Atoms in Generalized Orbital Configurations: Towards Atom-Dedicated Density Functionals
Abstract
:1. Introduction
2. Results and Discussion
2.1. The Energy of the Atom with a General Shell Occupation Scheme
2.2. A Methodology for the Decomposition of Two-Electron Terms
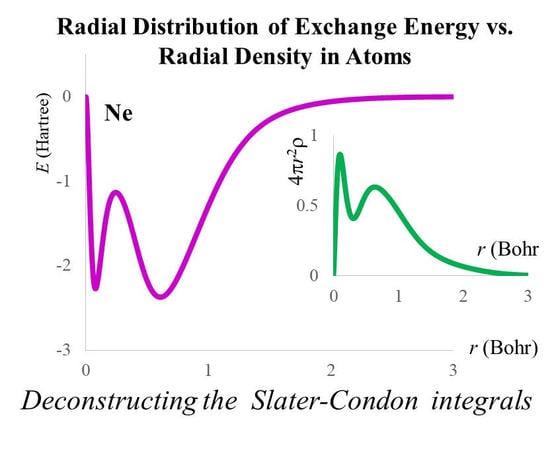
2.3. The Radial Distribution of the Exchange Energy in Atoms
3. Methods
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hehre, W.J.; Stewart, R.F.; Pople, J.A. Self-Consistent Molecular Orbital Methods. 1. Use of Gaussian expansions of Slater-type atomic orbitals. J. Chem. Phys. 1969, 51, 2657–2664. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods. 12. Further extensions of Gaussian-type basis sets for use in molecular-orbital studies of organic-molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
- Slater, J. Analytic atomic wave functions. Phys. Rev. 1932, 42, 33–43. [Google Scholar] [CrossRef]
- Foresman, J.B.; Frisch, A.E. Exploring Chemistry with Electronic Structure Methods, 3rd ed.; Gaussian, Inc.: Wallingford, CT, USA, 2015. [Google Scholar]
- Neese, F. The ORCA program system. WIREs. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Putz, M.V.; Cimpoesu, F.; Ferbinteanu, M. Structural Chemistry, Principles, Methods, and Case Studies; Springer: Cham, Germany, 2018; pp. 170–186. [Google Scholar]
- Nagy, B.; Jensen, F. Basis Sets in Quantum Chemistry. In Reviews in Computational Chemistry; Parrill, A.L., Lipkowitz, K.B., Eds.; John Willey & Sons: Hoboken, NJ, USA, 2017; Volume 30, pp. 93–149. [Google Scholar]
- Griffith, J.S. The Theory of Transition-Metal Ions; University Press: Cambridge, England, 1964. [Google Scholar]
- Koch, W.; Holthausen, M.C. A Chemist’s Guide to Density Functional Theory; VCH: Berlin, Germany, 2001. [Google Scholar]
- Parr, R.G.; Weitao, Y. Density-Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Ernzerhof, M.; Zupan, A.; Burke, K. Nonlocality of the density functional for exchange and correlation: Physical origins and chemical consequences. J. Chem. Phys. 1998, 108, 1522–1531. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Liechtenstein, A.I.; Anisimov, V.I.; Zaanen, J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 1995, 52, R5467. [Google Scholar] [CrossRef] [PubMed]
- Czyzyk, M.T.; Sawatzky, G.A. Local-density functional and on-site correlations: The electronic structure of La2CuO4 and LaCuO3. Phys. Rev. B 1994, 49, 14211. [Google Scholar] [CrossRef] [PubMed]
- Weber, V.; Daul, C.; Baltensperger, R. Radial numerical integrations based on the sinc function. Comput. Phys. Commun. 2004, 163, 133–142. [Google Scholar] [CrossRef]
- Holzwartha, N.A.W.; Tackettb, A.R.; Matthewsa, G.E. A Projector Augmented Wave (PAW) code for electronic structure calculations, Part I: Atompaw for generating atom-centered functions. Computer Phys. Comm. 2001, 135, 329–347. [Google Scholar] [CrossRef]
- Gonze, X.; Rignanese, G.M.; Verstraete, M.; Beuken, J.-M.; Pouillon, Y.; Caracas, R.; Jollet, F.; Torrent, M.; Zerah, G.; Mikami, M.; et al. A brief introduction to the ABINIT software package. Z. Kristallogr. 2005, 220, 558–562. [Google Scholar] [CrossRef]
- Boyd, R.J.; Coulson, C.A. Coulomb hole in some excited states of helium. J. Phys. B 1973, 6, 782–793. [Google Scholar] [CrossRef]
- Chakravorty, S.J.; Clementi, E. Soft Coulomb hole for the Hartree-Fock model to estimate atomic correlation energies. Phys. Rev. A 1989, 39, 2290–2296. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular Orbital Methods. 9. Extended Gaussian-type basis for molecular-orbital studies of organic molecules. J. Chem. Phys. 1971, 54, 724. [Google Scholar] [CrossRef]
- MATLAB and Statistics Toolbox Release 2018; The MathWorks Inc.: Natick, MA, USA, 2018; Available online: https://www.mathworks.com/academia.html (accessed on 1 September 2019).
- Eaton, J.W.; Bateman, D.; Hauberg, S.; Wehbring, R. GNU Octave Version 4.4.1; Free Software Foundation: Boston, MA, USA, 2018; Available online: https://www.gnu.org/software/octave/doc/v4.4.1/ (accessed on 1 September 2019).




| Shell Couples | s | p | d | f |
|---|---|---|---|---|
| s | ||||
| p | ||||
| d | ||||
| f |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toader, A.M.; Buta, M.C.; Maftei, D.; Putz, M.V.; Cimpoesu, F. Atoms in Generalized Orbital Configurations: Towards Atom-Dedicated Density Functionals. Int. J. Mol. Sci. 2019, 20, 5943. https://doi.org/10.3390/ijms20235943
Toader AM, Buta MC, Maftei D, Putz MV, Cimpoesu F. Atoms in Generalized Orbital Configurations: Towards Atom-Dedicated Density Functionals. International Journal of Molecular Sciences. 2019; 20(23):5943. https://doi.org/10.3390/ijms20235943
Chicago/Turabian StyleToader, Ana Maria, Maria Cristina Buta, Dan Maftei, Mihai V. Putz, and Fanica Cimpoesu. 2019. "Atoms in Generalized Orbital Configurations: Towards Atom-Dedicated Density Functionals" International Journal of Molecular Sciences 20, no. 23: 5943. https://doi.org/10.3390/ijms20235943