A Mission to Mars: Prediction of GCR Doses and Comparison with Astronaut Dose Limits
Abstract
:1. Introduction
2. Materials and Methods
2.1. Simulation of GCR Irradiation Using the FLUKA Transport Code
2.2. RBE Calculation by Means of the BIANCA Biophysical Model
3. Results and Discussion
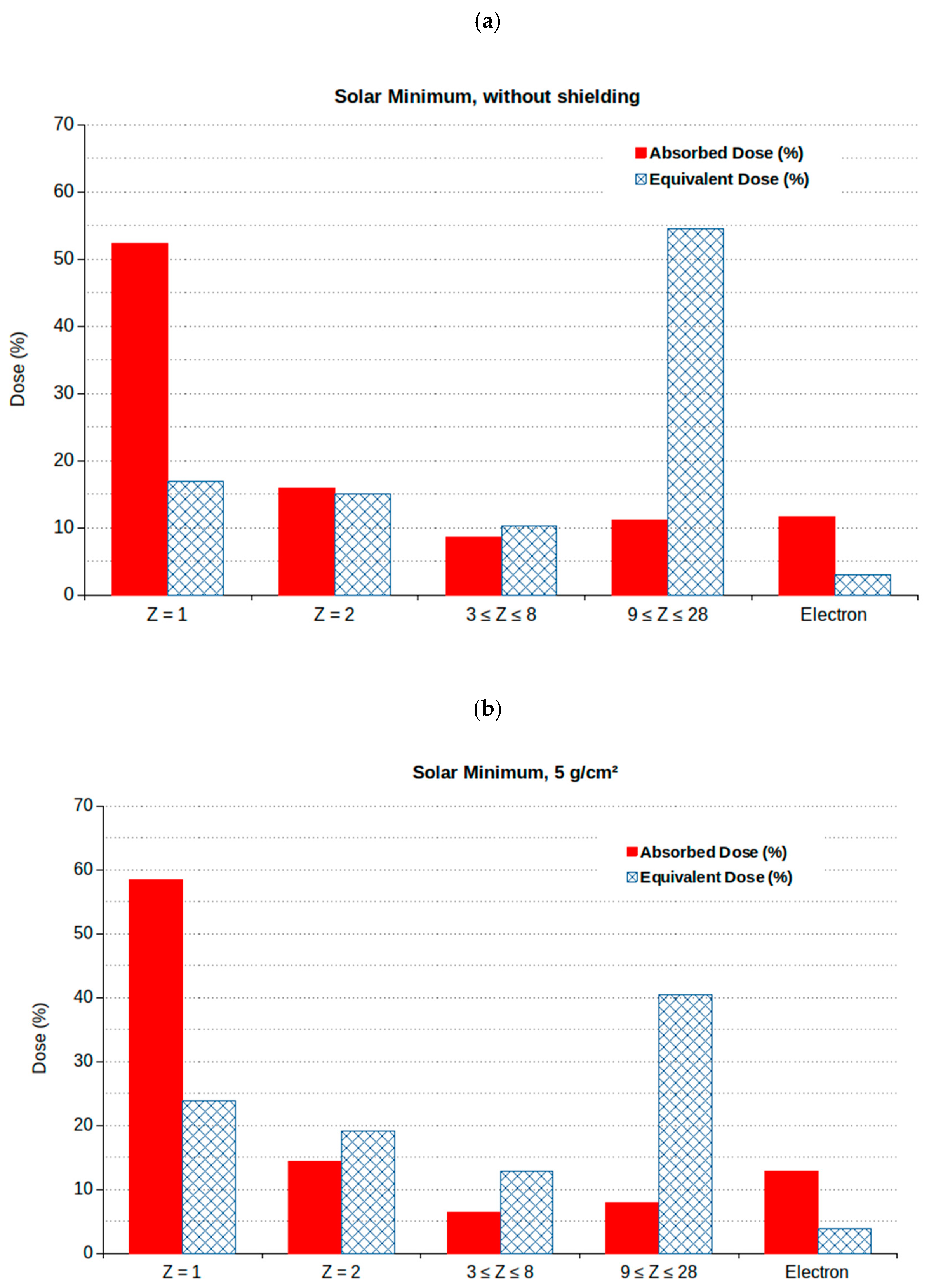
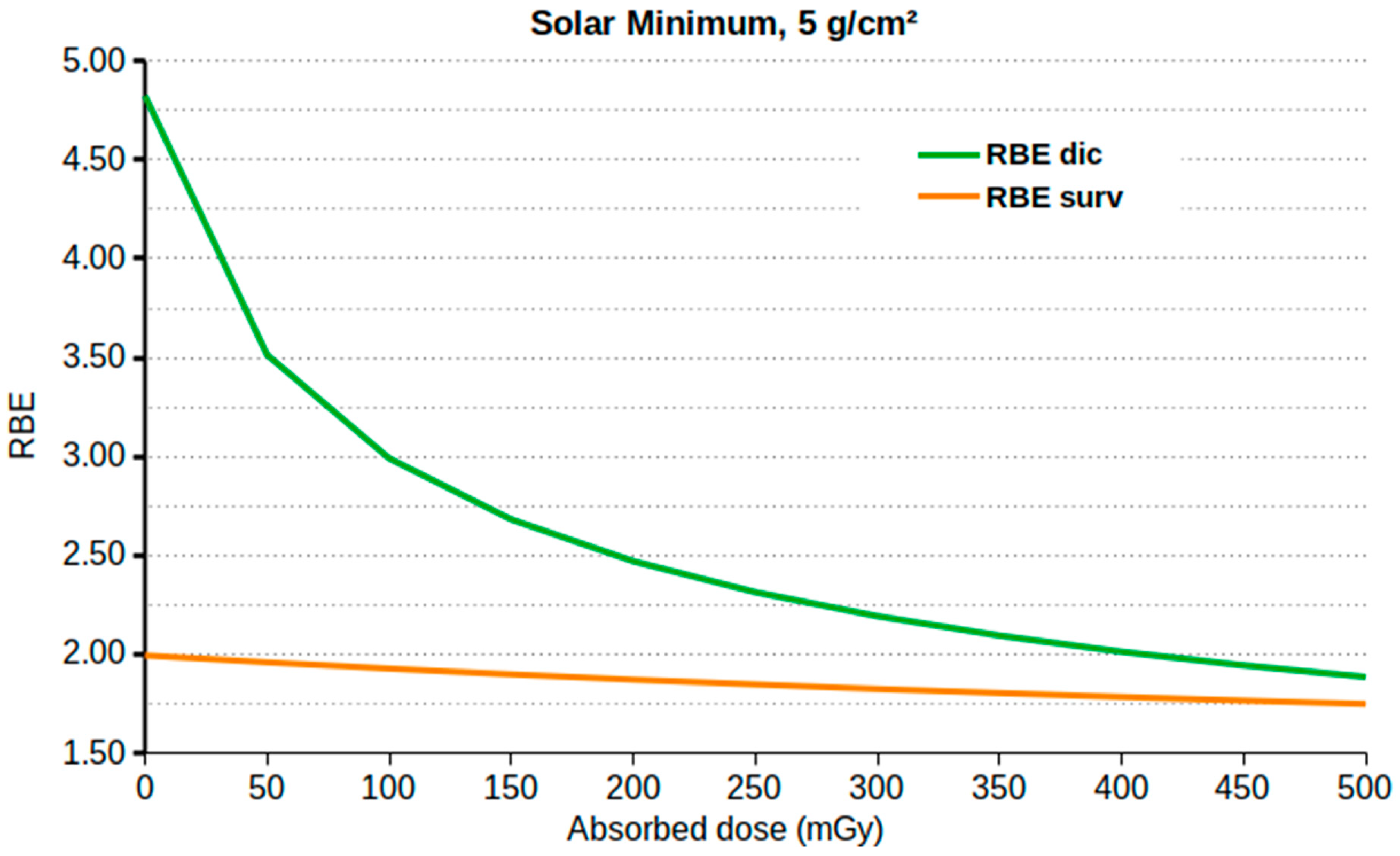
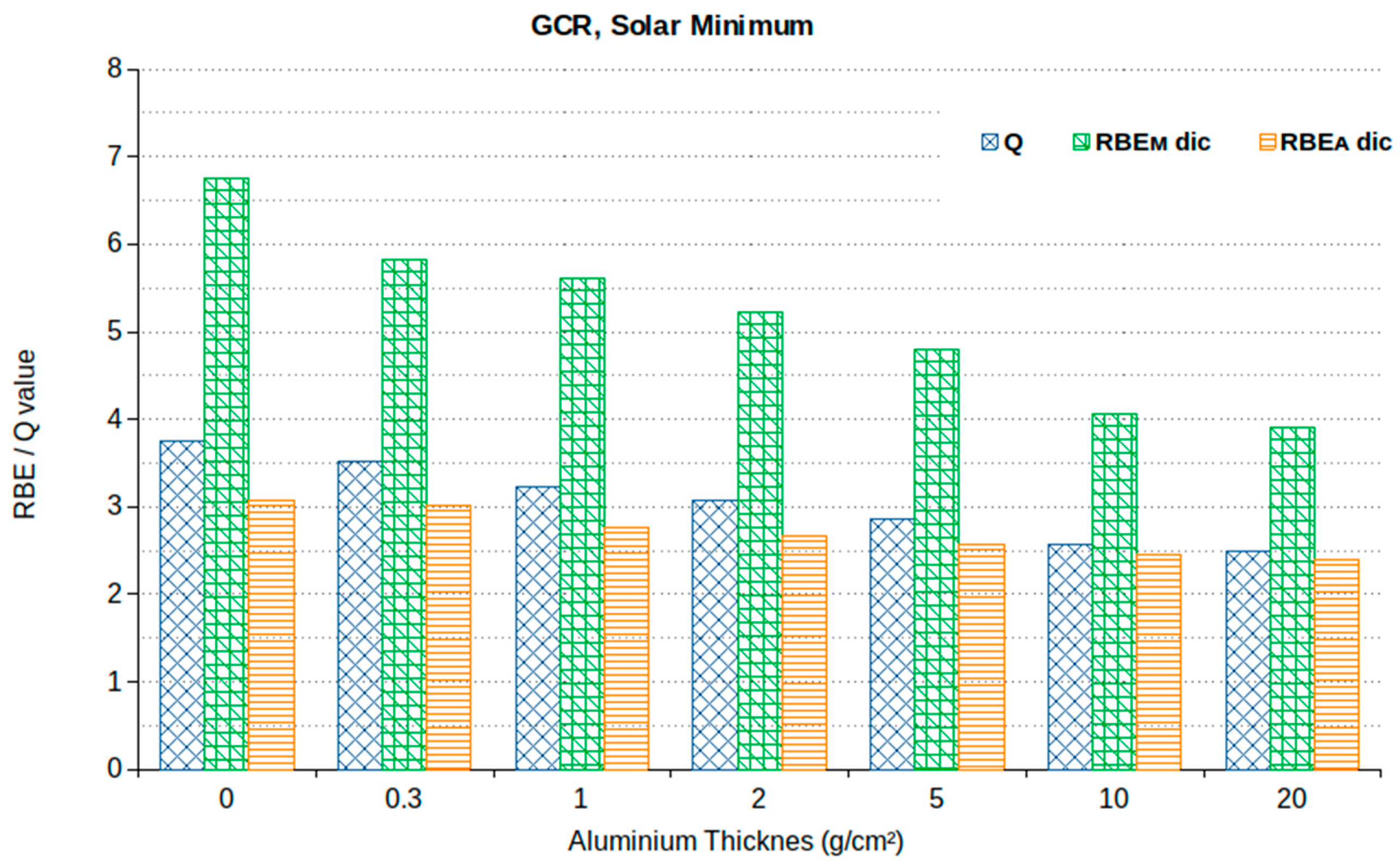
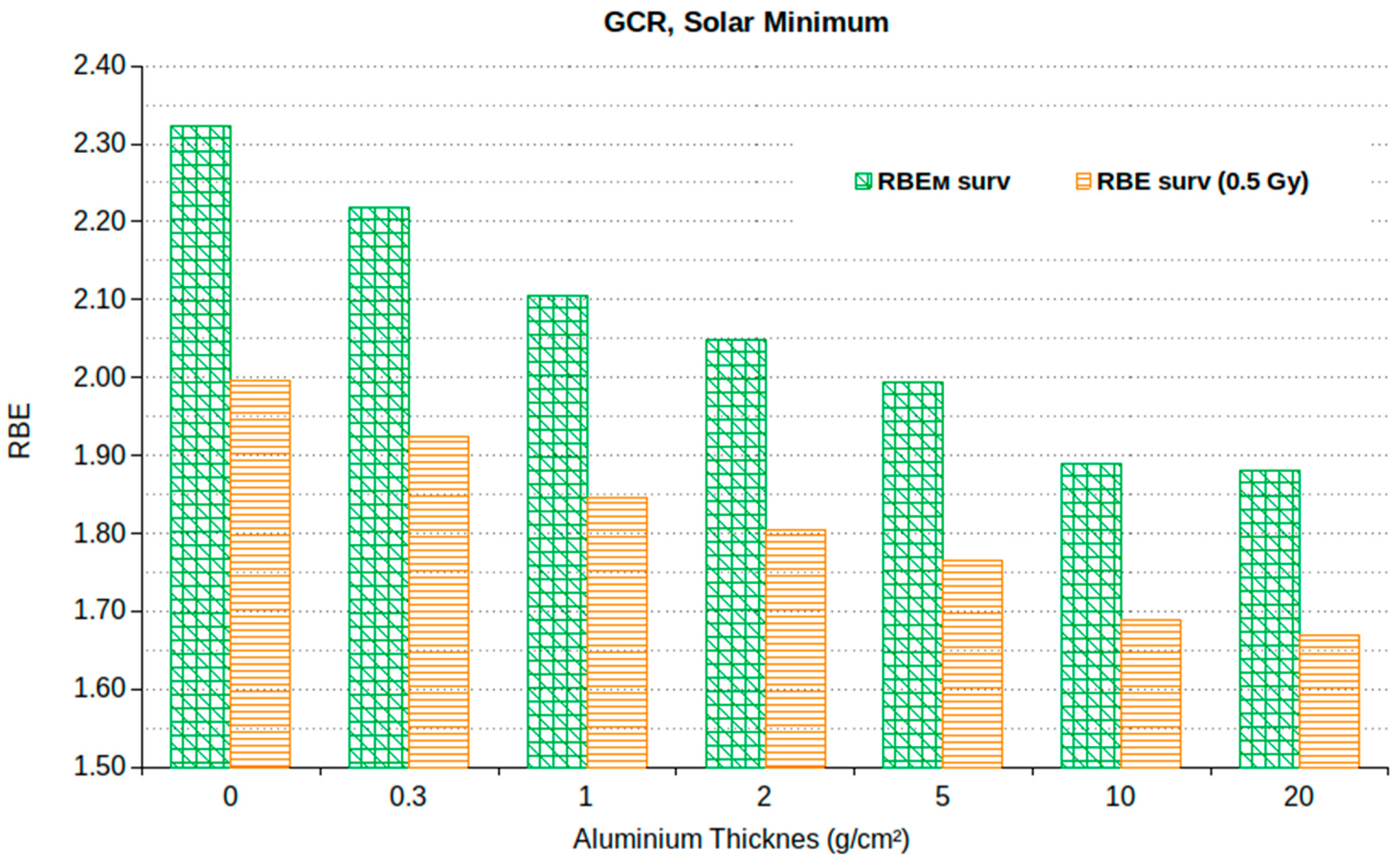
3.1. Absorbed Dose, Equivalent Dose and RBE
3.2. Stochastic Effects (Cancer)
3.3. Non-Cancer Effects
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Patel, S. The effects of microgravity and space radiation on cardiovascular health: From low-Earth orbit and beyond. Int. J. Cardiol. Heart. Vasc. 2020, 30, 100595. [Google Scholar] [CrossRef]
- Parihar, V.K.; Allen, B.D.; Caressi, C.; Kwok, S.; Chu, E.; Tran, K.K.; Chmielewski, N.N.; Giedzinski, E.; Acharya, M.M.; Britten, R.A.; et al. Cosmic radiation exposure and persistent cognitive dysfunction. Sci. Rep. 2016, 6, 34774. [Google Scholar] [CrossRef] [Green Version]
- Iwase, S.; Nishimura, N.; Tanaka, K.; Mano, T. Effects of microgravity on human physiology. In Beyond LEO-Human Health Issues for Deep Space Exploration; Reynolds, R.J., Ed.; IntechOpen: London, UK, 2020. [Google Scholar]
- Pagel, J.I.; Choukèr, A. Effects of isolation and confinement on humans-implications for manned space explorations. J. Appl. Physiol. 2016, 120, 1449–1457. [Google Scholar] [CrossRef] [Green Version]
- Campa, A.; Alloni, D.; Antonelli, F.; Ballarini, F.; Belli, M.; Dini, V.; Esposito, G.; Facoetti, A.; Friedland, W.; Furusawa, Y.; et al. DNA fragmentation induced in human fibroblasts by 56Fe ions: Experimental data and MC simulations. Radiat. Res. 2009, 171, 438–445. [Google Scholar] [CrossRef] [PubMed]
- Ballarini, F.; Battistoni, G.; Cerutti, F.; Fassò, A.; Ferrari, A.; Gadioli, E.; Garzelli, M.; Mairani, A.; Ottolenghi, A.; Paretzke, H.; et al. GCR and SPE organ doses in deep space with different shielding: Monte Carlo simulations based on the FLUKA code coupled to anthropomorphic phantoms. Adv. Space Res. 2006, 37, 1791–1797. [Google Scholar] [CrossRef]
- Berger, T.; Przybyla, B.; Matthiä, D.; Reitz, G.; Burmeister, S.; Labrenz, J.; Bilski, P.; Horwacik, T.; Twardak, A.; Hajek, M.; et al. DOSIS & DOSIS 3D: Long-term dose monitoring onboard the Columbus Laboratory of the International Space Station (ISS). J. Space Weather Space Clim. 2016, 6, 1–19. [Google Scholar]
- Kennedy, A.R. Biological effects of space radiation and development of effective countermeasures. Life Sci. Space Res. 2014, 1, 10–43. [Google Scholar] [CrossRef] [Green Version]
- Fornalski, K.W. Radioadaptation and radioresistance during deep space travels. J. Space Saf. Eng. 2022, 9, 385–389. [Google Scholar] [CrossRef]
- Cucinotta, F.A. Radiation Risk Acceptability and Limitations. 2010. Available online: https://three.jsc.nasa.gov/articles/astronautradlimitsfc.pdf (accessed on 14 December 2022).
- Space Radiation and Astronaut Health: Managing and Communicating Cancer Risks; The National Academies Press: Washington, DC, USA, 2021. [CrossRef]
- NASA regulations: 2022-01-05-NASA-STD-3001, Vol. 1, Rev. B. Available online: https://www.nasa.gov/sites/default/files/atoms/files/2022-01-05_nasa-std-3001_vol.1_rev._b_final_draft_with_signature_010522.pdf (accessed on 14 December 2022).
- Boscolo, D.; Durante, M. Dose Limits and Countermeasures for Mitigating Radiation Risk in Moon and Mars Exploration. Physics 2022, 4, 172–184. [Google Scholar] [CrossRef]
- Cucinotta, F.A.; Kim, M.H.Y.; Chappell, L.J. Space Radiation Cancer Risk Projections and Uncertainties. Report NASA/TP-2013-217375; The NASA STI Program Office: Hanover, MD, USA, 2013.
- NCRP. Radiation Protection Guidance for Activities in Low-Earth Orbit; NCRP Report No. 132; NCRP: Bethesda, MD, USA, 2000. [Google Scholar]
- NCRP. Information Needed to Make Radiation Protection Recommendations for Space Missions Beyond Low-Earth Orbit; NCRP Report No. 153; NCRP: Bethesda, MD, USA, 2006. [Google Scholar]
- McKenna-Lawlor, S.; Bhardwaj, A.; Ferrari, F.; Kuznetsov, N.; Lal, A.K.; Li, Y.; Nagamatsu, A.; Nymmik, R.; Panasyuk, M.; Petrov, V.; et al. Feasibility study of astronaut standardized career dose limits in LEO and the outlook for BLEO. Acta Astronaut. 2014, 104, 565–573. [Google Scholar] [CrossRef]
- National Academy of Sciences. Space Radiation and Astronaut Health; The National Academies Press: Washington, DC, USA, 2021. [Google Scholar]
- Cucinotta, F.A.; Schimmerling, W.; Blakely, E.A.; Hei, T.K. A proposed change to astronaut exposures limits is a giant leap backwards for radiation protection. Life Sci. Space Res. 2021, 31, 59–70. [Google Scholar] [CrossRef] [PubMed]
- Komiyama, T. Practicalities of dose management for Japanese astronauts staying at the International Space Station. Ann. ICRP 2020, 49, 194–199. [Google Scholar] [CrossRef] [PubMed]
- Durante, M.; Cucinotta, F.A. Heavy ion carcinogenesis and human space exploration. Nat. Rev. Cancer 2008, 8, 465–472. [Google Scholar] [CrossRef] [PubMed]
- Ballarini, F.; Carante, M. Chromosome aberrations and cell death by ionizing radiation: Evolution of a biophysical model. Radiat. Phys. Chem. 2016, 128C, 18–25. [Google Scholar] [CrossRef]
- Carante, M.P.; Aimè, C.; Cajiao, J.J.T.; Ballarini, F. BIANCA, a biophysical model of cell survival and chromosome damage by protons, C-ions and He-ions at energies and doses used in hadrontherapy. Phys. Med. Biol. 2018, 63, 075007. [Google Scholar] [CrossRef]
- Terence H Rabbitts. Chromosomal translocations in human cancer. Nature 1994, 372, 143–149. [Google Scholar] [CrossRef]
- Ottolenghi, A.; Ballarini, F.; Biaggi, M. Modelling chromosomal aberration induction by ionising radiation: The influence of interphase chromosome architecture. Adv. Space Res. 2001, 27, 369–382. [Google Scholar] [CrossRef]
- Ballarini, F.; Ottolenghi, A. A model of chromosome aberration induction and chronic myeloid leukaemia incidence at low doses. Radiat. Environ. Biophys. 2004, 43, 165–171. [Google Scholar] [CrossRef]
- Bonassi, S.; Hagmar, L.; Strömberg, U.; Montagud, A.; Tinnerberg, H.; Forni, A.; Heikkilä, P.; Wanders, S.; Wilhardt, P.; Hansteen, I.-L.; et al. Chromosomal aberrations in lymphocytes predict human cancer independently of exposure to carcinogens. Cancer Res. 2000, 60, 1619–1625. [Google Scholar]
- Ballarini, F.; Ottolenghi, A. A model of chromosome aberration induction: Applications to space research. Radiat. Res. 2005, 164, 567–570. [Google Scholar] [CrossRef]
- Bonassi, S.; Norppa, H.; Ceppi, M.; Stromberg, U.; Vermeulen, R.; Znaor, A.; Cebulska-Wasilewska, A.; Fabianova, E.; Fucic, A.; Gundy, S.; et al. Chromosomal aberration frequency in lymphocytes predicts the risk of cancer: Results from a pooled cohort study of 22 358 subjects in 11 countries. Carcinogenesis 2008, 29, 1178–1183. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carante, M.; Aricò, G.; Ferrari, A.; Kozlowska, W.; Mairani, A.; Ballarini, F. First benchmarking of the BIANCA model for cell survival predictions in a clinical hadron therapy scenario. Phys. Med. Biol. 2019, 64, 215008. [Google Scholar] [CrossRef] [PubMed]
- Carante, M.P.; Aricò, G.; Ferrari, A.; Karger, C.; Kozlowska, W.; Mairani, A.; Sala, P.; Ballarini, F. In vivo validation of the BIANCA biophysical model: Benchmarking against rat spinal cord RBE data. Int. J. Mol. Sci. 2020, 21, 3973. [Google Scholar] [CrossRef]
- Carante, M.; Embriaco, A.; Aricò, G.; Ferrari, A.; Mairani, A.; Mein, S.; Ramos, R.; Sala, P.; Ballarini, F. Biological effectiveness of He-3 and He-4 ion beams for cancer hadrontherapy: A study based on the BIANCA biophysical model. Phys. Med. Biol. 2021, 66, 195009. [Google Scholar] [CrossRef] [PubMed]
- Kozlowska, W.; Carante, M.; Aricò, G.; Ferrari, A.; Magro, G.; Mairani, A.; Sala, P.; Georg, D.; Ballarini, F. First application of the BIANCA model to carbon-ion patient cases. Phys. Med. Biol. 2022, 67, 115013. [Google Scholar] [CrossRef]
- Ferrari, A.; Sala, P.R.; Fassò, A.; Ranft, J. FLUKA: A multi-particle transport code. CERN 2005-10, INFN/TC_05/11, SLAC-R-773. 2005. Published in: CERN Yellow Reports: Monographs (DOI: 10.2172/877507, 10.5170/CERN-2005-010). Report number: CERN-2005-010, SLAC-R-773, INFN-TC-05-11, CERN-2005-10. Available online: https://www.osti.gov/biblio/877507 (accessed on 14 December 2022).
- Ballarini, F.; Battistoni, G.; Campanella, M.; Carboni, M.; Cerutti, F.; Empl, A.; Fassò, A.; Ferrari, A.; Gadioli, E.; Garzelli, M.V.; et al. The FLUKA code: An overview. J. Phys. Conf. Ser. 2006, 41, 151. [Google Scholar] [CrossRef] [Green Version]
- Bohlen, T.T.; Cerutti, F.; Chin, M.P.W.; Fassò, A.; Ferrari, A.; Ortega, P.G.; Mairani, A.; Sala, P.; Smirnov, G.; Vlachoudis, V. The FLUKA Code: Developments and Challenges for High Energy and Medical Applications. Nucl. Data Sheets 2014, 120, 211–214. [Google Scholar] [CrossRef] [Green Version]
- Ballarini, F.; Battistoni, G.; Belcari, N.; Bisogni, G.; Campanella, M.; Carante, M.P.; Dedes, G.; Degtiarenko, P.; Luque, P.d.l.T.; Augusto, R.d.S.; et al. FLUKA: Status and perspectives, Proceedings of the SATIF15 Workshop. submitted.
- Badhwar, G.D.; O’Neill, P.M. GCR Model and its Applications. Adv. Space Sci. 1996, 17, 7–17. [Google Scholar] [CrossRef]
- ICRP. Recommendations of the International Commission on Radiological Protection. ICRP Publication 60. Ann. ICRP 1991, 21, 1–3. [Google Scholar]
- ICRP. RBE for Deterministic Effects. ICRP Publication 58. Ann. ICRP 1990, 20. [Google Scholar]
- Simonsen, L.C.; Slaba, T.C.; Guida, P. Adam Rusek NASA’s first ground-based Galactic Cosmic Ray Simulator: Enabling a new era in space radiobiology research. PLoS Biol. 2020, 18, e3000669. [Google Scholar] [CrossRef] [PubMed]
- Ottolenghi, A.; Ballarini, F.; Merzagora, M. Modelling radiation induced biological lesions: From initial energy depositions to chromosome aberrations. Radiat. Environ. Biophys. 1999, 38, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Embriaco, A.; Ramos, R.L.; Carante, M.P.; Ferrari, A.; Sala, P.; Vercesi, V.; Ballarini, F. Healthy tissue damage following cancer ion therapy: A radiobiological database predicting lymphocyte chromosome aberrations based on the BIANCA biophysical model. Int. J. Mol. Sci. 2021, 22, 10877. [Google Scholar] [CrossRef] [PubMed]
- Ramos, R.L.; Embriaco, A.; Carante, M.P.; Ferrari, A.; Sala, P.; Vercesi, V.; Ballarini, F. Radiobiological damage by space radiation: Extension of the BIANCA model to heavy ions up to Iron, and pilot application to cosmic ray exposure. J. Radiol. Prot. 2022, 42, 021523. [Google Scholar] [CrossRef] [PubMed]
- Ramos, R.; Embriaco, A.; Carante, M.; Ferrari, A.; Sala, P.; Vercesi, V.; Ballarini, F. Extension of the BIANCA biophysical model up to Fe-ions and applications for space radiation research. Eur. Phys. J. Conf. 2022, 261, 03001. [Google Scholar] [CrossRef]
- Powojska, A.; Słonecka, I.; Fornalski, K. The Monte Carlo Method of Mixed Radiation Field Dose Assessment in the Cytogenetic Biodosimetry. Acta Phys. Pol. A 2018, 134. [Google Scholar] [CrossRef]
- ICRU. ICRP Report of the RBE Committee of the International Commissions on Radiological Protection and on Radiological Units. Health Phys. 1963, 9, 357–384. [Google Scholar]
- NRPB. Relative Biological Effectiveness of Neutrons for Stochastic Effects. Documents of the NRPB 8 (2); National Radiological Protection Board: Didcot, UK, 1997. [Google Scholar]
- ICRP. Relative Biological Effectiveness (RBE), Quality Factor (Q), and Radiation Weighting Factor (wR). ICRP Publication 92. Ann. ICRP 2003, 33. [Google Scholar]
- Trovati, S.; Ballarini, F.; Battistoni, G.; Cerutti, F.; Fassò, A.; Ferrari, A.; Gadioli, E.; Garzelli, M.; Mairani, A.; Ottolenghi, A.; et al. Human Exposure to Space Radiation: Role of Primary and Secondary Particles. Radiat. Prot. Dosim. 2006, 122, 362–366. [Google Scholar] [CrossRef]
- Cucinotta, F.A. A New Approach to Reduce Uncertainties in Space Radiation Cancer Risk Predictions. PLoS ONE 2015, 10, e0120717. [Google Scholar] [CrossRef]


| Age | Male (Sv) | Female (Sv) |
|---|---|---|
| 30 | 0.78 | 0.60 |
| 40 | 0.88 | 0.70 |
| 50 | 1.00 | 0.82 |
| 60 | 1.17 | 0.98 |
| Age at First Space Flight | Males (Sv) | Females (Sv) |
|---|---|---|
| 27–30 | 0.60 | 0.50 |
| 31–35 | 0.70 | 0.60 |
| 36–40 | 0.80 | 0.65 |
| 41–45 | 0.95 | 0.75 |
| >45 | 1.00 | 0.80 |
| 30-Day Limit (Gy-Eq) | 1-Year Limit (Gy-Eq) | Career Limit (Gy-Eq) | |
|---|---|---|---|
| Skin | 1.5 | 3.0 | 6.0 |
| Eye | 1.0 | 2.0 | 4.0 |
| BFO | 0.25 | 0.5 | N.A. |
| Heart | 0.25 | 0.5 | 1.0 |
| CNS | 0.5 | 1.0 | 1.5 |
| CNS (Z > 9) | N.A. | 0.10 Gy | 0.25 Gy |
| 30-Day Limit (Sv) | 1-Year Limit (Sv) | |
|---|---|---|
| Skin | 1.5 | 3.0 |
| Eye | 0.5 | 1.0 |
| BFO | 0.25 | 0.5 |
| 1-Week Limit (Sv) | 1-Year Limit (Sv) | Career Limit (Sv) | |
|---|---|---|---|
| Skin | 2.0 | 7.0 | 20.0 |
| Eye | 0.5 | 2.0 | 5.0 |
| BFOs | N.A. | 0.5 | N.A. |
| Testes | N.A. | 1.0 | N.A. |
| Al Thickness (g/cm2) | Equivalent Dose (mSv) | Equivalent Dose (mGy·RBEA) | Equivalent Dose (mGy·RBEM) |
|---|---|---|---|
| 0 | 986.7 | 809.8 | 1777.4 |
| 0.3 | 904.5 | 774.3 | 1496.0 |
| 1 | 812.1 | 693.5 | 1413.3 |
| 2 | 770.4 | 669.3 | 1312.7 |
| 5 | 729.0 | 658.9 | 1228.2 |
| 10 | 681.6 | 652.2 | 1077.7 |
| 20 | 708.5 | 680.9 | 1106.4 |
| Al Thickness (g/cm2) | Equivalent Dose (mSv) | Equivalent Dose RBEA Dic (mGy·RBEA) | Equivalent Dose RBEM Dic (mGy·RBEM) |
|---|---|---|---|
| 0 | 240.9 | 211.5 | 426.2 |
| 0.3 | 249.2 | 217.3 | 442.8 |
| 1 | 279.5 | 238.3 | 515.8 |
| 2 | 319.6 | 253.1 | 579.4 |
| 5 | 254.1 | 222.2 | 432.6 |
| 10 | 227.6 | 222.3 | 358.1 |
| 20 | 266.4 | 255.4 | 389.9 |
| Al Thickness (g/cm2) | 7 Days | 30 Days | 365 Days | 650 Days |
|---|---|---|---|---|
| 0 | 6.58 | 28.19 | 342.94 | 610.71 |
| 0.3 | 6.16 | 26.30 | 320.00 | 569.87 |
| 1 | 5.67 | 24.44 | 297.36 | 529.55 |
| 2 | 5.53 | 23.74 | 288.84 | 514.38 |
| 5 | 5.46 | 23.52 | 286.17 | 509.62 |
| 10 | 5.39 | 23.11 | 281.23 | 500.81 |
| 20 | 5.74 | 24.62 | 299.50 | 533.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos, R.L.; Carante, M.P.; Ferrari, A.; Sala, P.; Vercesi, V.; Ballarini, F. A Mission to Mars: Prediction of GCR Doses and Comparison with Astronaut Dose Limits. Int. J. Mol. Sci. 2023, 24, 2328. https://doi.org/10.3390/ijms24032328
Ramos RL, Carante MP, Ferrari A, Sala P, Vercesi V, Ballarini F. A Mission to Mars: Prediction of GCR Doses and Comparison with Astronaut Dose Limits. International Journal of Molecular Sciences. 2023; 24(3):2328. https://doi.org/10.3390/ijms24032328
Chicago/Turabian StyleRamos, Ricardo L., Mario P. Carante, Alfredo Ferrari, Paola Sala, Valerio Vercesi, and Francesca Ballarini. 2023. "A Mission to Mars: Prediction of GCR Doses and Comparison with Astronaut Dose Limits" International Journal of Molecular Sciences 24, no. 3: 2328. https://doi.org/10.3390/ijms24032328





