A Finite Element Model of a MEMS-based Surface Acoustic Wave Hydrogen Sensor
Abstract
:1. Introduction
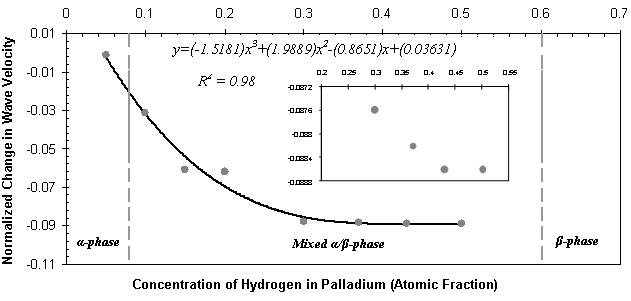
2. The Palladium Hydrogen System
3. Background
3.1. Piezoelectricity
3.2. Wave Equations
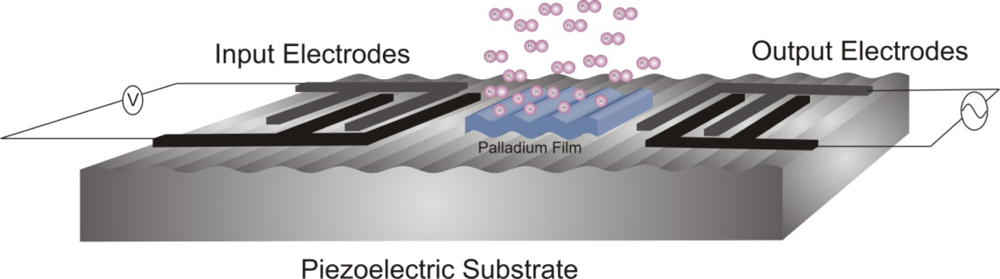
3.3. Inter-digital Transducers (IDT)
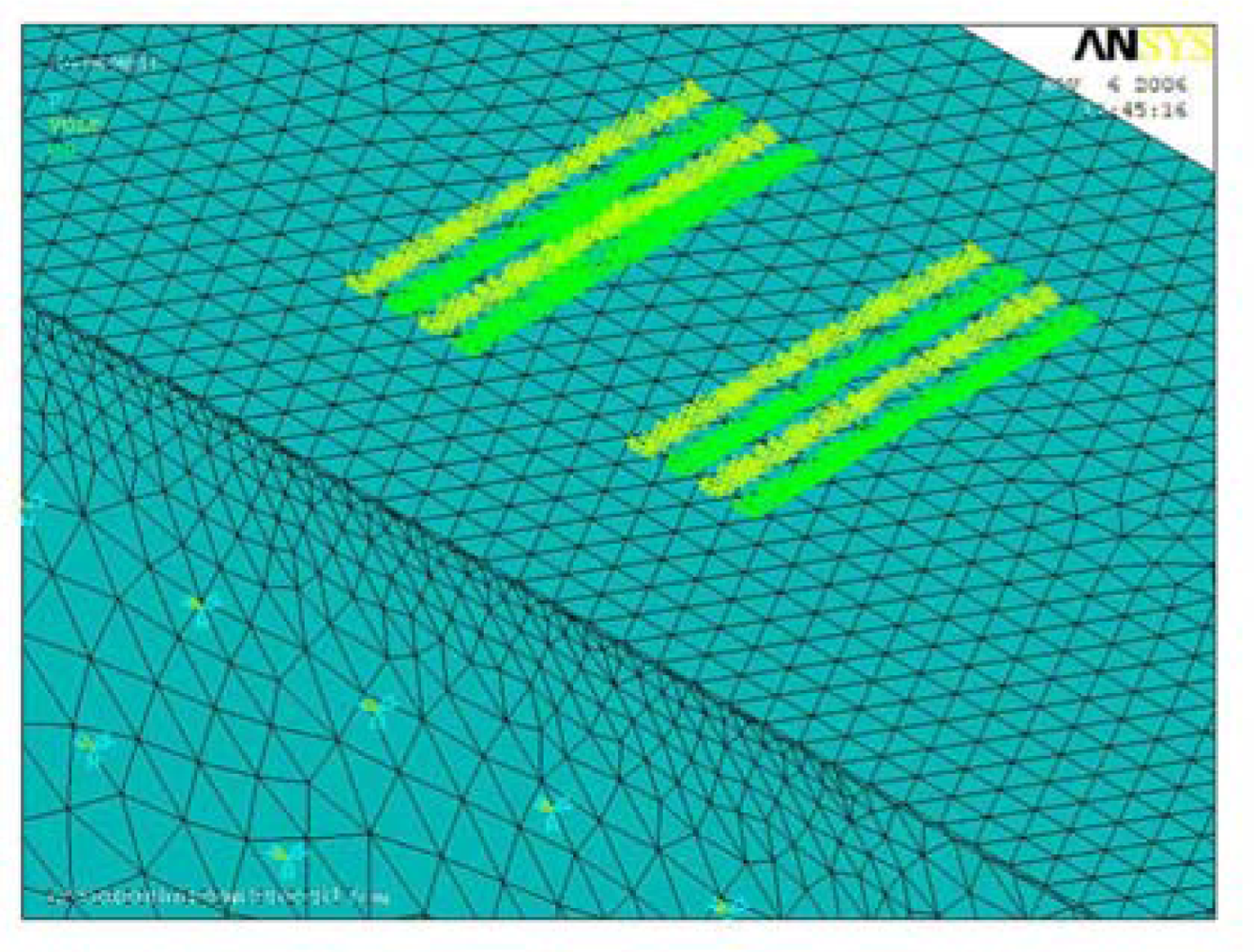
4. Numerical Modeling using Finite Element Analysis (FEA)
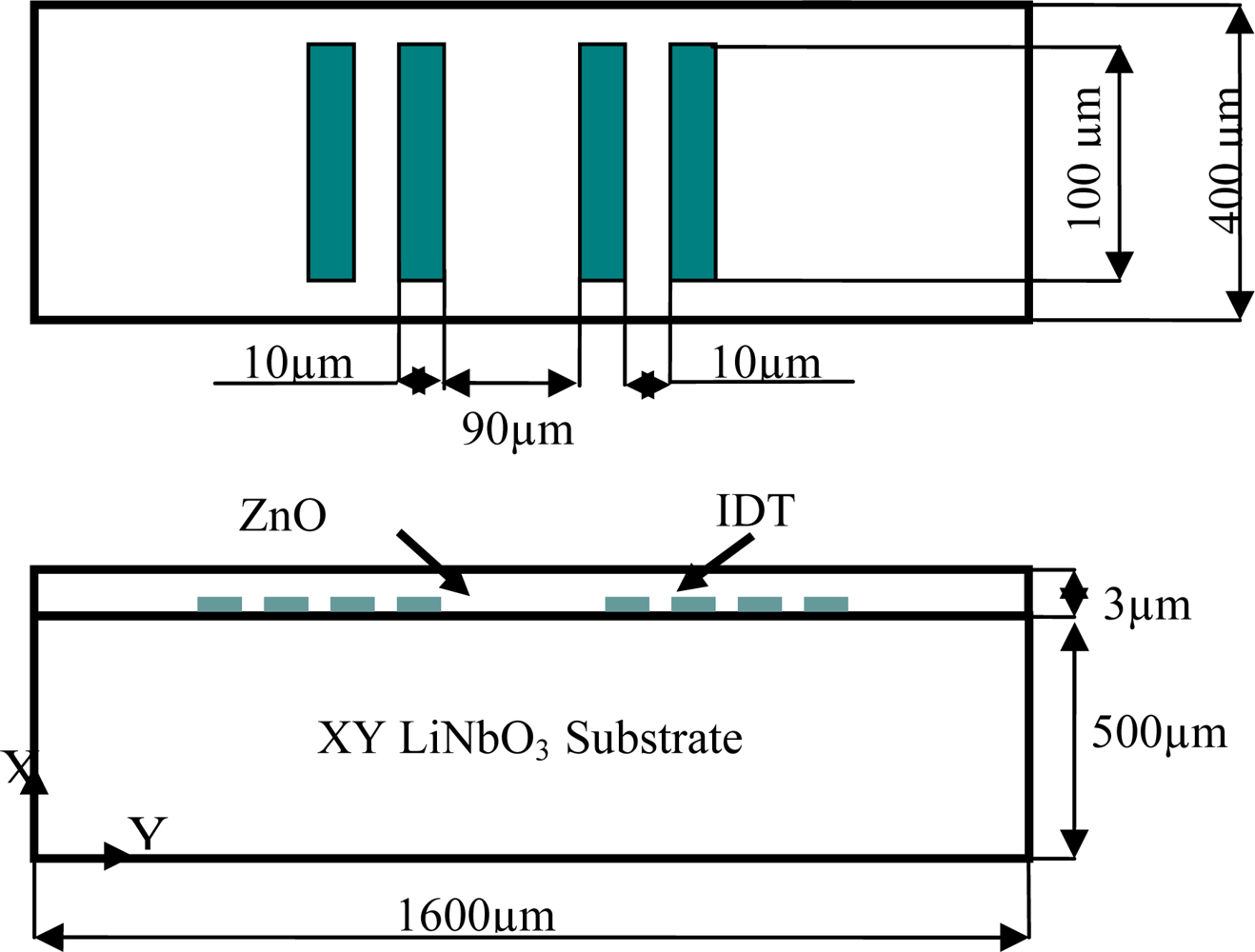
4.1. Verification Model (ZnO-XY LiNbO3)
- Clamped condition on the bottom surface A:
- Continuity of the displacement field components Ui for i = x, y, z and the voltage ϕ at interface I
- A Traction free boundary at the Free Surface S:
- The following Dirichlet conditions for the electric potential:
5. Finite Element Model of a SAW Sensor for Hydrogen Detection
5.1. Finite Element Analysis of the YZ-LiNbO3 SAW Sensor Model
- Clamped condition on the bottom of the substrate
- Same Dirichlet conditions for the electric potential at the electrodes
- Extension of the boundaries along the length and width of the substrate to avoid reflection
5.1.1. Palladium Film
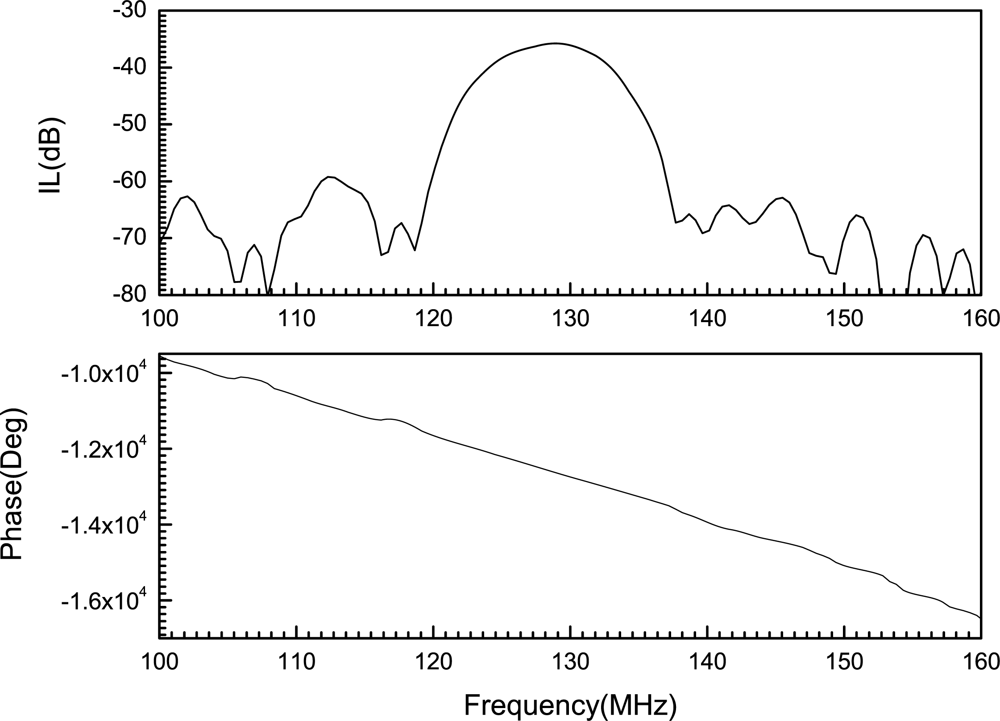
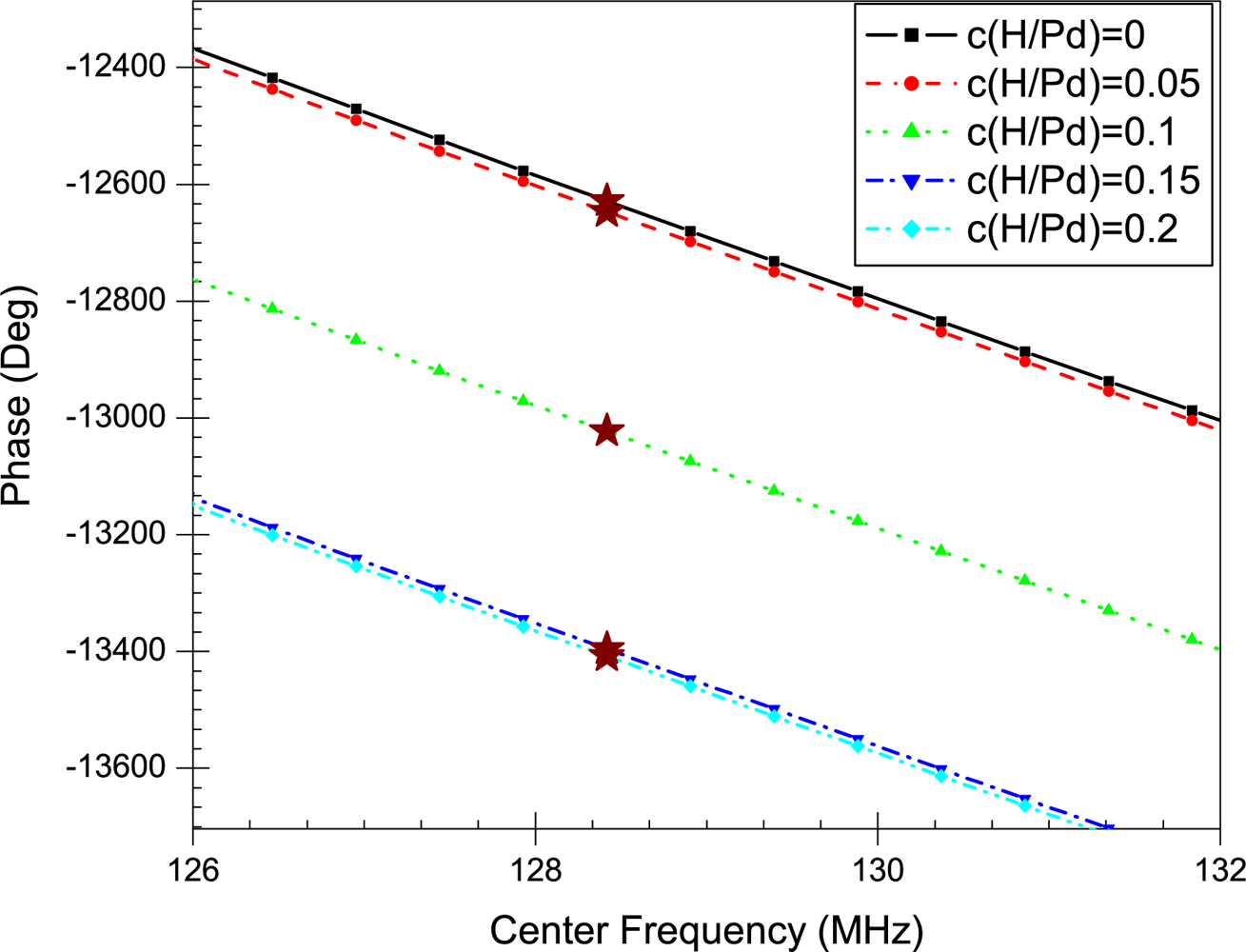
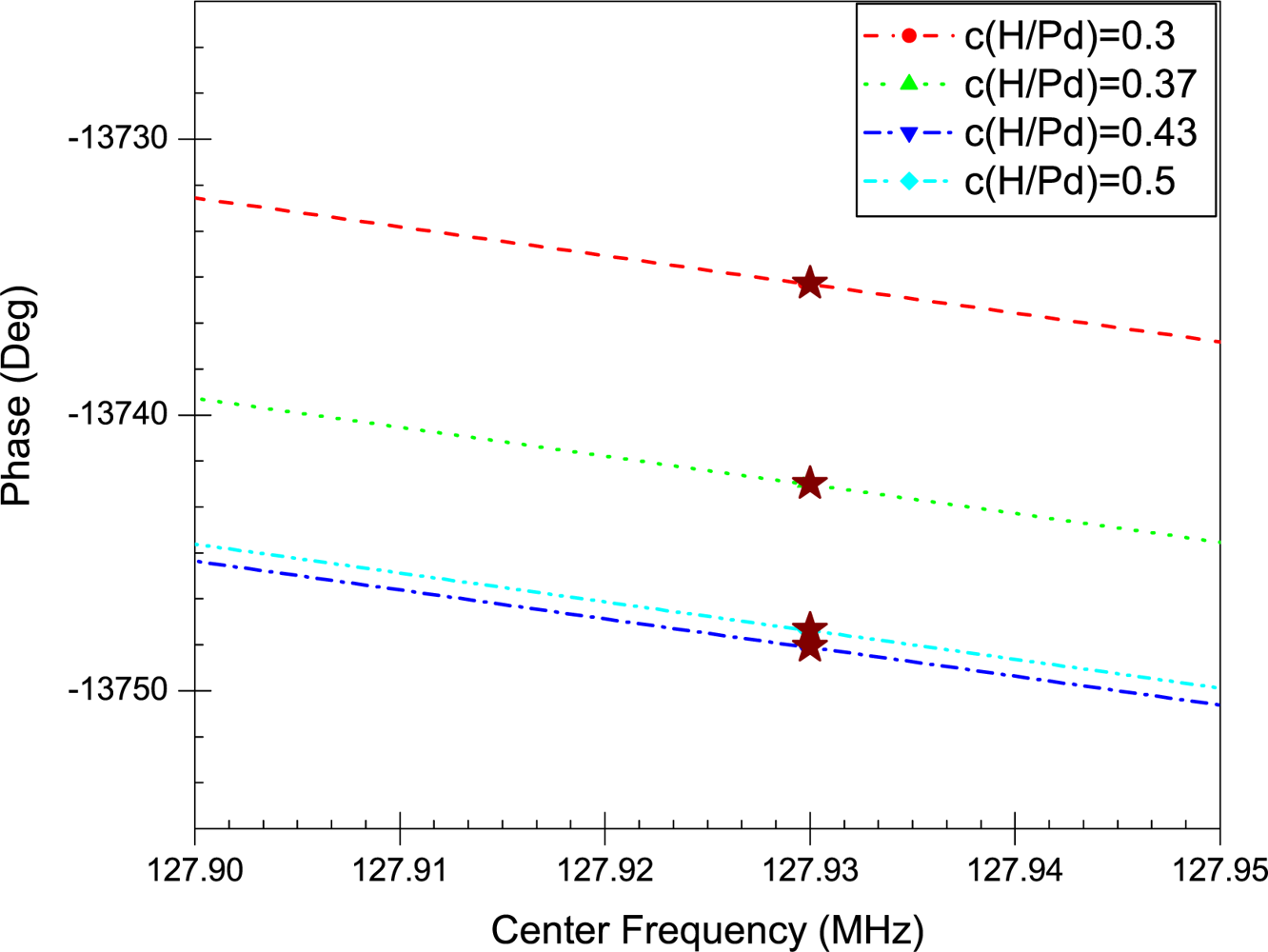
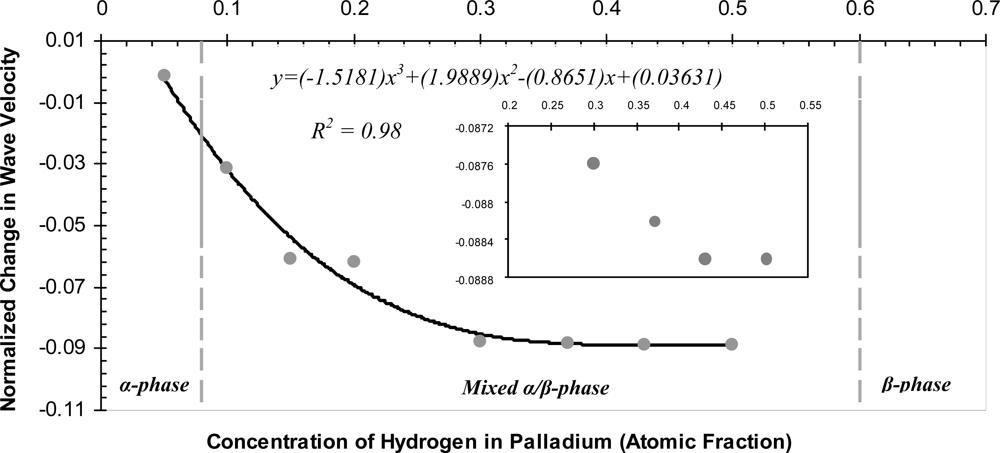
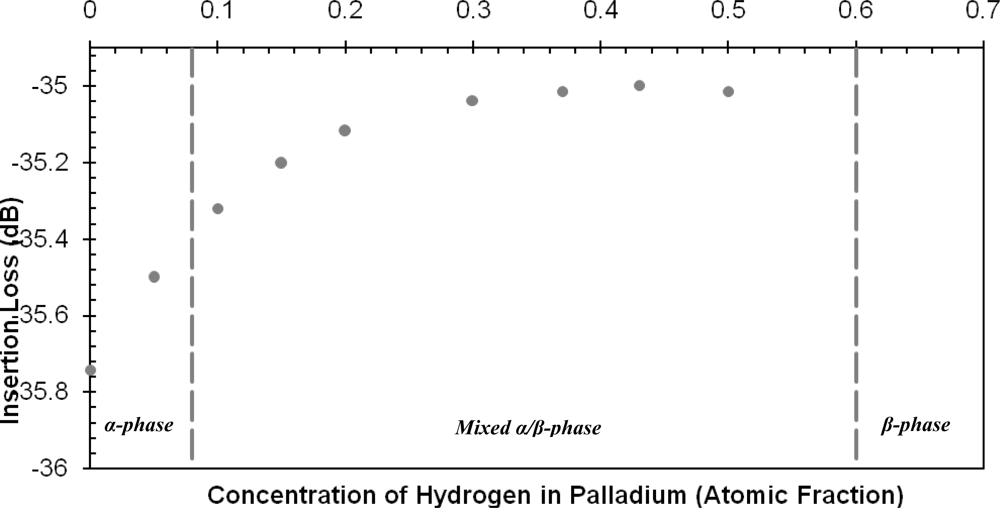
6. Results
7. Discussion
8. Conclusions
Acknowledgments
References and Notes
- White, R.M.; Voltmer, F.W. Direct Piezoelectric Coupling to Surface Elastic Waves. Appl. Phys. Lett 1965, 7, 314–316. [Google Scholar]
- Yamanaka, K.; Ishikawa, S.; Nakaso, N.; Takeda, N.; Mihara, T.; Tsukahara, Y. Ball SAW device for hydrogen gas sensor. IEEE Ultrasonics Symposium, Institute of Electrical and Electronics Engineers Inc, Honolulu, HI, USA, December 2003; pp. 299–302.
- D’Amico, A.; Zemel, J.N. Pyroelectric Enthalpimetric Detection. J. Appl. Phys 1985, 57, 2460–2463. [Google Scholar]
- Butler, M.A. Optical Fiber Hydrogen Sensor. Appl. Phys. Lett 1984, 45, 1007–1009. [Google Scholar]
- Kumar, R.V.; Fray, D.J. Development oF Solid State Hydrogen Sensors. Sens. Actuat 1988, 15, 185–191. [Google Scholar]
- Cabrera, A.L.; Aruayo-Soto, R. Hydrogen Absorption in Palladium Films Sensed by Changes in Their Resistivity. Catal. Lett 1997, 45, 79–83. [Google Scholar]
- Lukaszewski, M.; Czerwinski, A. Electrochemical Quartz Crystal Microbalance Study on Hydrogen Absorption and Desorption into/from Palladium and Palladium-Noble Metal Alloys. J. Electroanal. Chem 2006, 589, 87–95. [Google Scholar]
- Christofides, C.; Mandelis, A. Solid State Sensors for Trace Hydrogen Gas Detection. J. Appl. Phys 1990, 68, R1–R30. [Google Scholar]
- Anisimkin, V.I.; Kotelyanskii, I.M.; Verardi, P.; Verona, E. Elastic Properties of Thin-Film Palladium for Surface Acoustic Wave (SAW) Sensors. Sens. Actuat 1995, 23, 203–208. [Google Scholar]
- Kuschnereit, R.; Fath, H.; Kolomenskii, A.A.; Szabadi, M.; Hess, P. Mechaical and Elastic Properties of Amorphous Hydrogenated Silicon Films Studied by Broadband Surface Acoustic Wave Spectroscopy. Appl. Phys 1995, 61, 269–276. [Google Scholar]
- Jakubik, W.P.; Urbanczyk, M.; Meciak, E.; Pustelny, T. Surface Acoustic Wave Hydrogen Gas Sensor Based on Layered Structure of Palladium/Metal-Free Phthalocyanine. Bull. Pol. Acad. Sci-Chem 2008, 56, 133–138. [Google Scholar]
- D’Amico, A.; Palma, A.; Verona, E. Surface Acoustic Wave Hydrogen Sensor. Sens. Actuat 1982, 3, 31–39. [Google Scholar]
- Atashbar, M.Z.; Bazuin, B.J.; Simpeh, B.M.; Krishnamurthy, S. 3D FE Simulation of H2 SAW Gas Sensor. Sens. Actuat 2005, 111–112, 213–218. [Google Scholar]
- Lewis, F.A. The Palladium Hydrogen System; Academic Press Inc: London, UK, 1967. [Google Scholar]
- Baranowski, B.; Majchrzak, S.; Flanagan, T.B. The Volume Increase of FCC Metals and Alloys due to Interstitial Hydrogen over a Wide Range of Hydrogen Contents. J. Phys. F: Metal Phys 1971, 1, 258–261. [Google Scholar]
- Peisl, H. Topics in Applied Physics, Hydrogen in Metals I: Basic Properties; Springer-Verlag: Berlin, Germany, 1978; pp. 53–74. [Google Scholar]
- Fabre, A.; Finot, E.; Demoment, J.; Contreras, S. In Situ Measurement of Elastic Properties of PdHx, PdDx, and PdTx. J. Alloys. Compds 2003, 356–357, 372–376. [Google Scholar]
- Madou, M.J. Fundamentals of Microfabrication, 2nd ed; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Geerken, B.M.; Griessen, R.; Huisman, L.M. Contribution of Optical Phonon to the Elastic Moduli of PdHx and PdDx. Phys. Rev. B 1982, 26, 1637–1650. [Google Scholar]
- Harada, S.; Kasahara, T.; Tamaki, S. Elastic Constants and Thermal Expansion Coefficient of Hydrogenated Pd Alloys. J. Phys. Soc. Jpn 1985, 54, 168–174. [Google Scholar]
- Mason, W.P. Physical Acoustics Principles and Methods; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Auld, B.A. Acoustic Fields and Waves in Solids; John Wiley & Sons: New York, NY, USA, 1973. [Google Scholar]
- Datta, S. Surface Acoustic Wave Devices; Prentice-Hall: Englewood Cliffs, NJ, USA, 1986. [Google Scholar]
- Wong, K.; Tam, W. Analysis of the Frequency Response of SAW Filters Using Finite-Difference Time-Domain Method. IEEE Trans. Microwave. Theory 2005, 53, 3364–3370. [Google Scholar]
- Lerch, R. Simulation of Piezoelectric Devices by Two- and Three-Dimensional Finite Elements. IEEE T Ultrason. Ferroelectr 1990, 37, 233–247. [Google Scholar]
- Xu, G. Direct Finite-Element Analysis of The Frequency Response of A Y-Z Lithium Niobate SAW Filter. Smart Mater. Struct 2000, 9, 973–980. [Google Scholar]
- Ippolito, S.J.; Kalantar-Zadeh, K.; Powell, D.A.; Wlodarski, W. A 3-Dimensional Approach for Simulating Acoustic Wave Propagation in Layered SAW Devices. Proceedings of IEEE Ultrasonics Symposium, Honolulu, HI, USA, December 2003; pp. 303–306.
- Ventura, P.; Hode, J.M.; Solal, M. A New Efficient Combined FEM and Periodic Green’s Function Formalism for the Analysis of Periodic Structures. IEEE Ultrason. Symp 1995, 1, 263–268. [Google Scholar]
- Makkonen, T. Numerical Simulations of Micro-Acoustic Resonators and Filters, Ph.D. Thesis; Helsinki University of Technology: Helsinki, Finland, 2005.
- EL Gowini, M.M.; Moussa, W.A. A Reduced Three Dimensional Model for SAW Sensors Using Finite Element Analysis. Sensors 2009, 9, 9945–9964. [Google Scholar]
- Ippolito, S.J.; Kalantar-Zadeh, K.; Powell, D.A.; Wlodarski, W. A Finite Element Approach for 3-Dimensional Simulation of Layered Acoustic Wave Transducers. Proceedings of Conference on Optoelectronic and Microelectronic Materials and Devices, Sydney, NSW, Australia, December 2002; pp. 541–544.
- Wong, K.K. Properties of Lithium Niobate; INSPEC, The Institution for Electrical Engineers: London, UK, 2002. [Google Scholar]
- Didenko, I.S.; Hickernell, F.S.; Naumenko, N. The Experimental and Theoretical Characterization of the SAW Propagation Properties for Zinc Oxide Films on Silicon Carbide. IEEE T Ultrason. Ferroelectr 2000, 47, 179–187. [Google Scholar]
- Xu, G.; Jiang, Q. A Finite Element Analysis of Second Order Effects on the Frequency Response of A SAW Device. J. Intel. Mat. Syst. Struct 2001, 12, 69–77. [Google Scholar]
- Ippolito, S.J.; Kalantar-Zadeh, K.; Wlodarski, W.; Powell, D.A. Finite-Element Analysis for Simulation of Layered SAW Devices with XY LiNbO3 Substrate. Proceedings of Smart Structures, Devices, and Systems, Melbourne, Australia, December 2002; pp. 120–131.
- Ballantine, D.S.; White, R.M.; Martin, S.J.; Ricco, A.J.; Frye, G.C.; Zellers, E.T.; Wohltjen, H. Acoustic Wave Sensors; Theory, Design and Physico-Chemical Applications; Academic Press: San Diego, CA, USA, 1997. [Google Scholar]
- Rafizadeh, H. Lattice Dynamics of Metal Hydrides. Phys. Rev. B 1981, 23, 1628–1632. [Google Scholar]
- Wicke, E.; Brodowsky, H. Topics in Applied Physics, Hydrogen in Metals II: Application Oriented Properties; Springer-Verlag: Berlin, Germany, 1978. [Google Scholar]
- D’Amico, A.; Palma, A.; Veradi, P. Hydrogen Sensor Using a Palladium Coated Surface Acoustic Wave Delay-Line. Proceedings of IEEE Ultrasonsics Symposium, San Diego, CA, USA, November 1982; pp. 308–311.


| Elastic Matrix In Stiffness Form (x1011Pa) | Piezoelectric Matrix at Constant Strain(C/m2) | Permittivity Matrix at Constant Strain (x10−11F/m) | |||
|---|---|---|---|---|---|
| C11 | 2.03 | e15 | 3.7 | ε11 | 39 |
| C12 | 0.573 | e22 | 2.5 | ε33 | 20.4 |
| C13 | 0.752 | e31 | 0.2 | ||
| C14 | 0.085 | e33 | 1.3 | ||
| C33 | 2.424 | ||||
| C44 | 0.595 | ||||
| C66 | |||||
| Elastic Matrix In Stiffness Form (x1011Pa) | Piezoelectric Matrix at Constant Strain(C/m2) | Permittivity Matrix at Constant Strain (x10−11F/m) | |||
|---|---|---|---|---|---|
| C11 | 1.57 | e15 | −0.45 | ε11 | 7.35 |
| C12 | 0.89 | e31 | −0.51 | ε33 | 7.79 |
| C13 | 0.83 | e33 | 1.22 | ||
| C33 | 2.08 | ||||
| C44 | 0.38 | ||||
| C66 | |||||
| Center Frequency (MHz) | IL(dB) | |
|---|---|---|
| Experimental [31] | 103 | −34.3 |
| Simulation [31] | 100 | −37.5 |
| Current Simulation | 100.56 | −35.5 |
| Parameter | Value |
|---|---|
| Substrate Dimensions | 3,500 × 400 × 500 μm |
| Number of Electrode Pairs for each IDT | 12 |
| Wavelength (λ) | 26.5 μm |
| Electrode width and spacing between the electrodes | λ/4 |
| Propagation Distance | 523.2 μm |
| Electrode Length | 200 μm |
| Dimensions of Pd Film | 423 × 175 × 2 μm |
| mH (g/mol) | mpd (g/mol) | Thickness [h(μm)] | ||
|---|---|---|---|---|
| 0 | 0 | 1.008 | 106.42 | 2 |
| 0.05 | 0.0095 | 1.008 | 106.42 | 2.019 |
| 0.1 | 0.019 | 1.008 | 106.42 | 2.038 |
| 0.15 | 0.0285 | 1.008 | 106.42 | 2.057 |
| 0.2 | 0.038 | 1.008 | 106.42 | 2.076 |
| 0.3 | 0.057 | 1.008 | 106.42 | 2.114 |
| 0.37 | 0.0703 | 1.008 | 106.42 | 2.1406 |
| 0.43 | 0.0817 | 1.008 | 106.42 | 2.1634 |
| 0.5 | 0.095 | 1.008 | 106.42 | 2.19 |
| E(Gpa) | ρc (kg/m3) | |
|---|---|---|
| 0 | 128 | 12020 |
| 0.05 | 126.2 | 12019.98 |
| 0.1 | 124.5 | 12008.57 |
| 0.15 | 123 | 11985.84 |
| 0.2 | 121.36 | 11951.94 |
| 0.3 | 118.5 | 11851.5 |
| 0.37 | 116.83 | 11756.331 |
| 0.43 | 115 | 11659.352 |
| 0.5 | 113.73 | 11529.29 |
| Phase (ϕ) in Deg. | Frequency (MHz) | Insertion Loss (dB) | |||
|---|---|---|---|---|---|
| Pure Pd | −12629 | 0.00 | 0.00 | 128.42 | −35.743 |
| 0.05 | −12646.8 | 17.8 | 0.00141 | 128.42 | −35.5 |
| 0.1 | −13023 | 394 | 0.0312 | 128.42 | −35.32 |
| 0.15 | −13395.8 | 766.8 | 0.0607 | 128.42 | −35.202 |
| 0.2 | −13408 | 779 | 0.0617 | 128.42 | −35.12 |
| 0.3 | −13735 | 1106 | 0.0876 | 127.93 | −35.04 |
| 0.37 | −13743 | 1114 | 0.0882 | 127.93 | −35.014 |
| 0.43 | −13748 | 1119 | 0.0886 | 127.93 | −34.99 |
| 0.5 | −13748 | 1119 | 0.0886 | 127.93 | −35.01 |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
EL Gowini, M.M.; Moussa, W.A. A Finite Element Model of a MEMS-based Surface Acoustic Wave Hydrogen Sensor. Sensors 2010, 10, 1232-1250. https://doi.org/10.3390/s100201232
EL Gowini MM, Moussa WA. A Finite Element Model of a MEMS-based Surface Acoustic Wave Hydrogen Sensor. Sensors. 2010; 10(2):1232-1250. https://doi.org/10.3390/s100201232
Chicago/Turabian StyleEL Gowini, Mohamed M., and Walied A. Moussa. 2010. "A Finite Element Model of a MEMS-based Surface Acoustic Wave Hydrogen Sensor" Sensors 10, no. 2: 1232-1250. https://doi.org/10.3390/s100201232