Investigation into the Effect of Atmospheric Particulate Matter (PM2.5 and PM10) Concentrations on GPS Signals
Abstract
:1. Introduction
2. Physics of Atmospheric Refraction in GNSS
3. Methodology of Investigation and Experimental Data Description
4. Results, Analysis and Discussion
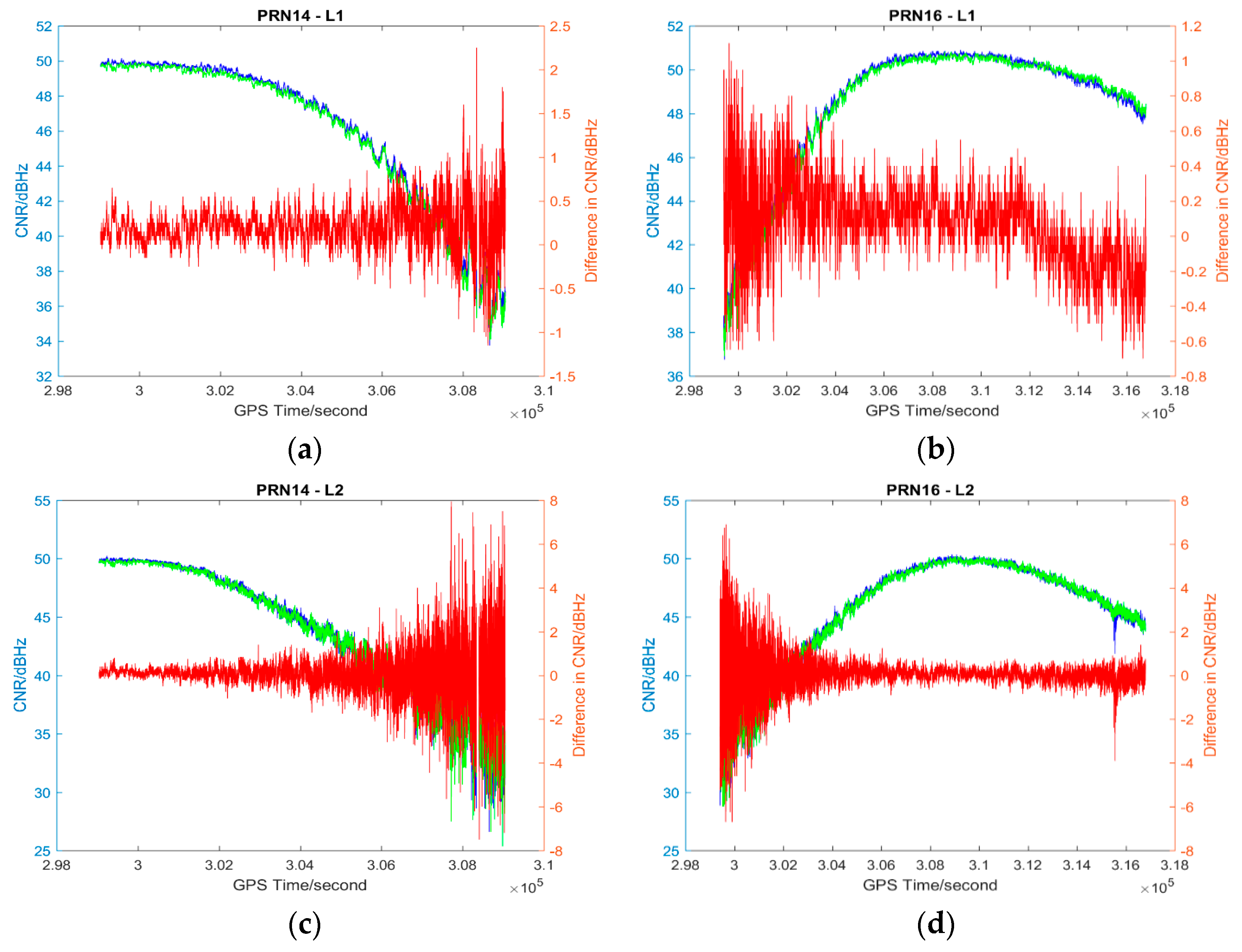
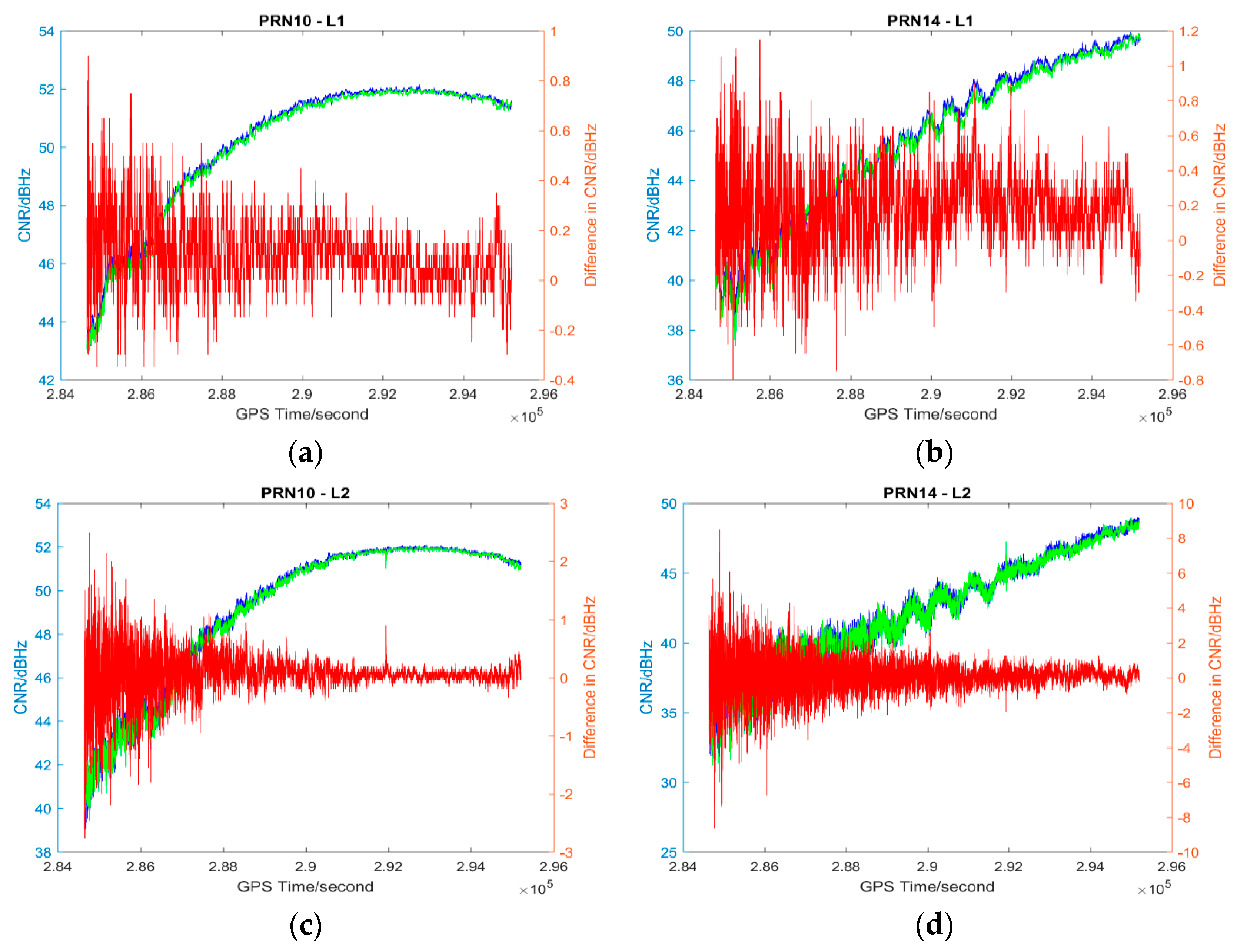
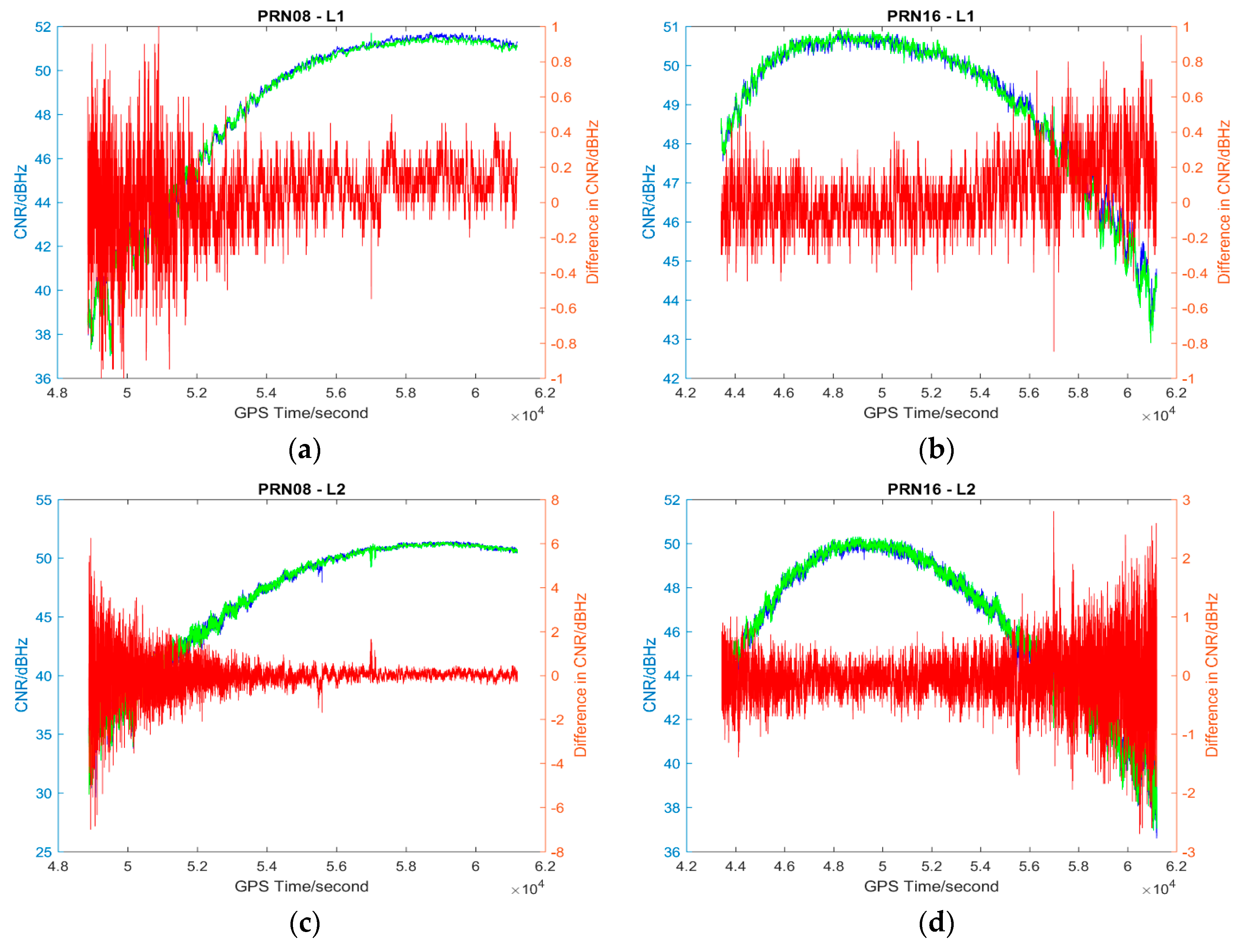
4.1. Description of Results
4.2. Analysis of Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lau, L.; Cross, P.; Steen, M. Flight Tests of Error-Bounded Heading and Pitch Determination with Two GPS Receivers. IEEE Trans Aerosp. Electron. Syst. 2012, 48, 388–404. [Google Scholar] [CrossRef]
- Klobuchar, J. Ionospheric Time-Delay Algorithms for Single-Frequency GPS Users. IEEE Trans Aerosp. Electron. Syst. 1987, 23, 325–331. [Google Scholar] [CrossRef]
- Radicella, S.M. The NeQuick Model Genesis, Uses and Evolution. Ann. Geophys. 2009, 52, 417–422. [Google Scholar]
- Hopfield, H.S. Two–quadratic tropospheric refractivity profile for correction satellite data. J. Geophys. Res. 1969, 74, 4487–4499. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric Correction for Troposphere and Stratosphere in Radio Ranging of Satellites. Geophys. Monogr. 1972, 15, 247–252. [Google Scholar]
- Xu, G. GPS: Theory, Algorithms and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Brook, R.D.; Rajagopalan, S.; Pope, C.A.; Brook, J.R.; Bhatnagar, A.; Diez-Roux, A.V.; Holguin, F.; Hong, Y.; Luepker, R.V.; Mittleman, M.A.; et al. Particulate Matter Air Pollution and Cardiovascular Disease. An Update to the Scientific Statement from the American Heart Association. Circulation 2010, 121, 2331–2378. [Google Scholar] [CrossRef] [PubMed]
- Xu, A.; Xu, Z.; Ge, M.; Xu, X.; Zhu, H.; Sui, X. Estimating Zenith Tropospheric Delays from BeiDou Navigation Satellite System Observations. Sensors 2013, 13, 4514–4526. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Ye, S.; Chen, D.; Liu, Y.; Xia, P. Retrieving Precipitable Water Vapor Data Using GPS Zenith Delays and Global Reanalysis Data in China. Remote Sens. 2016, 8, 389. [Google Scholar] [CrossRef]
- Solheim, F.S.; Vivekan, J.; Ware, R.H.; Rocken, C. Propagation delays induced in GPS signals by dry air, water vapor, hydrometeors and other atmospheric particulates. J. Geophys. Res. 1999, 104, 9663–9670. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Lau, L.; Cross, P. Development and Testing of a New Ray-Tracing Approach to GNSS Carrier-Phase Multipath Modelling. J. Geod. 2007, 81, 713–732. [Google Scholar] [CrossRef]
- Lau, L. Wavelet Packets Based Denoising Method for Measurement Domain Repeat-time Multipath Filtering in GPS Static High-Precision Positioning Applications. GPS Solut. 2016, 1–14. [Google Scholar] [CrossRef]
- Guo, J.; Miao, Y.; Zhang, Y.; Liu, H.; Li, Z.; Zhang, W.; He, J.; Lou, M.; Yan, Y.; Bian, L.; et al. The climatology of planetary boundary layer height in China derived from radiosonde and reanalysis data. Atmos. Chem. Phys. 2016, 16, 13309–13319. [Google Scholar] [CrossRef]
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying, 4th ed.; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Wang, G.; Huang, L.; Gao, S.; Gao, S.; Wang, L. Characterization of water-soluble species of PM10 and PM2.5 aerosols in urban area in Nanjing, China. Atmos. Environ. 2002, 36, 1299–1307. [Google Scholar] [CrossRef]
- Rusu-Zagar, G.; Rusu-Zagar, C.; Iorga, I.; Iorga, A. Air Pollution Particles PM10, PM2.5 and the Tropospheric Ozone Effects on Human Health. Procedia—Soc. Behav. Sci. 2013, 92, 826–831. [Google Scholar] [CrossRef]
- Jonasz, M. Size, shape, composition, and structure of microparticles from light scattering. In Principles, Methods and Application of Particle Size Analysis; Syvitski, J.P.M., Ed.; Cambridge University Press: Cambridge, UK, 1991; pp. 143–162. [Google Scholar]
- Molenar, J.V. Theoretical Analysis of PM2.5 Mass Measurements by Nephelometry—#11. Available online: http://vista.cira.colostate.edu/improve/publications/graylit/014_AerosolByNeph/AerosolbyNeph.pdf (accessed on 10 July 2016).
- Bhardwaja, P.S.; Herbert, J.; Charlson, R.J. Refractive Index of Atmospheric Particulate Matter: An in situ Method for Determination. Appl. Opt. 1974, 13, 731–734. [Google Scholar] [CrossRef] [PubMed]
- Bullrich, K. Scattered radiation in the atmosphere. Adv. Geophys. 1964, 10, 114. [Google Scholar]
- Gillespie, J.B.; Lindberg, J.D. Seasonal and geographic variations in imaginary refractive index of atmospheric particulate matter. Appl. Opt. 1992, 31, 2107–2111. [Google Scholar] [CrossRef] [PubMed]
- Lau, L. Comparison of Measurement and Position Domain Multipath Filtering Techniques with the Repeatable GPS Orbits for Static Antennas. Surv. Rev. 2012, 44, 9–16. [Google Scholar] [CrossRef]
- AirNow, Air Quality Index (AQI) Basics. Available online: https://airnow.gov/index.cfm?action=aqibasics.aqi (accessed on 23 June 2016).
- UNAVCO, TEQC—The Toolkit for GPS/GLONASS/Galileo/SBAS/Beidou/QZSS Data. Available online: https://www.unavco.org/software/data-processing/teqc/teqc.html (accessed on 18 July 2016).
- Lau, L.; Cross, P. A New Signal-to-Noise-Ratio Based Stochastic Model for GNSS High-Precision Carrier Phase Data Processing Algorithms in the Presence of Multipath Errors. In Proceedings of the ION GNSS 2006, Fort Worth, TX, USA, 26–29 September 2006; pp. 276–285.
- Moorthy, K.K.; Babu, S.S.; Badarinath, K.V.S.; Sunilkumar, S.V.; Kiranchand, T.R.; Ahmed, Y.N. Latitudinal distribution of aerosol black carbon and its mass fraction to composite aerosols over peninsular India during winter season. Geophys. Res. Lett. 2007, 34, L08802. [Google Scholar] [CrossRef]
- Geiling, T.; Dressler, L.; Welker, T.; Hoffmann, M. Fine Dust Measurement with Electrical Fields—Concept of a Hybrid Particle Detector. In Proceedings of the 9th International Conference and Exhibition on Ceramic Interconnect and Ceramic Microsystems Technologies, Orlando, FL, USA, 23–25 April 2013.
- Quan, Y.; Lau, L.; Roberts, G.W.; Meng, X. Measurement Signal Quality Assessment on All Available and New Signals of Multi-GNSS (GPS, GLONASS, Galileo, BDS, and QZSS) with Real Data. J. Navig. 2015, 69, 313–334. [Google Scholar] [CrossRef]
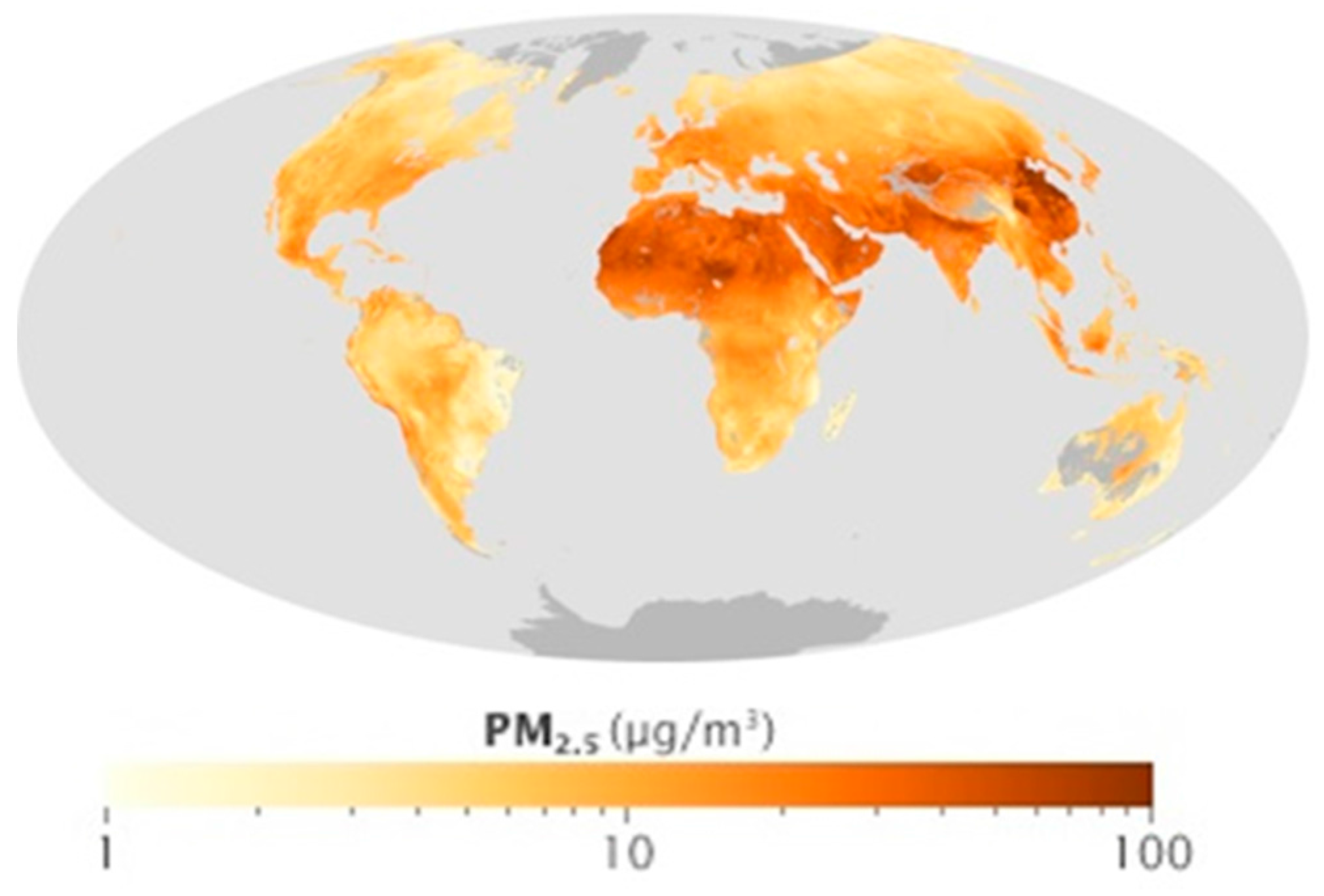
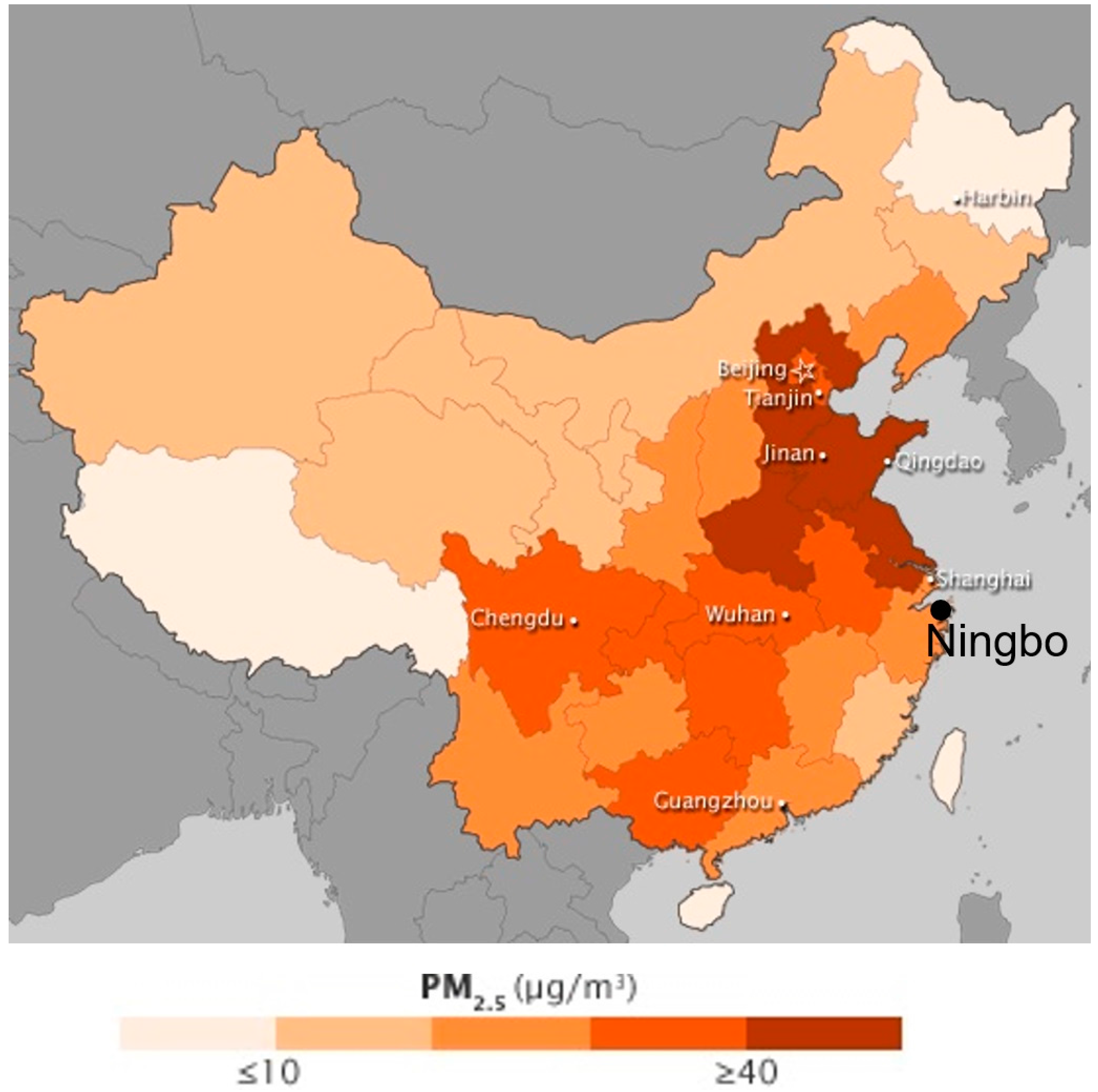

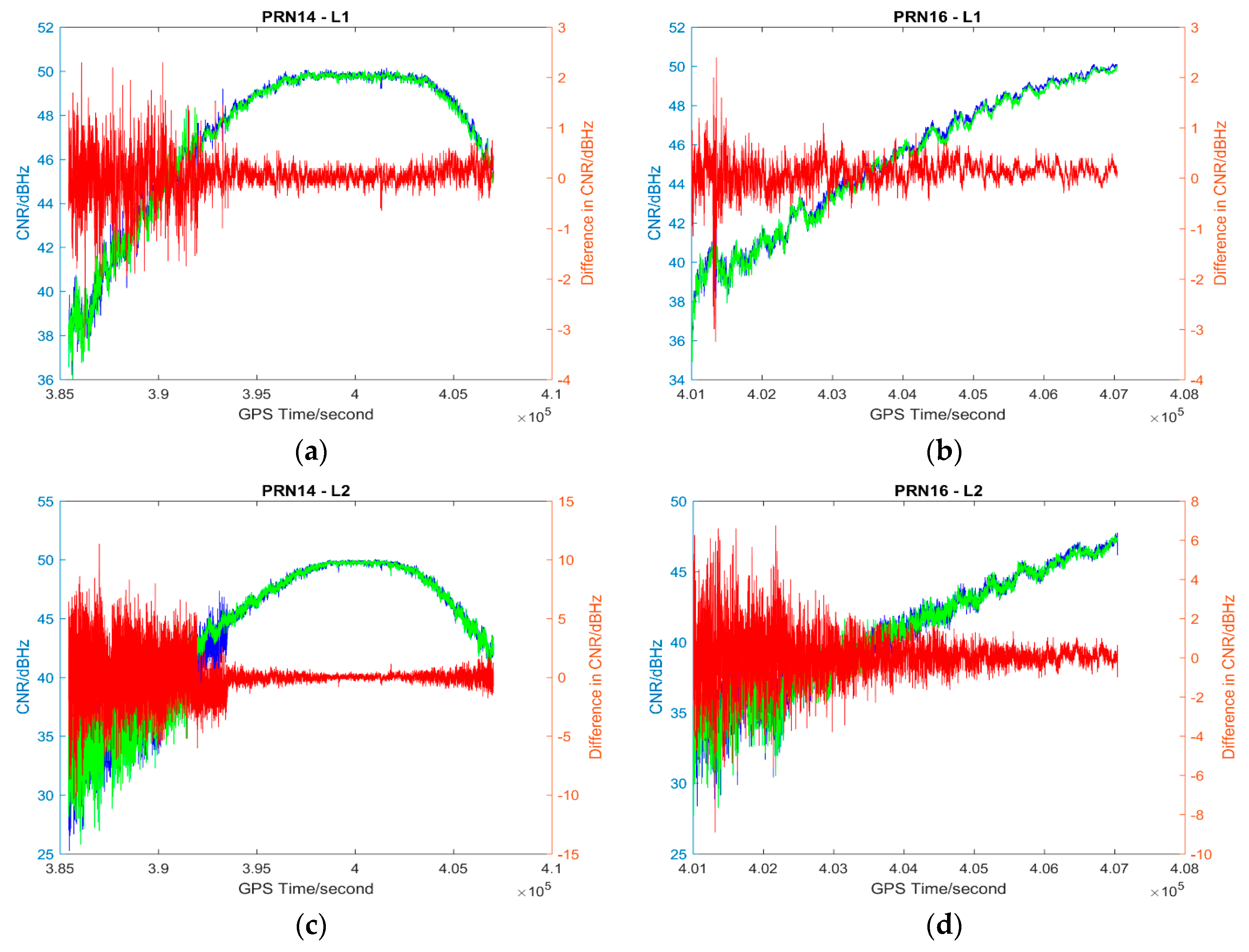


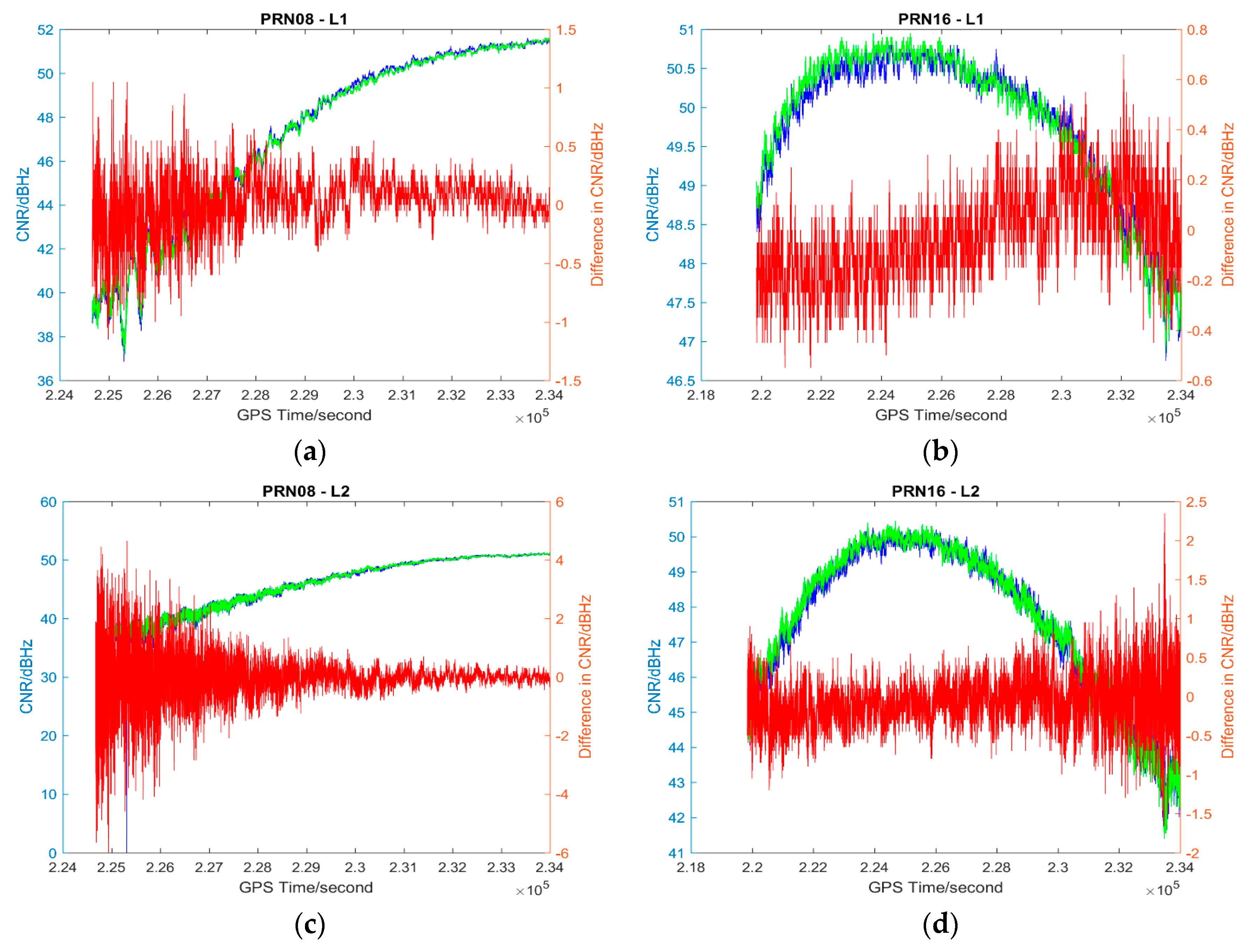
| Date | Time (hh:mm) | PM10 | PM2.5 | AQI | PM10 Ratio | PM2.5 Ratio | AQI Ratio |
|---|---|---|---|---|---|---|---|
| 6 November 2014 | 19:00 | 144 | 222 | 222 | 4.0 | 9.7 | 6.2 |
| 6 November 2014 | 20:00 | 130 | 203 | 203 | 3.9 | 9.2 | 6.2 |
| 6 November 2014 | 21:00 | 130 | 203 | 203 | 4.2 | 10.2 | 6.5 |
| 6 November 2014 | 22:00 | 142 | 216 | 216 | 4.3 | 9.8 | 6.5 |
| 6 November 2014 | 23:00 | 148 | 223 | 223 | 4.9 | 11.7 | 7.4 |
| 7 November 2014 | 00:00 | 147 | 221 | 221 | 4.7 | 11.1 | 7.1 |
| 7 November 2014 | 01:00 | 141 | 213 | 213 | 4.1 | 9.3 | 6.3 |
| 7 November 2014 | 02:00 | 136 | 207 | 207 | 3.0 | 6.9 | 4.6 |
| 7 November 2014 | 19:00 | 36 | 23 | 36 | - | - | - |
| 7 November 2014 | 20:00 | 33 | 22 | 33 | - | - | - |
| 7 November 2014 | 21:00 | 31 | 20 | 31 | - | - | - |
| 7 November 2014 | 22:00 | 33 | 22 | 33 | - | - | - |
| 7 November 2014 | 23:00 | 30 | 19 | 30 | - | - | - |
| 8 November 2014 | 00:00 | 31 | 20 | 31 | - | - | - |
| 8 November 2014 | 01:00 | 34 | 23 | 34 | - | - | - |
| 8 November 2014 | 02:00 | 45 | 30 | 45 |
| Date | Time (hh:mm) | PM10 | PM2.5 | AQI | PM10 Ratio | PM2.5 Ratio | AQI Ratio |
|---|---|---|---|---|---|---|---|
| 7 November 2014 | 16:00 | 38 | 26 | 38 | 0.9 | 0.7 | 0.9 |
| 7 November 2014 | 17:00 | 32 | 22 | 32 | 1.0 | 0.7 | 0.9 |
| 7 November 2014 | 18:00 | 30 | 19 | 30 | 0.9 | 0.6 | 0.9 |
| 7 November 2014 | 19:00 | 36 | 23 | 36 | 1.1 | 0.7 | 1.0 |
| 7 November 2014 | 20:00 | 33 | 22 | 33 | 1.0 | 0.7 | 1.0 |
| 7 November 2014 | 21:00 | 31 | 20 | 31 | 1.3 | 0.8 | 1.2 |
| 7 November 2014 | 22:00 | 33 | 22 | 33 | 1.8 | 1.1 | 1.7 |
| 7 November 2014 | 23:00 | 30 | 19 | 30 | 1.7 | 1.1 | 1.5 |
| 8 November 2014 | 00:00 | 31 | 20 | 31 | 1.3 | 0.9 | 1.3 |
| 8 November 2014 | 16:00 | 42 | 39 | 42 | - | - | - |
| 8 November 2014 | 17:00 | 32 | 30 | 36 | - | - | - |
| 8 November 2014 | 18:00 | 33 | 32 | 35 | - | - | - |
| 8 November 2014 | 19:00 | 34 | 35 | 35 | - | - | - |
| 8 November 2014 | 20:00 | 33 | 33 | 33 | - | - | - |
| 8 November 2014 | 21:00 | 23 | 26 | 26 | - | - | - |
| 8 November 2014 | 22:00 | 18 | 20 | 20 | - | - | - |
| 8 November 2014 | 23:00 | 18 | 18 | 20 | - | - | - |
| 9 November 2014 | 00:00 | 24 | 23 | 24 | - | - | - |
| Date | Time (hh:mm) | PM10 | PM2.5 | AQI | PM10 Ratio | PM2.5 Ratio | AQI Ratio |
|---|---|---|---|---|---|---|---|
| 15 December 2015 | 21:00 | 181 | 280 | 280 | 4.2 | 9.3 | 6.5 |
| 15 December 2015 | 22:00 | 191 | 295 | 295 | 4.0 | 8.9 | 6.1 |
| 15 December 2015 | 23:00 | 194 | 298 | 298 | 3.7 | 7.8 | 5.6 |
| 16 December 2015 | 00:00 | 192 | 293 | 293 | 3.6 | 7.0 | 5.4 |
| 16 December 2015 | 01:00 | 189 | 290 | 290 | 3.4 | 6.3 | 5.2 |
| 16 December 2015 | 21:00 | 43 | 30 | 43 | |||
| 16 December 2015 | 22:00 | 48 | 33 | 48 | |||
| 16 December 2015 | 23:00 | 53 | 38 | 53 | |||
| 17 December 2015 | 00:00 | 54 | 42 | 54 | |||
| 17 December 2015 | 01:00 | 56 | 46 | 56 |
| Date | Time (hh:mm) | PM10 | PM2.5 | AQI | PM10 Ratio | PM2.5 Ratio | AQI Ratio |
|---|---|---|---|---|---|---|---|
| 23 December 2015 | 19:00 | 200 | 314 | 314 | 4.9 | 6.0 | 6.0 |
| 23 December 2015 | 20:00 | 194 | 305 | 305 | 4.7 | 6.1 | 6.1 |
| 23 December 2015 | 21:00 | 189 | 295 | 295 | 4.5 | 5.7 | 5.7 |
| 23 December 2015 | 22:00 | 190 | 293 | 293 | 3.9 | 5.0 | 5.0 |
| 23 December 2015 | 23:00 | 191 | 294 | 294 | 3.7 | 4.7 | 4.7 |
| 24 December 2015 | 00:00 | 194 | 294 | 294 | 3.7 | 4.7 | 4.7 |
| 24 December 2015 | 19:00 | 41 | 52 | 52 | |||
| 24 December 2015 | 20:00 | 41 | 50 | 50 | |||
| 24 December 2015 | 21:00 | 42 | 52 | 52 | |||
| 24 December 2015 | 22:00 | 49 | 59 | 59 | |||
| 24 December 2015 | 23:00 | 51 | 62 | 62 | |||
| 25 December 2015 | 00:00 | 52 | 63 | 63 |
| Date | Time (hh:mm) | PM10 | PM2.5 | AQI | PM10 Ratio | PM2.5 Ratio | AQI Ratio |
|---|---|---|---|---|---|---|---|
| 23 December 2015 | 15:00 | 136 | 221 | 221 | 4.0 | 5.3 | 5.3 |
| 23 December 2015 | 16:00 | 143 | 229 | 229 | 3.3 | 4.2 | 4.2 |
| 23 December 2015 | 17:00 | 153 | 240 | 240 | 3.8 | 4.6 | 4.6 |
| 23 December 2015 | 18:00 | 166 | 258 | 258 | 4.2 | 5.0 | 5.0 |
| 24 December 2015 | 15:00 | 34 | 42 | 42 | |||
| 24 December 2015 | 16:00 | 44 | 55 | 55 | |||
| 24 December 2015 | 17:00 | 40 | 52 | 52 | |||
| 24 December 2015 | 18:00 | 40 | 52 | 52 |
| Date | Time (hh:mm) | PM10 | PM2.5 | AQI | PM10 Ratio | PM2.5 Ratio | AQI Ratio |
|---|---|---|---|---|---|---|---|
| 27 December 2015 | 20:00 | 55 | 48 | 55 | 0.7 | 0.6 | 0.7 |
| 27 December 2015 | 21:00 | 55 | 49 | 55 | 0.7 | 0.7 | 0.7 |
| 27 December 2015 | 22:00 | 56 | 50 | 56 | 0.7 | 0.6 | 0.7 |
| 27 December 2015 | 23:00 | 57 | 53 | 57 | 0.8 | 0.8 | 0.8 |
| 28 December 2015 | 00:00 | 56 | 50 | 56 | 0.8 | 0.7 | 0.7 |
| 28 December 2015 | 01:00 | 54 | 48 | 54 | 0.7 | 0.6 | 0.7 |
| 28 December 2015 | 20:00 | 75 | 74 | 75 | |||
| 28 December 2015 | 21:00 | 75 | 75 | 75 | |||
| 28 December 2015 | 22:00 | 76 | 78 | 78 | |||
| 28 December 2015 | 23:00 | 68 | 67 | 68 | |||
| 29 December 2015 | 00:00 | 74 | 75 | 75 | |||
| 29 December 2015 | 01:00 | 75 | 79 | 79 |
| Data Set 1 Great AQI Difference | L1 (dBHz) | L2 (dBHz) | ||
|---|---|---|---|---|
| PRN | Mean | S.D. | Mean | S.D. |
| 14 | 0.059 | 0.160 | −0.056 | 0.560 |
| 16 | 0.159 | 0.145 | 0.051 | 0.371 |
| 18 | 0.016 | 0.191 | 0.011 | 0.809 |
| 21 | −0.017 | 0.317 | 0.345 | 1.523 |
| 24 | −0.009 | 0.247 | 0.100 | 1.074 |
| Overall | 0.042 | 0.090 | ||
| Data set 2 Similar AQI | L1 (dBHz) | L2 (dBHz) | ||
| PRN | Mean | S.D. | Mean | S.D. |
| 14 | 0.124 | 0.127 | 0.079 | 0.221 |
| 15 | 0.184 | 0.196 | −0.975 | 1.085 |
| 18 | 0.097 | 0.144 | −0.043 | 0.386 |
| 24 | 0.157 | 0.167 | −0.702 | 0.744 |
| 29 | 0.167 | 0.191 | 0.072 | 0.857 |
| Overall | 0.146 | −0.314 | ||
| Data Set 3 Great AQI Diff | L1 (dBHz) | L2 (dBHz) | ||
|---|---|---|---|---|
| PRN | Mean | S.D. | Mean | S.D. |
| 08 | 0.077 | 0.125 | −0.012 | 0.257 |
| 16 | −0.029 | 0.1556 | −0.075 | 0.251 |
| 26 | −0.047 | 0.166 | −0.087 | 0.230 |
| 27 | 0.003 | 0.127 | 0.015 | 0.156 |
| Overall | 0.001 | −0.039 | ||
| Data set 4 Great AQI diff | L1 (dBHz) | L2 (dBHz) | ||
| PRN | Mean | S.D. | Mean | S.D. |
| 14 | 0.185 | 0.132 | 0.094 | 0.314 |
| 16 | 0.049 | 0.173 | 0.052 | 0.263 |
| 26 | 0.084 | 0.162 | 0.079 | 0.215 |
| 27 | −0.019 | 0.152 | −0.050 | 0.176 |
| Overall | 0.075 | 0.044 | ||
| Data set 5 Great AQI diff | L1 (dBHz) | L2 (dBHz) | ||
| Mean | S.D. | Mean | S.D. | |
| 10 | 0.092 | 0.097 | 0.072 | 0.171 |
| 12 | 0.168 | 0.147 | 0.101 | 0.346 |
| 14 | 0.193 | 0.147 | 0.108 | 0.414 |
| 18 | 0.088 | 0.109 | 0.058 | 0.205 |
| Overall | 0.135 | 0.085 | ||
| Data set 6 Similar AQI | L1 (dBHz) | L2 (dBHz) | ||
| Mean | S.D. | Mean | S.D. | |
| 08 | 0.077 | 0.125 | 0.013 | 0.220 |
| 16 | 0.041 | 0.150 | −0.041 | 0.286 |
| 26 | −0.019 | 0.121 | −0.041 | 0.209 |
| 27 | 0.050 | 0.124 | 0.025 | 0.164 |
| Overall | 0.037 | −0.011 | ||
| Data Set 1 | Day 1 ZTD (m) | Day 2 ZTD (m) | ΔZTD (m) |
|---|---|---|---|
| 19:00 | 2.460 | 2.459 | 0.0008 |
| 20:00 | 2.466 | 2.460 | 0.0063 |
| 21:00 | 2.468 | 2.462 | 0.0059 |
| 22:00 | 2.470 | 2.460 | 0.0103 |
| 23:00 | 2.471 | 2.471 | −0.0007 |
| 00:00 | 2.468 | 2.470 | −0.0027 |
| 01:00 | 2.466 | 2.475 | −0.0090 |
| 02:00 | 2.464 | 2.482 | −0.0179 |
| mean | −0.0009 | ||
| Data set 2 | Day 1 ZTD (m) | Day 2 ZTD (m) | ΔZTD (m) |
| 16:00 | 2.455 | 2.492 | −0.0364 |
| 17:00 | 2.457 | 2.493 | −0.0356 |
| 18:00 | 2.459 | 2.492 | −0.0332 |
| 19:00 | 2.459 | 2.493 | −0.0335 |
| 20:00 | 2.460 | 2.492 | −0.0322 |
| 21:00 | 2.462 | 2.491 | −0.0281 |
| 22:00 | 2.460 | 2.489 | −0.0294 |
| 23:00 | 2.471 | 2.484 | −0.0122 |
| 00:00 | 2.470 | 2.482 | −0.0112 |
| mean | −0.0280 | ||
| Data set 3 | Day 1 ZTD (m) | Day 2 ZTD (m) | ΔZTD (m) |
| 21:00 | 2.417 | 2.388 | 0.0284 |
| 22:00 | 2.419 | 2.389 | 0.0296 |
| 23:00 | 2.419 | 2.386 | 0.0329 |
| 00:00 | 2.418 | 2.385 | 0.0324 |
| 01:00 | 2.418 | 2.389 | 0.0286 |
| mean | 0.0304 | ||
| Data set 4 | Day 1 ZTD (m) | Day 2 ZTD (m) | ΔZTD (m) |
| 19:00 | 2.440 | 2.448 | −0.0085 |
| 20:00 | 2.439 | 2.446 | −0.0070 |
| 21:00 | 2.442 | 2.448 | −0.0052 |
| 22:00 | 2.444 | 2.448 | −0.0041 |
| 23:00 | 2.443 | 2.445 | −0.0017 |
| 00:00 | 2.444 | 2.444 | 0.0002 |
| mean | −0.0044 | ||
| Data set 5 | Day 1 ZTD (m) | Day 2 ZTD (m) | ΔZTD (m) |
| 15:00 | 2.437 | 2.451 | −0.0145 |
| 16:00 | 2.441 | 2.452 | −0.0114 |
| 17:00 | 2.443 | 2.450 | −0.0072 |
| 18:00 | 2.442 | 2.451 | −0.0088 |
| mean | −0.0105 | ||
| Data set 6 | Day 1 ZTD (m) | Day 2 ZTD (m) | ΔZTD (m) |
| 20:00 | 2.450 | 2.424 | 0.0260 |
| 21:00 | 2.446 | 2.420 | 0.0265 |
| 22:00 | 2.446 | 2.422 | 0.0239 |
| 23:00 | 2.442 | 2.422 | 0.0203 |
| 00:00 | 2.442 | 2.416 | 0.0260 |
| 01:00 | 2.442 | 2.415 | 0.0270 |
| mean | 0.0250 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lau, L.; He, J. Investigation into the Effect of Atmospheric Particulate Matter (PM2.5 and PM10) Concentrations on GPS Signals. Sensors 2017, 17, 508. https://doi.org/10.3390/s17030508
Lau L, He J. Investigation into the Effect of Atmospheric Particulate Matter (PM2.5 and PM10) Concentrations on GPS Signals. Sensors. 2017; 17(3):508. https://doi.org/10.3390/s17030508
Chicago/Turabian StyleLau, Lawrence, and Jun He. 2017. "Investigation into the Effect of Atmospheric Particulate Matter (PM2.5 and PM10) Concentrations on GPS Signals" Sensors 17, no. 3: 508. https://doi.org/10.3390/s17030508
APA StyleLau, L., & He, J. (2017). Investigation into the Effect of Atmospheric Particulate Matter (PM2.5 and PM10) Concentrations on GPS Signals. Sensors, 17(3), 508. https://doi.org/10.3390/s17030508







