Adaptive Obstacle Detection for Mobile Robots in Urban Environments Using Downward-Looking 2D LiDAR
Abstract
:1. Introduction
1.1. Motivation
1.2. Related Works
1.3. The proposed Approach
- (1)
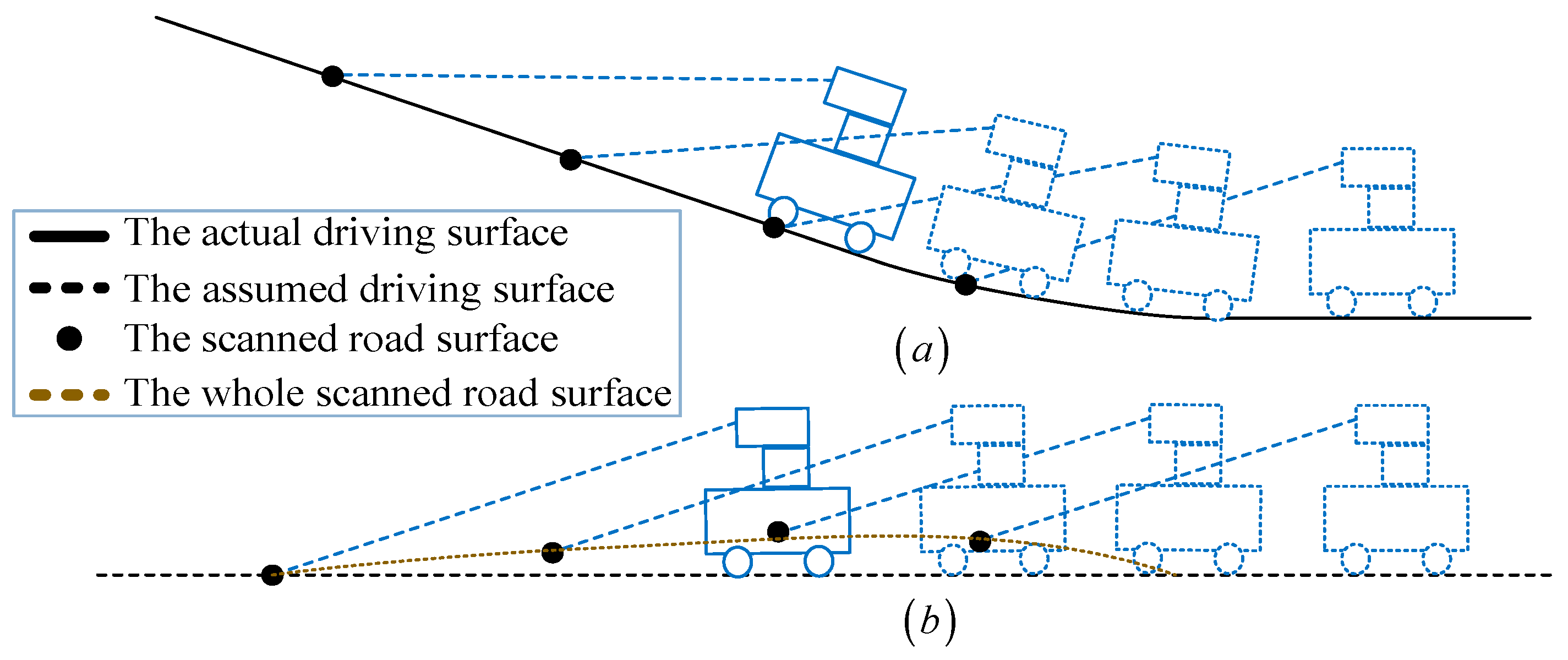
- Most previous studies did not deal with complex slopes and are poorly suited to different road conditions only using road height estimation. In order to improve the accuracy, we define the road vectors to well reflect the real situation of a road. We divide the line segments into ground and obstacle sections based on the average height of each line segment and the deviation of the line segment from the scanned road vector estimated from the previous measurements. By combining the height and the vector of the scanned road, our method can adapt to different road conditions.
- (2)
- The estimated road height and road vector in our method can vary with the changing road conditions, which improves the adaptivity of our method. The most recent characteristics of the road can be learnt by estimating the height and the vector a set of past scanned laser data, and then used for separation of obstacles at the next moment. The entire process is conducted iteratively so that a self-supervised learning system is realized to cope with uphill road, downhill road and sloping road.
- (3)
- We need not measure or estimate the roll and pitch angles of the LiDAR. During the whole design and application process, only the 2D planar position information and the steering angle of the robot are used, but we can also detect the road conditions and obstacles whether the robot is on an uphill road or a downhill road. The whole structure is simple and the algorithms are low time-consuming and applicable to small unmanned vehicles effectively in urban outdoor environments.
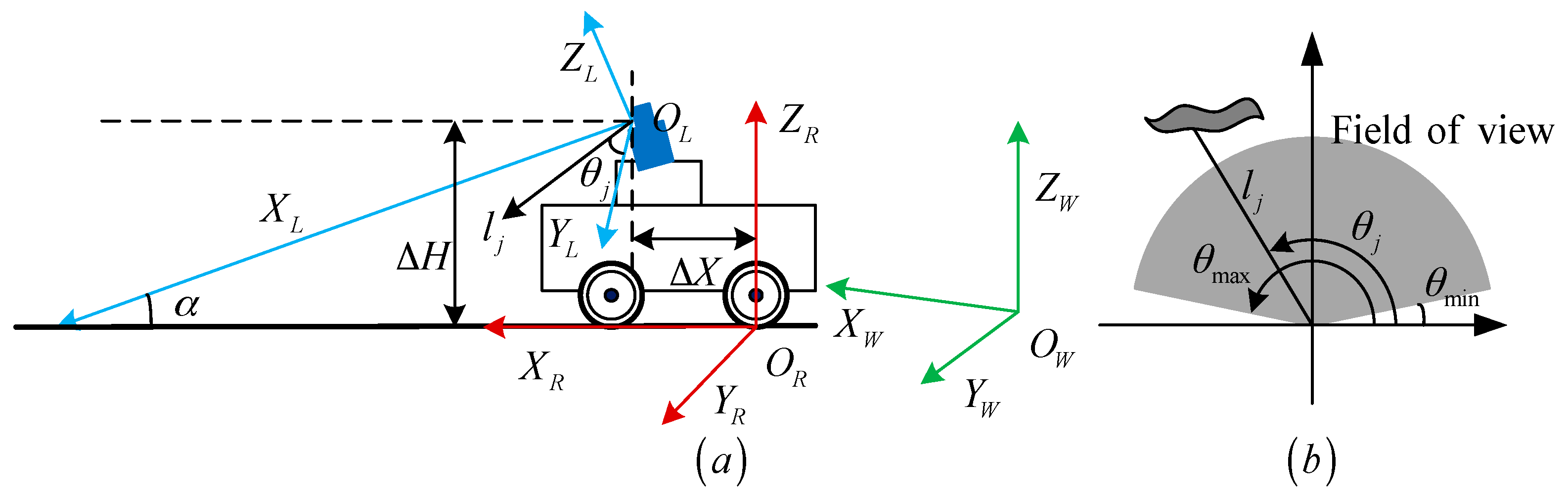
2. Definitions of System Coordinates
3. Scan Segmentation and Line Extraction
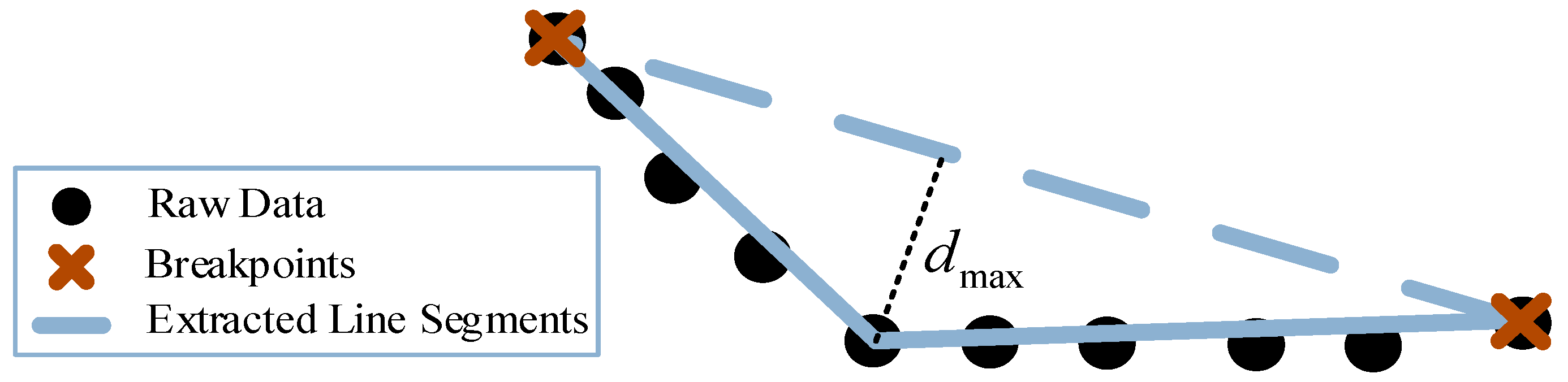
3.1. Breakpoint Detection
3.2. Line Extraction
- : The average height of .
- : The starting point of in .
- : The end point of in .
- : The starting point of in .
- : The end point of in .
- : The vector of .
- : The length of .
4. Obstacles Detection Algorithms
4.1. Road Height Estimation
| Algorithm 1: Height assessment of the scanned road surface. |
| INPUT: all point in range of (30°~150°) and . OUTPUT: Ω = ∅ (set Ω inital value is null set) 01 if ti = t0 02 hight (ti) = average 03 else 04 for all point pij in range of (30°~150°) 05 06 07 end 08 end 09 end 10 return height (ti) |
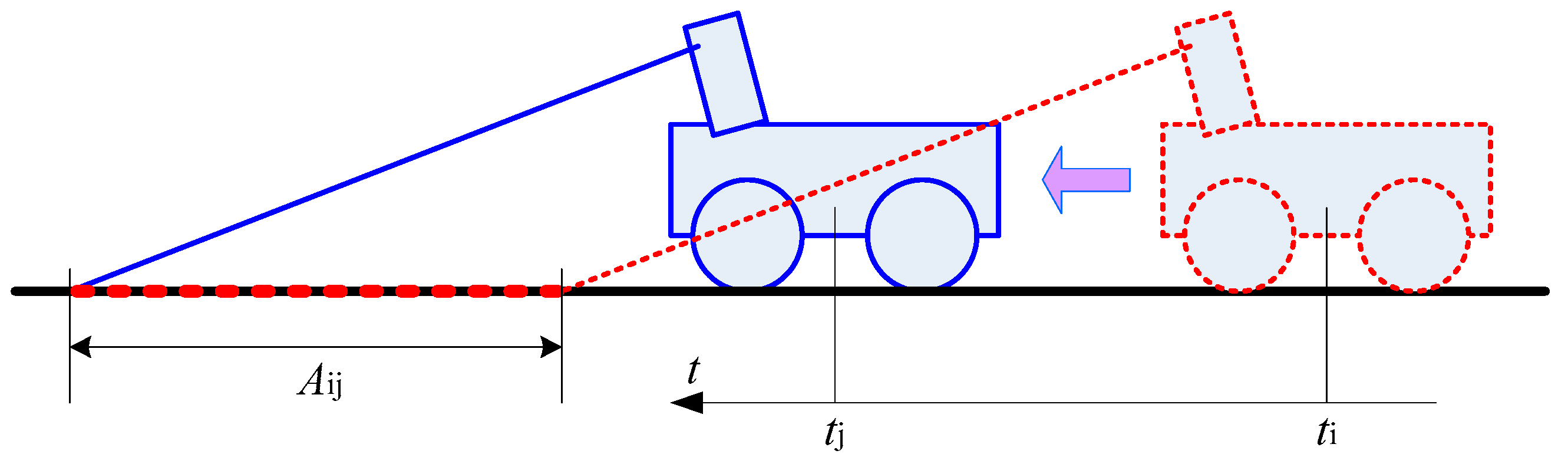
4.2. Road Vector Extraction
| Algorithm 2: Extract the vector of scanned road surface. |
| INPUT: road line segments sets , and . OUTPUT: 01 02 03 04 else 05 06 07 08 end 09 end 10 11 12 13 14 end return |
4.3. Obstacle Extraction
| Algorithm 3: Obstacles extraction. |
| INPUT: the average height of line , and . OUTPUT: 01 02 03 04 05 06 end 07 08 end 09 10 end 11 end return |
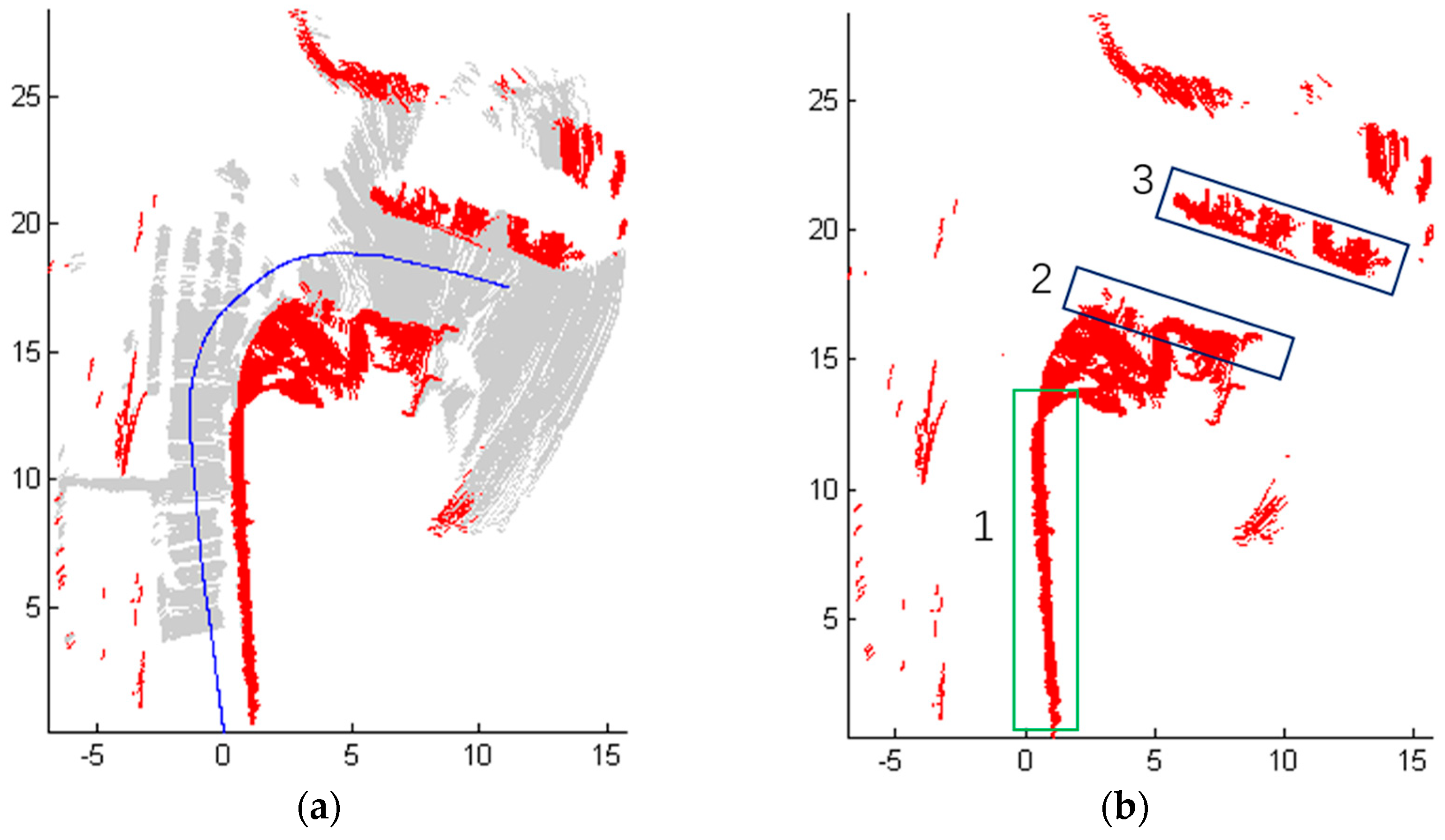
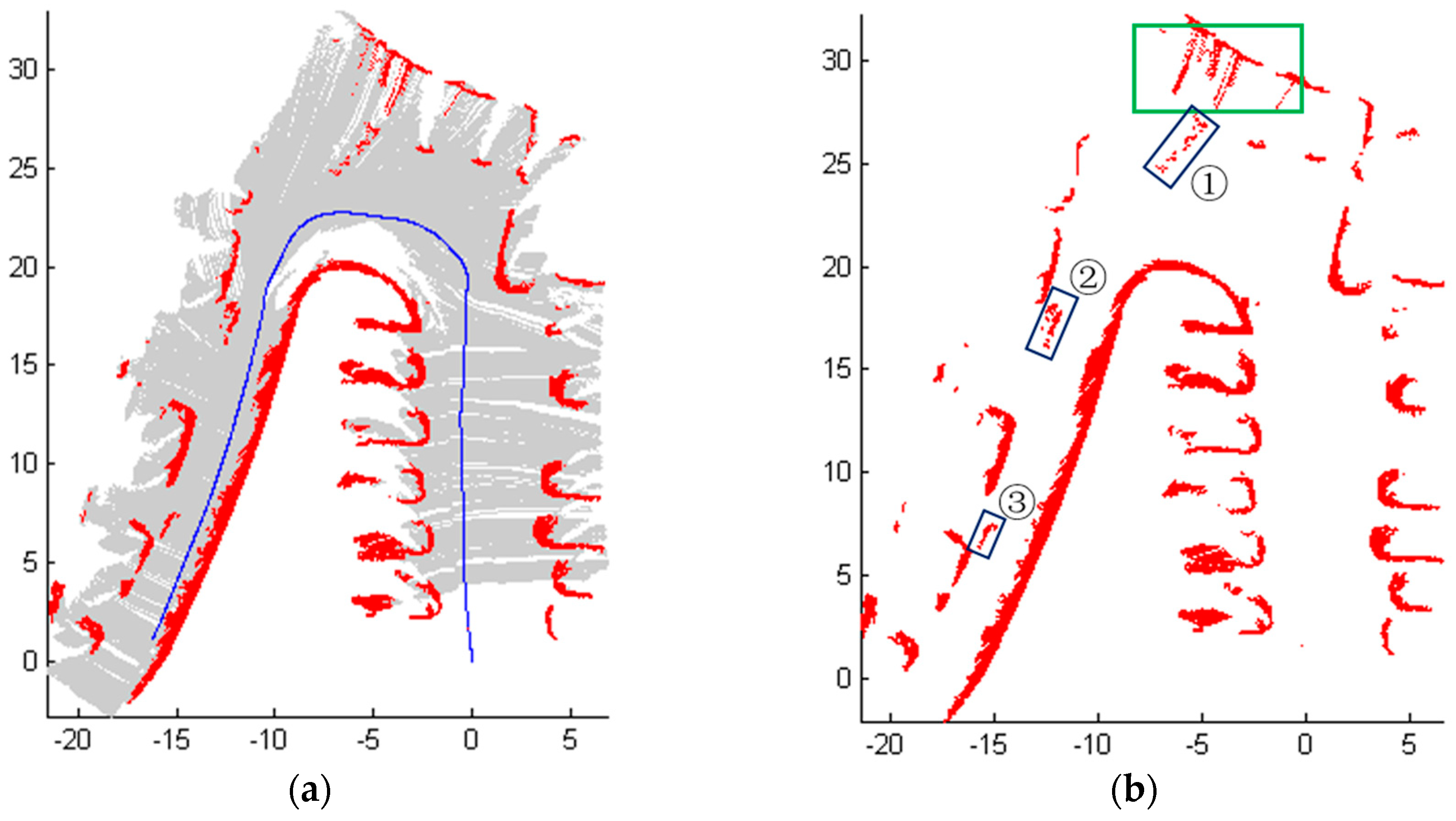
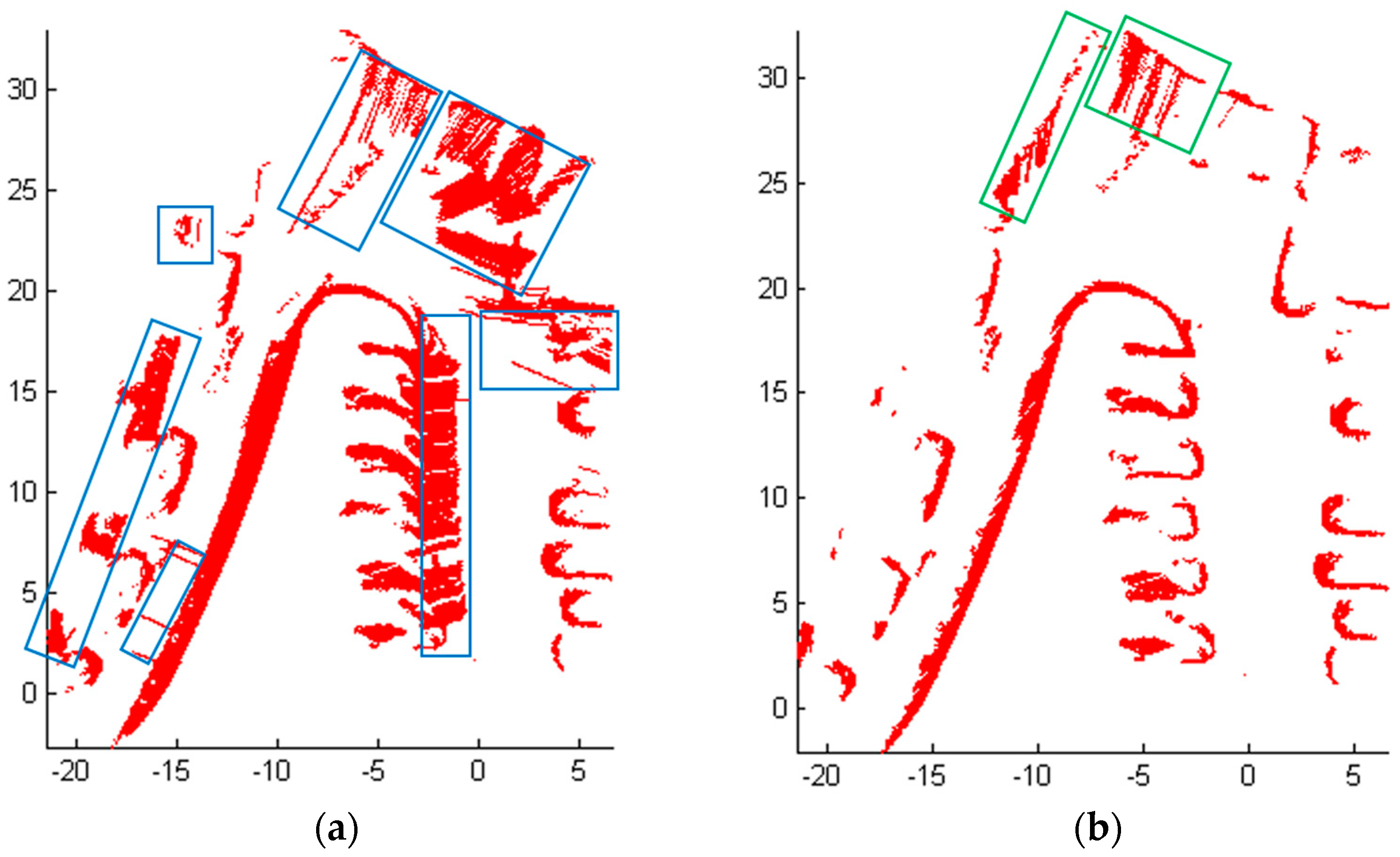
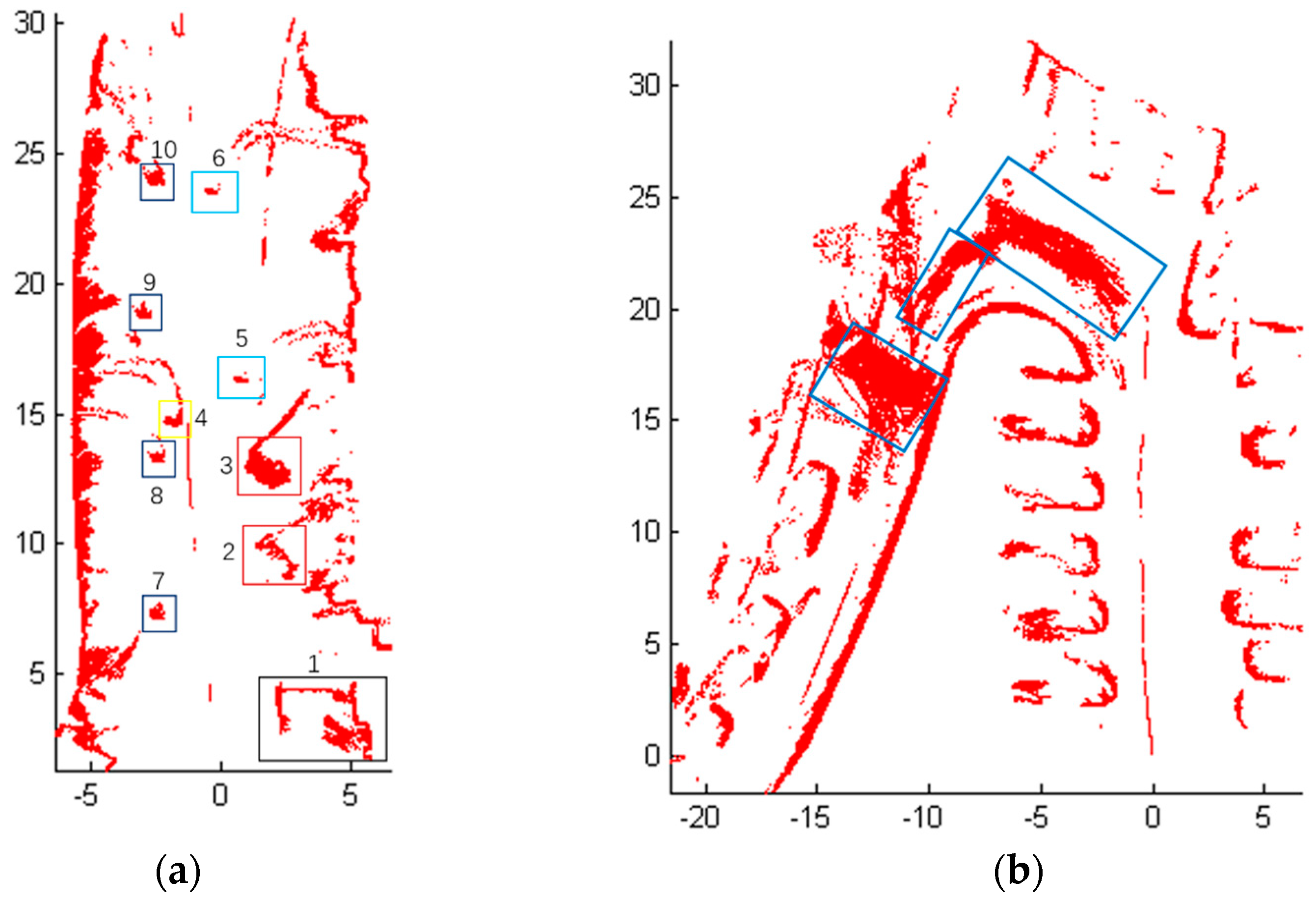
5. Experimental Results
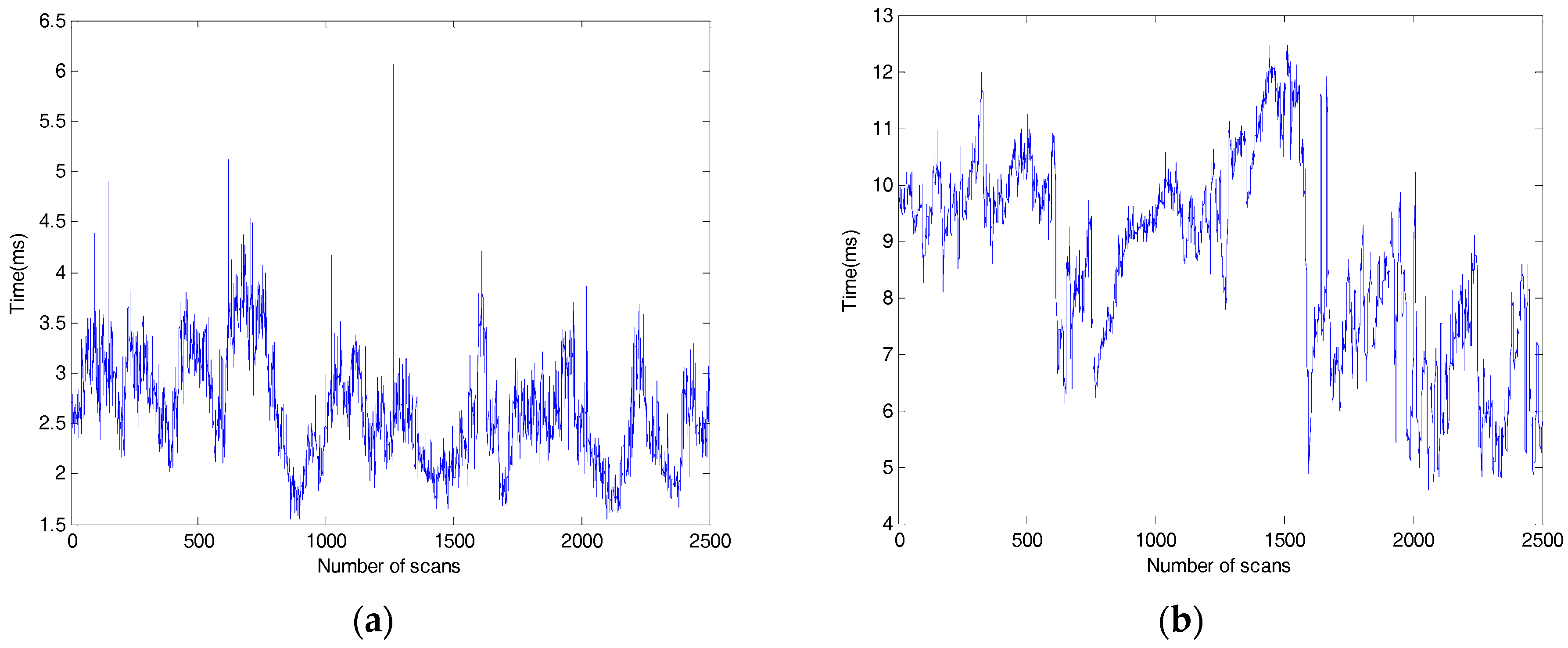
5.1. Parameters Analysis and Turning
5.2. Application Tests in Most Common Road Environment
5.3. Application Tests in Rare Complex Road Environment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kim, B.; Choi, B.; Park, S.; Kim, H.; Kim, E. Pedestrian/vehicle detection using a 2.5-d multi-layer laser scanner. IEEE Sens. J. 2016, 16, 400–408. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Liao, Y.; Xiong, R. Scalable Learning Framework for Traversable Region Detection Fusing With Appearance and Geometrical Information. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3267–3281. [Google Scholar] [CrossRef]
- Hillel, A.B.; Lerner, R.; Dan, L.; Raz, G. Recent progress in road and lane detection: A survey. IEEE Trans. Intell. Transp. Syst. 2014, 25, 727–745. [Google Scholar] [CrossRef]
- Hernández-Aceituno, J.; Arnay, R.; Toledo, J.; Acosta, L. Using Kinect on an Autonomous Vehicle for Outdoors Obstacle Detection. IEEE Sens. J. 2016, 16, 3603–3610. [Google Scholar] [CrossRef]
- Linegar, C.; Churchill, W.; Newman, P. Made to measure: Bespoke landmarks for 24-hour, all-weather localisation with a camera. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 787–794. [Google Scholar]
- Cherubini, A.; Spindler, F.; Chaumette, F. Autonomous visual navigation and laser-based moving obstacle avoidance. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2101–2110. [Google Scholar] [CrossRef]
- Lee, U.; Jung, J.; Shin, S.; Jeong, Y.; Park, K. EureCar turbo: A self-driving car that can handle adverse weather conditions. In Proceedings of the 2016 IEEE/RSJ International Conference on 2016 Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 2301–2306. [Google Scholar]
- Azim, A.; Aycard, O. Detection, classification and tracking of moving objects in a 3D environment. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium, Alcala de Henares, Spain, 3–7 June 2012; pp. 802–807. [Google Scholar]
- Asvadi, A.; Premebida, C.; Peixoto, P.; Nunes, U. 3D Lidar-based static and moving obstacle detection in driving environments: An approach based on voxels and multi-region ground planes. Robot. Auton. Syst. 2016, 83, 299–311. [Google Scholar] [CrossRef]
- Kusenbach, M.; Himmelsbach, M.; Wuensche, H.J. A new geometric 3D LiDAR feature for model creation and classification of moving objects. In Proceedings of the 2016 Intelligent Vehicles Symposium, Gothenburg, Sweden, 19–22 June 2016; pp. 272–278. [Google Scholar]
- Chen, X.; Kundu, K.; Zhu, Y.; Ma, H.; Fidler, S.; Urtasun, R. 3D object proposals using stereo imagery for accurate object class detection. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 1259–1272. [Google Scholar] [CrossRef] [PubMed]
- Zermas, D.; Izzat, I.; Papanikolopoulos, N. Fast segmentation of 3d point clouds: A paradigm on lidar data for autonomous vehicle applications. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017. [Google Scholar]
- Himmelsbach, M.; Hundelshausen, F.V.; Wuensche, H.J. Fast segmentation of 3D point clouds for ground vehicles. In Proceedings of the 2010 Intelligent Vehicles Symposium, San Diego, CA, USA, 21–24 June 2010. [Google Scholar]
- Chen, B.; Cai, Z.; Xiao, Z.; Yu, J.; Liu, L. Real-time detection of dynamic obstacle using laser radar. In Proceedings of the 2008 International Conference for Young Computer Scientists, Zhangjiajie, China, 18–21 November 2008; pp. 1728–1732. [Google Scholar]
- Chung, W.; Kim, H.; Yoo, Y.; Moon, C.B.; Park, J. The Detection and Following of Human Legs through Inductive Approaches for a Mobile Robot with a Single Laser Range Finder. IEEE Trans. Ind. Electron. 2012, 59, 3156–3166. [Google Scholar] [CrossRef]
- Kai, O.A.; Mozos, O.M.; Burgard, W. Using Boosted Features for the Detection of People in 2D Range Data. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 1050–4729. [Google Scholar]
- Thrun, S.; Montemerlo, M.; Dahlkamp, H.; Stavens, D.; Aron, A.; Diebel, J.; Fong, P.; Gale, J.; Halpenny, M.; Hoffmann, G.; et al. Stanley: The robot that won the DARPA Grand Challenge. J. Field Robot. 2006, 23, 661–692. [Google Scholar] [CrossRef]
- Qin, B.; Chong, Z.J.; Bandyopadhyay, T.; Ang, M.H. Curb-intersection feature based monte carlo localization on urban roads. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 2640–2646. [Google Scholar]
- Lee, L.K.; Oh, S.Y. Fast and efficient traversable region extraction using quantized elevation map and 2D laser rangefinder. In Proceedings of the 2016 International Symposium on Robotics, Munich, Germany, 21–22 June 2016; pp. 1–5. [Google Scholar]
- Ye, C.; Borenstein, J. A Method for Mobile Robot Navigation on Rough Terrain. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; pp. 1050–4729. [Google Scholar]
- Garcia, A.; Barrientos, A.; Medina, A.; Colmenarejo, P.; Mollinedo, L.; Rossi, C. 3D Path planning using a fuzzy logic navigational map for Planetary Surface Rovers. In Proceedings of the 2011 the 11th Symposium on Advanced Space Technologies in Robotics and Automation, Noordwijk, The Netherlands, 12–14 April 2011. [Google Scholar]
- Blas, M.R.; Blas, M.R.; Ravn, O.; Andersen, N.A.; Blanke, M. Traversable terrain classification for outdoor autonomous robots using single 2D laser scans. Integr. Comput. Aided Eng. 2006, 13, 223–232. [Google Scholar]
- Zhang, W. LiDAR-based road and road edge detection. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, San Diego, CA, USA, 21–24 June 2010; pp. 845–848. [Google Scholar]
- Han, J.; Kim, D.; Lee, M.; Sunwoo, M. Enhanced road boundary and obstacle detection using a downward-looking LIDAR sensor. IEEE Trans. Veh. Technol. 2016, 61, 971–985. [Google Scholar] [CrossRef]
- Wijesoma, W.S.; Kodagoda, K.R.S.; Balasuriya, A.P. Road-Boundary Detection and Tracking Using Ladar Sensing. IEEE Trans. Robot. Autom. 2004, 20, 456–464. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, J.; Liu, D. A New Curb Detection Method for Unmanned Ground Vehicles Using 2D Sequential Laser Data. Sensors 2013, 13, 1102–1120. [Google Scholar] [CrossRef] [PubMed]
- Tan, F.; Yang, J.; Huang, J.; Chen, W.; Wang, W. A corner and straight line matching localization method for family indoor monitor mobile robot. In Proceedings of the 2010 International Conference on Information and Automation, Harbin, China, 20–23 June 2010; pp. 1902–1907. [Google Scholar]
- Premebida, C.; Nunes, U. Segmentation and geometric primitives extraction from 2d laser range data for mobile robot applications. In Proceedings of the Robotica 2005—5th National Festival of Robotics Scientific Meeting, Coimbra, Portugal, 29 April–1 May 2005; pp. 17–25. [Google Scholar]
- Zhao, Y.; Chen, X. Prediction-Based geometric feature extraction for 2D laser scanner. Robot. Auton. Syst. 2011, 59, 402–409. [Google Scholar] [CrossRef]
- Li, Y.; Hua, L.; Tan, J.; Li, Z.; Xie, H.; Changjun, C. Scan Line Based Road Marking Extraction from Mobile LiDAR Point Clouds. Sensors 2016, 16, 903. [Google Scholar]
- Muñoz, L.R.; Villanueva, M.G.; Suárez, C.G. A tutorial on the total least squares method for fitting a straight line and a plane. Revista de Ciencia e Ingen. del Institute of Technology, Superior de Coatzacoalcos 2014, 1, 167–173. [Google Scholar]
- Sarkar, B.; Pal, P.K.; Sarkar, D. Building maps of indoor environments by merging line segments extracted from registered laser range scans. Robot. Auton. Syst. 2014, 62, 603–615. [Google Scholar] [CrossRef]
- Bu, Y.; Zhang, H.; Wang, H.; Liu, R.; Wang, K. Two-dimensional laser feature extraction based on improved successive edge following. Appl. Opt. 2015, 54, 4273–4279. [Google Scholar] [CrossRef]
- Norouzi, M.; Yaghobi, M.; Siboni, M.R.; Jadaliha, M. Recursive line extraction algorithm from 2d laser scanner applied to navigation a mobile robot. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Bangkok, Thailand, 22–25 February 2009; pp. 2127–2132. [Google Scholar]
- Borges, G.A.; Aldon, M.J. Line extraction in 2D range images for mobile robotics. J. Intell. Robot. Syst. 2004, 40, 267–297. [Google Scholar] [CrossRef]





| Reference | Sensor | Method | Advantages | Disadvantages |
|---|---|---|---|---|
| Zermas et al. [12] | 3D LiDAR | Iterative fashion using seed points | Rich information of obstacles | Expensive and height processing time |
| Himmelsbach et al. [13] | 3D LiDAR | Establishing binary labeling | ||
| Chen et al. [14] | Horizontally-looking 2D LiDAR | Based on occupancy grid map | Simple principle | The obstacles that are lower than the scanning height can not be detected |
| Chung et al. [15] | Horizontally-looking 2D LiDAR | Support vector data description | No geometric assumption and the robust tracking of dynamic object | |
| Lee et al. [19] | Downward-looking 2D LiDAR | Quantized digital elevation map and grayscale reconstruction | Data processing by using existing image processing techniques | Not discuss the conversion between different scene |
| Andersen et al. [22] | Downward-looking 2D LiDAR | Terrain classification based on derived models | Convenient and direct | Poorly suited to the changing conditions |
| Liu et al. [26] | Downward-looking 2D LiDAR | Dynamic digital elevation map | Adaptive curb model selection | Not discuss complex road conditions |
| Parameter | Description | Value |
|---|---|---|
| titled down angle | ||
| start scanning angle | ||
| stop scanning angle | ||
| angular resolution |
| Parameter | Description | Value |
|---|---|---|
| auxiliary parameter | ||
| residual variance | 0.02 m | |
| the minimum number of point | 8 | |
| height threshold of point | 0.15 m | |
| direction angle threshold | ||
| length threshold of line | 0.4 m | |
| segment threshold of noise | 0.0001 m | |
| height threshold of line | 0.14 m | |
| deviation | 0.2 m |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, C.; Zhong, X.; Hu, H.; Tian, J.; Peng, X.; Zeng, J. Adaptive Obstacle Detection for Mobile Robots in Urban Environments Using Downward-Looking 2D LiDAR. Sensors 2018, 18, 1749. https://doi.org/10.3390/s18061749
Pang C, Zhong X, Hu H, Tian J, Peng X, Zeng J. Adaptive Obstacle Detection for Mobile Robots in Urban Environments Using Downward-Looking 2D LiDAR. Sensors. 2018; 18(6):1749. https://doi.org/10.3390/s18061749
Chicago/Turabian StylePang, Cong, Xunyu Zhong, Huosheng Hu, Jun Tian, Xiafu Peng, and Jianping Zeng. 2018. "Adaptive Obstacle Detection for Mobile Robots in Urban Environments Using Downward-Looking 2D LiDAR" Sensors 18, no. 6: 1749. https://doi.org/10.3390/s18061749
APA StylePang, C., Zhong, X., Hu, H., Tian, J., Peng, X., & Zeng, J. (2018). Adaptive Obstacle Detection for Mobile Robots in Urban Environments Using Downward-Looking 2D LiDAR. Sensors, 18(6), 1749. https://doi.org/10.3390/s18061749






