Elastic Waves Excitation and Focusing by a Piezoelectric Transducer with Intermediate Layered Elastic Metamaterials with and without Periodic Arrays of Interfacial Voids
Abstract
:1. Introduction
2. Formulation of the Problem
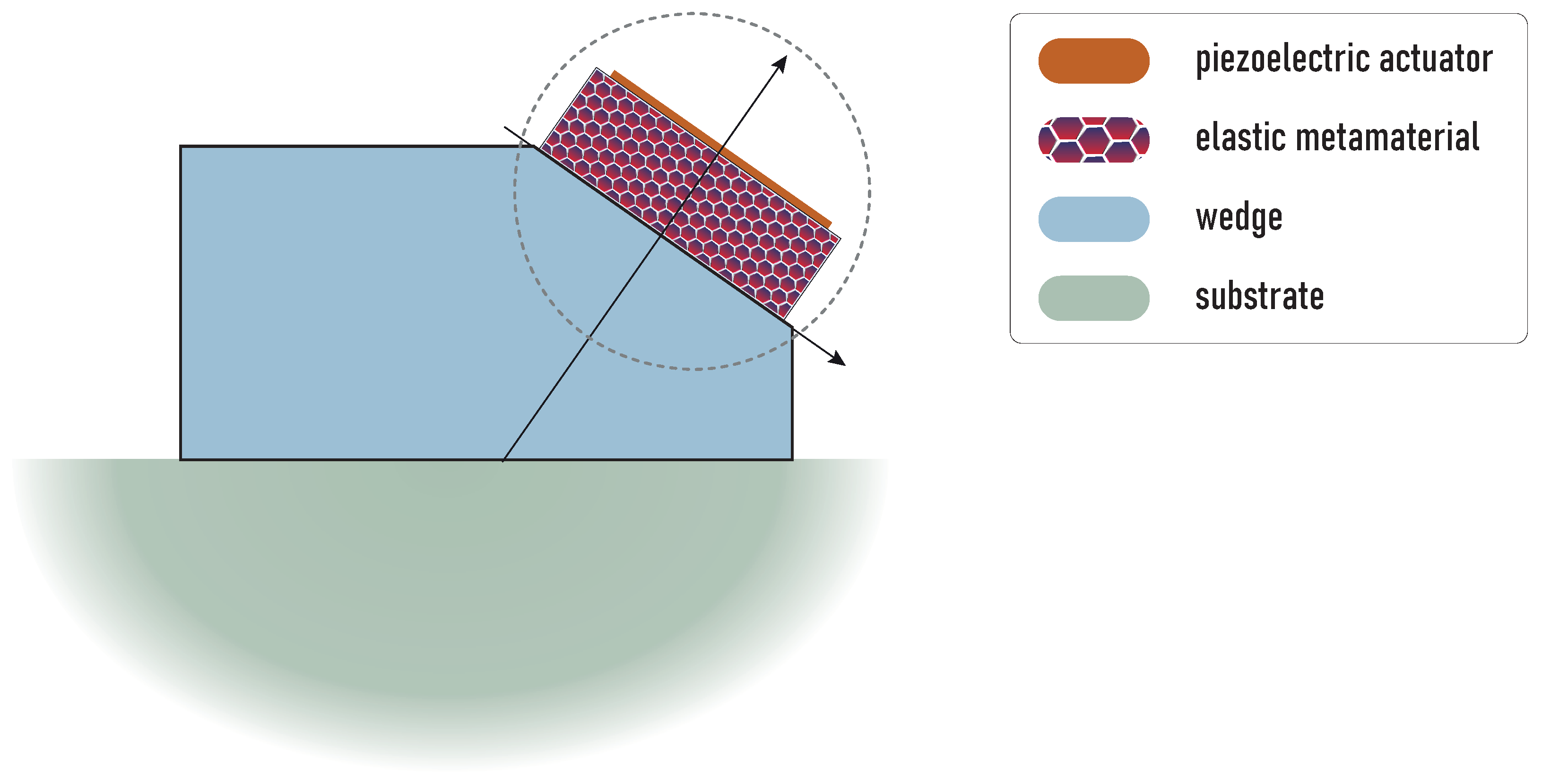
2.1. Aim and Design
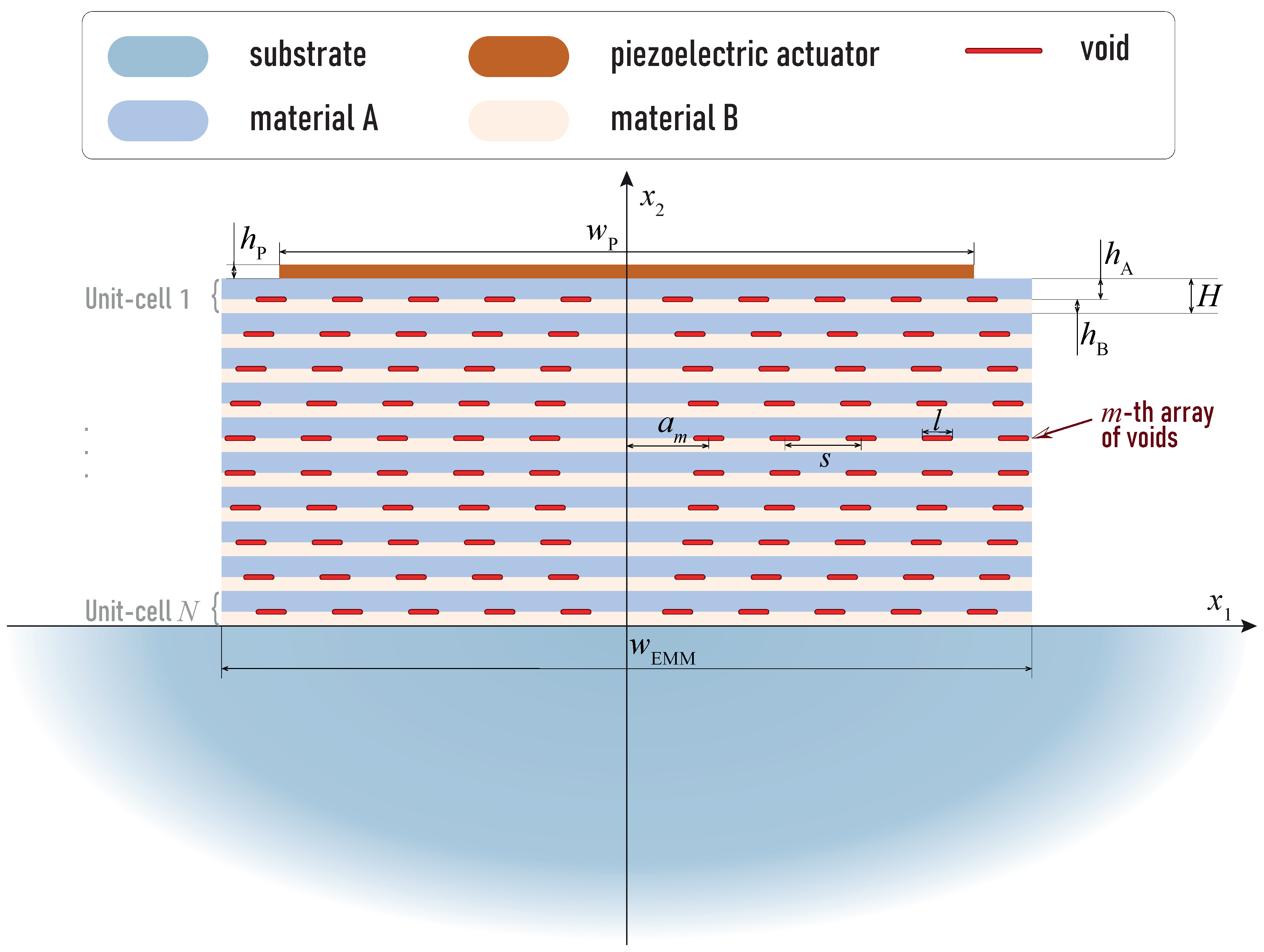
2.2. Mathematical Statement of the Problem
3. Transducer with EMM Intermediate without Voids
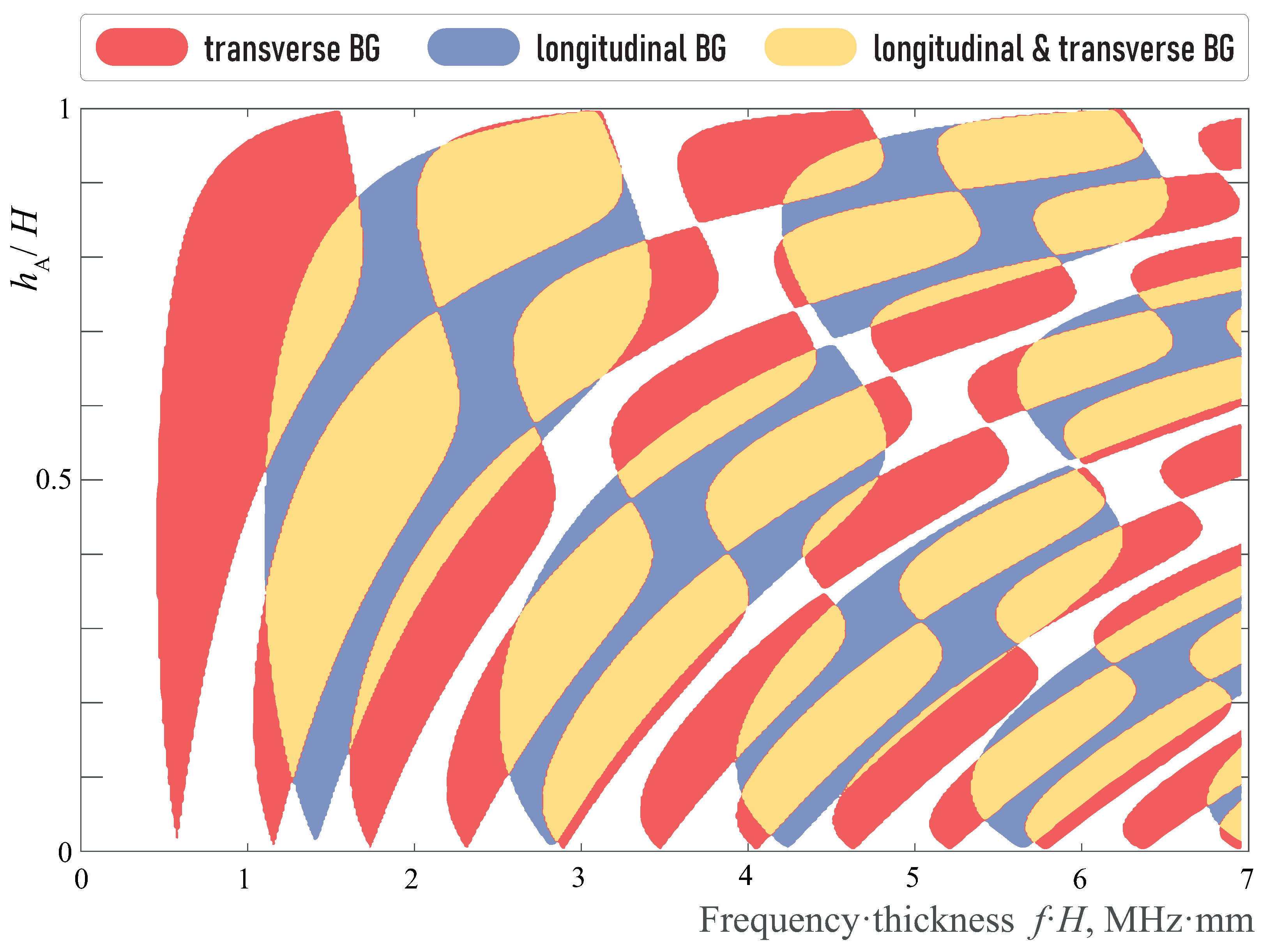
3.1. Plane Wave Propagation through a Periodic Layered Medium
3.1.1. Transfer Matrix Method
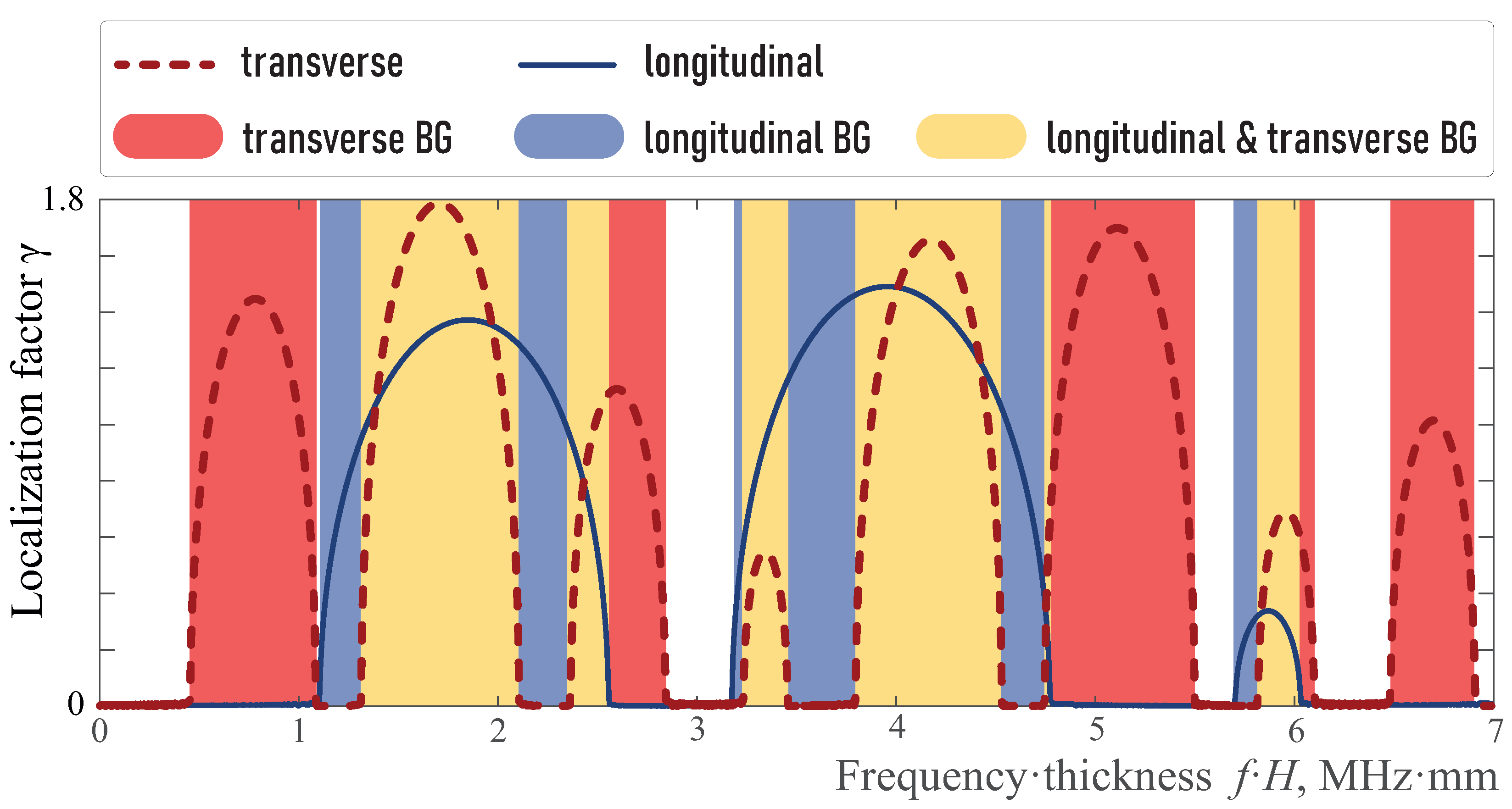
3.1.2. Energy Transmission Coefficient and Localization Factor
3.2. Wave Propagation Excited by Piezoelectric Transducer through a Half-Plane with EMM Layers
3.2.1. Semi-Analytical Hybrid Approach
3.2.2. Wave Energy Flux in Far-Field Zone
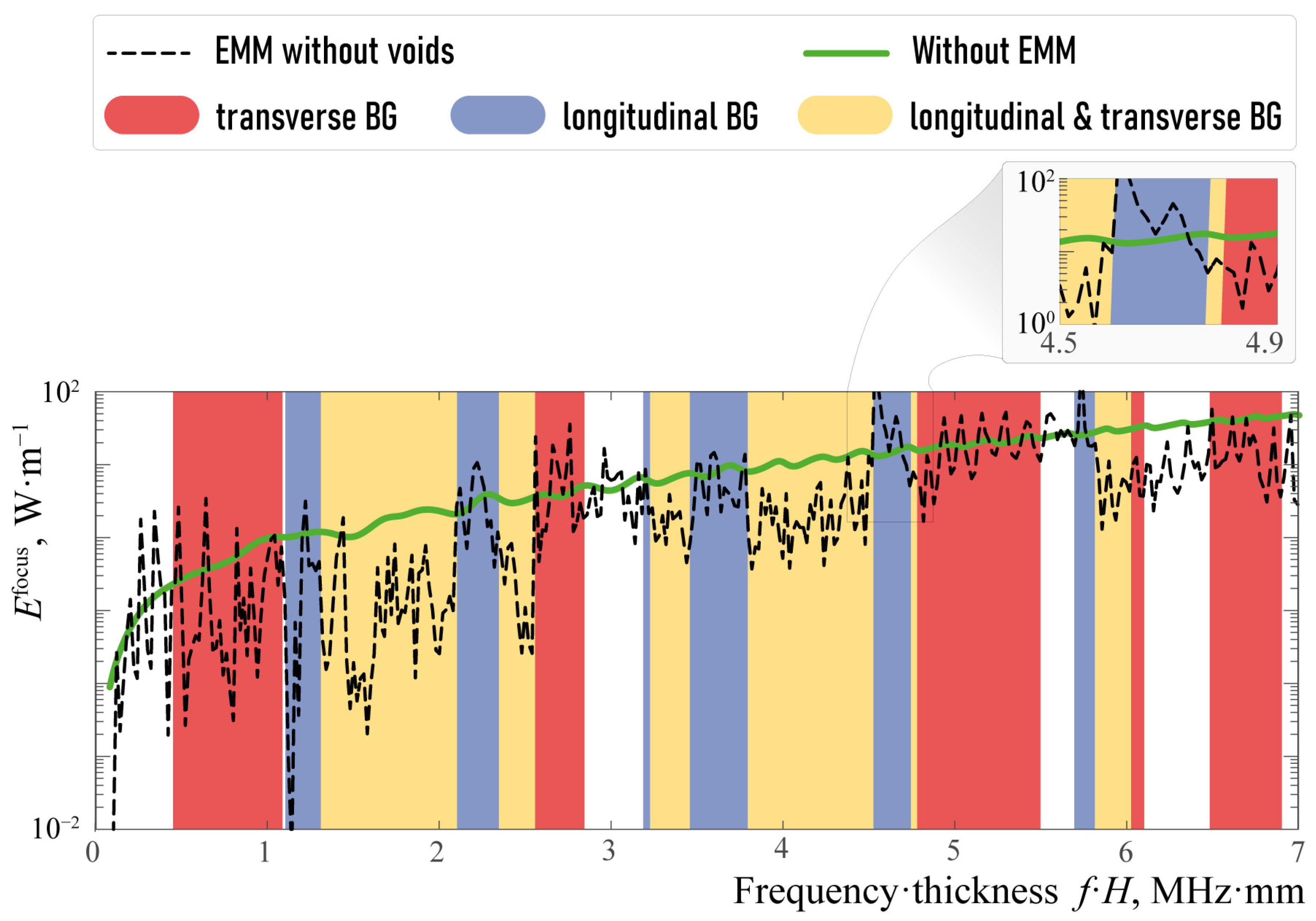
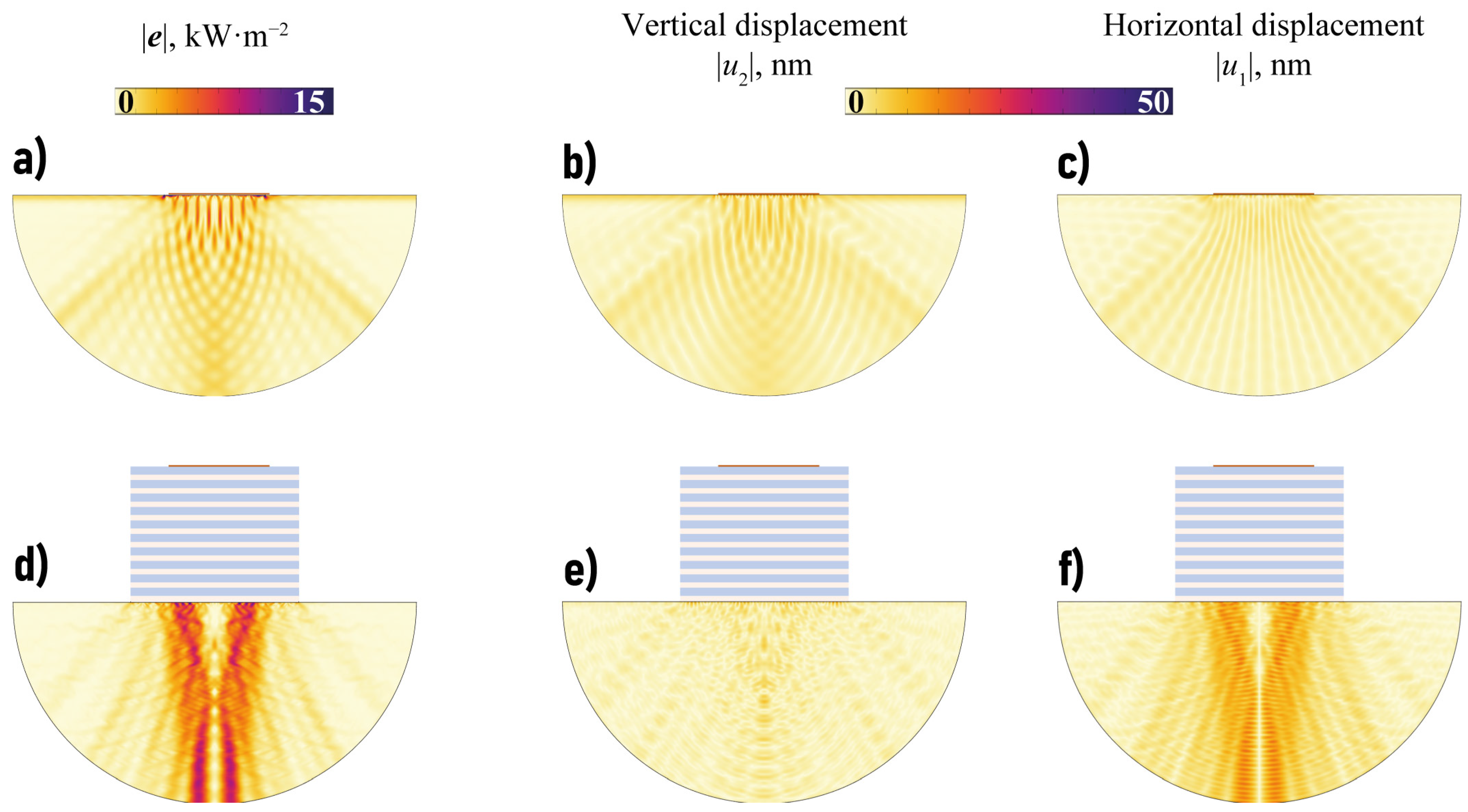
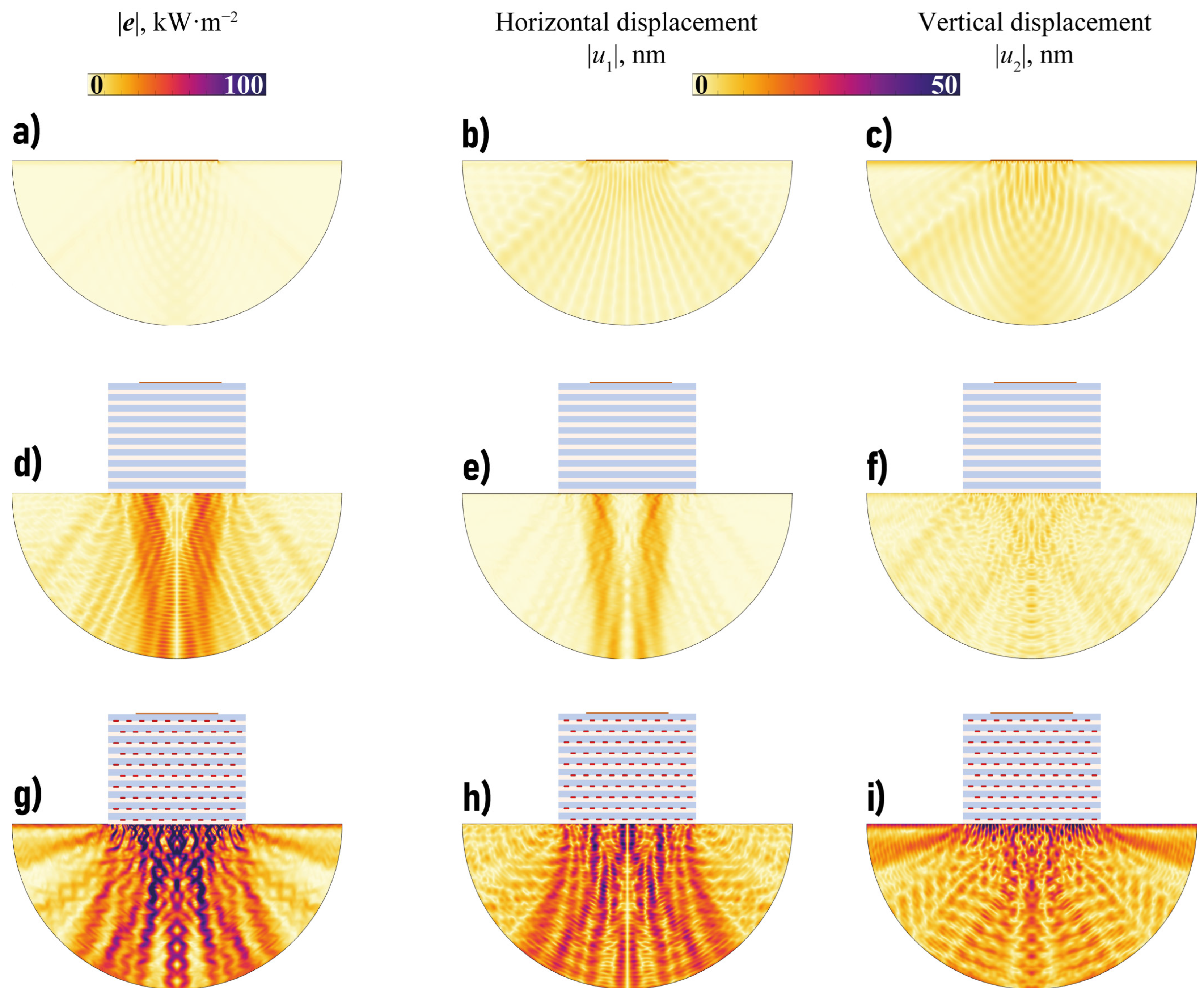
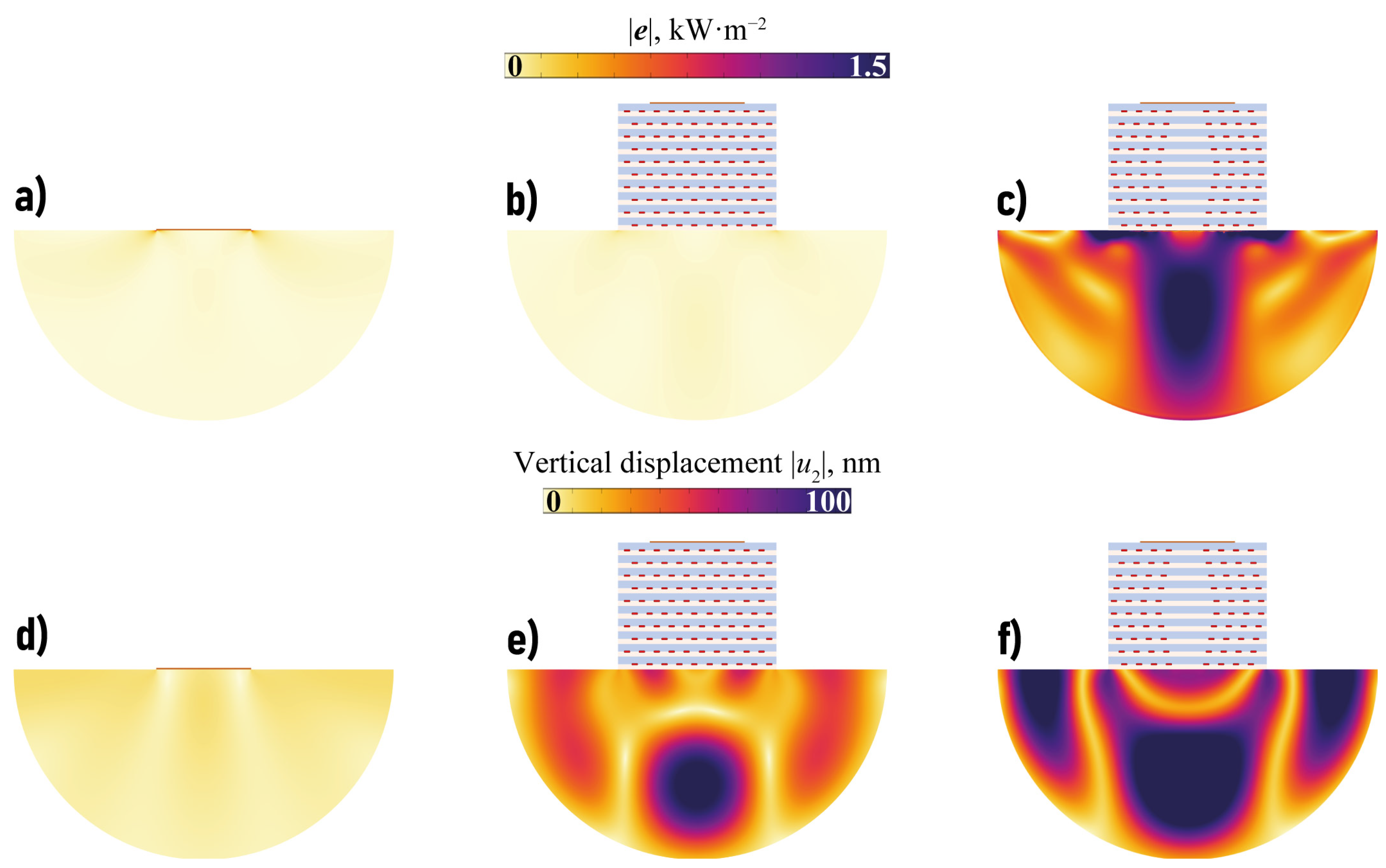
3.3. Analysis of Elastic Wave Energy Flux
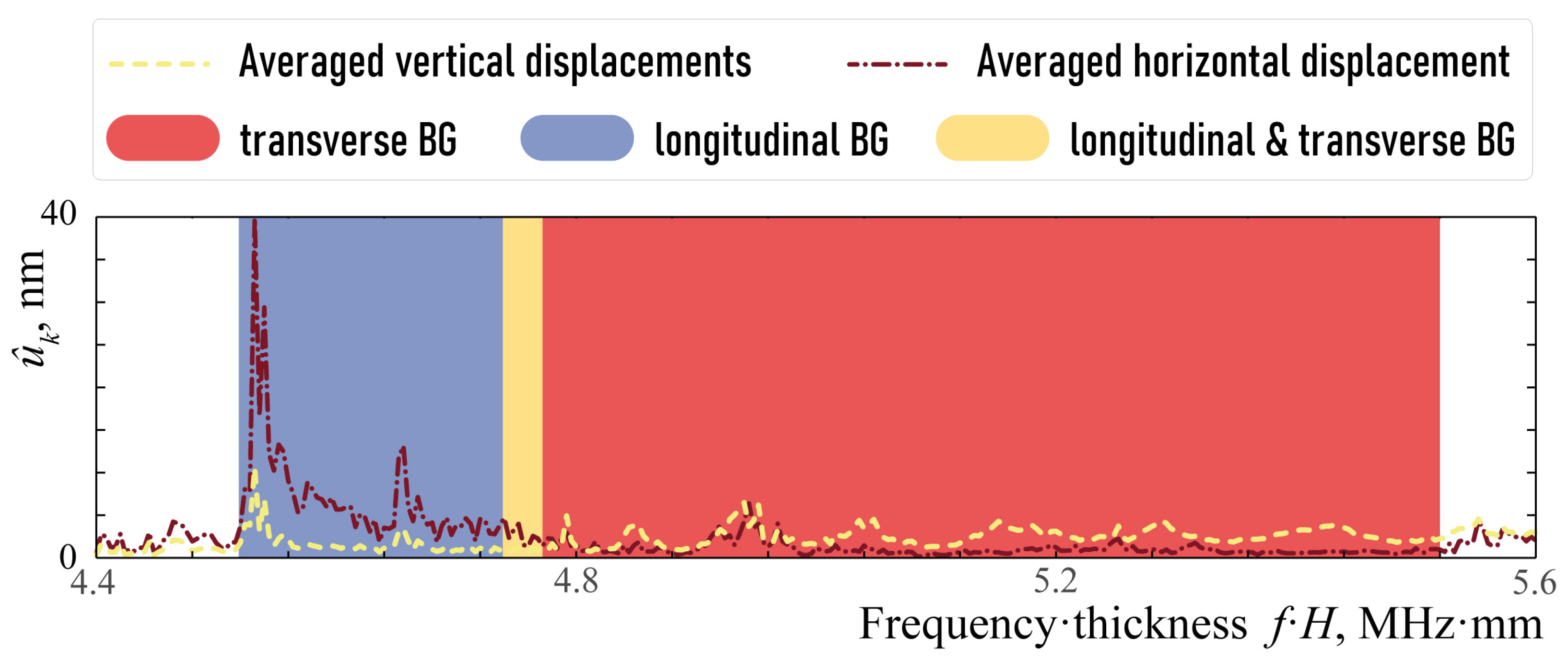
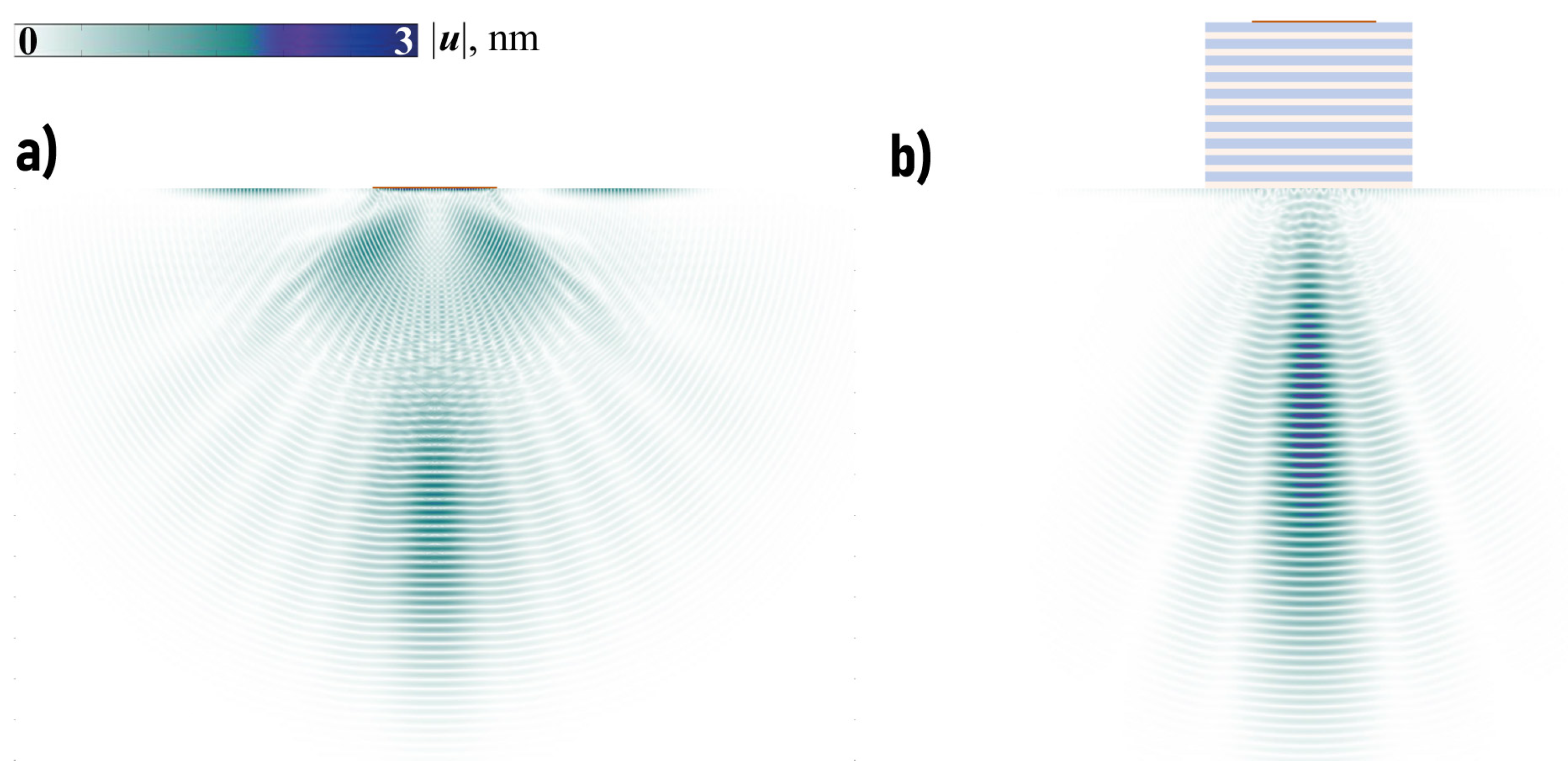
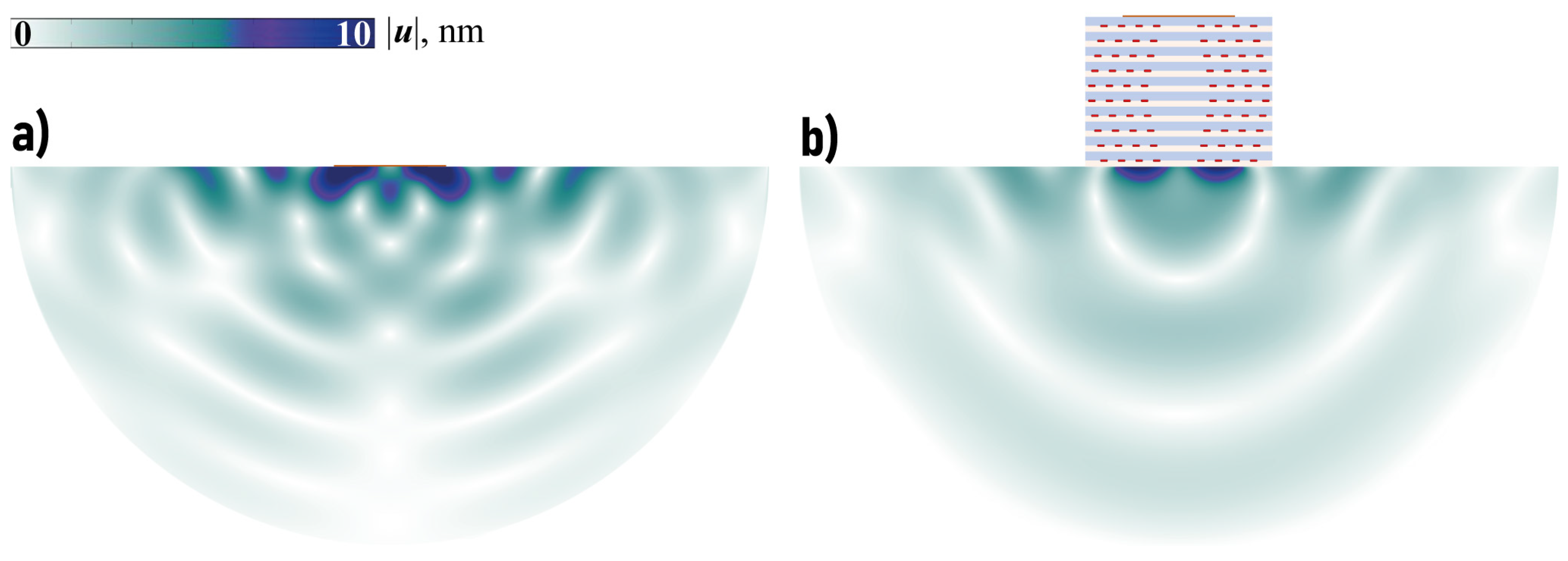
4. Transducer with EMM Intermediate with Arrays of Crack-like Voids
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mueller, I.; Fritzen, C.P. Inspection of Piezoceramic Transducers Used for Structural Health Monitoring. Materials 2017, 10, 71. [Google Scholar] [CrossRef] [PubMed]
- Ono, K.; Cho, H.; Vallen, H.; M’Closkey, R.T. Transmission Sensitivities of Contact Ultrasonic Transducers and Their Applications. Sensors 2021, 21, 4396. [Google Scholar] [CrossRef] [PubMed]
- Lematre, M.; Lethiecq, M. Enhancement of Guided Wave Detection and Measurement in Buried Layers of Multilayered Structures Using a New Design of V(z) Acoustic Transducers. Acoustics 2022, 4, 996–1012. [Google Scholar] [CrossRef]
- Diogo, A.R.; Moreira, B.; Gouveia, C.A.J.; Tavares, J.M.R.S. A Review of Signal Processing Techniques for Ultrasonic Guided Wave Testing. Metals 2022, 12, 936. [Google Scholar] [CrossRef]
- Mueller, I.; Memmolo, V.; Tschöke, K.; Moix-Bonet, M.; Möllenhoff, K.; Golub, M.V.; Venkat, R.S.; Lugovtsova, Y.; Eremin, A.A.; Moll, J. Performance Assessment for a Guided Wave-Based SHM System Applied to a Stiffened Composite Structure. Sensors 2022, 22, 7529. [Google Scholar] [CrossRef]
- Glushkov, E.; Glushkova, N.; Lammering, R.; Eremin, A.; Neumann, M.N. Lamb wave excitation and propagation in elastic plates with surface obstacles: Proper choice of central frequencies. Smart Mater. Struct. 2011, 20, 015020. [Google Scholar] [CrossRef]
- Shpak, A.N.; Mueller, I.; Golub, M.V.; Fritzen, C.P. Theoretical and experimental investigation of Lamb waves excited by partially debonded piezoelectric transducers. Smart Mater. Struct. 2020, 4, 045043. [Google Scholar] [CrossRef]
- Askari, M.; Hutchins, D.A.; Thomas, P.J.; Astolfi, L.; Watson, R.L.; Abdi, M.; Ricci, M.; Laureti, S.; Nie, L.; Freear, S.; et al. Additive manufacturing of metamaterials: A review. Addit. Manuf. 2020, 36, 101562. [Google Scholar] [CrossRef]
- Krushynska, A.O.; Torrent, D.; Aragón, A.M.; Ardito, R.; Bilal, O.R.; Bonello, B.; Bosia, F.; Chen, Y.; Christensen, J.; Colombi, A.; et al. Emerging topics in nanophononics and elastic, acoustic, and mechanical metamaterials: An overview. Nanophotonics 2023, 12, 659–686. [Google Scholar] [CrossRef]
- Kadic, M.; Milton, G.W.; van Hecke, M.; Wegener, M. 3D metamaterials. Nat. Rev. Phys. 2019, 1, 198–210. [Google Scholar] [CrossRef]
- Contreras, N.; Zhang, X.; Hao, H.; Hernandez, F. Application of elastic metamaterials/meta-structures in civil engineering: A review. Compos. Struct. 2024, 327, 117663. [Google Scholar] [CrossRef]
- Sofi, A.; Jane Regita, J.; Rane, B.; Lau, H.H. Structural health monitoring using wireless smart sensor network—An overview. Mech. Syst. Signal Process. 2022, 163, 108113. [Google Scholar] [CrossRef]
- Xiao, H.; Li, T.; Zhang, L.; Liao, W.H.; Tan, T.; Yan, Z. Metamaterial based piezoelectric acoustic energy harvesting: Electromechanical coupled modeling and experimental validation. Mech. Syst. Signal Process. 2023, 185, 109808. [Google Scholar] [CrossRef]
- Liao, G.; Luan, C.; Wang, Z.; Liu, J.; Yao, X.; Fu, J. Acoustic metamaterials: A review of theories, structures, fabrication approaches, and applications. Adv. Mater. Technol. 2021, 6, 2000787. [Google Scholar] [CrossRef]
- Zhang, T.; Mahdi, M.; Issa, M.; Xu, C.; Ozevin, D. Experimental Study on Monitoring Damage Progression of Basalt-FRP Reinforced Concrete Slabs Using Acoustic Emission and Machine Learning. Sensors 2023, 23, 8356. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Yang, D.Q.; Liu, S.L.; Yu, S.Y.; Lu, M.H.; Zhu, J.; Zhang, S.T.; Zhu, M.W.; Guo, X.S.; Wu, H.D.; et al. Broadband gradient impedance matching using an acoustic metamaterial for ultrasonic transducers. Sci. Rep. 2017, 7, 42863. [Google Scholar] [CrossRef] [PubMed]
- Mohammadgholiha, M.; Palermo, A.; Testoni, N.; Moll, J.; De Marchi, L. Finite Element Modeling and Experimental Characterization of Piezoceramic Frequency Steerable Acoustic Transducers. IEEE Sens. J. 2022, 22, 13958–13970. [Google Scholar] [CrossRef]
- Mori, N.; Biwa, S.; Kusaka, T. Damage localization method for plates based on the time reversal of the mode-converted Lamb waves. Ultrasonics 2019, 91, 19–29. [Google Scholar] [CrossRef]
- Piao, C.; Yang, X.; Kweun, J.M.; Kim, H.; Park, H.; Cho, S.H.; Kim, Y.Y. Ultrasonic flow measurement using a high-efficiency longitudinal-to-shear wave mode-converting meta-slab wedge. Sens. Actuators A Phys. 2020, 310, 112080. [Google Scholar] [CrossRef]
- Dong, H.W.; Zhao, S.D.; Oudich, M.; Shen, C.; Zhang, C.; Cheng, L.; Wang, Y.S.; Fang, D. Reflective Metasurfaces with Multiple Elastic Mode Conversions for Broadband Underwater Sound Absorption. Phys. Rev. Appl. 2022, 17. [Google Scholar] [CrossRef]
- Zhu, R.; Liu, X.; Huang, G. Study of anomalous wave propagation and reflection in semi-infinite elastic metamaterials. Wave Motion 2015, 55, 73–83. [Google Scholar] [CrossRef]
- Yang, X.; Chai, Y.; Li, Y. Metamaterial with anisotropic mass density for full mode-converting transmission of elastic waves in the ultralow frequency range. AIP Adv. 2021, 11, 125205. [Google Scholar] [CrossRef]
- Kweun, J.M.; Lee, H.J.; Oh, J.H.; Seung, H.M.; Kim, Y.Y. Transmodal Fabry-Pérot Resonance: Theory and Realization with Elastic Metamaterials. Phys. Rev. Lett. 2017, 118, 205901. [Google Scholar] [CrossRef]
- Yang, X.; Kweun, M.; Kim, Y.Y. Monolayer metamaterial for full mode-converting transmission of elastic waves. Appl. Phys. Lett. 2019, 115, 071901. [Google Scholar] [CrossRef]
- Chai, Y.; Yao, S.; Yang, X.; Li, Y. Asymmetric full mode-converting transmission of elastic waves. New J. Phys. 2023, 25, 053027. [Google Scholar] [CrossRef]
- Chai, Y.; Yang, X.; Li, Y. Full mode-converting transmission between longitudinal and bending waves in plates and beams. J. Sound Vib. 2023, 564, 117890. [Google Scholar] [CrossRef]
- Lee, J.; Kweun, M.; Lee, W.; Park, C.I.; Kim, Y.Y. Perfect transmission of elastic waves obliquely incident at solid-solid interfaces. Extrem. Mech. Lett. 2022, 51, 101606. [Google Scholar] [CrossRef]
- Barakat, M.A.Y. Fabrication of metal–polymer matching layers to improve some ultrasonic transducers for NDT and calibration. J. Mater. Sci. Mater. Electron. 2023, 34, 1–14. [Google Scholar] [CrossRef]
- Glushkov, E.; Glushkova, N.; Golub, M.; Eremin, A. Resonance blocking and passing effects in two-dimensional elastic waveguides with obstacles. J. Acoust. Soc. Am. 2011, 130, 113–121. [Google Scholar] [CrossRef]
- Šofer, M. Resonance phenomena of Lamb waves scattering by a horizontal crack of finite length. J. Sound Vib. 2021, 490, 115742. [Google Scholar] [CrossRef]
- Golub, M.V.; Doroshenko, O.V.; Fomenko, S.I.; Wang, Y.; Zhang, C. Elastic wave propagation, scattering and localization in layered phononic crystals with arrays of strip-like cracks. Int. J. Solids Struct. 2021, 212, 1–22. [Google Scholar] [CrossRef]
- Babeshko, V.; Glushkov, E.; Glushkova, N. Methods of constructing Green’s matrix of a stratified elastic half-space. USSR Comput. Math. Math. Phys. 1987, 27, 60–65. [Google Scholar] [CrossRef]
- Fomenko, S.I.; Golub, M.V.; Doroshenko, O.V.; Wang, Y.; Zhang, C. An advanced boundary integral equation method for wave propagation analysis in a layered piezoelectric phononic crystal with a crack or an electrode. J. Comput. Phys. 2021, 447, 110669. [Google Scholar] [CrossRef]
- Golub, M.V.; Shpak, A.N. Semi-analytical hybrid approach for the simulation of layered waveguide with a partially debonded piezoelectric structure. Appl. Math. Model. 2019, 65, 234–255. [Google Scholar] [CrossRef]
- Golub, M.; Fomenko, S.; Shpak, A.; Gu, Y.; Wang, Y.; Zhang, C. Semi-analytical hybrid approach for modelling guided wave-based SHM system for a laminate with multiple delaminations and surface-mounted inhomogeneities. Appl. Math. Model. 2023, 120, 812–832. [Google Scholar] [CrossRef]
- Sveshnikov, A.G. The limit absorption principle for a waveguide. Dokl. Akad. Nauk USSR 1951, 80, 345–347. [Google Scholar]
- Achenbach, J.D. Wave Propagation in Elastic Solids; North-Holland Publishing Company: Amsterdam, The Netherlands; London, UK, 1973; p. 440. [Google Scholar]
- Auld, B.A. Acoustic Fields and Waves in Solids; Wiley: New York, NY, USA, 1973; p. 431. [Google Scholar]
- Rupitsch, S.J.; Ilg, J. Complete characterization of piezoceramic materials by means of two block-shaped test samples. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 1403–1413. [Google Scholar] [CrossRef]
- Chen, A.L.; Wang, Y.S. Study on band gaps of elastic waves propagating in one-dimensional disordered phononic crystals. Phys. B Condens. Matter. 2007, 392, 369–378. [Google Scholar] [CrossRef]
- Fomenko, S.I.; Golub, M.V.; Bui, T.Q.; Zhang, C.; Wang, Y.S. In-plane elastic wave propagation and band-gaps in layered functionally graded phononic crystals. Int. J. Solids Struct. 2014, 51, 2491–2503. [Google Scholar] [CrossRef]
- Fomenko, S.I.; Golub, M.V.; Chen, A.; Wang, Y.; Zhang, C. Band-gap and pass-band classification for oblique waves propagating in a three-dimensional layered functionally graded piezoelectric phononic crystal. J. Sound Vib. 2019, 439, 219–240. [Google Scholar] [CrossRef]
- Kiselev, A. Energy flux of elastic waves. J. Sov. Math. 1982, 19, 1372–1375. [Google Scholar] [CrossRef]
- Glushkov, E.V. Energy distribution of a surface source in an inhomogeneous half-space. J. Appl. Math. Mech. 1984, 47, 70–75. [Google Scholar] [CrossRef]
- Glushkov, E.V.; Glushkova, N.V. Blocking property of energy vortices in elastic waveguides. J. Acoust. Soc. Am. 1997, 102, 1356–1360. [Google Scholar] [CrossRef]
- Glushkov, E.V.; Glushkova, N.V. On the efficient implementation of the integral equation method in elastodynamics. J. Comput. Acoust. 2001, 9, 889–898. [Google Scholar] [CrossRef]
- Sidorov, Y.V.; Fedoryuk, M.V.; Shabunin, M.I. Lectures on the Theory of Functions of a Complex Variable; Mir Publishers: Moscow, Russia, 1985. [Google Scholar]
- Glushkov, E.; Glushkova, N.; Fomenko, S. Wave energy transfer in elastic half-spaces with soft interlayers. J. Acoust. Soc. Am. 2015, 137, 1802–1812. [Google Scholar] [CrossRef]


| Material | Elastic Constants | Piezoelectric Constants | Dielectric Constants | Density [kg/m3] |
|---|---|---|---|---|
| [GPa] | [C/m2] | 10−9[F/m] | ||
| Aluminium | — | — | 2700 | |
| (Material A) | ||||
| Epoxy | — | — | 1200 | |
| (Material B) | ||||
| PIC155 | 7800 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Golub, M.V.; Fomenko, S.I.; Usov, P.E.; Eremin, A.A. Elastic Waves Excitation and Focusing by a Piezoelectric Transducer with Intermediate Layered Elastic Metamaterials with and without Periodic Arrays of Interfacial Voids. Sensors 2023, 23, 9747. https://doi.org/10.3390/s23249747
Golub MV, Fomenko SI, Usov PE, Eremin AA. Elastic Waves Excitation and Focusing by a Piezoelectric Transducer with Intermediate Layered Elastic Metamaterials with and without Periodic Arrays of Interfacial Voids. Sensors. 2023; 23(24):9747. https://doi.org/10.3390/s23249747
Chicago/Turabian StyleGolub, Mikhail V., Sergey I. Fomenko, Pavel E. Usov, and Artem A. Eremin. 2023. "Elastic Waves Excitation and Focusing by a Piezoelectric Transducer with Intermediate Layered Elastic Metamaterials with and without Periodic Arrays of Interfacial Voids" Sensors 23, no. 24: 9747. https://doi.org/10.3390/s23249747






