Implementing Intraday Model-Free Implied Volatility for Individual Equities to Analyze the Return–Volatility Relationship
Abstract
:1. Introduction
2. The VIX Methodology
3. Implementing Model-Free Implied Volatility for Individual Equities
3.1. Data and Data Processing
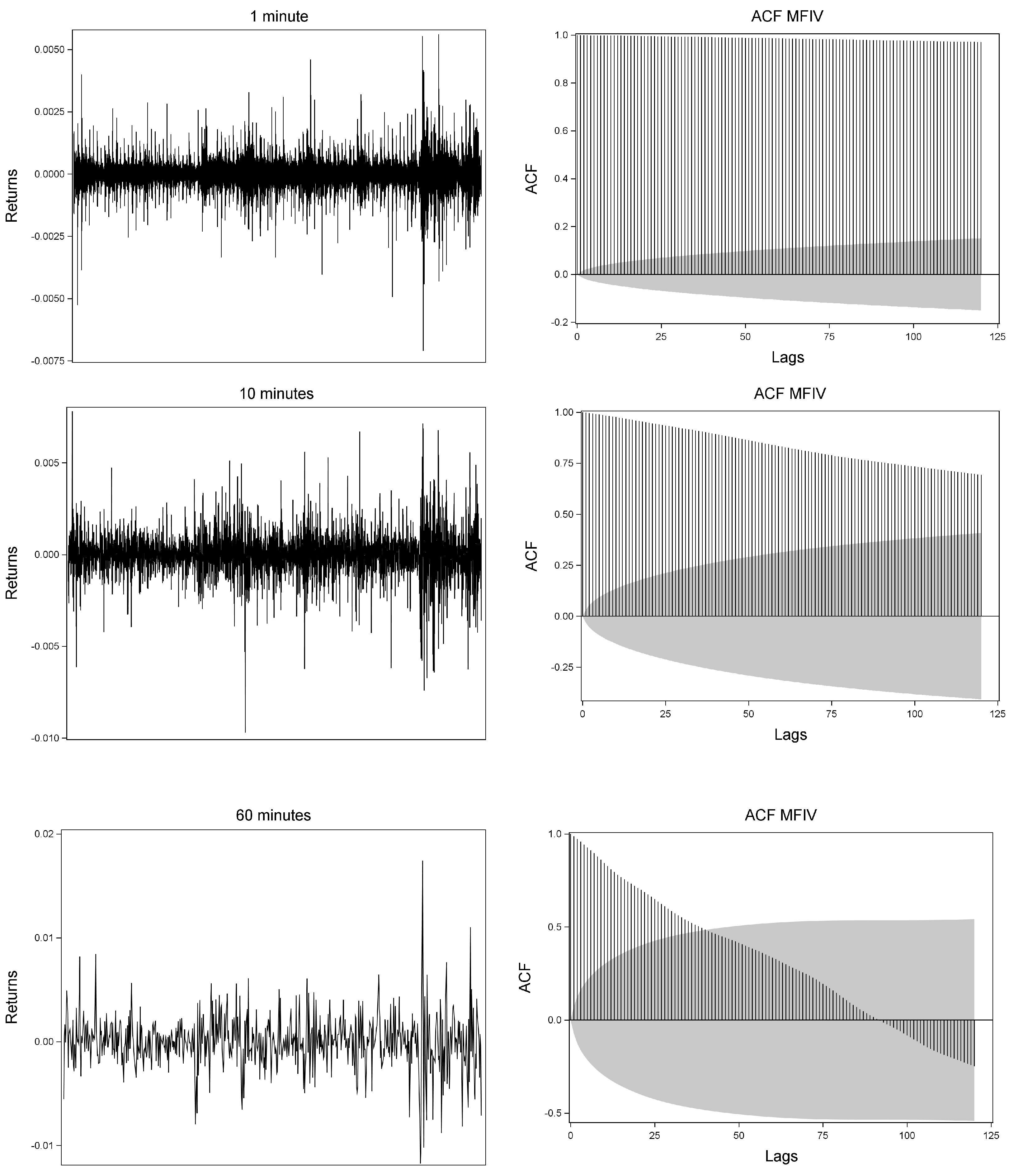
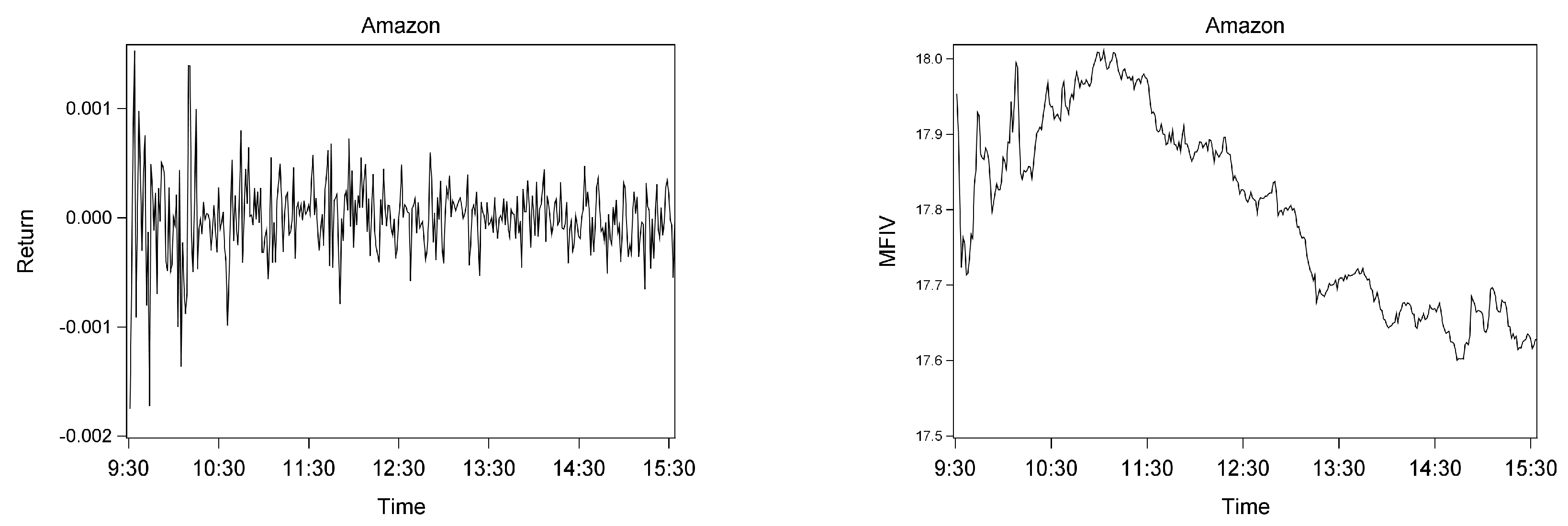
3.2. Descriptive Analyses on Model-Free Implied Volatility for Individual Equities
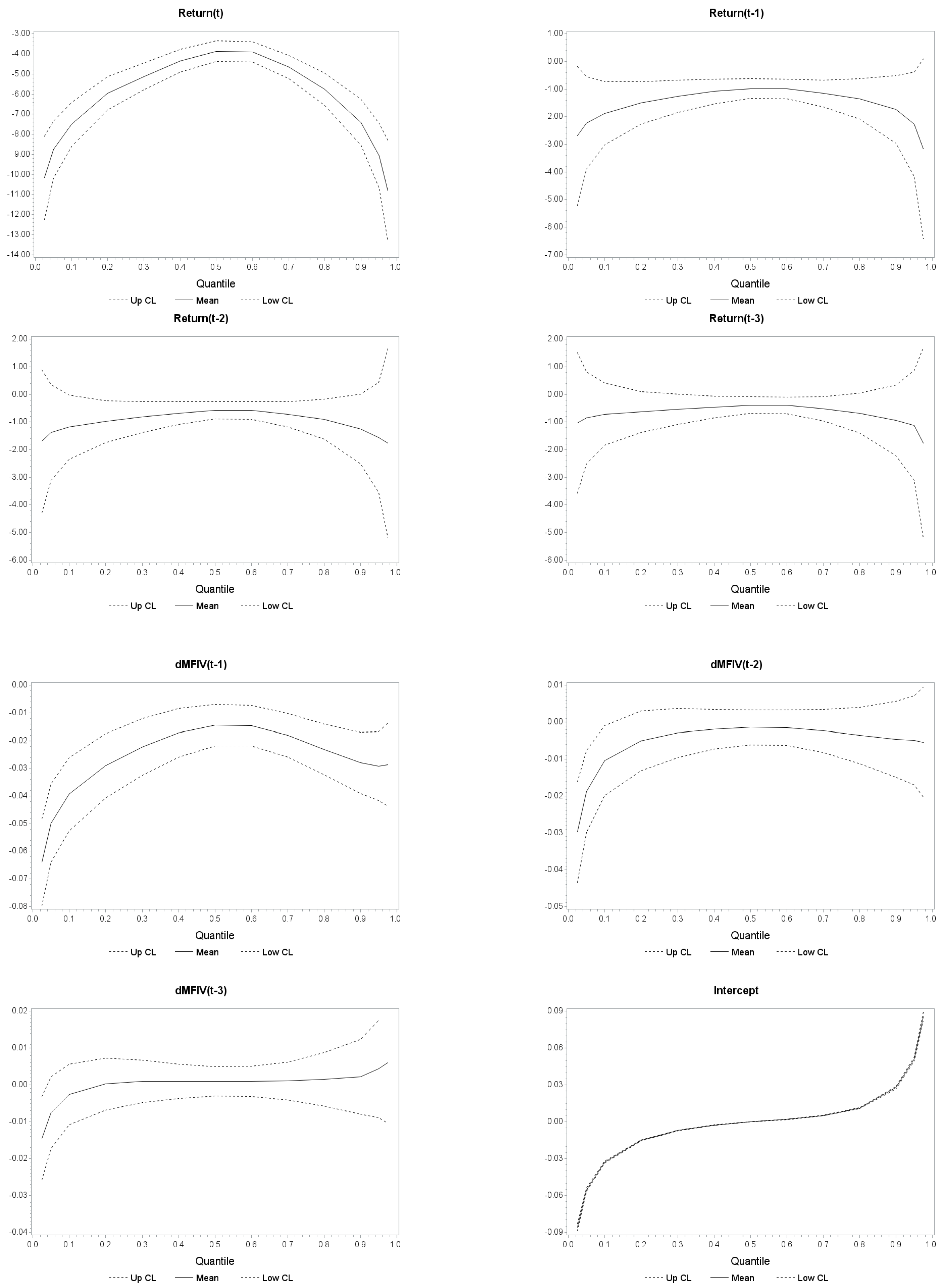
4. Analyzing the Intraday Return–Volatility Relationship
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of Model-Free Implied Volatility
Ito’s Lemma for ln(St)
Appendix B. Additional Figures and Tables


| 0.025 | 0.05 | 0.10 | 0.25 | 0.50 | 0.75 | 0.90 | 0.95 | 0.975 | |
|---|---|---|---|---|---|---|---|---|---|
| −13.764 | −11.538 | −9.993 | −9.201 | −9.043 | −9.732 | −10.825 | −12.316 | −14.233 | |
| (104/18) | (105/17) | (110/12) | (109/13) | (109/13) | (110/11) | (108/14) | (107/15) | (104/18) | |
| −1.470 | −1.253 | −1.015 | −0.988 | −0.958 | −1.154 | −1.926 | −2.195 | −3.723 | |
| (87/35) | (92/31) | (93/28) | (93/29) | (94/28) | (97/25) | (94/28) | (94/28) | (92/30) | |
| −0.438 | −0.532 | −0.365 | −0.182 | −0.165 | −0.364 | −0.763 | −1.368 | −2.889 | |
| (79/43) | (81/41) | (77/45) | (67/55) | (71/51) | (79/43) | (88/34) | (85/37) | (93/29) | |
| −0.202 | −0.552 | −0.356 | −0.188 | −0.228 | −0.323 | −0.695 | −1.203 | −1.550 | |
| (66/56) | (78/44) | (78/44) | (77/44) | (74/44) | (70/52) | (78/44) | (80/42) | (82/40) | |
| −0.12 | −0.09 | −0.07 | −0.05 | −0.03 | −0.03 | −0.05 | −0.09 | −0.15 | |
| (101/21) | (103/19) | (105/17) | (100/22) | (91/31) | (93/29) | (94/28) | (90/32) | (85/37) | |
| −0.063 | −0.041 | −0.029 | −0.016 | −0.009 | −0.009 | −0.020 | −0.040 | −0.071 | |
| (89/33) | (91/31) | (91/31) | (90/32) | (81/41) | (75/41) | (90/32) | (84/38) | (77/45) | |
| −0.025 | −0.017 | −0.012 | −0.005 | 0.000 | 0.000 | −0.004 | −0.013 | −0.032 | |
| (89/33) | (87/35) | (83/39) | (83/39) | (79/43) | (74/48) | (81/41) | (76/46) | (74/48) | |
| constant | −0.380 | −0.227 | −0.135 | −0.056 | −0.006 | 0.038 | 0.132 | 0.268 | 0.503 |
| (122/0) | (122/0) | (122/0) | (122/0) | (108/4) | (0/122) | (0/122) | (0/122) | (0/122) |
| 0.025 | 0.05 | 0.10 | 0.25 | 0.50 | 0.75 | 0.90 | 0.95 | 0.975 | |
|---|---|---|---|---|---|---|---|---|---|
| −13.764 | −11.538 | −9.993 | −9.201 | −9.043 | −9.732 | −10.825 | −12.316 | −14.233 | |
| (104/18) | (105/17) | (110/12) | (109/13) | (109/13) | (110/11) | (108/14) | (107/15) | (104/18) | |
| −1.470 | −1.253 | −1.015 | −0.988 | −0.958 | −1.154 | −1.926 | −2.195 | −3.723 | |
| (87/35) | (92/31) | (93/28) | (93/29) | (94/28) | (97/25) | (94/28) | (94/28) | (92/30) | |
| −0.438 | −0.532 | −0.365 | −0.182 | −0.165 | −0.364 | −0.763 | −1.368 | −2.889 | |
| (79/43) | (81/41) | (77/45) | (67/55) | (71/51) | (79/43) | (88/34) | (85/37) | (93/29) | |
| −0.202 | −0.552 | −0.356 | −0.188 | −0.228 | −0.323 | −0.695 | −1.203 | −1.550 | |
| (66/56) | (78/44) | (78/44) | (77/44) | (74/44) | (70/52) | (78/44) | (80/42) | (82/40) | |
| −0.12 | −0.09 | −0.07 | −0.05 | −0.03 | −0.03 | −0.05 | −0.09 | −0.15 | |
| (101/21) | (103/19) | (105/17) | (100/22) | (91/31) | (93/29) | (94/28) | (90/32) | (85/37) | |
| −0.063 | −0.041 | −0.029 | −0.016 | −0.009 | −0.009 | −0.020 | −0.040 | −0.071 | |
| (89/33) | (91/31) | (91/31) | (90/32) | (81/41) | (75/41) | (90/32) | (84/38) | (77/45) | |
| −0.025 | −0.017 | −0.012 | −0.005 | 0.000 | 0.000 | −0.004 | −0.013 | −0.032 | |
| (89/33) | (87/35) | (83/39) | (83/39) | (79/43) | (74/48) | (81/41) | (76/46) | (74/48) | |
| constant | −0.380 | −0.227 | −0.135 | −0.056 | −0.006 | 0.038 | 0.132 | 0.268 | 0.503 |
| (122/0) | (122/0) | (122/0) | (122/0) | (108/4) | (0/122) | (0/122) | (0/122) | (0/122) |
| 1 | We developed an R package for these calculations, which is currently available on https://github.com/m-g-h/R.MFIV, accessed on 20 November 2023. |
| 2 | Critically assessed, the notion of “model-freeness” is not entirely correct since an assumption about the underlying price process is still made. However, no option pricing model is required, which frees the IV from limitations due to potentially unrealistic model assumptions. |
| 3 | i.e., multiples of , with the ATM Black & Scholes IV and the time to maturity. |
| 4 | The VIX method is derived for European-style options only. Individual equity options, however, are American-style options and may be subject to an early exercise premium. As this premium can be assumed to be relatively small for out-of-the-money options and since we do not want to rely on a specific option pricing model for estimation, we do not account for it. |
| 5 | Jarque-Bera tests indicate the rejection of a normal distribution for all individual equity MFIVs. Detailed results are available upon request. |
| 6 | Compare Dennis et al. (2006), Fleming et al. (1995), Giot (2005), Hibbert et al. (2008), Carr and Wu (2017), and Talukdar et al. (2017). |
| 7 | |
| 8 | |
| 9 | Among others outlined by Hibbert et al. (2008) and Daigler et al. (2014), investors may view a high return and low risk (decreasing volatility) as representative of a good investment. Combined with an affect heuristic, where investors’ decisions may be governed or at least affected by intuition and instincts, they may act on the negative returns and high volatility, which are both negatively labeled and thereby cause a negative return–volatility relationship. |
References
- Agbeyegbe, Terence D. 2016. Modeling US stock market volatility-return dependence using conditional copula and quantile regression. Studies in Economic Theory 29: 597–621. [Google Scholar] [CrossRef]
- Andersen, Torben G., Oleg Bondarenko, and Maria T. Gonzalez-Perez. 2015. Exploring return dynamics via corridor implied volatility. The Review of Financial Studies 28: 2902–45. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Heiko Ebens. 2001. The distribution of realized stockrreturn volatility. Journal of Financial Economics 61: 43–76. [Google Scholar] [CrossRef]
- Andersen, Torben, Ilya Archakov, Leon Grund, Nikolaus Hautsch, Yifan Li, Sergey Nasekin, Ingmar Nolte, Manh Cuong Pham, Stephen Taylor, and Viktor Todorov. 2021. A Descriptive Study of High-Frequency Trade and Quote Option Data*. Journal of Financial Econometrics 19: 128–77. [Google Scholar] [CrossRef]
- Badshah, Ihsan Ullah. 2013. Quantile regression analysis of the asymmetric return-volatility relation: Quantile regression analysis. Journal of Futures Markets 33: 235–65. [Google Scholar] [CrossRef]
- Badshah, Ihsan, Bart Frijns, Johan Knif, and Alireza Tourani-Rad. 2016. Asymmetries of the intraday return-volatility relation. International Review of Financial Analysis 48: 182–92. [Google Scholar] [CrossRef]
- Bekaert, Geert, and Guojun Wu. 2000. Asymmetric Volatility and Risk in Equity Markets. The Review of Financial Studies 13: 1–42. [Google Scholar] [CrossRef]
- Bekiros, Stelios, Mouna Jlassi, Kamel Naoui, and Gazi Uddin. 2017. The asymmetric relationship between returns and implied volatility: Evidence from global stock markets. Journal of Financial Stability 30: 156–74. [Google Scholar]
- Black, Fischer. 1976. Studies of Stock Market Volatility Changes. Irvine: Scientific Research Publishing Inc., pp. 177–81. [Google Scholar]
- Black, Fischer, and Myron Scholes. 1973. The pricing of options and corporate liabilities. Journal of Political Economy 81: 637–54. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Julia Litvinova, and George Tauchen. 2006. Leverage and Volatility Feedback Effects in High-Frequency Data. Journal of Financial Econometrics 4: 353–84. [Google Scholar] [CrossRef]
- Breeden, Douglas T., and Robert H. Litzenberger. 1978. Prices of state-contingent claims implicit in option prices. Journal of Business 51: 621–51. [Google Scholar]
- Britten-Jones, Mark, and Anthony Neuberger. 2000. Option prices, implied price processes, and stochastic volatility. The Journal of Finance 55: 839–66. [Google Scholar] [CrossRef]
- Campbell, John Y., and Ludger Hentschel. 1992. No news is good news: An asymmetric model of changing volatility in stock returns. Journal of Financial Economics 31: 281–318. [Google Scholar] [CrossRef]
- Carr, Peter, and Dilip Madan. 1997. Towards a Theory of Volatility Trading. Cambridge: Cambridge University Press. [Google Scholar]
- Carr, Peter, and Liuren Wu. 2017. Leverage effect, volatility feedback, and self-exciting market disruptions. Journal of Financial and Quantitative Analysis 52: 2119–156. [Google Scholar] [CrossRef]
- CBOE. 2023. CBOE VIX Whitepaper. Available online: https://cdn.cboe.com/api/global/us_indices/governance/Volatility_Index_Methodology_Cboe_Volatility_Index.pdf (accessed on 20 November 2023).
- Chen, Jingjing, George J. Jiang, Chaowen Yuan, and Dongming Zhu. 2021. Breaking vix at open: Evidence of uncertainty creation and resolution. Journal of Banking & Finance 124: 106–60. [Google Scholar] [CrossRef]
- Christie, Andrew A. 1982. The stochastic behavior of common stock variances: Value, leverage and interest rate effects. Journal of Financial Economics 10: 407–32. [Google Scholar] [CrossRef]
- Cont, Rama. 2001. Empirical properties of asset returns: Stylized facts and statistical issues. Quantitative Finance 1: 223–36. [Google Scholar] [CrossRef]
- Daigler, Robert T., Ann Marie Hibbert, and Ivelina Pavlova. 2014. Examining the return–volatility relation for foreign exchange: Evidence from the euro vix. Journal of Futures Markets 34: 74–92. [Google Scholar] [CrossRef]
- Demeterfi, Kresimir, Emanuel Derman, Michael Kamal, and Joseph Zou. 1999. A guide to volatility and variance swaps. The Journal of Derivatives 6: 9–32. [Google Scholar] [CrossRef]
- Dennis, Patrick, Stewart Mayhew, and Chris Stivers. 2006. Stock returns, implied volatility innovations, and the asymmetric volatility phenomenon. Journal of Financial and Quantitative Analysis 41: 381–406. [Google Scholar] [CrossRef]
- Fleming, Jeff, Barbara Ostdiek, and Robert E. Whaley. 1995. Predicting stock market volatility: A new measure. Journal of Futures Markets 15: 265–302. [Google Scholar] [CrossRef]
- French, Kenneth R., G. William Schwert, and Robert F. Stambaugh. 1987. Expected stock returns and volatility. Journal of Financial Economics 19: 3–29. [Google Scholar] [CrossRef]
- Giot, Pierre. 2005. Relationships between implied volatility indexes and stock index returns. The Journal of Portfolio Management 31: 92–100. [Google Scholar] [CrossRef]
- Gonzalez-Perez, Maria T. 2015. Model-free volatility indexes in the financial literature: Areview. International Review of Economics & Finance 40: 141–59. [Google Scholar] [CrossRef]
- Green, Richard C., and Robert A. Jarrow. 1987. Spanning and completeness in markets with contingent claims. Journal of Economic Theory 41: 202–10. [Google Scholar] [CrossRef]
- Hibbert, Ann Marie, Robert T. Daigler, and Brice Dupoyet. 2008. A behavioral explanation for the negative asymmetric return–volatility relation. Journal of Banking & Finance 32: 2254–66. [Google Scholar] [CrossRef]
- Ishida, Isao, Michael McAleer, and Kosuke Oya. 2011. Estimating the leverage parameter of continuous-time stochastic volatility models using high frequency s&p 500 and VIX. Managerial Finance 37: 1048–67. [Google Scholar] [CrossRef]
- Jiang, George J., and Yisong S. Tian. 2005. The model-free implied volatility and its information content. The Review of Financial Studies 18: 1305–42. [Google Scholar] [CrossRef]
- Jiang, George J., and Yisong S. Tian. 2007. Extracting model-free volatility from option prices: An examination of the VIX index. The Journal of Derivatives 14: 35–60. [Google Scholar] [CrossRef]
- Kahneman, Daniel, and Amos Tversky. 2013. Prospect theory: An analysis of decision under risk. In Handbook of the Fundamentals of Financial Decision Making. Singapore: World Scientific Publishing, pp. 99–127. [Google Scholar] [CrossRef]
- Kalnina, Ilze, and Dacheng Xiu. 2017. Nonparametric estimation of the leverage effect: A trade-off between robustness and efficiency. Journal of the American Statistical Association 112: 384–96. [Google Scholar] [CrossRef]
- Koenker, Roger, and Gilbert Bassett. 1978. Regression quantiles. Econometrica 46: 33–50. [Google Scholar] [CrossRef]
- Latané, Henry A., and Richard J. Rendleman. 1976. Standard deviations of stock price ratios implied in option prices. The Journal of Finance 31: 369–81. [Google Scholar] [CrossRef]
- Nachman, David C. 1988. Spanning and completeness with options. The Review of Financial Studies 1: 311–28. [Google Scholar] [CrossRef]
- Poon, Ser-Huang, and Clive W. J. Granger. 2003. Forecasting volatility in financial markets: A review. Journal of Economic Literature 41: 478–539. [Google Scholar] [CrossRef]
- Talukdar, Bakhtear, Robert T. Daigler, and A. M. Parhizgari. 2017. Expanding the explanations for the return–volatility relation. Journal of Futures Markets 37: 689–716. [Google Scholar] [CrossRef]
- Taylor, Stephen J., Pradeep K. Yadav, and Yuanyuan Zhang. 2010. The information content of implied vlatilities and model-free volatility expectations: Evidence from options written on individual stocks. Journal of Banking & Finance 34: 871–81. [Google Scholar] [CrossRef]
- Whaley, Robert E. 1993. Derivatives on market volatility: Hedging tools long overdue. The Journal of Derivatives Fall 1: 71–84. [Google Scholar] [CrossRef]
- Whaley, Robert E. 2000. The investor fear gauge. The Journal of Portfolio Management 26: 12–17. [Google Scholar] [CrossRef]


| Size | MC | Calls | Puts | Max K | Min K | dK | n | P | R | R (sd) | MFIV |
|---|---|---|---|---|---|---|---|---|---|---|---|
| WK Set | |||||||||||
| Any | 101,337 | 11.0 | 13.8 | 1.75 | 2.31 | 0.274 | 178 | 104.37 | 0.0008 | 26.82 | |
| Mega | 485,985 | 11.4 | 18.1 | 1.93 | 3.11 | 0.337 | 21 | 205.50 | 0.0005 | 17.84 | |
| Large | 65,180 | 11.2 | 14.0 | 1.77 | 2.34 | 0.275 | 117 | 105.33 | 0.0008 | 25.08 | |
| Medium | 5692 | 10.0 | 11.0 | 1.61 | 1.82 | 0.237 | 33 | 51.52 | 0.0010 | 36.38 | |
| Small | 1359 | 10.8 | 9.8 | 1.65 | 1.67 | 0.238 | 7 | 34.04 | 0.0012 | 37.73 | |
| MN Set | |||||||||||
| Any | 101,337 | 8.2 | 10.1 | 2.06 | 2.74 | 0.436 | 178 | 104.37 | 0.0008 | 27.02 | |
| Mega | 485,985 | 9.1 | 14.4 | 2.30 | 3.84 | 0.539 | 21 | 205.50 | 0.0005 | 18.15 | |
| Large | 65,180 | 8.1 | 9.9 | 2.06 | 2.78 | 0.447 | 117 | 105.33 | 0.0008 | 25.34 | |
| Medium | 5692 | 8.0 | 8.4 | 1.93 | 2.11 | 0.344 | 33 | 51.52 | 0.0010 | 36.40 | |
| Small | 1359 | 8.1 | 6.7 | 1.92 | 1.84 | 0.374 | 7 | 34.04 | 0.0012 | 37.50 | |
| SP Set | |||||||||||
| Any | 101,337 | 9.0 | 11.8 | 3.27 | 3.80 | 0.349 | 178 | 104.37 | 0.0008 | 26.97 | |
| Mega | 485,985 | 9.6 | 16.4 | 3.86 | 5.34 | 0.407 | 21 | 205.50 | 0.0005 | 18.05 | |
| Large | 65,180 | 8.8 | 11.8 | 3.28 | 3.90 | 0.357 | 117 | 105.33 | 0.0008 | 25.28 | |
| Medium | 5692 | 9.2 | 9.8 | 2.90 | 2.74 | 0.290 | 33 | 51.52 | 0.0010 | 36.39 | |
| Small | 1359 | 7.5 | 3.02 | 2.43 | 0.321 | 7 | 34.04 | 0.0012 | 37.51 | ||
| Mean | Std. Dev. | Min | Max | Skewness | Kurtosis | |
|---|---|---|---|---|---|---|
| All | ||||||
| MFIV (MN) | 25.33 | 9.59 | 9.02 | 88.94 | 1.57 | 3.19 |
| MFIV (WK) | 25.03 | 9.74 | 9.71 | 86.82 | 1.58 | 3.33 |
| MFIV (SP) | 25.26 | 9.65 | 8.23 | 92.18 | 1.57 | 3.19 |
| Mega | ||||||
| MFIV (MN) | 22.50 | 7.35 | 9.02 | 88.94 | 2.27 | 9.18 |
| MFIV (WK) | 22.17 | 7.51 | 9.71 | 82.78 | 2.27 | 9.06 |
| MFIV (SP) | 22.42 | 7.38 | 8.23 | 92.18 | 2.24 | 8.95 |
| Large | ||||||
| MFIV (MN) | 33.00 | 7.37 | 13.88 | 68.63 | 0.63 | 0.58 |
| MFIV (WK) | 32.71 | 7.13 | 14.33 | 74.64 | 0.68 | 1.02 |
| MFIV (SP) | 32.95 | 7.45 | 17.60 | 65.08 | 0.73 | 0.88 |
| Medium | ||||||
| MFIV (MN) | 43.82 | 12.13 | 20.86 | 86.57 | 0.08 | −0.91 |
| MFIV (WK) | 43.93 | 12.43 | 21.44 | 86.82 | 0.17 | −0.75 |
| MFIV (SP) | 43.89 | 12.21 | 21.63 | 87.26 | 0.09 | −0.91 |
| Small | ||||||
| MFIV (MN) | 36.82 | 5.27 | 29.26 | 60.25 | 0.96 | 0.33 |
| MFIV (WK) | 37.77 | 5.76 | 26.28 | 57.44 | 0.53 | −0.93 |
| MFIV (SP) | 36.67 | 5.38 | 27.79 | 64.36 | 1.19 | 1.37 |
| Skewness | Kurtosis | Corr(MFIV, R) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 min | 10 min | 60 min | 1 min | 10 min | 60 min | 1 min | 10 min | 60 min | |
| All | 0.61 | 0.61 | 0.62 | −0.26 | −0.25 | −0.14 | 0.000 | −0.002 | −0.006 |
| Mega | 0.6 | 0.6 | 0.6 | −0.27 | −0.28 | −0.21 | 0.000 | 0.001 | 0.001 |
| Large | 0.62 | 0.63 | 0.68 | −0.3 | −0.21 | 0.15 | −0.001 | −0.014 | −0.037 |
| Medium | 0.68 | 0.68 | 0.69 | 0.18 | 0.16 | 0.17 | −0.001 | −0.004 | −0.016 |
| Small | 0.54 | 0.55 | 0.56 | −0.72 | −0.71 | −0.6 | −0.003 | −0.007 | −0.027 |
| 1 min | 10 min | 60 min | |
|---|---|---|---|
| −7.69 | −14.79 | −15.17 | |
| (66/1) | (65/14) | (69/15) | |
| −1.22 | −1.98 | −2.27 | |
| (25/5) | (52/9) | (31/7) | |
| −1.22 | −1.26 | −1.58 | |
| (24/1) | (28/6) | (25/4) | |
| −0.89 | −0.23 | −1.35 | |
| (21/2) | (12/5) | (20/5) | |
| −9.01 | −13.17 | −15.35 | |
| (81/1) | (74/14) | (74/14) | |
| −5.03 | −4.31 | −4.22 | |
| (52/1) | (47/10) | (42/4) | |
| −2.95 | −2.41 | −3.02 | |
| (35/2) | (32/8) | (24/7) | |
| −2.48 | −1.53 | −2.37 | |
| (16/3) | (21/6) | (19/6) | |
| −0.12 | −0.15 | −0.13 | |
| (88/0) | (92/0) | (64/0) | |
| −0.07 | −0.06 | −0.05 | |
| (55/2) | (53/1) | (37/1) | |
| −0.03 | −0.02 | −0.03 | |
| (31/2) | (22/0) | (26/2) | |
| 0.00 | 0.00 | −0.01 | |
| (14/25) | (39/26) | (38/30) | |
| 16 | 60 | 60 | |
| 19 | 38 | 26 |
| 0.025 | 0.05 | 0.10 | 0.25 | 0.50 | 0.75 | 0.90 | 0.95 | 0.975 | |
|---|---|---|---|---|---|---|---|---|---|
| −10.167 | −8.763 | −7.496 | −5.528 | −3.860 | −5.190 | −7.405 | −9.082 | −10.822 | |
| (112/2) | (110/3) | (108/4) | (103/8) | (95/5) | (100/8) | (104/5) | (107/2) | (106/3) | |
| −2.695 | −2.222 | −1.880 | −1.361 | −0.979 | −1.260 | −1.735 | −2.275 | −3.166 | |
| (67/3) | (73/3) | (83/5) | (82/5) | (80/5) | (72/5) | (73/6) | (69/4) | ( 64/4) | |
| −1.692 | −1.379 | −1.181 | −0.887 | −0.574 | −0.804 | −1.245 | −1.557 | −1.759 | |
| (50/4) | (54/1) | (64/0) | (73/0) | (79/1) | (66/1) | (60/1) | (52/2) | ( 43/5) | |
| −1.033 | −0.850 | −0.711 | −0.598 | −0.381 | −0.594 | −0.939 | −1.115 | −1.756 | |
| (32/4) | (36/0) | (39/0) | (52/1) | (56/1) | (57/2) | (45/1) | (42/4) | ( 39/3) | |
| −0.06 | −0.05 | −0.04 | −0.03 | −0.01 | −0.02 | −0.03 | −0.03 | −0.03 | |
| (108/4) | (107/1) | (111/1) | (104/0) | (90/0) | (88/0) | (86/5) | (83/10) | (72/19) | |
| −0.030 | −0.019 | −0.010 | −0.004 | −0.001 | −0.003 | −0.005 | −0.005 | −0.005 | |
| (95/13) | (81/13) | (70/13) | (42/10) | (21/5) | (36/7) | (41/24) | (46/29) | (46/33) | |
| −0.014 | −0.008 | −0.003 | 0.001 | 0.001 | 0.001 | 0.002 | 0.004 | 0.006 | |
| (68/17) | (60/21) | (23/48) | (18/20) | (7/11) | (10/11) | (13/23) | (16/35) | (25/43) | |
| constant | −0.783 | −0.527 | −0.331 | −0.162 | −0.037 | 0.091 | 0.347 | 0.608 | 0.910 |
| (122/0) | (121/0) | (122/0) | (120/0) | (61/47) | (0/122) | (0/122) | (0/122) | (0/122) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haas, M.G.; Peter, F.J. Implementing Intraday Model-Free Implied Volatility for Individual Equities to Analyze the Return–Volatility Relationship. J. Risk Financial Manag. 2024, 17, 39. https://doi.org/10.3390/jrfm17010039
Haas MG, Peter FJ. Implementing Intraday Model-Free Implied Volatility for Individual Equities to Analyze the Return–Volatility Relationship. Journal of Risk and Financial Management. 2024; 17(1):39. https://doi.org/10.3390/jrfm17010039
Chicago/Turabian StyleHaas, Martin G., and Franziska J. Peter. 2024. "Implementing Intraday Model-Free Implied Volatility for Individual Equities to Analyze the Return–Volatility Relationship" Journal of Risk and Financial Management 17, no. 1: 39. https://doi.org/10.3390/jrfm17010039







