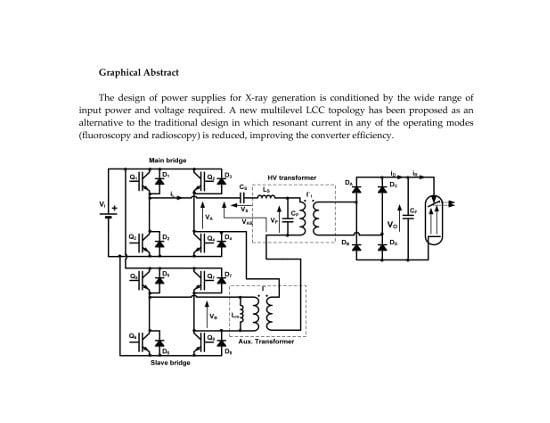
LCC Resonant Multilevel Converter for X-ray Applications
Abstract
:1. Introduction
2. Materials and Methods
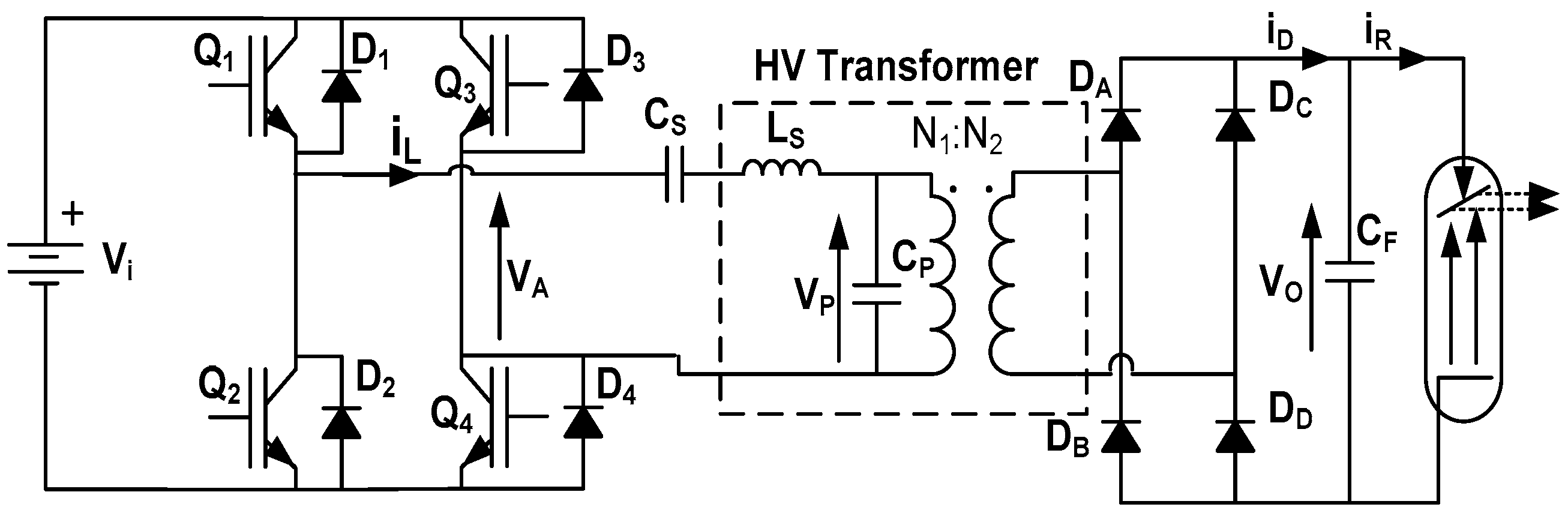
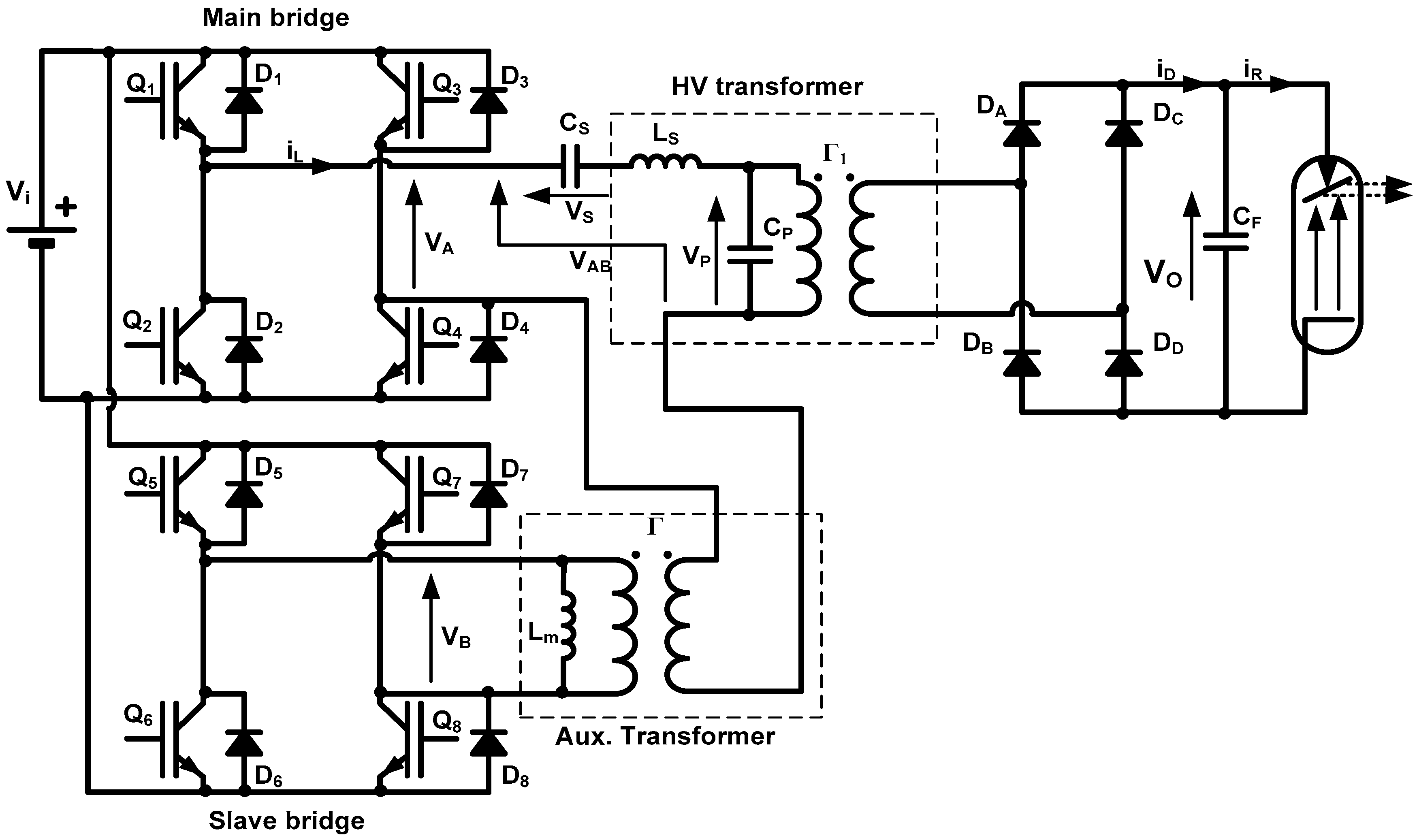
2.1. Topology
- -
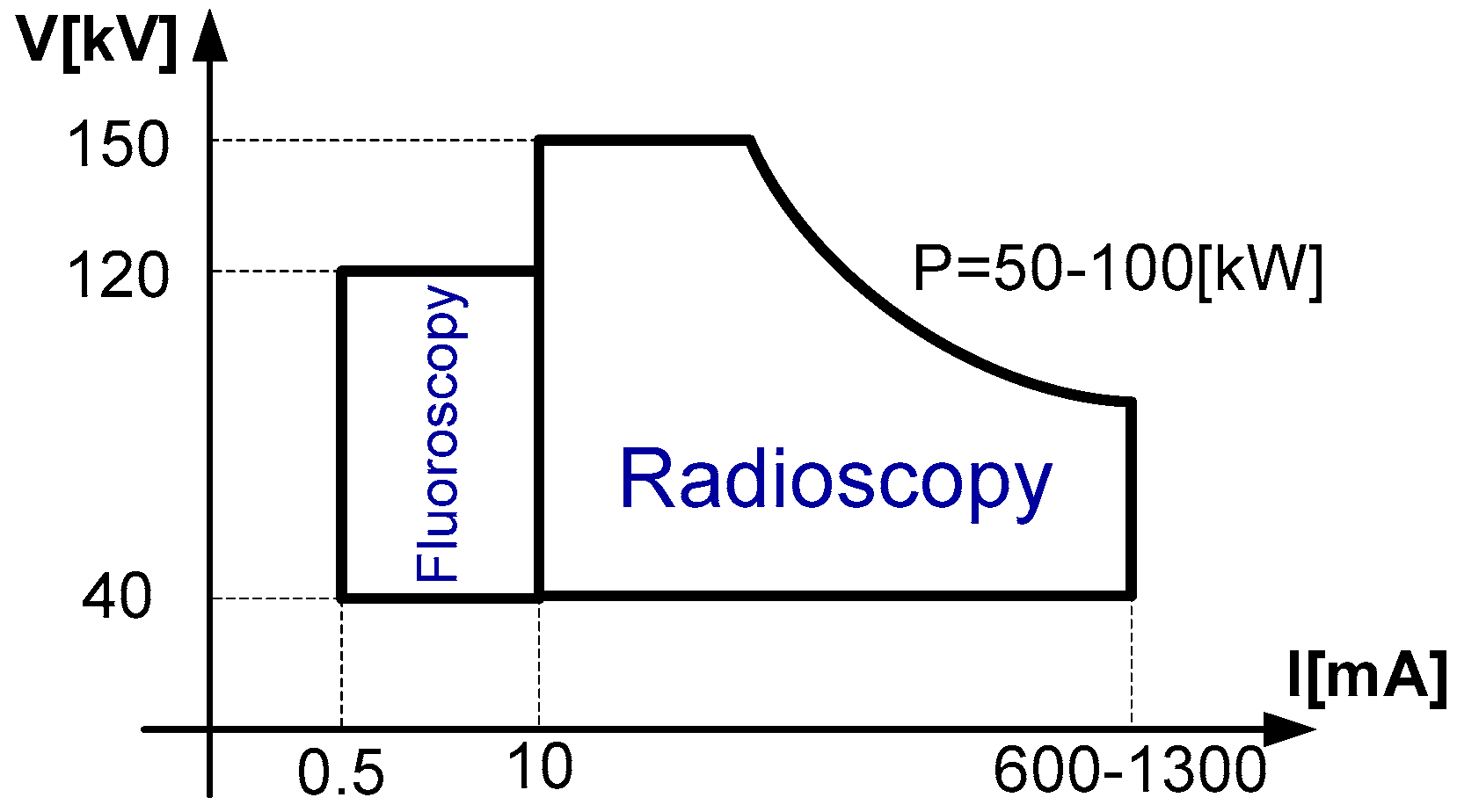
- Fluoroscopy: 1.2 kW–120 kV
- -
- Radioscopy: 100 kW–150 kV
2.2. High Voltage Transformer
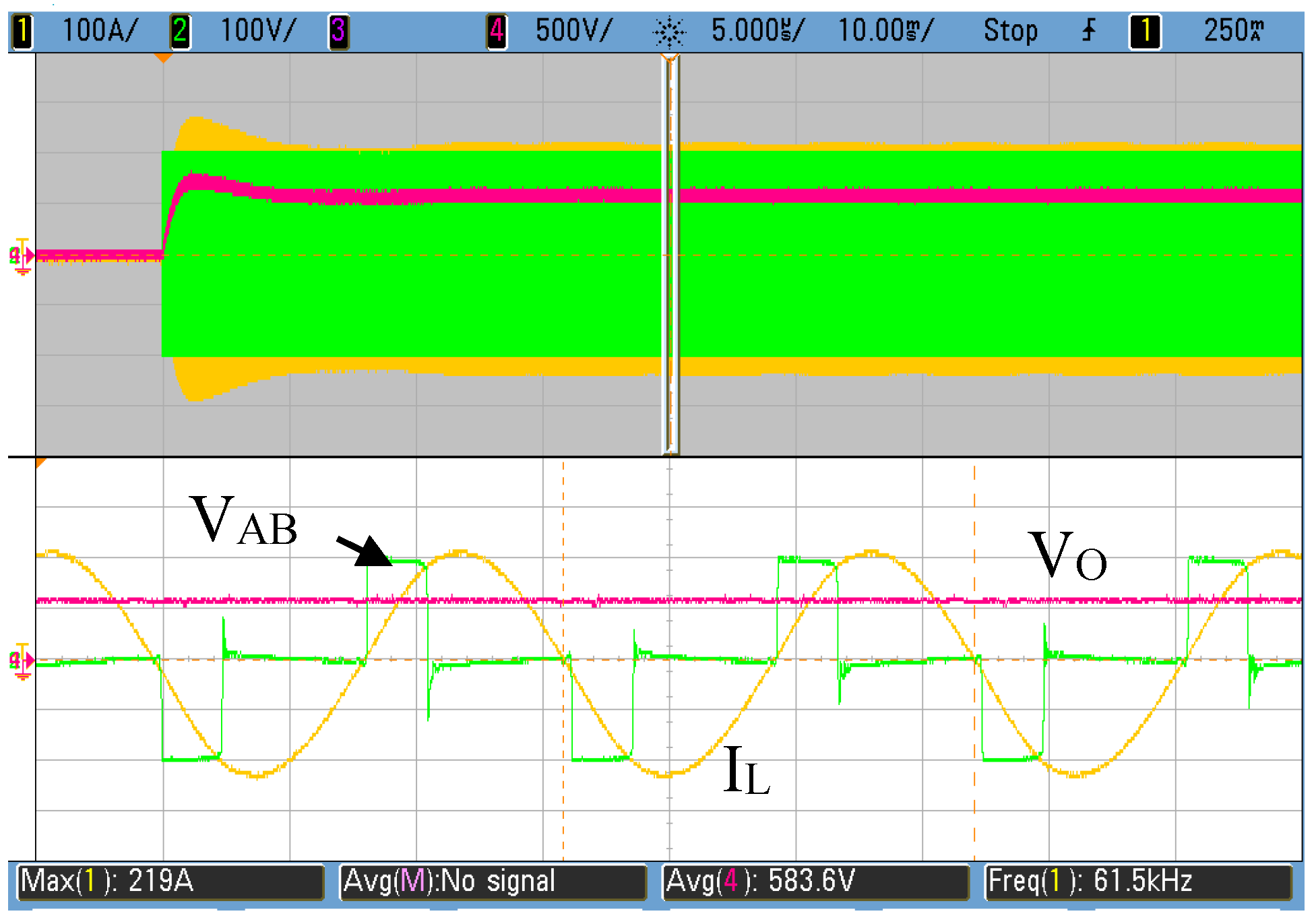
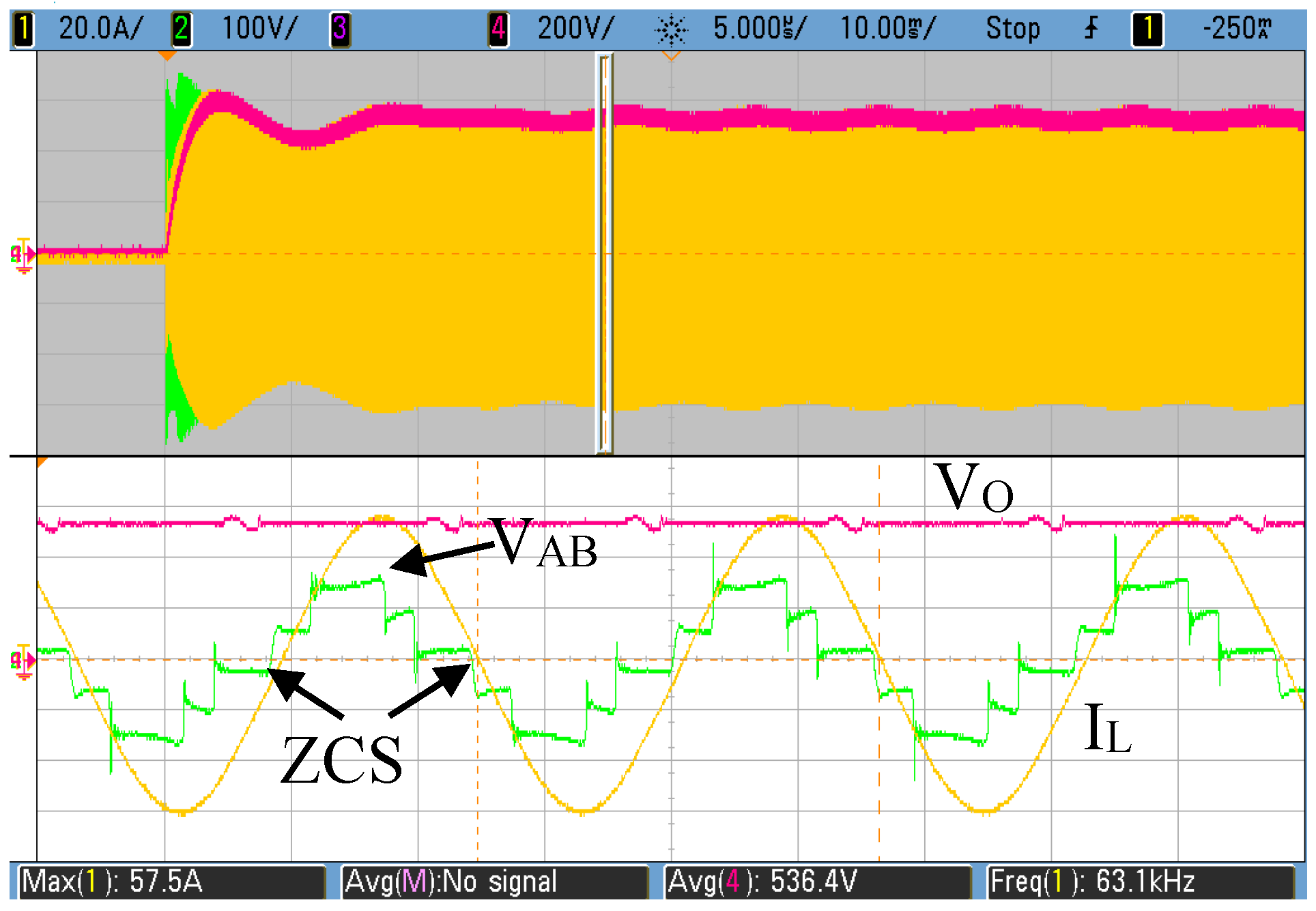
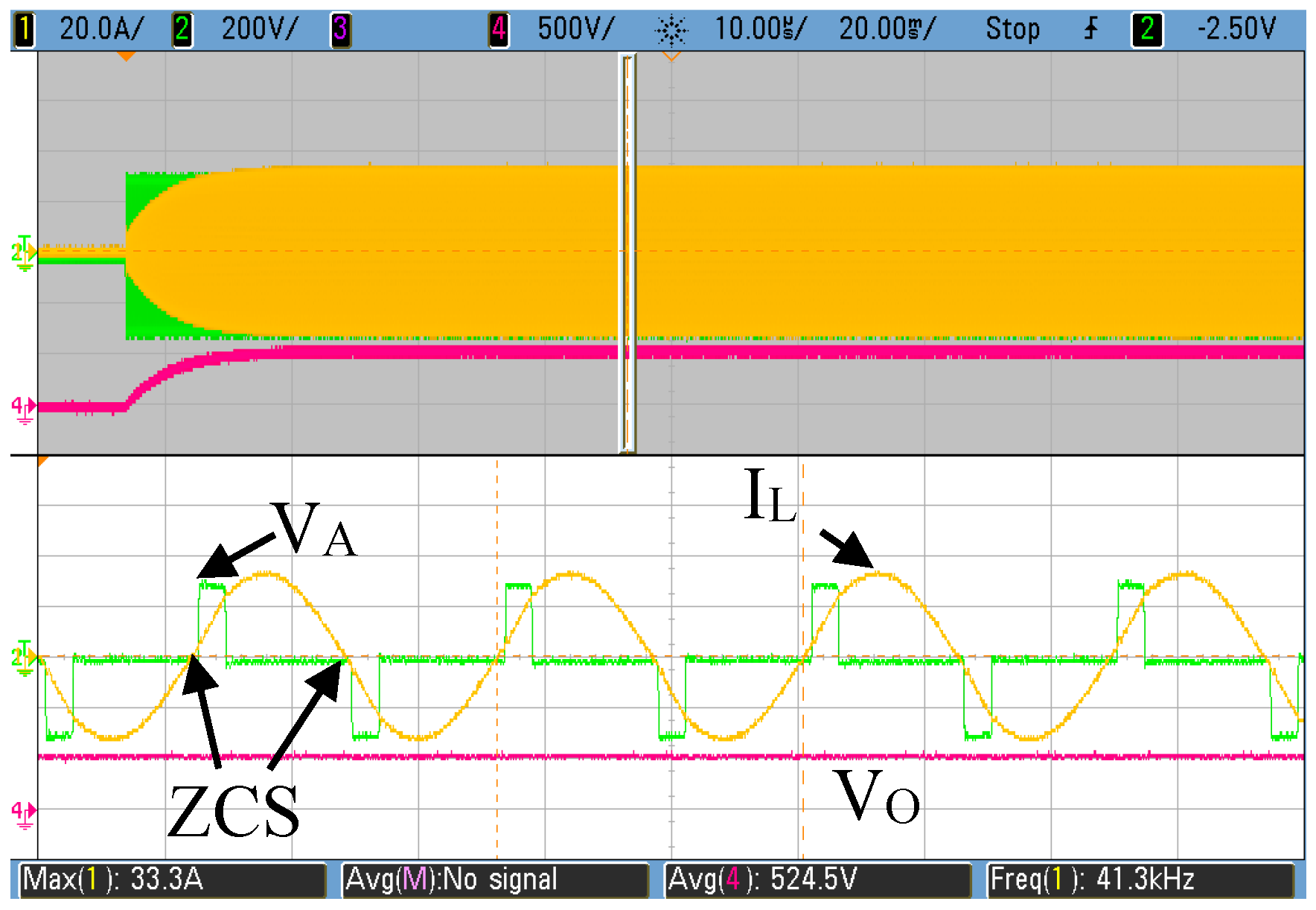
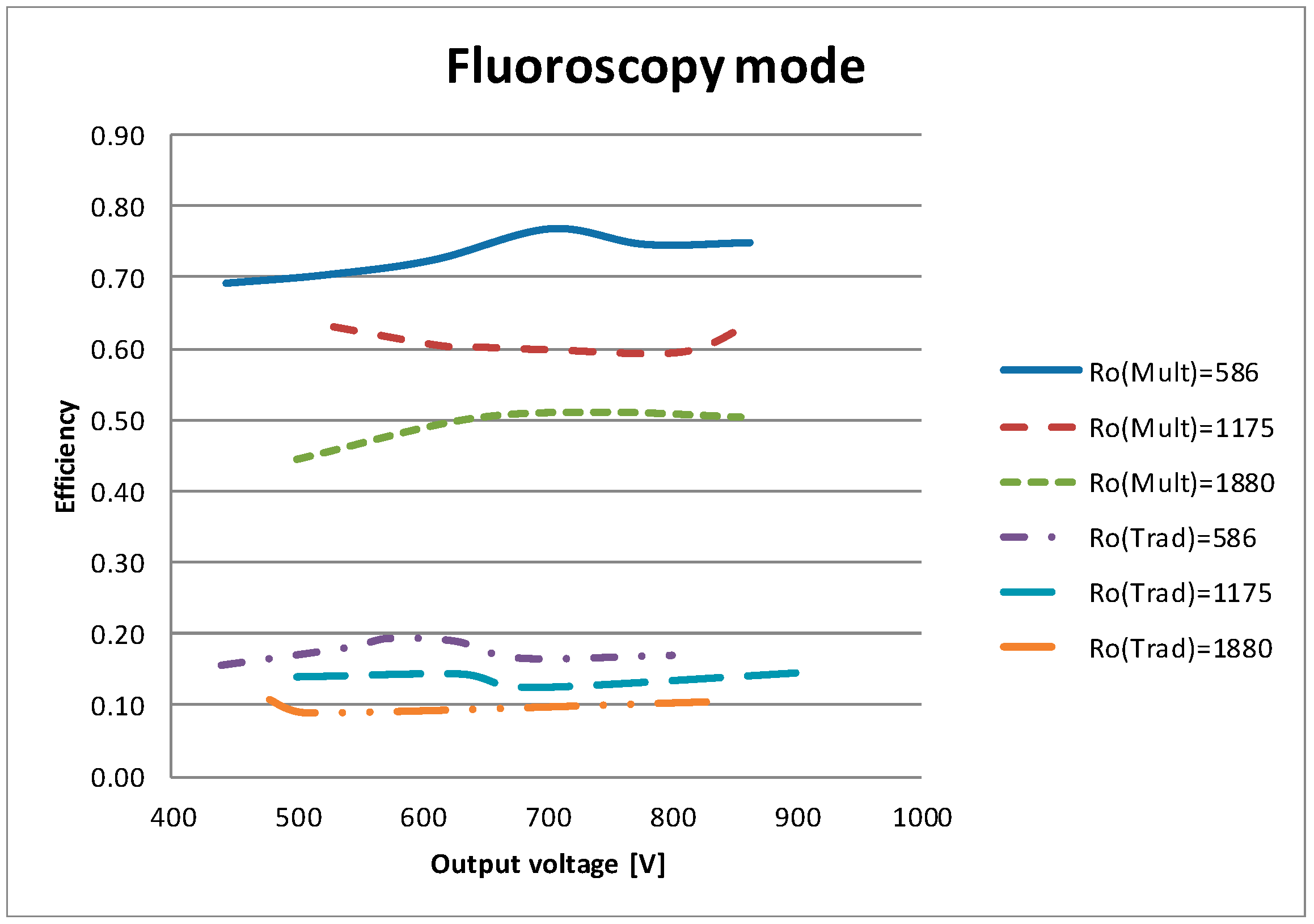
3. Results and Discussion
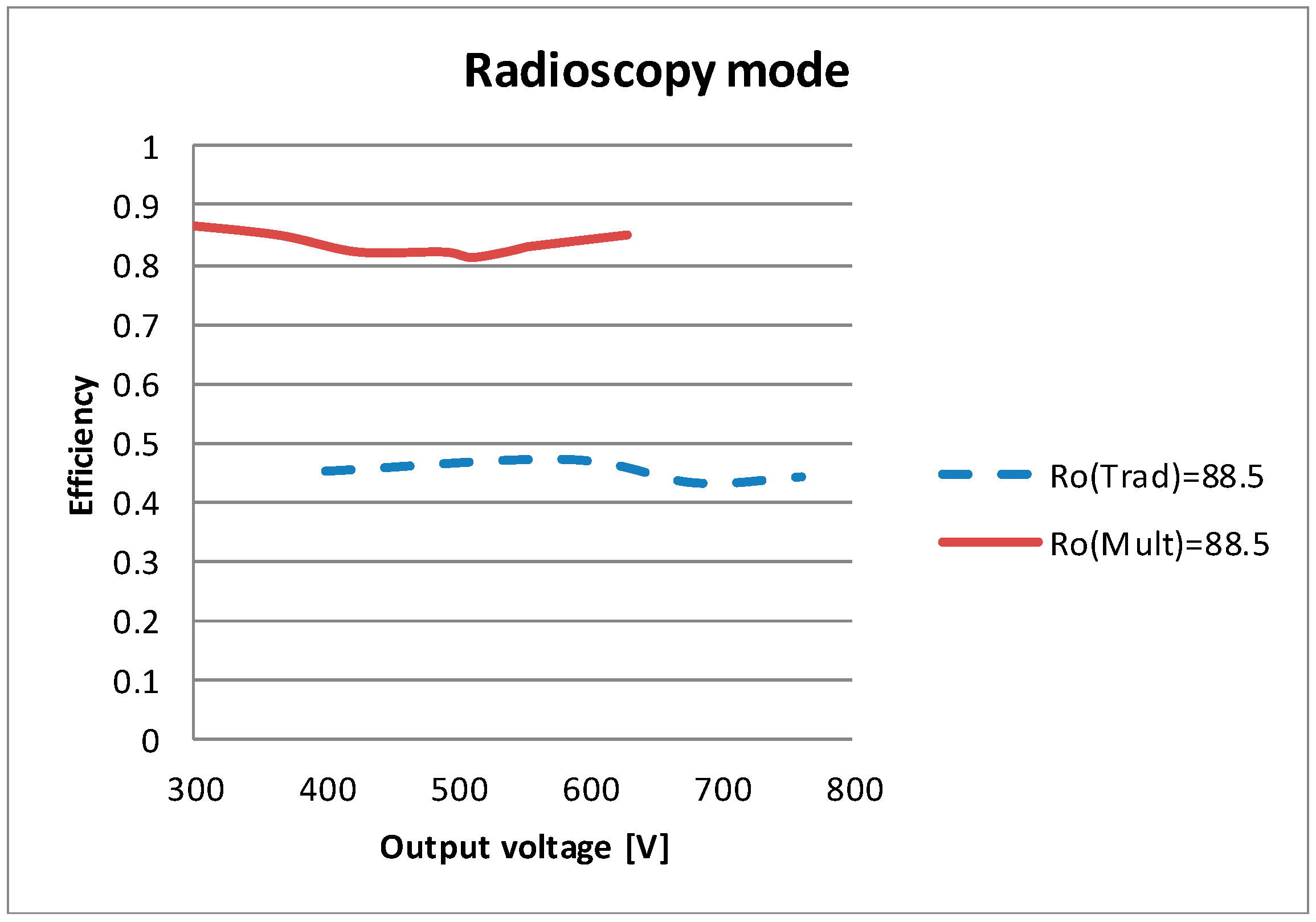
3.1. Operation in Radioscopy Mode
3.2. Operation in Fluoroscopy Mode
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Villegas, P.J.; Díaz, J.; Pernía, A.M.; Martínez, J.A.; Nuño, F.; Prieto, M.J. Filament Power Supply for Electron Beam Welding Machine. IEEE Trans. Ind. Electron. 2015, 62, 1421–1429. [Google Scholar] [CrossRef]
- Steigerwald, R.L. A comparison of half-bridge resonant converter topologies. IEEE Trans. Ind. Electron. 1988, 3, 174–182. [Google Scholar] [CrossRef]
- Sun, J.M.; Wang, S.P.; Nishimura, T.; Nakaoka, M. Resonant mode PWM DC-DC converter with a high-voltage transformer link and its control methods for medical-use X-ray power supply. In Proceedings of the European Power Electronics EPE´99, Lausanne, Switzerland, 7 September 1999. [Google Scholar]
- Van der Broek, H.; Rexhausen, W.; Wagner, B.; Geerkens, N. Power Supply Unit Including a PWM Inverter, Notably for an X-ray Generator. U.S. Patent 6,072,856, 6 June 2000. [Google Scholar]
- Jeong, B.H.; Cho, J.S.; Mok, H.S.; Choe, G.-H. A novel pulse power supply for magnetron using high voltage capacitor embedded high frequency transformer. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 22–26 February 2004; pp. 1819–1824. [Google Scholar]
- Casanueva, R.; Brañas, C.; Azcondo, F.J.; Díaz, F.J. Teaching resonant converters: Properties and applications for variable loads. IEEE Trans. Ind. Electron. 2010, 57, 3355–3363. [Google Scholar] [CrossRef]
- Shafiei, N.; Pahlevaninezhad, M.; Farzanehfard, H.; Bakhshai, A.; Jain, P. Analysis of a Fifth-Order Resonant Converter for High-Voltage DC Power Supplies. IEEE Trans. Power Electron. 2013, 28, 85–100. [Google Scholar] [CrossRef]
- Hsu, W.C.; Chen, J.F.; Hsieh, Y.P.; Wu, Y.M. Design and Steady-State Analysis of Parallel Resonant DC–DC Converter for High-Voltage Power Generator. IEEE Trans. Power Electron. 2017, 32, 957–966. [Google Scholar] [CrossRef]
- Ramos, J.M.; Diaz, J.; Pernía, A.M.; Nuño, F.; Lopera, J.M. Dynamic and steady-state models for the PRC-LCC resonant topology with a capacitor as output filter. IEEE Trans. Ind. Electron. 2007, 54, 2262–2275. [Google Scholar] [CrossRef]
- Bhat, A.K.S. Analysis and design of a series-parallel resonant converter with capacitive output filter. IEEE Trans. Ind. Appl. 1991, 27, 523–530. [Google Scholar] [CrossRef]
- Yang, R.; Ding, H.; Xu, Y.; Yao, L.; Xiang, Y. An Analytical Steady-State Model of LCC type Series-Parallel Resonant Converter with Capacitive Output Filter. IEEE Trans. Power Electron. 2014, 29, 328–338. [Google Scholar] [CrossRef]
- Diaz, J.; Jose, P.; Saiz, V.; Martin-Ramos, J.A.; Martin-Pernía, A.; Martinez, J.A. A High-Voltage AC/DC Resonant Converter Based on PRC with Single Capacitor as an Output Filter. IEEE Trans. Ind. Appl. 2010, 46, 2134–2142. [Google Scholar] [CrossRef]
- Martin-Ramos, J.A.; Villegas Saiz, P.J.; Pernía, A.M. Optimal Control of a High-Voltage Power Supply Based on the PRC-LCC Topology with a Capacitor as Output Filter. IEEE Trans. Ind. Appl. 2013, 49, 2323–2329. [Google Scholar] [CrossRef]
- Ivensky, G.; Kats, A.; Ben-Yaakov, S. An RC load model of parallel and series-parallel resonant DC-DC converters with capacitive output filter. IEEE Trans. Power Electron. 1999, 14, 515–521. [Google Scholar] [CrossRef]
- Takano, H.; Takahashi, J.; Sun, J.M.; Nakaoka, M. Comparative study of resonant and non-resonant DC-DC converter with parasitic LC components of high-voltage transformer. In Proceedings of the IEEE Industry Applications Society 33rd Annual Meeting (IAS), St. Louis, MO, USA, 12–15 October 1998; pp. 1580–1587. [Google Scholar]
- Kim, D.-K.; Moon, S.; Yeon, C.O.; Moon, G.-W. High Efficiency LLC Resonant Converter with High Voltage Gain Using Auxiliary LC Resonant Circuit. IEEE Trans. Power Electron. 2016, 31, 6901–6909. [Google Scholar] [CrossRef]
- Martin-Ramos, J.; Pernía, A.M.; Diaz, J.; Nuño, F.; Martínez, J.A. Power supply for a high voltage application. IEEE Trans. Power Electron. 2008, 23, 1608–1619. [Google Scholar] [CrossRef]
- Du, Y.; Wang, J.; Wang, G.; Huang, A.Q. Modeling of the High-Frequency Rectifier With 10-kV SiC JBS Diodes in High-Voltage Series Resonant Type DC-DC Converters. IEEE Trans. Power Electron. 2014, 29, 4288–4300. [Google Scholar] [CrossRef]
- Cavalcante, F.S.; Kolar, J.W. Small signal model of a 5 kW high-output voltage capacitive-loaded series–parallel resonant DC–DC converter. In Proceedings of the IEEE Power Electronics Specialists Conference PESC, Recife, Brazil, 16 June 2005; pp. 1271–1277. [Google Scholar]
- Wang, B.; Xin, X.; Wu, S.; Wu, H.; Ying, J. Analysis and Implementation of LLC Burst Mode for Light Load Efficiency Improvement. In Proceedings of the IEEE 2009 Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; pp. 58–64. [Google Scholar]
- Feng, W.; Lee, F.C.; Mattavelli, P.; Huang, D.; Prasantanakorn, C. LLC Resonant Converter Burst Mode Control with Constant Burst Time and Optimal Switching Pattern. In Proceedings of the Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 6–11 March 2011. [Google Scholar]
- Martín-Ramos, J.A.; Pardo-Vaquero, O.; Villegas, P.J.; Martínez, J.A.; Pernía, A.M. Multilevel PRC-LCC resonant converter for X-ray generation. Electron. Lett. 2015, 51, 1189–1191. [Google Scholar] [CrossRef]
- Debnath, S.; Qin, J.; Bahrani, B.; Saeedifard, M.; Barbosa, P. Operation, Control, and Applications of the Modular Multilevel Converter: A Review. IEEE Trans. Power Electron. 2015, 30, 37–53. [Google Scholar] [CrossRef]
- Zeng, R.; Xu, L.; Yao, L.; Williams, B.W. Design and Operation of a Hybrid Modular Multilevel Converter. IEEE Trans. Power Electron. 2015, 30, 1137–1146. [Google Scholar] [CrossRef]
- Pernía, A.M.; Lopera, J.M.; Nuño, F. 1D/2D transformer electric model for simulation in power converters. In Proceedings of the IEEE Power Electronic Specialist Conference PESC’95, Atlanta, GA, USA, 18–22 June 1995; Volume 2, pp. 1043–1049. [Google Scholar]


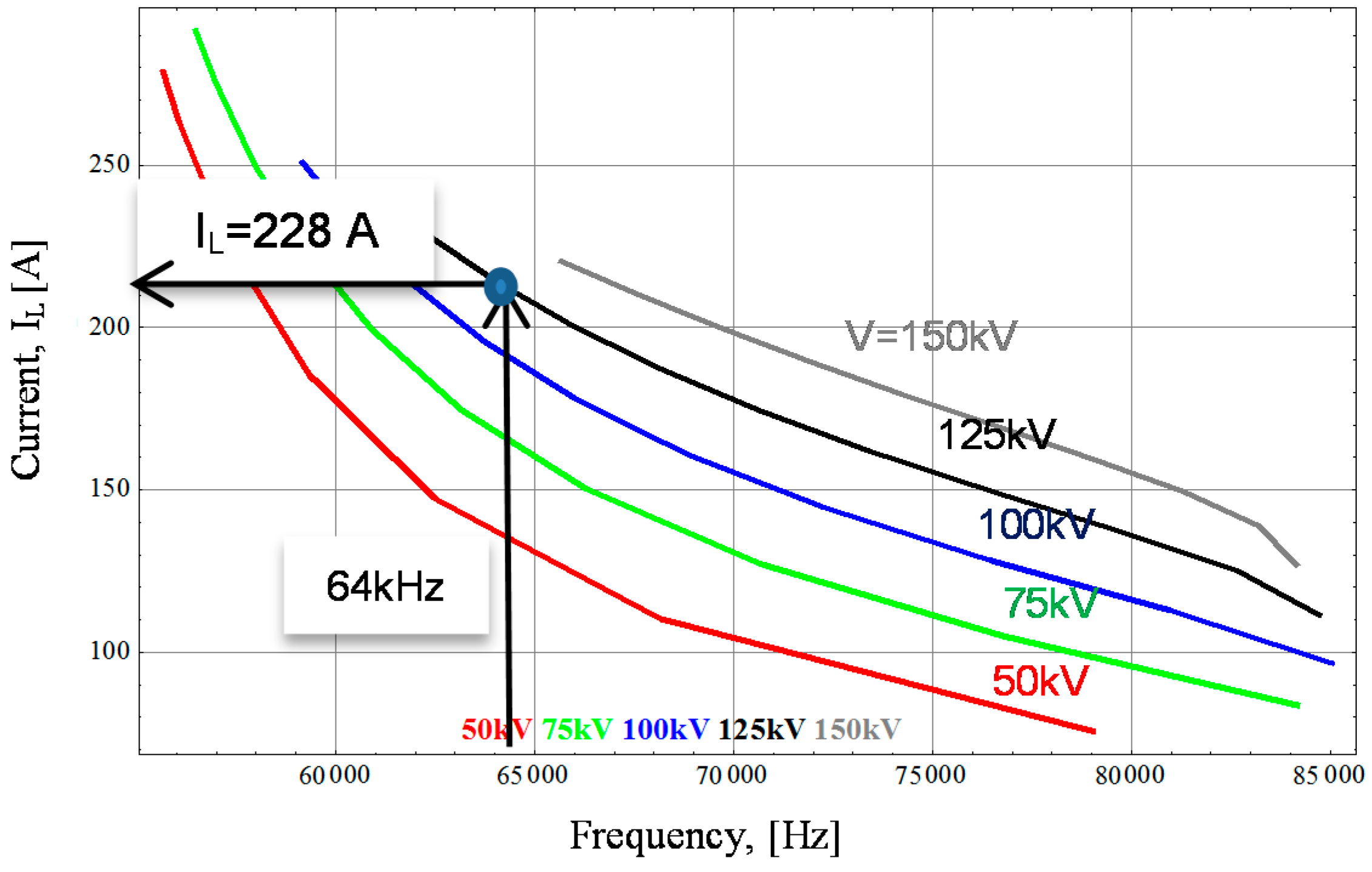
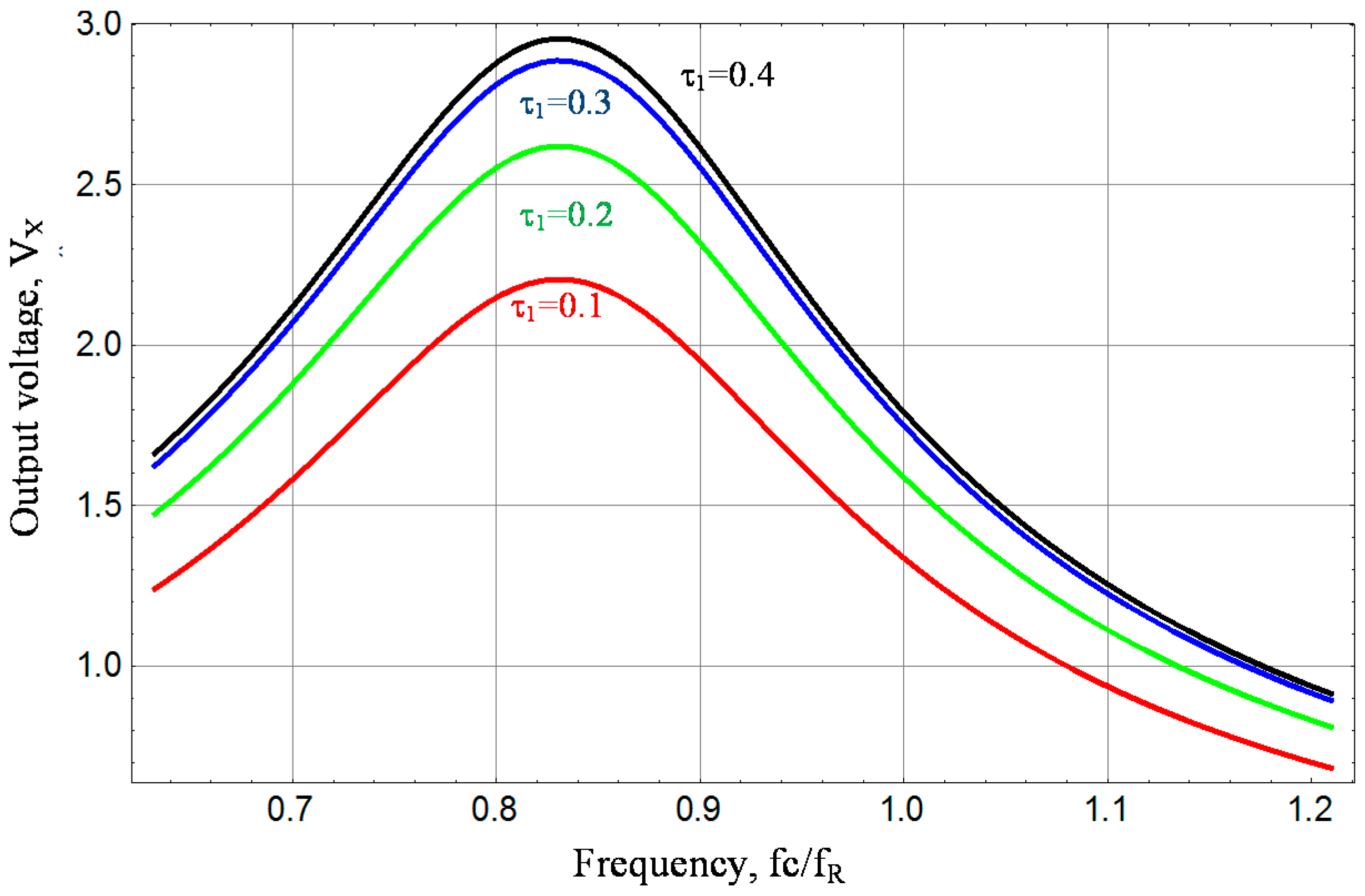
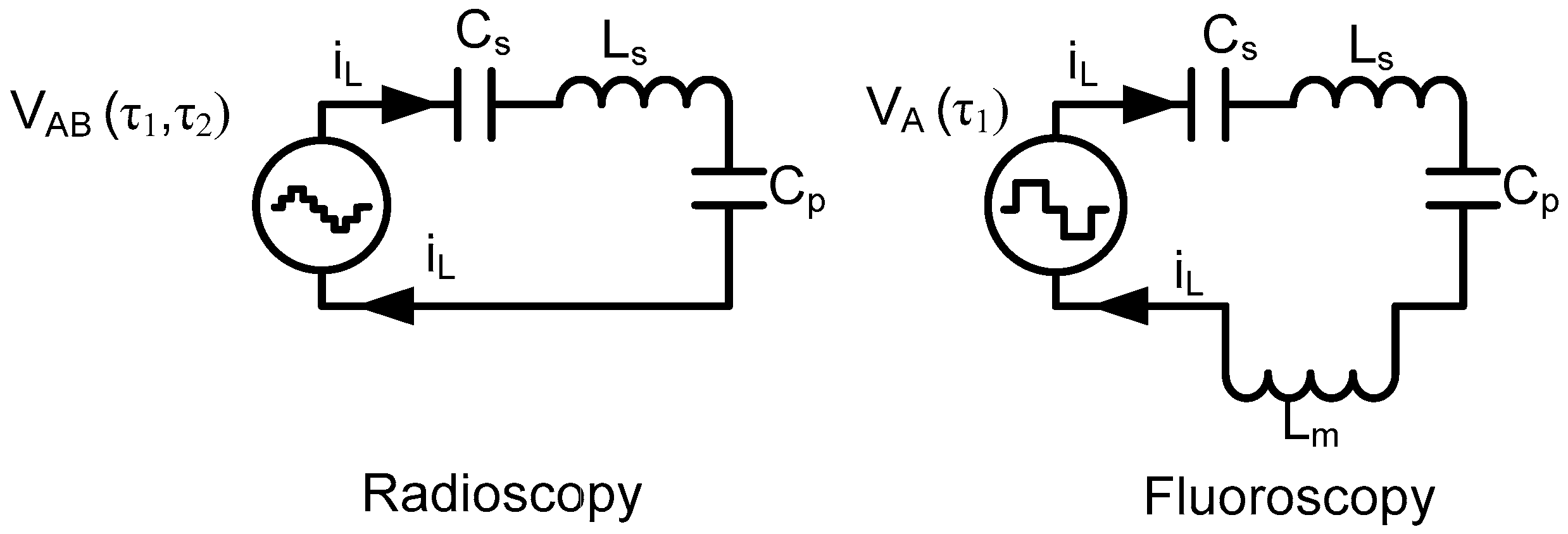

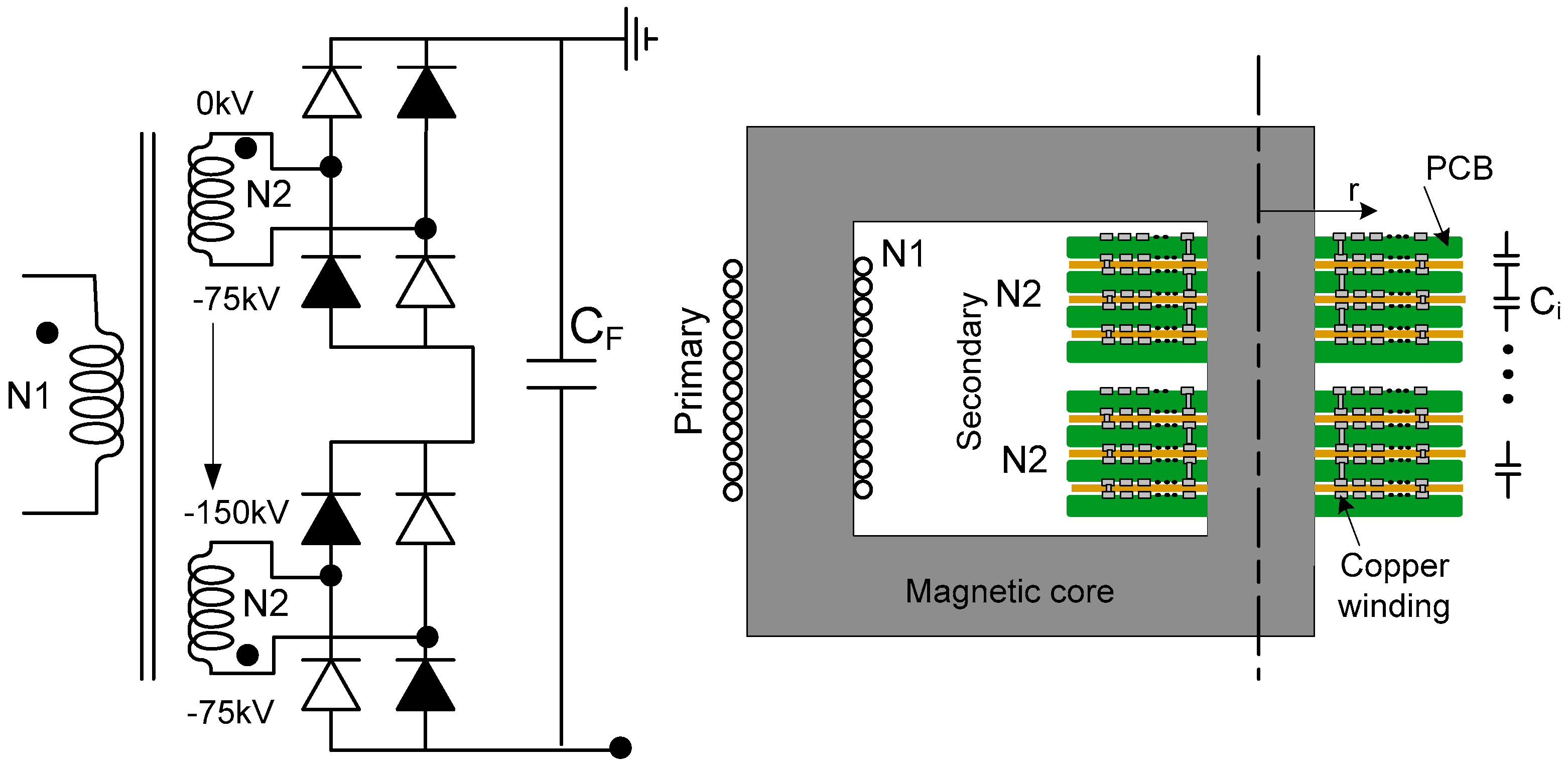




| A. Full Bridge. Traditional Design | ||||
| Vi | VO | PO | IL | fc |
| 400 V | 120 kV | 1200 W | 309 A | 80.5 kHz |
| 750 V | 120 kV | 1200 W | 310 A | 81.1 kHz |
| B. Full Bridge. Multilevel Design | ||||
| 400 V | 120 kV | 1200 W | 60 A | 53.7 kHz |
| 750 V | 120 kV | 1200 W | 61 A | 54.5 kHz |
| A. Full Bridge. Traditional Design (Radioscopy and Fluoroscopy) | ||||
| Cs | CP | Ls | Γ1 | fcmin |
| 950 nF | 630 nF | 10 µH | 80 | 50 kHz |
| B. Full Bridge. Multilevel Design (Radioscopy) | ||||
| Cs | CP | Ls | Γ1 | fcmin |
| 330 nF | 220 nF | 38 µH | 80 | 50 kHz |
| B. Full Bridge. Multilevel Design (Fluoroscopy) | ||||
| 330 nF | 220 nF | 163 µH | 80 | 50 kHz |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pernía, A.M.; Prieto, M.J.; Villegas, P.J.; Díaz, J.; Martín-Ramos, J.A. LCC Resonant Multilevel Converter for X-ray Applications. Energies 2017, 10, 1573. https://doi.org/10.3390/en10101573
Pernía AM, Prieto MJ, Villegas PJ, Díaz J, Martín-Ramos JA. LCC Resonant Multilevel Converter for X-ray Applications. Energies. 2017; 10(10):1573. https://doi.org/10.3390/en10101573
Chicago/Turabian StylePernía, A. M., Miguel J. Prieto, Pedro J. Villegas, Juan Díaz, and Juan A. Martín-Ramos. 2017. "LCC Resonant Multilevel Converter for X-ray Applications" Energies 10, no. 10: 1573. https://doi.org/10.3390/en10101573