Theoretical Analysis for Heat Transfer Optimization in Subcritical Electrothermal Energy Storage Systems
Abstract
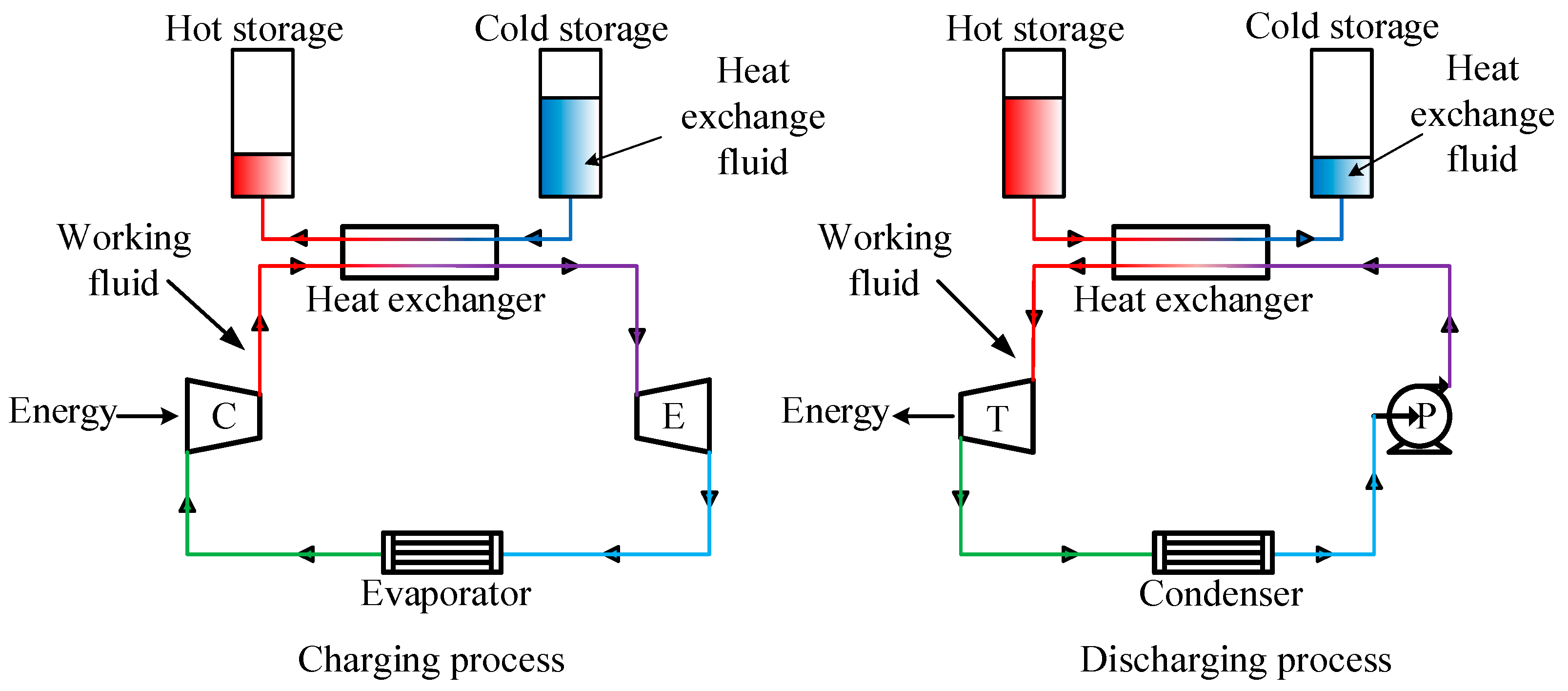
:1. Introduction
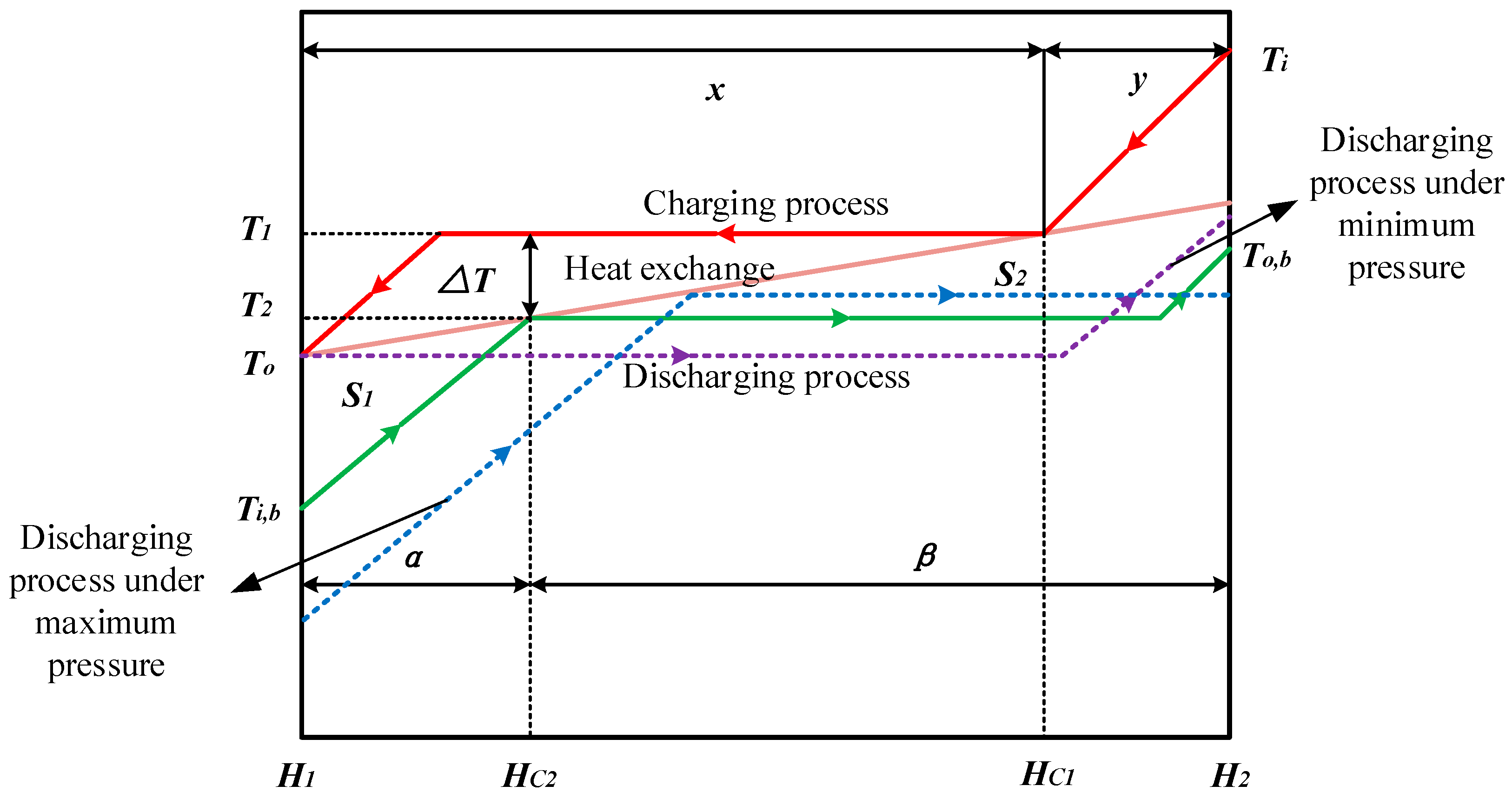
2. Theoretical Analysis
- The charging process is fixed, and the total heat exchange capacity of the charging and discharging process are equivalent, and the heat exchange is mainly based on the latent heat exchange;
- The variations of isobaric specific heat and latent heat with minor change of pressure can be ignored, thus the isobaric specific heat and latent heat are assumed to be constants;
- The pinch point temperature difference is assumed to be zero; the heat loss of the heat exchange process is taken no account.
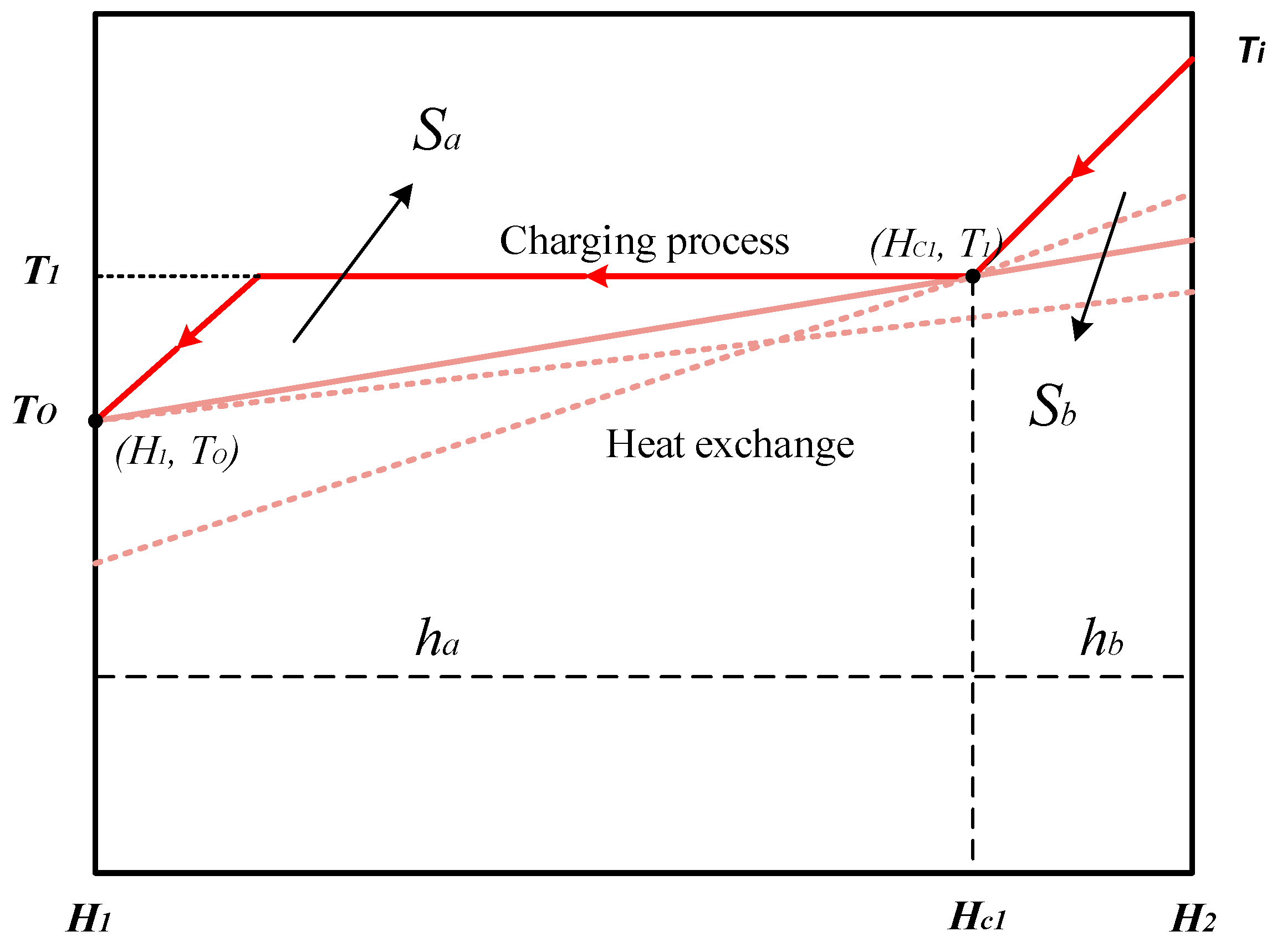
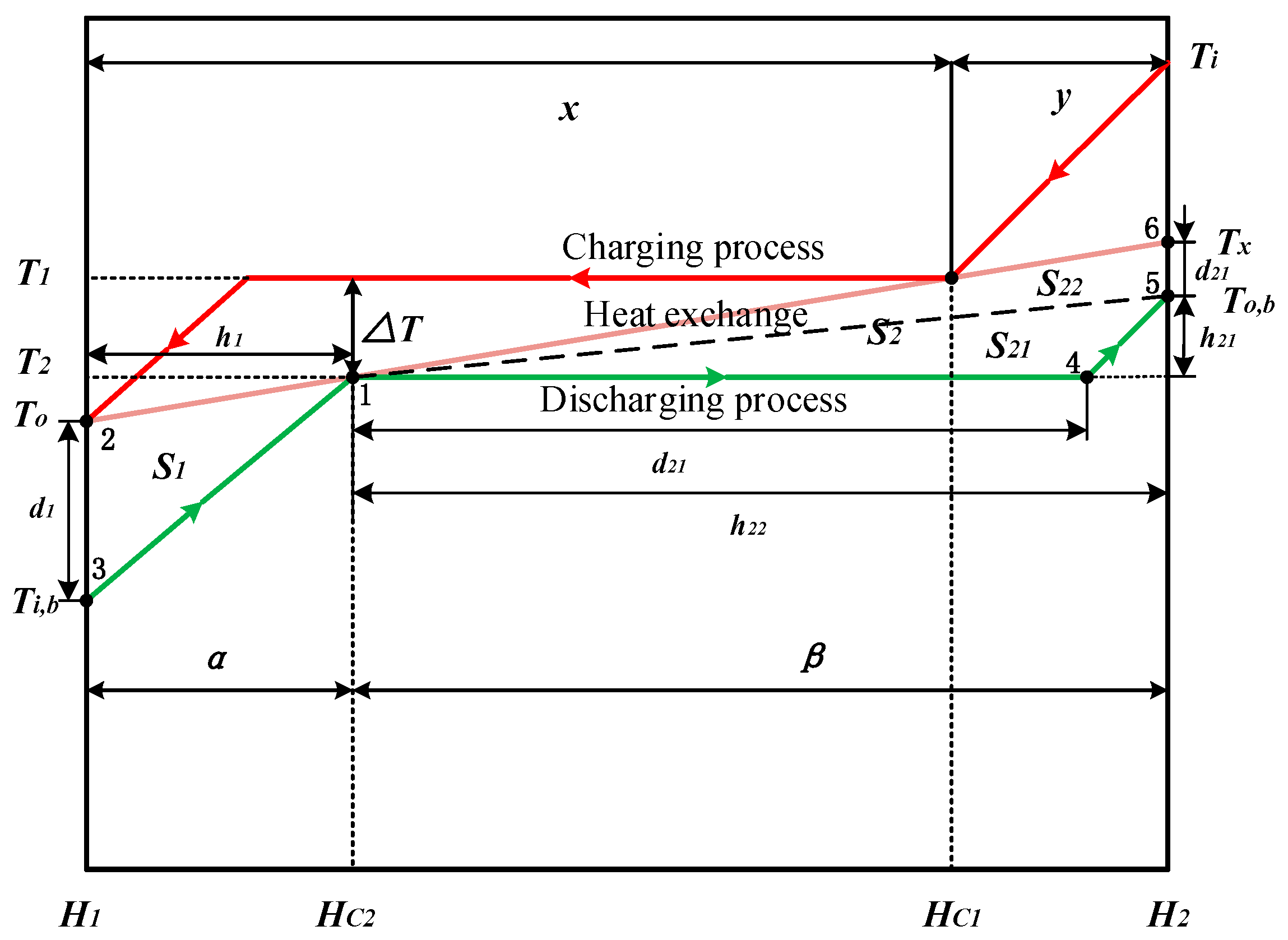
2.1. Optimum Heat Transfer at Different Mass Fluxes
2.2. Optimum Heat Transfer under Different Pressures
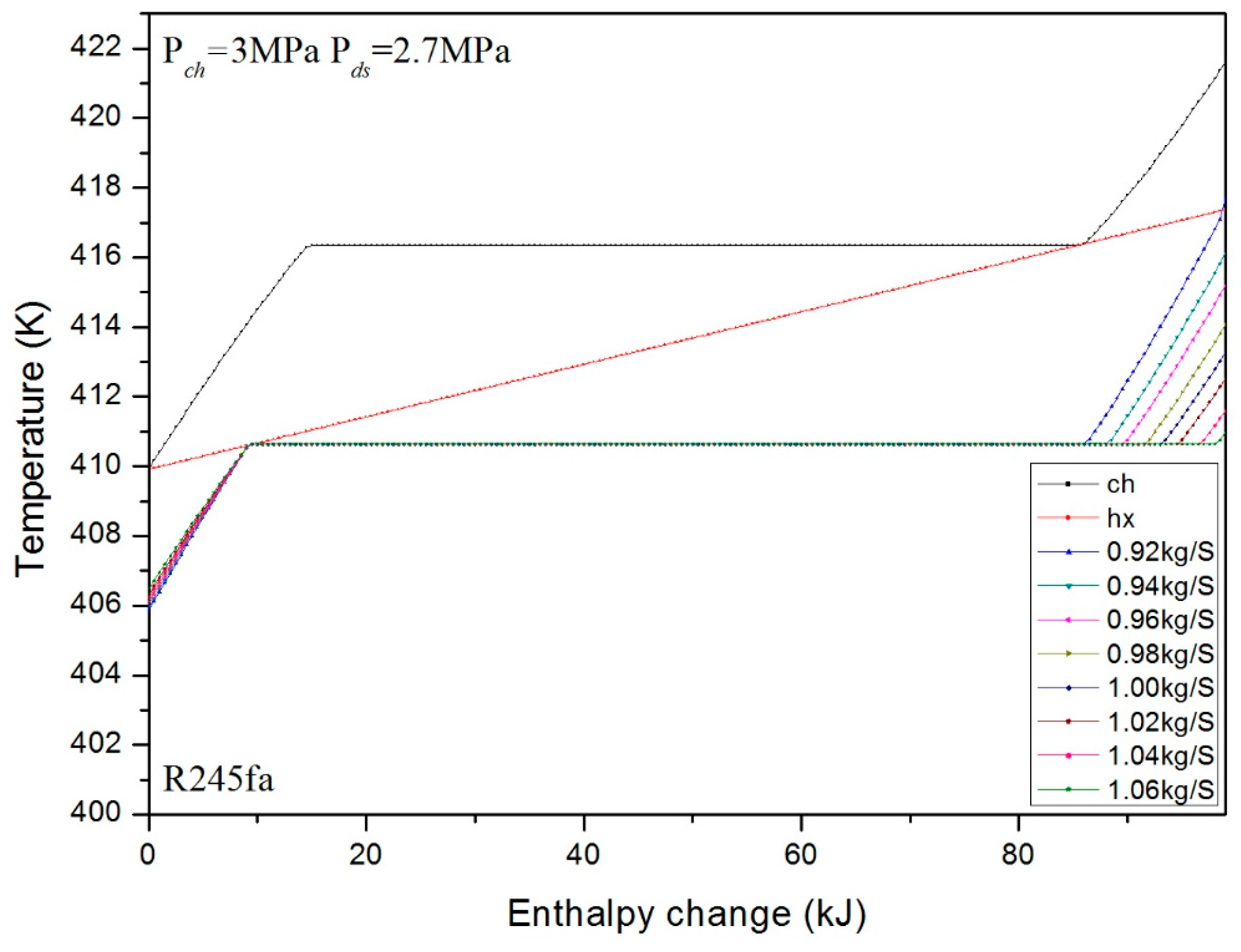
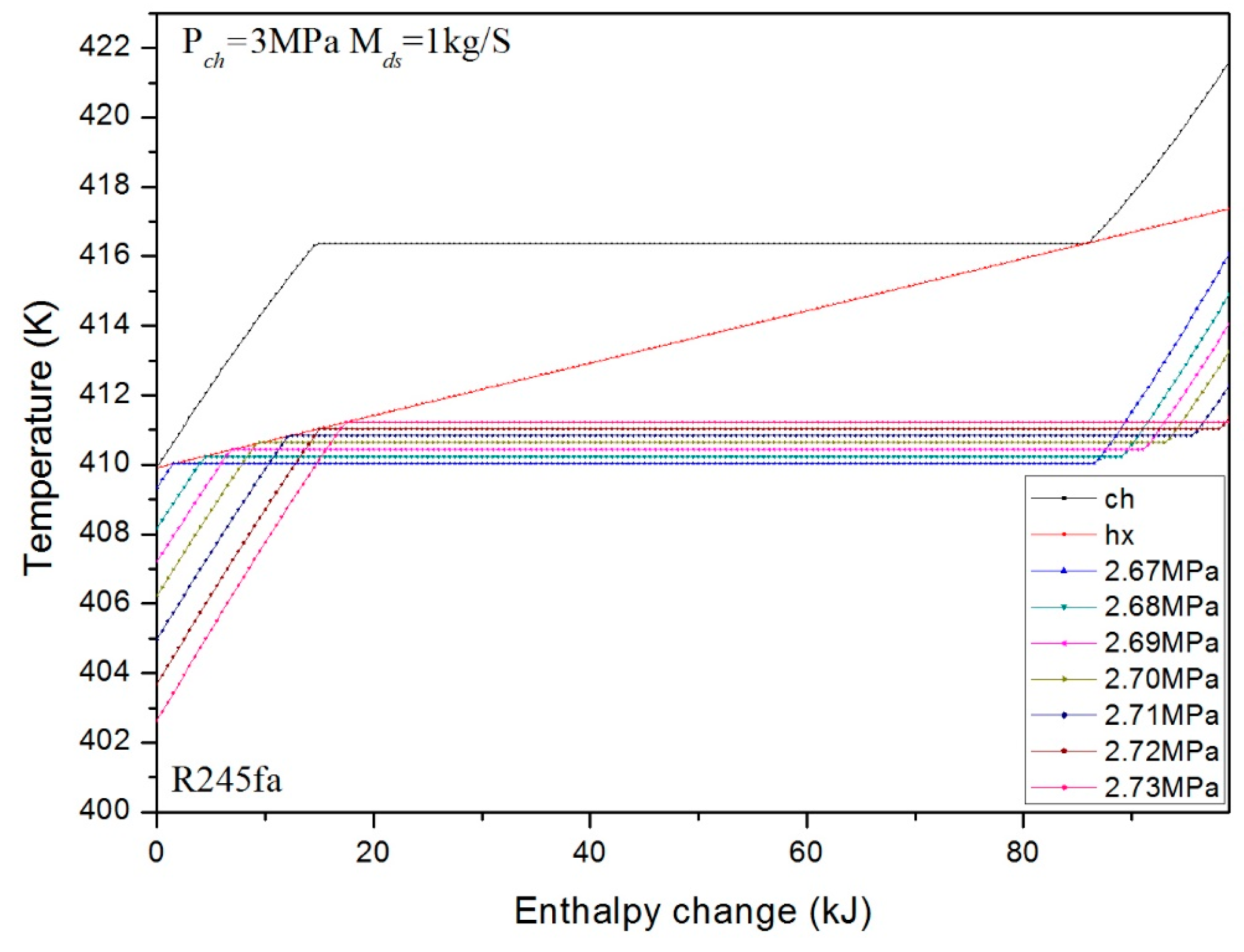
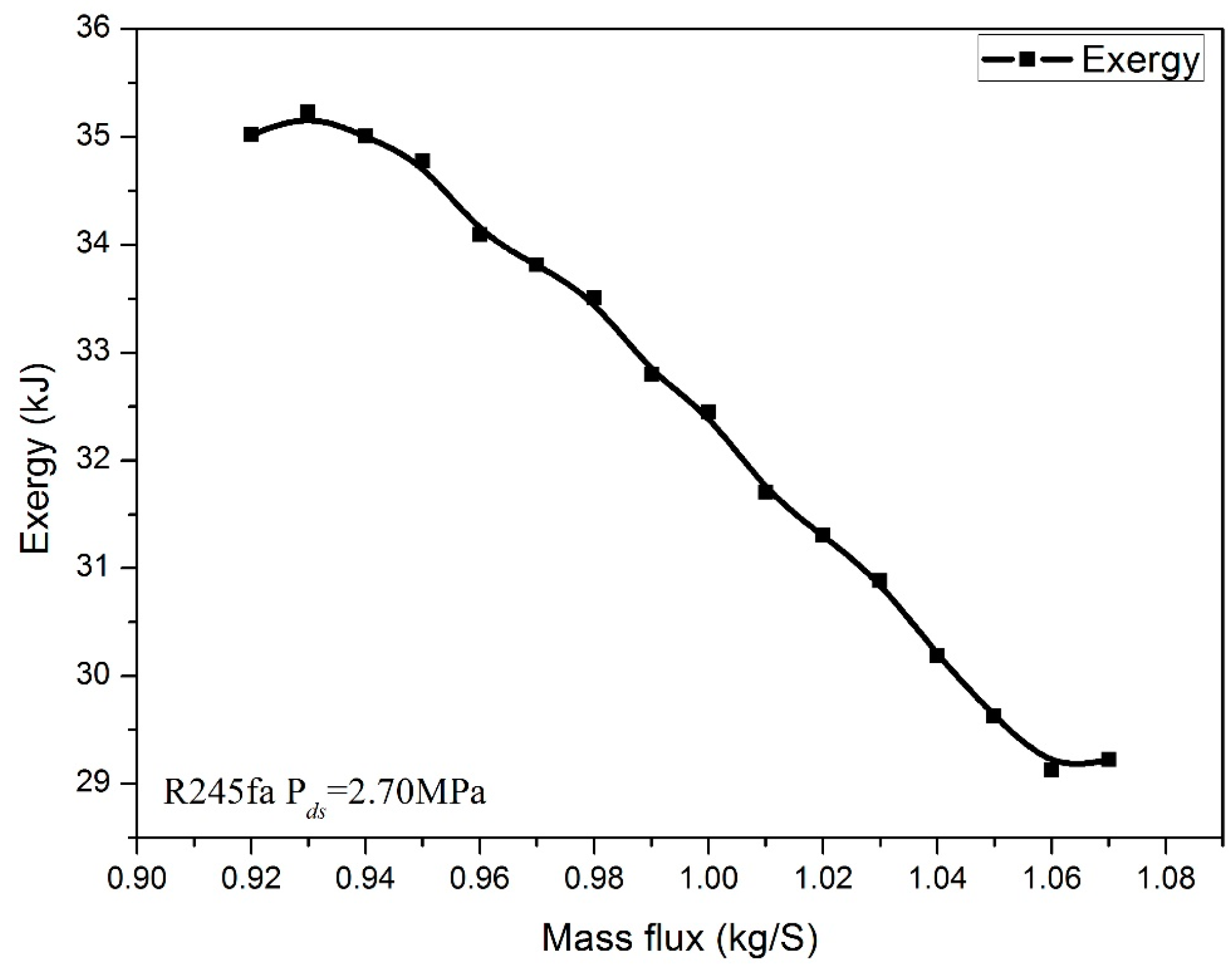
3. Numerical Confirmation of the Optimum Heat Transfer
4. Conclusions
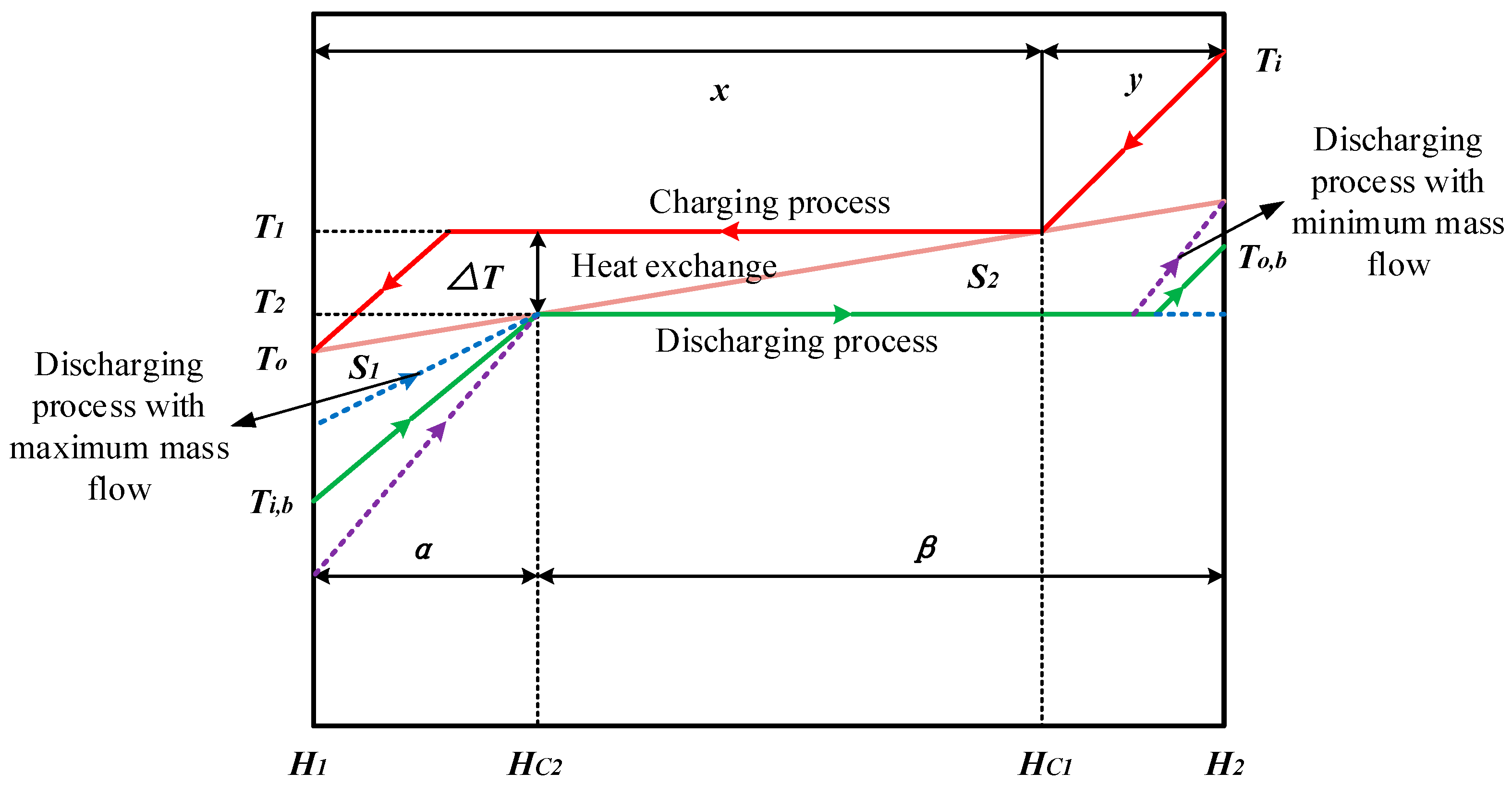
- For the different mass fluxes under fixed pressure, the mass fluxes to achieve the optimum heat transfer are different for different cases. The optimum mass flux is effected mainly by the latent heats of the charging and discharging processes. However, it is confirmed that the optimum mass flux appears at the minimum or maximum allowed value under the same pressure.
- Similarly, for the different pressures at fixed mass flux, the optimum pressure is effected mainly by the specific heat capacities of the liquid or vapor stages. The optimum heat transfer can be obtained under the minimum pressure with . We found the reason for this is the entransy dissipation is a monotonous decreasing function for this situation. However, for any other cases, there is an optimum pressure which depends on the extreme phase change temperature difference between charging and discharging processes.
- In order to demonstrate the validation of the model, the maximum exergy analysis based on the minimum entropy production principle has been carried out. The data of the numerical confirmation is compared with the result proposed by theoretical analysis. There is minor difference (around 0.19% in this study) between the variations of the exergy and entransy dissipation of R245fa.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Area | |
| Area of the triangle | |
| Area of the triangle | |
| Area of the triangle | |
| Liquid isobaric specific heat | |
| Vapor isobaric specific heat | |
| Base of the triangle | |
| Base of the triangle | |
| Base of the triangle | |
| Entransy | |
| Entransy dissipation | |
| Exergy | |
| Enthalpy | |
| Enthalpy of the beginning | |
| Enthalpy of the end | |
| Enthalpy of the phase change end in the charging process | |
| Enthalpy of the phase change beginning in the discharging process | |
| Latent heat | |
| Height of the triangle | |
| Height of the triangle | |
| Height of the triangle | |
| Slope of the heat exchange line | |
| Slope of the vapor stage in the discharging process | |
| Mass flux | |
| Pressure | |
| Δ123 | |
| Δ145 | |
| Δ156 | |
| Temperature | |
| Phase change temperature of the charging process | |
| Phase change temperature of the discharging process | |
| Inlet temperature of the charging process | |
| Outlet temperature of the charging process | |
| Inlet temperature of the discharging process | |
| Outlet temperature of the discharging process | |
| Environment temperature | |
| Outlet temperature of the heat exchange fluid | |
| Heat change | |
| Enthalpy difference between the end and the phase change beginning of the charging process | |
| Enthalpy difference between the beginning and the phase change beginning of the charging process | |
| The area difference between the process with the minimum and maximum mass flux | |
| Entropy production | |
| Phase change temperature difference between charging and discharging process | |
| Greek Symbols | |
| Enthalpy difference between the beginning and the phase change beginning of the discharging process | |
| Enthalpy difference between the phase change beginning and the end of the charging process | |
| Effect degree | |
| Thermodynamic properties | |
| Subscripts | |
| Extreme value | |
| Charging process | |
| Heat exchange | |
| Discharging process | |
| Minimum | |
| Maximum | |
References
- Khartchenko, N.V. Advanced Energy Systems; Institute of Energy Engineering & Technology University: Berlin, Germany, 1997. [Google Scholar]
- Hyman, L. Sustainable Thermal Storage Systems Planning Design and Operations; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Tyagi, V.V.; Buddhi, D. PCM thermal storage in buildings: A state of art. Renew. Sustain. Energy Rev. 2007, 11, 1146–1166. [Google Scholar] [CrossRef]
- Sowmy, D.S.; Prado, R.T. Assessment of energy efficiency in electric storage water heaters. Energy Build. 2008, 40, 2128–2132. [Google Scholar] [CrossRef]
- El Qarnia, H. Numerical analysis of a coupled solar collector latent heat storage unit using various phase change materials for heating the water. Energy Convers. Manag. 2009, 50, 247–254. [Google Scholar] [CrossRef]
- Regin, A.F.; Solanki, S.; Saini, J. Latent heat thermal energy storage using cylindrical capsule: Numerical and experimental investigations. Renew. Energy 2006, 31, 2025–2041. [Google Scholar] [CrossRef]
- Cahn, R. Thermal Energy Storage by Means of Reversible Heat Pumping. US Patent 4,089,744, 5 September 1978. [Google Scholar]
- Desrues, T.; Ruer, J.; Marty, P.; Fourmigué, J.F. A thermal energy storage process for large scale electric applications. Appl. Therm. Eng. 2010, 30, 425–432. [Google Scholar] [CrossRef]
- Baik, Y.; Kim, M.; Cho, J.; Ra, H.; Lee, Y.; Chang, K. Performance Variation of the TEES According to the Changes in Cold-Side Storage Temperature. Int. J. Mech. Aerosp. Ind. Mechatron. Manuf. Eng. 2014, 8, 1413–1416. [Google Scholar]
- Marguerre, F. Ueber ein neues Verfahren zur Aufspeicherung elektrischer Energie. Mitt. Ver. Elektr. 1924, 354, 27–35. [Google Scholar]
- Marguerre, F. Das thermodynamische speicherverfahren von marguerre. Escher-Wyss Mitt. 1933, 6, 67–76. [Google Scholar]
- Peterson, R.B. A concept for storing utility-scale electrical energy in the form of latent heat. Energy 2011, 36, 6098–6109. [Google Scholar] [CrossRef]
- Henchoz, S.; Buchter, F.; Favrat, D.; Morandin, M.; Mercangoz, M. Thermoeconomic analysis of a solar enhanced energy storage concept based on thermodynamic cycles. Energy 2012, 45, 358–365. [Google Scholar] [CrossRef]
- White, A.; Parks, G.; Markides, C.N. Thermodynamic analysis of pumped thermal electricity storage. Appl. Therm. Eng. 2013, 53, 291–298. [Google Scholar] [CrossRef]
- Mercangöz, M.; Hemrle, J.; Kaufmann, L.; Z’Graggen, A.; Ohler, C. Electrothermal energy storage with transcritical CO2 cycles. Energy 2012, 45, 407–415. [Google Scholar] [CrossRef]
- Kim, Y.; Shin, D.; Lee, S.; Favrat, D. Isothermal transcritical CO2 cycles with TES (thermal energy storage) for electricity storage. Energy 2013, 49, 484–501. [Google Scholar] [CrossRef]
- Morandin, M.; Mercangöz, M.; Hemrle, J.; Maréchal, F.; Favrat, D. Thermoeconomic design optimization of a thermo-electric energy storage system based on transcritical CO2 cycles. Energy 2013, 58, 571–587. [Google Scholar] [CrossRef]
- Morandin, M.; Marechal, F.; Mercangoz, M.; Buchter, F. Conceptual design of a thermoeelectrical energy storage system based on heat integration of thermodynamic cycles e part A: Methodology and base case. Energy 2012, 45, 375–385. [Google Scholar] [CrossRef]
- Morandin, M.; Marechal, F.; Mercangoz, M.; Buchter, F. Conceptual design of a thermoeelectrical energy storage system based on heat integration of thermodynamic cycles e part B: Alternative system configurations. Energy 2012, 45, 386–396. [Google Scholar] [CrossRef]
- Baik, Y.; Heo, J.; Koo, J.; Kim, M. The effect of storage temperature on the performance of a thermoelectric energy storage using a transcritical CO2 cycle. Energy 2014, 75, 204–215. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Production Minimization; CRC Press: Boca Raton, FL, USA, 1996; pp. 47–112. [Google Scholar]
- Johannessen, E.; Nummedal, L.; Kjelstrup, S. Minimizing the entropy production in heat exchange. Int. J. Heat Mass Transf. 2002, 45, 2649–2654. [Google Scholar] [CrossRef]
- Balkan, F. Application of EoEP principle with variable heat transfer coefficient in minimizing entropy production in heat exchangers. Energy Convers. Manag. 2005, 46, 2134–2144. [Google Scholar] [CrossRef]
- Guo, Z.; Zhu, H.; Liang, X. Entransy—A physical quantity describing heat transfer ability. Int. J. Heat Mass Transf. 2007, 50, 2545–2556. [Google Scholar] [CrossRef]
- JiangFeng, G.; MingTian, X.; Lin, C. Principle of equipartition of entransy dissipation for heat exchanger design. Sci. China Technol. Sci. 2010, 53, 1309–1314. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, P.; Zhang, G.-W.; Chen, L.-X.; Liu, M.-H. Theoretical Analysis for Heat Transfer Optimization in Subcritical Electrothermal Energy Storage Systems. Energies 2017, 10, 198. https://doi.org/10.3390/en10020198
Hu P, Zhang G-W, Chen L-X, Liu M-H. Theoretical Analysis for Heat Transfer Optimization in Subcritical Electrothermal Energy Storage Systems. Energies. 2017; 10(2):198. https://doi.org/10.3390/en10020198
Chicago/Turabian StyleHu, Peng, Gao-Wei Zhang, Long-Xiang Chen, and Ming-Hou Liu. 2017. "Theoretical Analysis for Heat Transfer Optimization in Subcritical Electrothermal Energy Storage Systems" Energies 10, no. 2: 198. https://doi.org/10.3390/en10020198
APA StyleHu, P., Zhang, G.-W., Chen, L.-X., & Liu, M.-H. (2017). Theoretical Analysis for Heat Transfer Optimization in Subcritical Electrothermal Energy Storage Systems. Energies, 10(2), 198. https://doi.org/10.3390/en10020198




