Fuzzy Logic-Based Operation of Battery Energy Storage Systems (BESSs) for Enhancing the Resiliency of Hybrid Microgrids
Abstract
:1. Introduction
- In contrast to the existing literature, where microgrids have been used as a resiliency resource, an algorithm for enhancing the resiliency of microgrids themselves is proposed.
- Uncertain nature of disturbance events is considered and realized through fuzzy logic in contrast to the literature, where uncertain nature of renewables and market price are focused.
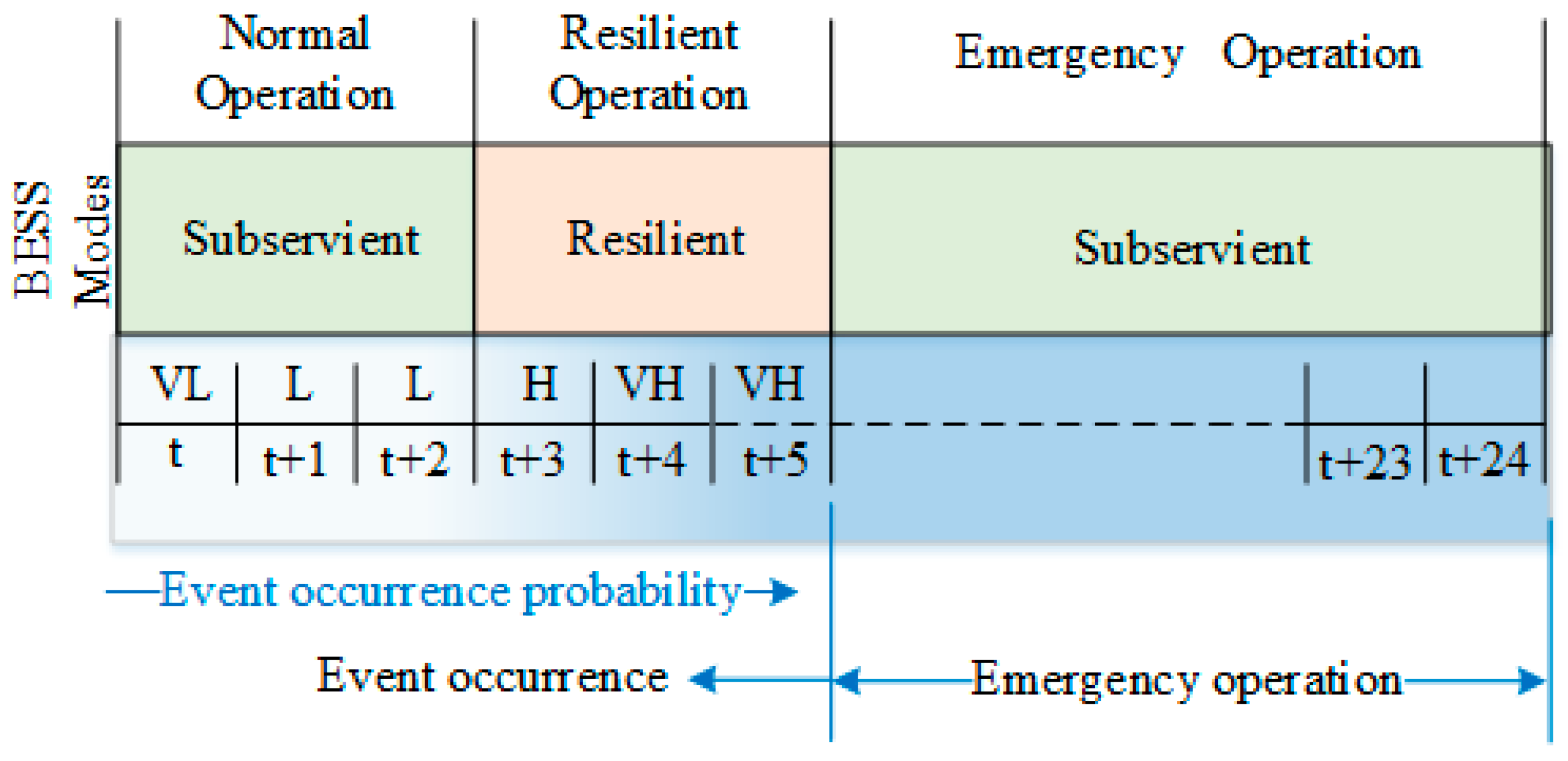
- In addition to normal and emergency modes of microgrids, an additional mode (resilient mode) is suggested in this study to ensure the survivability of critical loads during disturbance intervals.
- Two operation modes (subservient and resilient) have been suggested for the BESS units to minimize the operation cost and to prepare the microgrid for feasible islanding.
2. Fuzzy Logic-Based Operation of Battery Energy Storage System (BESS)
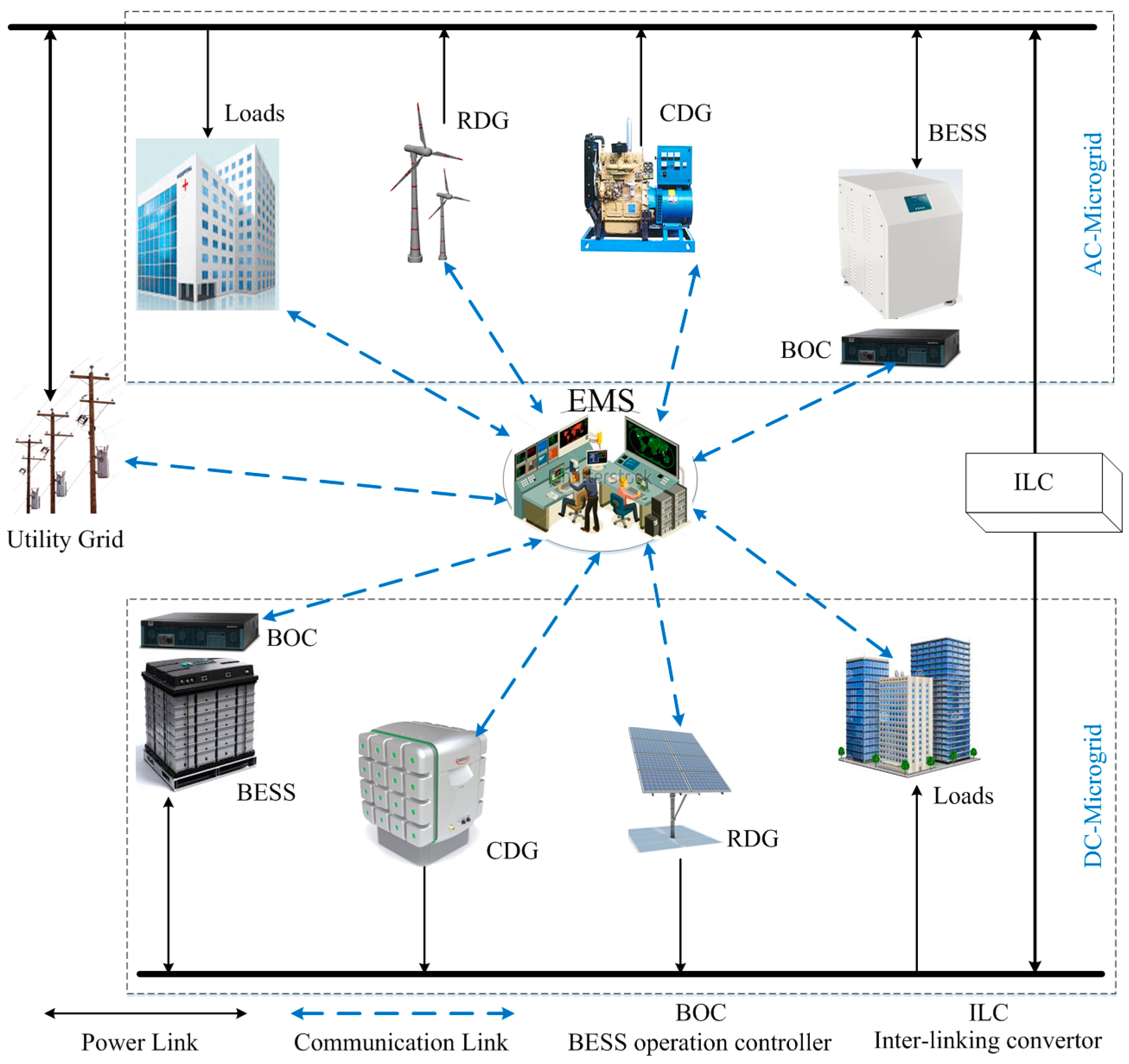
2.1. System Configuration
2.2. BESS Operation Modes
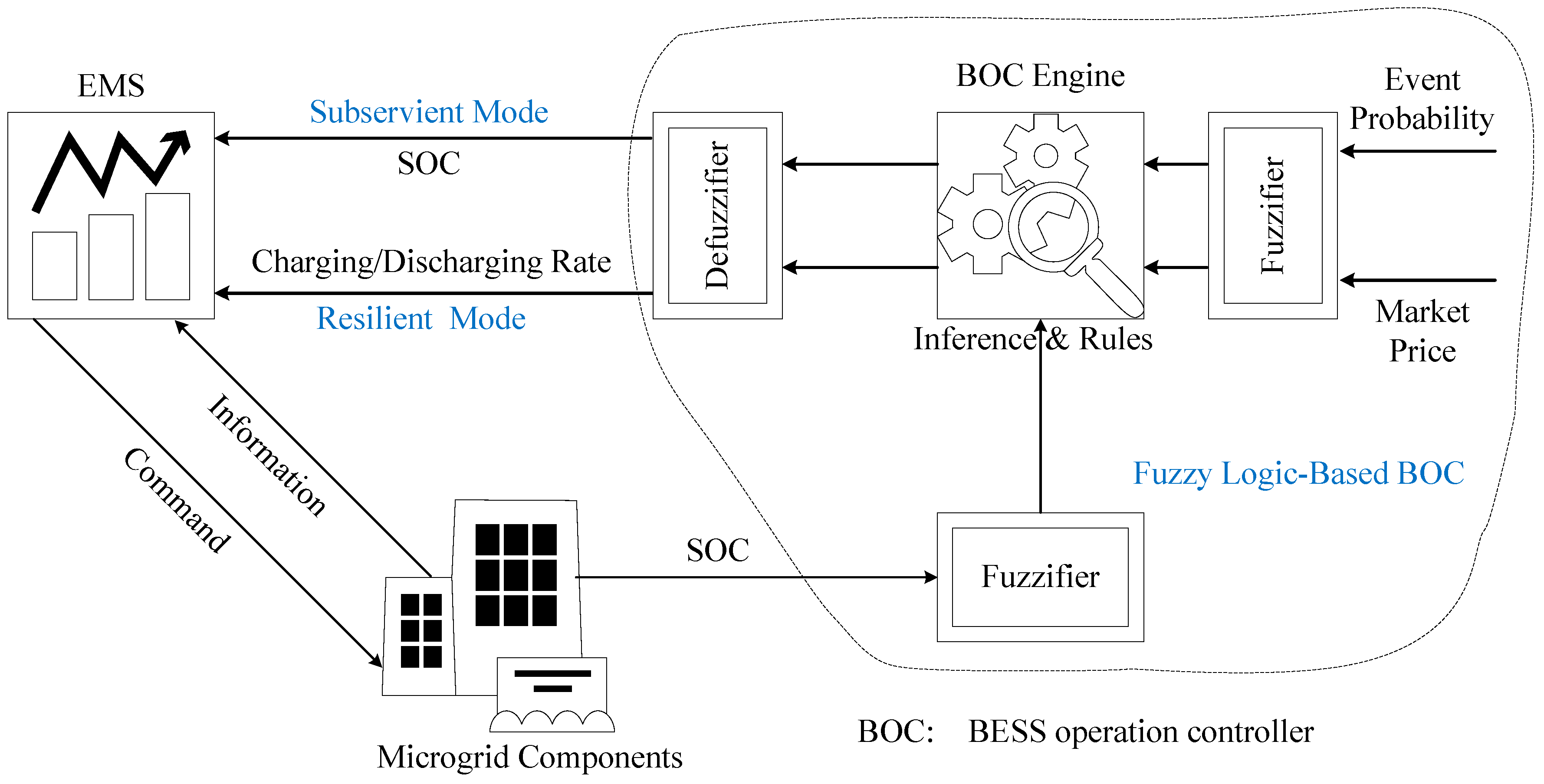
2.3. Interaction between the EMS and the BESS Operation Controller
- EMS receives the information about the components of the microgrid and shares the required information (market price and BESS SOC) with the BESS operation controller.
- The BESS operation controller receives event occurrence information from a separate entity and also uses the information provided by the EMS and decides the operation modes of the BESS units.
- The BESS operation controller informs the EMS about the decided operation modes of the BESS units and related information i.e., BESS SOC or charging/discharging rates.
- In the subservient mode, the BESS follows the commands of the EMS while in the case of resilient mode, the EMS charges/discharges the BESS units according to the rates decided by the BESS operation controller.
- The EMS evaluates the operation mode of microgrid and chooses one of the three optimization algorithms, as formulated in Section 3.
- After optimization, all the components of the microgrid are informed with the optimal results by the EMS.
- The same process is repeated till the end of the scheduling horizon.
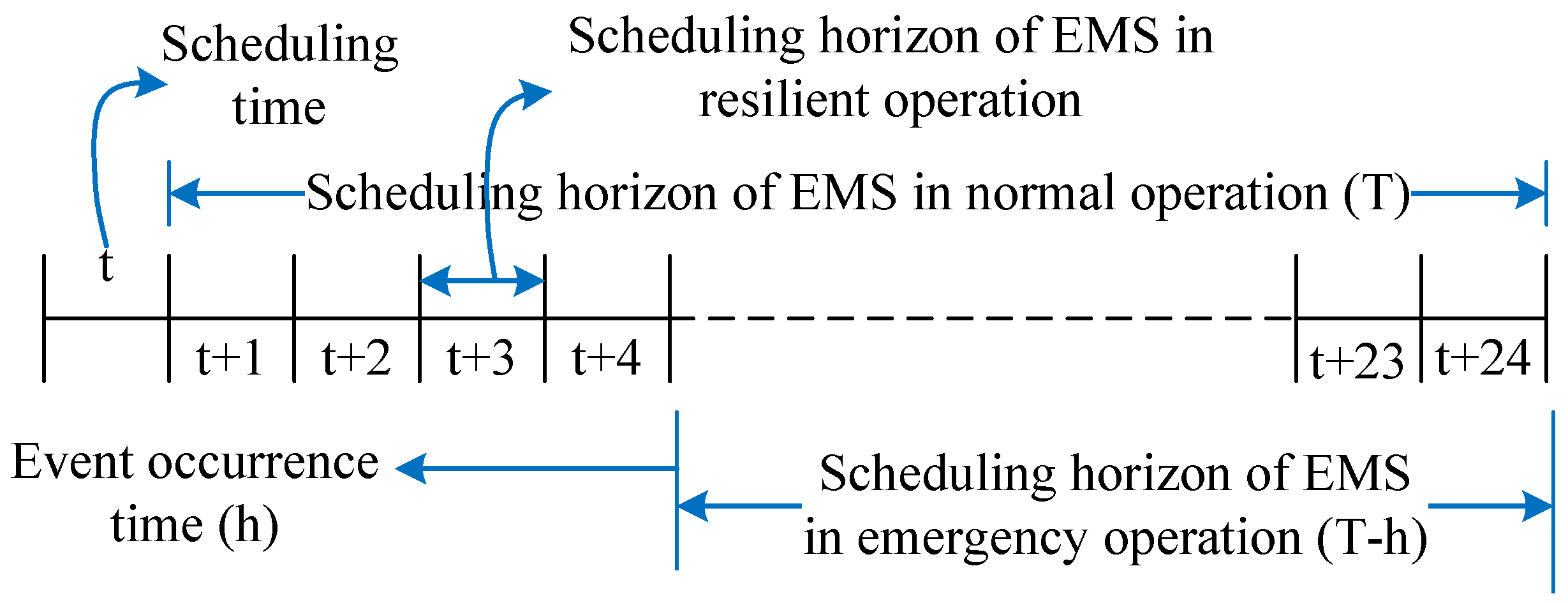
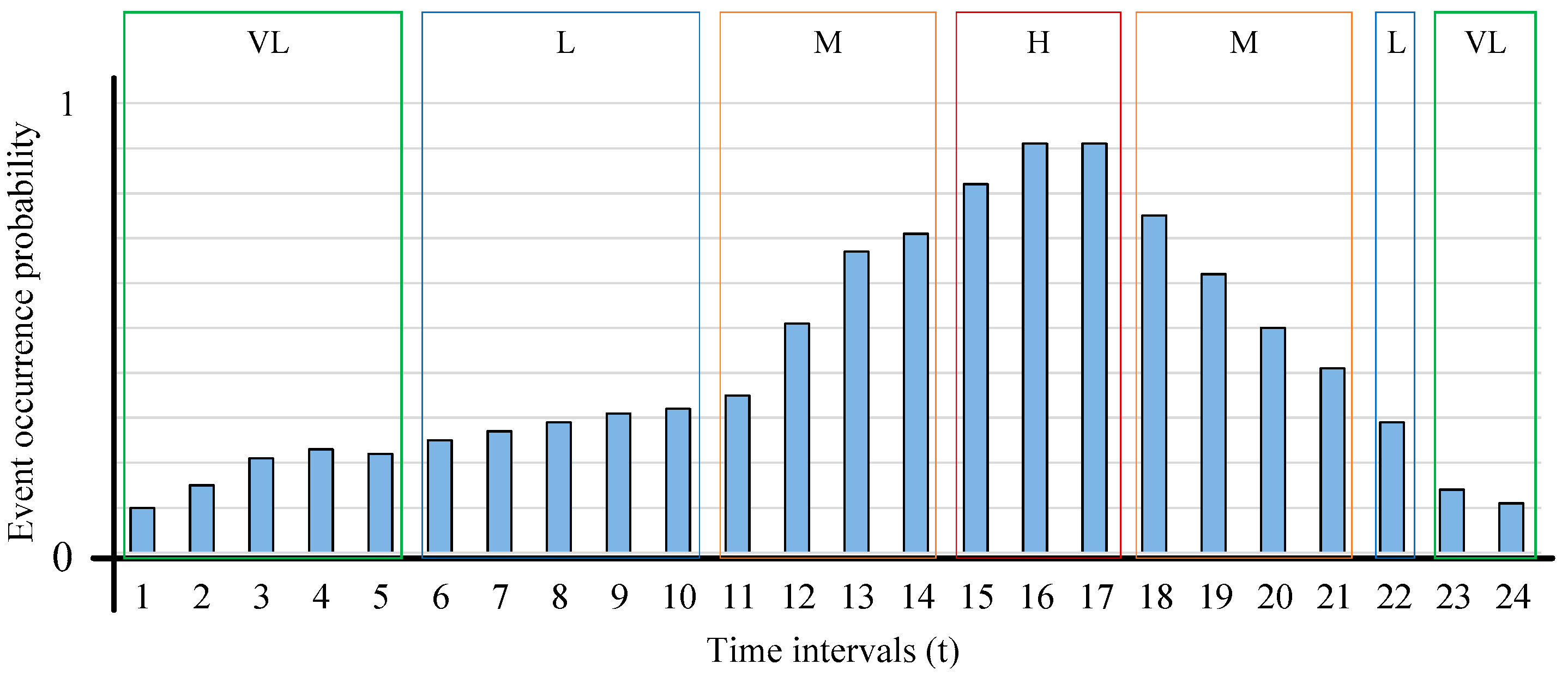
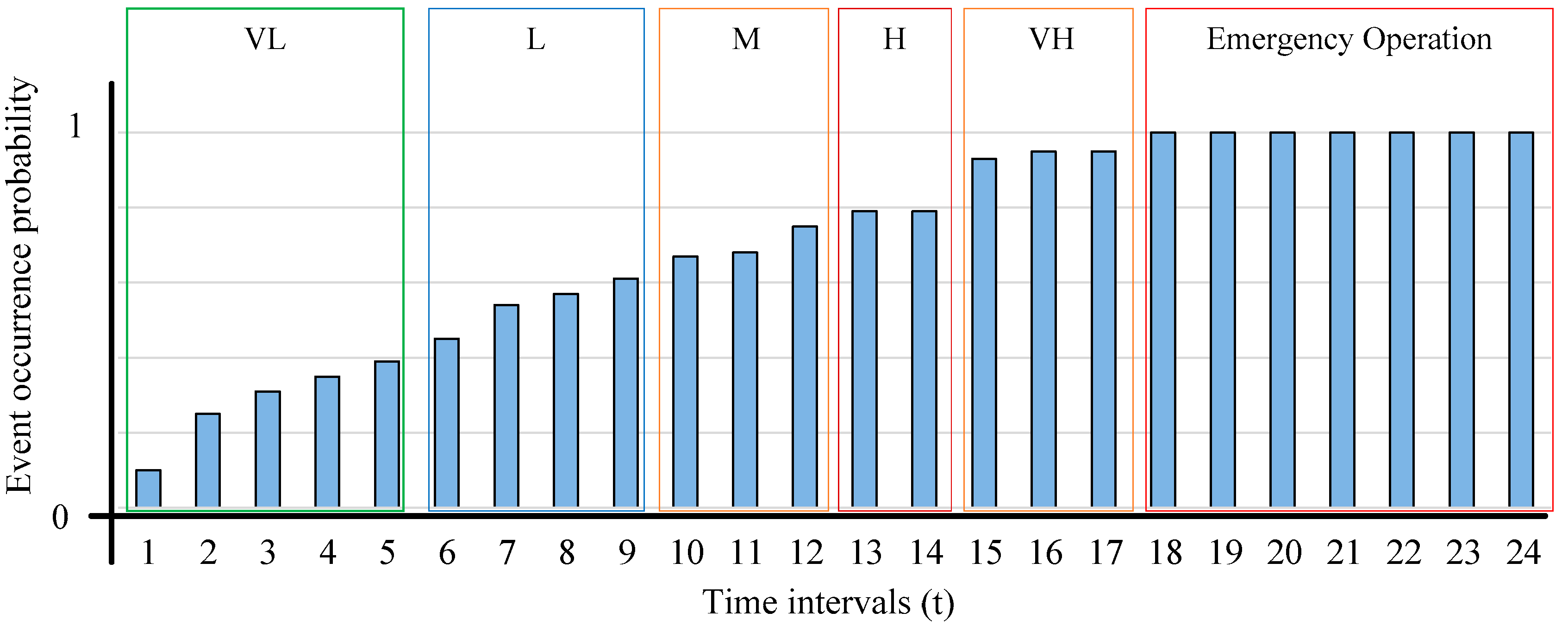
2.4. Scheduling Horizons
3. Problem Formulation
3.1. Normal Operation
3.1.1. Objective Function
3.1.2. Load Balancing Constraints
3.1.3. Constraints for Controllable Generators
3.1.4. Battery Constraints
3.2. Resilient Mode
3.2.1. Objective Function
3.2.2. BESS Charging/Discharging Rate Constraints
3.2.3. Other Constraints
3.3. Emergency Mode
3.3.1. Objective Function
3.3.2. Load Balancing Constraints
3.3.3. Other Constraints
4. Numerical Simulations
4.1. Input Parameters
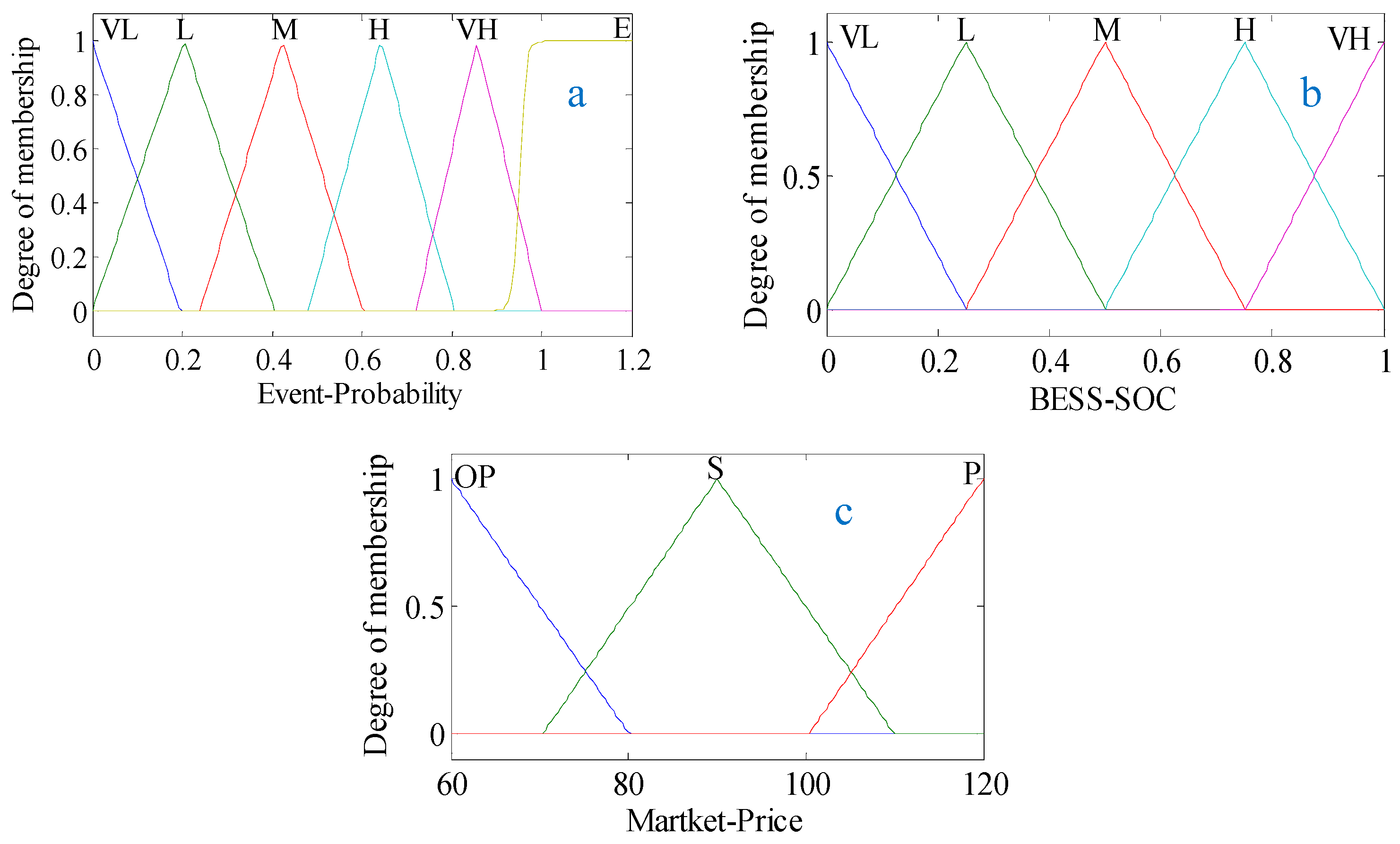
4.2. Control Surfaces for BESS Operation Controller
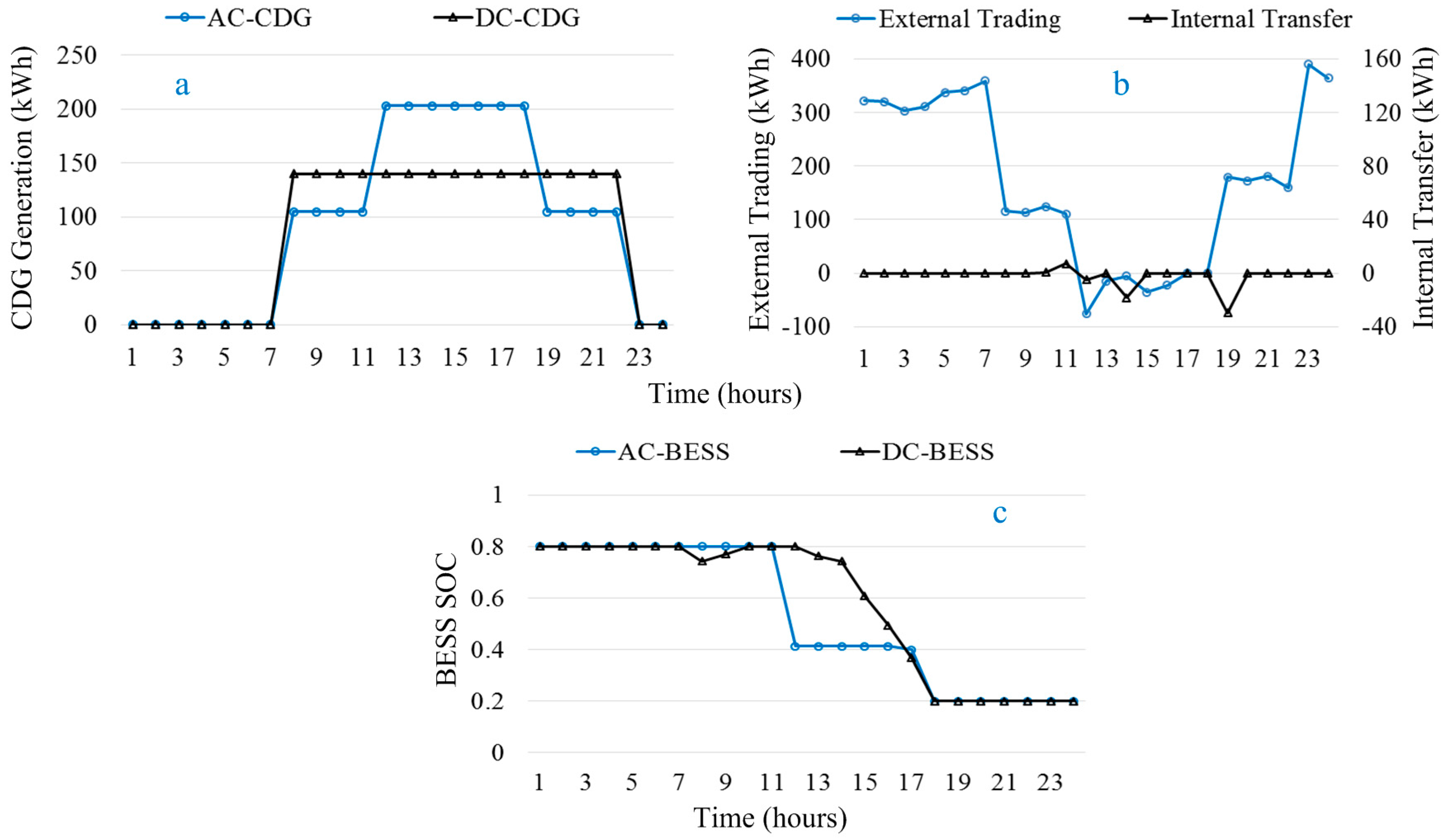
4.3. Normal Operation Mode
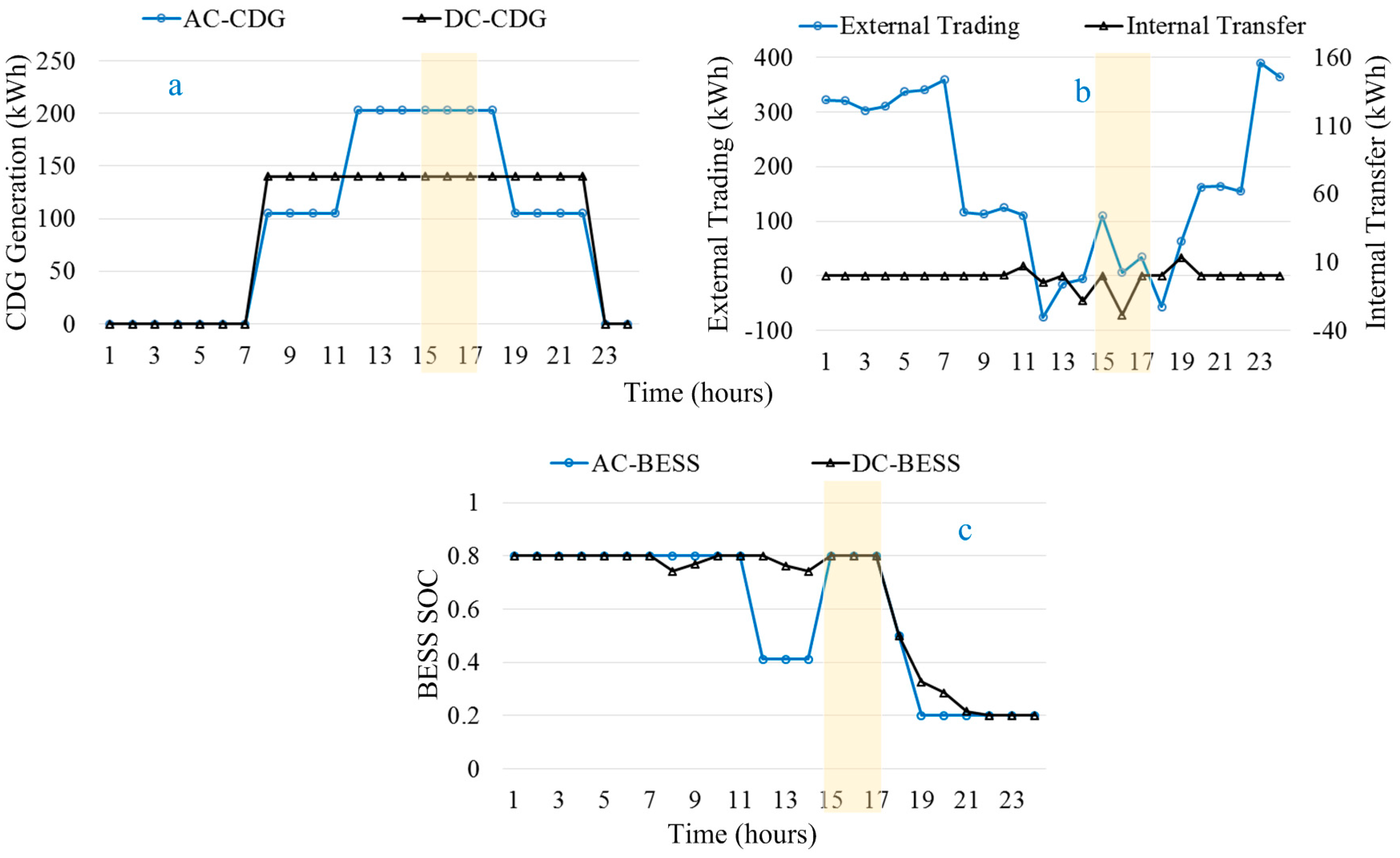
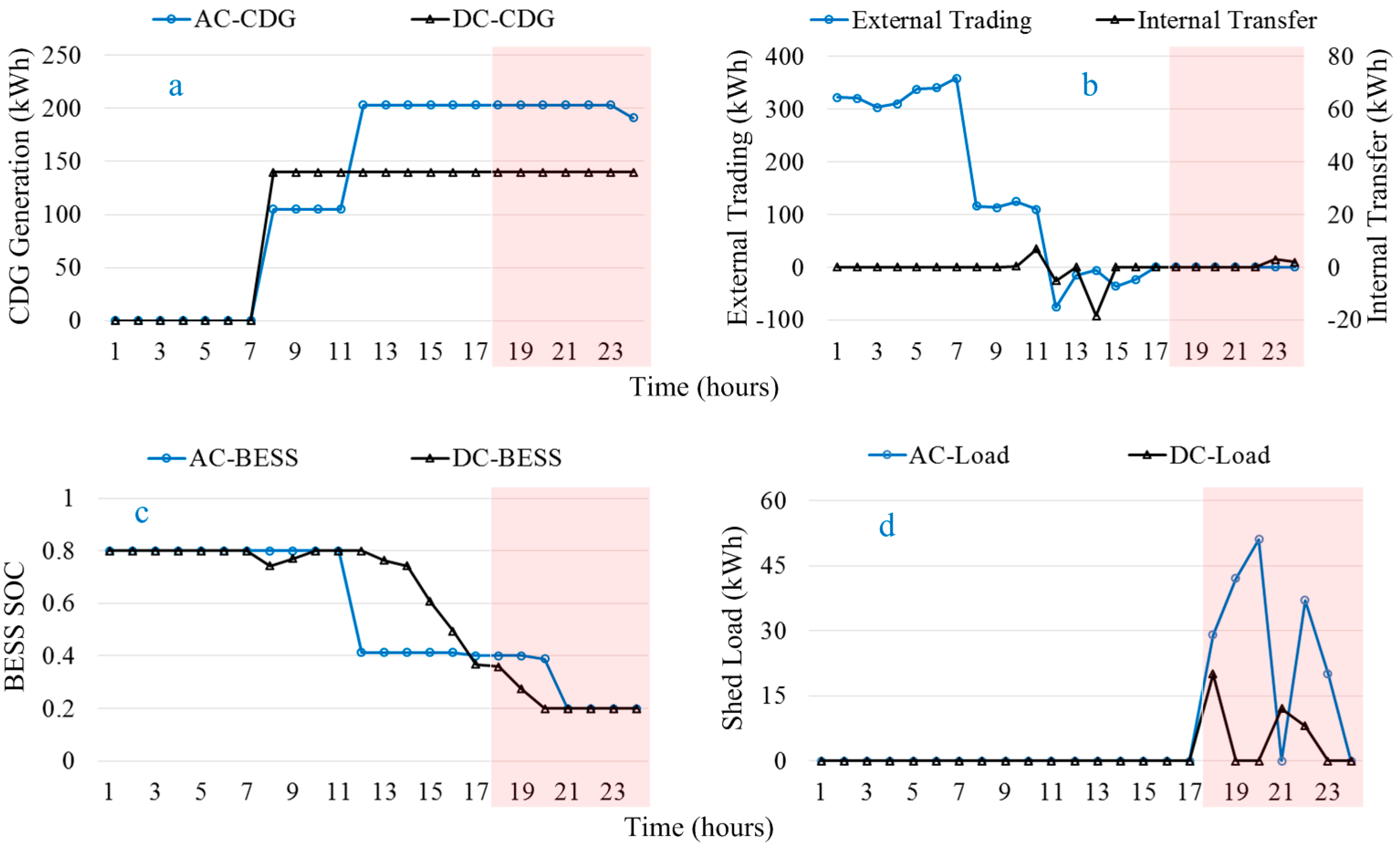
4.4. Emergency Operation Mode
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Index of time, running from 1 to | |
| Index for total, AC side, and DC side CDGs, respectively | |
| Commitment, startup, and shutdown status identifier of gth CDG at t | |
| Generation cost of CDG unit at t | |
| , | Start-up and shutdown cost of CDG unit at t |
| , | Price for buying and selling power to/from the utility grid at t |
| Amount of power generated by CDG g at t | |
| , | Total amount of power bought from and sold to the utility grid at t |
| , | Amount of power bought from and sold to the utility grid by AC microgrid at t |
| , | Amount of power bought from and sold to the utility grid by DC microgrid at t |
| Forecasted electric load of AC and DC side microgrids at t | |
| Amount of power transferred from DC to AC and AC to DC microgrids at t | |
| Amount of power generated by AC and DC side RDG units at t | |
| Capacity and efficiency of interlinking converter | |
| Minimum and maximum generation amount of gth CDG unit | |
| Ramp-up and Ramp-down time of gth CDG unit | |
| , | Amount of electrical energy charged/discharged to/from BESS at t |
| , | Charging and discharging losses of X-type BESS unit |
| Capacity and SOC of BESS X-type BESS unit | |
| Lower and upper limits for SOC of X-type BESS unit | |
| C-rates for charging and discharging of BESS units | |
| Amount of load shed from AC and DC side microgrids at t | |
| Total amount of shed load and penalty cost for load shedding at t |
References
- Khodaei, A. Resiliency-oriented microgrid optimal scheduling. IEEE Trans. Smart Grid 2014, 5, 1584–1591. [Google Scholar] [CrossRef]
- Arghandeh, R.; Von, M.A.; Mehrmanesh, L.; Mili, L. On the definition of cyber-physical resilience in power systems. Renew. Sustain. Energy Rev. 2016, 58, 1060–1069. [Google Scholar] [CrossRef]
- Simonov, M. Dynamic partitioning of DC microgrid in resilient clusters using event-driven approach. IEEE Trans. Smart Grid 2014, 5, 2618–2625. [Google Scholar] [CrossRef]
- Schneider, K.; Tuffner, F.; Elizondo, M.; Liu, C.C.; Xu, Y.; Ton, D. Evaluating the feasibility to use microgrids as a resiliency resource. IEEE Trans. Smart Grid 2016, 8. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.H.; Kim, H.M. A resilient and privacy-preserving energy management strategy for networked microgrids. IEEE Trans. Smart Grid 2016, pp. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J.; Chen, C. Networked microgrids for self-healing power systems. IEEE Trans. Smart Grid 2016, 7, 310–319. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J. Self-healing resilient distribution systems based on sectionalization into microgrids. IEEE Trans. Power Syst. 2015, 30, 3139–3149. [Google Scholar] [CrossRef]
- Balasubramaniam, K.; Saraf, P.; Hadidi, R.; Makram, E.B. Energy management system for enhanced resiliency of microgrids during islanded operation. Electr. Power Syst. Res. 2016, 137, 133–141. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.H.; Kim, H.M. Optimal operation of hybrid microgrids for enhancing resiliency considering feasible islanding and survivability. IET Renew. Power Gener. 2017. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, C.; Wang, J.; Baldick, R. Research on resilience of power systems under natural disasters—A review. IEEE Trans. Power Syst. 2016, 31, 1604–1613. [Google Scholar] [CrossRef]
- Panteli, M.; Mancarella, P. Influence of extreme weather and climate change on the resilience of power systems: Impacts and possible mitigation strategies. Electr. Power Syst. Res. 2015, 127, 259–270. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Fouad, M. Control and Optimization of Distributed Generation Systems; Springer: London, UK, 2015. [Google Scholar]
- García, P.; Torreglosa, J.P.; Fernández, L.M.; Jurado, F. Optimal energy management system for stand-alone wind turbine/photovoltaic/hydrogen/battery hybrid system with supervisory control based on fuzzy logic. Int. J. Hydrog. Energy 2013, 38, 14146–14158. [Google Scholar] [CrossRef]
- Li, S.G.; Sharkh, S.M.; Walsh, F.C.; Zhang, C.N. Energy and battery management of a plug-in series hybrid electric vehicle using fuzzy logic. IEEE Trans. Veh. Technol. 2011, 60, 3571–3585. [Google Scholar] [CrossRef]
- Chen, Y.K.; Wu, Y.C.; Song, C.C.; Chen, Y.S. Design and implementation of energy management system with fuzzy control for DC microgrid systems. IEEE Trans. Power Electron. 2013, 28, 1563–1570. [Google Scholar] [CrossRef]
- Kyriakarakos, G.; Dounis, A.I.; Arvanitis, K.G.; Papadakis, G. A fuzzy logic energy management system for polygeneration microgrids. Renew. Energy 2012, 41, 315–327. [Google Scholar] [CrossRef]
- Sayed, K.; Gabbar, H.A. Electric vehicle to power grid integration using three-phase three-level AC/DC converter and PI-fuzzy controller. Energies 2016, 9, 532. [Google Scholar] [CrossRef]
- Koirala, B.P.; Chaves, Á.J.P.; Gómez, T.; Hakvoort, R.A.; Herder, P.M. Local alternative for energy supply: Performance assessment of integrated community energy systems. Energies 2016, 9, 981. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Salmasi, F.R. Power management of an isolated hybrid AC/DC micro-grid with fuzzy control of battery banks. IET Renew. Power Gener. 2015, 9, 484–493. [Google Scholar] [CrossRef]
- Aryani, D.R.; Song, H. Coordination control strategy for AC/DC hybrid microgrids in stand-alone mode. Energies 2016, 9, 469. [Google Scholar] [CrossRef]
- Baboli, P.T.; Shahparasti, M.; Moghaddam, M.P.; Haghifam, M.R.; Mohamadian, M. Energy management and operation modelling of hybrid AC–DC microgrid. IET Gener. Transm. Distrib. 2014, 8, 1700–1711. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, X.; Wang, X.; Lin, C.; Guerrero, J.M. A coordinated control for photovoltaic generators and energy storages in low-voltage AC/DC hybrid microgrids under islanded mode. Energies 2016, 9, 651. [Google Scholar] [CrossRef]
- STI Policy Profiles: Facing New Challenges, Technology to Manage Natural Disasters and Catastrophes. Available online: http://www.wmo.int/pages/index_en.html (accessed on 22 February 2017).
- Hussain, A.; Bui, V.H.; Kim, H.M. Robust optimization-based scheduling of multi-microgrids considering uncertainties. Energies 2016, 9, 278. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.H.; Kim, H.M.; Im, Y.H.; Lee, J.Y. Optimal operation of tri-generation microgrids considering demand uncertainties. Int. J. Smart Home 2016, 10, 131–144. [Google Scholar] [CrossRef]
- Battery University-C-Rates. Available online: http://batteryuniversity.com/learn/article/what_is_the_c_rate (accessed on 22 February 2017).
- Texas Instruments. Characteristics of Rechargeable Batteries; Texas Instruments: Dallas, TX, USA, 2011. [Google Scholar]
- Bai, Y.; Wang, D. Fundamentals of fuzzy logic control—Fuzzy sets, fuzzy rules and defuzzifications. In Advanced Fuzzy Logic Technologies in Industrial Applications; Springer: London, UK, 2006. [Google Scholar]





| Time (Hours) | Electric Load (kWh) | Renewable Power (kWh) | Market Price Signals (KRW) | |||
|---|---|---|---|---|---|---|
| AC-MG | DC-MG | PV | WT | Buying Price | Selling Price | |
| 1 | 215 | 110 | 0 | 5 | 100 | 80 |
| 2 | 206 | 119 | 0 | 7 | 100 | 80 |
| 3 | 197 | 114 | 0 | 10 | 100 | 80 |
| 4 | 209 | 111 | 0 | 12 | 100 | 80 |
| 5 | 216 | 125 | 0 | 6 | 100 | 80 |
| 6 | 212 | 130 | 0 | 4 | 100 | 80 |
| 7 | 219 | 140 | 0 | 3 | 100 | 80 |
| 8 | 228 | 158 | 4 | 7 | 115 | 100 |
| 9 | 227 | 142 | 9 | 9 | 115 | 100 |
| 10 | 242 | 144 | 12 | 12 | 115 | 100 |
| 11 | 237 | 147 | 14 | 15 | 115 | 100 |
| 12 | 234 | 162 | 17 | 17 | 135 | 125 |
| 13 | 216 | 169 | 20 | 28 | 135 | 125 |
| 14 | 199 | 182 | 19 | 20 | 135 | 125 |
| 15 | 181 | 189 | 16 | 14 | 135 | 125 |
| 16 | 190 | 179 | 11 | 10 | 135 | 125 |
| 17 | 214 | 178 | 7 | 8 | 135 | 125 |
| 18 | 255 | 184 | 3 | 3 | 135 | 125 |
| 19 | 261 | 169 | 0 | 6 | 115 | 100 |
| 20 | 274 | 150 | 0 | 7 | 115 | 100 |
| 21 | 280 | 157 | 0 | 11 | 115 | 100 |
| 22 | 275 | 144 | 0 | 15 | 115 | 100 |
| 23 | 265 | 141 | 0 | 19 | 100 | 80 |
| 24 | 237 | 148 | 0 | 24 | 100 | 80 |
| MGs | BESS | CDG1 | CDG2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (%) | (%) | (kWh) | (kWh) | (kWh) | (kWh) | (KRW/kWh) | (kWh) | (kWh) | (KRW/kWh) | |
| AC MG | 2 | 2 | 50 | 250 | 0 | 105 | 112 | 0 | 98 | 118 |
| DC MG | 2 | 2 | 50 | 250 | 0 | 75 | 106 | 0 | 65 | 103 |
| Total | 4 | 4 | 100 | 500 | 0 | 180 | - | 0 | 163 | - |
| Cases | Generation (kWh) | Internal Trading (kWh) | External Trading (kWh) | Operation Cost (KRW) * |
|---|---|---|---|---|
| Conventional | 4361 | 60.48 | 4358.85 | 895,255 |
| Proposed | 4361 | 72.96 | 4358.1 | 898,797 |
| Cases | Generation (kWh) | Internal Trading (kWh) | External Trading (kWh) | Load Shed (kWh) | Operation Cost (KRW) * |
|---|---|---|---|---|---|
| Conventional | 5427.08 | 35.89 | 2912.73 | 219.2 | 981,143.4 |
| Proposed | 5427.08 | 169.23 | 2969.26 | 17.73 | 919,046.6 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, A.; Bui, V.-H.; Kim, H.-M. Fuzzy Logic-Based Operation of Battery Energy Storage Systems (BESSs) for Enhancing the Resiliency of Hybrid Microgrids. Energies 2017, 10, 271. https://doi.org/10.3390/en10030271
Hussain A, Bui V-H, Kim H-M. Fuzzy Logic-Based Operation of Battery Energy Storage Systems (BESSs) for Enhancing the Resiliency of Hybrid Microgrids. Energies. 2017; 10(3):271. https://doi.org/10.3390/en10030271
Chicago/Turabian StyleHussain, Akhtar, Van-Hai Bui, and Hak-Man Kim. 2017. "Fuzzy Logic-Based Operation of Battery Energy Storage Systems (BESSs) for Enhancing the Resiliency of Hybrid Microgrids" Energies 10, no. 3: 271. https://doi.org/10.3390/en10030271
APA StyleHussain, A., Bui, V.-H., & Kim, H.-M. (2017). Fuzzy Logic-Based Operation of Battery Energy Storage Systems (BESSs) for Enhancing the Resiliency of Hybrid Microgrids. Energies, 10(3), 271. https://doi.org/10.3390/en10030271








