Real-Power Rescheduling of Generators for Congestion Management Using a Novel Satin Bowerbird Optimization Algorithm

Abstract

In this paper, an efficient meta-heuristic satin bowerbird optimization (SBO) algorithm is presented for congestion management (CM) in the deregulated power system. The main objective of CM is to relieve congestion in the transmission lines using a generation rescheduling-based approach, while satisfying all the constraints with minimum congestion cost. The SBO is a nature-inspired algorithm, developed based on the ‘male-attracts-the-female for breeding’ principle of the specialized stick structure mechanism of satin birds. The proposed approach is effectively tested on small and large test systems, namely, modified IEEE 30-bus, modified IEEE 57-bus, and IEEE 118-bus test systems. The constraints like line loading, line limits, generator limits, and bus voltage impact, etc., are incorporated into this study. The proposed technique gives superior results with regards to congestion cost and losses compared with various recent optimization algorithms.

1. Introduction

The electric power industry is switching over from being vertically integrated into being a deregulated utility. The vertical utility system has common control over all the transmissions, distributions, and generations in the power system. In a deregulated utility system, the transmission, distribution, and generation systems work independently of the environment and, thus, it becomes a challenge for independent system operators (ISOs) to manage [1]. Congestion management (CM) plays a vital role in the deregulated electricity market environment. The power flowing through the transmission network is limited by the voltage, thermal, and stability limits. Whenever constraints imposed by the operation and physical limits of the transmission network become active, it is said to be Congestion. Congestion occurs in the transmission network due to natural hazards, transmission line failure due to miss-operation, and all the market participants purchasing the power from the cheapest sources of the area at the same time. To relieve the congestion in overloaded lines, various methods and approaches are used, as given in [2,3]. To manage the operation of transmission systems in a deregulated power system based on optimal power flow (OPF), price–area congestion control and a transaction-based model CM problem have been analyzed in depth [4]. In [5], a thorough study has been done of a CM problem solution, based on re-dispatch and a unified framework for a mathematical representation of the market dispatch in various electricity markets all over the world. Phase-shifters and multi-tap transformers can assist in avoiding the difficulty of congestion without re-dispatching generation from the preferred schedules of transactions. The effect of contingency-imposed limits on CM, by an independent system operator (ISO), to lesser adjustments to the preferred schedules to overcome the congestion in the system, has also been analyzed [6]. Mathematical models of evolutionary approaches solved zonal congestion based on sensitivity indices, which are termed as Real-power and Reactive-power Transmission Congestion Distribution Factors [7]. The rescheduling of generators for CM with a three block structure, offered by the generating companies (GENCOs), has been analyzed and carried out for a hybrid power market considering constant impedance, current, and power [8]. In [9], an efficient particle swarm optimization (PSO) was made use of for the real-power rescheduling of generators for CM in a deregulated environment. Use of the random search method (RSM) for solving various optimization problems has been analyzed [10]. Rescheduling of generators for CM with flexible AC transmission system flexible alternating current transmission system (FACTS) in a deregulated electricity market has been evaluated [11]. In [12], a real-coded genetic algorithm (RCGA) was used to locate the optimal generation rescheduling for CM in a deregulated environment. Nature-inspired algorithms based on swarm intelligence [13], like the firefly algorithm [14], flower pollination algorithm [15], bat algorithm [16], etc., have exhibited their worth and, consequently, become popular and broadly used by scholars. In [17], a novel symbiotic organism search (SOS) algorithm was the focus. It is based on the symbiotic interactions of organisms coexisting in an ecosystem. The key advantages of the SOS algorithm compared with other meta-heuristic algorithms are the fast convergence rate, the shorter computational time, and the fact that no specific parameters are required. This paper puts forth an SBO algorithm, for CM to lessen the losses and congestion cost of the system by a generator rescheduling method.

1.1. Inspiration of SBO

The proposed new optimization algorithms effectively solve CM problems with various contingency case studies by changing the real-power of the generators with less cost. The major inspiration behind the introduction of this work is as follows:

(a)

SBO provides competitive or slightly better performance compared with other bio-inspired algorithms in a stand test function;

(b)

SBO has good exploitation capabilities, which optimize the solution through small and reasonable changes in variables;

(c)

SBO performs with real-world data sets, unlike other bio-inspired algorithms; and

(d)

SBO focuses on the best solution while constantly searching for new solutions in the search space.

1.2. Objective of the Present Work

The main purpose of this work is documented below:

(a)

SBO algorithm tool effectively minimizes the changing generator real-power rescheduling cost;

(b)

Effectively relieves the congestion in overloaded lines with different contingency cases; and

(c)

Minimizes the losses indifferent contingencies of the test system cases.

2. Mathematical Problem Formulation

The mathematical formulation of the CM problem with minimum cost is stated in Equation (1) [9]:

$$\mathrm{Minimize}{\mathrm{C}}_{\mathrm{t}}={{\displaystyle \sum }}_{j\in {\mathrm{N}}_{\mathrm{g}}}({\mathrm{C}}_{\mathrm{tG}}\Delta {\mathrm{P}}_{\mathrm{Gj}}^{+}+{\mathrm{D}}_{\mathrm{tG}}\Delta {\mathrm{P}}_{\mathrm{Gj}}^{-})\$/\mathrm{h}$$

(1)

where Z_t, C_tG, D_tG, ${\mathrm{N}}_{\mathrm{g}}$, $\Delta {\mathrm{P}}_{\mathrm{Gj}}^{+}$, and $\Delta {\mathrm{P}}_{\mathrm{Gj}}^{-}$ represent the total cost of changing the generator real-power output ($/h),the total number of generators, the incremental/decremental price bid by the generator company ($/MWh), the real-power increment of the jth generator (MW), and the real-power decrement of the jth generator (MW), respectively.

2.1. Equality Constraints

The mathematical formulation of the equality constraints corresponds to the CM representation. The power flow equations are stated by the following equations (Equations (2)–(5)) [18].

$${\mathrm{P}}_{\mathrm{Gk}}-{\mathrm{P}}_{\mathrm{Dk}}={\displaystyle \sum }_{\mathrm{j}}\left|{\mathrm{V}}_{\mathrm{j}}\right|\left|{\mathrm{V}}_{\mathrm{k}}\right|\left|{\mathrm{Y}}_{\mathrm{kj}}\right|\cos ({\mathsf{\delta }}_{\mathrm{k}}-{\mathsf{\delta }}_{\mathrm{j}}-{\mathsf{\theta }}_{\mathrm{kj}});\mathrm{j}=1,2,\dots ,{\mathrm{N}}_{\mathrm{b}},$$

(2)

$${\mathrm{Q}}_{\mathrm{Gk}}-{\mathrm{Q}}_{\mathrm{Dk}}={\displaystyle \sum }_{\mathrm{j}}\left|{\mathrm{V}}_{\mathrm{j}}\right|\left|{\mathrm{V}}_{\mathrm{k}}\right|\left|{\mathrm{Y}}_{\mathrm{kj}}\right|\sin ({\mathsf{\delta }}_{\mathrm{k}}-{\mathsf{\delta }}_{\mathrm{j}}-{\mathsf{\theta }}_{\mathrm{kj}});\mathrm{j}=1,2,\dots ,{\mathrm{N}}_{\mathrm{b}},$$

(3)

$${\mathrm{P}}_{\mathrm{Gk}}={\mathrm{P}}_{\mathrm{Gk}}^{\mathrm{c}}+\Delta {\mathrm{P}}_{\mathrm{Gk}}^{+}-\Delta {\mathrm{P}}_{\mathrm{Gk}}^{-};\mathrm{k}=1,2,\dots ,{\mathrm{N}}_{\mathrm{g}},$$

(4)

$${\mathrm{P}}_{\mathrm{Dj}}={\mathrm{P}}_{\mathrm{Dj}}^{\mathrm{c}};\mathrm{j}=1,2,\dots ,{\mathrm{N}}_{\mathrm{d}},$$

(5)

where P_Gk and Q_Gk represent the generated real and reactive powers at the kth bus; P_Dk and Q_Dk represent the real and reactive load powers at the kth bus; V_j and V_k represent the voltages at the jth bus and kth bus; δ_j and δ_k represent the bus voltage angle at the jth and kth buses; θ_kj is the admittance angle of the line connecting the kth and jth buses; N_b, N_g, N_d are the number of used buses, generators and loads, respectively; and ${\mathrm{P}}_{\mathrm{Gk}}^{\mathrm{c}}$ and ${\mathrm{P}}_{\mathrm{Dj}}^{\mathrm{c}}$ are the real-power produced by the kth generator and the real-power consumed by the jth load, respectively. Equations (2) and (3) note the real and reactive powers at each node, whereas (4) and (5) note the market clearing price.

2.2. Inequality Constraints

The operational and physical limits of the generators, transmission lines, and transformers-as stated by the following equations-are-

$${\mathrm{P}}_{\mathrm{Gk}}^{\min }\le {\mathrm{P}}_{\mathrm{Gk}}\le {\mathrm{P}}_{\mathrm{Gk}}^{\max },\forall \mathrm{k}\in {\mathrm{N}}_{\mathrm{g}}$$

(6)

$${\mathrm{Q}}_{\mathrm{Gk}}^{\min }\le {\mathrm{Q}}_{\mathrm{Gk}}\le {\mathrm{Q}}_{\mathrm{Gk}}^{\max },\forall \mathrm{k}\in {\mathrm{N}}_{\mathrm{g}}$$

(7)

$$({\mathrm{P}}_{\mathrm{Gk}}-{\mathrm{P}}_{\mathrm{Gk}}^{\min })=\Delta {\mathrm{P}}_{\mathrm{Gk}}^{\min }\le \Delta {\mathrm{P}}_{\mathrm{Gk}}\le \Delta {\mathrm{P}}_{\mathrm{Gk}}^{\max }=({\mathrm{P}}_{\mathrm{Gk}}^{\max }-{\mathrm{P}}_{\mathrm{Gk}})$$

(8)

$${\mathrm{V}}_{\mathrm{n}}^{\min }\le {\mathrm{V}}_{\mathrm{n}}\le {\mathrm{V}}_{\mathrm{n}}^{\max },\forall \mathrm{k}\in {\mathrm{N}}_{\mathrm{l}}$$

(9)

$${\mathrm{P}}_{\mathrm{ij}}\le {\mathrm{P}}_{\mathrm{ij}}^{\max }$$

(10)

where the superscript ‘min’ represents the minimum and ‘max’ represents the maximum values of the respective parameters;${\mathrm{N}}_{\mathrm{g}}$represents the number of generators and N_l represents the number of lines.

3. Satin Bowerbird Optimization (SBO)

The SBO algorithm is bio-inspired by theprinciple of themale-attracting-the-female for breeding the male bowerbird attracts the female with the construction of a specialized bower. This optimization algorithm is new in terms of application toa power system but, in [19], its unimodal and multimodal standard test functions were tested. It showed better performance compared with other optimization techniques such as the Antlion algorithm (ALO), Firefly algorithm (FA), Artificial bee colony algorithm (ABC), Particle swarm optimization algorithm (PSO) and Genetic algorithm (GA).

3.1. Introduction of SBO

Satin bowerbirds live in the rainforest and mesic forest in Australia. They are closely related to the other bowerbirds. Mainly, they live in a particular local area throughout their lives. During autumn and winter seasons, they leave their forest environment and move into open woodlands to eat fruits and pests. However, during the breeding season, they flock together in small groups, inhabiting territories which they apparently occupy year after year.

Male satin bowerbirds construct specialized stick structures called bowers, where male bowerbirds attract the female by dancing and by making a noble bower and decking the surrounding area. The bowers are decorated with flowers, berries, feathers, etc. [20]. Males compete by thieving decorations from other males and destroying the bowers of neighbors [21]. Female birds visit several bowers before choosing a mating partner.

In the SBO algorithm, adult males begin to construct a bower with different materials on their land during the mating season. According to the moralities of satin bowerbird life, the SBO algorithm is structured in several stages as follows.

3.2. SBO Algorithm

3.2.1. Generating a Set of Random Bowers

The SBO algorithm begins with the creation of a random initial population, similar to other meta-heuristic algorithms. The initial population is a set of positions for bowers. Each position is an n-dimensional vector of parameters that must be optimized. These values are randomly initialized so that a uniform distribution is considered between the lower and upper limit parameters. The parameters of each bower are the same as the variables in the optimization problem. The combination of parameters determines the attractiveness of the bower.

3.2.2. Calculating the Probability of Each Population Member

The probability is the attractiveness of a bower. A female satin bowerbird selects a bower (built) based on its probability. Similarly, a male mimics bower building through selecting a bower based on the probability assigned to it. This probability is calculated using Equation (11). In this equation, Fit_i is fitness of the ith solution and NB is the number of bowers. In this equation, the value of Fit_i is achieved using Equation (12).

$${\mathrm{Prob}}_{\mathrm{i}}=\frac{{\mathrm{Fit}}_{\mathrm{i}}}{{{\displaystyle \sum }}_{\mathrm{n}=1}^{\mathrm{NB}}{\mathrm{fit}}_{\mathrm{n}}}$$

(11)

$${\mathrm{Fit}}_{\mathrm{i}}=\{\begin{array}{cc}\hfill \frac{1}{1+\mathrm{f}\left({\mathrm{x}}_{\mathrm{i}}\right)},& \mathrm{f}\left({\mathrm{x}}_{\mathrm{i}}\right)\ge 0\\ \hfill 1+\left|\mathrm{f}\left({\mathrm{x}}_{\mathrm{i}}\right)\right|,& \mathrm{f}\left({\mathrm{x}}_{\mathrm{i}}\right)<0\end{array}$$

(12)

In this equation, f(x_i) is the value of the cost function in the ith position or ith bower. The cost function is a function optimized by Equation (12) which has two parts. The first part calculates the final fitness where values are greater than or equal to zero, while the second part calculates the fitness for values less than zero. This equation has two main characteristics.

3.2.3. Elitism

Elitism is one of the important features of evolutionary algorithms. Elitism allows the best solution(s) to be preserved at every stage of the optimization process. All birds normally build their nests using their natural instincts. The male satin bowerbird is like all other birds in the mating season and uses his natural instinct to build his bower and decorate it. This means that all males use materials to decorate their bowers. However, an important factor in attracting more attention to the bower of a particular male is his experience. This experience helps a lot in both the dramatic gestures and the building of the bower. This means that older males can attract more attention from others to their bowers. In other words, experienced males build better bowers, and these bowers have greater fitness than the other bowers. In this work, the position of the best bower built by birds (best position) is intended as the elite of the iteration. Since the position of the elite has the highest fitness, it should be able to influence the other positions.

3.2.4. Determining New Changes in Any Position

In each cycle of the algorithm, new changes at any bower are calculated according to Equation (13).

$${\mathrm{x}}_{\mathrm{ik}}^{\mathrm{new}}={\mathrm{x}}_{\mathrm{ik}}^{\mathrm{old}}+{\mathsf{\lambda }}_{\mathrm{k}}\left(\left(\frac{{\mathrm{x}}_{\mathrm{jk}}+{\mathrm{x}}_{\mathrm{elite},\mathrm{k}}}{2}\right)-{\mathrm{x}}_{\mathrm{ik}}^{\mathrm{old}}\right)$$

(13)

In this equation, x_i is the ith bower or solution vector and x_ik is the kth member of this vector. The value of x_j is determined as the target solution among all solutions in the current iteration. In Equation (3), value j is calculated based on probabilities derived from positions. In fact, the value j is calculated by the roulette wheel procedure, which means that a solution having a larger probability will have more chance to be selected as x_j; x_elite indicates the position of the elite, which is saved in each cycle of the algorithm. In fact, the position of the elite is the position of a bower whose fitness is the highest in the current iteration. The parameter λ_k determines the attraction power in the goal bower. It determines the amount of step, calculated for each variable. This parameter is determined by Equation (14).

$${\mathsf{\lambda }}_{\mathrm{k}}=\frac{\mathsf{\alpha }}{1+{\mathrm{p}}_{\mathrm{j}}}$$

(14)

In Equation (14), α is the greatest step size and p_j is the probability obtained by Equation (11) using the goal bower. Since the obtained probability values are between 0 and 1, the denominator of this equation contains a sum with 1 to avoid 0 in the denominator of Equation (14). As is obvious from Equation (14), the step size is inversely proportional to the probability of the target position. In other words, when the probability of the target position is greater (due to the constant α), movement to that position is more carefully done. The highest step size occurs when the probability of the target position is 0; the step size in this case will be α. On the other hand, the lowest step size occurs when the probability of target position is 1; the step size will then be α/2.

3.2.5. Mutation

When males are building a bower on the ground, they may be attacked by other animals or be completely ignored. In many cases, stronger males steal materials from weaker males or may even destroy their bowers. Therefore, at the end of each cycle of the algorithm, random changes are applied with a certain probability. In this step, random changes are applied to x_ik with a certain probability. Here, for the mutation process, a normal distribution (N) is employed with an average of ${\mathrm{x}}_{\mathrm{ik}}^{\mathrm{old}}$ and variance of σ², as seen in Equation (15).

$${\mathrm{x}}_{\mathrm{ik}}^{\mathrm{new}}~\mathrm{N}({\mathrm{x}}_{\mathrm{ik}}^{\mathrm{old}},{\mathsf{\sigma }}^2)$$

(15)

$$\mathrm{N}({\mathrm{x}}_{\mathrm{ik}}^{\mathrm{old}},{\mathsf{\sigma }}^2)={\mathrm{x}}_{\mathrm{ik}}^{\mathrm{old}}+\left(\mathsf{\sigma }\times \mathrm{N}\left(0,1\right)\right)$$

(16)

In Equation (16), the value of σ is proportional to the space width, as calculated in Equation (17).

$$\mathsf{\sigma }=\mathrm{z}\times ({\mathrm{var}}_{\max }-{\mathrm{var}}_{\min })$$

(17)

In Equation (17), var_max and var_min are the upper and lower bounds respectively assigned to the variables; z is the percentage of the difference between the upper and lower limits and is variable.

3.2.6. Combining the Old Population and the Population Obtained from Changes

At the end of each cycle, the old population and the population obtained from changes are evaluated. After the evaluation, these two populations are combined and sorted (based on the values obtained from the cost function) and the new population is created according to the previously defined number, while the others are deleted.

3.3. Pseudocode for SBO Algorithm

Algorithm

Initialize the first population of bowers randomly

Calculate the cost of bowers

Find the best bower and assume it as elite

Return best bower

4. Proposed SBO Algorithm for CM Application

In this work, the number of generators taken up has dimensions (D) for the CM problem. The penalty functions are added to the objective function in order to construct the fitness function by transferring inequality constraints. In the present work, during Newton–Raphson power flow, the equality and reactive-power inequality constraints are efficiently handled, while the real-power inequality constraints are handled during the iteration process. Other inequality constraints line power flow and load bus voltages are considered as quadratic penalty functions. The fitness function of the CM problem is described by the following:

$$\begin{gathered} \mathrm{Minimize}\mathrm{ZZ}={\mathrm{C}}_{\mathrm{t}}+{\mathrm{P}}_{{\mathrm{f}}_1}\times {{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{ovli}}\left({\mathrm{P}}_{\mathrm{ij}}-{\mathrm{P}}_{\mathrm{ij}}^{\max }\right)+{\mathrm{P}}_{{\mathrm{f}}_2}\times {{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{VBL}}\left({\left(∆{\mathrm{V}}_{\mathrm{j}}\right)}^2{}_{\mathrm{j}}+{\mathrm{P}}_{\mathrm{ij}}^{\max }\right)+{\mathrm{P}}_{{\mathrm{f}}_3}\times \\ {\left(∆{\mathrm{P}}_{\mathrm{G}}\right)}^2 \end{gathered}$$

(18)

where

$$∆{\mathrm{V}}_{\mathrm{j}}=\{\begin{array}{c}\left({\mathrm{V}}_{\mathrm{j}}^{\min }-{\mathrm{V}}_{\mathrm{j}}\right);\mathrm{if} {\mathrm{V}}_{\mathrm{j}}\le {\mathrm{V}}_{\mathrm{j}}^{\min },\\ \left({\mathrm{V}}_{\mathrm{j}}-{\mathrm{V}}_{\mathrm{j}}^{\max }\right);\mathrm{if} {\mathrm{V}}_{\mathrm{j}}\le {\mathrm{V}}_{\mathrm{j}}^{\max },\end{array}$$

(19)

$$∆{\mathrm{P}}_{\mathrm{G}}=\{\begin{array}{c}\left({\mathrm{P}}_{\mathrm{G}}^{\min }-{\mathrm{P}}_{\mathrm{G}}\right);\mathrm{if} {\mathrm{P}}_{\mathrm{G}}\le {\mathrm{P}}_{\mathrm{G}}^{\min },\\ \left({\mathrm{P}}_{\mathrm{G}}-{\mathrm{P}}_{\mathrm{G}}^{\max }\right);\mathrm{if} {\mathrm{P}}_{\mathrm{G}}\le {\mathrm{P}}_{\mathrm{G}}^{\max }.\end{array}$$

(20)

Here, ZZ is the fitness function;$\mathrm{ovli}$,$\mathrm{VBL}$represents set of overloaded lines, violated load bus voltage; and ${\mathrm{P}}_{{\mathrm{f}}_{\mathrm{i}}}$(${\mathrm{f}}_{\mathrm{i}}$ = 1, 2, 3) represents a large penalty factor, taken to be 10,000 throughout the simulation procedure [9].

Computational Procedure for SBO Algorithm for CM

The following procedure is applied to the CM problem based on the above discussion.

Step 1 Initialization: Initialize the population of bowerbirds, which are a set of generations (i.e., ${\mathrm{P}}_{\mathrm{Gj}}^{+}$ and ${\mathrm{P}}_{\mathrm{Gj}}^{-}$) constrained by the upper and lower limits of the generation to regulate the congestion.

Step 2 Fitness function evaluation: The objective function is evaluated for the bowerbird population and the best solution is stored as elite.

Step 3 Deterministic changes: The attraction power of the bower is calculated based on Equations (11), (12), and (14). The new solution is obtained from the older solution following deterministic changes (13). These new solutions are the new set of values for generation rescheduling. The solutions are implemented in the objective function, and the fitness of the solution is evaluated.

Step 4 Mutation: Random changes are applied to the existing solutions based on a certain probability as in Equations (15) and (16). The fitness of the obtained solution is evaluated using the objective function.

Step 5 Elitism: For each iteration, the best solution is preserved as the “elite” solution. After the end of the iterations, the elite solution corresponds to the solution of the problem.

5. Simulation Results and Discussion

In the present proposed work, the SBO for CM was implemented using MATLAB R2014a software on a computer system based on an Intel core i3 Processor, with 2.20 GHz and 2 GB of RAM. The effectiveness of the proposed approach was put to the test on various networks, namely, a modified IEEE 30-bus system [9], modified IEEE 57-Bus test system [9], and IEEE 118-Bus test system [22]. The load bus lower and upper voltage were taken as 0.9 p.u. and 1.1 p.u. In this algorithm, throughout the simulation, the population size taken was 50, step size(α) was 0.94, the percentage of the difference between the upper and lower limit z was 0.002, mutation probability (p) was 0.05, and maximum iterations was taken as 100. The incremental/decremental price bids are exhibited in the Appendix A in

Table A1. Price bids submitted by the generator companies for modified IEEE 30-bus, modified IEEE 57-bus, and IEEE-118 bus test systems.

Bus Number	Increment (CtG), $/MWh	Decrement (DtG), $/MWh	Bus Number	Increment (CtG), $/MWh	Decrement (DtG,) $/MWh
Modified IEEE 30-bus test system [7]
1	22	18	4	43	37
2	21	19	5	43	35
3	42	38	6	41	39
Modified IEEE 57-bus test system [7]
1	44	41	5	42	39
2	43	39	6	44	40
3	42	38	7	44	41
4	43	37
IEEE 118-bus test system [19]
1	40	38	65	25	17
4	43	35	66	26	18
6	41	38	69	28	15
8	44	39	70	43	39
10	22	17	72	47	38
12	23	18	73	44	36
15	45	35	74	43	39
18	41	38	76	44	36
19	44	36	77	47	38
24	45	35	80	23	15
25	27	18	85	43	39
26	23	18	87	25	17
27	41	39	89	44	36
31	45	35	90	42	38
32	24	18	91	41	38
34	43	37	92	44	36
36	44	36	99	43	37
40	43	35	100	42	36
42	47	38	103	24	17
46	45	35	104	44	38
49	25	18	105	43	39
54	32	30	107	42	38
55	42	36	110	43	37
56	43	37	111	22	18
59	23	17	112	42	38
61	26	16	113	47	33
62	44	36	116	45	35

. The different test systems with different testing approaches considered for validation of the present work and details are shown in

Table 1. Details of simulated test systems with test cases.

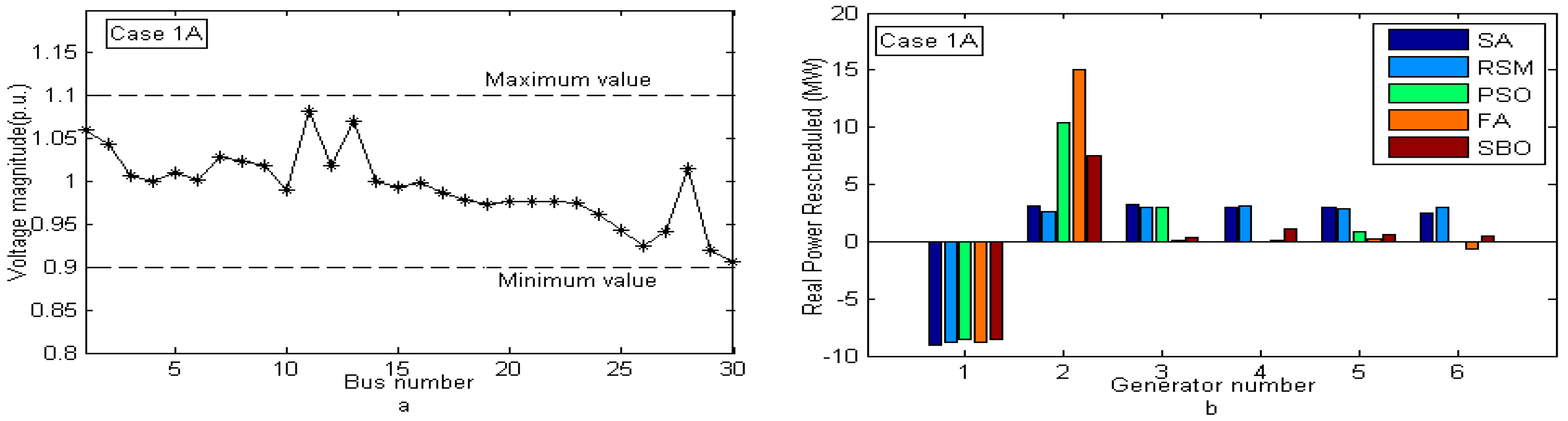
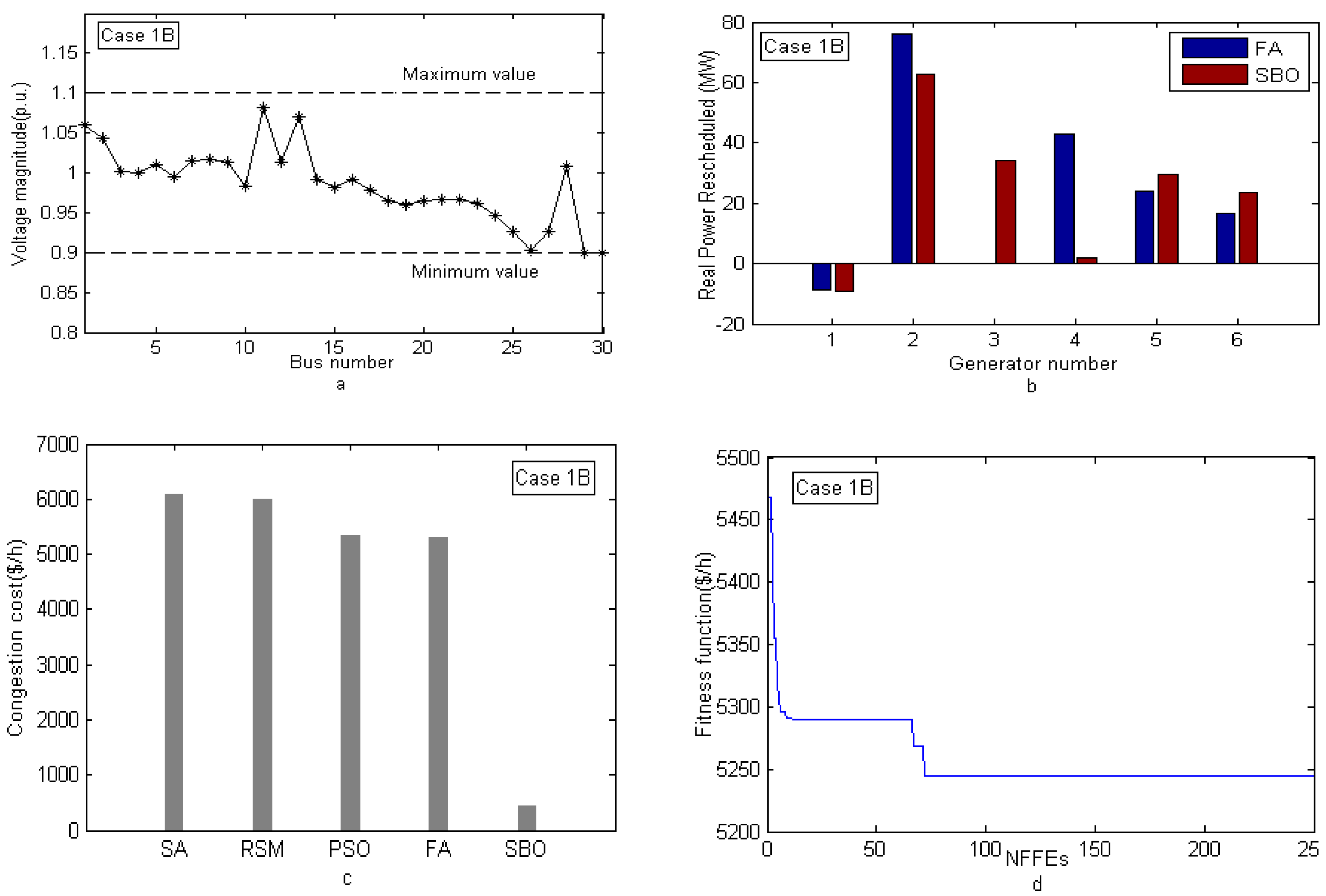
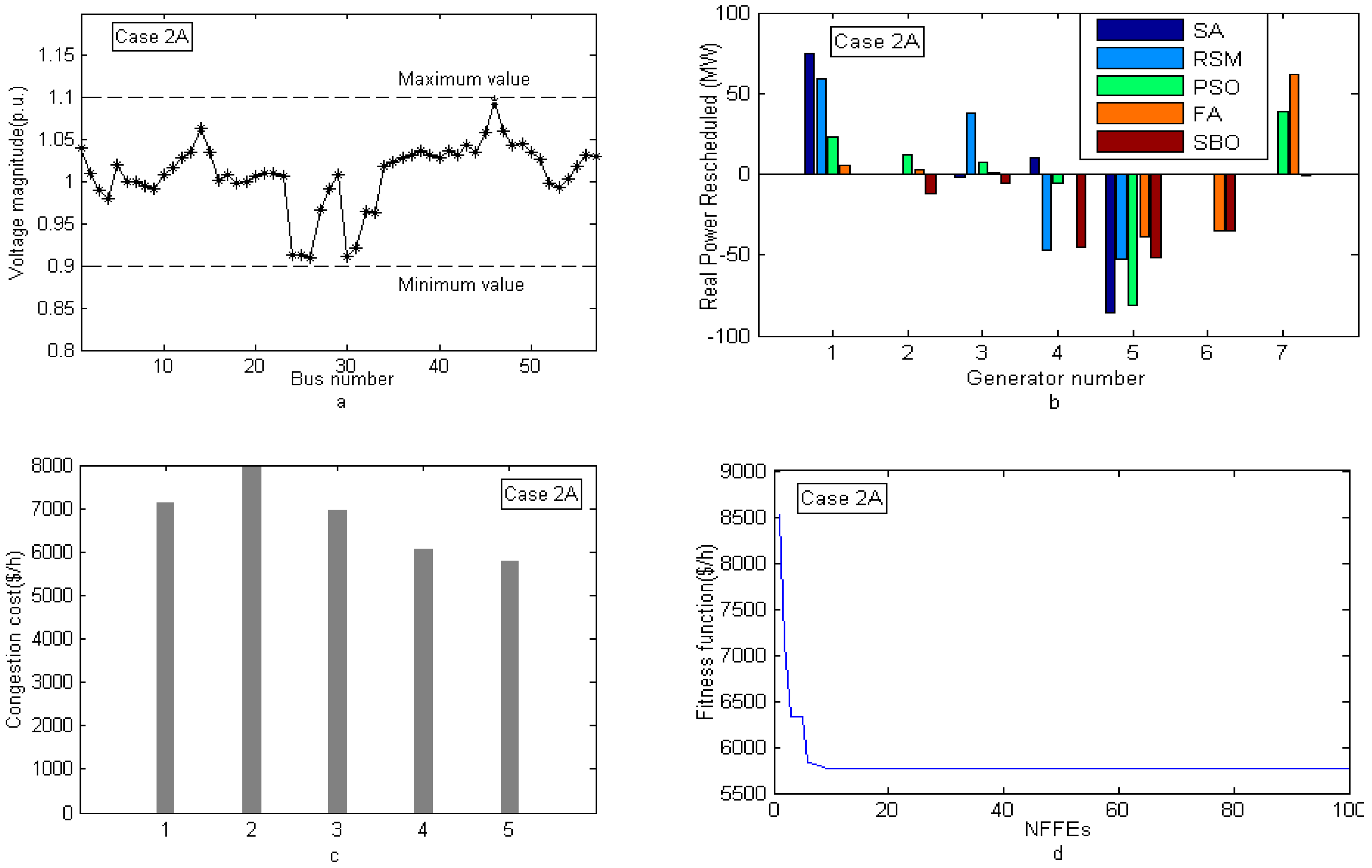
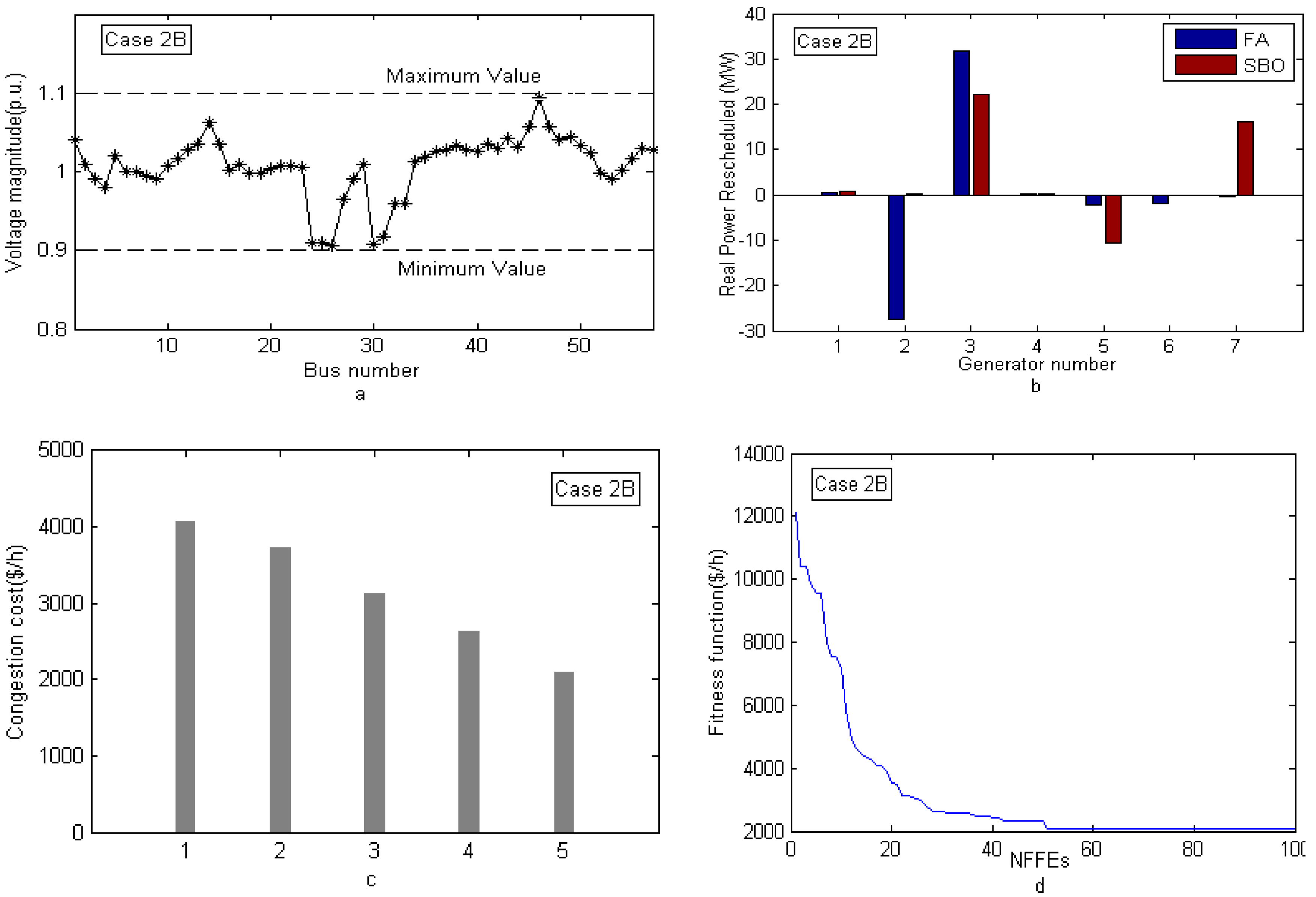
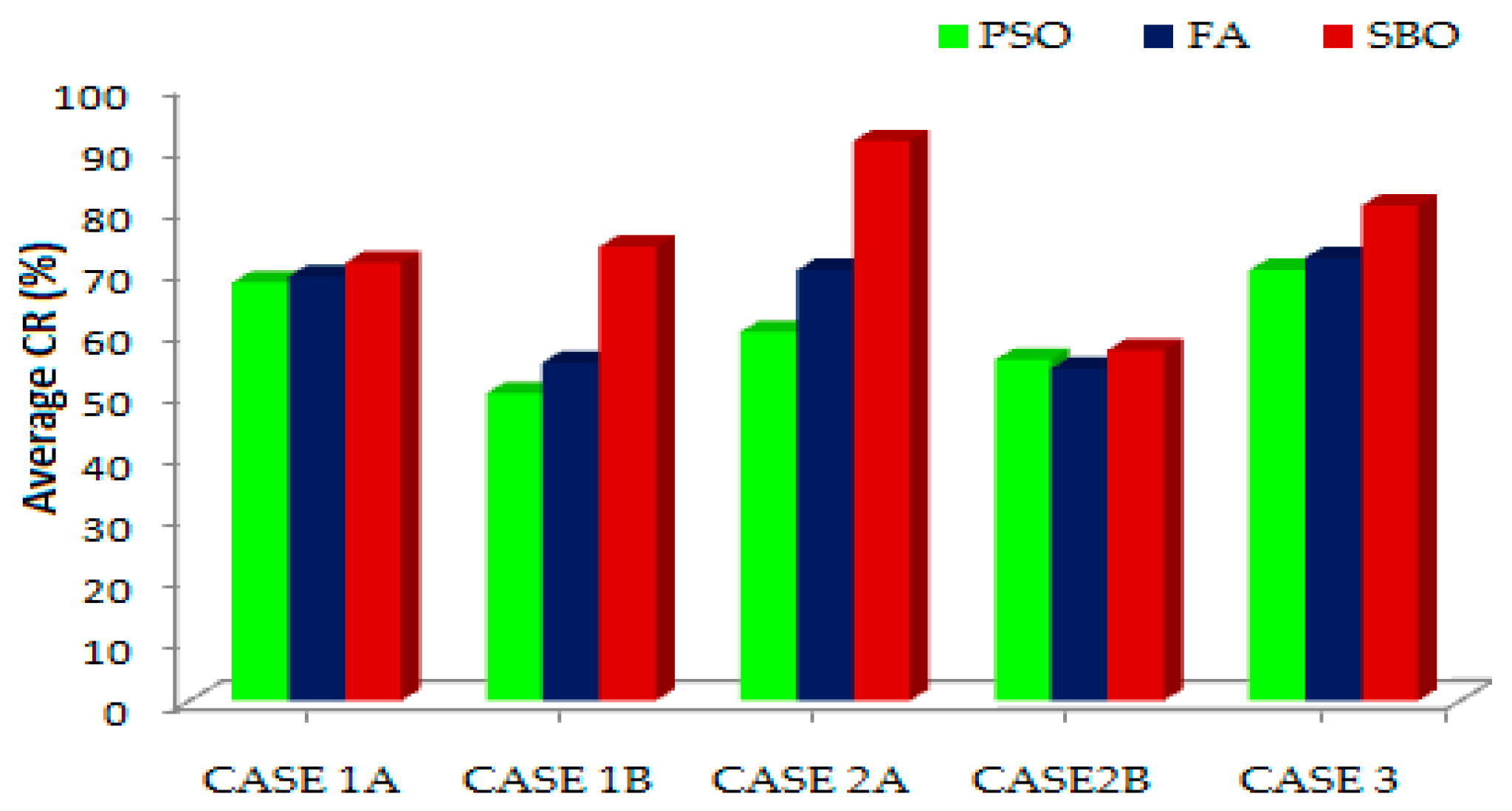
Test System	Test Case	Contingency Considered
Modified	1A	Line outage between 1 and 2
IEEE 30-bus	1B	Line outage between 1 and 7 with load increase 50% at all buses
Modified	2A	Lines capacity reduction from 200 to 175 MW and 50 to 35 MW between 5–6 and 6–12
IEEE 57-bus	2B	Line capacity reduction from 85 to 20 MW between lines 2 and 3
IEEE 118-bus	3	Line outage between 8 and 5 with load increase of 57% at buses 11–20

.

The amount of electric power transmitted between the congested lines before and after CM is given in

Table 2. Details of congested line flow for different test systems. CM: congestion management.

Test Case	Congested Lines	Line Flow, MW		Specified Line Limit, MW
		Before CM	After CM
1A	1–7	147.57	130	130
	7–8	140.23	123.54	130
1B	1–2	314.01	130	130
	2–8	97.86	61.46	65
	2–9	103.66	64.39	65
2A	5–6	188.69	168.47	175
	6–12	49.53	16.85	35
2B	2–3	36.60	16.78	20
3	16–17	209.24	97.65	175
	30–17	580.29	496.80	500
	8–30	363.52	143.08	175

.

5.1. Modified IEEE 30-Bus Test System

The modified IEEE 30-bus test system contains 41 transmission lines, 6 generator buses, and 24 load buses. The total testing network real-power is 283.4 MW and reactive-power is 126.2 MVAR. In this test system, two different cases are taken up for analysis of the proposed algorithm, viz., Cases 1A and 1B shown in Table 1.

In Case 1A, congestion is created in the test system by considering an outage of the line between the buses 1 and 2. Due to the outage of the line, congestion occurs in the lines between 1–7 and 7–8. The details of the amount of line flow are shown in Table 2. For secured operation, corrective actions are taken to alleviate these overloading lines. The proposed SBO algorithm is applied for the minimization of congestion cost. The obtained optimal values of congestion cost by the proposed SBO method are compared with those reported in the literature like simulated annealing(SA) [9], random search method (RSM) [9], particle swarm optimization (PSO) [9], and firefly algorithm (FA) [23] in

Table 3. Comparison of simulation results for modified IEEE 30-bus test power system. SA: simulated annealing; RSM: random search method; (PSO): particle swarm optimization; FA: firefly algorithm; SBO: satin bowerbird optimization.

Variables	SA [9]	RSM [9]	PSO [9]	FA [23]	SBO [Proposed]
Case 1A
TC, $/h	719.86	716.25	538.95	511.8737	421.58
ΔPG1, MW	−9.076	−8.808	−8.61	−8.7783	−8.59617
ΔPG2, MW	3.133	2.647	10.4	15.0008	7.57019
ΔPG3, MW	3.234	2.953	3.03	0.1068	0.35246
ΔPG4, MW	2.968	3.063	0.02	0.0653	1.09699
ΔPG5, MW	2.954	2.913	0.85	0.1734	0.56891
ΔPG6, MW	2.443	2.952	−0.01	−0.6180	0.52286
TRRG, MW	23.809	23.33	22.93	24.7425	18.70758
Case 1B
TC, $/h	6068.7	5988	5335.5	5304.40	5238.93
ΔPG1, MW	NL	NL	NL	−8.5798	−9.00148
ΔPG2, MW	NL	NL	NL	75.9954	62.90304
ΔPG3, MW	NL	NL	NL	0.0575	34.24745
ΔPG4, MW	NL	NL	NL	42.9944	2.05959
ΔPG5, MW	NL	NL	NL	23.8325	29.45485
ΔPG6, MW	NL	NL	NL	16.5144	23.47373
TRRG, MW	164.53	164.5	168	167.974	161.14013

TC—total cost of the congestion; TRRG—total real-power rescheduling generators; NL—not given in the literature.

. The optimal value of total congestion cost obtained using the proposed SBO algorithm was found to be 421.58 $/h, as shown in Table 3.

The voltage magnitude was obtained after CM using SBO, and is shown in Figure 1a. It is observed that, after CM, the voltage magnitude is within limits between 0.9 and 1.1. A comparative graphical representation of the real-power rescheduling and congestion cost with different algorithms is shown in Figure 1b,c. The system real-power losses reduce from 16.13 MW to 12.665 MW after the CM.

In Case 1B, outage of line between 1 and 7, along with the increase in load to 1.5 times as much, causes overloading in the lines 1–2, 2–8, and 2–9. Table 2 shows the line flows in between the overloaded lines in this case. Table 3 illustrates the results for minimization of the congestion cost and changes in the real power of generators. A comparative graphic view of the change in real-power of generators and total congestion cost is presented in Figure 2b,c. The cost for CM is less for the proposed SBO method than for the other comparative methods. In addition, the total system loss is initially 37.24 MW; after CM, it reduces to 14.59 MW. Figure 2a shows the proposed SBO method-based variation in output voltage at all the buses after the CM.

5.2. Modified IEEE 57-Bus Test System

The modified IEEE 57-bus test system consists of 80 transmission lines, 50 load buses, and 7 generator buses. The total test network real-power is 1250.8 MW and the reactive-power is 336 MVAR. The two different cases considered for this simulation, viz., Cases 2A and 2B, are shown in Table 1.

In Case 2A, the line limits were reduced to 175 MW and 35 MW in the lines 5–6 and 6–12, instead of 200 MW and 50 MW. The details of the congested line flow before and after CM are provided in Table 2. Due to this congestion, lines between 5–6 and 6–12 get overloaded and the total power violation becomes 28.22 MW. The optimum value of the generator real-power rescheduling performed using the proposed SBO algorithm completely alleviates the violation of the overloading lines.

Table 4. Comparison of simulation results for modified IEEE 57-bus test power system.

Variables	SA [9]	RSM [9]	PSO [9]	FA [23]	SBO [Proposed]
Case 2A
TC, $/h	7114.3	7967.1	6951.9	6050.1	5773.27
ΔPG1, MW	74.499	59.268	23.13	5.6351	−0.05437
ΔPG2, MW	0	0	12.44	2.5230	−11.72790
ΔPG3, MW	−1.515	37.452	7.49	0.5098	−5.81154
ΔPG4, MW	9.952	−47.39	−5.38	0.107	−45.26118
ΔPG5, MW	−85.92	−52.12	−81.21	−39.1514	−51.32093
ΔPG6, MW	0	0	0	−35.1122	−34.86761
ΔPG7, MW	0	0	39.03	62.1938	−0.53486
TRRG, MW	171.87	196.23	168.78	145.227	144.57839
Case 2B
TC, $/h	4072.9	3717.9	3117.6	2618.1	2084.78
ΔPG1, MW	NL	NL	NL	0.3704	0.76179
ΔPG2, MW	NL	NL	NL	−27.5084	0.08662
ΔPG3, MW	NL	NL	NL	31.6294	22.04924
ΔPG4, MW	NL	NL	NL	0.3308	0.17019
ΔPG5, MW	NL	NL	NL	−2.2549	−10.50832
ΔPG6, MW	NL	NL	NL	−1.9354	−0.00000
ΔPG7, MW	NL	NL	NL	−0.5101	16.00743
TRRG, MW	97.88	89.32	76.314	64.5393	49.58359

TC—total cost of the congestion; TRRG—total real-power rescheduled generators; NL—not given in the literature.

shows the minimum cost achieved by the proposed SBO method compared to those achieved by earlier algorithms. The SBO method-based bus voltages, as obtained after the application of CM, are displayed in Figure 3a and are acceptable. The real-power rescheduling and congestion cost of the proposed SBO method compared with that of other algorithms is shown in Figure 3b,c. Figure 3d shows the convergence profile. The total system loss before CM was 69.64 MW; this decreased to 24.558 MW after the CM.

In Case 2B, shown in Table 1, the line limit of line 2–3 was reduced from 85 MW to 20 MW to create line overloading. The details of the line flow data before and after CM are shown in Table 2. The results obtained after applying the proposed SBO and other methods are listed in Table 4. Table 4 clearly shows that the cost incurred for CM is only 2084.78 $/h for the proposed SBO method, which is the lowest among all the costs obtained so far as reported in [9]. Comparative congestion costs offered by different algorithms and the proposed SBO method are displayed in Figure 4c. The system loss reduces to 28.22 MW after CM as compared to 78.23 MW during congestion. Figure 4 indicates that the proposed SBO method gives the best results after CM compared with others in the literature.

5.3. IEEE 118-Bus Test System

The test system comprising 54 generator buses, 64 load buses, and 186 transmission lines is taken into account in this work. In this simulation, Case 3 disconnects the line between 8 and 5 along with increasing the load between 11 and 20 to 1.57 times the original load in order to create contingency for simulation purposes; this is projected in Table 1. The particulars related to the congested line flow for this case are shown in Table 2.

The data in

Table 5. Comparison of simulation results for IEEE 118-bus test power system.EP: evolutionary programming algorithm, RCGA: real coded genetic algorithm, PSO: particle swarm optimization, HPSO: hybrid particle swarm optimization, DE: differential evolution.

Variables	EP [22]	RCGA [22]	PSO [22]	HPSO [22]	DE [22]	SBO [Proposed]
TC, $/h	42,886	17,693	17,742	17,365	16,080	12,336.05
ΔPG1	38.11	26.274	24.502	11.59	6.4705	6.35066
ΔPG2	0	0	0	0	0	3.45815
ΔPG3	63.06	31.422	1.0259	6.568	12.295	5.01763
ΔPG4	−7.48	11.349	1.3148	−0.046	−0.056	8.99506
ΔPG5	−200.6	−219.3	−21.82	−207.7	−208.1	−203.28939
ΔPG6	48.58	101.42	105.32	80.126	105.32	8.81232
ΔPG7	0	0	0	0	0	22.22845
ΔPG8	49.17	0.0029	16.815	6.0059	1.9946	0.61579
ΔPG9	64.056	8.0582	23.665	−0.239	1.2884	6.78422
ΔPG10	0	0	0	0	0	2.32609
ΔPG11	121.51	114.69	121.51	121.51	49.697	−0.2996
ΔPG12	25.918	116.31	116.31	108.06	113.29	1.06873
ΔPG13	85.37	7.4155	3.0092	10.752	0.8125	0.62895
ΔPG14	32.857	−0.0019	0.0177	−0.536	2.1836	4.24786
ΔPG15	31.616	28.095	8.8665	11.254	89.669	12.42693
ΔPG16	39.071	1.7508	7.1475	0.0731	0.7819	0.21691
ΔPG17	37.552	0.0004	0.4916	−0.394	−0.041	0.49255
ΔPG18	0	0	0	0	0	1.48727
ΔPG19	0	0	0	0	0	0.46018
ΔPG20	89.001	1.7478	6.0792	4.3096	−0.089	−0.34758
ΔPG21	96.075	18.528	19.359	77.661	102.85	−1.09116
ΔPG22	93.828	33.426	36.798	72.901	7.3786	−0.24492
ΔPG23	0	0	0	0	0	0.36291
ΔPG24	0	0	0	0	0	0.25945
ΔPG25	0	0	0	0	0	1.53135
ΔPG26	0	0	0	0	0	−5.89327
ΔPG27	0	0	0	0	0	0.3658
ΔPG28	0	0	0	0	0	−112.36346
ΔPG29	0	0	0	0	0	−6.58455
ΔPG30	−450.9	0	10.702	0.6525	4.904	−4.10322
ΔPG31	0	0	0	0	0	0.90951
ΔPG32	0	0	0	0	0	0.40333
ΔPG33	0	0	0	0	0	0.17212
ΔPG34	0	0	0	0	0	0.78747
ΔPG35	0	0	0	0	0	0.14819
ΔPG36	0	0	0	0	0	0.18178
ΔPG37	0	0	0	0	0	−3.22489
ΔPG38	0	0	0	0	0	0.32378
ΔPG39	0	0	0	0	0	−0.80088
ΔPG40	0	0	0	0	0	−74.35625
ΔPG41	0	0	0	0	0	0.19709
ΔPG42	0	0	0	0	0	0.15209
ΔPG43	0	0	0	0	0	1.21754
ΔPG44	0	0	0	0	0	0.13011
ΔPG45	0	0	0	0	0	−0.54271
ΔPG46	0	0	0	0	0	−3.72569
ΔPG47	0	0	0	0	0	1.82584
ΔPG48	0	0	0	0	0	0.36729
ΔPG49	0	0	0	0	0	0.15896
ΔPG50	0	0	0	0	0	0.99087
ΔPG51	0	0	0	0	0	−0.90559
ΔPG52	0	0	0	0	0	0.27131
ΔPG53	0	0	0	0	0	0.78541
ΔPG54	0	0	0	0	0	1.05513
TRRG	1574.9	719.8998	717.7839	720.4816	707.3281	515.98823

TC—total cost of the congestion; TRRG—total real-power rescheduled generators.

list the cost of the congestion and generator real-power rescheduling obtained by SBO algorithm compared with those of other algorithms given in literature. From Table 5, it is made clear that overloaded lines are totally relieved by generation rescheduling with the cost of 12,336.05 $/h, which is the lowest when compared with all other optimization algorithms enlisted in [22] such as evolutionary programming algorithm (EP), real coded genetic algorithm (RCGA), particle swarm optimization (PSO), hybrid particle swarm optimization (HPSO), and differential evolution (DE). The loss of the total system before CM is 277.301 MW, and is then decreased to 230.505 MW. Further, it is assessed through the tests that the SBO provides the best optimal solution in every independent trial run and continues to be consistent even for large systems as well. The bus voltage and convergence profile obtained after the CM are plotted in Figure 5. Figure 5a shows the voltage magnitudes at all the buses.

6. Convergence Mobility and Effectiveness of SBO

To examine the performance of the SBO proposed for solving CM issues, the worth of the convergence rate (CR) [24] was set for all the cases so as to check the convergence speed. Here, a general scheme was adopted to search out the worth of the CR for any number of optimization algorithms in line; the explicit adopted procedure is as follows:

(a)

Run the algorithms up to the maximum of NFFE (number of fitness function evaluation) (NFFE^max);

(b)

Based on convergence, determine NFFER, which is the NFFE corresponding to the minimum objective value; and

(c)

Compute the CR for the algorithm by using Equation (21).

$$\mathrm{CR}=\left(1-\frac{{\mathrm{NFFE}}^{\mathrm{R}}}{{\mathrm{NFFE}}^{\max }}\right)\times 100\%,$$

(21)

where CR ∈ [0,1] and the values of CR equal to 1 and 0 respectively specify the best and worst convergence rate of the considered algorithm. The CR of the proposed SBO method has the highest average value, which clearly shows that this algorithm converges to the optimum solution faster than other optimization algorithms shown in Figure 6. The details of parameter values of the various algorithms are shown in

Table 6. Parameter values of various algorithms. FFA: firefly algorithm.

PSO	FFA	SBO
No. of particles = 40; Inertia weight ${\mathsf{\omega }}_{\max }$ = 0.9; ${\mathsf{\omega }}_{\min }$ = 0.4; ${\mathrm{C}}_1$ =${\mathrm{C}}_2$ = 2	Fireflies = 40; α and γ = 0 to 1; ${\mathsf{\beta }}_{\mathrm{o}}$ = 10	Population size = 40, step size (α) = 0.94; z = 0.002; p = 0.05
Maximum iterations = 150	Maximum iterations = 150	Maximum iterations = 150

.

7. Conclusions

A new approach for CM in an electricity market with open access is proposed in the paper. The problem was formulated as a multi-objective function with cost and losses as major objectives satisfying several electrical constraints. To solve this problem, Satin Bowerbird Optimization (SBO)- a modern meta-heuristic algorithm-was employed. In addition, contingencies such as tripping lines and overloading lines were considered. The proposed approach of utilizing SBO was compared with contemporary algorithms such as SA, RSM, PSO, FA, EP, RCGA, HPSO, and DE as reported in the literature, and the results depict the superiority of SBO over these algorithms. The approach was applied successfully to the standard test systems such as the IEEE 30-bus, 57-bus, and 118-bus systems. The comparative study clearly shows that the proposed SBO-based approach of generator rescheduling produces less cost compared with other algorithms for all the adopted test cases. The convergence mobility of the proposed method is the fastest among all methods. It can also be inferred from the single-objective and multi-objective cases that the optimization of one of the objectives has a deteriorating effect on the other objective. Hence, care must be taken while designing a solution based on the method described in the paper.