Design, Evaluation and Implementation of an Islanding Detection Method for a Micro-grid
Abstract
:1. Introduction
2. Islanding Detection Method for an MG Based on the Instantaneous Active and Reactive Power at the PCC
2.1. Calculation of the Instantaneous Active and Reactive Power
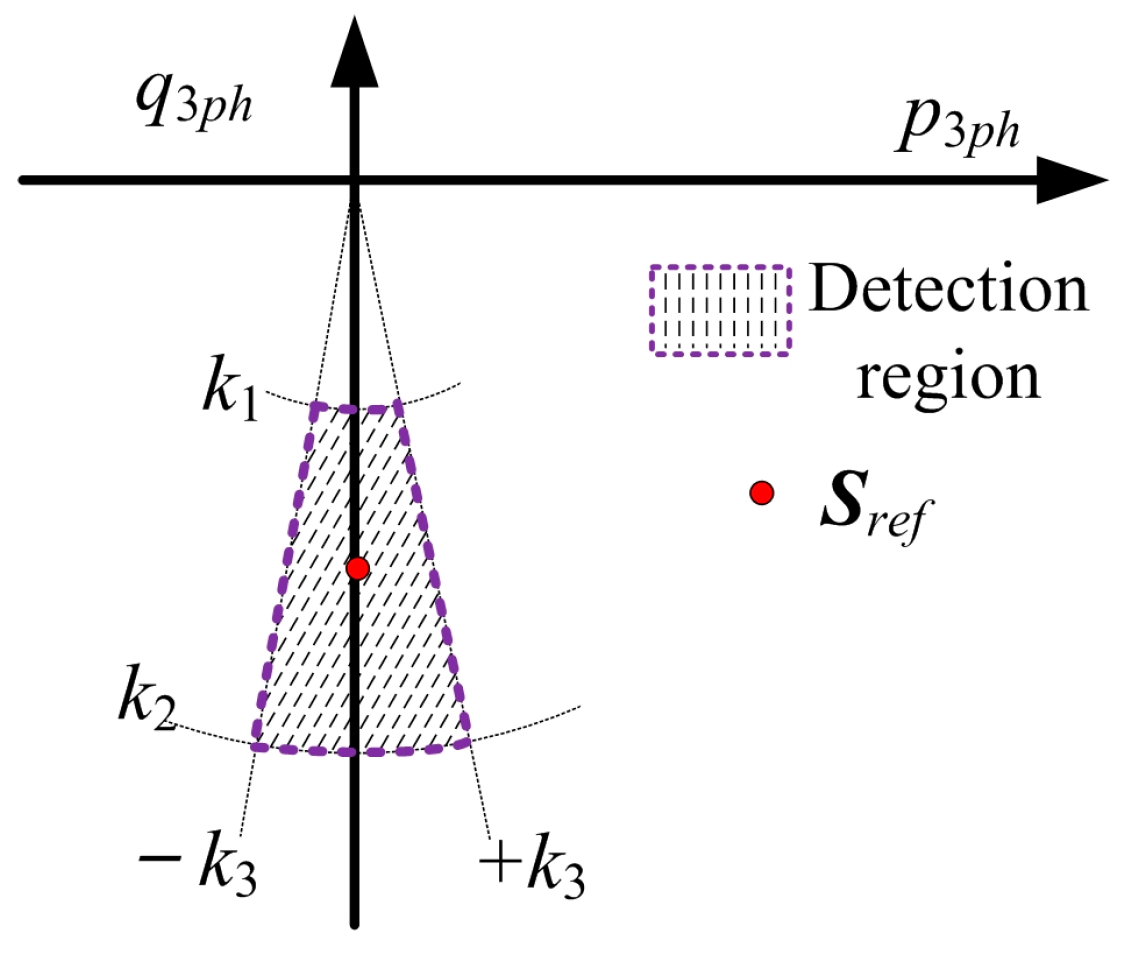
2.2. Islanding Detection Method Based on the Instantaneous Active and Reactive Power at the PCC
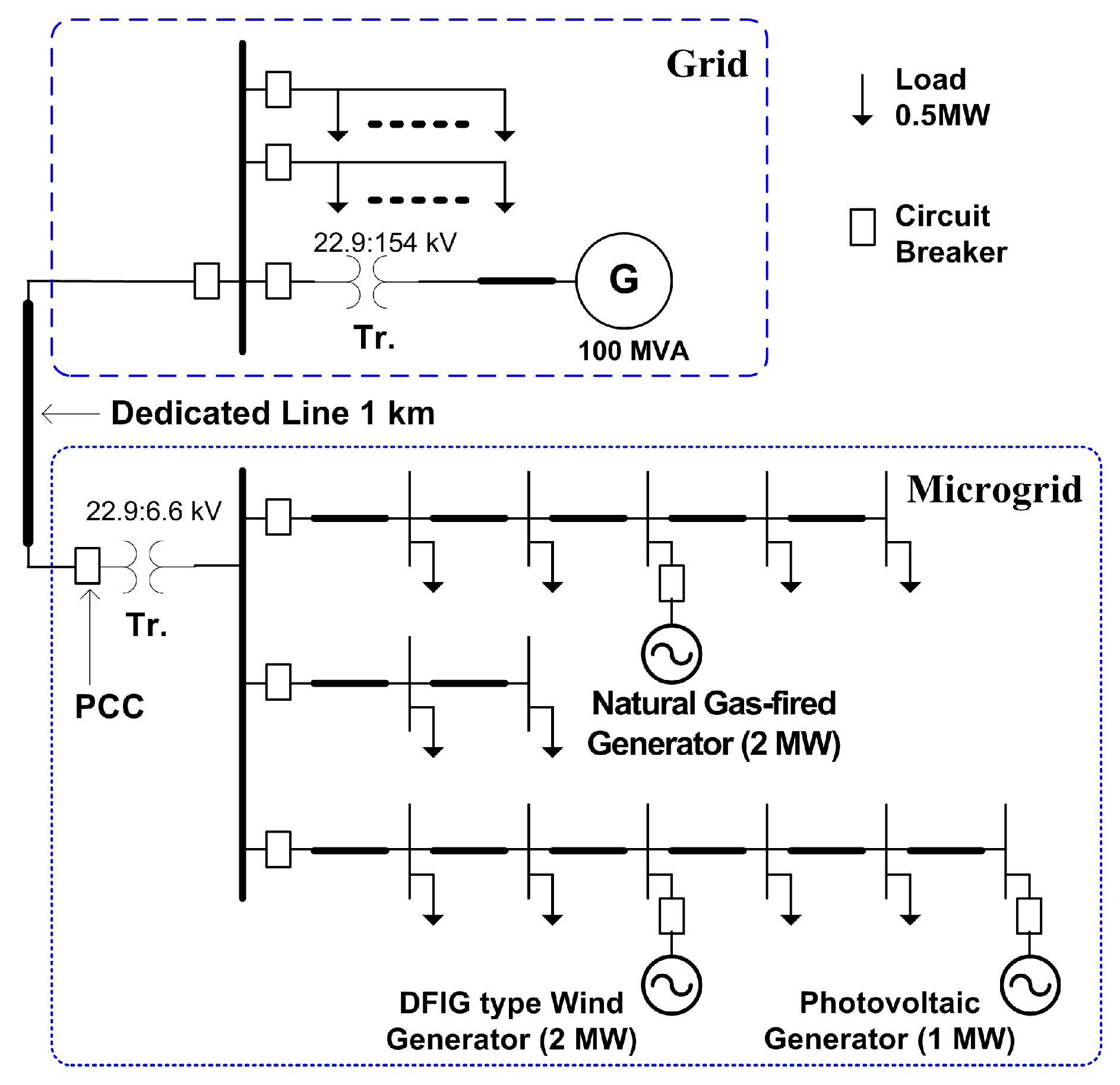
3. Case Studies
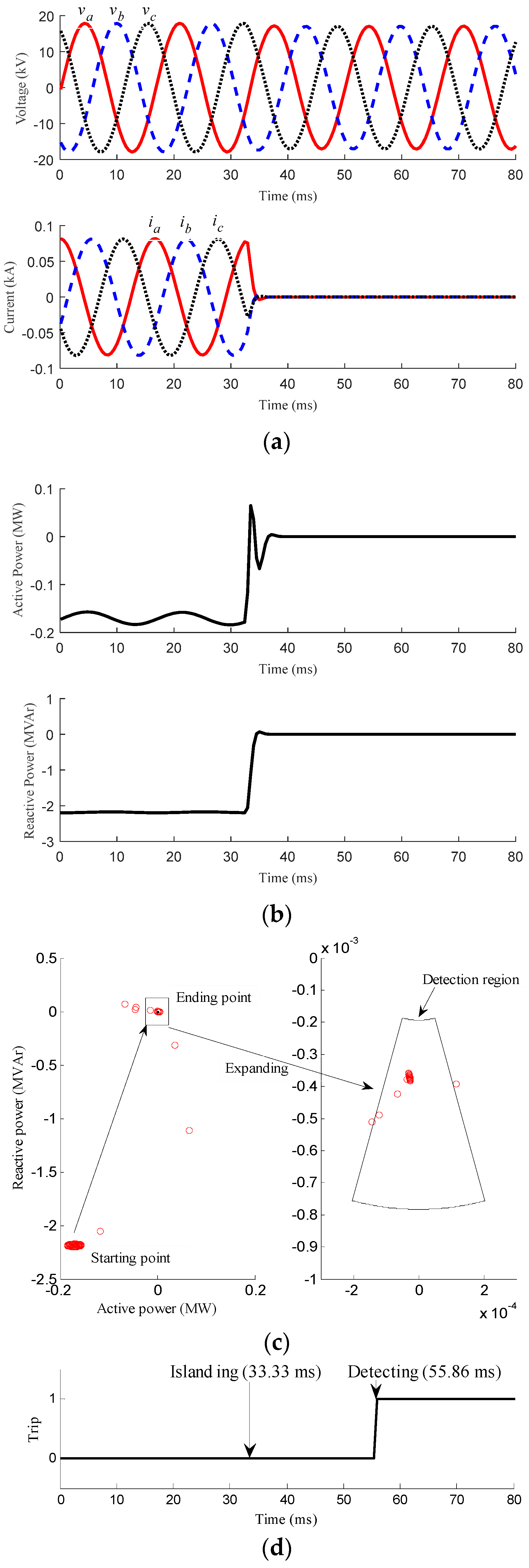
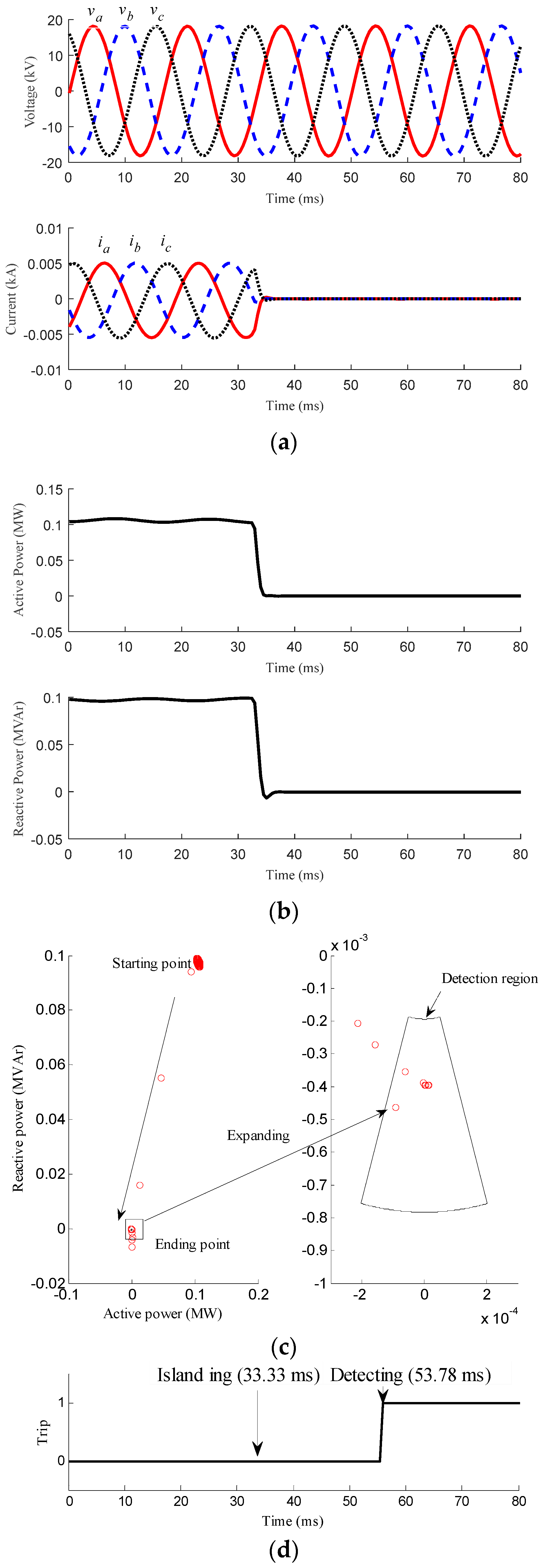
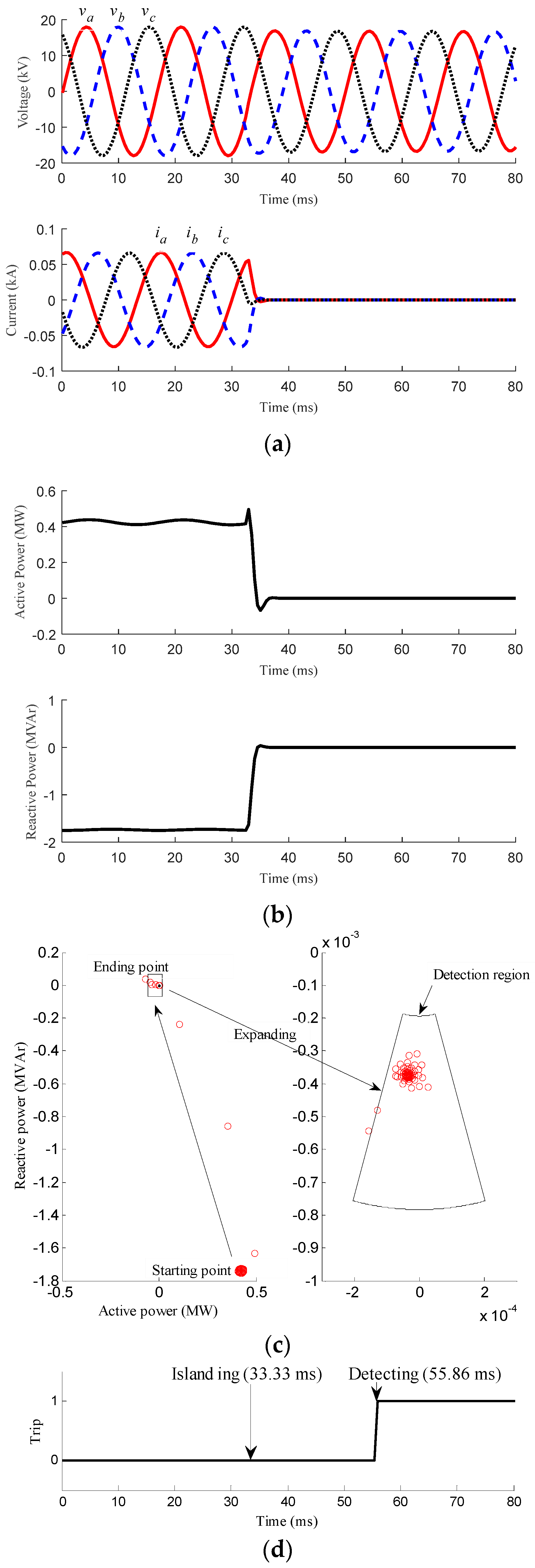
3.1. Islanding Conditions
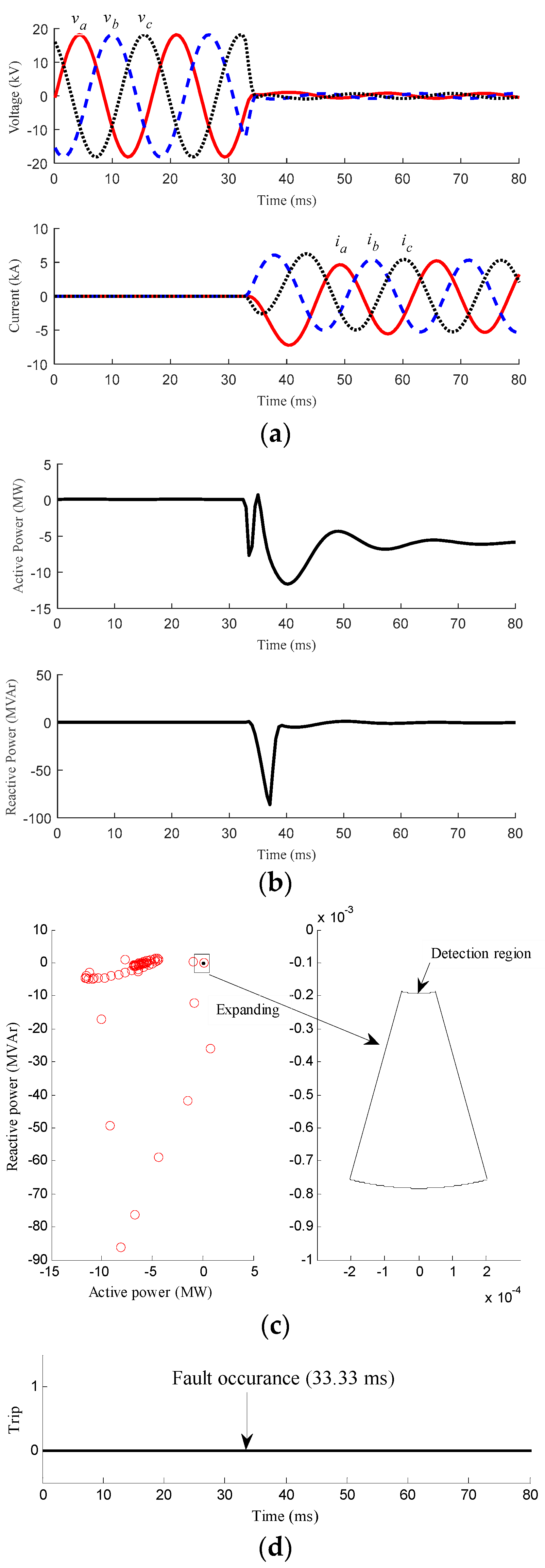
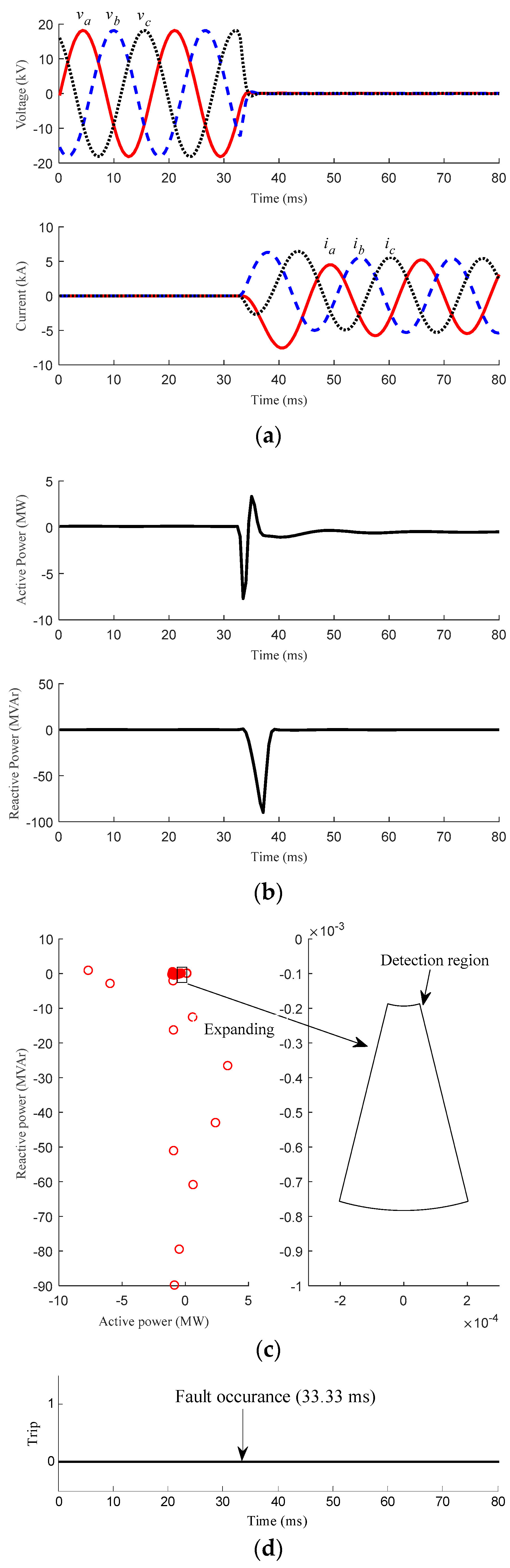
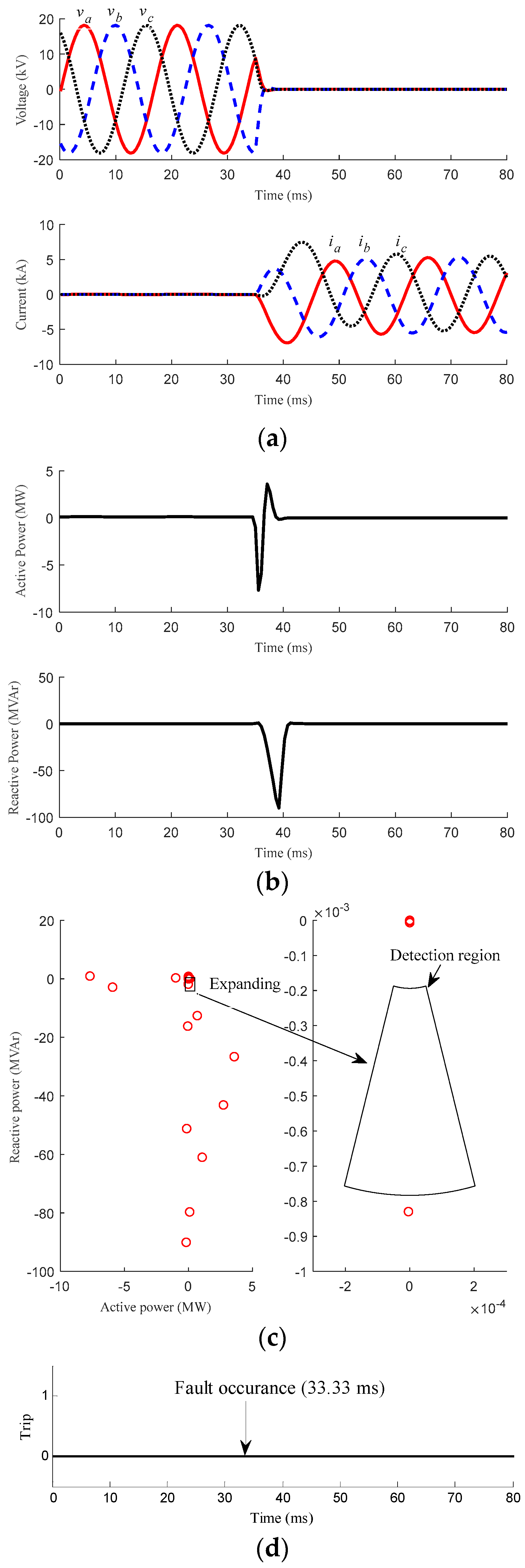
3.2. Fault Conditions
3.2.1. Faults with Different Position
3.2.2. Faults with Different Inception Angle
3.2.3. Faults with Different Type
3.2.4. Faults with Different Fault Impedance
4. Hardware Implementation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ackermann, T.; Andersson, G.; Söder, L. Distributed generation: A definition. Electr. Power Syst. Res. 2001, 57, 195–204. [Google Scholar] [CrossRef]
- Chiradeja, P.; Ramakumar, R. An approach to quantify the technical benefits of distributed generation. IEEE Trans. Energy Convers. 2004, 19, 764–773. [Google Scholar] [CrossRef]
- Ochoa, L.F.; Padilha-Feltrin, A.; Harrison, G.P. Evaluating distributed generation impacts with a multi objective index. IEEE Trans. Power Deliv. 2006, 21, 1452–1458. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Venkataramanan, G.; Marnay, C. A larger role for microgrids. IEEE Power Energy Mag. 2008, 6, 78–82. [Google Scholar] [CrossRef]
- Lasseter, R.; Akhil, A.; Marnay, C.; Stephens, J.; Dagle, J.; Guttromson, R.; Sakis Meliopoulous, A.; Yinger, R.; Eto, J. Integration of Distributed Energy Resources: The CERTS Microgrid Concept; Technical Report for the California Energy Commission: Sacramento, CA, USA, 2002.
- Katiraei, F.; Iravani, M.R.; Lehn, P.W. Micro-grid autonomous operation during and subsequent to islanding process. IEEE Trans. Power Deliv. 2005, 20, 248–257. [Google Scholar] [CrossRef]
- Jayawarna, N.; Jenkins, N.; Barnes, M.; Lorentzou, M.; Papthanassiou, S.; Hatziargyriou, N. Safety analysis of a microgrid. In Proceedings of the International Conference on Future Power System, Amsterdam, The Netherlands, 16–18 November 2005. [Google Scholar]
- Eltawil, M.A.; Zhao, Z. Grid-connected photovoltaic power systems: Technical and potential problems—A review. Renew. Sustain. Energy Rev. 2010, 14, 112–129. [Google Scholar] [CrossRef]
- Ahmad, K.N.E.K.; Selvaraj, J.; Rahim, N.A. A review of the islanding detection methods in grid-connected PV inverters. Renew. Sustain. Energy Rev. 2013, 21, 756–766. [Google Scholar] [CrossRef]
- Bower, W.; Ropp, M. Evaluation of Islanding Detection Methods for Photovoltaic Utility-Interactive Power Systems; Technical Report IEA PVPS T5-09; International Energy Agency: Paris, France, 2002. [Google Scholar]
- Velasco, D.; Trujillo, C.L.; Garcera, G.; Figueres, E. Review of anti-islanding techniques in distributed generators. Renew. Sustain. Energy Rev. 2010, 14, 1608–1614. [Google Scholar] [CrossRef]
- Khamis, A.; Shareef, H.; Bizkevelci, E.; Khatib, T. A review of islanding detection techniques for renewable distributed generation systems. Renew. Sustain. Energy Rev. 2013, 28, 483–493. [Google Scholar] [CrossRef]
- Yu, B.; Matsui, M.; Yu, G. A review of current anti-islanding methods for photovoltaic power system. Sol. Energy 2010, 84, 745–754. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, G.; Li, C.; Wang, W.; Wang, G.; Kliber, J. A power line signaling based technique for anti-islanding protection of distributed generators—Part I: Scheme and analysis. IEEE Trans. Power Deliv. 2007, 22, 1758–1766. [Google Scholar] [CrossRef]
- Wang, W.; Kliber, J.; Zhang, G.; Xu, W.; Howell, B.; Palladino, T. A power line signaling based scheme for anti-islanding protection of distributed generators—Part II: Field test results. IEEE Trans. Power Deliv. 2007, 22, 1767–1772. [Google Scholar] [CrossRef]
- De Mango, F.; Liserre, M.; Aquila, A.D. Overview of anti-islanding algorithms for PV systems. Part II: Active methods. In Proceedings of the EPE-PEMC, Portorož, Slovenia, 30 August–1 September 2006. [Google Scholar]
- Ropp, M.E.; Begovic, M.; Rohatgi, A. Analysis and performance assessment of the active frequency drift method of islanding prevention. IEEE Trans. Energy Convers. 1999, 14, 810–816. [Google Scholar] [CrossRef]
- Kobayashi, H.; Takigawa, K.; Hashimoto, E.; Kitamura, A.; Matsuda, H. Method for preventing phenomenon of utility grid with a number of small scale PV systems. In Proceedings of the 22nd IEEE Photovoltaic Specialists Conference, Las Vegas, NV, USA, 7–11 October 1991. [Google Scholar]
- Ropp, M.E.; Begovic, M.; Rohatgi, A. Prevention of islanding in grid-connected photovoltaic systems. Prog. Photovolt. 1999, 7, 39–59. [Google Scholar] [CrossRef]
- Rioual, P.; Pouliquen, H.; Louis, J. Regulation of a PWM rectifier in the unbalanced network state using a generalized model. IEEE Trans. Power Electron. 1996, 11, 495–502. [Google Scholar] [CrossRef]
- Song, H.; Nam, K. Dual current control scheme for PWM converter under unbalanced input voltage conditions. IEEE Trans. Ind. Electron. 1999, 46, 953–959. [Google Scholar] [CrossRef]
- Stankovic, A.M.; Lev-Ari, H. Frequency-domain observations on definitions of reactive power. IEEE Power Eng. Rev. 2000, 20, 46–48. [Google Scholar] [CrossRef]
- Suh, Y.S.; Tijeras, V.; Lipo, T.A. A control method in dq synchronous frame for PWM boost rectifier under generalized unbalanced operating conditions. In Proceedings of the IEEE PESC, Cairns, Australia, 23–27 June 2002. [Google Scholar]
- Suh, Y.S.; Lipo, T.A. Control scheme in hybrid synchronous stationary frame for PWMAC/DC converter under generalized unbalanced operating conditions. IEEE Trans. Ind. Appl. 2006, 42, 825–835. [Google Scholar]
- International Electrotechnical Commission. Instrument Transformers—Part 1: Current Transformers; IEC 60044-1:2003; International Electrotechnical Commission: Geneva, Switzerland, 2003. [Google Scholar]
- International Electrotechnical Commission. Instrument Transformers—Part 2: Inductive Voltage Transformers; IEC 60044-2:2003; International Electrotechnical Commission: Geneva, Switzerland, 2003. [Google Scholar]
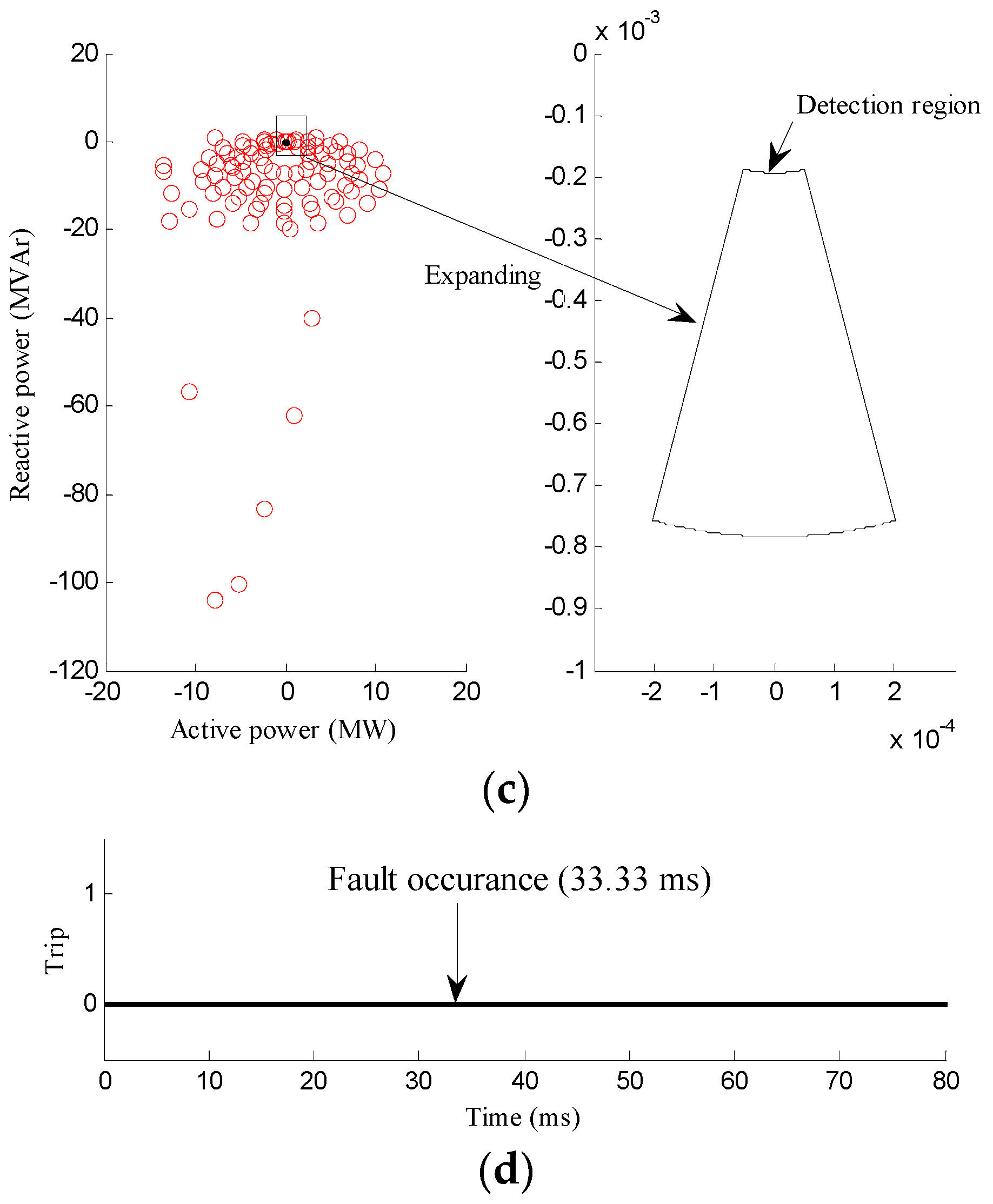
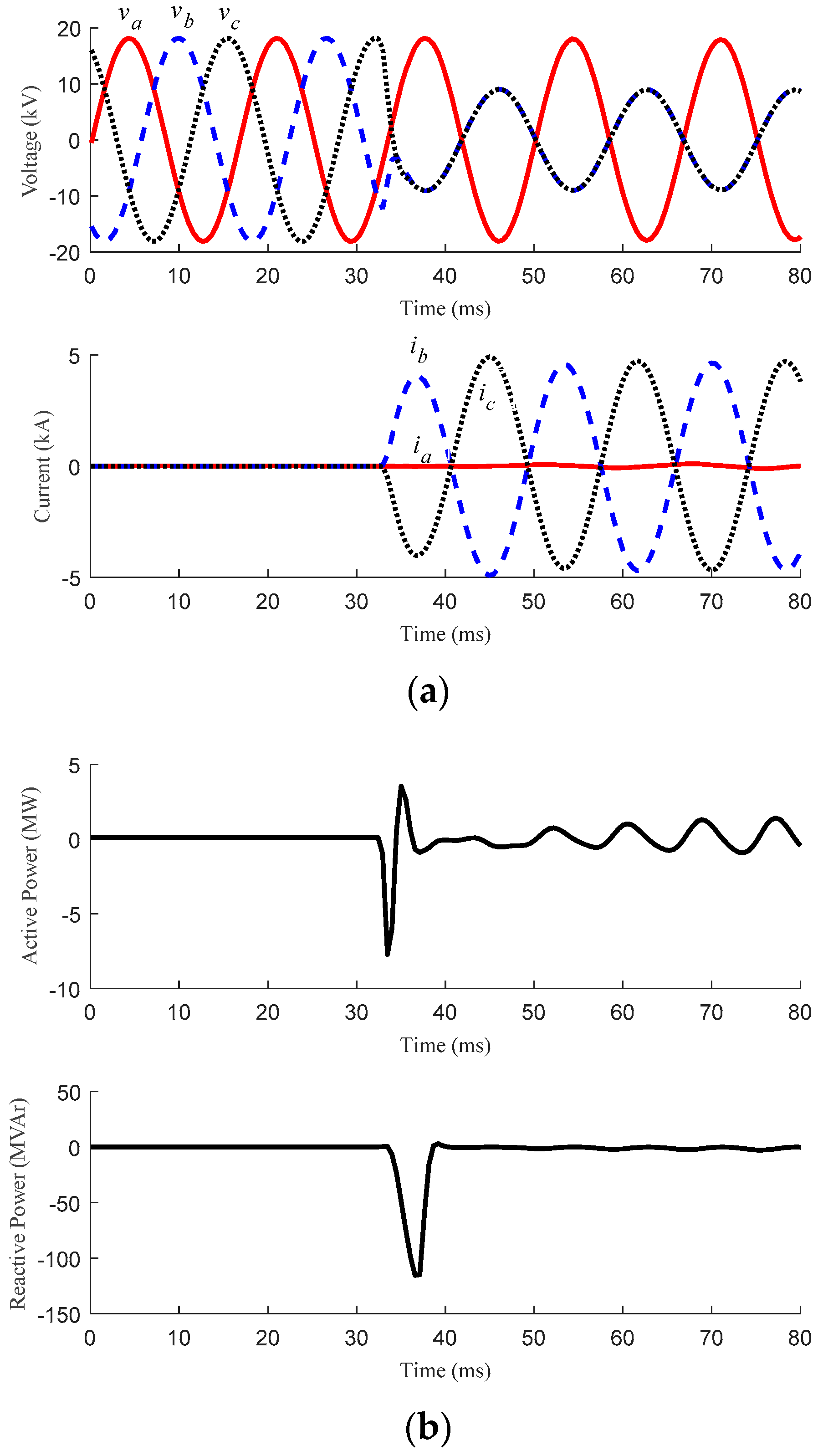
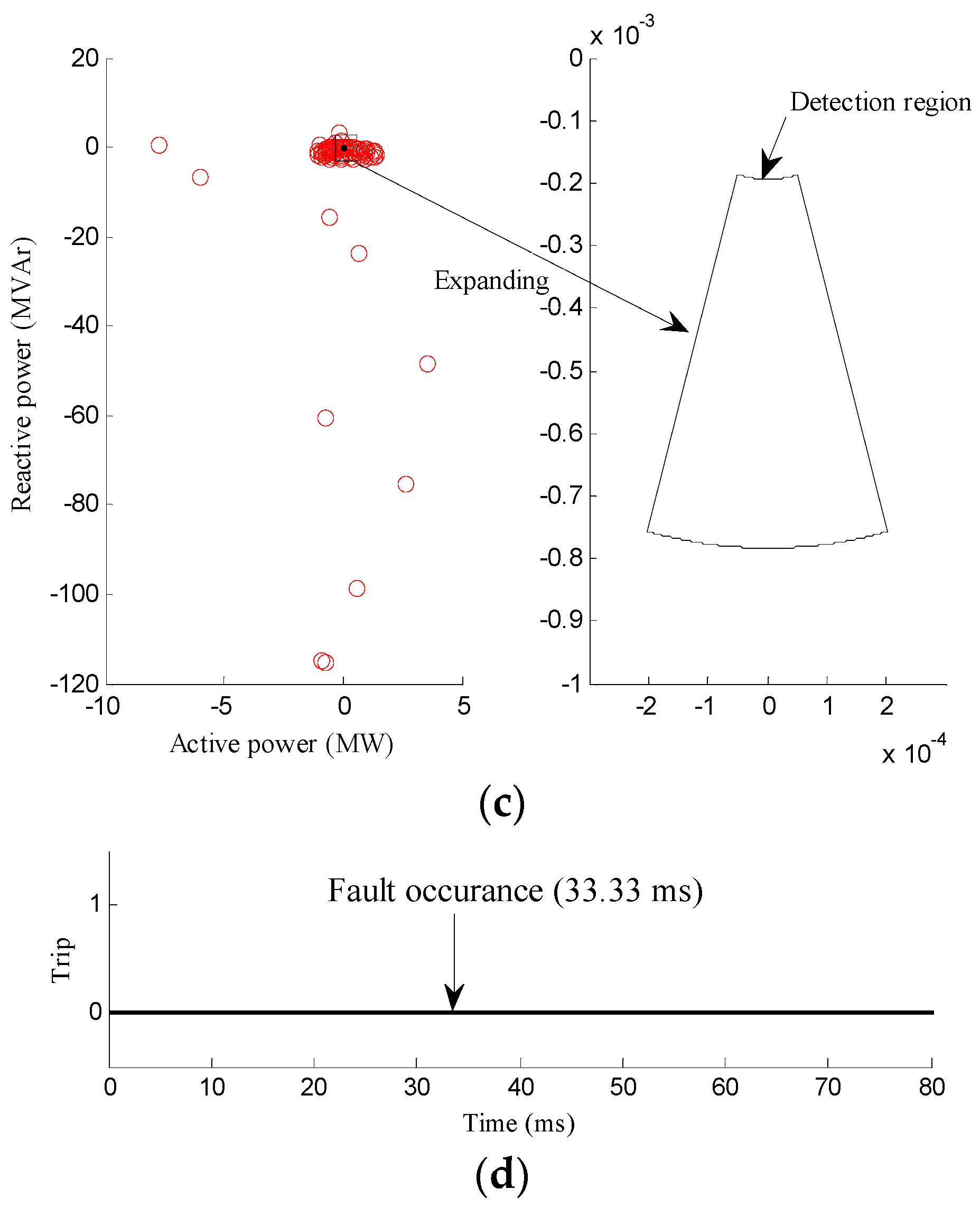
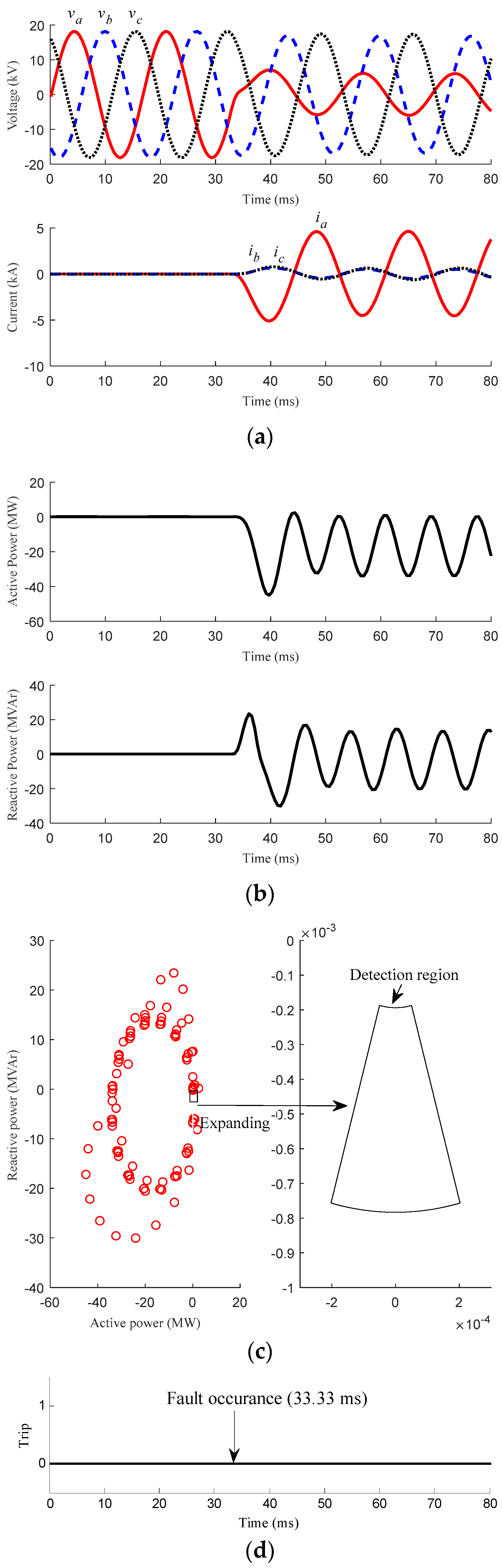
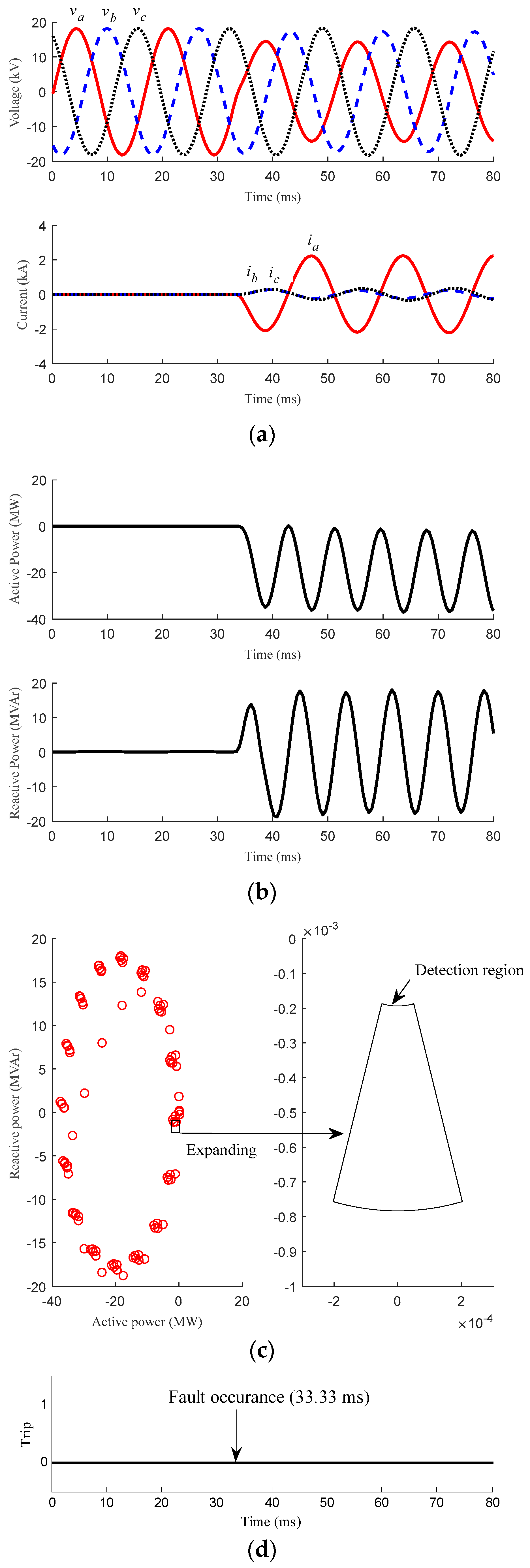
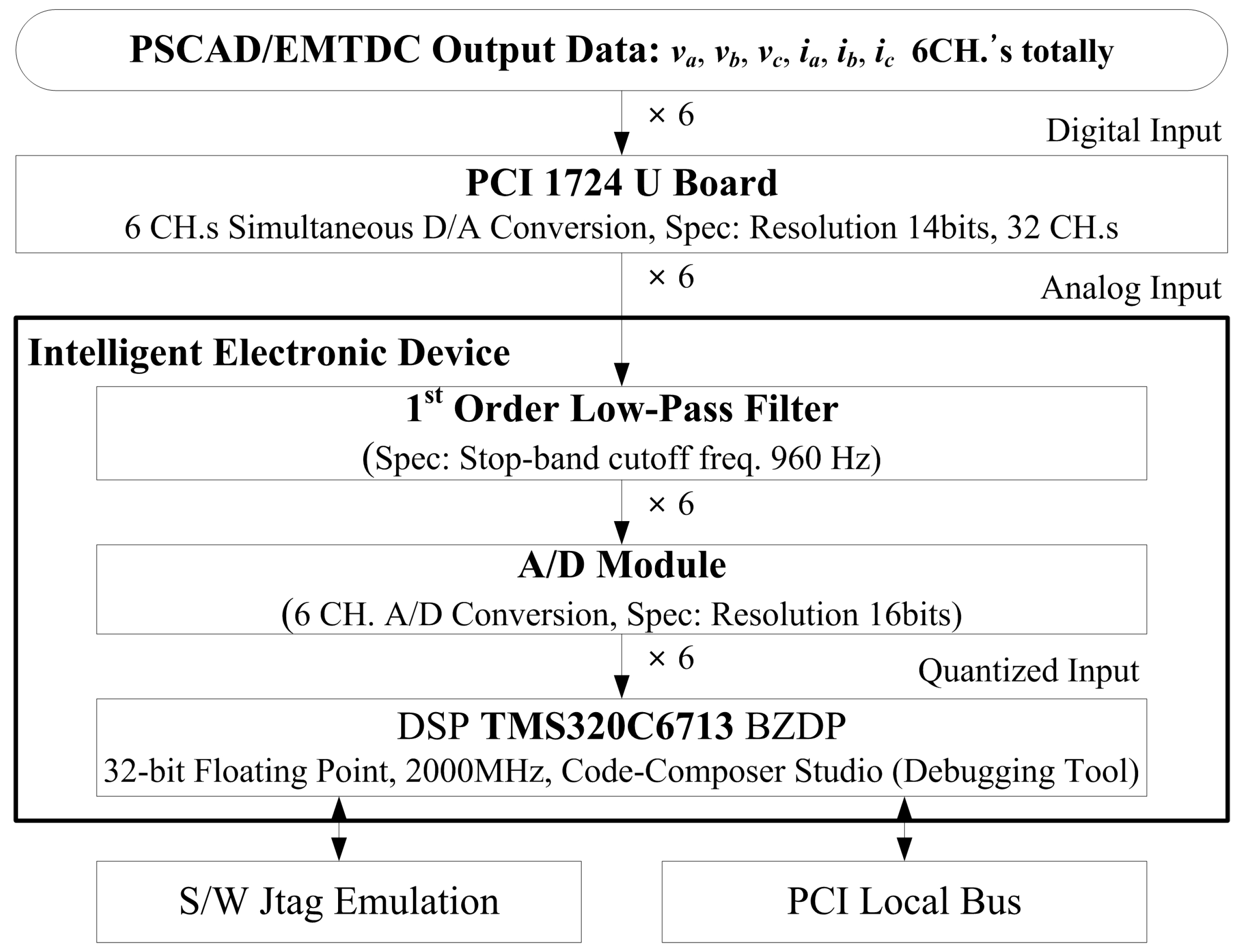
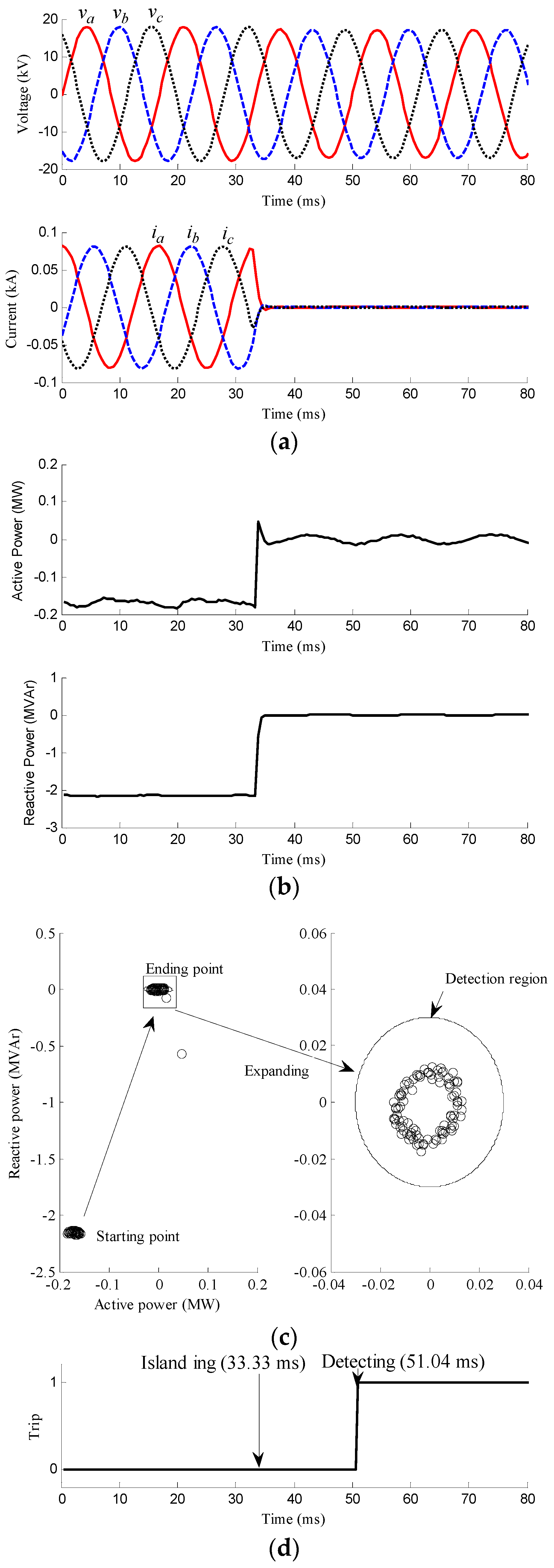
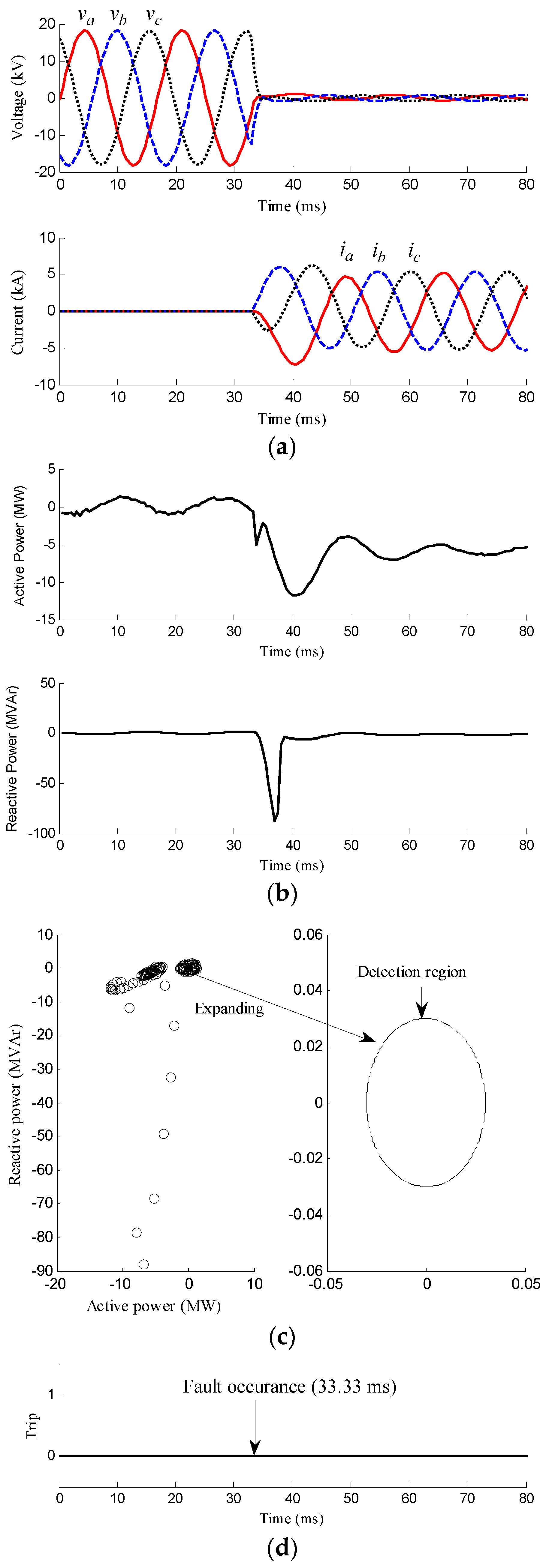
| Scenario | Case No. | Description | Figure | Detection Signal |
|---|---|---|---|---|
| Islanding | Case 1 | Generating power of the MG < local loads of the MG | Figure 3 | Should be activated |
| Case 2 | Generating power of the MG ≈ local loads of the MG | Figure 4 | ||
| Case 3 | Generating power of the MG > local loads of the MG | Figure 5 |
| Scenario | Case No. | Fault Position | Fault Inception Angle | Fault Type | Fault Impedance | Figure | Detection Signal |
|---|---|---|---|---|---|---|---|
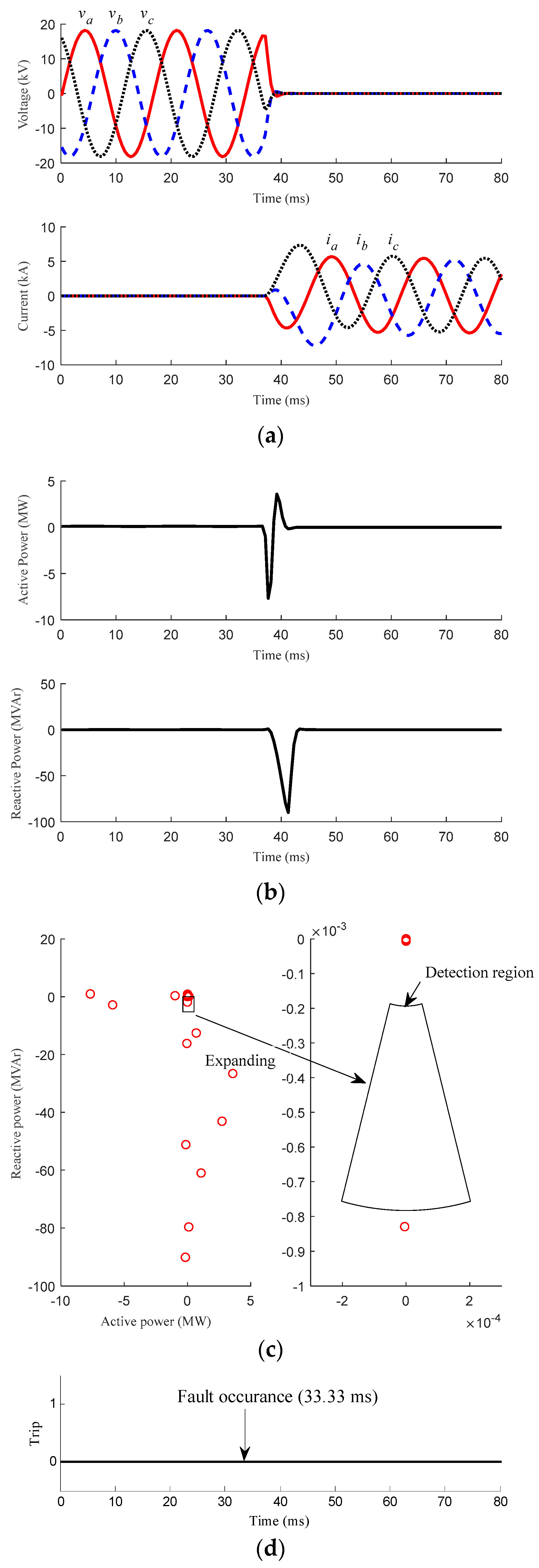
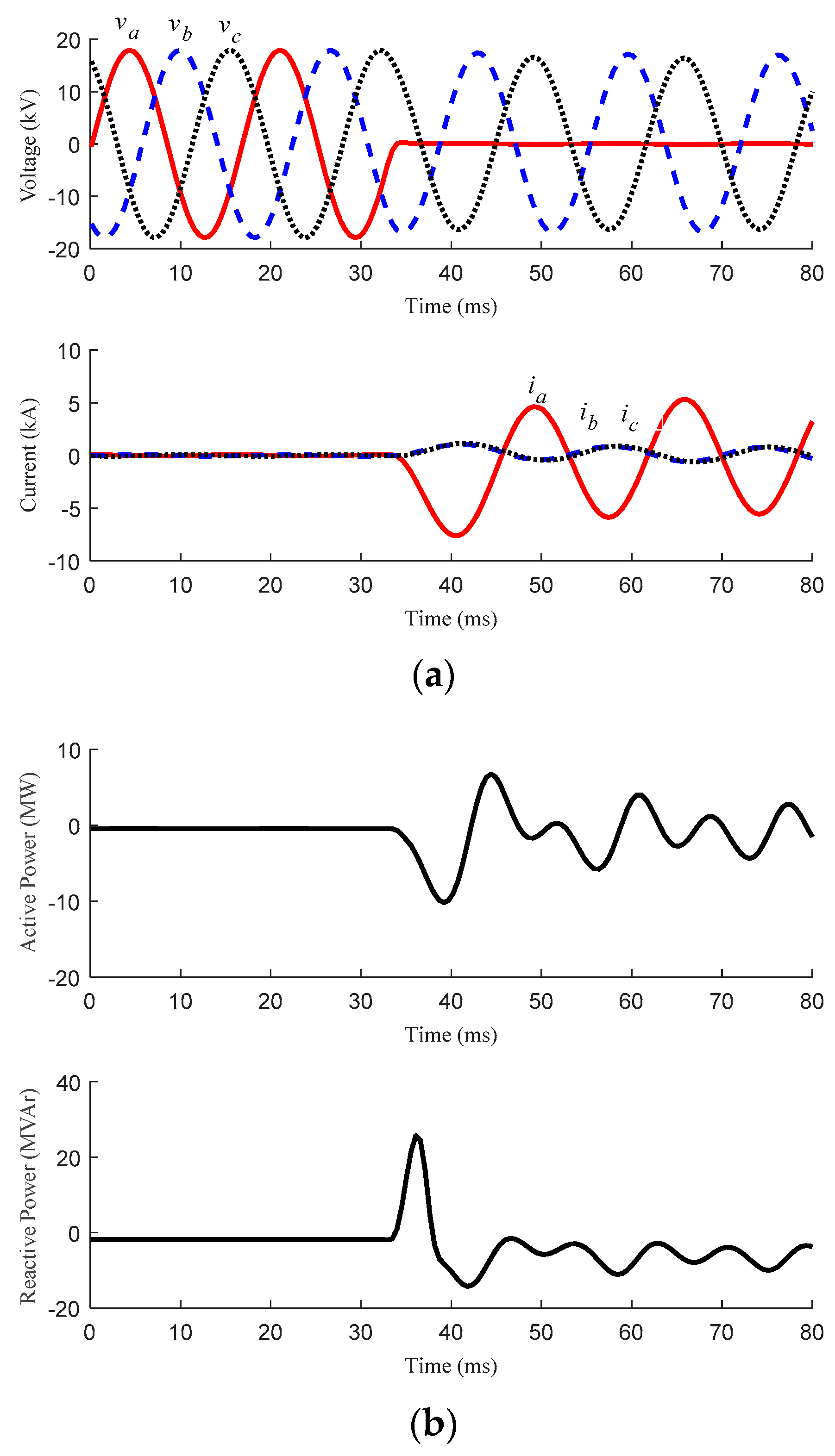
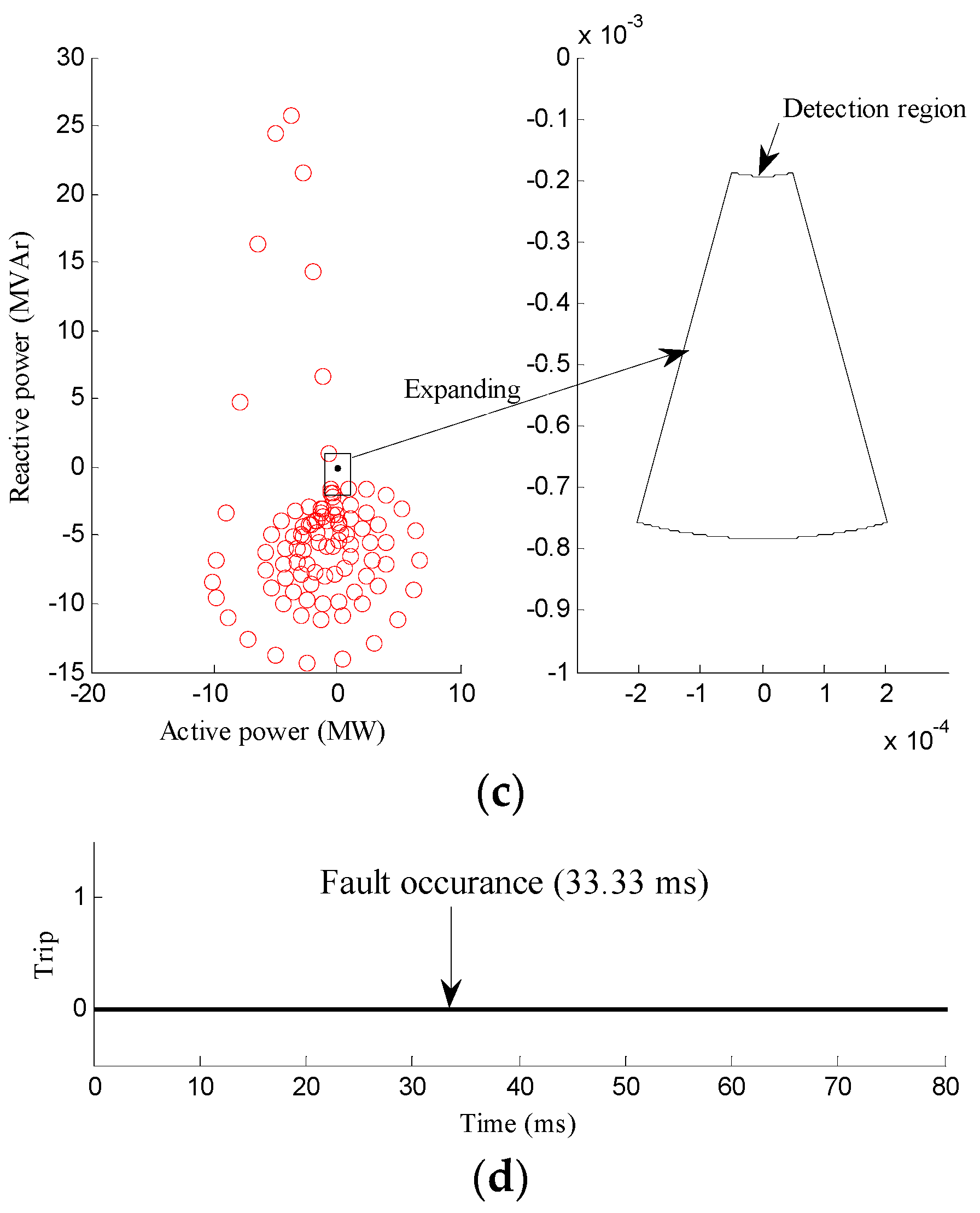
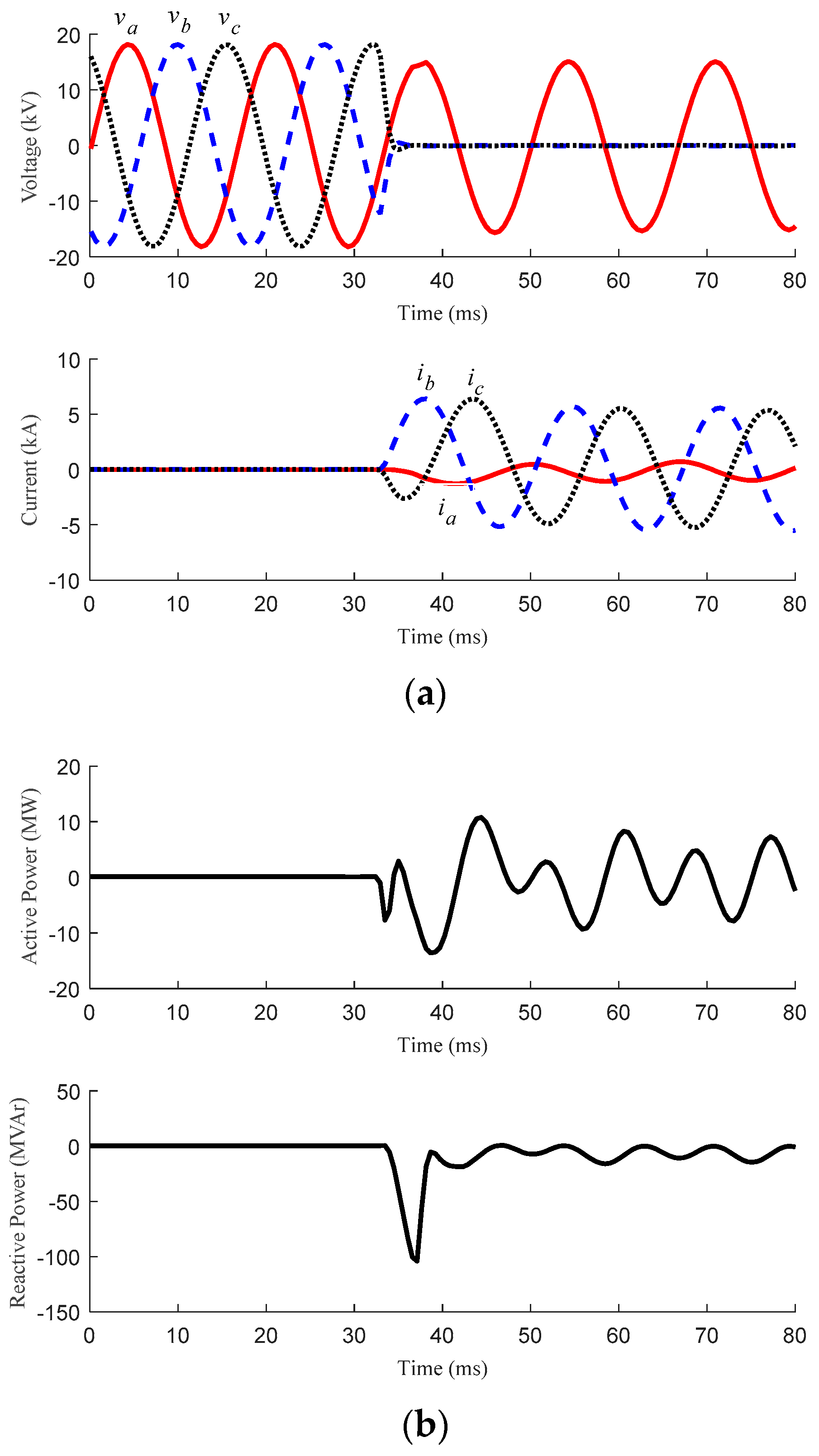
| Fault | Case 4 | Distribution line of the MG | 0° | Three-phase | 0 Ω | Figure 6 | Should NOT be activated |
| Case 5 | Dedicated line | 0° | Three-phase | 0 Ω | Figure 7 | ||
| Case 6 | Dedicated line | 45° | Three-phase | 0 Ω | Figure 8 | ||
| Case 7 | Dedicated line | 90° | Three-phase | 0 Ω | Figure 9 | ||
| Case 8 | Dedicated line | 0° | Single line-to-ground | 0 Ω | Figure 10 | ||
| Case 9 | Dedicated line | 0° | Double line-to-ground | 0 Ω | Figure 11 | ||
| Case 10 | Dedicated line | 0° | Line-to-line | 0 Ω | Figure 12 | ||
| Case 11 | Dedicated line | 0° | Single line-to-ground | 1 Ω | Figure 13 | ||
| Case 12 | Dedicated line | 0° | Single line-to-ground | 5 Ω | Figure 14 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, T.; Yang, H.; Zhao, R.; Kang, Y.C.; Terzija, V. Design, Evaluation and Implementation of an Islanding Detection Method for a Micro-grid. Energies 2018, 11, 323. https://doi.org/10.3390/en11020323
Zheng T, Yang H, Zhao R, Kang YC, Terzija V. Design, Evaluation and Implementation of an Islanding Detection Method for a Micro-grid. Energies. 2018; 11(2):323. https://doi.org/10.3390/en11020323
Chicago/Turabian StyleZheng, Taiying, Huan Yang, Rongxiang Zhao, Yong Cheol Kang, and Vladimir Terzija. 2018. "Design, Evaluation and Implementation of an Islanding Detection Method for a Micro-grid" Energies 11, no. 2: 323. https://doi.org/10.3390/en11020323
APA StyleZheng, T., Yang, H., Zhao, R., Kang, Y. C., & Terzija, V. (2018). Design, Evaluation and Implementation of an Islanding Detection Method for a Micro-grid. Energies, 11(2), 323. https://doi.org/10.3390/en11020323




