Investigation of Water Hammer Protection in Water Supply Pipeline Systems Using an Intelligent Self-Controlled Surge Tank
Abstract
:1. Introduction
2. Numerical Model
2.1. Governing Equations
2.2. Method of Characteristics
2.3. Boundary Conditions
2.3.1. Reservoirs
2.3.2. Valve
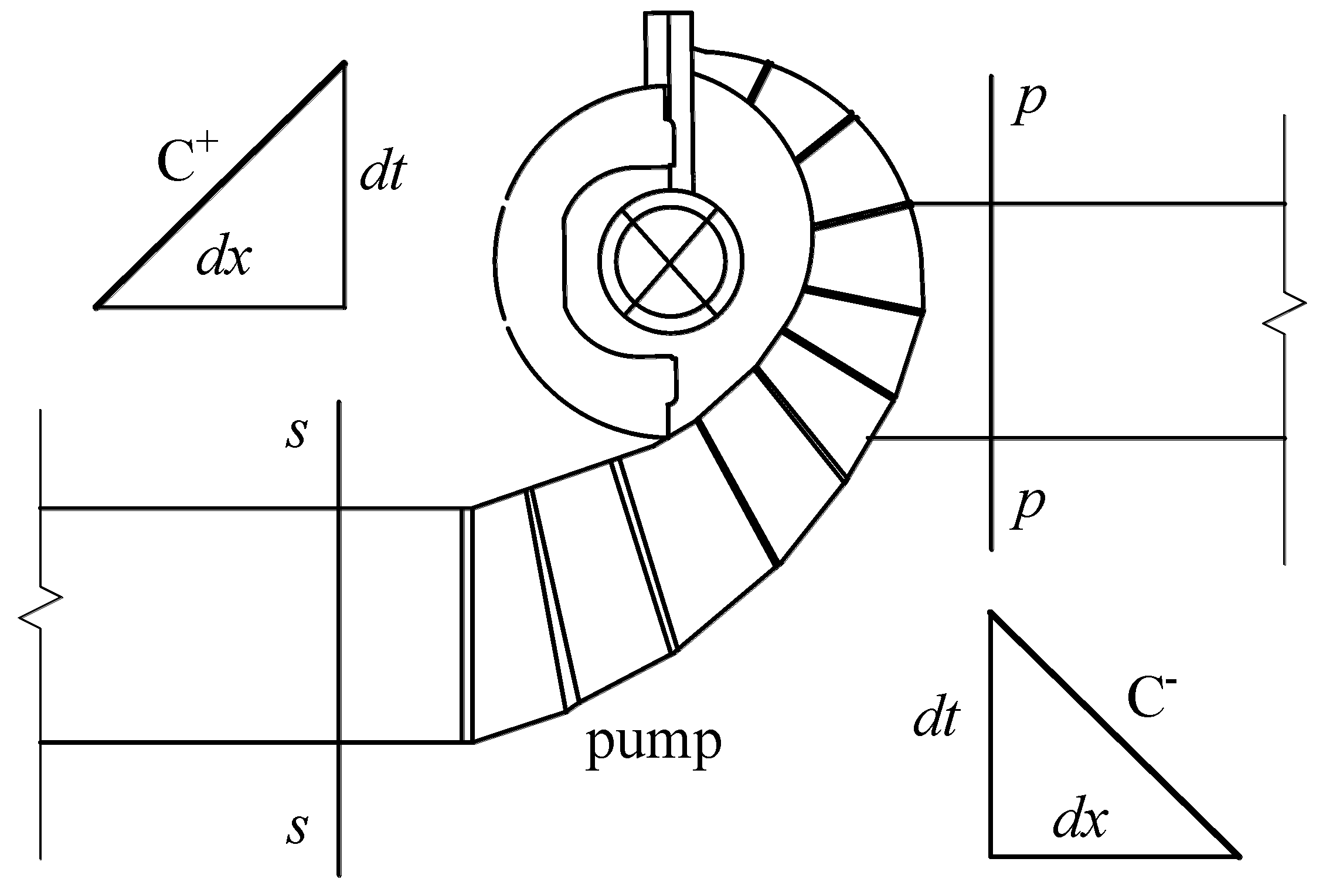
2.3.3. Pumps
2.3.4. Normal Surge Tanks
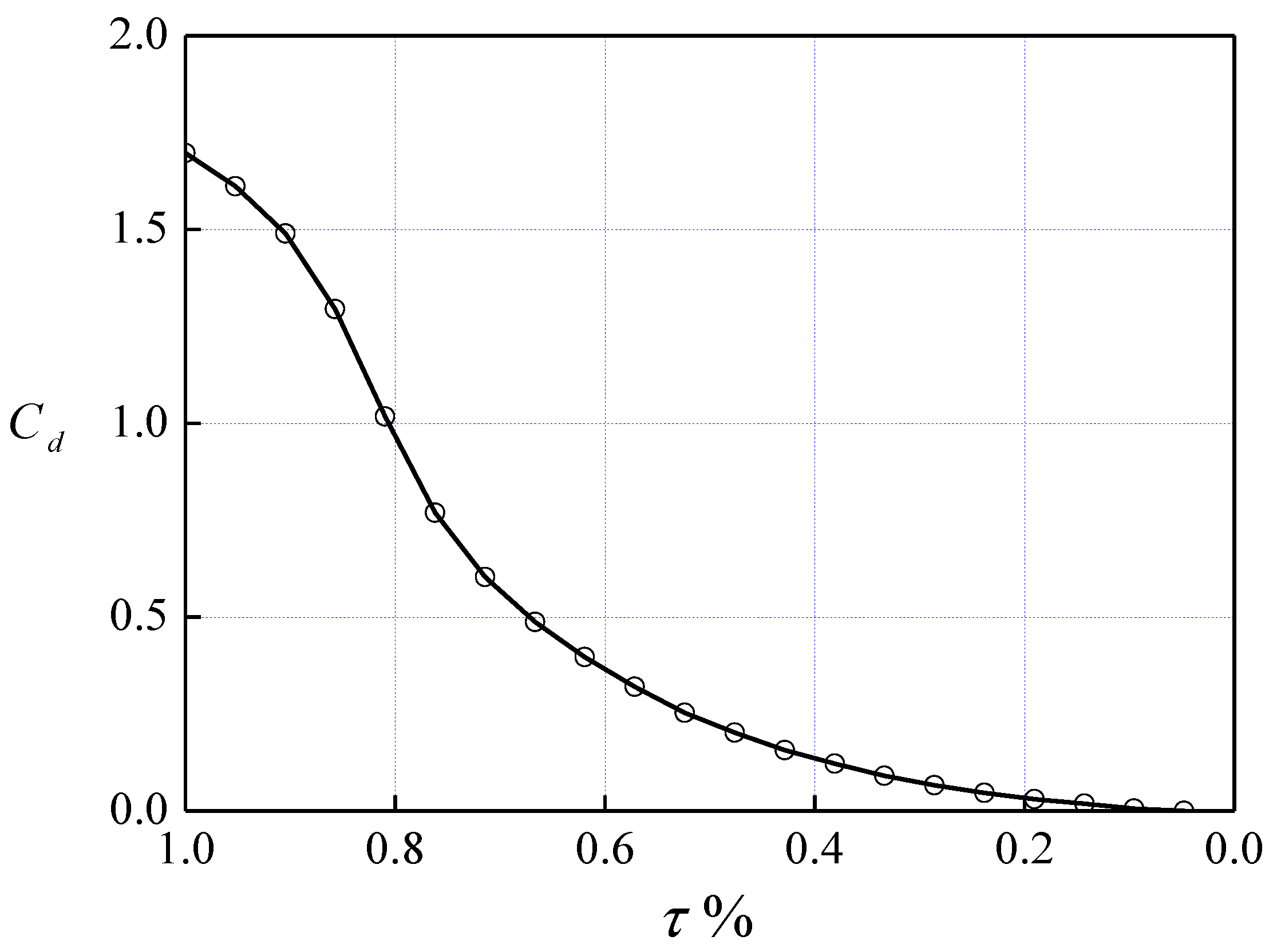
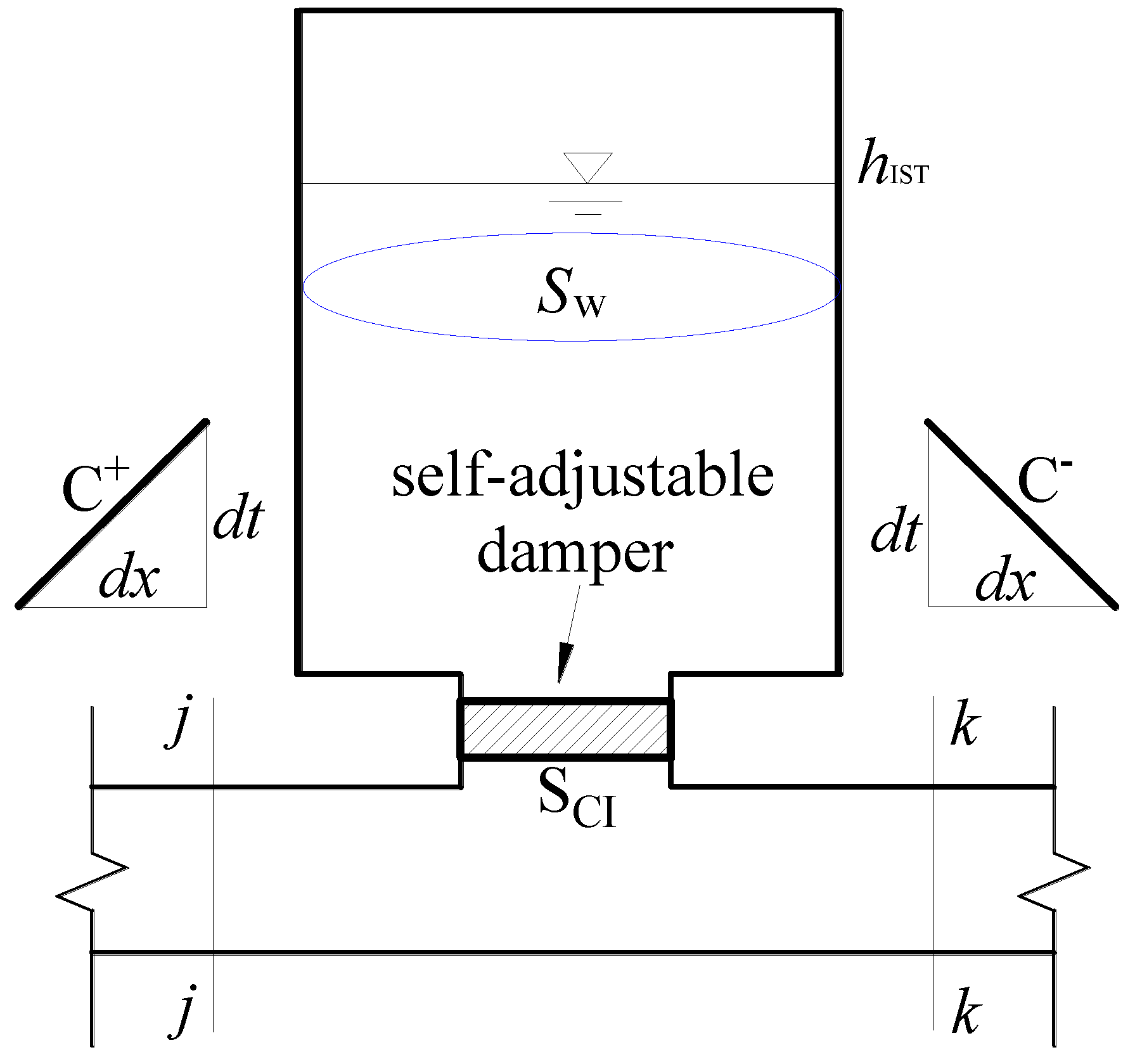
2.3.5. Intelligent Self-Controlled Surge Tanks
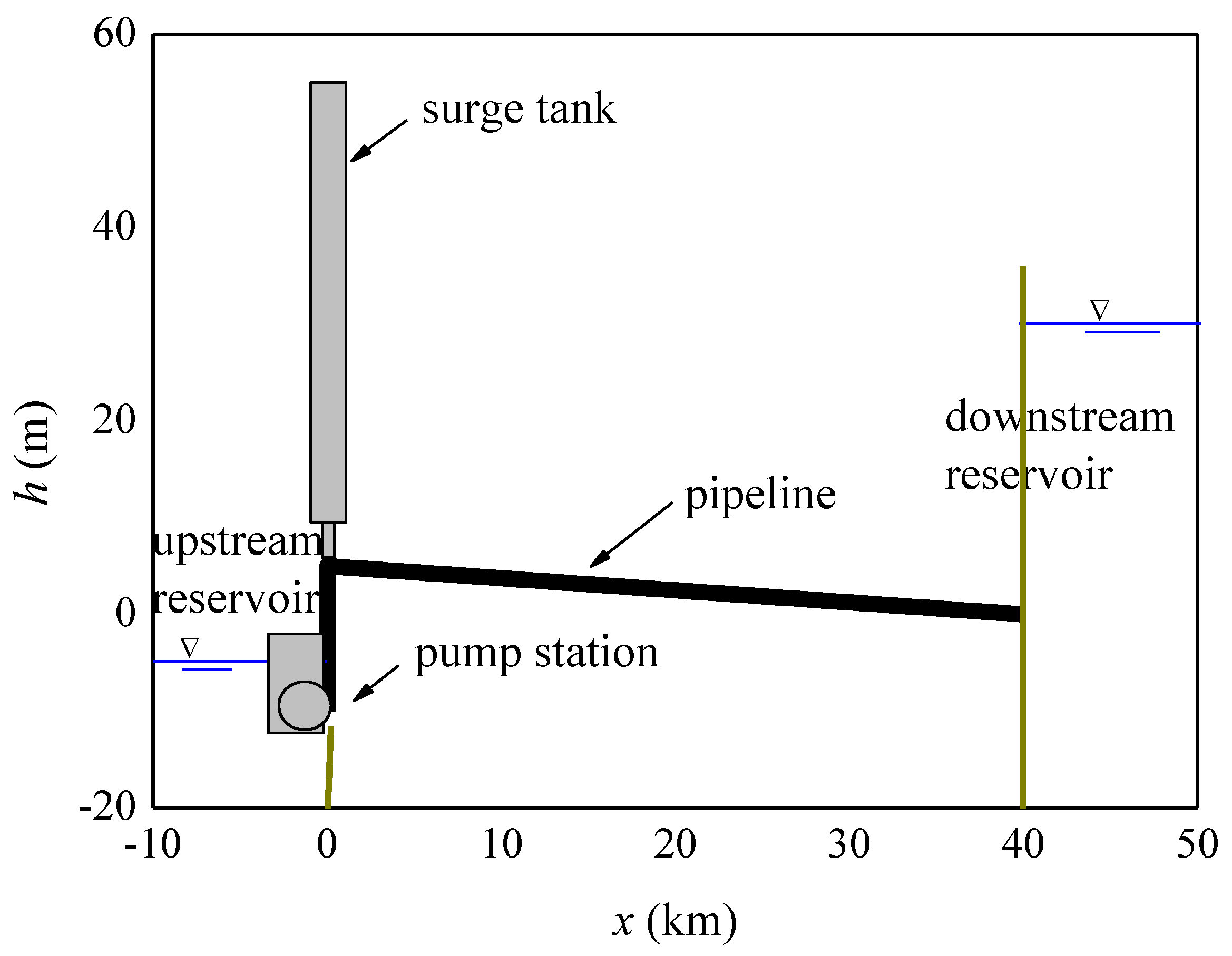
3. Simulation and Analysis
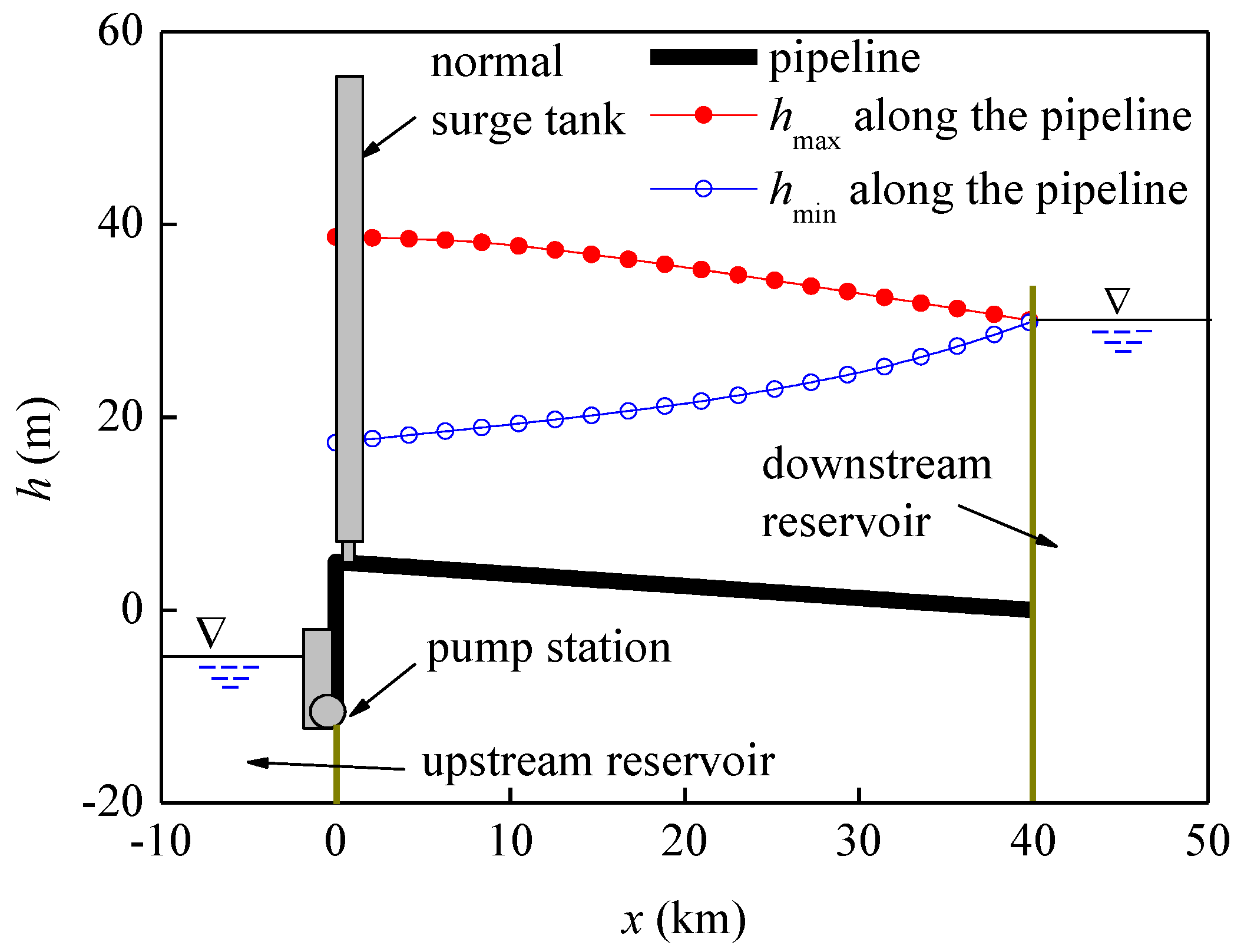
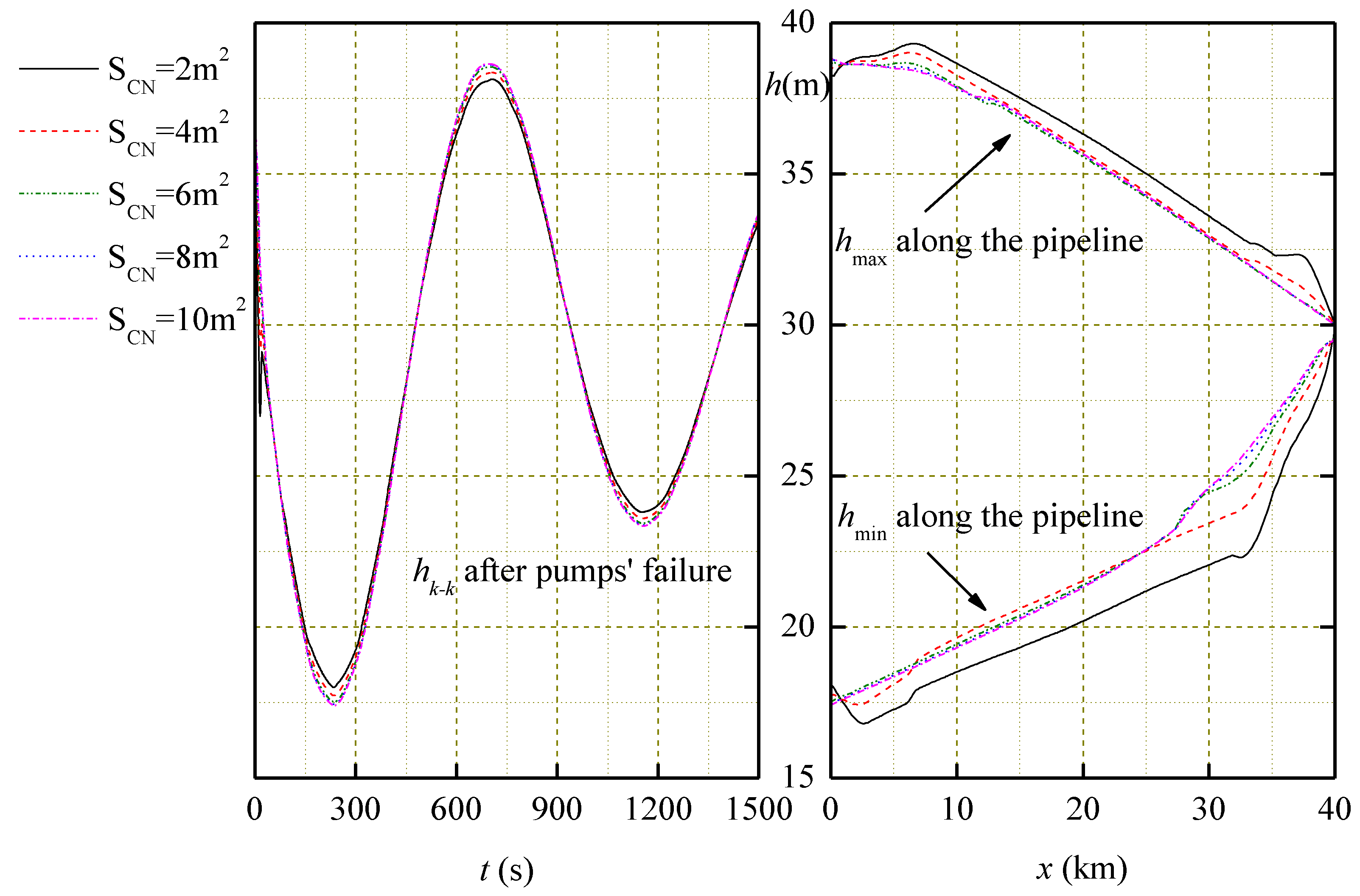
3.1. Transient Response of Normal Surge Tanks
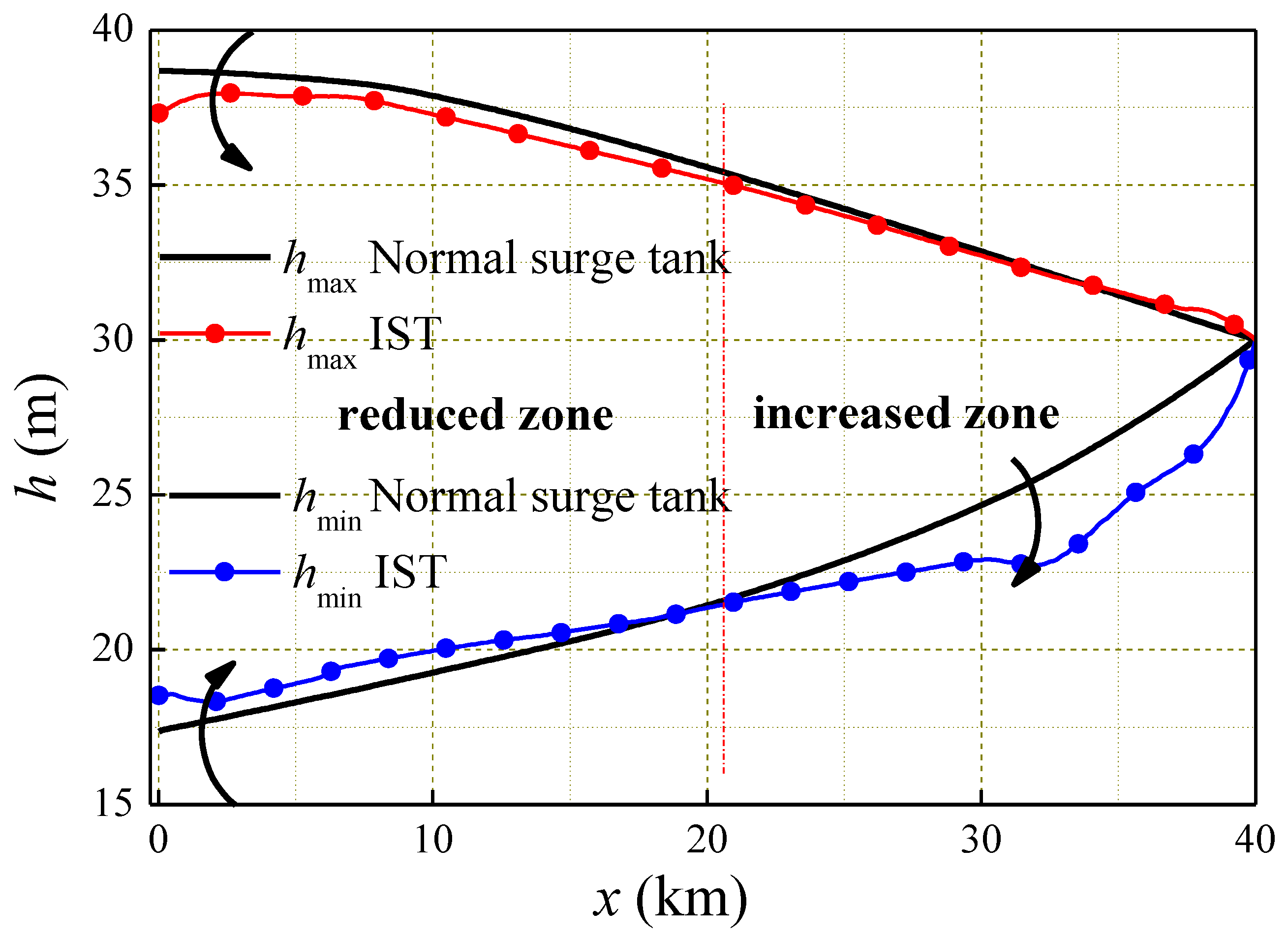
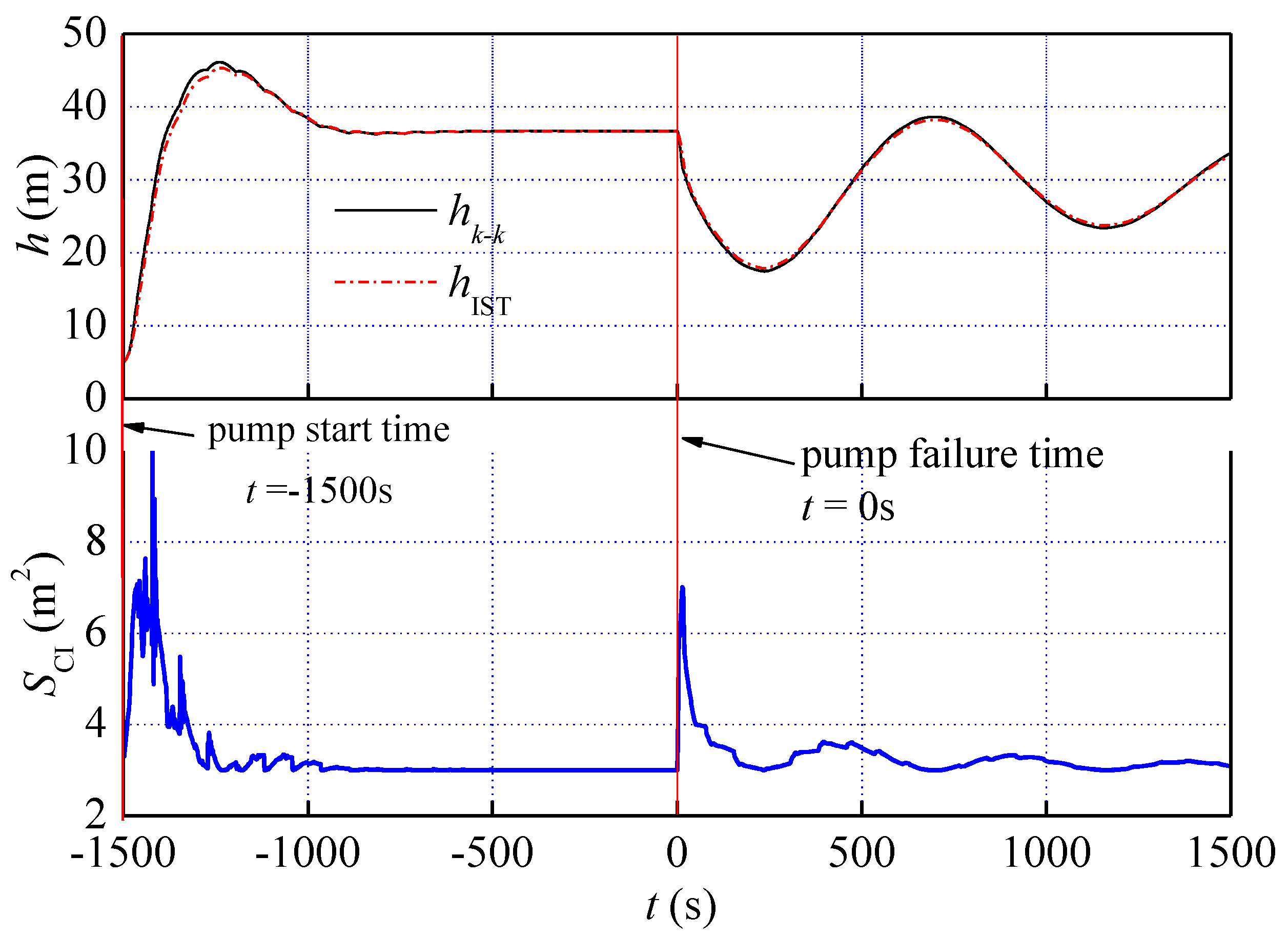
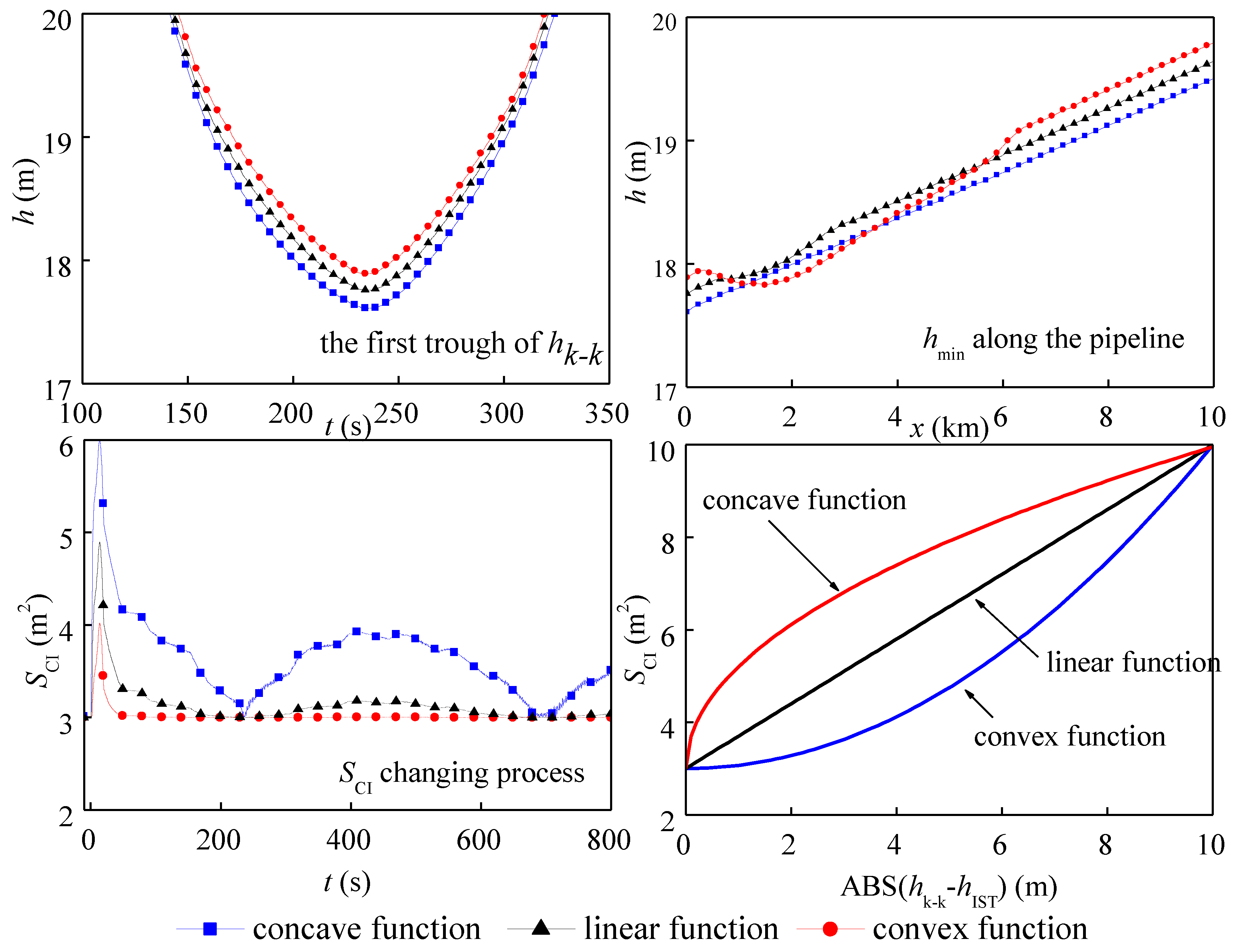
3.2. Transient Response of Intelligent Self-Controlled Surge Tanks
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| Acceleration of gravity (m/s2) | |
| Pressure head (m) | |
| Distance along pipe from inlet (m) | |
| Time, as subscript to denote time (s) | |
| Flow velocity (m/s) | |
| Instantaneous wall shear stress | |
| The quasi-steady component | |
| The unsteady component | |
| The angle between pipe and the horizontal plane. | |
| Speed of pressure wave (m/s) | |
| Darcy friction factor | |
| Main pipe diameter (m) | |
| Serial number of nodes (s) | |
| Time step (s) | |
| Discharge (m3/s) | |
| Length of segment (m) | |
| Head of upstream reservoir (m) | |
| Number of sections | |
| Head of downstream reservoir (m) | |
| Discharge through the valve (m3/s) | |
| Discharge coefficient | |
| Valve opening ratio | |
| Cross area (m2) | |
| Head difference of valve’s two sides (m) | |
| Instantaneous position of pump operation | |
| Constant | |
| Dimensionless discharge of the pump | |
| Dimensionless rotated speed of the pump | |
| Head of the pump (m) | |
| Rated head of the pump (m) | |
| Rotate speed of the pump | |
| Rated speed of the pump | |
| Discharge through the pump (m3/s) | |
| Rated discharge of the pump (m3/s) | |
| Torque of the pump (Nm) | |
| Rated torque of the pump (Nm) | |
| Head difference of pump’s two sides (m) | |
| The weight of rotating parts plus entrained liquid (kg) | |
| The radius of gyration of the rotating mass (m) | |
| Cross area of normal surge tank (m2) | |
| Head in normal surge tank (m) | |
| The local energy loss coefficient of normal surge tank connector | |
| The discharge through the normal surge tank connector (m3/s) | |
| Cross area of the normal surge tank connector (m2) | |
| Head at the connector in pipe (m) | |
| Head in IST (m) | |
| The local energy loss coefficient of IST connector | |
| The discharge through the IST connector (m3/s) | |
| Cross area of the IST damper (m2) | |
| Maximum head along pipeline (m) | |
| Minimum head along pipeline (m) | |
| The extreme water hammer amplitude (m) | |
| Acronyms | |
| MOC | Method of Characteristics |
| IST | Intelligent Self-controlled Surge Tank |
References
- Yu, X.D.; Zhang, J.; Miao, D. Innovative Closure Law for Pump-Turbines and Field Test Verification. J. Hydraul. Eng. 2015, 141, 05014010. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L.; Suo, L. Fluid Transients in Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Kim, S.H. Impulse response method for pipeline systems equipped with water hammer protection devices. J. Hydraul. Eng. 2008, 134, 961–969. [Google Scholar] [CrossRef]
- Vereide, K.; Svingen, B.; Nielsen, T.K.; Lia, L. The Effect of Surge Tank Throttling on Governor Stability, Power Control, and Hydraulic Transients in Hydropower Plants. IEEE Trans. Energy Convers. 2017, 32, 91–98. [Google Scholar] [CrossRef]
- Stephenson, D. Effects of air valves and pipework on water hammer pressures. J. Transp. Eng.-ASCE 1997, 123, 101–106. [Google Scholar] [CrossRef]
- Bergant, A.; Kruisbrink, A.; Arregui, F. Dynamic Behaviour of Air Valves in a Large-Scale Pipeline Apparatus. Strojniski Vestnik-J. Mech. Eng. 2012, 58, 225–237. [Google Scholar] [CrossRef]
- Ghidaoui, M.S.; Zhao, M.; McInnis, D.A.; Axworthy, D.H. A review of water hammer theory and practice. Appl. Mech. Rev. 2005, 58, 49–76. [Google Scholar] [CrossRef]
- Chaudhry, M.; Hussaini, M. Second-order accurate explicit finite-difference schemes for waterhammer analysis. J. Fluids Eng. 1985, 107, 523–529. [Google Scholar] [CrossRef]
- Kochupillai, J.; Ganesan, N.; Padmanabhan, C. A new finite element formulation based on the velocity of flow for water hammer problems. Int. J. Press. Vessels Pip. 2005, 82, 1–14. [Google Scholar] [CrossRef]
- Triki, A. Further investigation on the resonance of free-surface waves provoked by floodgate maneuvers: Negative surge waves. Ocean Eng. 2017, 133, 133–141. [Google Scholar] [CrossRef]
- Triki, A. Resonance of Free-Surface Waves Provoked by Floodgate Maneuvers (vol 19, pg 1124, 2014). J. Hydrol. Eng. 2016, 21. [Google Scholar] [CrossRef]
- Karney, B.W.; McInnis, D. Efficient Calculation of Transient Flow in Simple Pipe Networks. J. Hydraul. Eng.-ASCE 1992, 118, 1014–1030. [Google Scholar] [CrossRef]
- Fang, H.Q.; Chen, L.; Dlakavu, N.; Shen, Z.Y. Basic Modeling and simulation tool for analysis of hydraulic transients in hydroelectric power plants. IEEE Trans. Energy Convers. 2008, 23, 834–841. [Google Scholar] [CrossRef]
- Nagode, K.; Skrjanc, I. Modelling and Internal Fuzzy Model Power Control of a Francis Water Turbine. Energies 2014, 7, 874–889. [Google Scholar] [CrossRef] [Green Version]
- Zhou, D.; Chen, H.; Zhang, L. Investigation of Pumped Storage Hydropower Power-Off Transient Process Using 3D Numerical Simulation Based on SP-VOF Hybrid Model. Energies 2018, 11, 1020. [Google Scholar] [CrossRef]
- Vournas, C.D.; Papaioannou, G. Modeling and Stability of Hydro Plant with 2 Surge Tanks. IEEE Trans. Energy Convers. 1995, 10, 368–375. [Google Scholar] [CrossRef]
- Demello, F.P.; Koessler, R.J.; Agee, J.; Anderson, P.M.; Doudna, J.H.; Fish, J.H.; Hamm, P.A.L.; Kundur, P.; Lee, D.C.; Rogers, G.J.; et al. Hydraulic-turbine and turbine control-models for system dynamic studies. IEEE Trans. Power Syst. 1992, 7, 167–179. [Google Scholar]
- Cheng, Y.G.; Li, J.P.; Yang, J.D. Free surface-pressurized flow in ceiling-sloping tailrace tunnel of hydropower plant: Simulation by VOF model. J. Hydraul. Res. 2007, 45, 88–99. [Google Scholar] [CrossRef]
- Yang, J.D.; Wang, M.J.; Wang, C.; Guo, W.C. Linear Modeling and Regulation Quality Analysis for Hydro-Turbine Governing System with an Open Tailrace Channel. Energies 2015, 8, 11702–11717. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.D.; Wang, H.; Guo, W.C.; Yang, W.J.; Zeng, W. Simulation of Wind Speed in the Ventilation Tunnel for Surge Tanks in Transient Processes. Energies 2016, 9, 95. [Google Scholar] [CrossRef]
- Riasi, A.; Tazraei, P. Numerical analysis of the hydraulic transient response in the presence of surge tanks and relief valves. Renew. Energy 2017, 107, 138–146. [Google Scholar] [CrossRef]
- Skulovich, O.; Bent, R.; Judi, D.; Perelman, L.S.; Ostfeld, A. Piece-wise mixed integer programming for optimal sizing of surge control devices in water distribution systems. Water Resour. Res. 2015, 51, 4391–4408. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Xu, Y.; Zheng, Y.; Zhang, Y. Optimization of Guide Vane Closing Schemes of Pumped Storage Hydro Unit Using an Enhanced Multi-Objective Gravitational Search Algorithm. Energies 2017, 10, 911. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Mazzetti, E.; Laucelli, D.B.; Borta, G. Hydraulic characterization and transient response of pressure reducing valves: Laboratory experiments. J. Hydroinform. 2017, 19, 798–810. [Google Scholar] [CrossRef]
- Meniconi, S.; Duan, H.F.; Brunone, B.; Ghidaoui, M.S.; Lee, P.J.; Ferrante, M. Further Developments in Rapidly Decelerating Turbulent Pipe Flow Modeling. J. Hydraul. Eng. 2014, 140, 04014028. [Google Scholar] [CrossRef] [Green Version]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, W.; Zhang, B. Investigation of Water Hammer Protection in Water Supply Pipeline Systems Using an Intelligent Self-Controlled Surge Tank. Energies 2018, 11, 1450. https://doi.org/10.3390/en11061450
Wan W, Zhang B. Investigation of Water Hammer Protection in Water Supply Pipeline Systems Using an Intelligent Self-Controlled Surge Tank. Energies. 2018; 11(6):1450. https://doi.org/10.3390/en11061450
Chicago/Turabian StyleWan, Wuyi, and Boran Zhang. 2018. "Investigation of Water Hammer Protection in Water Supply Pipeline Systems Using an Intelligent Self-Controlled Surge Tank" Energies 11, no. 6: 1450. https://doi.org/10.3390/en11061450
APA StyleWan, W., & Zhang, B. (2018). Investigation of Water Hammer Protection in Water Supply Pipeline Systems Using an Intelligent Self-Controlled Surge Tank. Energies, 11(6), 1450. https://doi.org/10.3390/en11061450





