How Elastic Demand Affects Bidding Strategy in Electricity Market: An Auction Approach
Abstract
:1. Introduction
2. The Basic Model
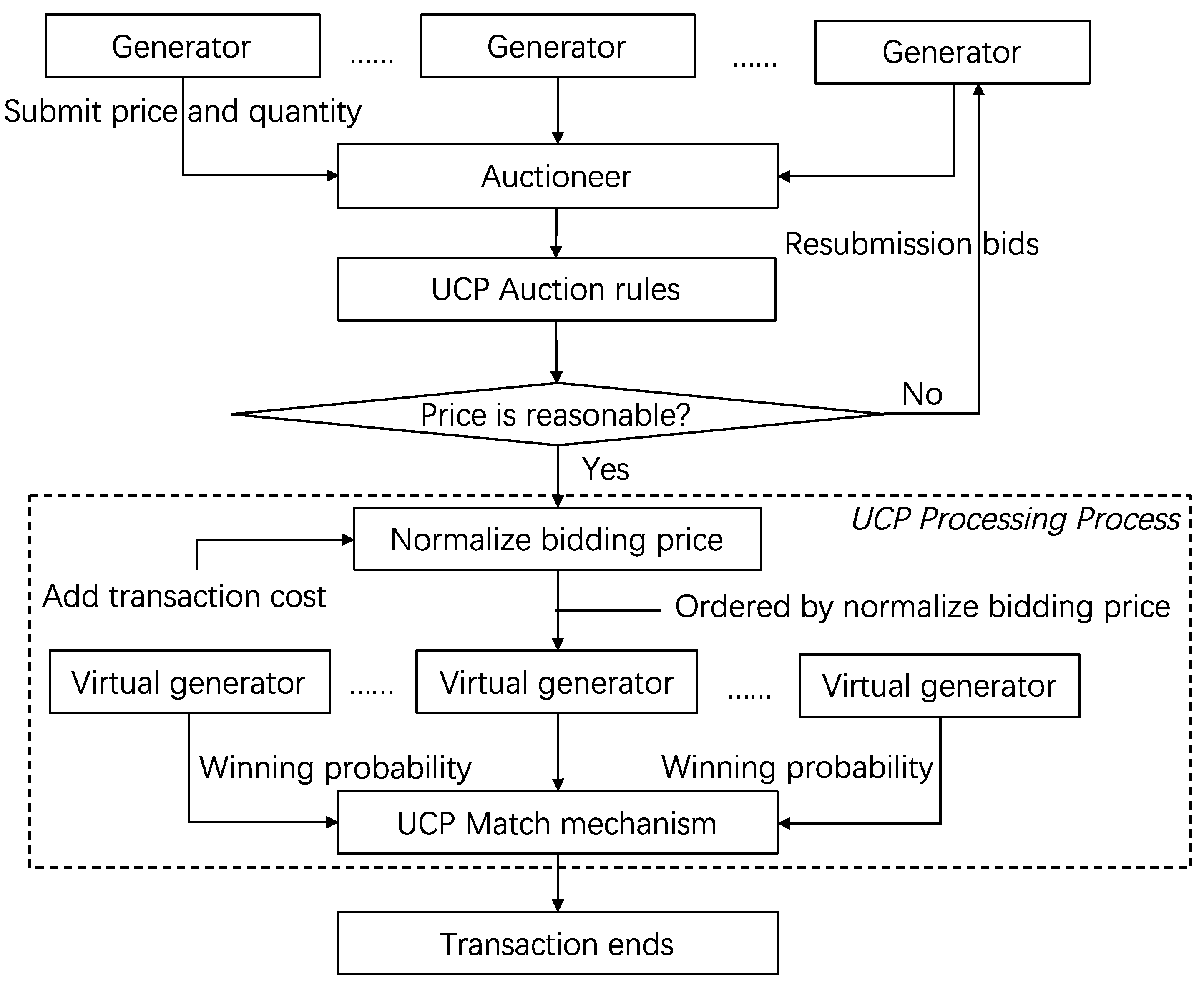
2.1. Electricity Market and MCP
- (1)
- The auctioneer releases market information according to market operation rules, including the demand information and the bidding history of participant generators.
- (2)
- Each generator simultaneously and independently submits a bidding price at which it is willing to supply its maximum production up to quantity .
- (3)
- These bids are ranked in terms of the bidding price .
- (4)
- The lower price generator is assigned with the demand quantity first. If his quantity cannot satisfy the demand, the higher price bidders produce the residual demand. If the bidders submit equal bids, then they split the market equally.
- (5)
- MCP is the highest price that produces the demand. Generators would not participate in a bid if their bidding prices were higher than the MCP.
- Step 1:
- Information acquisition. The generators get related information from the auctioneer, including the demand information and the bidding history of participant generators.
- Step 2:
- Price normalization. The generators normalize the bidding prices integrating the transaction cost.
- Step 3:
- Winning probability. The generators calculate the winning probability based on private costs.
- Step 4:
- Optimal strategy. The generators submit the optimal bids.
- Step 5:
- Nash equilibrium. Market equilibrium is the intersection of the demand function and the bidding curves.
2.2. Winning Probabilities
2.3. The Optimal Bidding Strategy of the Generators
- (1)
- For, each generatorcommits a production schedule, that satisfies Equations (1) and (13).
- (2)
- Period-day-ahead demand shockis realized and day-ahead MCPis determined. Production and profits are fulfilled in period.
3. Numerical Examples
3.1. Generators’ Optimal Bidding Strategy with Uniform Cost Distribution
3.2. Impact of Demand Scenario on Generators’ Optimal Bidding Behaviors
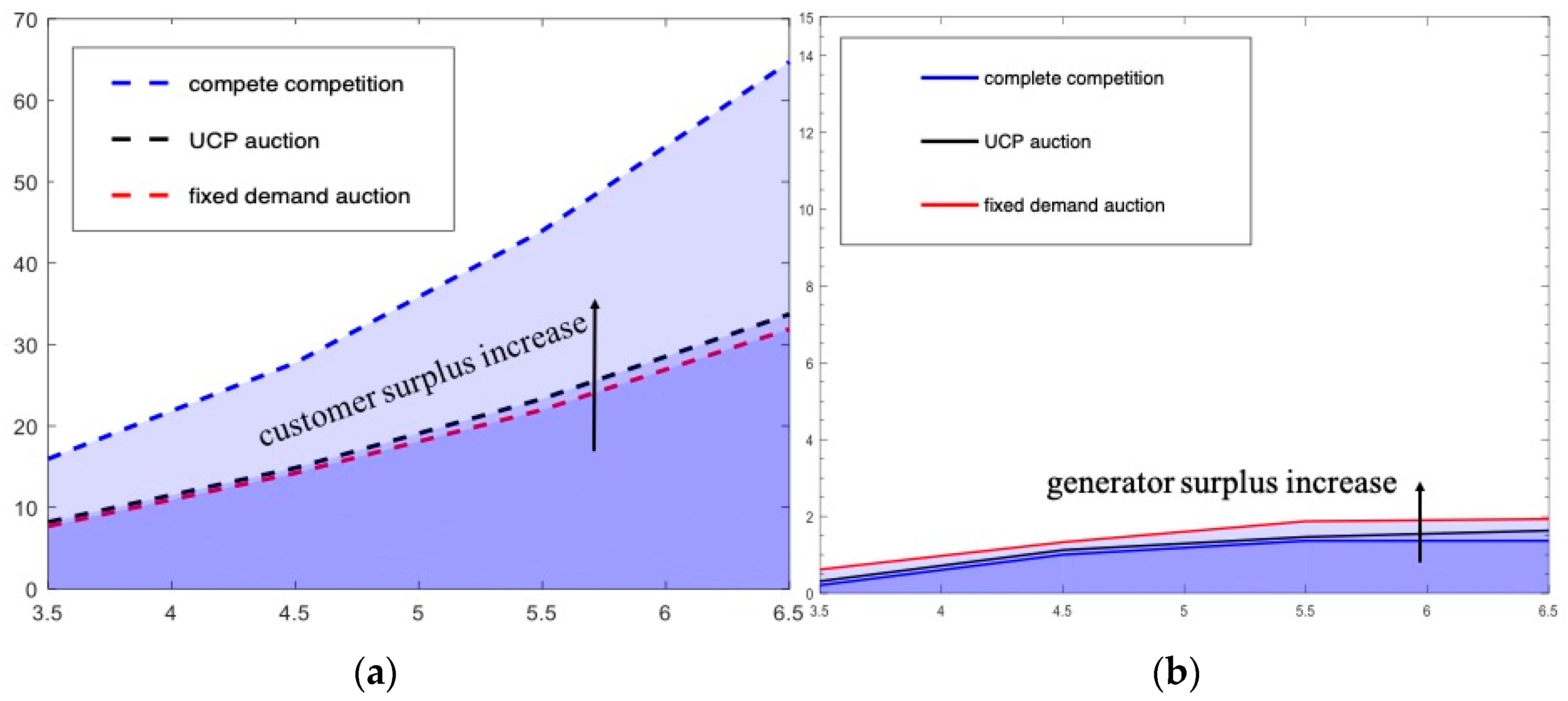
3.3. Market Power to Derive Electricity Prices and Social Welfare
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gountis, V.P.; Bakirtzis, A.G. Bidding strategies for electricity producers in a competitive electricity marketplace. IEEE Trans. Power Syst. 2004, 19, 356–365. [Google Scholar] [CrossRef]
- The State Council. Several Opinions on Further Deepening the Reform of Electric Power System (No. 9 Document). Available online: http://www.gov.cn/zhengce/content/2017-09/13/content_5223177.htm (accessed on 20 December 2018).
- Tang, Y.; Ling, J.; Ma, T.; Chen, N.; Liu, X.; Gao, B. A Game Theoretical Approach Based Bidding Strategy Based Bidding Strategy Optimization for Power Producers in Power Markets with Renewable Electricity. Energies 2017, 10, 627. [Google Scholar] [CrossRef]
- Main Problems Faced by China’s Power System Reform. Available online: http://shupeidian.bjx.com.cn/html/20140828/541427.shtml (accessed on 20 December 2018).
- Sunar, N.; Birge, J. Strategic Commitment to a Production Schedule with Uncertain Supply and Demand: Renewable Energy in Day-Ahead Electricity Markets. 2018. Available online: https://doi.org/10.1287/mnsc.2017.2961 (accessed on 20 December 2018).
- Borenstein, S.; Bushnell, J.; Wolak, F. Measuring Market Inefficiencies in California’s Restructured Wholesale Electricity Market. Am. Econ. Rev. 2002, 92, 1376–1405. [Google Scholar] [CrossRef]
- Aparicio, J.; Ferrando, J.; Meca, A.; Sancho, J. Strategic bidding in continuous electricity auctions: An application to the Spanish electricity market. Ann. Oper. Res. 2008, 158, 229–241. [Google Scholar] [CrossRef]
- Li, G.; Shi, J.; Qu, X. Modeling methods for GenCo bidding strategy optimization in the liberalized electricity spot market—A state-of-the-art review. Energy 2011, 36, 4686–4700. [Google Scholar] [CrossRef]
- Aliabadi, D.; Kaya, M.; Şahin, G. An agent-based simulation of power generation company behavior in electricity markets under different market-clearing mechanisms. Energy Policy 2017, 100, 191–205. [Google Scholar] [CrossRef]
- Aparicio, J.; Monforti, F.; Volker, P.; Zucker, A.; Careri, F.; Huld, T.; Badger, J. Simulating European wind power generation applying statistical downscaling to reanalysis data. Appl. Energy 2017, 199, 155–168. [Google Scholar] [CrossRef]
- Wang, J.; Zhi, A.; Botterud, A. An evolutionary game approach to analyzing bidding strategies in electricity markets with elastic demand. Energy 2011, 36, 3459–3467. [Google Scholar] [CrossRef]
- Jain, P.; Bhakar, R.; Singh, S. Influence of Bidding Mechanism and Spot Market Characteristics on Market Power of a Large Genco Using Hybrid DE/BBO. J. Energy Eng. 2015, 141, 04014028. [Google Scholar] [CrossRef] [Green Version]
- Soleymani, S. Bidding strategy of generation companies using PSO combined with SA method in the pay as bid markets. Int. J. Electr. Power Energy Syst. 2011, 33, 1272–1278. [Google Scholar] [CrossRef]
- Elmaghraby, W. The Effect of Asymmetric Bidder Size on an Auction’s Performance: Are More Bidders Always Better? Manag. Sci. 2005, 51, 1763–1776. [Google Scholar] [CrossRef]
- Anderson, E.; Cau, T. Modeling Implicit Collusion Using Coevolution. Oper. Res. 2009, 57, 439–455. [Google Scholar] [CrossRef]
- Xu, T. Information Revelation in Auctions with Common and Private Values. Games Econ. Behav. 2016, 97, 147–165. [Google Scholar]
- Atakan, A.E.; Ekmekci, M. Auctions, Actions, and the Failure of Information Aggregation. Am. Econ. Rev. 2014, 104, S45–S46. [Google Scholar] [CrossRef]
- Bompard, E.; Ma, Y.; Napoli, R.; Abrate, G. The Demand Elasticity Impacts on the Strategic Bidding Behavior of the Electricity Producers. IEEE Trans. Power Syst. 2007, 22, 188–197. [Google Scholar] [CrossRef]
- Motalleb, M.; Ghorbani, R. Non-cooperative game-theoretic model of demand response aggregator competition for selling stored energy in storage devices. Appl. Energy 2017, 202, 581–596. [Google Scholar] [CrossRef]
- Hao, S. A study of basic bidding strategy in clearing pricing auctions. IEEE Trans. Power Syst. 2000, 15, 975–980. [Google Scholar]
- Mcafee, R.; Mcmillan, J. Auctions and Bidding. J. Econ. Lit. 1987, 25, 699–738. [Google Scholar]
- Yin, X.; Zhao, J.; Saha, T.; Dong, Z. Developing GENCO’s strategic bidding in an electricity market with incomplete information. In Proceedings of the IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–7. [Google Scholar]
- Li, T.; Shahidehpour, M. Strategic bidding of transmission-constrained GENCOs with incomplete information. IEEE Trans. Power Syst. 2005, 20, 437–447. [Google Scholar] [CrossRef]
- Banaei, M.; Buygi, M.; Zareipour, H. Impacts of Strategic Bidding of Wind Power Producers on Electricity Markets. IEEE Trans. Power Syst. 2016, 31, 4544–4553. [Google Scholar] [CrossRef]
- Rahimiyan, M.; Baringo, L. Strategic Bidding for a Virtual Power Plant in the Day-Ahead and Real-Time Markets: A Price-Taker Robust Optimization Approach. IEEE Trans. Power Syst. 2016, 31, 2676–2687. [Google Scholar] [CrossRef]
- Ruddell, K.; Philpottt, A.; Downward, A. Supply Function Equilibrium with Taxed Benefits. Oper. Res. 2017, 65, 1–18. [Google Scholar] [CrossRef]
- Samuelson, W. Auctions: Advances in Theory and Practice; Game Theory and Business Applications; Springer: New York, NY, USA, 2014; pp. 323–366. [Google Scholar]
- Soleymani, S.; Ranjbar, A.; Shirani, A. Strategic bidding of generating units in competitive electricity market with considering their reliability. Electr. Power Energy Syst. 2008, 30, 193–201. [Google Scholar] [CrossRef]
- Kalashnikov, V.; Bulavsky, V.; Kalashnikov, V.V., Jr.; Kalashnykova, N.I. Structure of demand and consistent conjectural variations equilibrium (CCVE) in a mixed oligopoly model. Ann. Oper. Res. 2014, 217, 281–297. [Google Scholar] [CrossRef]
- Iria, J.; Soaresa, F.; Matos, M. Optimal supply and demand bidding strategy for an aggregator of small prosumers. Appl. Energy 2018, 213, 658–669. [Google Scholar] [CrossRef]
- Rao, C.; Zhao, Y.; Zheng, J.; Wang, C. An extended uniform-price auction mechanism of homogeneous divisible goods: Supply optimisation and non-strategic bidding. Int. J. Prod. Res. 2016, 54, 1–15. [Google Scholar] [CrossRef]
- Fang, D.; Wu, J.; Tang, D. A double auction model for competitive generators and large consumers considering power transmission cost. Int. J. Electr. Power Energy Syst. 2012, 43, 880–888. [Google Scholar] [CrossRef]

| 1 | 2 | 3 | 4 | |
| 0.120 | 0.220 | 0.303 | 0.372 |
| Bidder | Private Cost | Bid Quantity | Optimal Bidding Price |
|---|---|---|---|
| 1 | 1.1425 | 1 | 1.2329 |
| 2 | 1.3510 | 3 | 1.4594 |
| 3 | 1.5499 | 1 | 1.6151 |
| 4 | 1.6221 | 2 | 1.6879 |
| 5 | 1.8530 | 1 | 1.8763 |
| Bidder | Private Cost | Bid Quantity | Optimal Bidding Price | |||
|---|---|---|---|---|---|---|
| 1 | 1.1425 | 1 | 1.2487 | 1.2529 | 1.2572 | 1.2617 |
| 2 | 1.3510 | 3 | 1.4534 | 1.4594 | 1.4667 | 1.478 |
| 3 | 1.5499 | 1 | 1.6093 | 1.6151 | 1.6224 | 1.6312 |
| 4 | 1.6221 | 2 | 1.6825 | 1.6879 | 1.6947 | 1.7033 |
| 5 | 1.8530 | 1 | 1.8734 | 1.8763 | 1.8801 | 1.8854 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, D.; Ren, Q.; Yu, Q. How Elastic Demand Affects Bidding Strategy in Electricity Market: An Auction Approach. Energies 2019, 12, 9. https://doi.org/10.3390/en12010009
Fang D, Ren Q, Yu Q. How Elastic Demand Affects Bidding Strategy in Electricity Market: An Auction Approach. Energies. 2019; 12(1):9. https://doi.org/10.3390/en12010009
Chicago/Turabian StyleFang, Debin, Qiyu Ren, and Qian Yu. 2019. "How Elastic Demand Affects Bidding Strategy in Electricity Market: An Auction Approach" Energies 12, no. 1: 9. https://doi.org/10.3390/en12010009




