Preliminary Ray Tracing and Experimental Study on the Effect of Mirror Coating on the Optical Efficiency of a Solid Dielectric Compound Parabolic Concentrator

Abstract

This study aims to determine the necessity of applying a mirror coating on the side of a truncated solid dielectric CPC (compound parabolic concentrator) since ray tracing analysis has revealed that part of the incoming rays do not undergo total internal reflection, even within the half acceptance angle of the CPC. An experiment was designed and conducted indoors and outdoors to study the effect of mirror coating on the optical performance of a solid dielectric CPC. Ray tracing was also employed for the detailed analysis and its results are compared with the measurements. Based on these, a concept of partial coating is proposed and verified through simulation. The results show that a partly coated solid dielectric CPC may have a better optical efficiency than a solid CPC without coating for a certain range of incidence angles.

1. Introduction

Photovoltaic (PV) research is one of the most popular topics in the field of solar energy and has been extensively conducted worldwide [1,2,3,4]. Concentration PV in particular has attracted an increasing attention because the cost of the solar cells account for more than 70% of the total cost of a conventional flat PV system. This factor has prevented PV technology from fully penetrating the electricity generation market [5]. For concentration PV applications, a compound parabolic concentrator (CPC) has some advantages. Firstly, it has a large half acceptance angle and does not require a tracking system. When the concentration ratio is below 3, it can be used for stationary installation, thereby avoiding the reliability and accuracy issues associated with moving parts. Secondly, the receiver is located on the base of the concentrator and does not cast a shadow on the reflector surface, which is beneficial for high concentration efficiency. Thirdly, it has economic benefits because of its simple structure. In addition, it only requires a one-off installation, thus it can reduce the cost of the tracking or monitoring equipment.

Non-imaging static concentrators have been designed and tested using converging lenses as refractive elements [6,7]. In comparison, a solid dielectric CPC concentrates light via reflection and refraction by incorporating a solid dielectric refractive material into the CPC structure. Refraction at the front interface of a solid CPC causes a larger acceptable angle than the mirror CPC of the same size. In addition, the total internal reflection within the the solid CPC has a high reflectance and therefore may lead to a higher optical efficiency. Mallick et al. [8,9] have investigated an asymmetric CPC consisting of two different parabolas using a transparent dielectric material. Saitoh and Yoshioka [10] presented a review of the general concepts, designs, and optical properties of 2D and 3D concentration lenses suitable for static concentrators. Winston et al. [11,12] stated that a solid dielectric CPC has an increased angular acceptance and reduced optical loss compared with its non-dielectric counterpart. Scharlack [13], Goodman [14], and Zacharopoulos et al. [15] conducted further research on CPC design and analysis of total internal reflection. For the conditions prevalent in Sydney, Australia, a non-imaging static concentrator lens was able to achieve a geometrical concentration ratio of 2.0 with a lens efficiency of 94% [16]. The performance of the solid dielectric CPC is also a popular research topic in building-integrated PV applications. Although the cost of the dielectric concentrator may outweigh the PV material cost savings, especially when the price of PVs has fallen significantly, a reduction of up to 53% could be expected in volume production instead of the small number of systems currently manufactured [9].

Total internal reflection occurs when the incidence angle on an interface is larger than the critical angle; otherwise, rays would be refracted across the interface. For a solid dielectric CPC, the common impression is that the total internal reflection happens for all the incoming rays when the incidence angle is smaller than the half acceptance angle of the CPC. However, through ray tracing analysis of solid dielectric CPCs, we have noticed that this may be not always the case for part of these incoming rays. This finding has therefore stimulated the work presented here. This paper will first present ray tracing analysis of a solid dielectric CPC at different incidence angles to find the proportion of the incoming rays that undergoes the total internal reflection. The effect of mirror coating on the optical efficiency of the truncated solid dielectric CPC will be then investigated using both ray tracing simulation and experimental verification. Particularly, the concept of partial mirror coating will be put forward to increase the optical efficiency of a truncated solid dielectric CPC.

2. Experimental Study

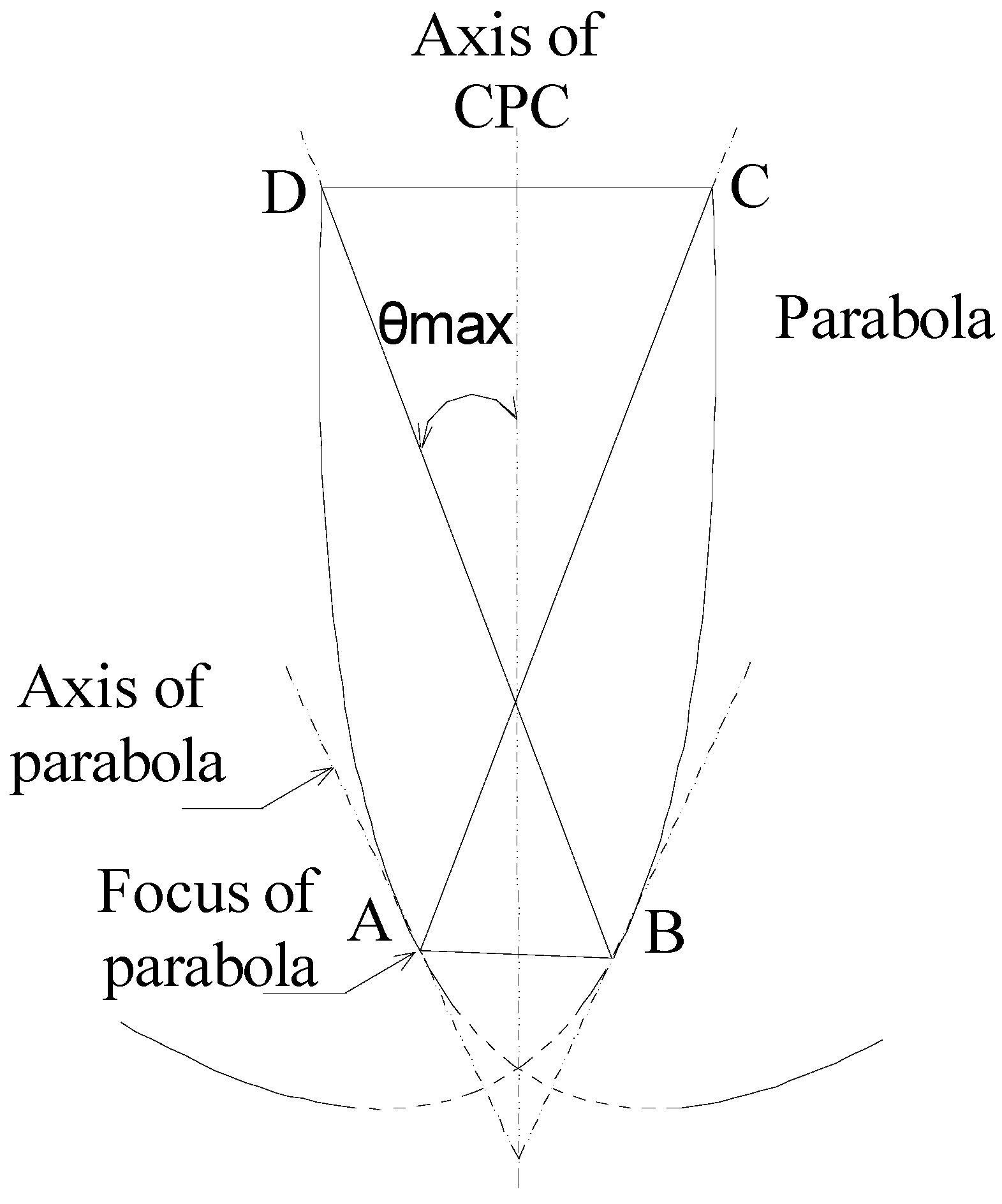
A symmetrical CPC [17] consists of two identical parabolic reflectors that funnel radiation from the aperture to the absorber. The right-hand side and the left-hand side parabolas are axisymmetric. The axis of either parabola and the axis of the CPC make a so-called half acceptance angle ${\theta }_{\max }$, as shown in Figure 1. The focuses of two parabolas form the base of the CPC.

Figure 1. A symmetrical CPC.

Figure 1. A symmetrical CPC.

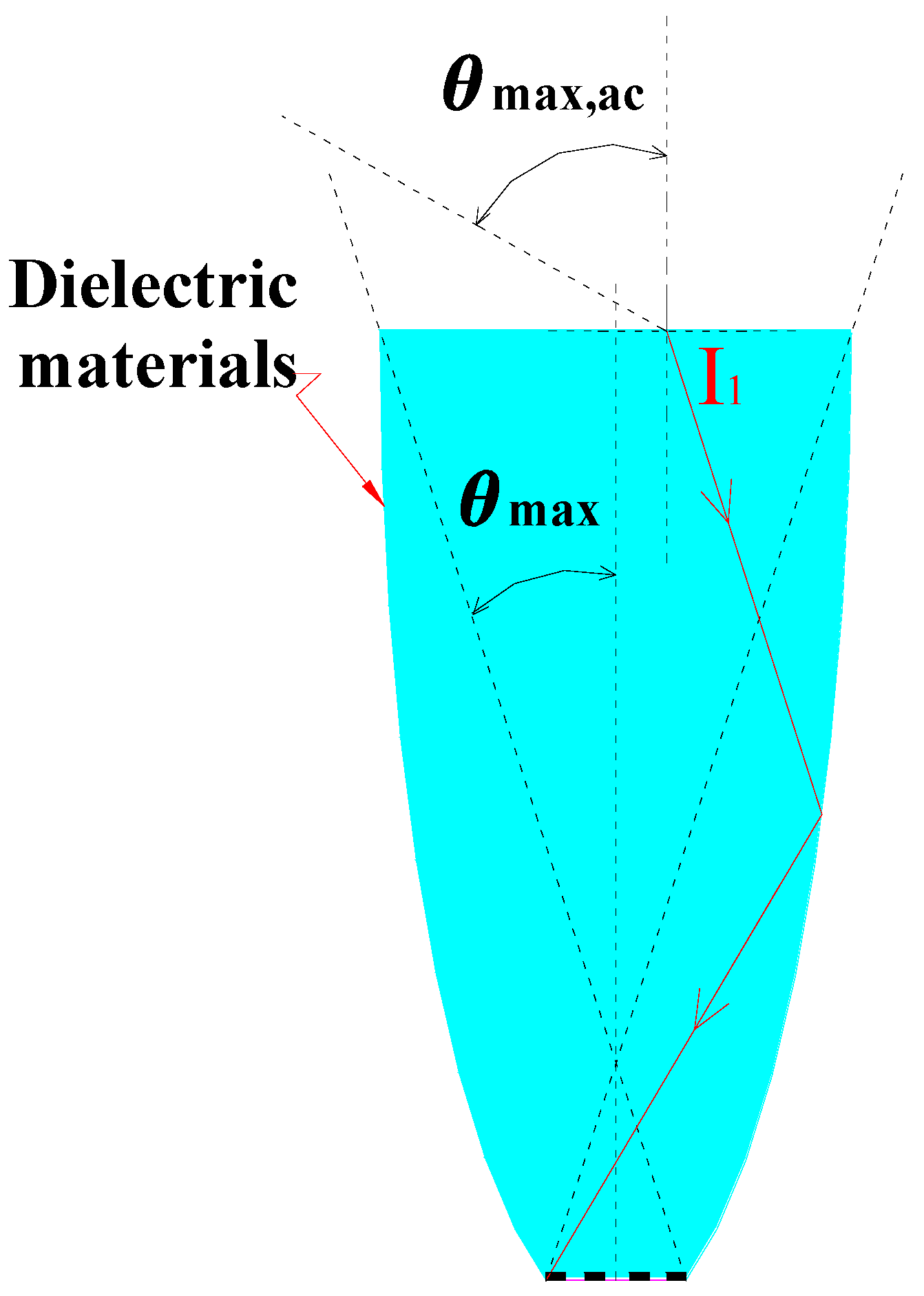
A solid dielectric CPC has a larger half acceptance angle because of refraction on the air-dielectric interface, as shown in Figure 2, which changes the incidence angle to be smaller when a ray comes through air into a dielectric material with higher refractive index. For the solid dielectric CPC, an external half acceptance angle ${\theta }_{\max ,ac}$ may be defined. When the incidence angles of the incoming rays are smaller than ${\theta }_{\max ,ac}$, the rays would undergo total internal reflection or mirror reflection to reach the base of CPC. Otherwise, the rays cannot be collected. The relationship between the geometrical concentration ratio (CR) and the external half acceptance angle ${\theta }_{\max ,ac}$ can be expressed as follows:

$$CR=(\frac{S_1}{S_2})=\frac{n}{\sin {\theta }_{\max ,ac}}$$

(1)

where S₁ is the area of the CPC front aperture, S₂ is the area of the CPC base, and n is the refractive index.

According to the above description, two sample solid CPCs truncated were made by laser cutting an acrylic panel. The full height CPCs had the geometrical concentration ratio of 2.5. Considering the economic factor in real applications, the sample solid CPCs were truncated by 27.73%.

Figure 2. Working principle of the solid dielectric CPC.

Figure 2. Working principle of the solid dielectric CPC.

The truncated sample CPCs had the geometrical concentration ratio of 2.41 cm, the height of 2.7 cm and the base width of 1 cm. In order to study the effect of mirror coating, one of the sample solid CPCs was mirror coated with evaporated aluminum, see the right-hand side image in Figure 3.

Figure 3. A photograph of the solid dielectric CPC module with and without coating.

Figure 3. A photograph of the solid dielectric CPC module with and without coating.

Each sample CPC was attached with a small monocrystalline silicon PV cell to form a mini solid dielectric CPC PV module. The experiment was carried out for three situations. The first testing was conducted indoors using a solar simulator (equipped with PHILIPS MSR 575/2 lamps), in which a digital multimeter was used to measure the output short circuit current and the open circuit voltage of the two types of solid dielectric CPC PV modules for different incidence angles. The beam irradiation on the aperture of CPC was recorded using a pyranometer. The second experiment was aimed to find the characteristic current-voltage (I-V) curve of the CPC PV modules, so a sliding rheostat was used. The I-V characteristic curves of the solid dielectric CPC PV module with and without mirror coating were compared. Finally, the solid CPC PV modules were placed outdoors with the east–west orientation to measure the short circuit current I_sc at different times on a sunny day. A PV cell of same size without solar concentration was also used in the entire experiment for comparison.

According to Bernardo et al. [18], the relative uncertainties of the measuring instruments stated by the manufacturers are estimated for ideal measurement and installation conditions. In practice, somewhat higher relative uncertainties were assumed to take into account any inaccuracies related to the installation and operation of those instruments. The relative uncertainties of the pyranometer, ammeter, and voltmeter were assumed to be ±2%, ±3.8%, and ±1.1%, respectively. Using the standard method of the square root of the quadratic sum for the uncertainty propagation, the global uncertainty of the efficiency measurements was estimated to be approximately ±4.4%.

3. Rays Tracing Analysis

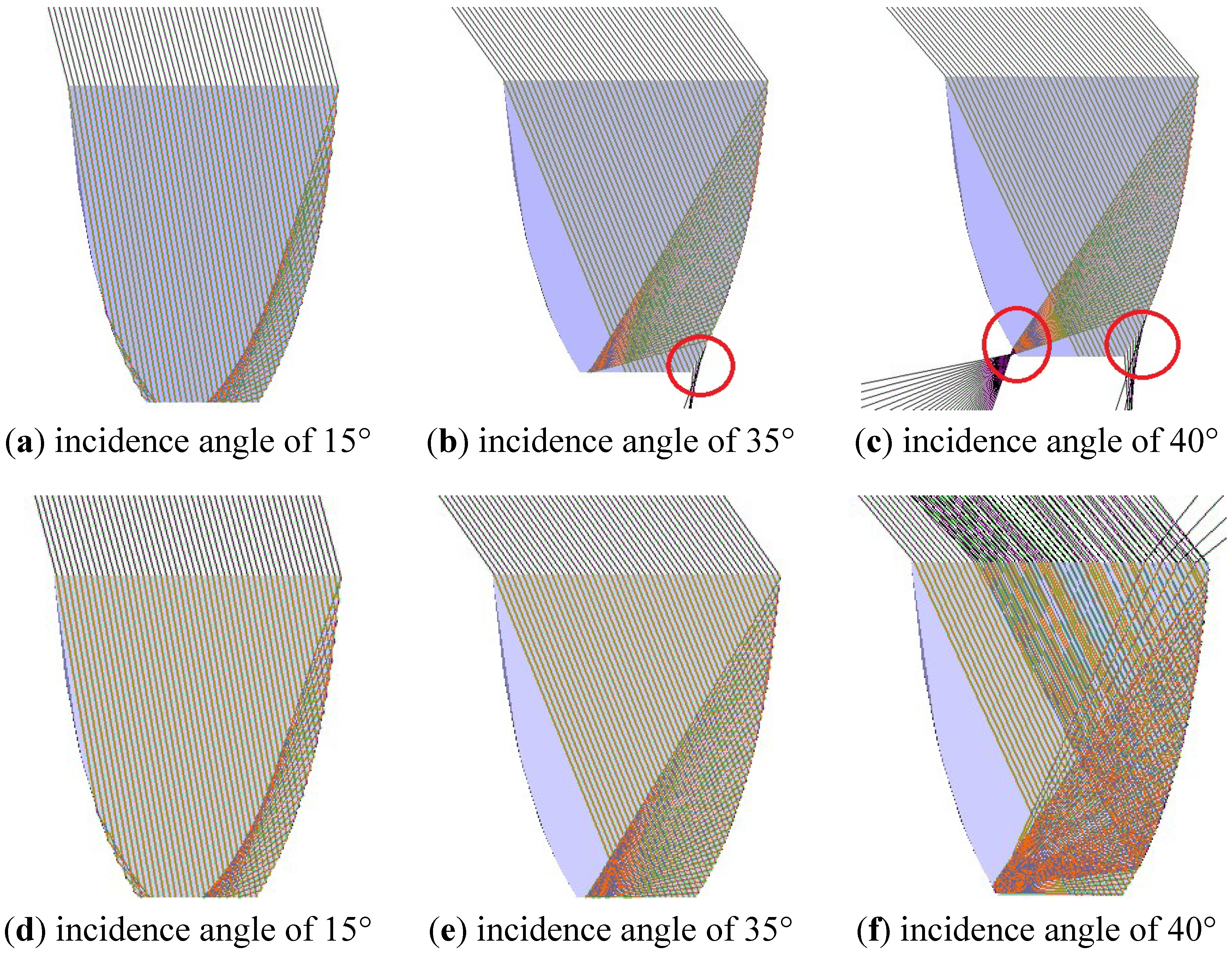
The LightTools software was used to study the behavior of rays within the experimental sample solid dielectric CPCs for different incidence angles. As described above, the aperture width of the truncated solid CPC was 2.41 cm and the base width was 1 cm. According to these, the geometry model of the sample CPCs were created in LightTools for ray tracing analysis. The schematic diagram of ray tracing results is shown in Figure 4. A total of 1000 rays were traced. The refractive index of the material is 1.5. The ray tracing analysis was conducted for nine different incidence angles, namely, 0°, 5°, 10°, 15°, 20°, 25°, 30°, 35°, and 40°.

Figure 4. Schematic diagram of ray tracing results for the experimental solid CPC. (a), (b) and (c): for the incidence angles of 15°, 35°, 40° respectively and no coating; (d), (e) and (f): for the incidence angle of 15°, 35°, 40° respectively and with mirror coating.

Figure 4. Schematic diagram of ray tracing results for the experimental solid CPC. (a), (b) and (c): for the incidence angles of 15°, 35°, 40° respectively and no coating; (d), (e) and (f): for the incidence angle of 15°, 35°, 40° respectively and with mirror coating.

It is clear from Figure 4 that when the incidence angle is small, for example, 15° in the conditions (a) and (d), the truncated solid dielectric CPC with or without mirror coating has the same ray path. When the incidence angle becomes larger, Figure 4b indicates that part of rays escape from the lower side of the solid CPC without coating, whereas this could be prevented when the solid CPC has a mirror coating (Figure 4e), even when the incidence angle is less than the half acceptance angle. Therefore, this exhibits an interesting contradiction against the common impression that the total internal reflection always occurs in a solid CPC when the incidence angle is less than the half acceptance angle. The issue becomes more evident for larger incidence angle, as shown in Figure 4c,f. This finding implies the necessity of applying a mirror coating on the outside of the solid CPC to increase its optical performance, particularly when the incidence angle is larger.

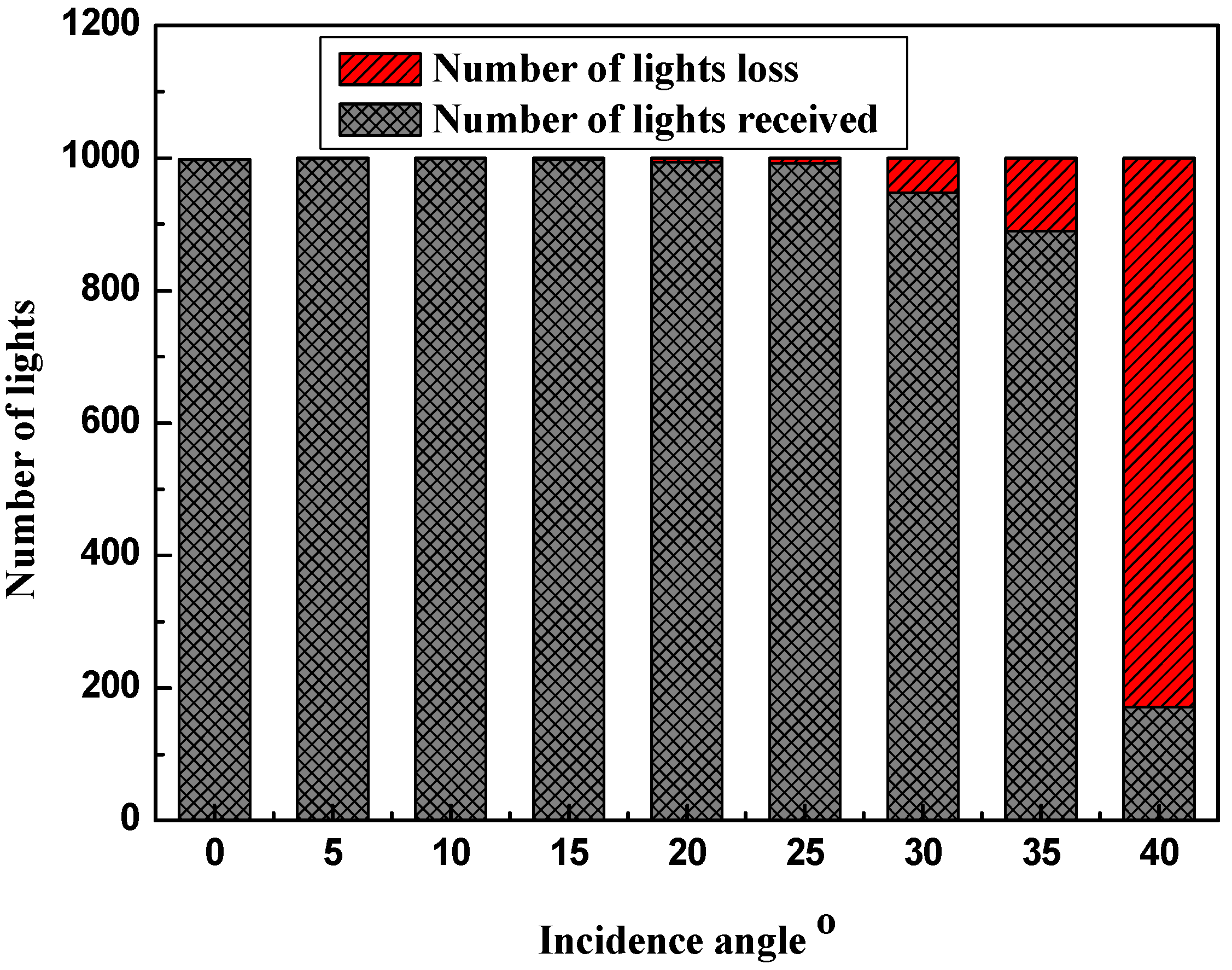
Figure 5 shows the number of rays received on the base of the solid CPCs or lost due to side escaping for the solid CPC without a mirror coating. It is apparent that when the incidence angle is smaller than the half external acceptable angle (36.8°) of the solid CPC, the number of rays undergoing total internal reflection has a much larger proportion in the total number of rays. However, this proportion becomes smaller when the incidence angle increases, also can be seen from Figure 4. The proportion of the rays undergoing total internal reflection is almost 100% for 0° to 15° incidence angle. When the incidence angle is equal to 35°, quite close to the external half acceptance angle of 36.8°, the proportion of the side-escaped rays without undergoing total internal reflection is approximately 12%, also as shown in Figure 4b. In addition, as the incidence angle exceeds the external half acceptance angle, the proportion of the side-escaped rays is very large; meanwhile, due to truncation, a small proportion of the rays directly reach the base of the CPC (also see Figure 4c).

A similar ray tracing analysis was also conducted for the solid CPC with a mirror coating. It was found that the proportion of the side-escaped rays would be reduced by the side mirror coating only for the incidence angle less than the external half acceptance angle. Beyond that, the rays would be bounced back by the mirror coating. However the mirror coating usually has a lower reflectance than the total internal reflection, so the coating may have positive or negative effect on the optical performance of a solid CPC. This will be discussed in more detail in the following section.

Figure 5. Ray tracing outcome for the solid dielectric CPC without mirror coating.

Figure 5. Ray tracing outcome for the solid dielectric CPC without mirror coating.

4. Results and Discussions

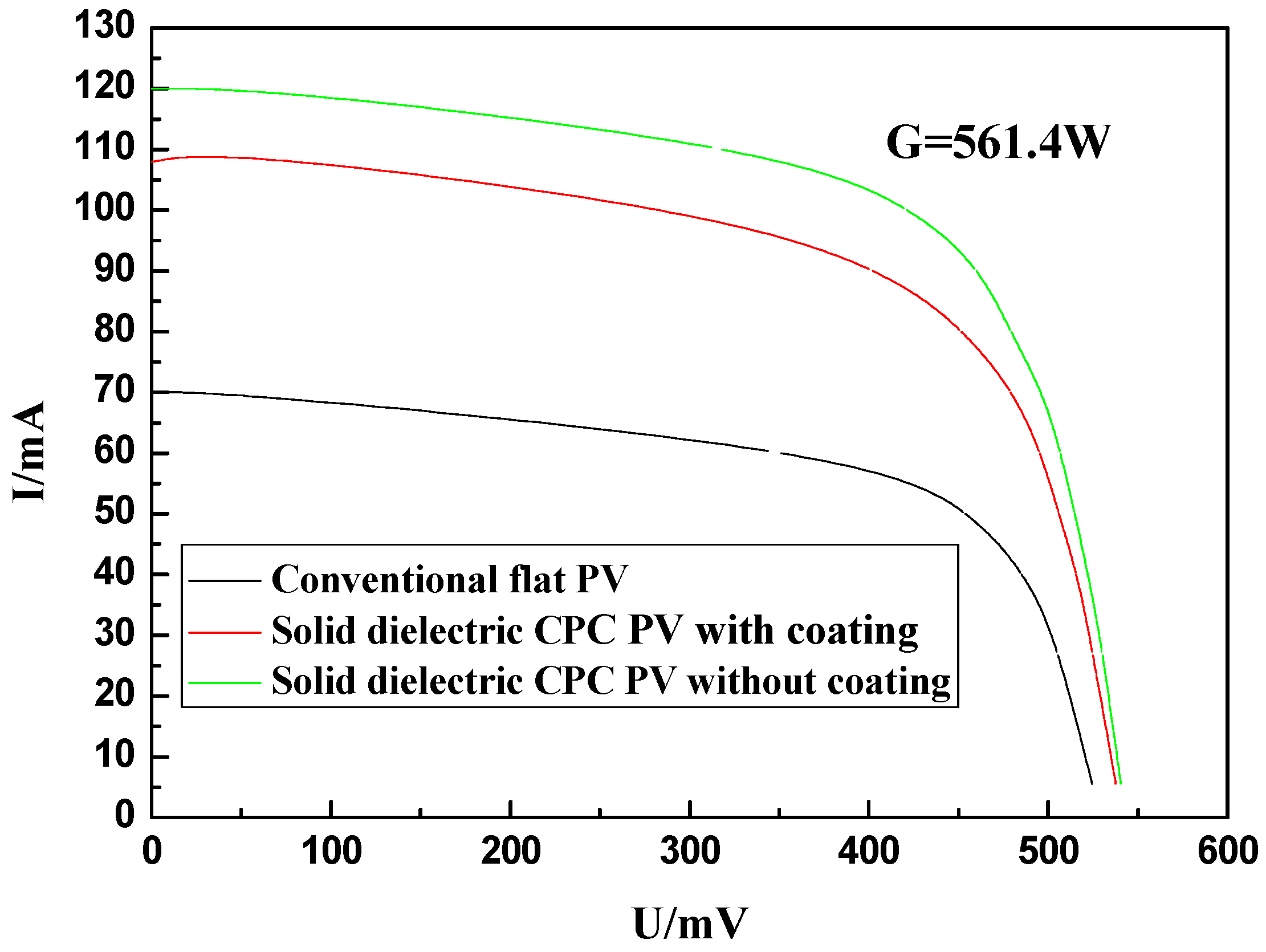
During the comparative experiments in the laboratory, the PV cell temperature was maintained close to the ambient temperature of about 12 °C ± 0.5 °C. Figure 6 shows the I-V characteristics of the solid dielectric CPC PV with and without coating and the flat PV of the same size when the incidence angle of rays was 0° under the same radiation. The short circuit current I_sc of the solid dielectric CPC PV without coating was the highest, followed by the solid dielectric CPC PV with coating, and the lowest is the flat PV. The open circuit voltages of the three PV modules were quite close.

Figure 6. I-V curve for 0° incidence angle.

Figure 6. I-V curve for 0° incidence angle.

The current I_max and voltage V_max corresponding the maximum power output were obtained from the I-V curve. Subsequently, the maximum power P_m and the fill-factor FF were calculated as follows [19]:

$$FF=\frac{I_{\max }{V}_{\max }}{I_{sc}{V}_{oc}}$$

(2)

The ratio of the output power to incidence irradiance η is called the efficiency of the solar PV module [20]:

$$\eta =\frac{P_m}{A{P}_{in}}=\frac{FF\cdot I_{sc}{V}_{oc}}{A{P}_{in}}$$

(3)

where A is the area of the CPC front aperture, S₁ is the solid dielectric CPC PV, and P_in is the incident irradiance.

The above parameters for the 0° incidence angle are shown in Table 1. Based on the data, the output power of the solid CPC PV without coating is higher by 13.5% than that of the solid CPC PV with coating. The two solid CPCs had the same dielectric material and size, so the lower reflectance of the evaporated aluminum coating may have caused a lower efficiency compared with the high reflectance of total internal reflection.

Table 1. Performance parameters of CPCs with the incidence angle of 0°.

Parameters	Solid dielectric CPC PV without coating	Solid dielectric CPC PV with coating	Non-concentration flat PV
Isc (mA)	120	108	70
Pm (mW)	44.80	39.45	25.86
FF	0.69	0.68	0.70
η(%)	7.98	7.03	11.52

Table 1. Performance parameters of CPCs with the incidence angle of 0°.

Parameters	Solid dielectric CPC PV without coating	Solid dielectric CPC PV with coating	Non-concentration flat PV
Isc (mA)	120	108	70
Pm (mW)	44.80	39.45	25.86
FF	0.69	0.68	0.70
η(%)	7.98	7.03	11.52

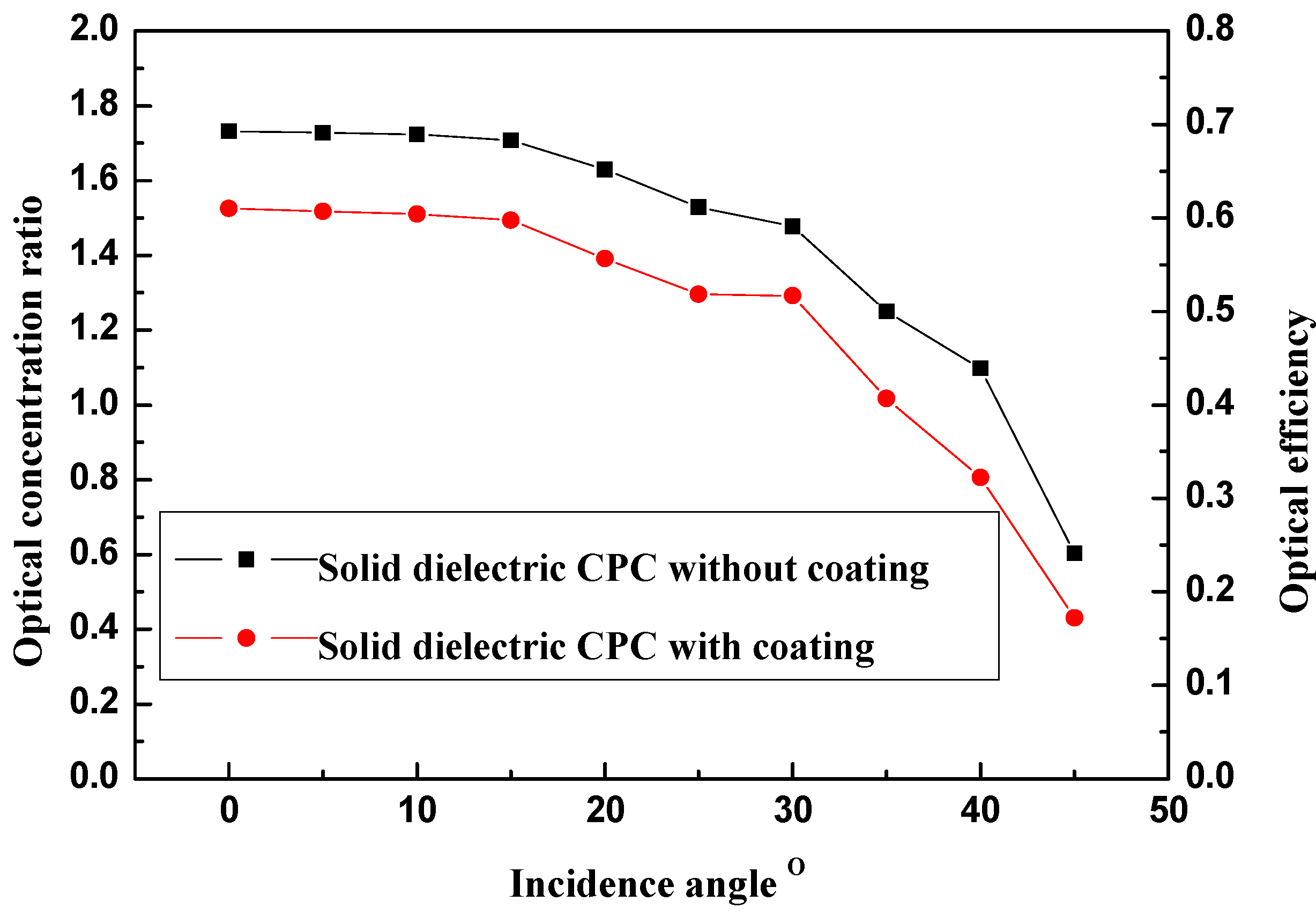
For the present study, it would be useful to know the optical efficiency of the solid CPCs, which may be calculated by dividing the short circuit current of the solid CPC PV module by that of the flat PV cell of the same size and the geometrical concentration ratio. The optical concentration ratio is the product of the optical efficiency and the geometrical concentration ratio. As can be seen from Figure 7, with increasing incidence angle, the optical concentration ratio and optical efficiency of the solid dielectric CPC with or without coating showed a decreasing trend. This is in consistent with the pattern shown in Figure 5, but manufacturing errors and parallel degree of radiation may have caused deviation. Evidently, the performance of the solid CPC without coating is superior to that of the solid CPC with coating, indicating that the reflectance of the evaporated aluminum coating had lower than the total internal reflection.

Figure 7. Optical concentration ratio and efficiency for different incidence angles.

Figure 7. Optical concentration ratio and efficiency for different incidence angles.

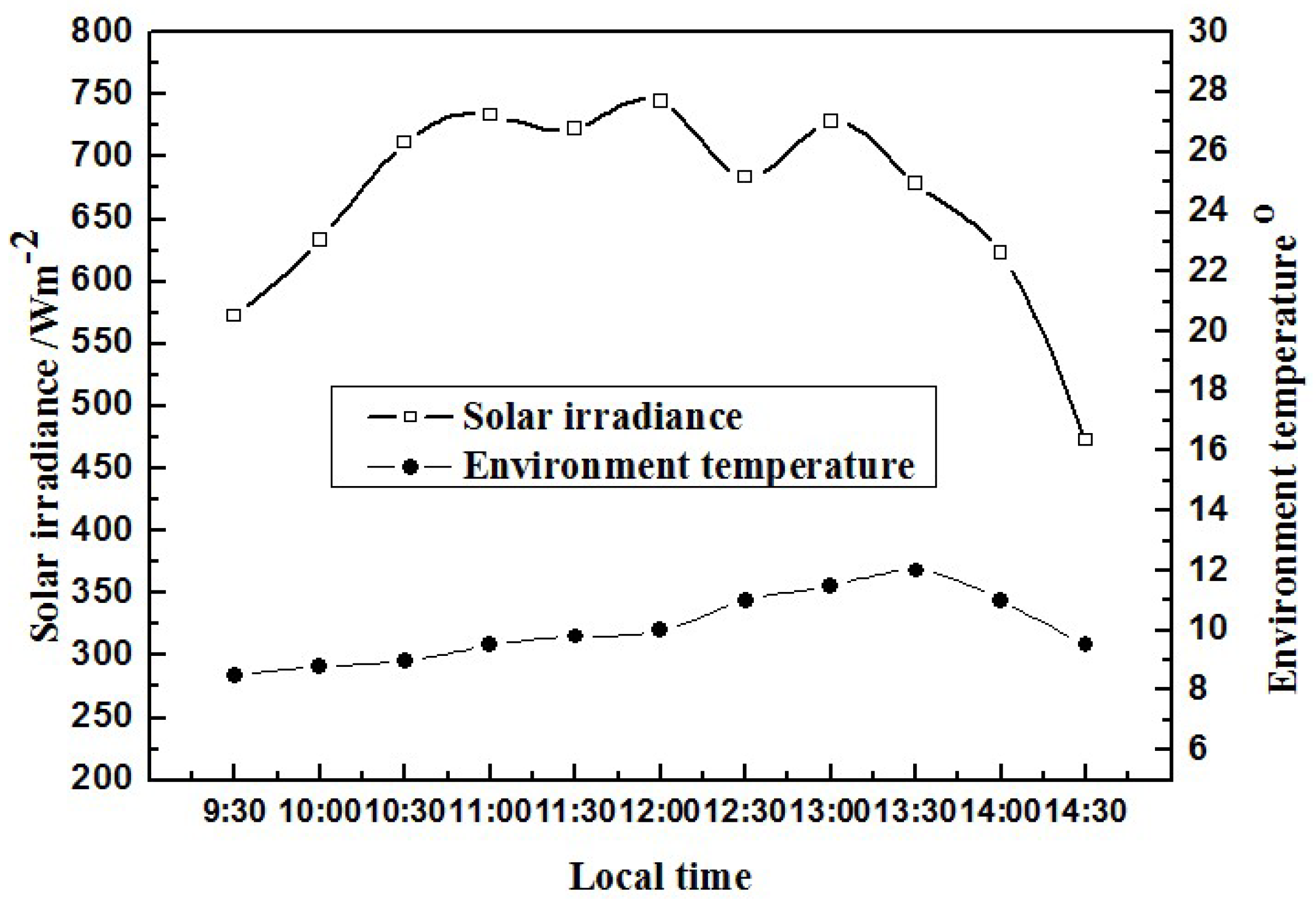
Another experiment was conducted on a sunny day in Nottingham, UK (N52°56′25.51″, W1°11′49.20″) to examine the performance of the solid CPCs in the real outdoor condition. The flat PV cell of the same size was also used for comparison. The solid CPC PV modules and the flat PV cell were tilted at 52° and oriented in the east–west direction. Figure 8 shows the solar irradiance and environment temperature of a sunny day in winter. The lowest solar irradiance value during the test was approximately 470 W, and the environment temperature remained relatively stable.

Figure 8. Weather parameter with local time.

Figure 8. Weather parameter with local time.

Figure 9 shows that the short circuit current I_sc of the solid CPC without coating is higher than that with coating. The ratio of short circuit current of the solid CPC PV modules to the flat PV may indicate the optical concentration ratio of the solid CPCs. The optical concentration ratio of the solid CPC without coating is approximately 1.7~1.8. The optical concentration ratio of the solid dielectric CPC with coating is about 1.5~1.6. The short circuit current or the optical concentration ratio of the solid CPC without coating is higher by approximately 14% than that of the coated solid CPC. This is satisfactorily in consistence with the results gained from the indoor testing.

Figure 9. Changes in short circuit current with local time.

Figure 9. Changes in short circuit current with local time.

The ratio of short circuit current between the solid CPC with and without mirror coating is actually an indicator of the coating reflectance as the total internal reflection is usually considered to have a reflectance of about 99%. According to the results given in Figure 7 and Figure 9, the reflectance of mirror coating was found to be about 0.8. By comparing the simulation results with the measured data, the average transmissivity was determined to be 0.92 per 6 mm. Taking these optical properties into consideration, a further ray tracing simulation using LightTools was given to predict the optical efficiency of the solid CPCs. 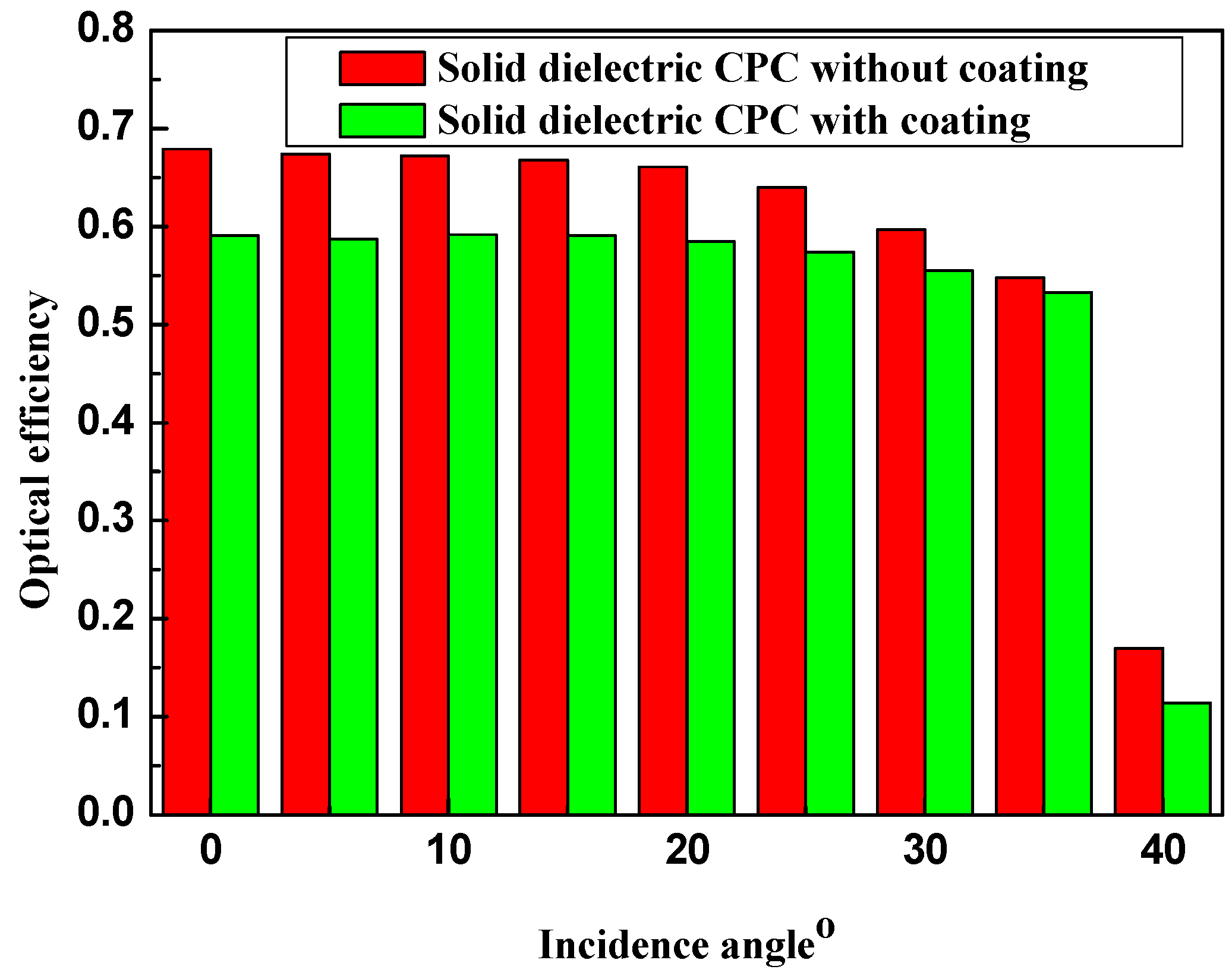Figure 10 shows the variation in the calculated optical efficiencies of the solid dielectric CPCs. Similar to the experimental finding, the difference in the calculated optical efficiency between the solid dielectric CPC with and without coating becomes smaller when the incidence angle increases. At the incidence angle around 35°, they are very close because the effect of mirror reflectance may be just compensated by avoidance of side optical escape.

Figure 10. Optical efficiency of the truncated solid dielectric CPC with and without mirror coating at different incidence angles.

Figure 10. Optical efficiency of the truncated solid dielectric CPC with and without mirror coating at different incidence angles.

The results in Figure 10 may lead to a wrong conclusion, that is, it may be meaningless to apply mirror coating on a solid CPC. However, the outcome would be different if the coating reflectance is higher or the coating is applied partially. From ray path shown in Figure 4, side optical escape mainly occurs near the base of the solid CPC, so this means only part of side needs to be mirror coated. Therefore, a concept of partial coating is formed. To verify this, a further ray tracing analysis was carried out for the partly coated CPC. 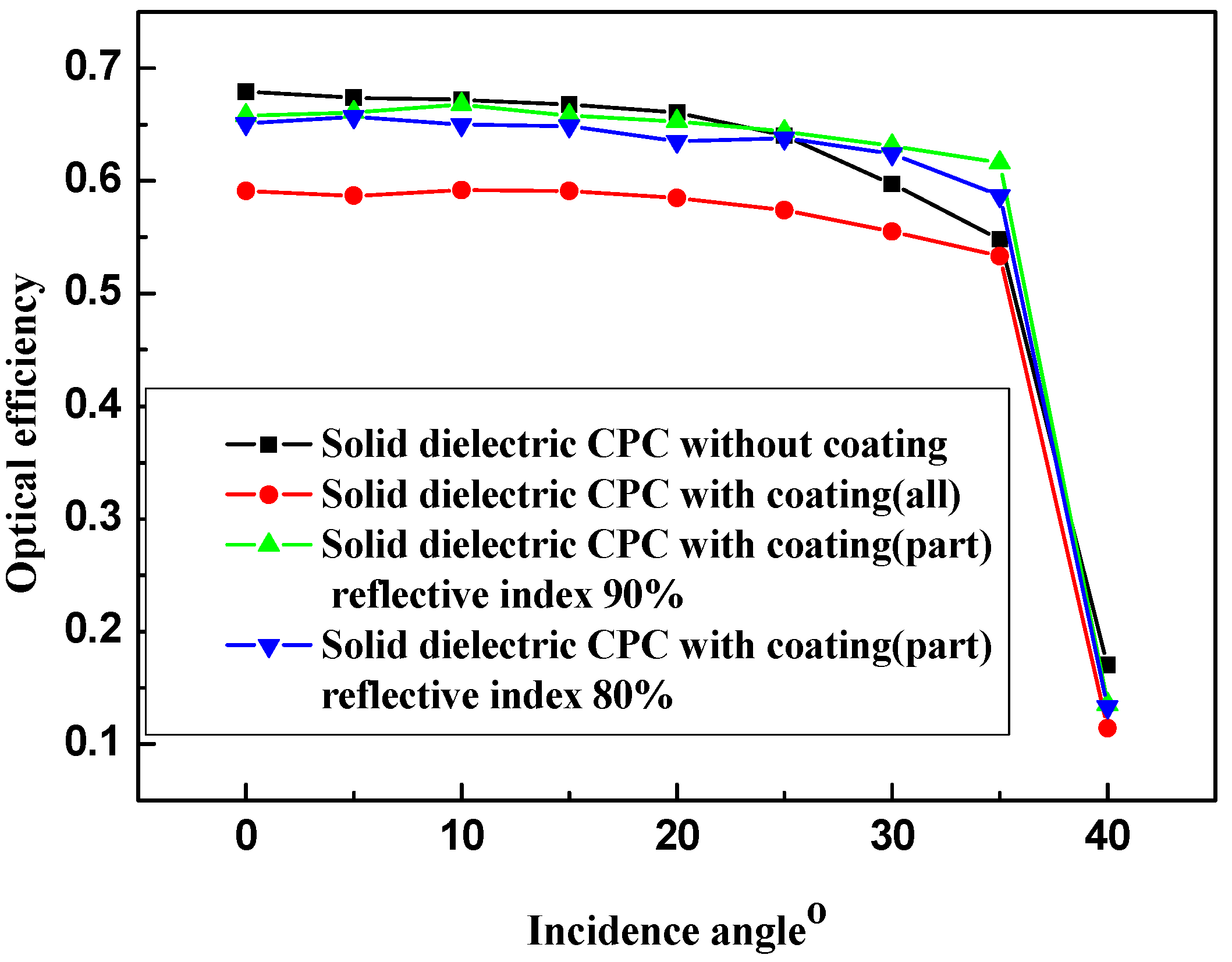Figure 11 is the schematic diagram of the solid CPC partly coated. It is apparent that the area of the reflector surface coated is small, so any negative effect of coating could be minimized. Through a preliminary estimation based on the results in Figure 4, the height of mirror coating was assumed to be 4mm from the base of CPC. Partly coating combines the advantage of the total internal reflection and mirror reflection, and may lead to a better optical performance. This expectation is confirmed by the simulation results given Figure 12. It is clear that the solid CPC partly coated has a higher optical efficiency than that without coating for the incidence angle range of 25~35 °C. The situation would be much better if the mirror coating has a higher reflectance such as 0.90, which is easily achievable through a quality coating process.

Figure 11. A schematic diagram of the partially coated truncated solid dielectric CPC.

Figure 11. A schematic diagram of the partially coated truncated solid dielectric CPC.

Figure 12. Comparison of optical efficiencies of the truncated solid CPC without mirror coating, with full or partial coating, respectively.

Figure 12. Comparison of optical efficiencies of the truncated solid CPC without mirror coating, with full or partial coating, respectively.

It is worthwhile to mention that the above ray tracing analysis was conducted for the 2D situation, however the conclusion would also apply to the 3D situation. For the 3D situation, i.e., the incoming rays have an azimuth angle to the meridian of the solid CPC, our previous study has shown that the optical efficiency of a CPC depends on the so-called projected incidence angle on the meridian of the solid CPC (Su et al. [21]), so the comparison of the solid CPCs with and without coating is not subject to the azimuth angle. Actually, this is also evident by comparing the estimated optical efficiency from the indoor measurement (Figure 7) and outdoor monitoring (Figure 9).

5. Conclusions

Ray tracing analysis of the solid dielectric CPCs has revealed that part of the incoming rays do not undergo total internal reflection, even when their incidence angle is smaller than the half acceptance angle of the CPC. It is therefore suggested that a mirror coating could be applied to the side of a solid CPC to prevent the side optical escape, which occurs on the lower side of a solid CPC. An experiment has been designed to investigate the actual effect of coating on the optical performance of a solid CPC. The indoor testing results show that the optical efficiency or the optical concentration ratio of the solid dielectric CPC without coating is higher by 13.5% than the solid CPC with a mirror coating. The outdoor monitoring has indicated a similar difference. However, further analysis has identified that this was caused by the lower reflectance of the unsatisfactory aluminum coating, therefore a concept of partial coating has been put forward. Ray tracing results show that the partially coated solid dielectric CPC has a higher optical efficiency than that without coating for a certain range of incidence angles just closed to the half acceptance angle. This would be better if the partial coating has a higher reflectance. Therefore, the solid dielectric CPC partly coated would be a suggested design as an alternative to the common solid CPC without coating.