Numerical Investigation on the Effect of Cementing Properties on the Thermal and Mechanical Stability of Geothermal Wells
Abstract
:1. Introduction
2. Laboratory Experiments
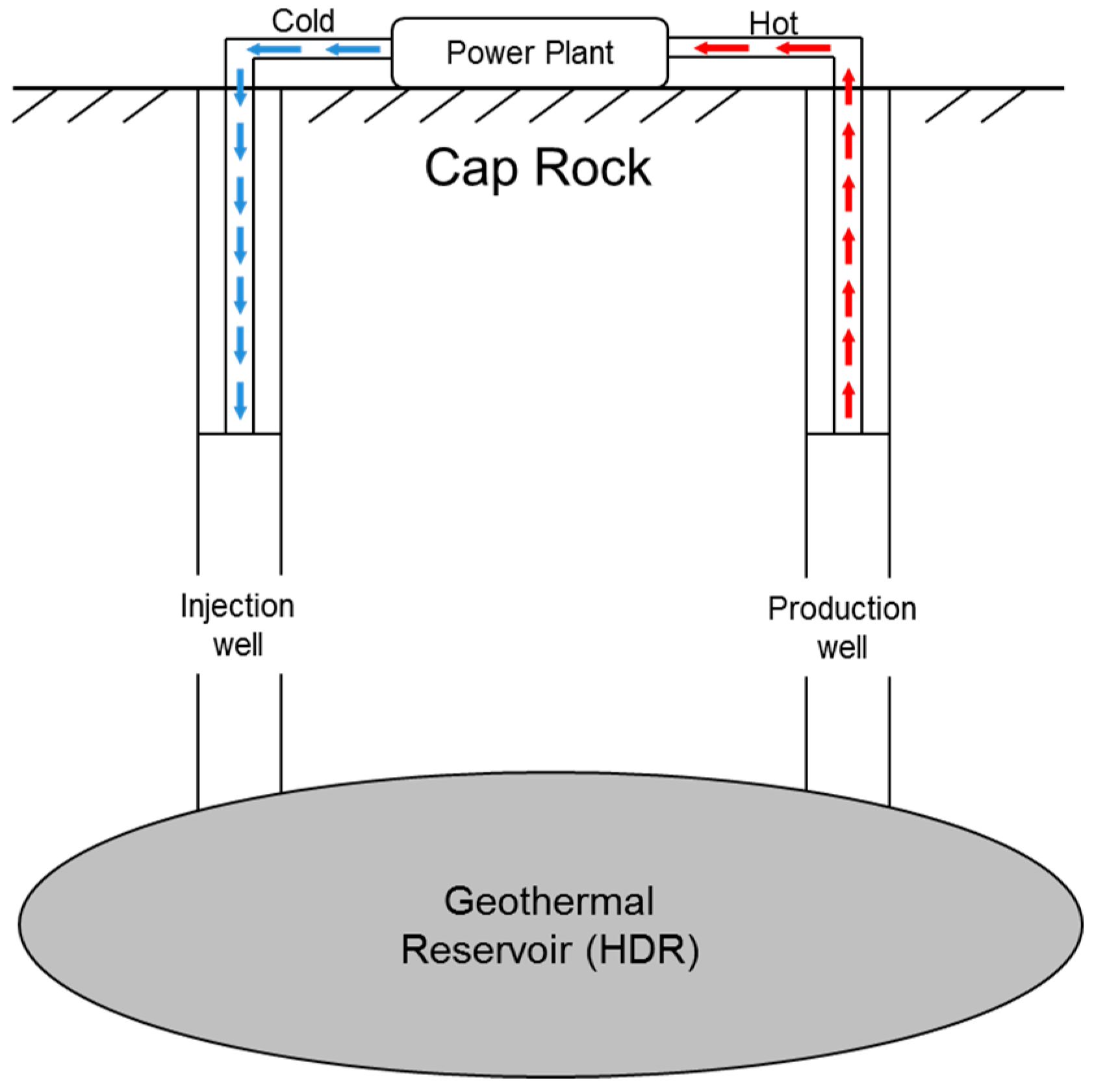
3. 2-D Numerical Modeling of the Geothermal Well
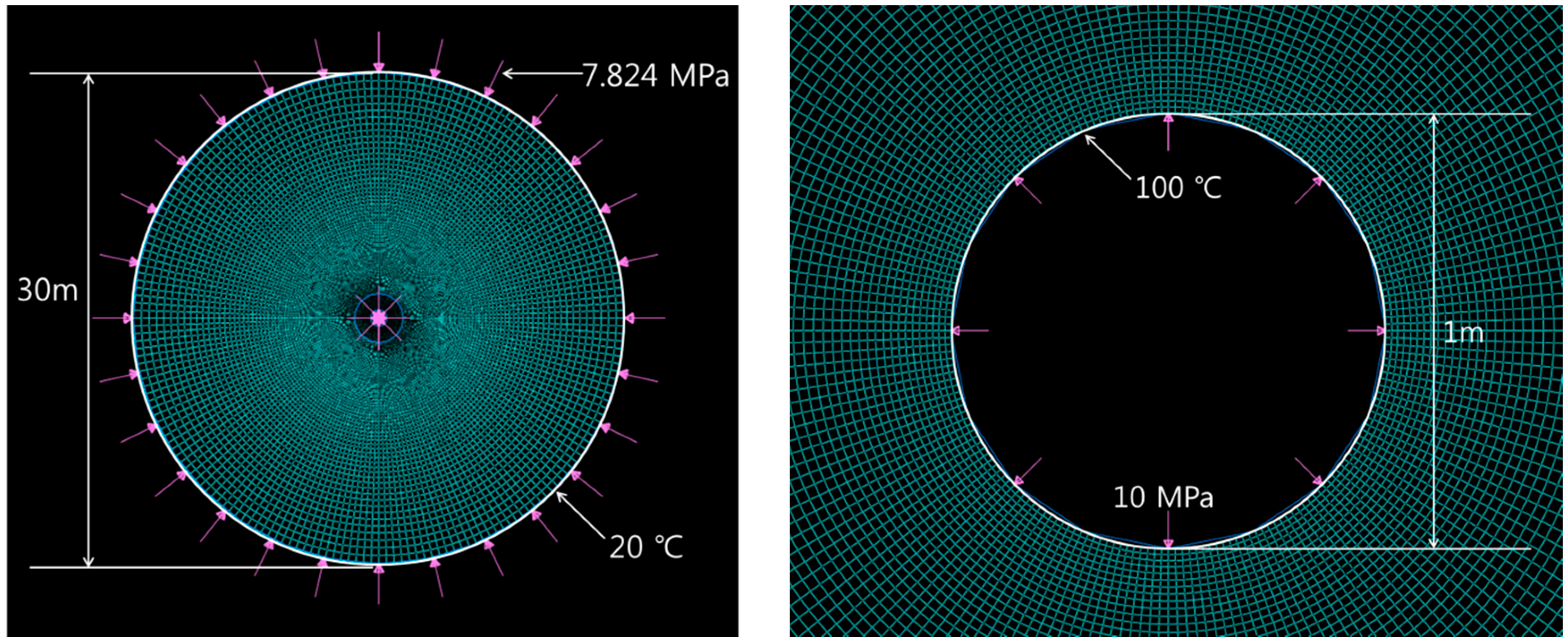
3.1. Preliminary Investigation
3.2. Geothermal Well Modeling
3.3. Numerical Simulation of Geothermal Well
4. Parametric Study for Cementing Component
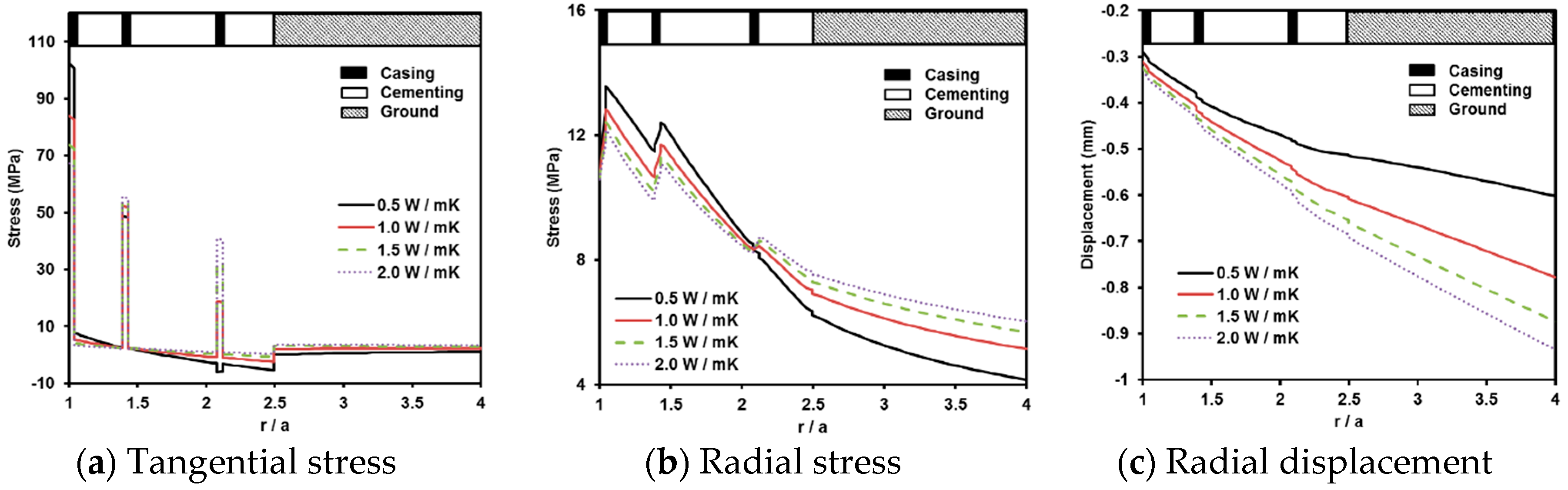
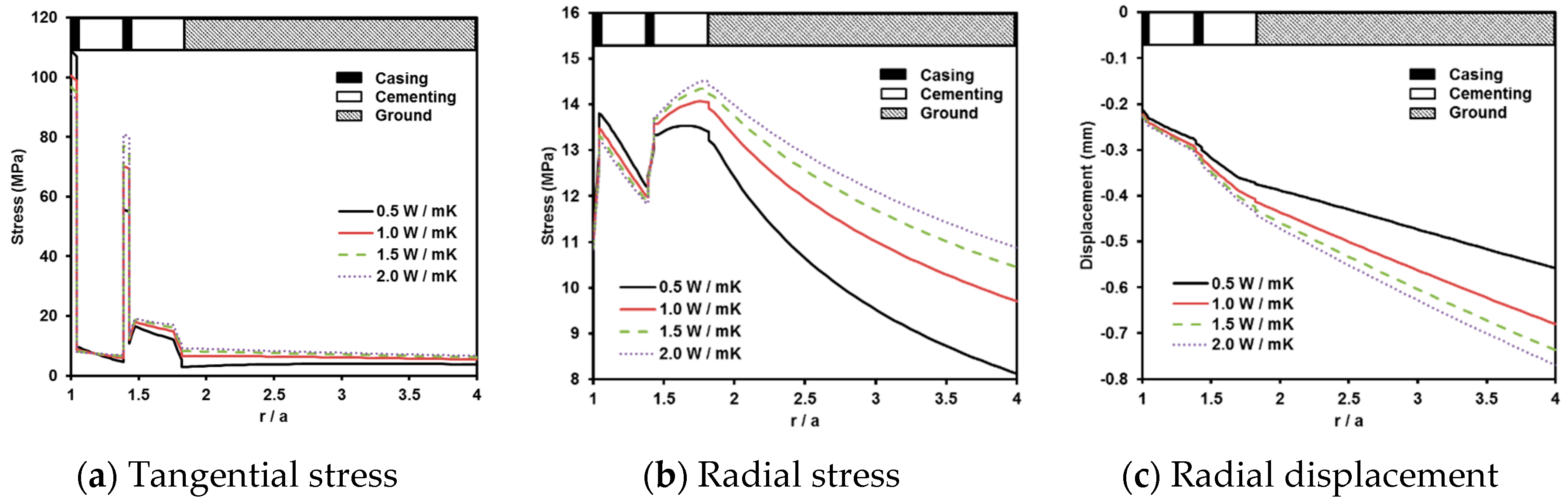
4.1. Effect of Thermal Conductivity
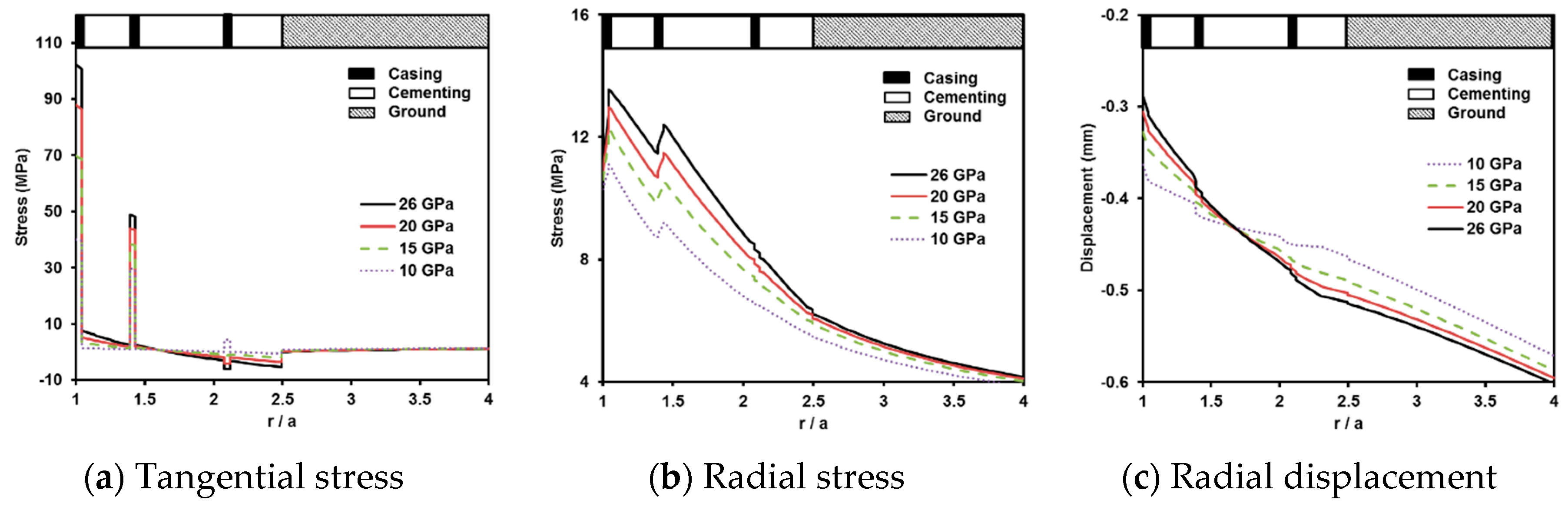
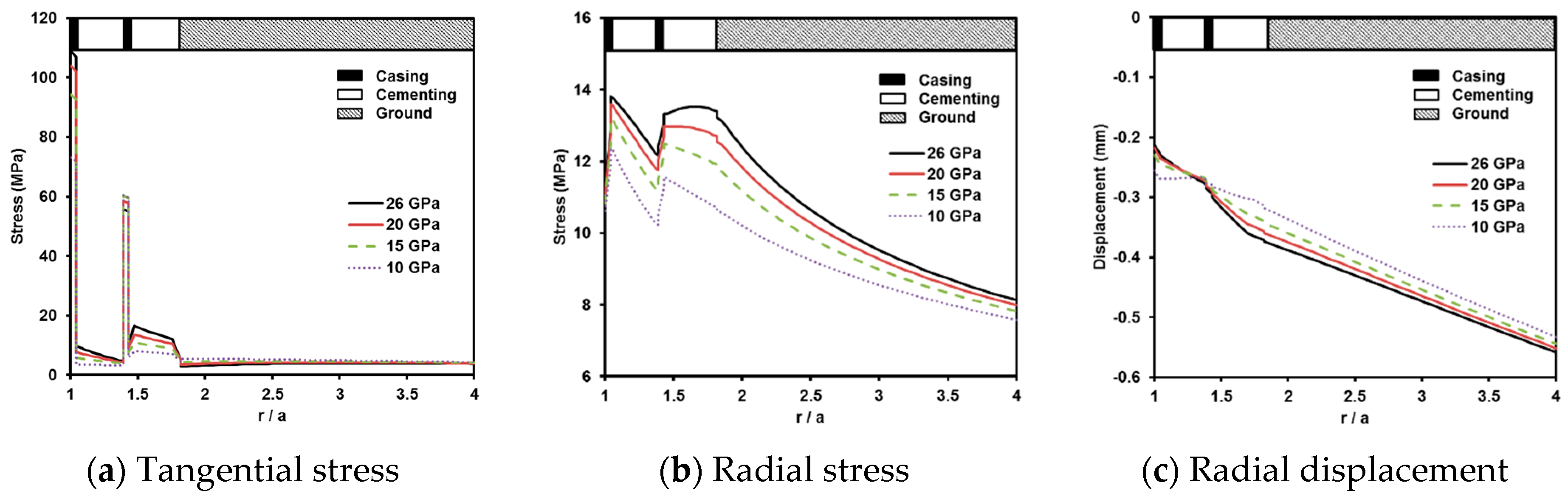
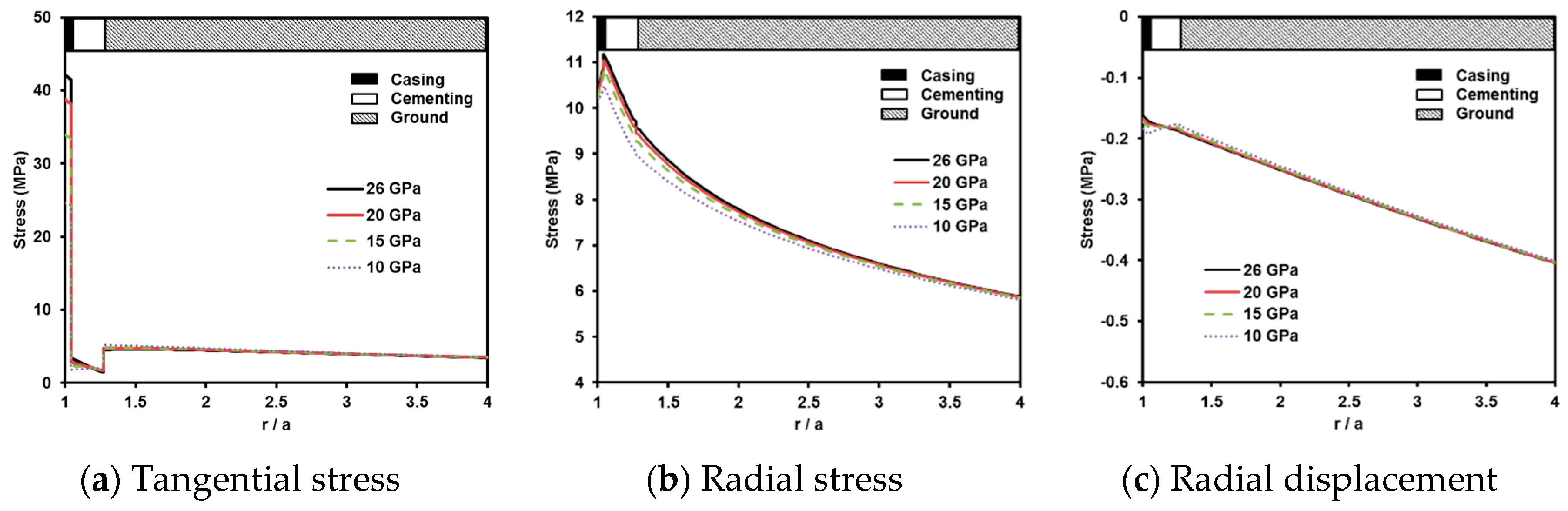
4.2. Effect of Young’s Modulus
5. Conclusions
- (1)
- The FE analysis of the geothermal well at five different depths revealed that the outer cementing undergoes relatively high tangential stress compared with the surrounding ground formation due to the relatively higher Young’s modulus. In addition, increasing the number of casings can lessen the tangential stress concentration in the cementing component.
- (2)
- During numerically simulating operation of the geothermal power plants, the geothermal well experiences expansion outward (i.e., negative-signed radial displacement) at all designated depths and all components of the geothermal well because of the combined effect of the inner fluid pressure and the thermal expansion.
- (3)
- Relatively low thermal conductivity of G-class cement (0.62–0.68 W/mK) might be suitable for geothermal wells to prevent heat loss in the production well, but it may still induce more concentration of tangential stress at the most inner casing based on the FE analysis. However, the low thermal conductivity of the cementing is effective to decrease the well expansion.
- (4)
- The variation of the tangential and radial stress, and radial displacement according to the thermal conductivity decreases as the depth of the geothermal well increases, which is caused by the temperature difference between the geothermal well and the surrounding ground formation.
- (5)
- The tangential and radial stress exerted in the geothermal well increase with an increase in the Young’s modulus of the cementing component. However, the variation of the stress and displacement along with the Young’s modulus decreases as the depth of the geothermal well increases.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Leibowitz, L.P. California’s geothermal resource potential. Energy Sources 1978, 3, 293–311. [Google Scholar] [CrossRef]
- Lee, Y.; Park, S.; Kim, J.; Kim, H.C.; Koo, M.H. Geothermal resource assessment in Korea. Renew. Sustain. Energy Rev. 2010, 14, 2392–2400. [Google Scholar] [CrossRef]
- Xu, T.; Apps, J.A.; Pruess, K. Mineral sequestration of carbon dioxide in a sandstone-shale system. Chem. Geol. 2005, 217, 295–318. [Google Scholar] [CrossRef]
- Chen, H.; Goswami, D.Y.; Stefanakos, E.K. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067. [Google Scholar] [CrossRef]
- Brown, D.W. A hot dry rock geothermal energy concept utilizing supercritical CO2 instead of water. In Proceedings of the Twenty-Fifth Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 24–26 January 2000; pp. 233–238.
- Pruess, K. Enhanced geothermal systems (EGS) using CO2 as working fluid—A novel approach for generating renewable energy with simultaneous sequestration of carbon. Geothermics 2006, 35, 351–367. [Google Scholar] [CrossRef]
- Sasaki, S. Characteristics of microseismic events induced during hydraulic fracturing experiments at the Hijiori hot dry rock geothermal energy site, Yamagata, Japan. Tectonophysics 1998, 289, 171–188. [Google Scholar] [CrossRef]
- Pearson, C. The relationship between microseismicity and high pore pressures during hydraulic stimulation experiments in low permeability granitic rocks. J. Geophys. Res. Solid Earth 1981, 86, 7855–7864. [Google Scholar] [CrossRef]
- Edwards, L.M.; Chilingar, G.V.; Rieke, H.H., III; Fertl, W.H. Handbook of Geothermal Energy; Gulf Publishing Co.: Houston, TX, USA, 1982. [Google Scholar]
- Sugama, T. Advanced Cements for Geothermal Wells; Brookhaven Science Laboratories under Contract No. DEAC02-98Ch10886 with the US Department of Energy; Brookhaven Science Laboratories: Upton, NY, USA, 2006. [Google Scholar]
- Philippacopoulos, A.J.; Berndt, M.L. Characterization and modeling of cements for geothermal well casing remediation. Trans. Geotherm. Resour. Counc. 2000, 24, 81–86. [Google Scholar]
- Kestin, J.; Wakeham, W.A. A contribution to the theory of the transient hot-wire technique for thermal conductivity measurements. Phys. A Stat. Mech. Appl. 1978, 92, 102–116. [Google Scholar] [CrossRef]
- Roder, H.M. A transient hot wire thermal conductivity apparatus for fluids. J. Res. Natl. Bur. Stand 1981, 86, 457–493. [Google Scholar] [CrossRef]
- Coquard, R.; Baillis, D.; Quenard, D. Experimental and theoretical study of the hot-wire method applied to low-density thermal insulators. Int. J. Heat Mass Transf. 2006, 49, 4511–4524. [Google Scholar] [CrossRef]
- Won, J.; Lee, D.; Na, K.; Lee, I.M.; Choi, H. Physical properties of G-class cement for geothermal well cementing in South Korea. Renew. Energy 2015, 80, 123–131. [Google Scholar] [CrossRef]
- ASTM International. Standard Test Method for Compressive Strength and Elastic Moduli of Intact Rock Core Specimens under Varying States of Stress and Temperatures; ASTM D7012-14; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Hoek, E.; Brown, E.T. Underground Excavations in Rock; No. Monograph; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Lee, T.J. Development of Exploitation Technologies for Geothermal Resources; Research Report GP2007-002-01-2007; Korea Institute of Geoscience and Mineral Resources (KIGAM): Daejeon, Korea, 2007; p. 161. [Google Scholar]
- Bae, S.H.; Jeon, S.W.; Kim, J.M.; Kim, J.S. Characteristics of the regional rock stress field at shallow depth in the Kyungsang Basin with in-situ rock stress measurement. J. Korean Soc. Rock Mech. 2008, 18, 149–161. [Google Scholar]
- Bullard, E.C. Heat flow in South Africa. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1939, 173, 474–502. [Google Scholar] [CrossRef]
- Beck, A.E.; Sass, J.H. A preliminary value of heat flow at the Muskox Intrusion near Coppermine, N.W.T., Canada. Earth Planet. Sci. Lett. 1966, 1, 123–129. [Google Scholar] [CrossRef]
- Cruz, C.R.; Gillen, M. Thermal expansion of Portland cement paste, mortar and concrete at high temperatures. Fire Mater. 1980, 4, 66–70. [Google Scholar] [CrossRef]
- Fu, X.; Chung, D.D.L. Effects of silica fume, latex, methylcellulose, and carbon fibers on the thermal conductivity and specific heat of cement paste. Cem. Concr. Res. 1997, 27, 1799–1804. [Google Scholar] [CrossRef]
- European Committee. Eurocode 3: Design of Steel Structures—Part 1.2: General Rules—Structural Fire Design; European Committee for Standardization: Brussels, Belgium, 1993; pp. 1–2. [Google Scholar]
- Tester, J.W.; Anderson, B.; Batchelor, A.; Blackwell, D.; DiPippo, R.; Drake, E.; Petty, S. The Future of Geothermal Energy: Impact of Enhanced Geothermal Systems (EGS) on the United States in the 21st Century; Massachusetts Institute of Technology: Cambridge, MA, USA, 2006; p. 209. [Google Scholar]
- Lee, T.J.; Song, Y.; Yoon, W.S.; Kim, K.; Jeon, J.; Min, K.; Cho, Y. The first enhanced geothermal system project in Korea. In Proceedings of the 9th Asian Geothermal Symposium, Kagoshima, Japan, 7–9 November 2011; Volume 7, p. 9.




| Mix Type | Cement | Silica Flour | Water | Bentonite | Dispersant |
|---|---|---|---|---|---|
| 40SF | 1 | 0.4 | 0.55 | 0.034 | 0.012 |
| Surrounding Temperature (°C) | Thermal Conductivity (W/mK) |
|---|---|
| 20 | 0.6798 |
| 50 | 0.6243 |
| Curing Method | Dry (100 °C) | Water (21 °C) |
|---|---|---|
| E (MPa) | 6224 | 26216 |
| qu (MPa) | 23.04 | 28.97 |
| Case No. | Boundary Conditions |
|---|---|
| 1 | Horizontal stress only (7.824 MPa) |
| 2 | Horizontal stress + inner fluid pressure (10 MPa) |
| 3 | Horizontal stress + thermal stress |
| 4 | Horizontal stress + inner fluid pressure + temperature stress |
| Themal Conductivity (W/mK) | Thermal Expansion Coefficient (/°C) | Young’s Modulus (GPa) | Poisson’s Ratio | Specific Heat (J/kg·°C) |
|---|---|---|---|---|
| 2.8 | 1.345 × 10−5 | 9.7 | 0.3 | 818.0 |
| Property | Casing | Cementing |
|---|---|---|
| Thermal conductivity(W/mK) | 75 | 0.5 (1.0, 1.5, 2.0) |
| Coefficient of thermal expansion(/°C) | 1.2 × 10−5 | 1 × 10−5 |
| Specific heat(J/kg·°C) | 460.24 | 750 |
| Young’s modulus(GPa) | 205.6 | 26 (20, 15, 10) |
| Poisson’s ratio | 0.29 | 0.21 |
| Density (kg/m3) | 7850 | 1920 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Won, J.; Choi, H.-J.; Lee, H.; Choi, H. Numerical Investigation on the Effect of Cementing Properties on the Thermal and Mechanical Stability of Geothermal Wells. Energies 2016, 9, 1016. https://doi.org/10.3390/en9121016
Won J, Choi H-J, Lee H, Choi H. Numerical Investigation on the Effect of Cementing Properties on the Thermal and Mechanical Stability of Geothermal Wells. Energies. 2016; 9(12):1016. https://doi.org/10.3390/en9121016
Chicago/Turabian StyleWon, Jongmuk, Hyun-Jun Choi, Hyobum Lee, and Hangseok Choi. 2016. "Numerical Investigation on the Effect of Cementing Properties on the Thermal and Mechanical Stability of Geothermal Wells" Energies 9, no. 12: 1016. https://doi.org/10.3390/en9121016
APA StyleWon, J., Choi, H.-J., Lee, H., & Choi, H. (2016). Numerical Investigation on the Effect of Cementing Properties on the Thermal and Mechanical Stability of Geothermal Wells. Energies, 9(12), 1016. https://doi.org/10.3390/en9121016







