Chaotic Manifold Analysis of Four-Screw Extruders Based on Lagrangian Coherent Structures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Government Equations
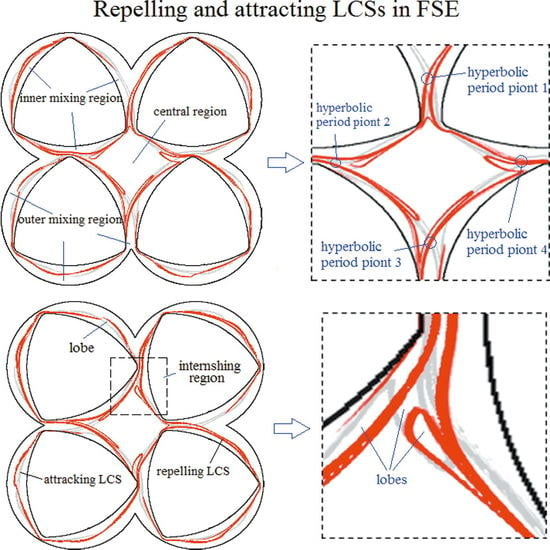
2.2. FTLE and LCS
2.3. Configurations of Three Types of Four-Screw Extruders
2.4. FE Models and Computational Details
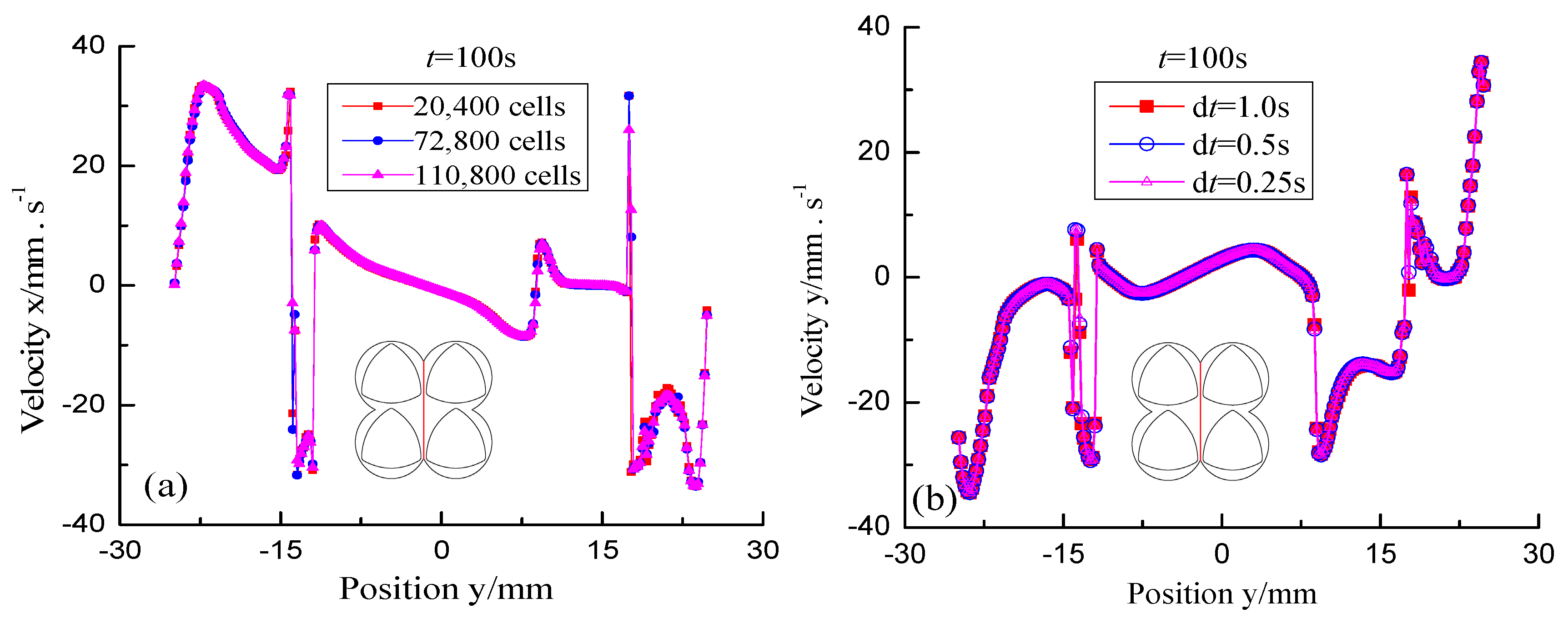
2.5. Grid Independence and Time-Step Validations
3. Results and Discussion
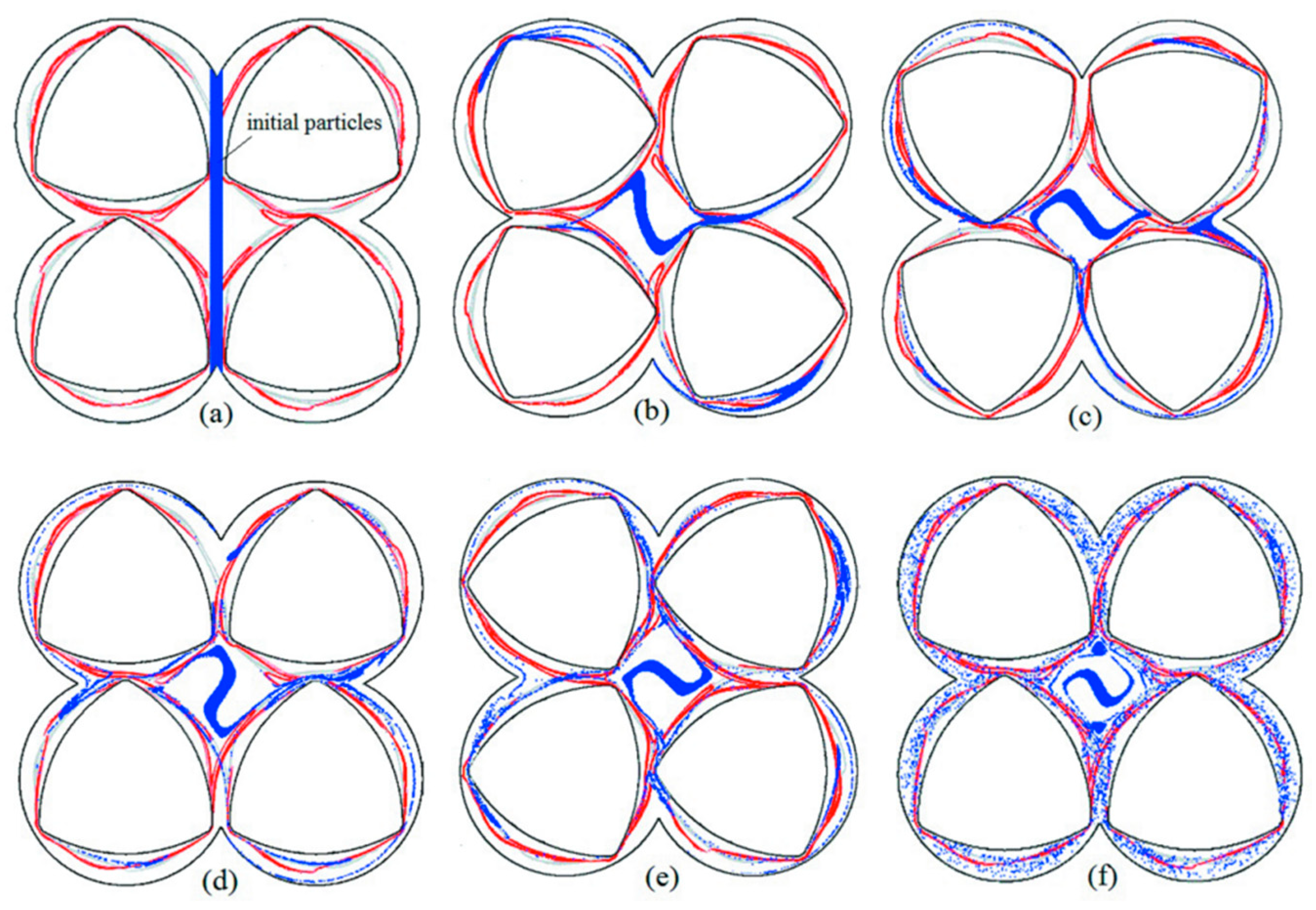
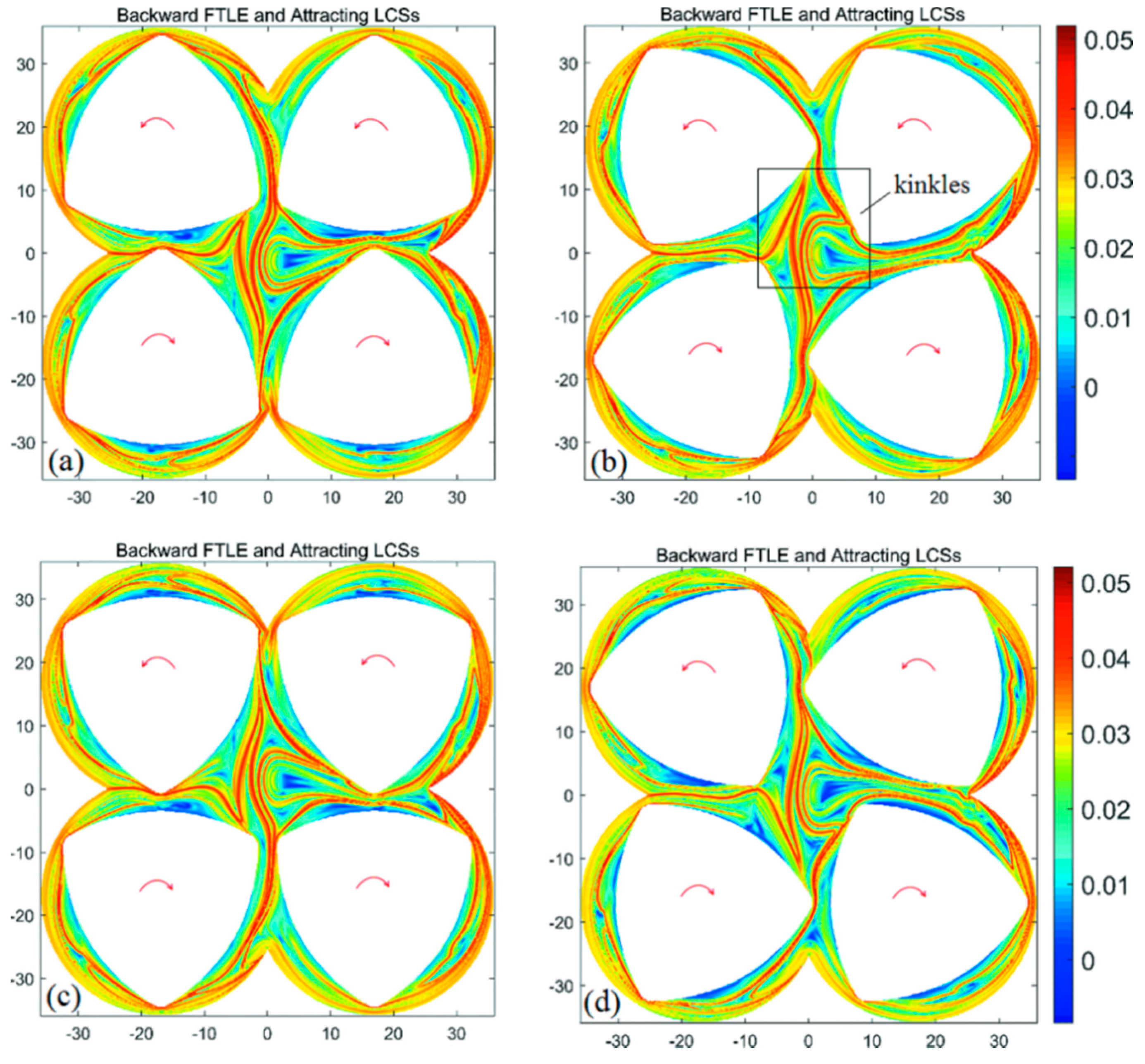
3.1. Chaotic Manifolds in the Basic System
3.2. Chaotic Manifolds in CRS and SEDS
3.3. Comparisons of Poincaré Sections
3.4. Quantitative Mixing Comparisons
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lawal, A.; Kalyon, D.M. Mechanisms of mixing in single and co-rotating twin screw extruders. Polym. Eng. Sci. 1995, 35, 1325–1338. [Google Scholar] [CrossRef]
- Yao, W.G.; Takahashi, K.; Koyama, K.; Dai, G.C. Experimental study on distributive mixing characteristics of a new type of pin mixing section. Polym. Eng. Sci. 1997, 37, 615–622. [Google Scholar] [CrossRef]
- Nakayama, Y.; Takeda, E.; Shigeishi, T.; Kajiwara, T. Melt-mixing by novel pitched-tip kneading disks in a co-rotating twin-screw extruder. Chem. Eng. Sci. 2011, 66, 103–110. [Google Scholar] [CrossRef] [Green Version]
- Ishikawa, T.; Amano, T.; Kihara, S.I.; Funatsu, K. Flow patterns and mixing mechanisms in the screw mixing element of a co-rotating twin-screw extruder. Chem. Eng. Sci. 2002, 42, 925–939. [Google Scholar] [CrossRef]
- Zhu, X.Z.; Xie, Y.J.; Yuan, H.Q. Numerical simulation of flow characteristics of co-rotating intermeshing four-screw extruder. J. Reinf. Plast. Compos. 2008, 27, 321–334. [Google Scholar] [CrossRef]
- Hutchinson, B.C.; Rios, A.C.; Osswald, T.A. Modeling the distributive mixing in an internal batch mixer. Int. Polym. Process. 1999, 14, 315–321. [Google Scholar] [CrossRef]
- Bravo, V.L.; Hrymak, A.N.; Wright, J.D. Numerical simulation of pressure and velocity profiles in kneading elements of a co-rotating twin screw extruder. Polym. Eng. Sci. 2000, 40, 525–541. [Google Scholar] [CrossRef]
- Erol, M.; Kalyon, D.M. Assessment of the degree of mixedness of filled polymers. Int. Polym. Process. 2005, 20, 228–237. [Google Scholar] [CrossRef]
- Luo, P.; Jia, H.; Xin, C. An Experimental study of liquid mixing in a multi-orifice-impinging transverse jet mixer using plif. Chem. Eng. J. 2013, 228, 554–564. [Google Scholar] [CrossRef]
- Connelly, R.K.; Kokini, J.L. Examination of the mixing ability of single and twin screw mixers using 2D finite element method simulation with particle tracking. J. Food Eng. 2007, 79, 956–969. [Google Scholar] [CrossRef]
- Domingues, N.; Gaspar-Cunha, A.; Covas, J.A. A quantitative approach to assess the mixing ability of single-screw extruders for polymer extrusion. J. Polym. Eng. 2012, 32, 81–94. [Google Scholar] [CrossRef]
- Zhang, X.M.; Feng, L.F.; Chen, W.X. Numerical simulation and experimental validation of mixing performance of kneading discs in a twin screw extruder. Polym. Eng. Sci. 2009, 49, 1772–1783. [Google Scholar] [CrossRef]
- Nakayama, Y.; Takeda, E.; Shigeishi, T.; Kajiwara, T. Comparative study of internal batch mixer such as cam, boundary and roller. Chem. Eng. Sci. 2011, 66, 2502–2511. [Google Scholar]
- Dhakal, P.; Das, S.R.; Poudyal, H.; Chandy, A.J. Numerical simulations of partially-filled rubber mixing in a 2-wing rotor-equipped chamber. J. Appl. Polym. Sci. 2016, 134, 44250. [Google Scholar] [CrossRef]
- Das, S.R.; Poudyal, H.; Chandy, A.J. Numerical Investigation of Effect of Rotor Phase Angle in Partially-Filled Rubber Mixing. Int. Polym. Process. 2017, 32, 343–354. [Google Scholar] [CrossRef]
- Wiggins, S.; Ottino, J.M. Foundations of chaotic mixing. Math. Phys. Eng. Sci. 2004, 362, 937–970. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xia, H.M.C.; Shu, S.; Wan, Y.; Chew, T. Influence of the reynolds number on chaotic mixing in a spatially periodic micromixer and its characterization using dynamical system techniques. J. Micromech. Microeng. 2006, 16, 53–61. [Google Scholar] [CrossRef]
- Lee, T.H.; Kwon, T.H. A new representative measure of chaotic mixing in a chaos single-screw extruder. Adv. Polym. Technol. 1999, 18, 53–68. [Google Scholar] [CrossRef]
- Hwang, W.R.; Kwon, T.H. Chaotic volumetric transports in a single-screw extrusion process. Polym. Eng. Sci. 2003, 43, 783–797. [Google Scholar] [CrossRef]
- Hwang, W.R.; Kwon, T.H. Dynamical modeling of chaos single-screw extruder and its three-dimensional numerical analysis. Polym. Eng. Sci. 2000, 40, 702–714. [Google Scholar] [CrossRef]
- Niu, X.; Lee, Y.K. Efficient spatial-temporal chaotic mixing in microchannels. J. Micromech. Microeng. 2003, 13, 454–462. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Manas-Zloczower, I.; Kaufman, M. Entropy time evolution in a twin-flight single-screw extruder and its relationship to chaos. Chem. Eng. Sci. 2005, 192, 405–423. [Google Scholar] [CrossRef]
- Haller, G.; Yuan, G. Lagrangian coherent structures and mixing in two-dimensional turbulence. Phys. D 2000, 147, 352–370. [Google Scholar] [CrossRef]
- Haller, G. Finding finite-time invariant manifolds in two-dimensional velocity fields. Chaos 2000, 10, 99–108. [Google Scholar] [CrossRef] [PubMed]
- Haller, G. Lagrangian coherent structures. Annu. Rev. Fluid Mech. 2015, 47, 137–162. [Google Scholar] [CrossRef]
- Santitissadeekorn, N.; Bohl, D.; Bollt, E.M. Analysis and modeling of an experimental device by finite-time lyapunov exponent method. Int. J. Bifurcat. Chaos 2011, 19, 993–1006. [Google Scholar] [CrossRef]
- Robinson, M.; Cleary, P.W. The influence of cam geometry and operating conditions on chaotic mixing of viscous fluids in a twin cam mixer. AIChE J. 2011, 57, 581–598. [Google Scholar] [CrossRef]
- Robinson, M.; Cleary, P.W. Flow and mixing performance in helical ribbon mixers. Chem. Eng. Sci. 2012, 84, 382–398. [Google Scholar] [CrossRef]
- Conti, G.; Badin, G. Hyperbolic Covariant Coherent Structures in Two-Dimensional Flows. Fluids 2017, 2, 50. [Google Scholar] [CrossRef]
- O’Farrell, C.; Dabiri, J.O. A lagrangian approach to identifying vortex pinch-off. Chaos 2010, 20, 261–300. [Google Scholar] [CrossRef] [PubMed]
- Bozorgmagham, A.E.; Ross, S.D. Atmospheric lagrangian coherent structures considering unresolved turbulence and forecast uncertainty. Commun. Nonlinear Sci. 2015, 22, 964–979. [Google Scholar] [CrossRef]
- Prant, S.V. Chaotic lagrangian transport and mixing in the ocean. Eur. Phys. J. Spec. Top. 2015, 223, 2723–2743. [Google Scholar] [CrossRef]
- Mukiibi, D.; Badin, G.; Serra, N. Three dimensional chaotic advection by mixed layer baroclinic instabilities. J. Phys. Oceanogr. 2016, 46, 1509–1529. [Google Scholar] [CrossRef]
- Green, M.A.; Rowley, C.W.; Smits, A.J. Using hyperbolic lagrangian coherent structures to investigate vortices in bioinspired fluid flows. Chaos 2010, 20, 017510. [Google Scholar] [CrossRef] [PubMed]
- Borgogno, D.; Rubino, G.; Veranda, M.; Cappello, S.; Grasso, D. Detection of magnetic barriers in a chaotic domain: first application of finite time lyapunov exponent method to a magnetic confinement configuration. Plasma Phys. Control. Fusion 2015, 57, 401–406. [Google Scholar]
- Connelly, R.K.; Kokini, J.L. The effect of shear thinning and differential viscoelasticity on mixing in a model 2D mixer as determined using FEM with particle tracking. J. Non-Newton. Fluid Mech. 2004, 123, 1–17. [Google Scholar] [CrossRef]
- Shadden, S.C.; Lekien, F.; Marsden, J.E. Definition and properties of lagrangian coherent structures from finite-time lyapunov exponents in a two-dimensional periodic flows. Phys. D 2005, 212, 271–304. [Google Scholar] [CrossRef]
- Ortega-Casanova, J. CFD study on mixing enhancement in a channel at a low Reynolds number by pitching a square cylinder. Comput. Fluids 2017, 145, 141–152. [Google Scholar] [CrossRef]
- Ottino, J.M. Mixing, chaotic advection, and turbulence. Annu. Rev. Fluid Mech. 1990, 22, 207–254. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| Barrel diameter R0 | 18.5 mm |
| Screw root diameter R1 | 13 mm |
| Screw tip diameter R2 | 17 mm |
| Centerline distance of four screws L | 33 mm |
| Screw clearance | 3 mm |
| Clearance of screw and barrel | 1.5 mm |
| Rotational speed of four screws | 0.5 r/min |
| Leads of our screws | 3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.Z.; Tong, Y.; Hu, Y.X. Chaotic Manifold Analysis of Four-Screw Extruders Based on Lagrangian Coherent Structures. Materials 2018, 11, 2272. https://doi.org/10.3390/ma11112272
Zhu XZ, Tong Y, Hu YX. Chaotic Manifold Analysis of Four-Screw Extruders Based on Lagrangian Coherent Structures. Materials. 2018; 11(11):2272. https://doi.org/10.3390/ma11112272
Chicago/Turabian StyleZhu, Xiang Zhe, Ying Tong, and Yue Xin Hu. 2018. "Chaotic Manifold Analysis of Four-Screw Extruders Based on Lagrangian Coherent Structures" Materials 11, no. 11: 2272. https://doi.org/10.3390/ma11112272