Computation of Propagating and Non-Propagating Lamb-Like Wave in a Functionally Graded Piezoelectric Spherical Curved Plate by an Orthogonal Function Technique
Abstract
:1. Introduction
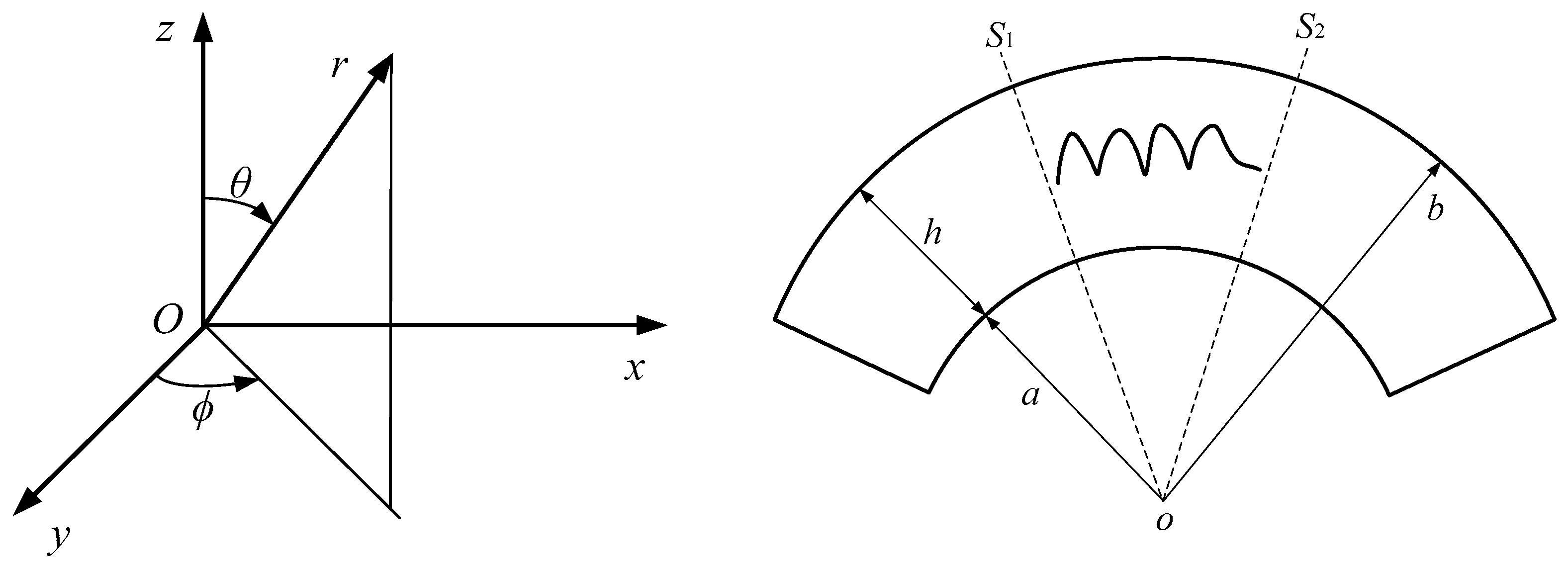
2. Statement of the Problem and Basic Equations
3. Numerical Results
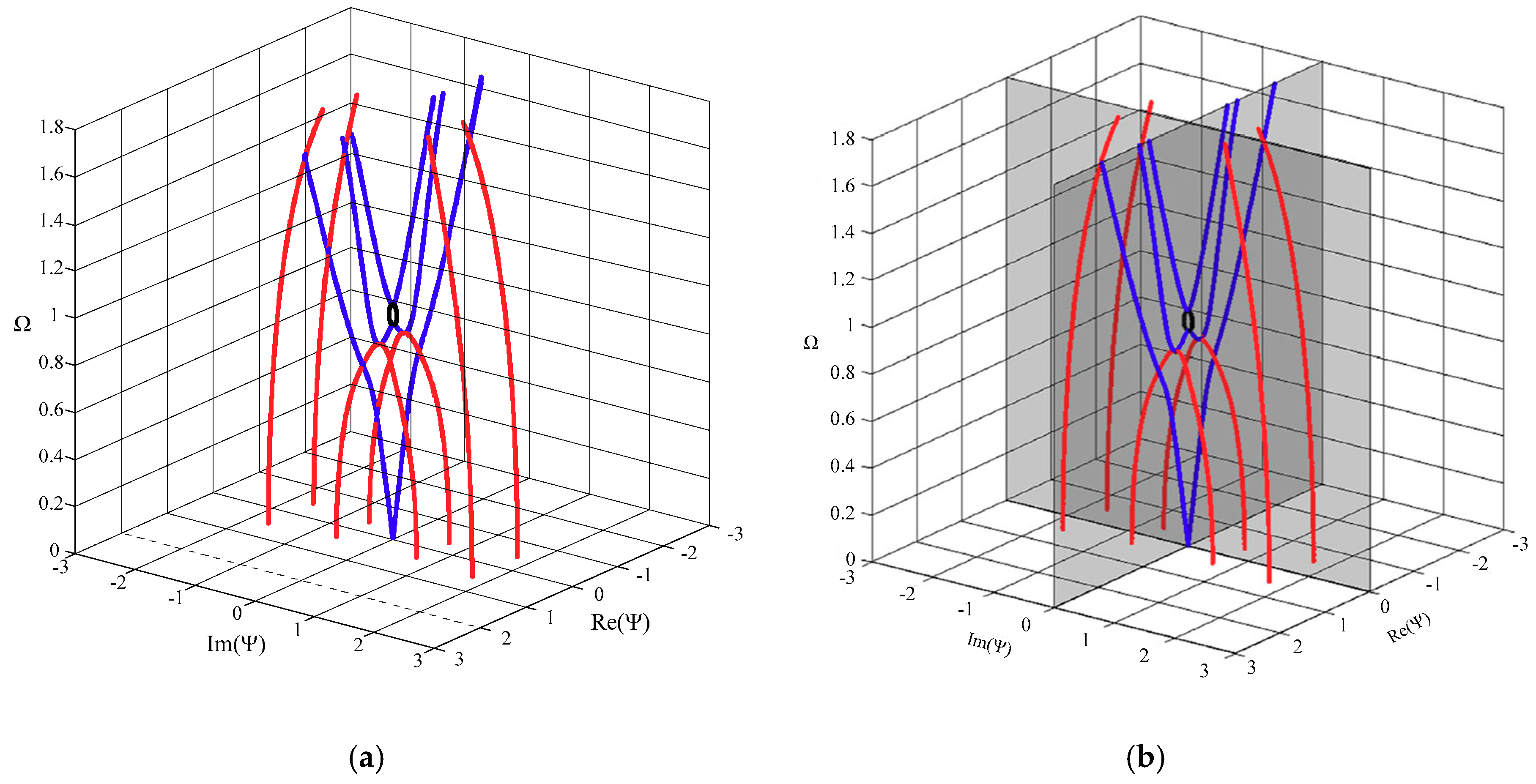
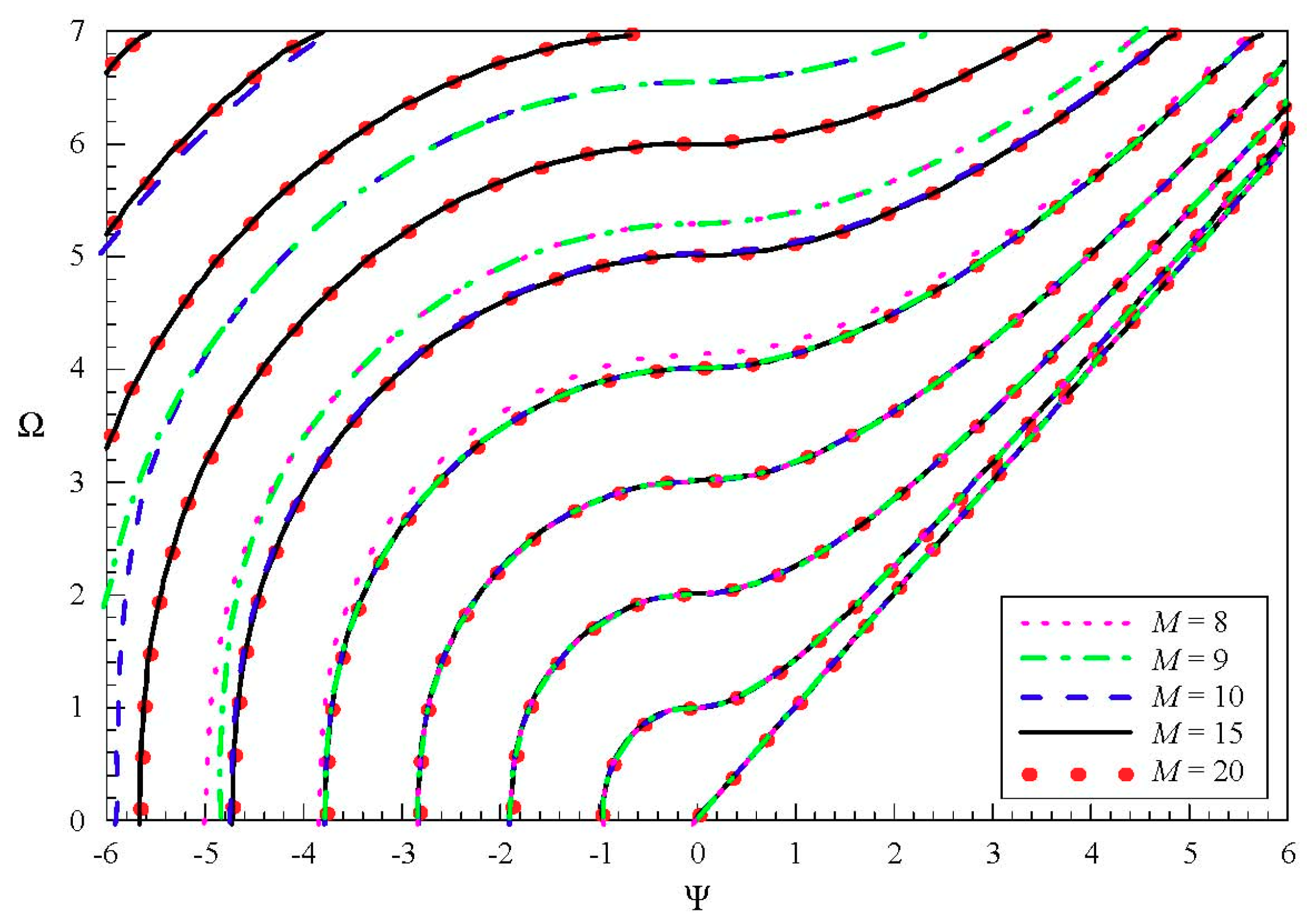
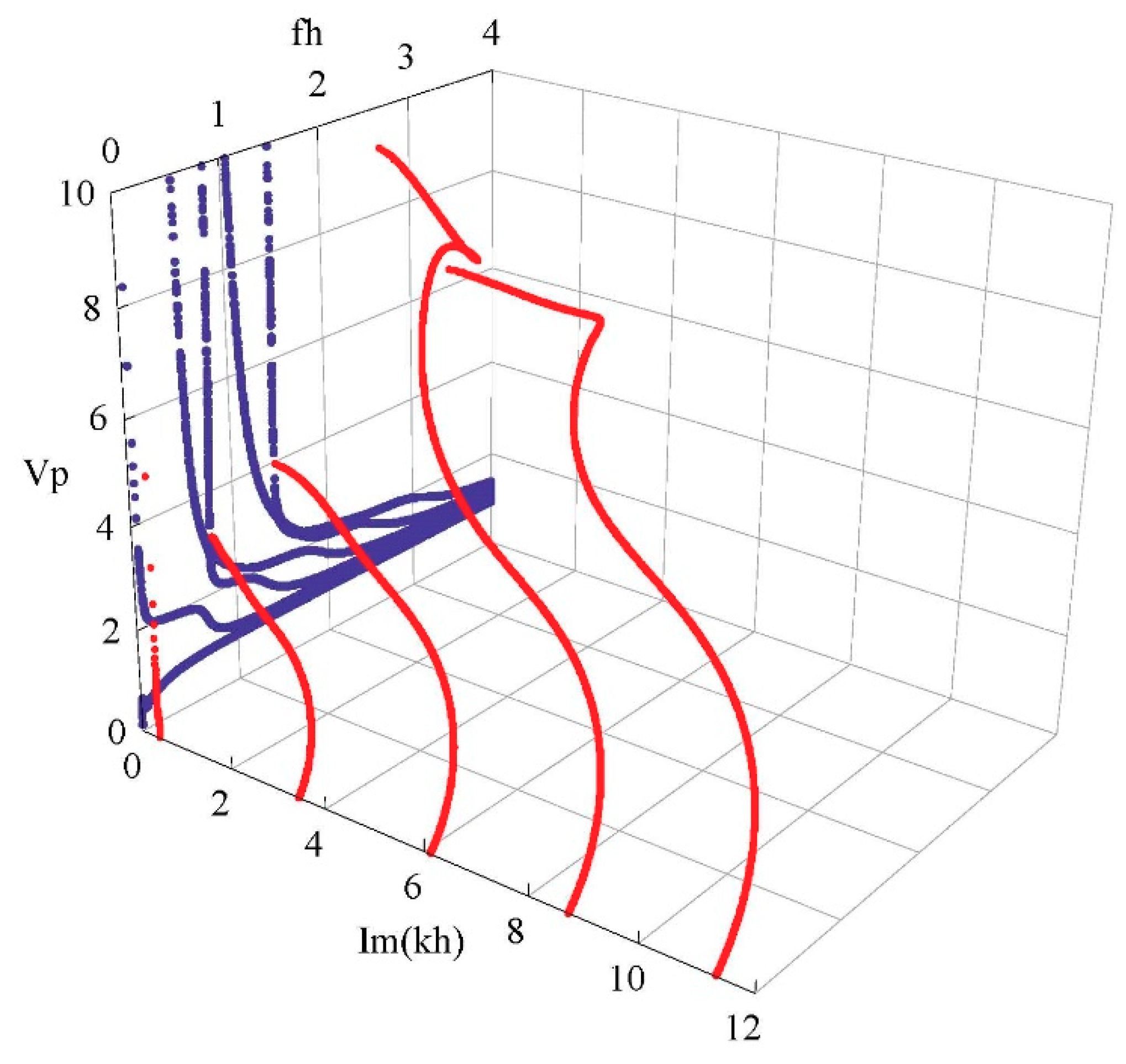
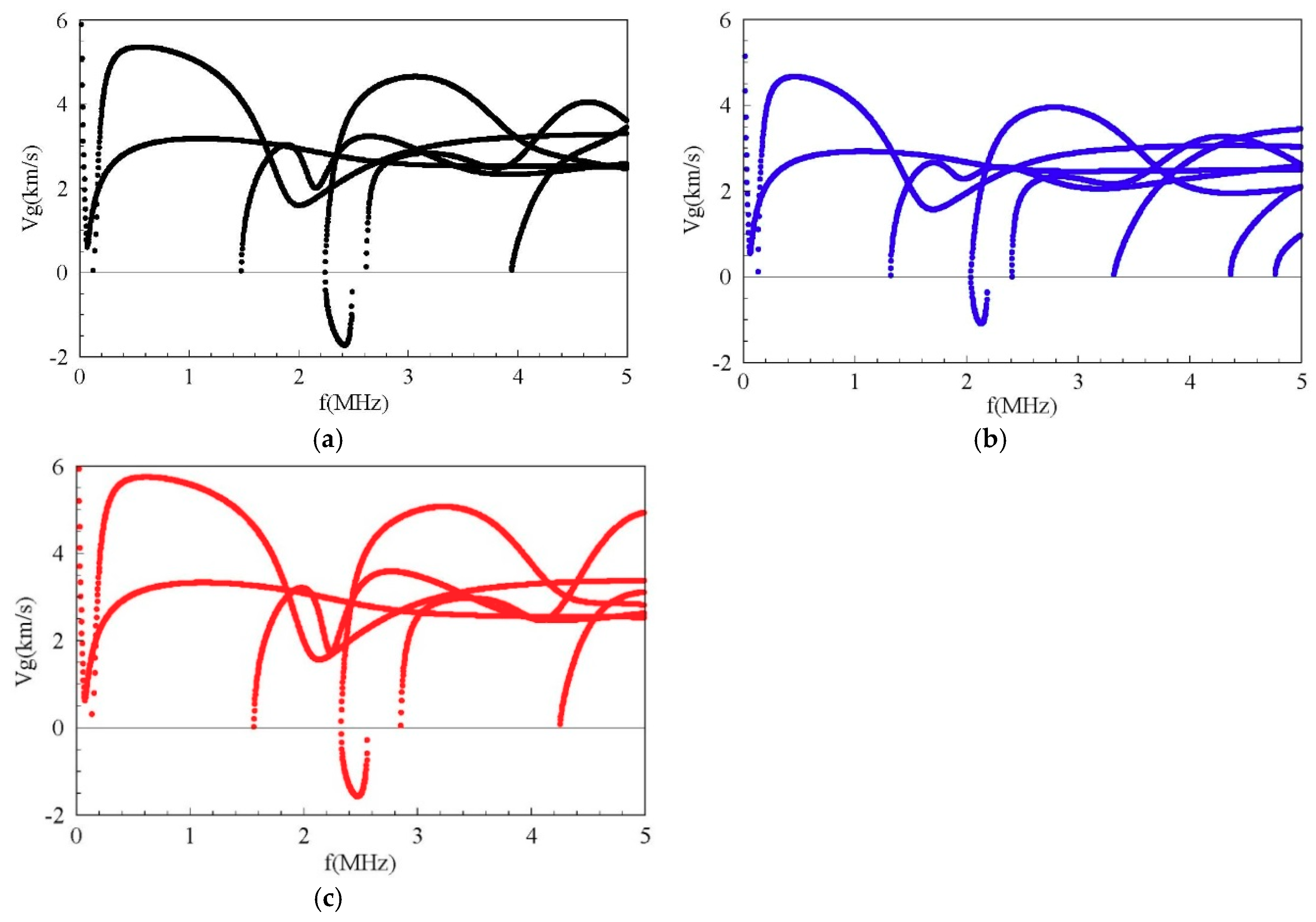
3.1. Approach Validation and Convergence of the Problem
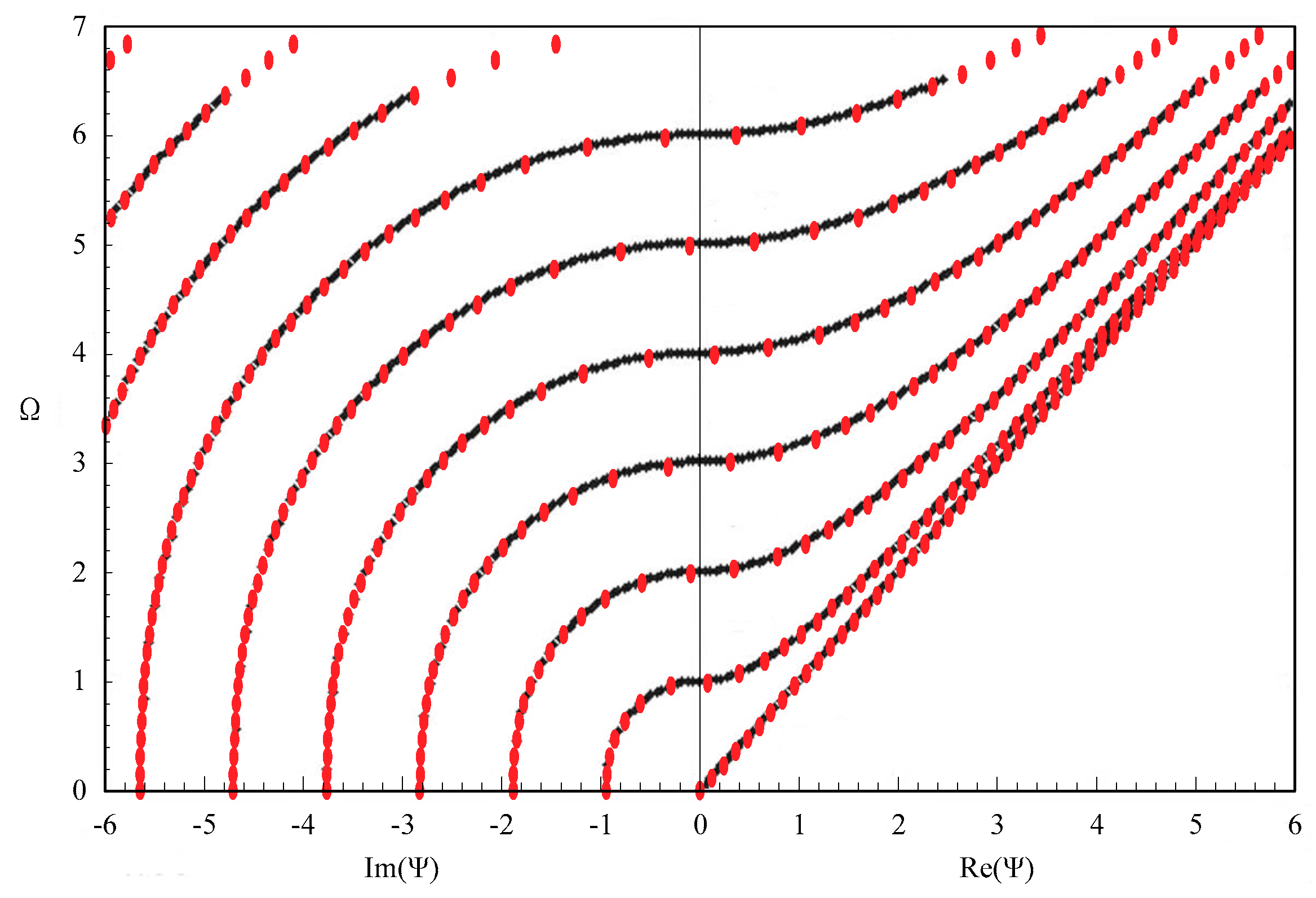
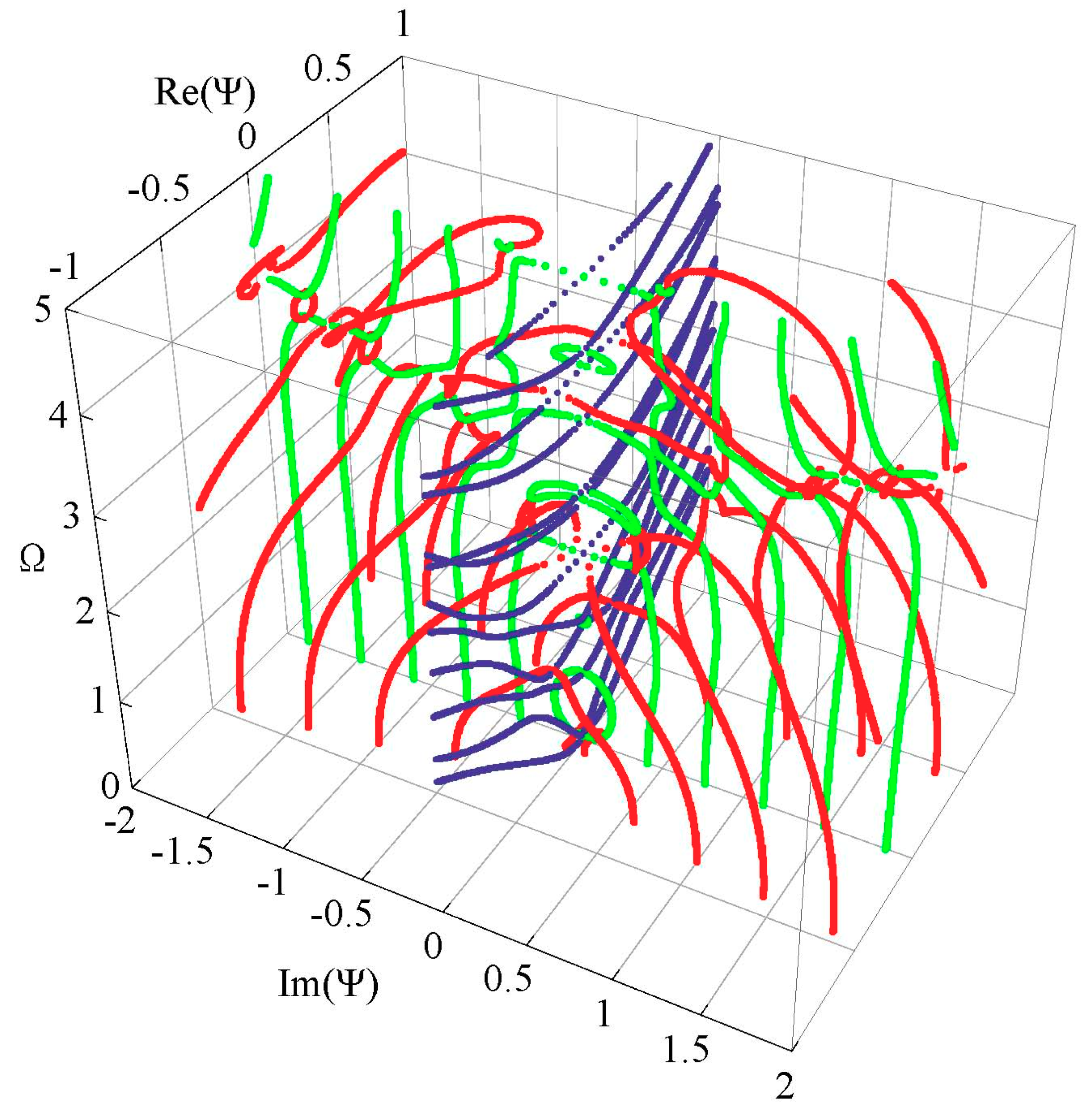
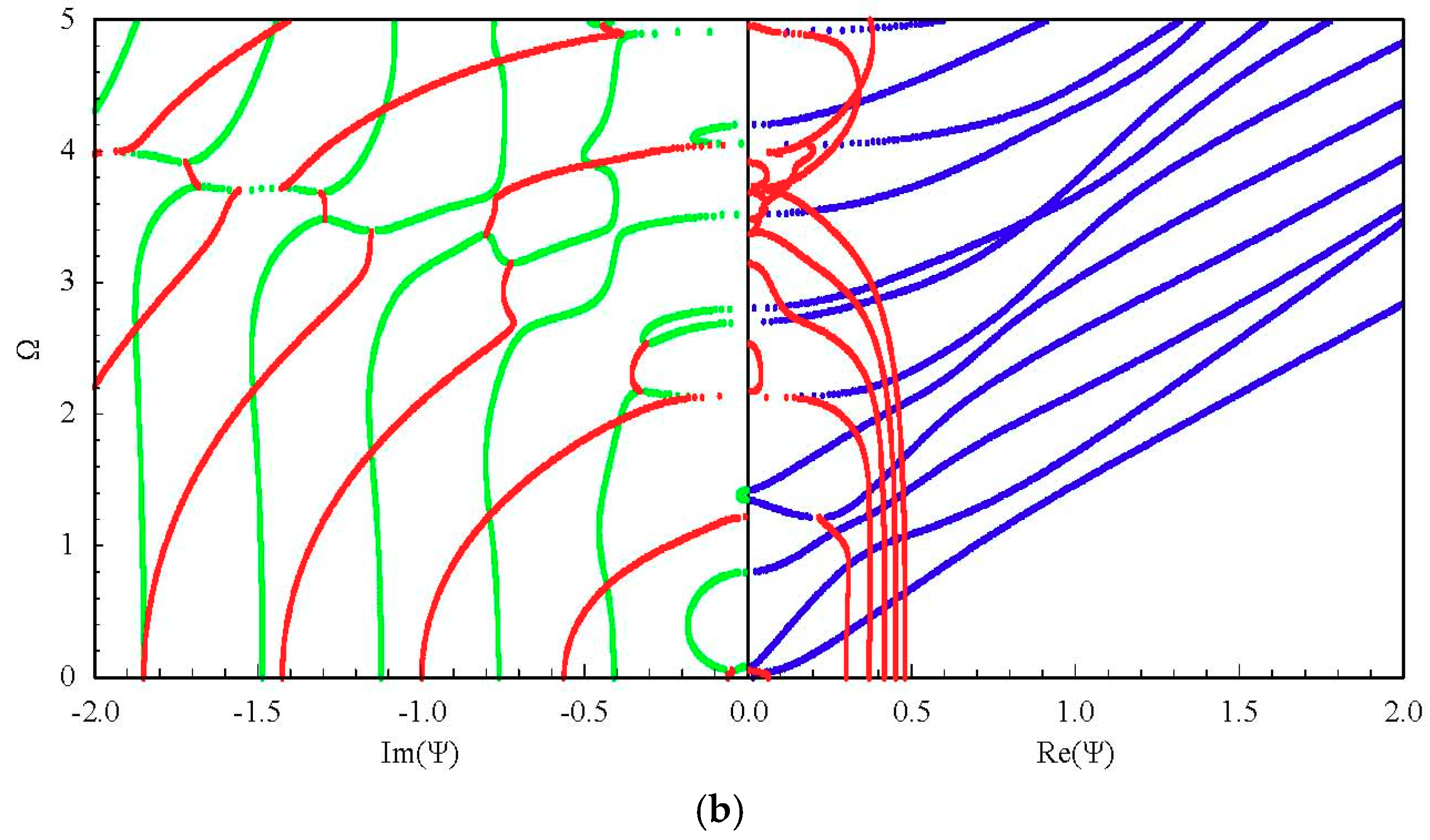
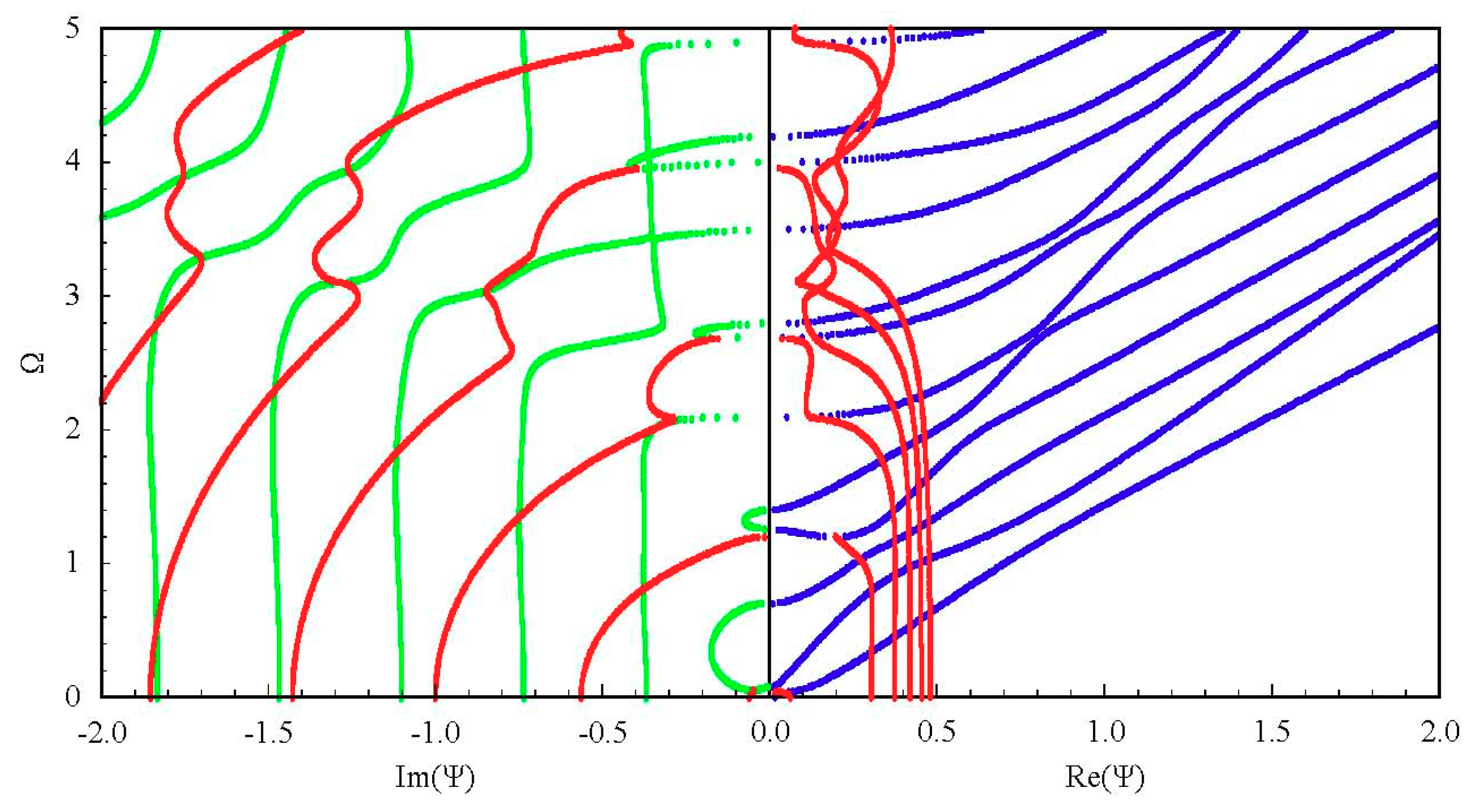
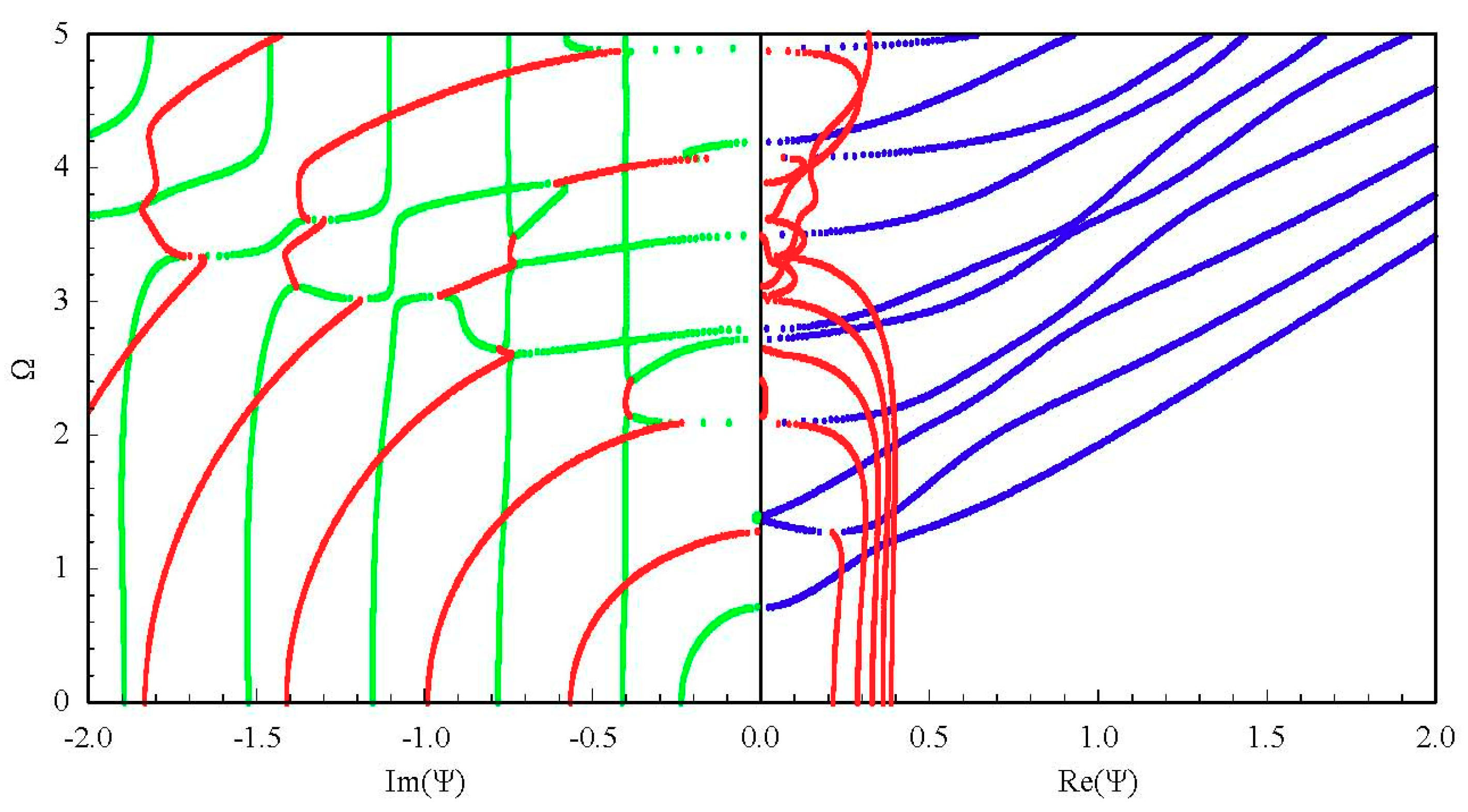
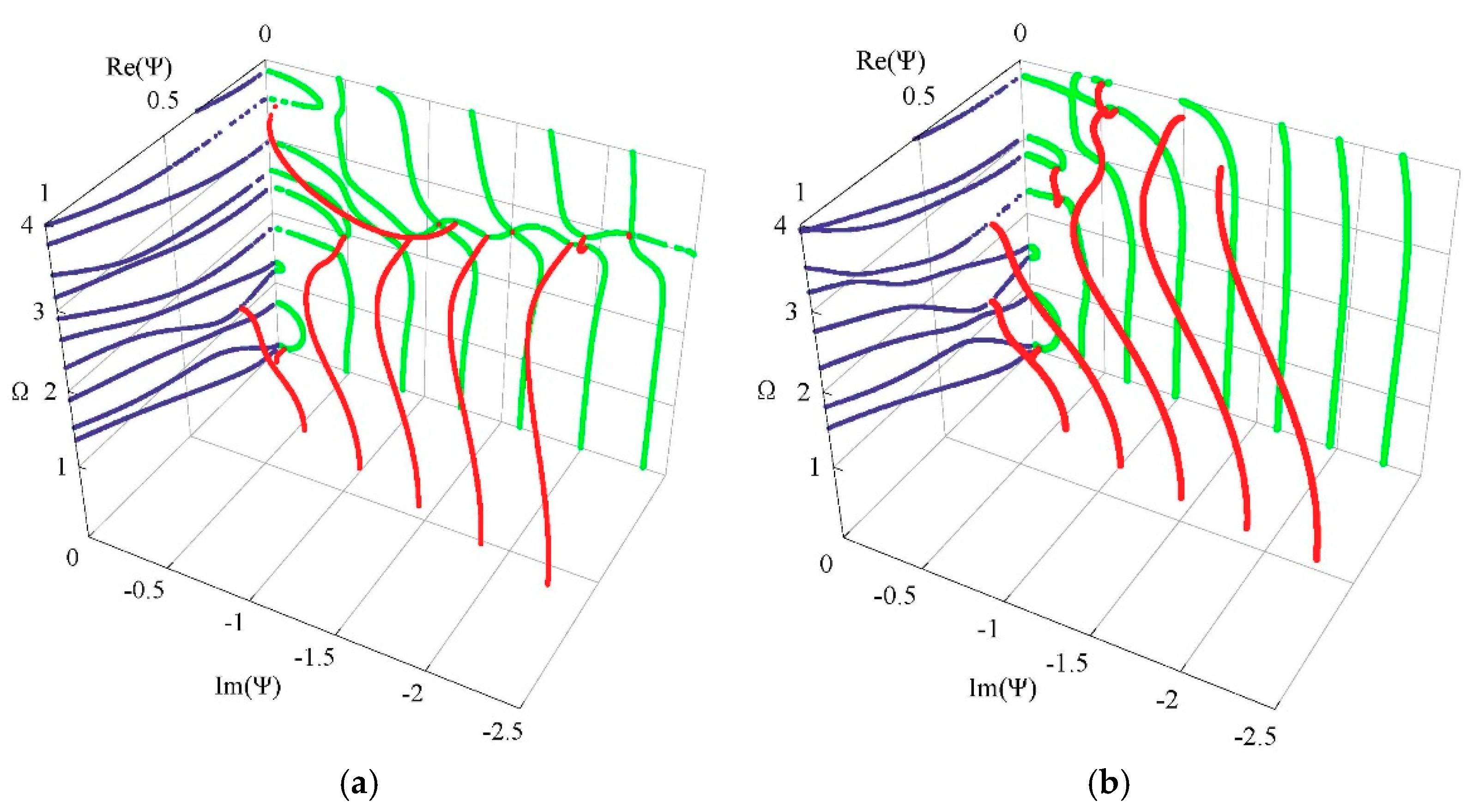
3.2. Complete Frequency Spectrum for a FGPM Spherical Curved Plate
3.3. Influences of Piezoelectricity and Boundary Conditions on Frequency Spectrum
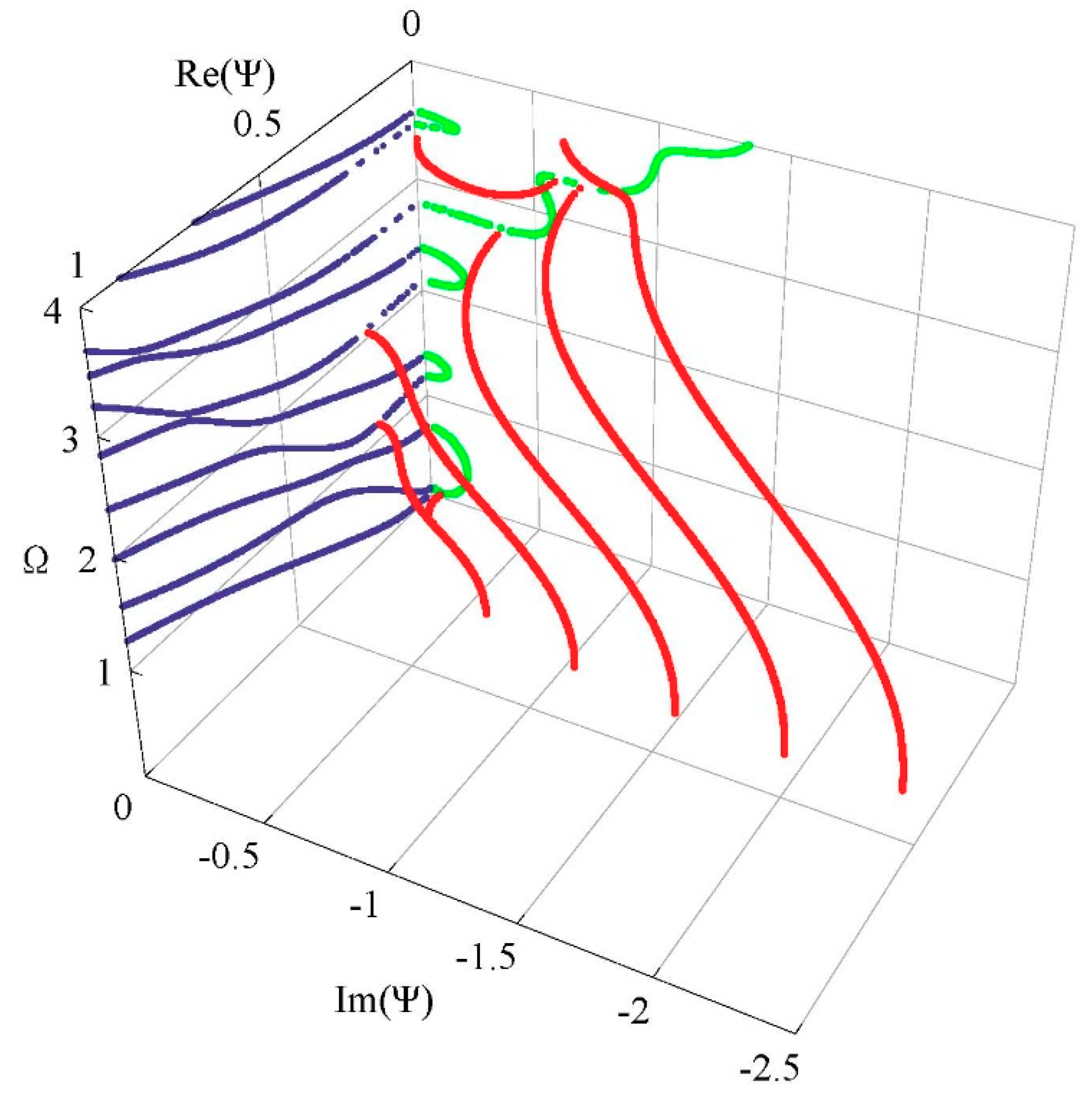
3.4. Influences of Graded Field on the Frequency Spectrum
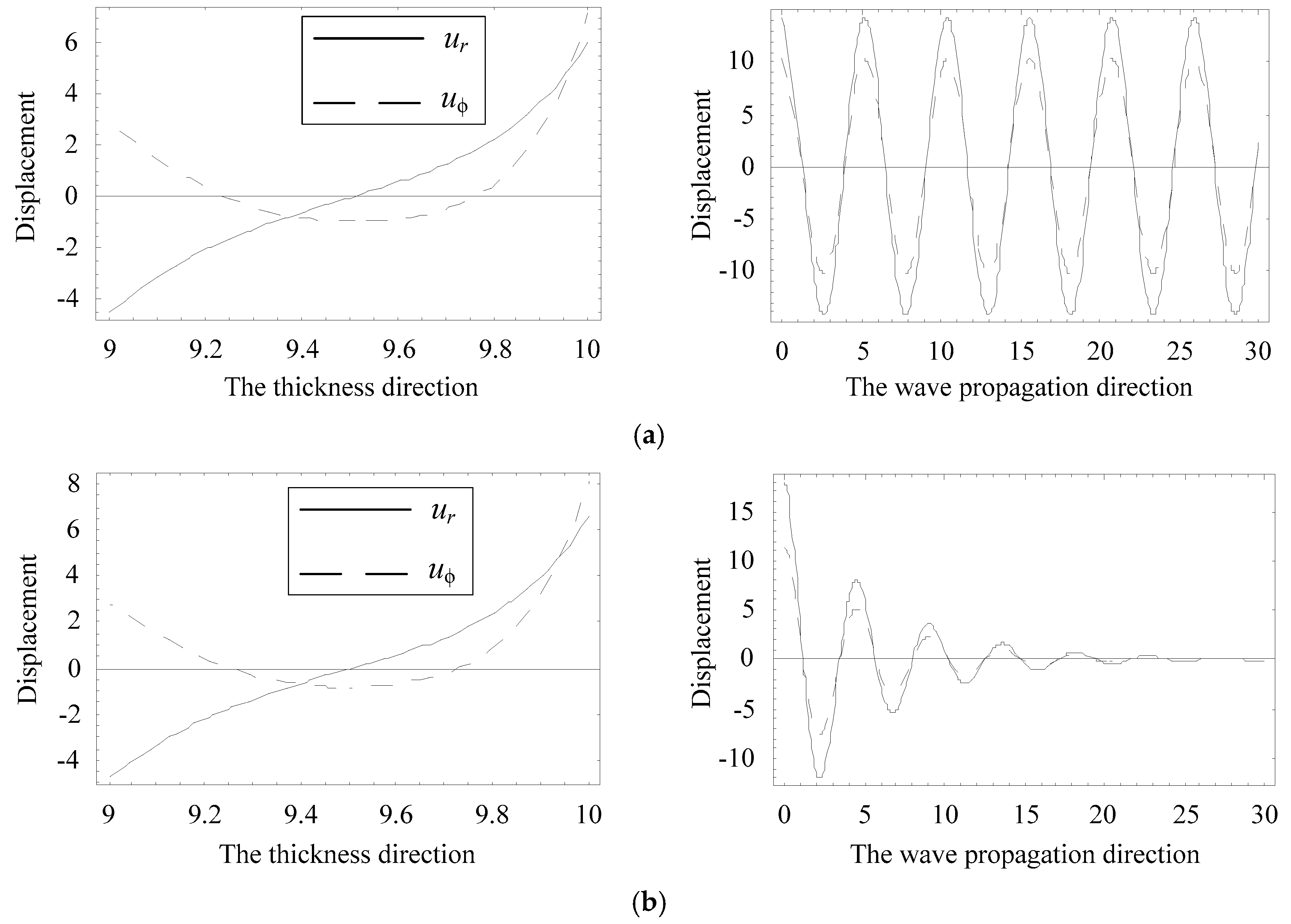
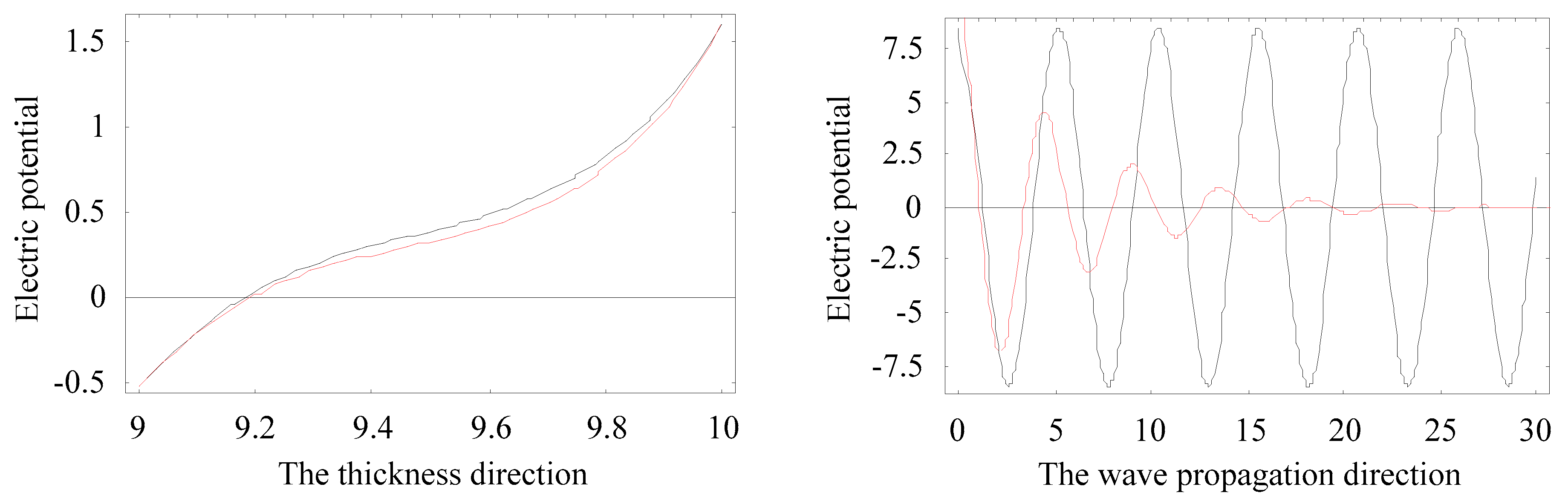
3.5. Displacement and Electric Potential Fields
4. Conclusions
- (1)
- The presented method can transform the set of differential wave equations into an eigenvalue problem, thus obtaining the complete solution straightforwardly, which avoids the iterative search procedure of the traditional methods to find the complex roots;
- (2)
- Some complex branches of the Lamb-like waves can propagate a quite long distance (more than 10 times the plate thickness). These modes will turn into the propagating modes with increasing frequency. Complex non-propagating modes exhibit both local vibration and local propagation, and purely imaginary non-propagating modes exhibit only local vibration and no local propagation;
- (3)
- Some non-propagating modes have a noticeably higher phase velocity than the propagating modes. Also, the wave dispersion of the non-propagating mode is quite weak in a certain frequency range;
- (4)
- The piezoelectricity, graded field, and mechanical and electrical boundary conditions have significant influences on non-propagating waves.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Alleyne, D.; Cawley, P. The interaction of lamb waves with defects. IEEE Trans Ultrason. Ferroelectr. Freq. Control. 1992, 39, 381–397. [Google Scholar] [CrossRef] [PubMed]
- Castaings, M.; Cawley, P. The generation, propagation, and detection of Lamb waves in plates using air-coupled ultrasonic transducers. J. Acoust. Soc. Am. 1996, 100, 3070–3077. [Google Scholar] [CrossRef]
- Pagneux, V. Revisiting the edge resonance for Lamb waves in a semi-infinite plate. J. Acoust. Soc. Am. 2006, 120, 649–656. [Google Scholar] [CrossRef]
- Lawrie, J.B.; Kaplunov, J. Edge waves and resonance on elastic structures: An overview. Math. Mech. Solids. 2011, 17, 4–16. [Google Scholar] [CrossRef]
- Puzyrev, V.; Storozhev, V. Wave propagation in axially polarized piezoelectric hollow cylinders of sector cross section. J. Sound Vib. 2011, 330, 4508–4518. [Google Scholar] [CrossRef]
- Qiu, J.; Tani, J.; Ueno, T.; Morita, T.; Takahashi, H.; Du, H. Fabrication and high durability of functionally graded piezoelectric bending actuators. Smart Mater. Struct. 2003, 12, 115–121. [Google Scholar] [CrossRef]
- Cao, X.S.; Jin, F.; Wang, Z.K. Theoretical investigation on horizontally shear waves in a functionally gradient piezoelectric material plate. Adv. Mater. Res. 2008, 33–37, 707–712. [Google Scholar] [CrossRef]
- Collet, B.; Destrade, M.; Maugin, G.A. Bleustein–Gulyaev waves in some functionally graded materials. Eur. J. Mech. 2006, 25, 695–706. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.S.; Shi, J.P.; Jin, F. Lamb wave propagation in the functionally graded piezoelectric-piezomagnetic material plate. Acta Mech. 2012, 223, 1081–1091. [Google Scholar] [CrossRef]
- Wu, B.; Yu, J.G.; He, C.F. Wave propagation in non-homogeneous magneto-electro-elastic plates. J. Sound Vib. 2008, 317, 250–264. [Google Scholar]
- Othmani, C.; Takali, F.; Njeh, A.; Ghozlen, M.H.B. Numerical simulation of Lamb waves propagation in a functionally graded piezoelectric plate composed of GaAs-AlAs materials using Legendre polynomial approach. Opt. Int. J. Light Electron Opt. 2017, 142, 401–411. [Google Scholar] [CrossRef]
- Han, X.; Liu, G.R. Elastic waves in a functionally graded piezoelectric cylinder. Smart Mater. Struct. 2003, 12, 962–971. [Google Scholar] [CrossRef]
- Qian, Z.-H.; Jin, F.; Lu, T.; Kishimoto, K. Transverse surface waves in an FGM layered structure. Acta Mech. 2009, 207, 183–193. [Google Scholar] [CrossRef]
- Sahu, S.A.; Singhal, A.; Chaudhary, S. Surface wave propagation in functionally graded piezoelectric material: An analytical solution. J. Intell. Mater. Syst. Struct. 2018, 29, 423–437. [Google Scholar] [CrossRef]
- Chakraborty, A. Wave Propagation in Porous Piezoelectric Media. Comput. Model. Eng. Sci. 2009, 40, 105–132. [Google Scholar]
- Amor, M.B.; Salah, I.B.; Ghozlen, M.H.B. Propagation behavior of lamb waves in functionally graded piezoelectric plates. Acta Acust. United Acust. 2015, 101, 435–442. [Google Scholar] [CrossRef]
- Lyon, R.H. Response of an Elastic Plate to Localized Driving Forces. J. Acoust. Soc. Am. 1955, 27, 259–265. [Google Scholar] [CrossRef]
- Mindlin, R.D. Waves and vibrations in isotropic, elastic plates. Struct. Mech. 1960, 199–232. [Google Scholar]
- Pagneux, V.; Maurel, A. Determination of Lamb mode eigenvalues. J. Acoust. Soc. Am. 2001, 110, 1307–1314. [Google Scholar] [CrossRef] [PubMed]
- Quintanilla, F.H.; Lowe, M.J.S.; Craster, R.V. Full 3D dispersion curve solutions for guided waves in generally anisotropic media. J. Sound Vib. 2016, 363, 545–559. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Wang, J.; Du, J.; Yang, J. Propagation of shear-horizontal waves in piezoelectric plates of cubic crystals. Arch. Appl. Mech. 2016, 86, 517–528. [Google Scholar] [CrossRef]
- Daros, C.H. On modelling SH-waves in a class of inhomogeneous anisotropic media via the Boundary Element Method. ZAMM J. Appl. Math. Mech. 2010, 90, 113–121. [Google Scholar] [CrossRef]
- Yan, X.; Yuan, F.G. A semi-analytical approach for SH guided wave mode conversion from evanescent into propagating. Ultrasonics 2018, 84, 430–437. [Google Scholar] [CrossRef] [PubMed]
- Dubuc, B.; Ebrahimkhanlou, A.; Salamone, S. Computation of propagating and non-propagating guided modes in nonuniformly stressed plates using spectral methods. J. Acoust. Soc. Am. 2018, 143, 3220. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Yu, J.G.; Zhang, X.M.; Ming, P.M. Complex guided waves in functionally graded piezoelectric cylindrical structures with sectorial cross-section. Appl. Math. Model. 2018, 63, 288–302. [Google Scholar] [CrossRef]
- Zhang, X.M.; Li, Z.; Yu, J.G. The Computation of complex dispersion and properties of evanescent Lamb wave in Functionally graded piezoelectric-piezomagnetic plates. Materials 2018, 11, 1186. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre, J.E.; Yu, J.G.; Ratolojanahary, F.E.; Elmaimouni, L.; Xu, W.J.; Gryba, T. Mapped orthogonal functions method applied to acoustic waves-based devices. AIP Adv. 2016, 6, 065307. [Google Scholar] [CrossRef] [Green Version]
- Dahmen, S.; Amor, M.; Ghozlen, M.H.B. Investigation of the coupled Lamb waves propagation in viscoelastic and anisotropic multilayer composites by Legendre polynomial method. Compos. Struct. 2016, 153, 57–568. [Google Scholar] [CrossRef]
- Onoe, M.; Mcniven, H.D.; Mindlin, R.D. Dispersion of Axially Symmetric Waves in Elastic Rods. J. Appl. Mech. 1962, 29, 729–734. [Google Scholar] [CrossRef]


| Property | C11 | C12 | C13 | C22 | C23 | C33 | C44 | C55 | C66 |
| Ba2NaNb5O15 | 23.9 | 10.4 | 5.0 | 24.7 | 5.2 | 13.5 | 6.5 | 6.6 | 7.6 |
| PZT-4 | 13.9 | 7.8 | 7.4 | 13.9 | 7.4 | 11.5 | 2.56 | 2.56 | 3.05 |
| e15 | e24 | e31 | e32 | e33 | ϵ11 | ϵ22 | ϵ33 | ρ | |
| Ba2NaNb5O15 | 2.8 | 3.4 | −0.4 | −0.3 | 4.3 | 196 | 201 | 28 | 5.3 |
| PZT-4 | 12.7 | 12.7 | −5.2 | −5.2 | 15.1 | 650 | 650 | 560 | 7.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Liang, S.; Han, X.; Li, Z. Computation of Propagating and Non-Propagating Lamb-Like Wave in a Functionally Graded Piezoelectric Spherical Curved Plate by an Orthogonal Function Technique. Materials 2018, 11, 2363. https://doi.org/10.3390/ma11122363
Zhang X, Liang S, Han X, Li Z. Computation of Propagating and Non-Propagating Lamb-Like Wave in a Functionally Graded Piezoelectric Spherical Curved Plate by an Orthogonal Function Technique. Materials. 2018; 11(12):2363. https://doi.org/10.3390/ma11122363
Chicago/Turabian StyleZhang, Xiaoming, Shunli Liang, Xiaoming Han, and Zhi Li. 2018. "Computation of Propagating and Non-Propagating Lamb-Like Wave in a Functionally Graded Piezoelectric Spherical Curved Plate by an Orthogonal Function Technique" Materials 11, no. 12: 2363. https://doi.org/10.3390/ma11122363





