Phase Change Material Used for Masonry Joints to Reduce the Thermal Bridge Effect
Abstract
:1. Introduction
1.1. Importance of Energy Conservation and Emissions Reduction
1.2. Literature Review
1.3. Research Ideas in This Paper
2. Materials and Methods
2.1. Introduction of Materials and the Wall Structures
2.2. Traditional Theoretical Equation for the Wall Heat Transfer Coefficient
2.3. The Derived Equation for the Wall Steady-State Heat Transfer Coefficient
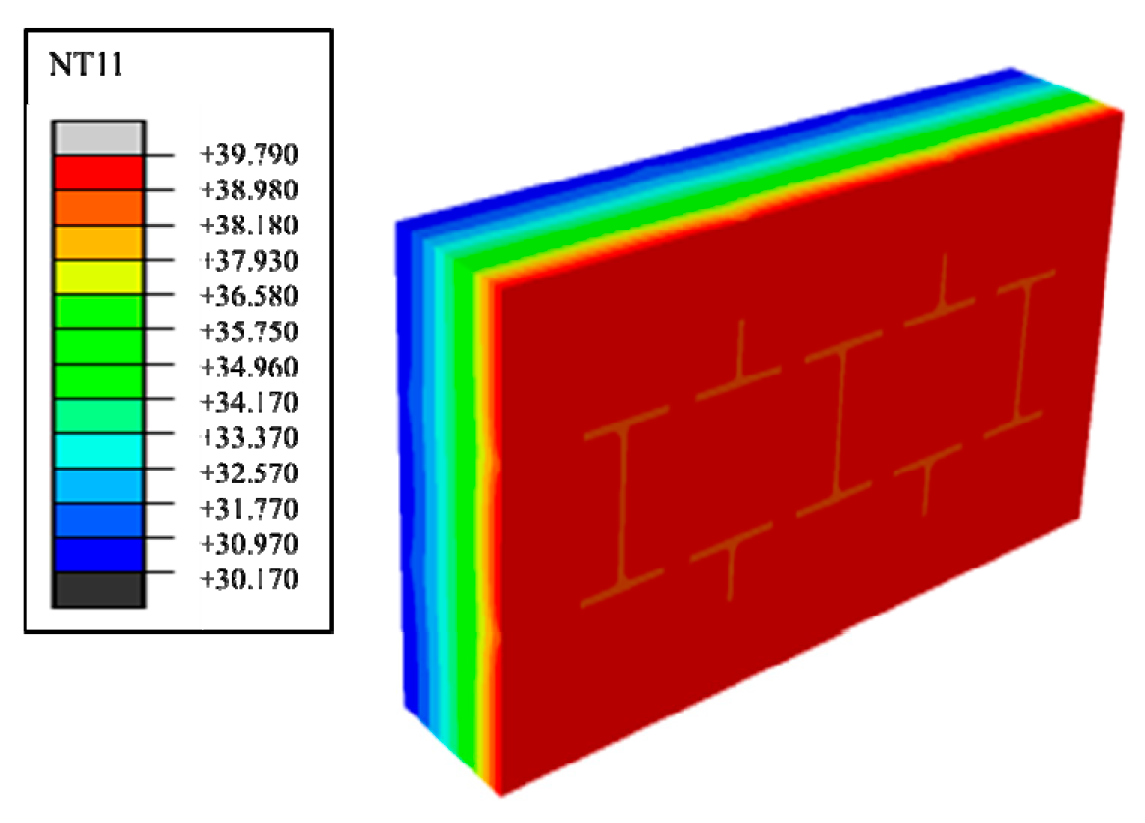
- In Equation (2), and are the temperature boundary conditions of the outer and inner surfaces of the wall, whose values are 40 °C and 30 °C, respectively. The initial temperature of the wall parts is the same as the inner surface temperature. In the process of a numerical calculation of wall parts using a finite element analysis, the research object is divided into a large number of micro-elements, and the entire heat transfer situation can be reflected by the interference superposition of the heat transfer situation of countless elements that are in steady state. Therefore, the derived heat transfer coefficient equation can be deduced reversibly by using the element mean given in the field output of the finite element analysis software as follows:
- In Equation (3), the average heat transfer (QAHF) of a single grid integral point under steady state of the wall is Watt, which is directly given by the output file of the finite element analysis software field; and are the number of grids in the direction of the thickness and height extension paths of the wall, respectively; and is the temperature range between the inner and outer surface of the wall in steady state.
2.4. The Derived Equation for Transient Heat Transfer Coefficient in the PCM Wall
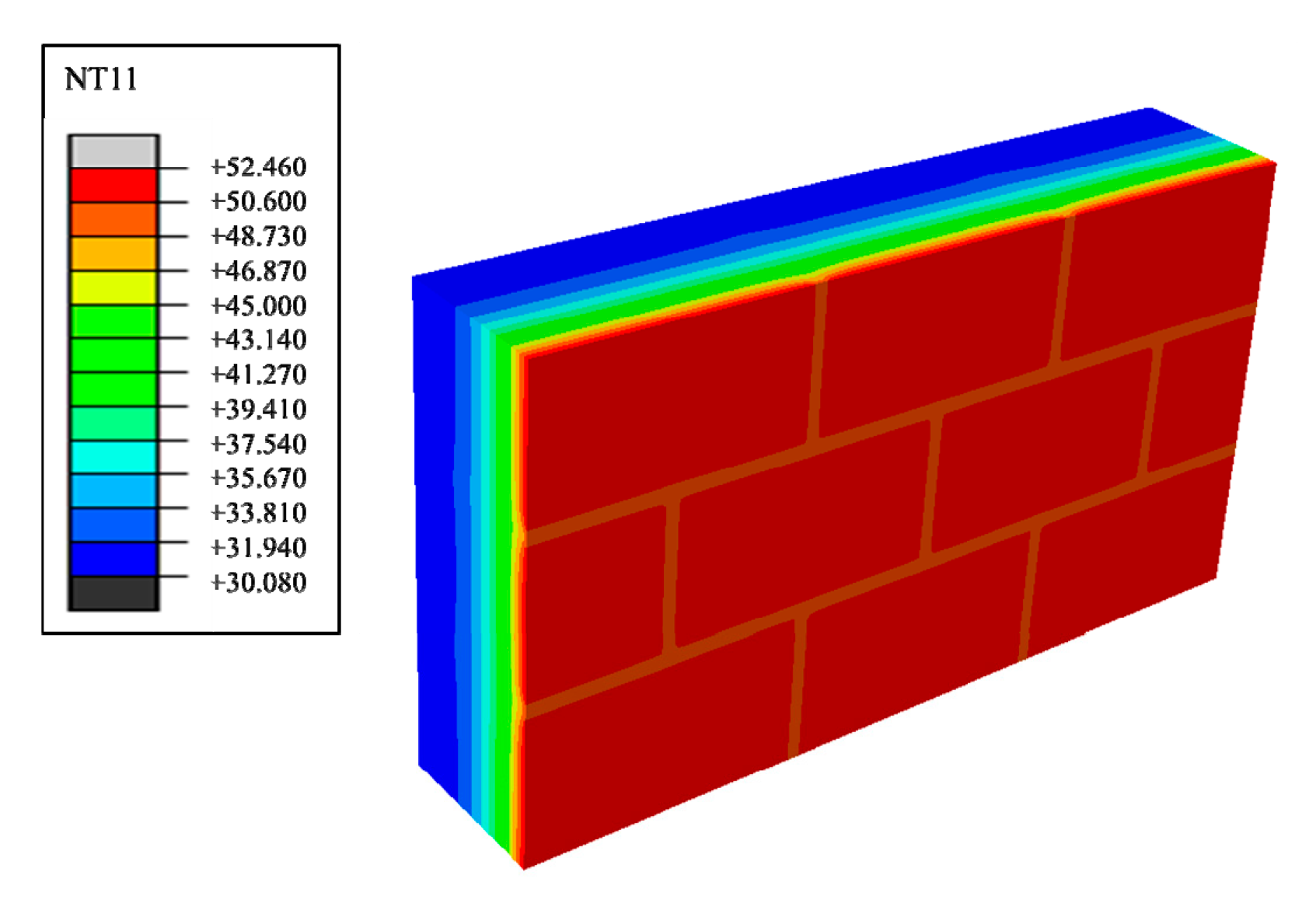
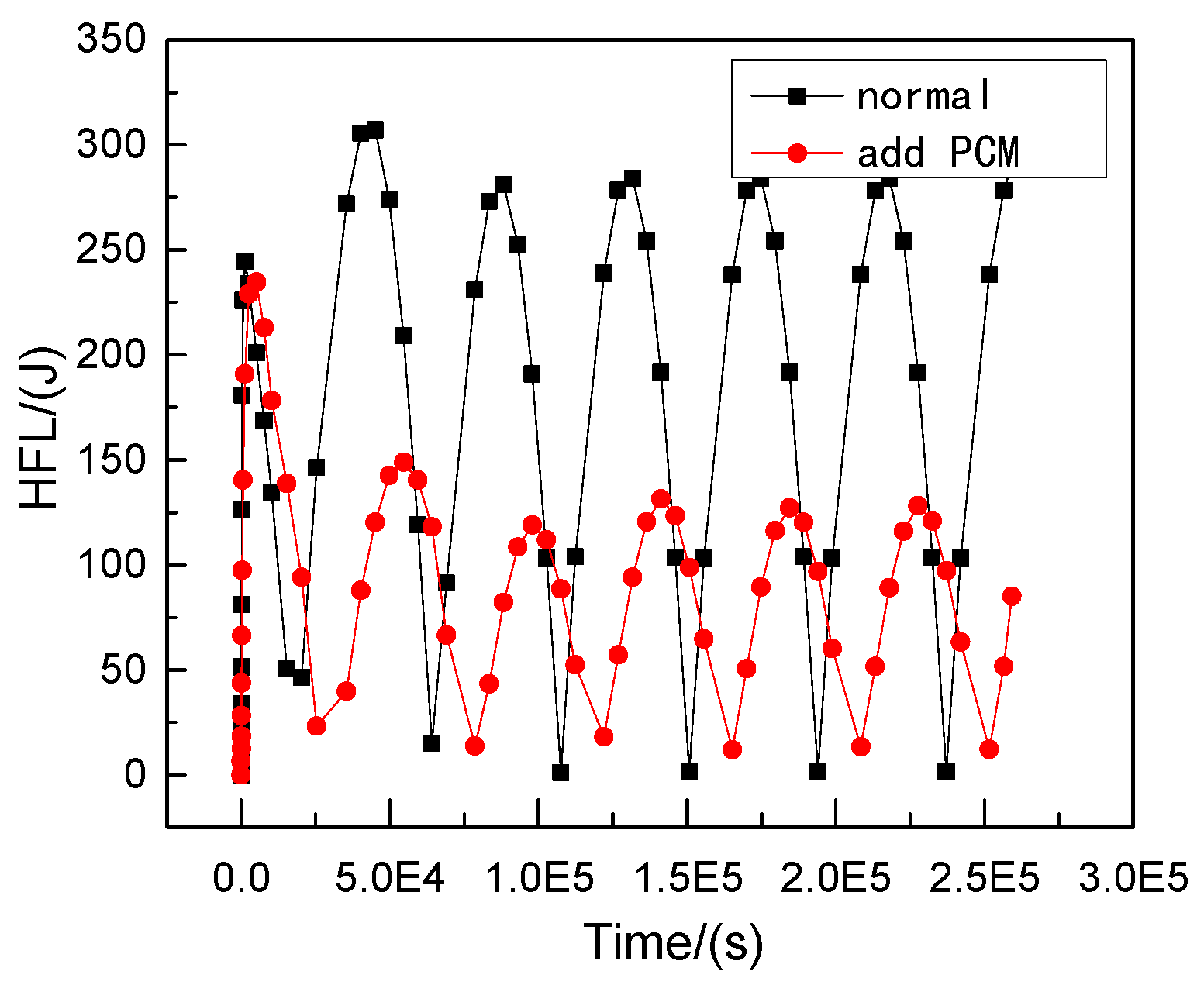
- In Equation (4), is the total heat flux from the outer wall to the inner wall in a single period after the transient heat transfer temperature waveform changes stably, J/m2; is the calculating effective time period, s.On the basis of model 2, the transient temperature boundary conditions are set as follows:
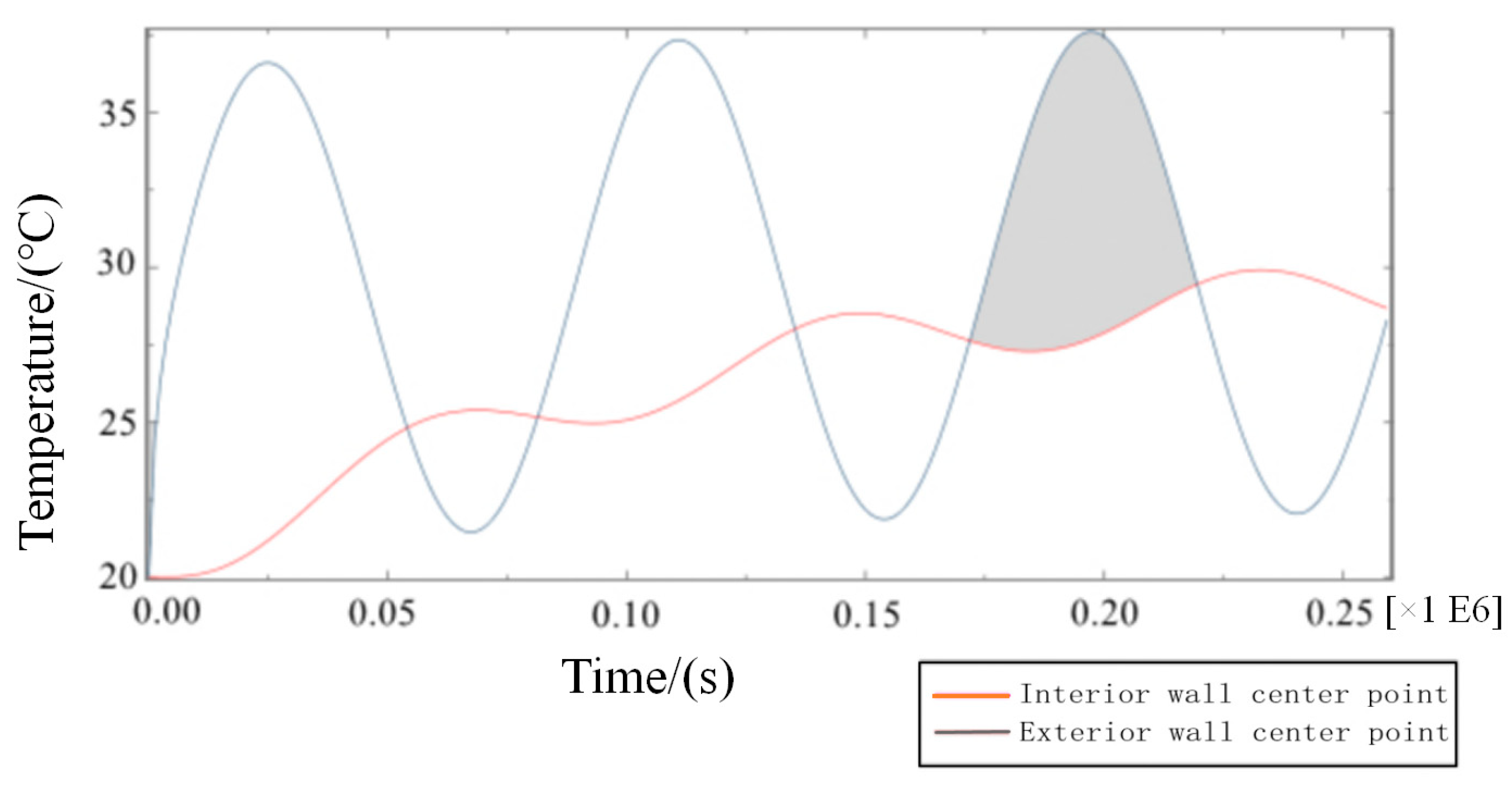
- In Equation (5), the amplitude of the periodic function A = 10, the intercept C = 30, the integral refers to the ambient temperature of the external wall as a reference, and 10 °C is the up and down vibration amplitude fluctuation. Additionally, the initial phase is zero, referring to when t = 86,400 s, and the vibration completes a cycle to simulate the actual service time state from 6 a.m. to 6 a.m. the next day. To determine a reasonable cycle period in the study, the characteristic temperature curve is obtained by numerical calculation for the total step size of six days, as shown in Figure 9.
- From Figure 9, the following waveforms are almost unchanged from the third waveform, that is, when the cycle period is ≥3 days, the fluctuation range of temperature inside the wall tends to be stable because the true value of temperature cycle in the actual environment is ≤3 days. The maximum temperature difference in the process of heat transfer in the wall direction is the duration of the heat transfer process from the outer wall to the inner wall in a single cycle after the transient heat transfer temperature waveform changes stably, as shown in the shadowed area of the third cycle of the curve of the temperature change between the feature points of the outer wall and the feature points (the center of masonry joints) of the inner wall in Figure 10.
3. Results
3.1. High Temperature Phase Change Material’s Proportion
3.2. Low Temperature Phase Change Material’s Proportion
- Equation (9) reflects the linear correlation between the correction coefficient of the transient heat transfer and the proportion of a cryogenic phase change material. This equation is referred to as the characteristic curve of the proportion of a cryogenic phase change material-heat transfer coefficient. The definition domain of the proportion x is (0 < x < 25), and it can be determined from the figure that when the proportion of decanoic acid is 0%, the intercept obtained is 0.4958 (W·m−2·°C−1) when there is no phase change material, which is slightly different from the intercept of the characteristic curve of the decanoic acid’s proportion-heat transfer coefficient, and the latter is closer to the transient heat transfer coefficient. It can be seen that the correction of the transient heat transfer coefficient of wall parts containing phase change materials at a high temperature is more accurate than that of wall parts containing phase change materials at a low temperature.
4. Discussion
5. Conclusions
- The transient heat transfer coefficient has been developed that can be used to characterize the heat preservation performance of wall parts under transient heat transfer. After adding phase change materials, such as decanoic acid, the correction method of the value is determined, and the transient correction heat transfer coefficient is obtained.
- The larger the temperature range of the phase change material is as a sub-range of the environmental temperature range, the better the effect of the phase change material is, and the range of the phase change material is unaffected by its location in the temperature range.
- The larger the mass fraction of the phase change material is in the composite phase change mortar, the more the heat preservation performance of the wall parts is improved, and the linear relationship is satisfied.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| the internal surface coefficient of heat transfer (8.7 W·m−2·°C−1) | |
| the external surface coefficient of heat transfer (19 W·m−2·°C−1) | |
| the thermal conductivity of the blocks (W·m−1·°C−1) | |
| the thermal conductivity of masonry joints (W·m−1·°C−1) | |
| the length of the wall (mm) | |
| the height of the wall (mm) | |
| the width of the wall (mm) | |
| the width of masonry joints (mm) | |
| the temperature boundary condition of the outer surface of the wall (°C) | |
| the temperature boundary condition of the inner surface of the wall (°C) | |
| the average heat transfer of a single grid integral point under steady state of the wall (W) | |
| the number of grids in the direction of the thickness extension paths of the wall (1) | |
| the number of grids in the direction of the height extension paths of the wall (1) | |
| temperature range between the inner and outer surface of the wall under steady state (°C) | |
| the total heat flux from the outer wall to the inner wall in a single period after the transient heat transfer temperature waveform changes stably (J·m−2) | |
| the latent heat flux from the outer wall to the inner wall in a single period after the transient heat transfer temperature waveform changes stably (J·m−2) | |
| the theoretical heat transfer coefficient of the wall under steady state (W·m−2·°C−1) | |
| the heat transfer resistance of the wall under steady state (W−1·m2·°C) | |
| the numerical heat transfer coefficient of the wall under steady state (W·m−2·°C−1) | |
| the numerical heat transfer coefficient of the model under steady state (W·m−2·°C−1) | |
| the corrected numerical heat transfer coefficient of the model under steady state (W·m−2·°C−1) | |
| the calculating effective time period (s) |
References
- Vanmarcke, E.M.; Shinozuka, M.; Nakagiri, S.; Schueller, G.I.; Grigoriu, M. Random-fields and stochastic finite-element. Struct. Saf. 1986, 3, 143–166. [Google Scholar] [CrossRef]
- Zhou, D.; Eames, P. Phase Change Material Wallboard (PCMW) melting temperature optimisation for passive indoor temperature control. Renew. Energy 2019, 139, 507–514. [Google Scholar] [CrossRef]
- Liu, L.; Xiang, M.; Lyu, D.; Men, Y. Encapsulation of polar phase change materials via multiemulsification and crosslinking method and its application in building. J. Appl. Polym. Sci. 2019, 136, 47837. [Google Scholar] [CrossRef]
- Yao, C.; Kong, X.; Li, Y.; Du, Y.; Qi, C. Numerical and experimental research of cold storage for a novel expanded perlite-based shape-stabilized phase change material wallboard used in building. Energy Convers. Manag. 2018, 155, 20–31. [Google Scholar] [CrossRef]
- Forzano, C.; Baggio, P.; Buonomano, A.; Palombo, A. Building integrating phase change materials: A dynamic hygrothermal simulation model for system analysis. J. Sustain. Dev. Energy Water Environ. Syst. -Jsdewes 2019, 7, 325–342. [Google Scholar] [CrossRef]
- Kuznik, F.; Virgone, J.; Noel, J. Optimization of a phase change material wallboard for building use. Appl. Therm. Eng. 2008, 28, 1291–1298. [Google Scholar] [CrossRef] [Green Version]
- Diaconu, B.M.; Cruceru, M. Novel concept of composite phase change material wall system for year-round thermal energy savings. Energy Build. 2010, 42, 1759–1772. [Google Scholar] [CrossRef]
- Hadjieva, M.; Kanev, S.; Argirov, J. Thermophysical properties of some paraffins applicable to thermal energy storage. Sol. Energy Mater. Sol. Cells 1992, 27, 181–187. [Google Scholar] [CrossRef]
- Hunter, L.W.; Kuttler, J.R. The enthalpy method for heat conduction problems with moving boundaries. J. Heat Transf. 1989, 111, 239–242. [Google Scholar] [CrossRef]
- Ahmad, M.; Bontemps, A.; Sallée, H.; Quenard, D. Experimental investigation and computer simulation of thermal behaviour of wallboards containing a phase change material. Energy Build. 2006, 38, 357–366. [Google Scholar] [CrossRef]
- Aadmi, M.; Karkri, M.; El Hammouti, M. Heat transfer characteristics of thermal energy storage of a composite phase change materials: Numerical and experimental investigations. Energy 2014, 72, 381–392. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, Y.; Wang, X.; Lin, K.; Xiao, W. An assessment of mixed type PCM-gypsum and shape-stabilized PCM plates in a building for passive solar heating. Sol. Energy 2007, 81, 1351–1360. [Google Scholar] [CrossRef]
- Zhu, N.; Hu, P.; Xu, L. A simplified dynamic model of double layers shape-stabilized phase change materials wallboards. Energy Build. 2013, 67, 508–516. [Google Scholar] [CrossRef]
- Zhu, N.; Liu, P.; Hu, P.; Liu, F.; Jiang, Z. Modeling and simulation on the performance of a novel double shape-stabilized phase change materials wallboard. Energy Build. 2015, 107, 181–190. [Google Scholar] [CrossRef]
- Zhu, N.; Liu, P.; Liu, F.; Hu, P.; Wu, M. Energy performance of double shape-stabilized phase change materials wallboards in office building. Appl. Therm. Eng. 2016, 105, 180–188. [Google Scholar] [CrossRef]
- Costanzo, V.; Evola, G.; Marletta, L.; Nocera, F. The effectiveness of phase change materials in relation to summer thermal comfort in air-conditioned office buildings. Build. Simul. 2018, 11, 1145–1161. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB 50176-2016 Code for Thermal Design of Civil Building, 2nd ed.; China Building Industry Press: Beijing, China, 2016; pp. 11–16.














| Material | Density/(kg·m−3) | Thermal Conductivity/(W·m−1·°C−1) | Latent Heat/(J·kg−1) | Specific Heat/(J·kg−1·°C−1) |
|---|---|---|---|---|
| Decanoic acid | 880 | 0.20 | 5000 | / |
| Mortar | 2000 | 0.87 | / | 820 |
| Slag brick | 400 | 0.07 | / | 800 |
| Concrete | 2500 | 1.74 | / | 920 |
| Lightweight insulating brick | 800 | 0.26 | / | 840 |
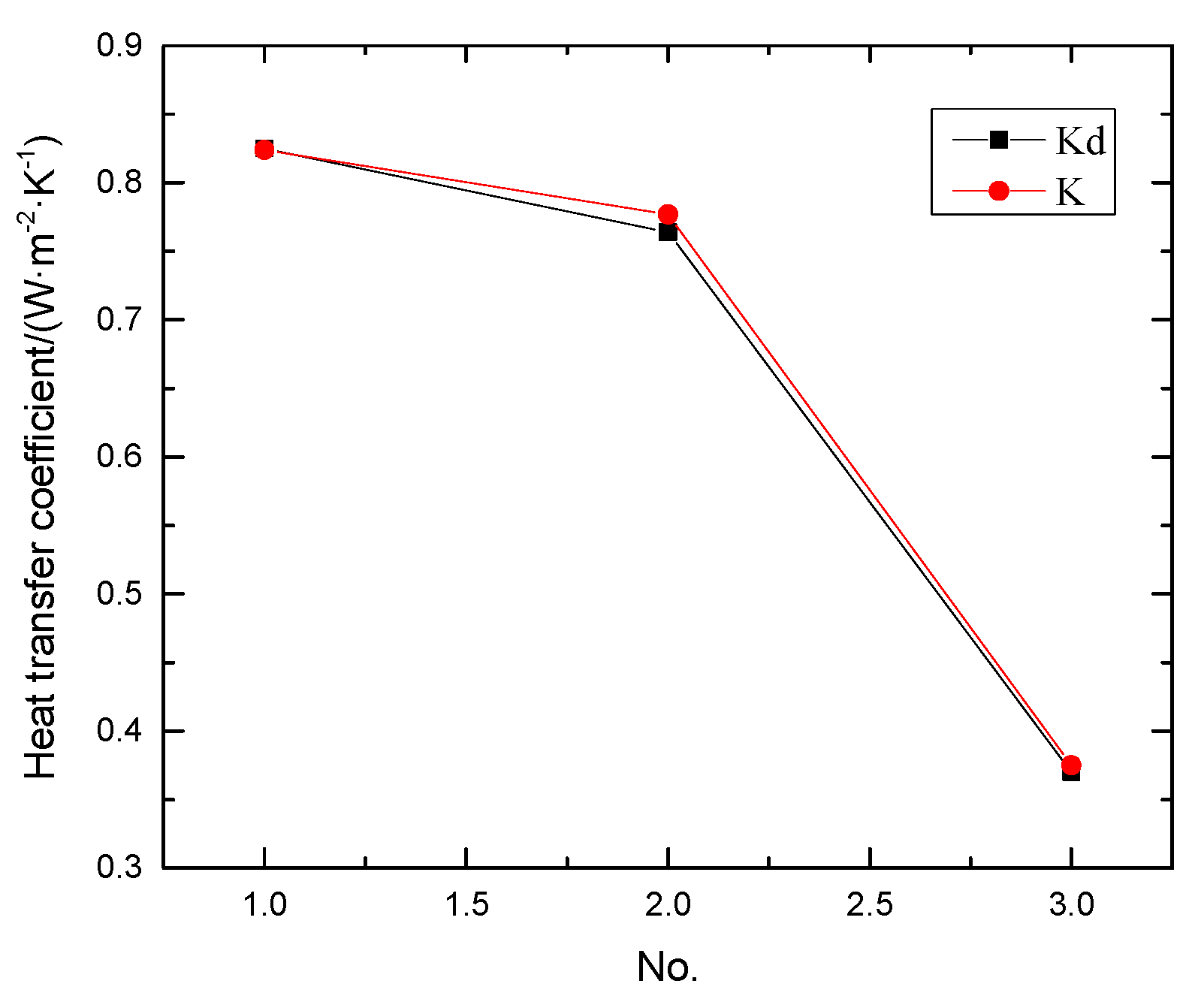
| No. | Material | K/(W·m−2·°C−1) | QAHF/(W) | Kd/(W·m−2·°C−1) |
|---|---|---|---|---|
| 1 | Mortar, lightweight insulating brick and concrete | 0.824 | 0.041 | 0.825 |
| 2 | Mortar, concrete and slag brick | 0.777 | 0.038 | 0.764 |
| 3 | Mortar, lightweight insulating brick and slag brick | 0.375 | 0.018 | 0.370 |
| Proportion/(%) | Q/(J·m−2) | Compound Latent Heat/(J·kg−1) | Km′/(W·m−2·°C−1) |
|---|---|---|---|
| 2 | 251,361.77 | 2857 | 0.4602 |
| 2.5 | 249,415.34 | 3571 | 0.4554 |
| 3 | 247,872.41 | 4286 | 0.4511 |
| 3.5 | 246,735.02 | 5000 | 0.4477 |
| 4 | 244,682.50 | 5714 | 0.4425 |
| 4.5 | 242,945.82 | 6429 | 0.4380 |
| 5 | 239,951.68 | 7143 | 0.4311 |
| Proportion/(%) | Q/(J·m−2) | Compound Latent Heat/(J·kg−1) | /(W·m−2·°C−1) |
|---|---|---|---|
| 5 | 86,740.399 | 2500 | 0.4680 |
| 10 | 84,398.755 | 5000 | 0.4411 |
| 15 | 81,750.851 | 7500 | 0.4125 |
| 20 | 79,462.629 | 10,000 | 0.3859 |
| 25 | 76,886.171 | 12,500 | 0.3577 |
| /(°C) | /(°C) | /(°C) | /(s) | Stabilized Wall Centre Temperature/(°C) | Stabilized Masonry Joints Centre Temperature/(°C) |
|---|---|---|---|---|---|
| 30 | 40 | 7 | 133,200 | 34.913 | 34.921 |
| 33 | 40 | 5.5 | 128,400 | 34.939 | 34.959 |
| 30 | 37 | 5.5 | 128,400 | 34.942 | 34.960 |
| 35 | 40 | 3.5 | 124,800 | 34.975 | 35.002 |
| 30 | 35 | 3.5 | 124,800 | 34.969 | 34.991 |
| 37 | 40 | 1.5 | 123,600 | 35.258 | 35.588 |
| 30 | 33 | 1.5 | 123,600 | 35.306 | 35.705 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W.; Liu, D. Phase Change Material Used for Masonry Joints to Reduce the Thermal Bridge Effect. Materials 2019, 12, 1895. https://doi.org/10.3390/ma12121895
Jiang W, Liu D. Phase Change Material Used for Masonry Joints to Reduce the Thermal Bridge Effect. Materials. 2019; 12(12):1895. https://doi.org/10.3390/ma12121895
Chicago/Turabian StyleJiang, Wei, and Dan Liu. 2019. "Phase Change Material Used for Masonry Joints to Reduce the Thermal Bridge Effect" Materials 12, no. 12: 1895. https://doi.org/10.3390/ma12121895





