An Anisotropic Auxetic 2D Metamaterial Based on Sliding Microstructural Mechanism
Abstract
:1. Introduction
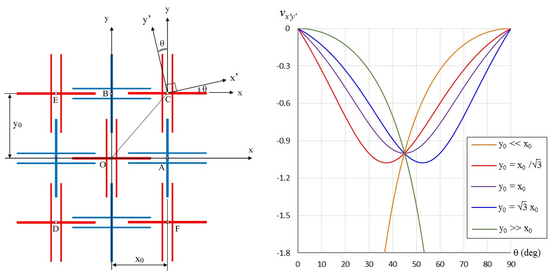
2. Analysis
3. Results and Discussion
4. Conclusions
Funding
Conflicts of Interest
Appendix A

References
- Lakes, R. Foam structures with negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Lakes, R. Negative Poisson’s ratio materials. Science 1987, 238, 551. [Google Scholar] [CrossRef] [PubMed]
- Wojciechowski, K.W. Constant thermodynamic tension Monte-Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Two-dimensional isotropic system with a negative Poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Wojciechowski, K.W.; Branka, A.C. Negative Poisson ratio in a two-dimensional ‘‘isotropic’’ solid. Phys. Rev. A 1989, 40, 7222–7225. [Google Scholar] [CrossRef]
- Choi, J.B.; Lakes, R.S. Design of a fastener based on negative Poisson’s ratio foam. Cell. Polym. 1991, 10, 205–212. [Google Scholar]
- Caddock, B.D.; Evans, K.E. Negative Poisson ratios and strain-dependent mechanical properties in arterial prostheses. Biomaterials 1995, 16, 1109–1115. [Google Scholar] [CrossRef]
- Martz, E.O.; Lakes, R.S.; Goel, V.K.; Park, J.B. Design of an artificial intervertebral disc exhibiting a negative Poisson’s ratio. Cell. Polym. 2005, 24, 127–138. [Google Scholar] [CrossRef]
- Dolla, W.J.S.; Fricke, B.A.; Becker, B.R. Structural and drug diffusion models of conventional and auxetic drug-eluting stents. J. Med. Dev. 2007, 1, 47–55. [Google Scholar] [CrossRef]
- Scarpa, F. Auxetic materials for bioprostheses. IEEE Signal Process. Mag. 2008, 25, 125–126. [Google Scholar] [CrossRef]
- Lakes, R.S.; Lowe, A. Negative Poisson’s ratio foam as seat cushion material. Cell. Polym. 2000, 19, 157–167. [Google Scholar]
- Wang, Y.C.; Lakes, R.S. Analytical parametric analysis of the contact problem of human buttocks and negative Poisson’s ratio foam cushions. Int. J. Solids Struct. 2002, 39, 4825–4838. [Google Scholar] [CrossRef]
- Alderson, A.; Rasburn, J.; Ameer-Bag, S.; Mullarkey, P.G.; Perrie, W.; Evans, K.E. An auxetic filter: A tuneable filter displaying enhanced size selectivity or defouling properties. Ind. Eng. Chem. Res. 2000, 39, 654–655. [Google Scholar] [CrossRef]
- Alderson, A.; Davies, P.J.; Evans, K.E.; Alderson, K.L.; Grima, J.N. Modelling of the mechanical and mass transport properties of auxetic molecular sieves: An idealised inorganic (zeolitic) host-guest system. Mol. Simul. 2005, 31, 889–896. [Google Scholar] [CrossRef]
- Alderson, A.; Davies, P.J.; Williams, M.R.; Evans, K.E.; Alderson, K.L.; Grima, J.N. Modelling of the mechanical and mass transport properties of auxetic molecular sieves: An idealised organic (polymeric honeycomb) host-guest system. Mol. Simul. 2005, 31, 897–905. [Google Scholar] [CrossRef]
- Lim, T.C.; Acharya, R.U. Performance Evaluation of Auxetic Molecular Sieves with Re-Entrant Structures. J. Biomed. Nanotechnol. 2010, 6, 718–724. [Google Scholar] [CrossRef]
- Scarpa, F.; Giacomin, J.; Zhang, Y.; Pastorino, P. Mechanical performance of auxetic polyurethane foam for antivibration glove applications. Cell. Polym. 2005, 24, 253–268. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L. Expanding materials and applications: Exploiting auxetic textiles. Tech. Text. Int. 2005, 14, 29–34. [Google Scholar]
- Park, K.O.; Choi, J.B.; Lee, S.J.; Choi, H.H.; Kim, J.K. Polyurethane foam with Negative Poisson’s ratio for diabetic shoe. Key Eng. Mater. 2005, 288–289, 677–680. [Google Scholar] [CrossRef]
- Ellul, B.; Muscat, M.; Grima, J.N. On the effect of the Poisson’s ratio (positive and negative) on the stability of pressure vessel heads. Phys. Status Solidi B 2009, 246, 2025–2032. [Google Scholar] [CrossRef]
- Salit, V.; Weller, T. On the feasibility of introducing auxetic behavior into thin-walled structures. Acta Mater. 2009, 57, 125–135. [Google Scholar] [CrossRef]
- Whitty, J.P.M.; Henderson, B.; Myler, P.; Chirwa, C. Crash performance of cellular foams with reduced relative density part 2: Rib deletion. Int. J. Crashworthiness 2007, 12, 689–698. [Google Scholar]
- Park, K.O.; Choi, J.B.; Park, J.C.; Park, D.J.; Kim, J.K. An improvement in shock absorbing behavior of polyurethane foam with a negative Poisson effect. Key Eng. Mater. 2007, 342–343, 845–848. [Google Scholar] [CrossRef]
- Shodja, H.M.; Ahmadi, S.F.; Eskandari, M. Boussinesq indentation of a transversely isotropic half-space reinforced by a buried inextensible membrane. Appl. Math. Model. 2014, 38, 2163–2172. [Google Scholar] [CrossRef]
- Ahmadi, S.F.; Samea, P.; Eskandari, M. Axisymmetric response of a bi-material full-space reinforced by an interfacial thin film. Int. J. Solids Struct. 2016, 90, 251–260. [Google Scholar] [CrossRef]
- Mitschke, H.; Schwerdtfeger, J.; Schury, F.; Stingl, M.; Körner, C.; Singer, R.F.; Robins, V.; Mecke, K.; Schröder-Turk, G.E. Finding auxetic frameworks in periodic tessellations. Adv. Mater. 2011, 23, 2669–2674. [Google Scholar] [CrossRef]
- Mitschke, H.; Robins, V.; Mecke, K.; Schröder-Turk, G.E. Finite auxetic deformations of plane tessellations. Proc. R. Soc. A 2013, 469, 20120465. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R. Perforated sheets exhibiting negative Poisson’s ratios. Adv. Eng. Mater. 2010, 12, 460–464. [Google Scholar] [CrossRef]
- Taylor, M.; Francesconi, L.; Gerendás, M.; Shanian, A.; Carson, C.; Bertoldi, K. Low porosity metallic periodic structures with negative Poisson’s ratio. Adv. Mater. 2014, 26, 2365–2370. [Google Scholar] [CrossRef]
- Francesconi, L.; Taylor, M.; Bertoldi, K.; Baldi, A. Static and modal analysis of low porosity thin metallic auxetic structures using speckle interferometry and digital image correlation. Exp. Mech. 2018, 58, 283–300. [Google Scholar] [CrossRef]
- Jiang, J.W.; Kim, S.Y.; Park, H.S. Auxetic nanomaterials: Recent progress and future development. Appl. Phys. Rev. 2016, 3, 041101. [Google Scholar] [CrossRef] [Green Version]
- Saxena, K.K.; Das, R.; Calius, E.P. Three decades of auxetics research—Materials with negative Poisson’s ratio: A review. Adv. Eng. Mater. 2016, 18, 1847–1870. [Google Scholar] [CrossRef]
- Park, H.S.; Kim, S.Y. A perspective on auxetic nanomaterials. Nano Converg. 2017, 4, 10. [Google Scholar] [CrossRef] [PubMed]
- Lim, T.C. Analogies across auxetic models based on deformation mechanism. Phys. Status Solidi RRL 2017, 11, 1600440. [Google Scholar] [CrossRef]
- Kolken, H.M.A.; Zadpoor, A.A. Auxetic mechanical metamaterials. RSC Adv. 2017, 7, 5111–5129. [Google Scholar] [CrossRef] [Green Version]
- Lakes, R.S. Negative-Poisson’s-ratio materials: Auxetic solids. Ann. Rev. Mater. Res. 2017, 47, 63–81. [Google Scholar] [CrossRef]
- Lim, T.C. Auxetic Materials and Structures; Springer: Singapore, 2015; ISBN 978-981-287-274-6. [Google Scholar]
- Ravirala, N.; Alderson, A.; Alderson, K.L. Interlocking hexagons model for auxetic behavior. J. Mater. Sci. 2007, 42, 7433–7445. [Google Scholar] [CrossRef]
- Alderson, A.; Scarpa, F. We’ve Created a New Vibration-Proof ‘Metamaterial’ That Could Save Premature Babies’ Lives. The Conversation, 2017. Available online: https://theconversation.com/weve-created-a-new-vibration-proof-metamaterial-that-could-save-premature-babies-lives-70872 (accessed on 30 January 2019).
- Lim, T.C. Functionally graded beam for attaining Poisson-curving. J. Mater. Sci. Lett. 2002, 21, 1899–1901. [Google Scholar] [CrossRef]
- Lim, T.C. Shear deformation in beams with negative Poisson’s ratio. J. Mater. Des. Appl. 2015, 229, 447–454. [Google Scholar] [CrossRef]
- Lim, T.C. Torsion of semi-auxetic rods. J. Mater. Sci. 2011, 46, 6904–6909. [Google Scholar] [CrossRef]
- Lim, T.C. Longitudinal wave velocity in auxetic rods. J. Eng. Mater. Technol. 2015, 137, 024502. [Google Scholar] [CrossRef]
- Lim, T.C. Auxeticity of concentric auxetic-conventional foam rods with high modulus interface adhesive. Materials 2018, 11, 223. [Google Scholar] [CrossRef]
- Sobieszczyk, P.; Majka, M.; Kuźma, D.; Lim, T.C.; Zieliński, P. Effect of longitudinal stress on wave propagation in width-constrained elastic plates with arbitrary Poisson’s ratio. Phys. Status Solidi B 2015, 252, 1615–1619. [Google Scholar] [CrossRef]
- Lim, T.C. Bending stresses in triangular auxetic plates. J. Eng. Mater. Technol. 2016, 138, 014501. [Google Scholar] [CrossRef]
- Lim, T.C. Longitudinal wave motion in width-constrained auxetic plates. Smart Mater. Struct. 2016, 25, 054008. [Google Scholar] [CrossRef]
- Lim, T.C. Simply-supported elliptical auxetic plates. J. Mech. 2016, 32, 413–419. [Google Scholar] [CrossRef]
- Lim, T.C. An accurate design equation for the maximum deflection in a class of auxetic sectorial plates. Phys. Status Solidi B 2017, 254, 1600784. [Google Scholar] [CrossRef]
- Lim, T.C. Shear deformation in a class of thick hexagonal plates. Phys. Status Solidi B 2017, 254, 1700014. [Google Scholar] [CrossRef]
- Lim, T.C. Refined shear correction of polygonal plates with static loads. Proc. Inst. Civil Eng. – Eng. Comput. Mech. 2017, 170, 167–173. [Google Scholar] [CrossRef]
- Gorodtsov, V.A.; Lisovenko, D.S.; Lim, T.C. Three-layered plate exhibiting auxeticity based on stretching and bending modes. Compos. Struct. 2018, 194, 643–651. [Google Scholar] [CrossRef]
- Lim, T.C. Spherical auxetic shells. Adv. Mater. Res. 2013, 804, 146–150. [Google Scholar] [CrossRef]
- Lim, T.C. Thermal stresses in auxetic plates and shells. Mech. Adv. Mater. Struct. 2015, 22, 205–212. [Google Scholar] [CrossRef]
- Lim, T.C. Out-of-plane modulus of semi-auxetic laminates. Eur. J. Mech. A Solids 2009, 28, 752–756. [Google Scholar] [CrossRef]
- Lim, T.C. In-plane stiffness of semiauxetic laminates. J. Eng. Mech. 2010, 136, 1176–1180. [Google Scholar] [CrossRef]
- Lim, T.C.; Acharya, U.R. Longitudinal modulus of semi-auxetic unidirectional fiber composites. J. Reinf. Plast. Compos. 2010, 29, 1441–1445. [Google Scholar] [CrossRef]
- Lim, T.C. Coefficient of thermal expansion of stacked auxetic and negative thermal expansion laminates. Phys. Status Solidi B 2011, 248, 140–147. [Google Scholar] [CrossRef]
- Lim, T.C.; Rajendra Acharya, U. Counterintuitive modulus from semi-auxetic laminates. Phys. Status Solidi B 2011, 248, 60–65. [Google Scholar] [CrossRef]
- Lim, T.C. Mixed auxeticity of auxetic sandwich structures. Phys. Status Solidi B 2012, 249, 1366–1372. [Google Scholar] [CrossRef]
- Boldrin, L.; Hummel, S.; Scarpa, F.; Di Maio, D.; Lira, C.; Ruzzene, M.; Remillat, C.D.L.; Lim, T.C.; Rajasekaran, R.; Patsias, S. Dynamic behavior of auxetic gradient composite hexagonal honeycombs. Compos. Struct. 2016, 149, 114–124. [Google Scholar] [CrossRef]
- Lim, T.C. Composite microstructures with Poisson’s ratio sign switching upon stress reversal. Compos. Struct. 2019, 209, 34–44. [Google Scholar] [CrossRef]
- Lim, T.C. 2D structures exhibiting negative area compressibility. Phys. Status Solidi B 2017, 254, 1600682. [Google Scholar] [CrossRef]
- Lim, T.C. Metamaterials with Poisson’s ratio sign toggling by means of microstructural duality. SN Appl. Sci. 2019, 1, 176. [Google Scholar]





© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, T.-C. An Anisotropic Auxetic 2D Metamaterial Based on Sliding Microstructural Mechanism. Materials 2019, 12, 429. https://doi.org/10.3390/ma12030429
Lim T-C. An Anisotropic Auxetic 2D Metamaterial Based on Sliding Microstructural Mechanism. Materials. 2019; 12(3):429. https://doi.org/10.3390/ma12030429
Chicago/Turabian StyleLim, Teik-Cheng. 2019. "An Anisotropic Auxetic 2D Metamaterial Based on Sliding Microstructural Mechanism" Materials 12, no. 3: 429. https://doi.org/10.3390/ma12030429