Application of a New, Energy-Based ΔS* Crack Driving Force for Fatigue Crack Growth Rate Description
Abstract
:1. Introduction
2. Kinetic Fatigue Fracture Diagrams for 10HNAP, 18G2A, and the Eiffel bridge 19th-Century Puddle Iron
3. Conclusions
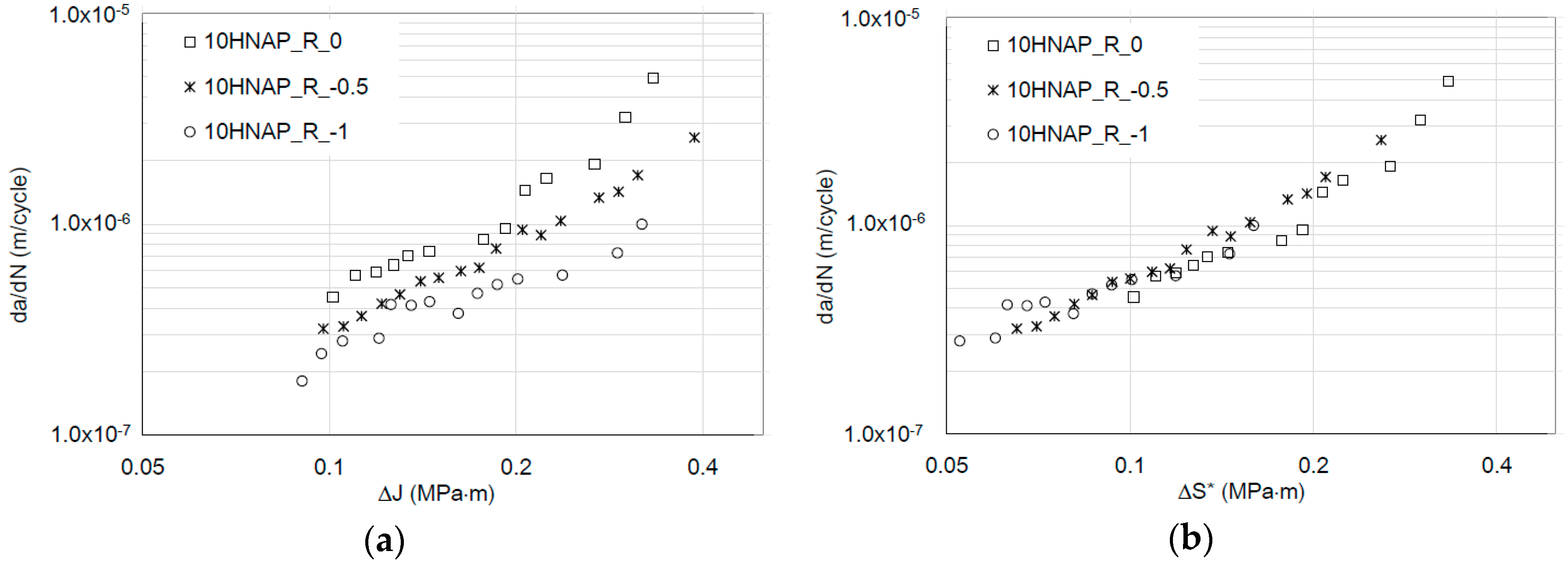
- In contrast to J, S* unambiguously describes the fatigue crack kinetics for 10HNAP and 18G2A steels in the range of non-positive stress ratio R (considering elastic-plastic conditions).
- In contrast to J, S* unambiguously describes the fatigue crack kinetics for 19th-century puddle iron from the Eiffel bridge in the range of positive stress ratio R (considering linear elastic fracture mechanics conditions).
- In each case, the description of KFFD including S* resulted in higher values of R2 data fitting coefficient for the power-law description of the FCGR in the Paris regime.
- A good physical interpretation of S* as opposed to H allows for its easy implementation into the numerical environment.
Funding
Conflicts of Interest
References
- Paris, P.C.; Erdogan, F. A critical analysis of crack propagation laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Forman, R.G.; Kearney, V.E.; Engle, R.M. Numerical analysis of crack propagation in cyclic loaded structures. J. Basic Eng. 1967, 89, 459–463. [Google Scholar] [CrossRef]
- Walker, K. The effect of stress ratio during crack propagation and fatigue for 2024-T3 and 7075-TO Aluminum. ASTM Int. 1970, 462, 1–14. [Google Scholar]
- Elber, W. Fatigue crack closure under cyclic tension. Eng. Fract. Mech. 1970, 2, 37–45. [Google Scholar]
- Forman, R.G.; Mettu, S.R. Behavior of Surface and Corner Cracks Subjected to Tensile and Bending Loads in Ti–6Al–4V Alloy. In Fracture Mechanics: 22nd Symposium; Ernst, H.A., Saxena, A., McDowell, D.L., Eds.; American Society for Testing and Materials: Philadelphia, PA, USA, 1992; Volume 1, pp. 519–546. [Google Scholar]
- Koçak, M. FITNET fitness-for-service procedure: An overview. Weld. World 2007, 51, 94–105. [Google Scholar] [CrossRef]
- Huffman, P.J.; Ferreira, J.; Correia, J.A.F.O.; De Jesus, A.M.P.; Lesiuk, G.; Berto, F.; Glinka, G. Fatigue crack propagation prediction of a pressure vessel mild steel based on a strain energy density model. Frat. Struct. Integrity 2017, 11, 74–84. [Google Scholar] [CrossRef]
- Shi, K.K.; Cai, L.X.; Chen, L.; Wu, S.C.; Bao, C. Prediction of fatigue crack growth based on low cycle fatigue properties. Int. J. Fatigue 2014, 61, 220–225. [Google Scholar] [CrossRef]
- Chen, L.; Cai, L.; Yao, D. A new method to predict fatigue crack growth rate of materials based on average cyclic plasticity strain damage accumulation. Chin. J. Aeronaut. 2013, 26, 130–135. [Google Scholar] [CrossRef] [Green Version]
- Boljanović, S.; Maksimović, S.; Djurić, M. Analysis of crack propagation using the strain energy density method. Sci. Tech. Rev. 2009, 59, 12–17. [Google Scholar]
- Khelil, F.; Aour, B.; Belhouari, M.; Benseddiq, N. Modeling of fatigue crack propagation in aluminum alloys using an energy based approach. Eng. Tech. Appl. Sci. Res. 2013, 3, 488–496. [Google Scholar]
- Hadi Hafezi, M.; Nik Abdullah, N.; Correia, J.F.; De Jesus, A.M. An assessment of a strain-life approach for fatigue crack growth. Int. J. Struct. Integrity 2012, 3, 344–376. [Google Scholar] [CrossRef]
- Correia, J.A.; Jesus, A.M.D.; Ribeiro, A.S.; Fernandes, A.A. Strain-based approach for fatigue crack propagation simulation of the 6061-T651 Aluminium alloy. Int. J. Mater. Struct. Integrity 2017, 11, 1–15. [Google Scholar] [CrossRef]
- Zhu, S.P.; Liu, Y.; Liu, Q.; Yu, Z.Y. Strain energy gradient-based LCF life prediction of turbine discs using critical distance concept. Int. J. Fatigue 2018, 113, 33–42. [Google Scholar] [CrossRef]
- Kujawski, D. A fatigue crack driving force parameter with load ratio effects. Int. J. Fatigue 2001, 23, 239–246. [Google Scholar] [CrossRef]
- Kujawski, D. A new (ΔK + Kmax) 0.5 driving force parameter for crack growth in Aluminum alloys. Int. J. Fatigue 2001, 23, 733–740. [Google Scholar] [CrossRef]
- Stoychev, S.; Kujawski, D. Analysis of crack propagation using ΔK and Kmax. Int. J. Fatigue 2005, 27, 1425–1431. [Google Scholar] [CrossRef]
- Dinda, S.; Kujawski, D. Correlation and prediction of fatigue crack growth for different R-ratios using Kmax and ΔK+ parameters. Eng. Fract. Mech. 2004, 71, 1779–1790. [Google Scholar] [CrossRef]
- Ranganathan, N.; Chalon, F.; Méo, S. Some aspects of the energy based approach to fatigue crack propagation. Int. J. Fatigue 2008, 30, 1921–1929. [Google Scholar] [CrossRef]
- Mazari, M.; Benguediab, M.; Zemri, M.; Bouchouicha, B. Influence of Structural Parameters on the Resistance on the Crack of Aluminium Alloy. In Aluminium Alloys-New Trends in Fabrication and Applications; InTech: London, UK, 2012. [Google Scholar] [Green Version]
- Szata, M.; Lesiuk, G. A new method of constructing the kinetic fatigue fracture diagrams - crack propagation equation based on energy approach. FME Trans. 2008, 36, 74–80. [Google Scholar]
- Szata, M.; Lesiuk, G. Algorithms for the estimation of fatigue crack growth using energy method. Arch. Civ. Mech. Eng. 2009, 9, 118–134. [Google Scholar] [CrossRef]
- Szata, M. Description of the Fatigue Fracture Development in Terms of Energy Approach; Oficyna Wydawnicza PWr: Wrocław, Poland, 2002. (In Polish) [Google Scholar]
- Lesiuk, G.; Szata, M.; Rozumek, D.; Marciniak, Z.; Correia, J.; De Jesus, A. Energy response of S355 and 41Cr4 steel during fatigue crack growth process. J. Strain Anal. Eng. Des. 2018, 53, 663–675. [Google Scholar] [CrossRef]
- Ferreira, J.; Correia, J.A.; Lesiuk, G.; González, S.B.; Gonzalez, M.C.R.; de Jesus, A.M.; Fernández-Canteli, A. Pre-Strain Effects on Mixed-Mode Fatigue Crack Propagation Behaviour of the P355NL1 Pressure Vessels Steel. In ASME 2018 Pressure Vessels and Piping Conference, Prague, Czech Republic, 15–20 July 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; p. V06AT06A027. [Google Scholar]
- Lesiuk, G.; Katkowski, M.; Correia, J.; Jesus, A.M.D.; Błażejewski, W. Fatigue crack growth rate in CFRP reinforced constructional old steel. Int. J. Struct. Integr. 2018, 9, 381–395. [Google Scholar] [CrossRef]
- Rozumek, D.; Marciniak, Z.; Lesiuk, G.; Correia, J.A.; de Jesus, A.M. Experimental and numerical investigation of mixed mode I+ II and I+ III fatigue crack growth in S355J0 steel. Int. J. Fatigue 2018, 113, 160–170. [Google Scholar] [CrossRef]
- Lesiuk, G.; Kucharski, P.; Correia, J.A.; de Jesus, A.M.P.; Rebelo, C.; da Silva, L.S. Mixed mode (I + II) fatigue crack growth in puddle iron. Eng. Fract. Mech. 2017, 185, 175–192. [Google Scholar] [CrossRef]
- Dowling, N.E.; Begley, J.A. Fatigue crack growth during gross yielding and the J-integral. In Mechanics of Crack Growth; ASTM STP 590; American Society for Testing and Materials: Philadelphia, PA, USA, 1976; pp. 82–103. [Google Scholar]
- Dowling, N.E. Geometry effects and the J-integral approach to elasticplastic fatigue crack growth. In Cracks and Fracture; ASTM STP 601; American Society for Testing and Materials: Philadelphia, PA, USA, 1976; pp. 19–32. [Google Scholar]
- Lamba, H.S. The J-integral approach applied to cyclic loading. Eng. Fract. Mech. 1975, 7, 693–703. [Google Scholar] [CrossRef]
- Wüthrich, C. The extension of the J-integral concept to fatigue cracks. Int. J. Fract. 1982, 20, 35–37. [Google Scholar] [CrossRef]
- Wüthrich, C.; Hoffelner, W. Fatigue crack growth at high strain amplitudes. Mech. Behav. Mater. 1984, 911–917. [Google Scholar]
- Tanaka, K. The cyclic J-integral as a criterion for fatigue crack growth. Int. J. Fract. 1983, 22, 91–104. [Google Scholar] [CrossRef]
- Gasiak, G.; Rozumek, D. ΔJ-integral range estimation for fatigue crack growth rate description. Int. J. Fatigue 2004, 26, 135–140. [Google Scholar] [CrossRef]
- Rozumek, D.; Macha, E. Elastic–plastic fatigue crack growth in 18G2A steel under proportional bending with torsion loading. Fatigue Fract. Eng. Mater. Struct. 2006, 29, 135–144. [Google Scholar] [CrossRef]
- Rozumek, D.; Macha, E. Description of the Fatigue Crack Development in Elastic-Plastic Materials with Proportional Torsion-Bending Load; Oficyna Wydawnicza Politechniki Opolskiej: Opole, Poland, 2006. (In Polish) [Google Scholar]
- Rozumek, D. Mixed Mode Fatigue Cracks of Constructional Materials, Studies and Monographs; Oficyna Wydawnicza Politechniki Opolskiej: Opole, Poland, 2009; p. 152. (In Polish) [Google Scholar]
- Rozumek, D. Survey of formulas used to describe the fatigue crack growth rate. Mater. Sci. 2014, 49, 723–733. [Google Scholar] [CrossRef]
- Joyce, J.A.; Hackett, E.M.; Roe, C. Effects of cyclic loading on the deformation and elastic-plastic fracture behaviour of a cast stainless steel. In Fracture Mechanics; Landes, J.D., McCabe, D.E., Boulet, J.A., Eds.; American Society for Testing and Materials: Philadelphia, PA, USA, 1994; Volume 24, pp. 722–741. [Google Scholar]
- Kasprzak, W.; Lysik, B.; Rybaczk, M. Measurement, Dimensions, Invariant Models and Fractals; Spolom: Lviv, Ukraine, 2004. [Google Scholar]
- Rybaczuk, M. Geometrical methods of dimensional analysis in problems of mechanics. Scientific Papers of the Institute of Materials Science and Applied Mechanics of the Technical University of Wroclaw, Wrocław, Poland, 1993. (In Polish) [Google Scholar]
- Lesiuk, G.; Szata, M.; Correia, J.A.; De Jesus, A.M.P.; Berto, F. Kinetics of fatigue crack growth and crack closure effect in long term operating steel manufactured at the turn of the 19th and 20th centuries. Eng. Fract. Mech. 2017, 185, 160–174. [Google Scholar] [CrossRef]
- Lesiuk, G. Mixed mode (I + II, I + III) fatigue crack growth rate description in P355NL1 and 18G2A steel using new energy parameter based on j-integral approach. Eng. Fail. Anal. 2019. submitted for publication. [Google Scholar]
- Breitbarth, E.; Besel, M. Energy based analysis of crack tip plastic zone of AA2024-T3 under cyclic loading. Int. J. Fatigue 2017, 100, 263–273. [Google Scholar] [CrossRef]
- De Oliveira Correia, J.A.F. An integral probabilistic approach for fatigue lifetime prediction of mechanical and structural components. Ph.D. Thesis, Universidade do Porto, Porto, Portugal, 2015. [Google Scholar]
- ASTM E647: Standard Test Method for Measurement of Fatigue Crack Growth Rates. In Annual Book of ASTM Standards; ASTM: West Conshohocken, PA, USA, 2011.
- Becker, T.H.; Mostafavi, M.; Tait, R.B.; Marrow, T.J. An approach to calculate the J-integral by digital image correlation displacement field measurement. Fatigue Fract. Eng. Mater. Struct. 2012, 35, 971–984. [Google Scholar] [CrossRef]
- Vavrik, D.; Jandejsek, I. Experimental evaluation of contour J integral and energy dissipated in the fracture process zone. Eng. Fract. Mech. 2014, 129, 14–25. [Google Scholar] [CrossRef] [Green Version]








| Material | C | Mn | Si | P | S | Cr | Ni | Cu | Fe |
|---|---|---|---|---|---|---|---|---|---|
| 10HNAP [37] | 0.14 | 0.88 | 0.31 | 0.066 | 0.027 | 0.73 | 0.30 | 0.345 | bal. |
| 18G2A [36] | 0.20 | 1.49 | 0.33 | 0.023 | 0.024 | 0.01 | 0.01 | 0.035 | bal. |
| tested puddle iron | 0.01 | 0.01 | 0.07 | 0.354 | 0.045 | - | - | - | bal. |
| Material | Ultimate Tensile Strength UTS (MPa) | Yield Strength σpl/σ0.2 (MPa) | Young Modulus E (GPa) | Poisson Ratio ν (-) | Fracture Toughness JIC (MPa·m) |
|---|---|---|---|---|---|
| 10HNAP [37] | 566 | 418 | 215 | 0.29 | 0.178 |
| 18G2A [36] | 535 | 357 | 210 | 0.3 | 0.320 |
| Eiffel Bridge puddle iron [46] | 342 | 292 | 193 | 0.3 | n/a |
| Material | Fatigue Strength Coefficient σf’ (MPa) | Fatigue Ductility Coefficient εf’ (-) | Fatigue Strength Exponent b (-) | Fatigue Ductility Exponent c (-) |
|---|---|---|---|---|
| 10HNAP [37] | 746 | 0.442 | −0.080 | −0.601 |
| 18G2A [36] | 782 | 0.693 | −0.118 | −0.410 |
| Puddle Iron Eiffel Bridge [46] | 603 | 0.160 | −0.078 | −0.797 |
| All Data from FCGR Tests | R2 da/dN-(ΔJ) Equation (19) | R2 da/dN-(ΔS*) Equation (20) |
|---|---|---|
| 10HNAP | 0.73 | 0.94 |
| 18G2A | 0.54 | 0.91 |
| Puddle Iron from the Eiffel Bridge | 0.64 | 0.97 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lesiuk, G. Application of a New, Energy-Based ΔS* Crack Driving Force for Fatigue Crack Growth Rate Description. Materials 2019, 12, 518. https://doi.org/10.3390/ma12030518
Lesiuk G. Application of a New, Energy-Based ΔS* Crack Driving Force for Fatigue Crack Growth Rate Description. Materials. 2019; 12(3):518. https://doi.org/10.3390/ma12030518
Chicago/Turabian StyleLesiuk, Grzegorz. 2019. "Application of a New, Energy-Based ΔS* Crack Driving Force for Fatigue Crack Growth Rate Description" Materials 12, no. 3: 518. https://doi.org/10.3390/ma12030518





