An Alternative Digital Image Correlation-Based Experimental Approach to Estimate Fracture Parameters in Fibrous Soft Materials
Abstract
:1. Introduction
2. Materials and Methods
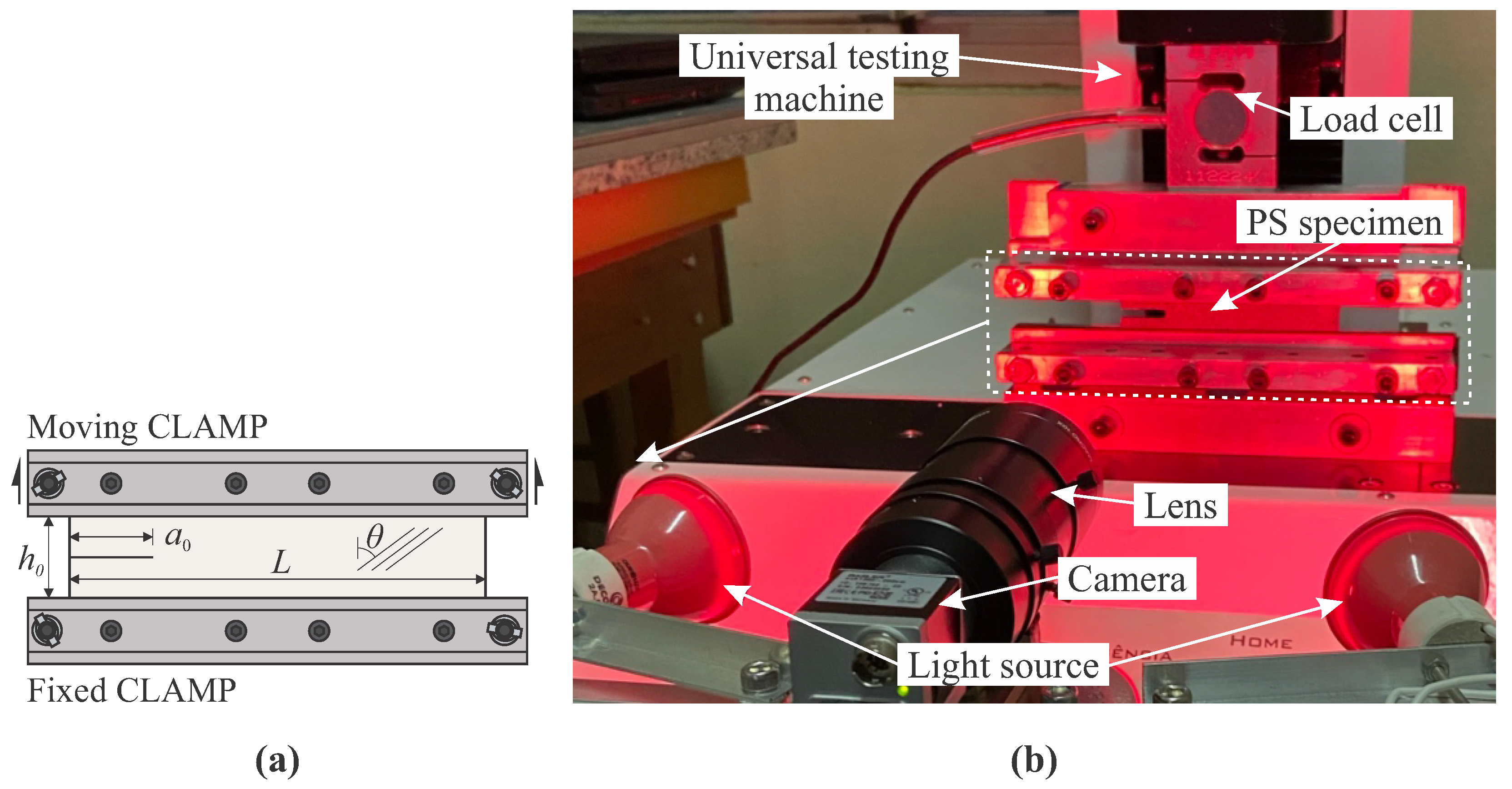
2.1. Specimen Fabrication and Experimental Setup
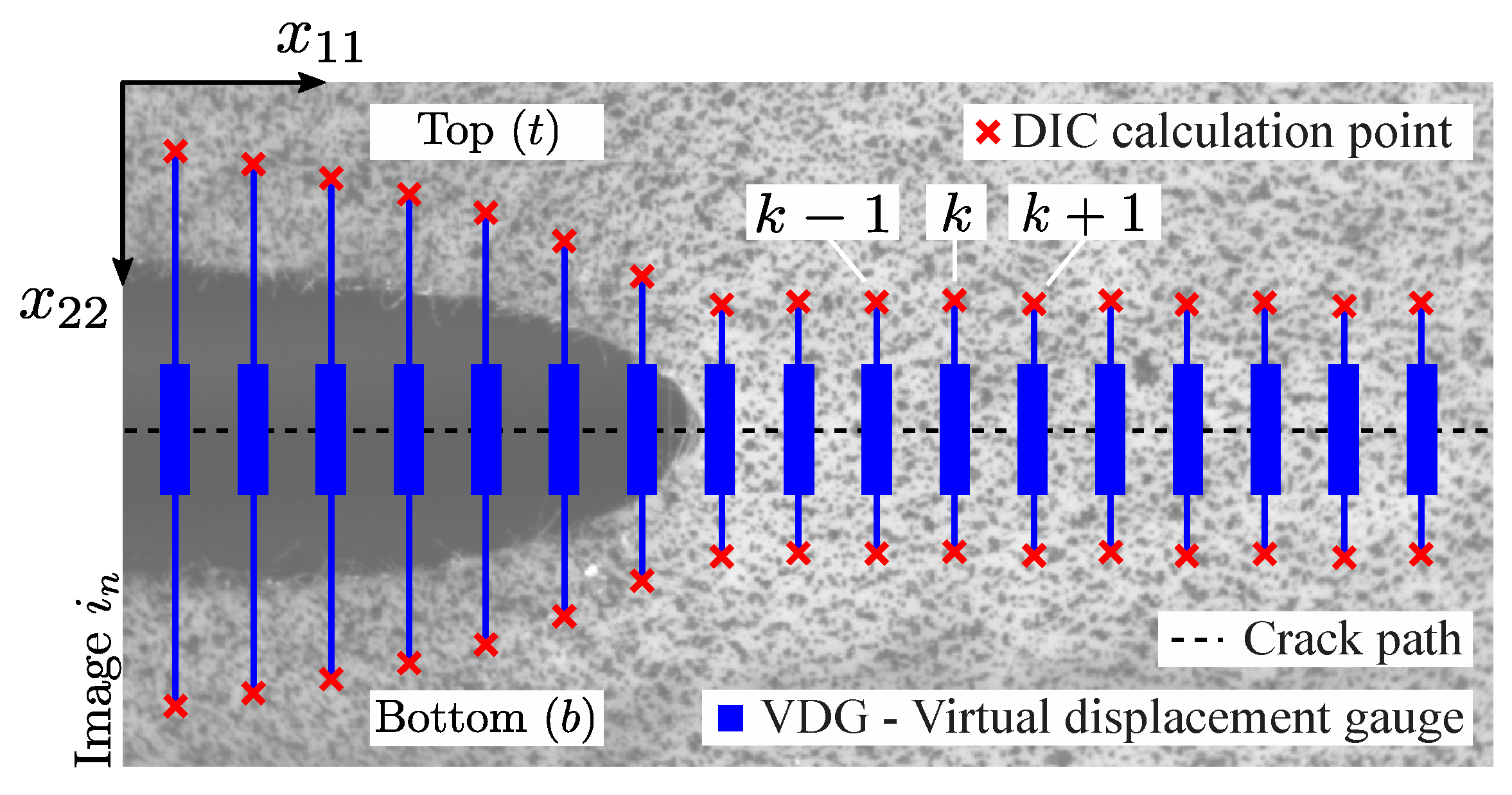
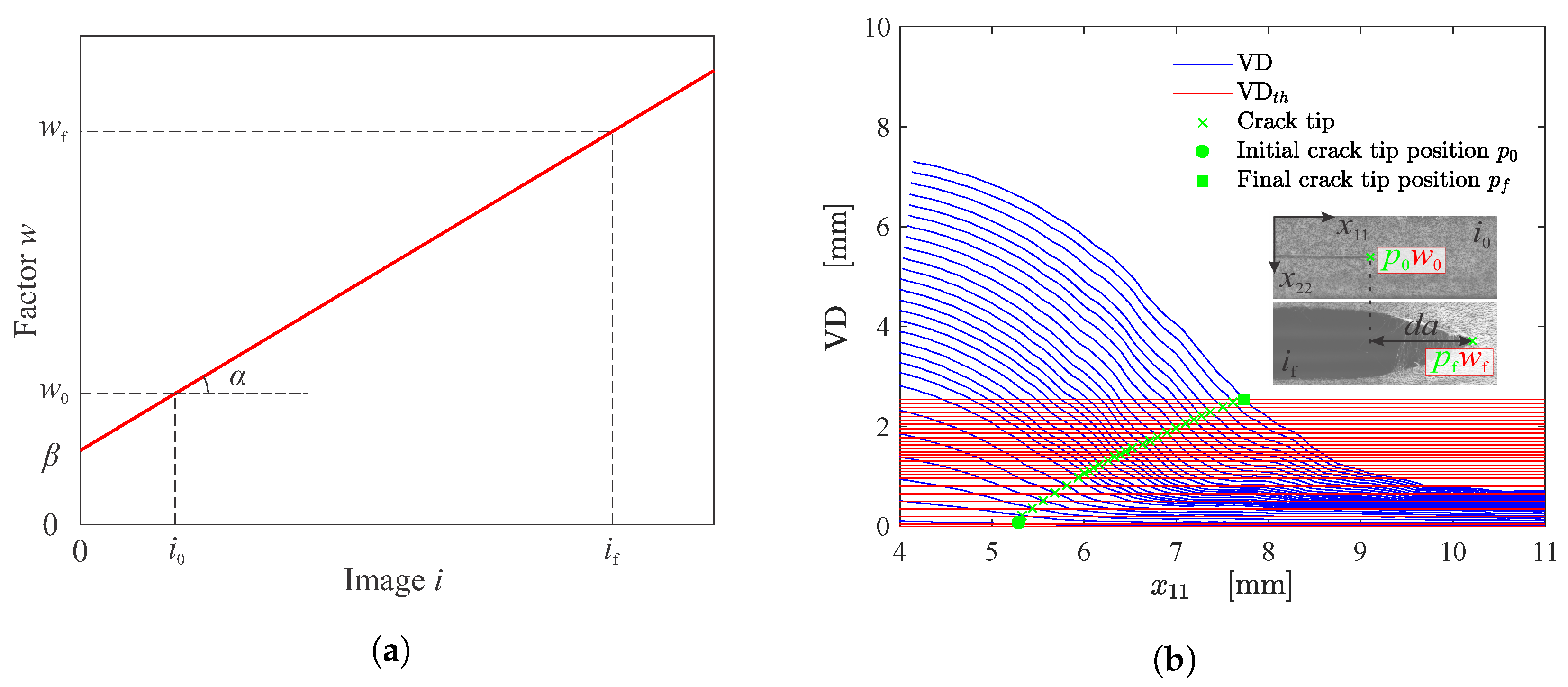
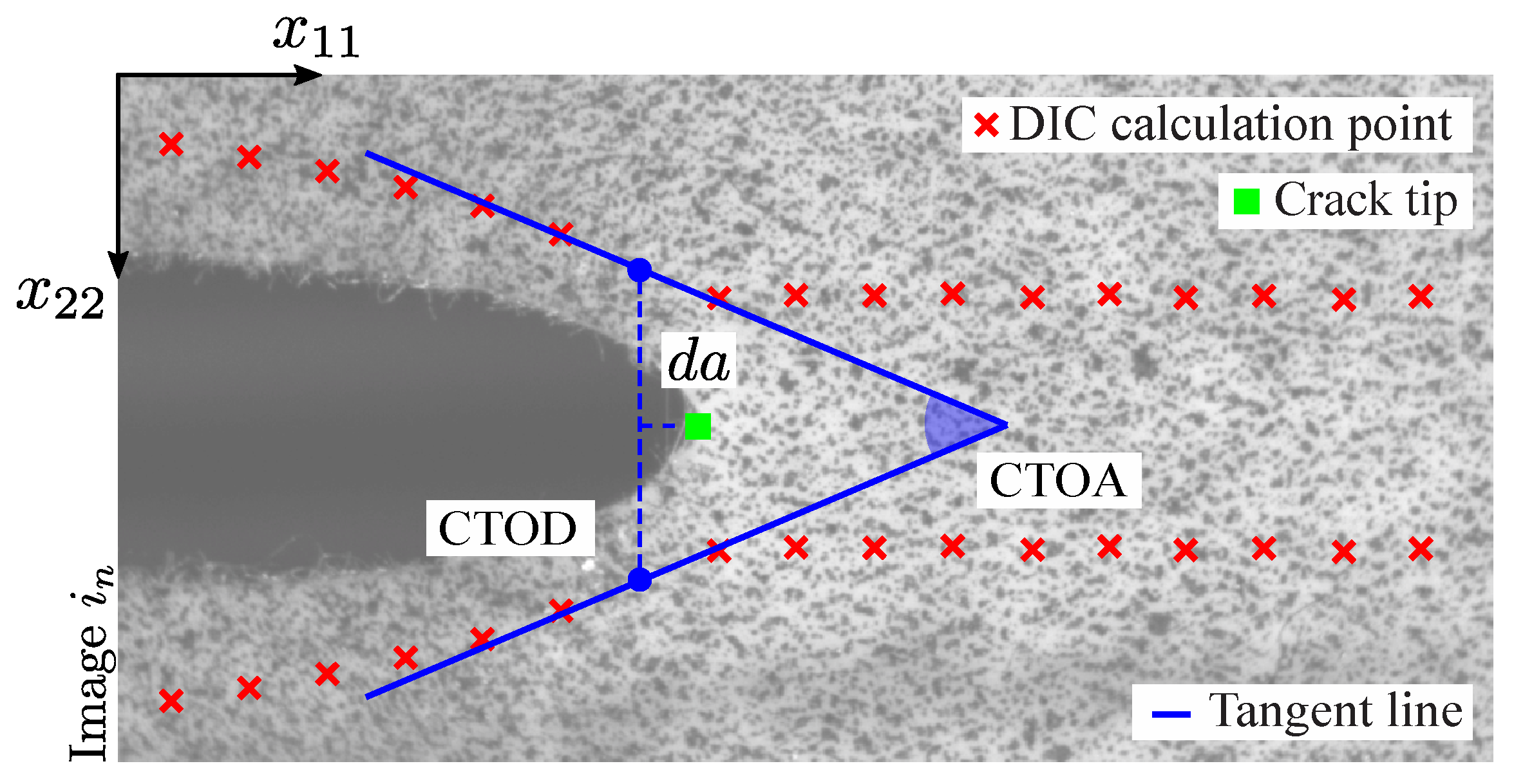
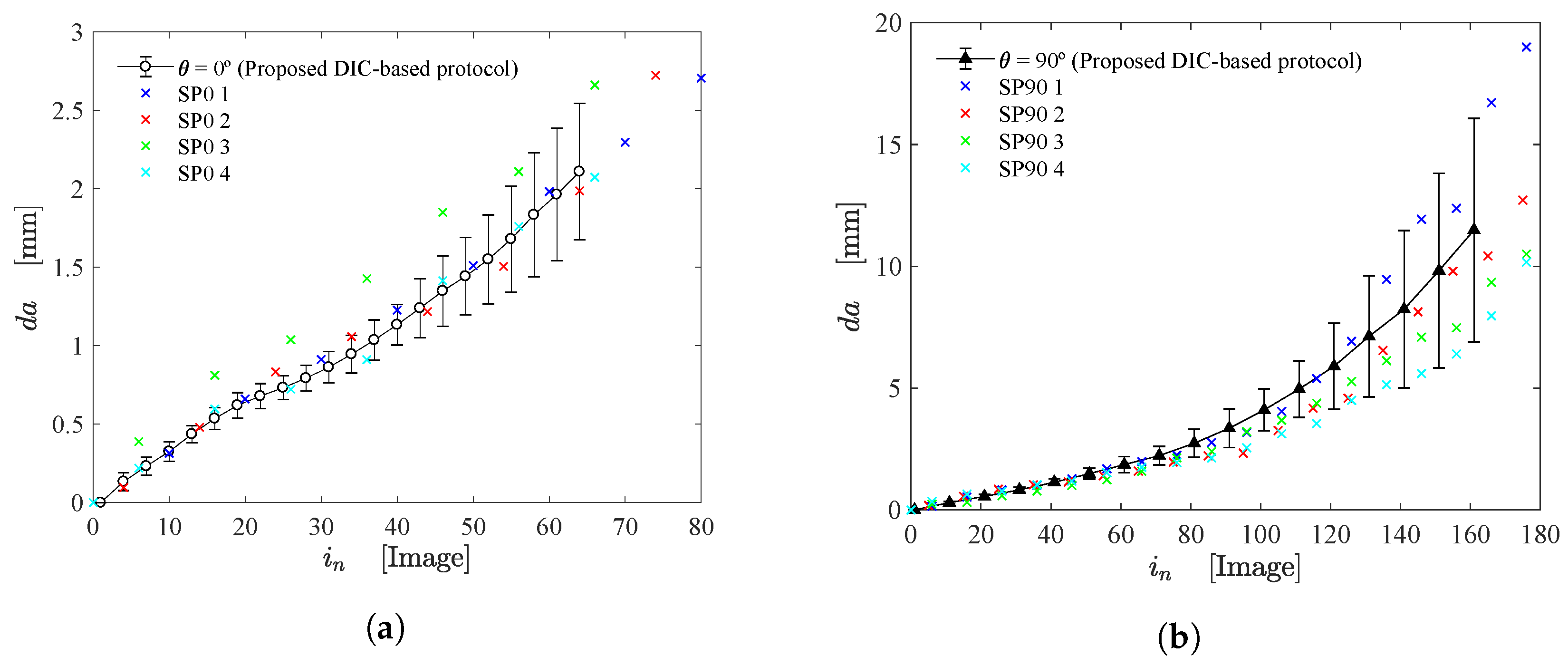
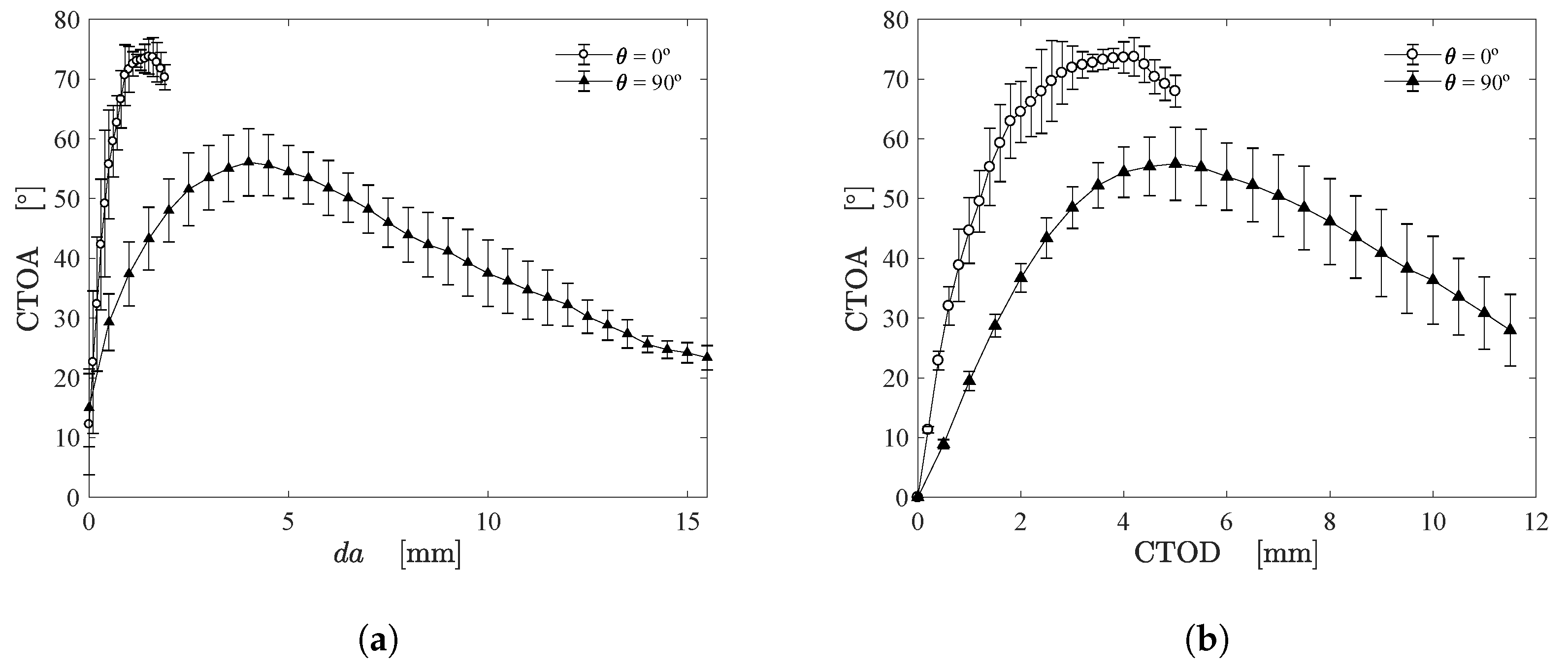
2.2. Evaluation of Crack Growth (), CTOD and CTOA
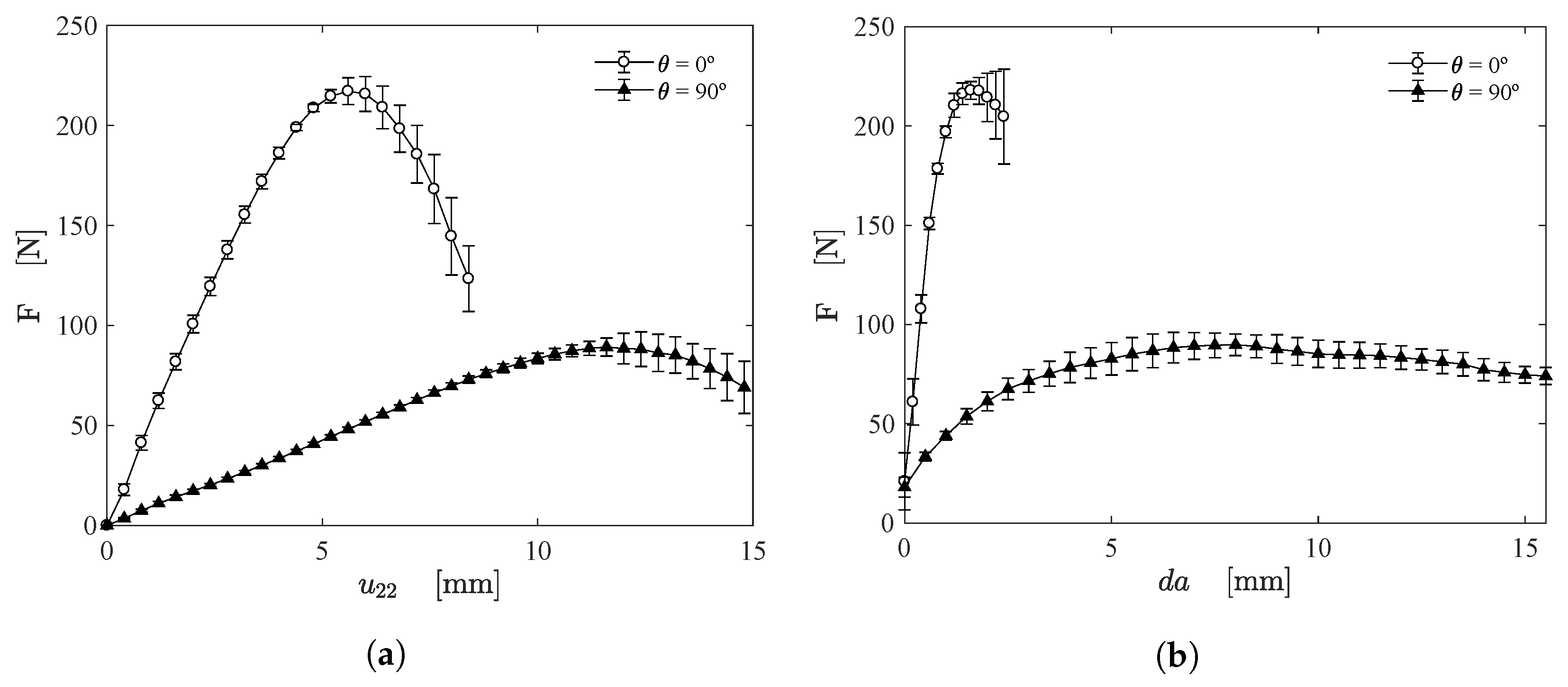
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Guimarães, C.F.; Gasperini, L.; Marques, A.P.; Reis, R.L. The stiffness of living tissues and its implications for tissue engineering. Nat. Rev. Mater. 2020, 5, 351–370. [Google Scholar] [CrossRef]
- Gültekin, O.; Hager, S.P.; Dal, H.; Holzapfel, G.A. Computational modeling of progressive damage and rupture in fibrous biological tissues: Application to aortic dissection. Biomech. Model. Mechanobiol. 2019, 18, 1607–1628. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- FitzGibbon, B.; McGarry, P. Development of a test method to investigate mode II fracture and dissection of arteries. Acta Biomater. 2021, 121, 444–460. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Sherman, V.R.; Gludovatz, B.; Schaible, E.; Stewart, P.; Ritchie, R.O.; Meyers, M.A. On the tear resistance of skin. Nat. Commun. 2015, 6, 6649. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Von Forell, G.A.; Hyoung, P.S.; Bowden, A.E. Failure modes and fracture toughness in partially torn ligaments and tendons. J. Mech. Behav. Biomed. Mater. 2014, 35, 77–84. [Google Scholar] [CrossRef]
- Deprest, J.A.; Flake, A.W.; Gratacos, E.; Ville, Y.; Hecher, K.; Nicolaides, K.; Johnson, M.P.; Luks, F.I.; Adzick, N.S.; Harrison, M.R. The making of fetal surgery. Prenat. Diagn. 2010, 30, 653–667. [Google Scholar] [CrossRef] [PubMed]
- Verghese, T.S.; Champaneria, R.; Kapoor, D.S.; Latthe, P.M. Obstetric anal sphincter injuries after episiotomy: Systematic review and meta-analysis. Int. Urogynecol. J. 2016, 27, 1459–1467. [Google Scholar] [CrossRef] [Green Version]
- Humphrey, J. Review Paper: Continuum biomechanics of soft biological tissues. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2003, 459, 3–46. [Google Scholar] [CrossRef] [Green Version]
- Cappello, R.; Pitarresi, G.; Xavier, J.; Catalanotti, G. Experimental determination of mode I fracture parameters in orthotropic materials by means of Digital Image Correlation. Theor. Appl. Fract. Mech. 2020, 108, 102663. [Google Scholar] [CrossRef]
- Maimí, P.; Wagih, A.; Ortega, A.; Xavier, J.; Blanco, N.; Ponces Camanho, P. On the experimental determination of the J-curve of quasi-brittle composite materials. Int. J. Fract. 2020, 224, 199–215. [Google Scholar] [CrossRef]
- Samadian, K.; Hertelé, S.; De Waele, W. Measurement of CTOD along a surface crack by means of digital image correlation. Eng. Fract. Mech. 2019, 205, 470–485. [Google Scholar] [CrossRef]
- Majano-Majano, A.; Lara-Bocanegra, A.J.; Xavier, J.; Morais, J. Measuring the Cohesive Law in Mode I Loading of Eucalyptus globulus. Materials 2019, 12, 23. [Google Scholar] [CrossRef] [Green Version]
- Majano-Majano, A.; Lara-Bocanegra, A.J.; Xavier, J.; Morais, J. Experimental Evaluation of Mode II fracture Properties of Eucalyptus globulus L. Materials 2020, 13, 745. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oliveira, J.; Xavier, J.; Pereira, F.; Morais, J.; de Moura, M. Direct Evaluation of Mixed Mode I + II Cohesive Laws of Wood by Coupling MMB Test with DIC. Materials 2021, 14, 374. [Google Scholar] [CrossRef] [PubMed]
- Xavier, J.; Oliveira, M.; Monteiro, P.; Morais, J.; de Moura, M. Direct Evaluation of Cohesive Law in Mode I of Pinus pinaster by Digital Image Correlation. Exp. Mech. 2014, 54, 829–840. [Google Scholar] [CrossRef]
- Silva, A.; de Jesus, A.; Xavier, J.; Correia, J.; Fernandes, A. Combined analytical-numerical methodologies for the evaluation of mixed-mode (I + II) fatigue crack growth rates in structural steels. Eng. Fract. Mech. 2017, 185, 124–138. [Google Scholar] [CrossRef]
- Mohan, A.; Poobal, S. Crack detection using image processing: A critical review and analysis. Alex. Eng. J. 2018, 57, 787–798. [Google Scholar] [CrossRef]
- Catalanotti, G.; Camanho, P.; Xavier, J.; Dávila, C.; Marques, A. Measurement of resistance curves in the longitudinal failure of composites using digital image correlation. Compos. Sci. Technol. 2010, 70, 1986–1993. [Google Scholar] [CrossRef] [Green Version]
- Haslach, H.W.; Leahy, L.N.; Fathi, P.; Barrett, J.M.; Heyes, A.E.; Dumsha, T.A.; McMahon, E.L. Crack Propagation and Its Shear Mechanisms in the Bovine Descending Aorta. Cardiovasc. Eng. Technol. 2015, 6, 501–518. [Google Scholar] [CrossRef]
- Haslach, H.W.; Siddiqui, A.; Weerasooriya, A.; Nguyen, R.; Roshgadol, J.; Monforte, N.; McMahon, E. Fracture mechanics of shear crack propagation and dissection in the healthy bovine descending aortic media. Acta Biomater. 2018, 68, 53–66. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Nunes, L. Crack-craze opening profiles near a crack tip in a polytetrafluoroethylene. Polym. Test. 2012, 31, 375–383. [Google Scholar] [CrossRef] [Green Version]
- Qi, Y.; Zou, Z.; Xiao, J.; Long, R. Mapping the nonlinear crack tip deformation field in soft elastomer with a particle tracking method. J. Mech. Phys. Solids 2019, 125, 326–346. [Google Scholar] [CrossRef]
- Moreira, C.; Nunes, L. Simple shearing of rubberlike materials filled with parallel fibers at large strain. J. Compos. Mater. 2017, 51, 1643–1651. [Google Scholar] [CrossRef]
- Bernardi, L.; Hopf, R.; Ferrari, A.; Ehret, A.; Mazza, E. On the large strain deformation behavior of silicone-based elastomers for biomedical applications. Polym. Test. 2017, 58, 189–198. [Google Scholar] [CrossRef]
- Chagnon, G.; Rebouah, M.; Favier, D. Hyperelastic Energy Densities for Soft Biological Tissues: A Review. J. Elast. 2015, 120, 129–160. [Google Scholar] [CrossRef] [Green Version]
- Shahani, A.R.; Shooshtar, H.; Baghaee, M. On the determination of the critical J-integral in rubber-like materials by the single specimen test method. Eng. Fract. Mech. 2017, 184, 101–120. [Google Scholar] [CrossRef]
- Zhu, X.K.; Joyce, J.A. Review of fracture toughness (G, K, J, CTOD, CTOA) testing and standardization. Eng. Fract. Mech. 2012, 85, 1–46. [Google Scholar] [CrossRef] [Green Version]
- Roucou, D.; Diani, J.; Brieu, M.; Mbiakop-Ngassa, A. Critical strain energy release rate for rubbers: Single edge notch tension versus pure shear tests. Int. J. Fract. 2019, 216, 31–39. [Google Scholar] [CrossRef]
- Rivlin, R.S.; Thomas, A.G. Rupture of rubber. I. Characteristic energy for tearing. J. Polym. Sci. 1953, 10, 291–318. [Google Scholar] [CrossRef]
- Jones, E.; Iadicola, M. A Good Practices Guide for Digital Image Correlation. International Digital Image Correlation Society. 2018. Available online: https://idics.org/guide/ (accessed on 6 March 2022).
- Pan, B.; Dafang, W.; Yong, X. Incremental calculation for large deformation measurement using reliability-guided digital image correlation. Opt. Lasers Eng. 2012, 50, 586–592. [Google Scholar] [CrossRef]
- OpenCV Packages for Python. Available online: https://pypi.org/project/opencv-python/ (accessed on 28 October 2021).
- Baranwal, A.; Agnihotri, P.K.; McGarry, J. The influence of fibre alignment on the fracture toughness of anisotropic soft tissue. Eng. Fract. Mech. 2020, 239, 107289. [Google Scholar] [CrossRef]
- Kowaluk, G. Properties of Lignocellulosic Composites Containing Regenerated Cellulose Fibers. BioResources 2014, 9, 5339–5348. [Google Scholar] [CrossRef] [Green Version]





| Correlation Parameters | Value |
|---|---|
| Reference subset size | 21 × 21 pixels |
| Target subset size | 71 × 71 pixels |
| Mean calibration factor | 38.7 pixels/mm |
| Elements in direction | 200 (for ) and 400 (for ) |
| Elements in direction | 1 |
| Image interpolation (Bicubic spline) | 10× |
| Subpixel level (Bicubic spline) | 10 |
| Correlation function | TM_CCORR_NORMED [33] |
| Correlation criterion | 0.9 |
| Correlation approach | Incremental |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filho, J.; Xavier, J.; Nunes, L. An Alternative Digital Image Correlation-Based Experimental Approach to Estimate Fracture Parameters in Fibrous Soft Materials. Materials 2022, 15, 2413. https://doi.org/10.3390/ma15072413
Filho J, Xavier J, Nunes L. An Alternative Digital Image Correlation-Based Experimental Approach to Estimate Fracture Parameters in Fibrous Soft Materials. Materials. 2022; 15(7):2413. https://doi.org/10.3390/ma15072413
Chicago/Turabian StyleFilho, João, José Xavier, and Luiz Nunes. 2022. "An Alternative Digital Image Correlation-Based Experimental Approach to Estimate Fracture Parameters in Fibrous Soft Materials" Materials 15, no. 7: 2413. https://doi.org/10.3390/ma15072413







