Coupling Computational Homogenization with Crystal Plasticity Modelling for Predicting the Warm Deformation Behaviour of AA2060-T8 Al-Li Alloy
Abstract
:1. Introduction
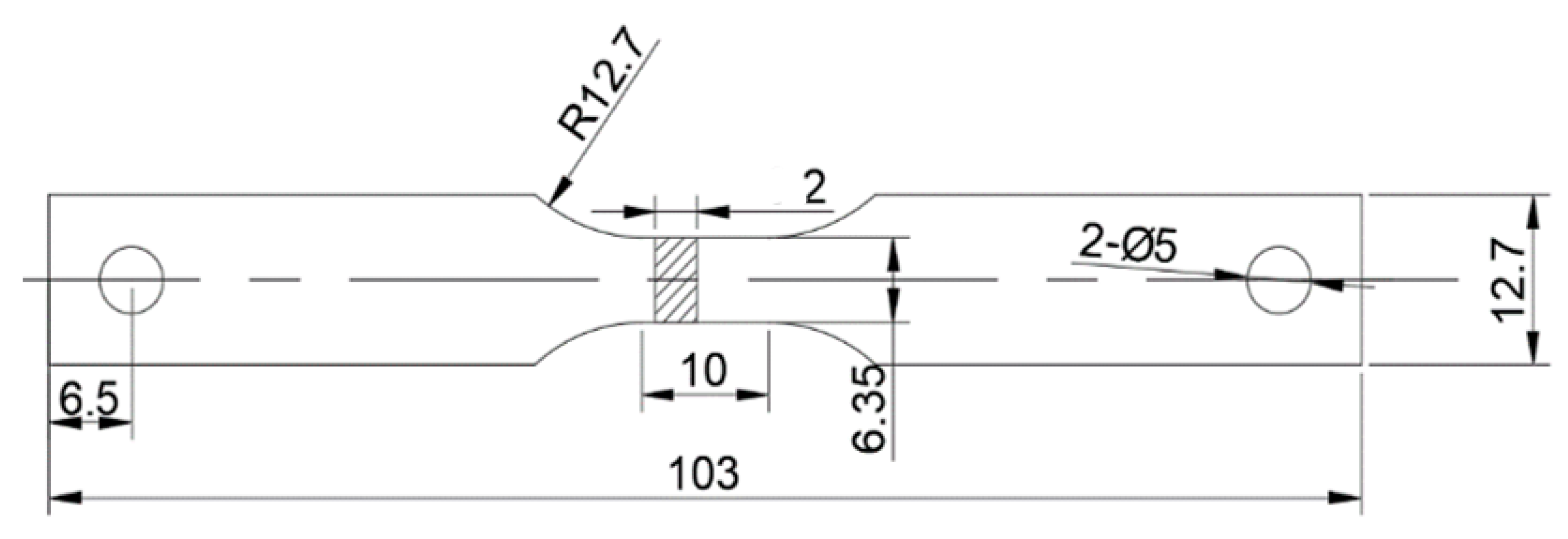
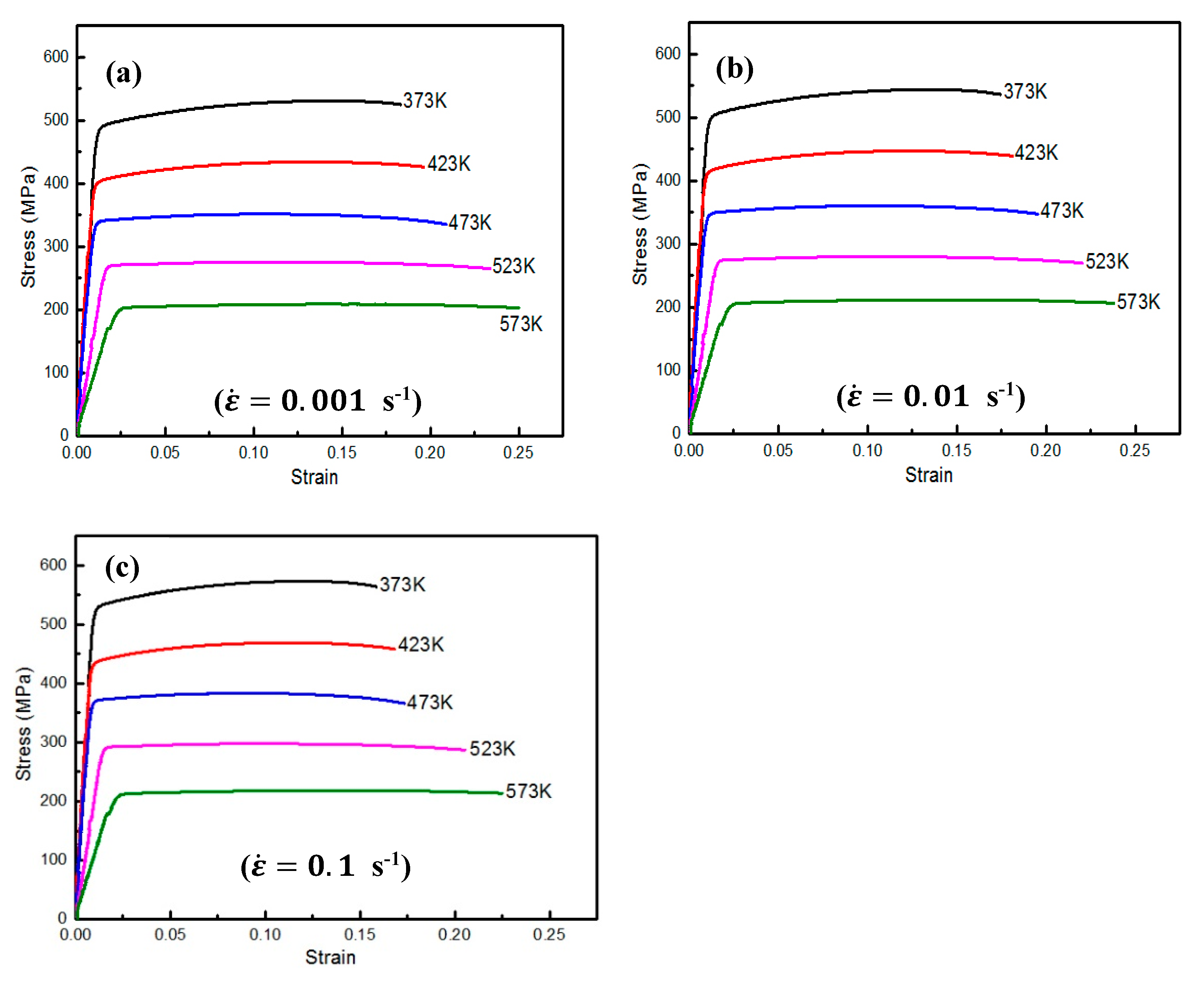
2. Experimental Procedure
3. Coupling CH with CP Modelling and Numerical Implementation
3.1. CP Modeling
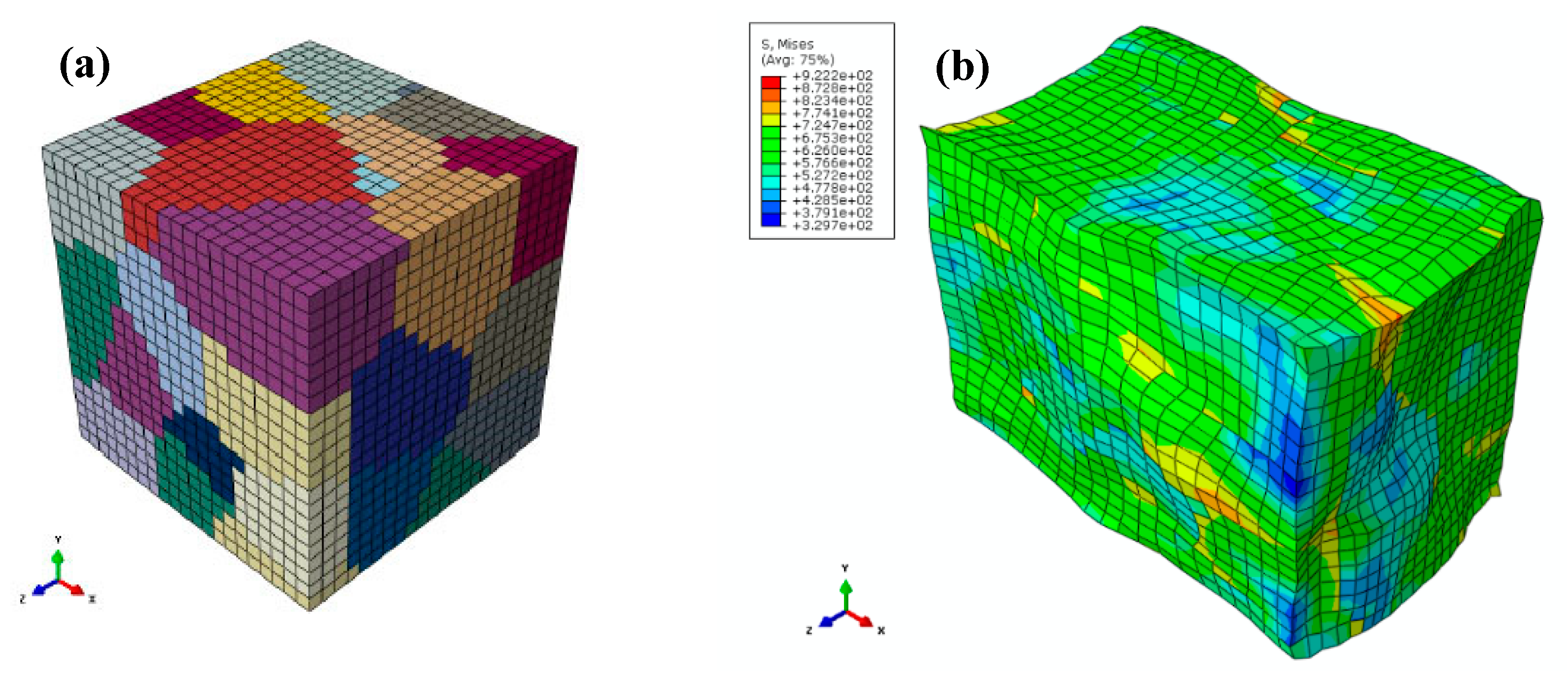
3.2. CH Procedures
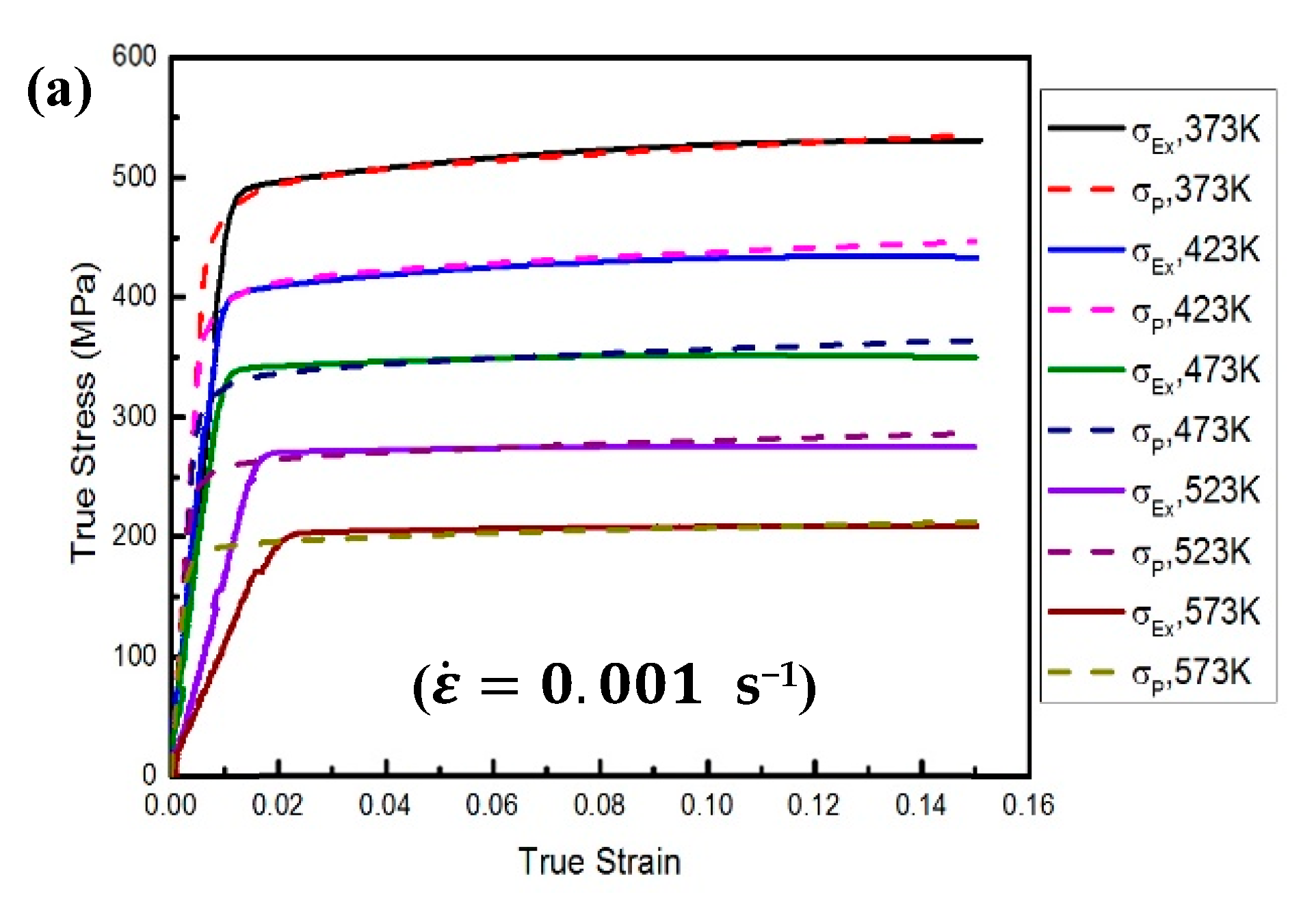
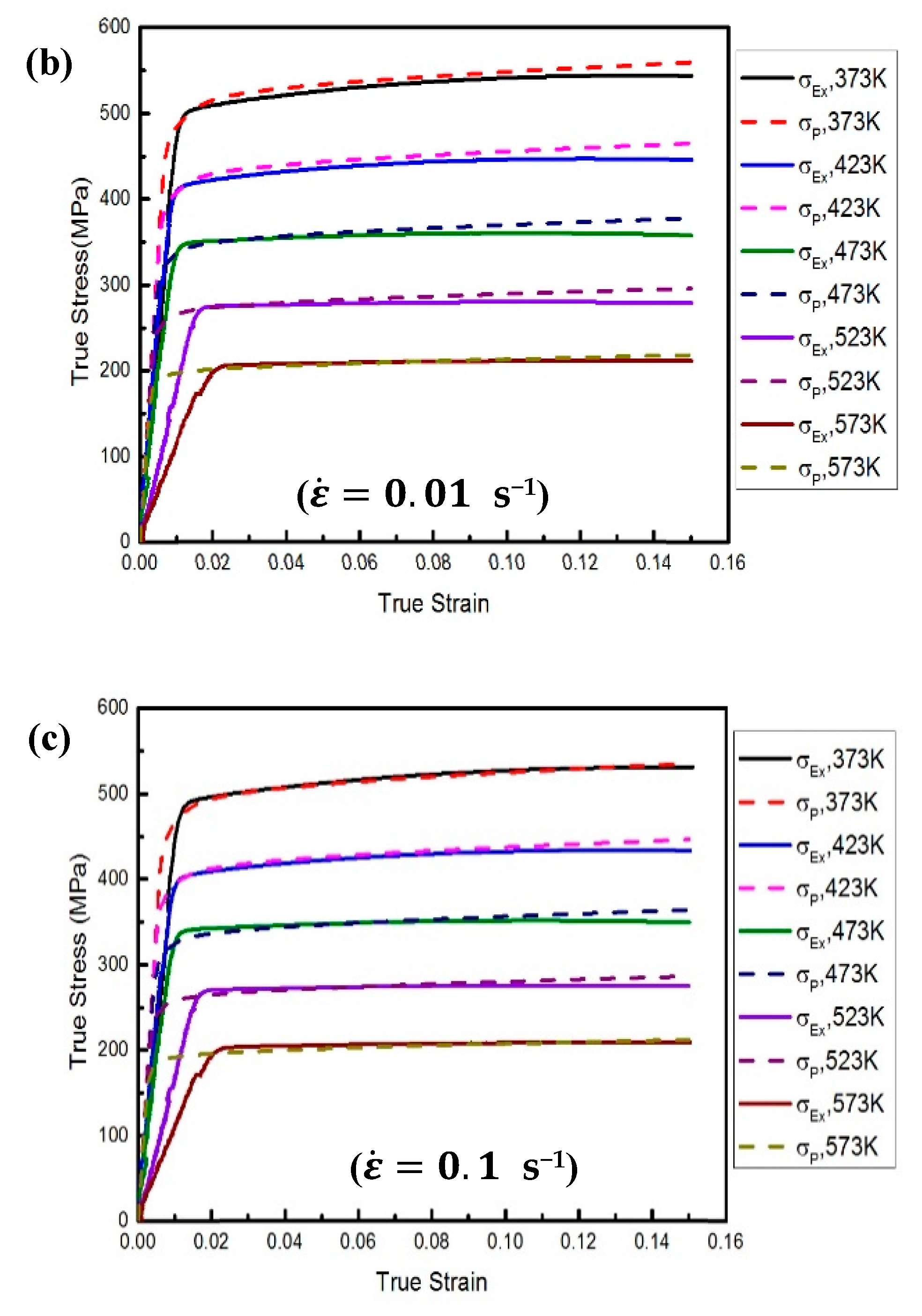
4. Verification of the Proposed Approach

5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abd El-Aty, A.; Xu, Y.; Guo, X.; Zhang, S.; Ma, Y.; Chen, D. Strengthening mechanisms, deformation behavior, and anisotropic mechanical properties of Al-Li alloys: A review. J. Adv. Res. 2018, 10, 49–67. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Myung, D.; Park, J.K.; Min, J.; Lee, H.-R.; El-Aty, A.A.; Lee, M.-G. A Review of Characterization and Modelling Approaches for Sheet Metal Forming of Lightweight Metallic Materials. Materials 2023, 16, 836. [Google Scholar] [CrossRef] [PubMed]
- El-Aty, A.A.; Guo, X.; Lee, M.-G.; Tao, J.; Hou, Y.; Hu, S.; Li, T.; Wu, C.; Yang, Q. A review on flexibility of free bending forming technology for manufacturing thin-walled complex-shaped metallic tubes. Int. J. Lightweight Mater. Manuf. 2023, 6, 165–188. [Google Scholar] [CrossRef]
- Li, T.; Wang, H.; El-Aty, A.A.; Li, J.; Zhang, Y.; Wei, W.; Chen, H.; Cheng, X.; Tao, J.; Guo, X. Theoretical modelling and finite element simulation of AA6061 involute components based on 3D free bending process. Int. J. Mech. Sci. 2020, 178, 105607. [Google Scholar] [CrossRef]
- Khokhlatova, L.B.; Kolobnev, N.I.; Oglodkov, M.S.; Mikhaylov, E.D. Aluminum-lithium alloys for aircraft building. Metallurgist 2012, 56, 336–341. [Google Scholar] [CrossRef]
- Dong, F.; Huang, S.; Yi, Y.; He, H.; Huang, K.; Gao, S.; Jia, Y.; Yu, W. Effect of increased stretching deformation at cryogenic temperature on the precipitation behavior and mechanical properties of 2060 Al–Li alloy. Mater. Sci. Eng. A 2022, 834, 142585. [Google Scholar] [CrossRef]
- Dong, F.; Yi, Y.; Huang, S.; Wang, B.; He, H.; Huang, K.; Wang, C. Cryogenic formability and deformation behavior of 2060 Al–Li alloys with water-quenched and T4 aged temper. Mater. Sci. Eng. A 2021, 823, 141722. [Google Scholar] [CrossRef]
- Zheng, X.; Luo, P.; Yue, G.; Hu, Y. Analysis of microstructure and high-temperature tensile properties of 2060 Al-Li alloy strengthened by laser shock peening. J. Alloys Compd. 2020, 860, 158539. [Google Scholar] [CrossRef]
- Liu, T.; Zhao, Y.; Kang, Y.; Zhan, X. Effect of micro morphology in different zones on mechanical properties of 2060 Al-Li alloy laser welded joints. J. Manuf. Process. 2020, 50, 336–344. [Google Scholar] [CrossRef]
- Abd El-Aty, A.; Xu, Y.; Zhang, S.; Ha, S.; Yan, Y.; Chen, D. Impact of high strain rate deformation on the mechanical behavior, fracture mechanisms and anisotropic response of 2060 Al-Cu-Li alloy. J. Adv. Res. 2019, 18, 19–37. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, K.; Song, Y.; Ali, R.A.; Chen, W.; Wang, X. Constitutive behavior and microstructural evolution of 2060 Al–Li alloy under high strain rate: Experiment and simulation. Mater. Sci. Eng. A 2022, 844, 143048. [Google Scholar] [CrossRef]
- El-Aty, A.A.; Xu, Y.; Zhang, S.-H.; Yan, M.; Guo, X.; Tao, J.; Hou, Y.; Lee, M.-G. Dynamic Deformation Behaviour of Al-Li Alloys Under High Strain Rate Deformation; Inal, K., Levesque, J., Worswick, M., Butcher, C., Eds.; NUMISHEET 2022; The Minerals, Metals & Materials Series; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- El-Aty, A.A.; Zhang, S.-H.; Guo, X.; Xu, Y.; Yan, M.; Chen, D.; Tao, J. The High-Speed Deformation Behavior of High-Strength Lightweight Al-Li Alloy Sheets. In Forming the Future; Daehn, G., Cao, J., Kinsey, B., Tekkaya, E., Vivek, A., Yoshida, Y., Eds.; The Minerals, Metals & Materials Series; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Xia, L.; Zhang, S.-H.; Xu, Y.; Chen, S.; El-Aty, A.A.; Pokrovsky, A.I.; Bakinovskaya, A.A. Study of the ductility enhancement of 5A90 Al–Mg–Li alloy sheets with stress relaxation. Philos. Mag. 2021, 101, 2449–2472. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, S.; Banabic, D.; Xu, Y.; Abd El-Aty, A.; Chen, D.; Cheng, M.; Song, W.; Pokrovsky, A.; Chen, G. Investigation on Formability Enhancement of 5A06 Aluminum Sheet by Impact Hydroforming. CIRP Ann. Manuf. Technol. 2018, 67, 281–284. [Google Scholar] [CrossRef]
- Abd El-Aty, A.; Xu, Y.; Zhang, S.; Ma, Y.; Chen, D. Experimental investigation of tensile properties and anisotropy of 1420, 8090 and 2060 Al-Li alloys sheet undergoing different strain rates and fibre orientation: A comparative study. Procedia Eng. 2017, 207, 13–18. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, Y.; Xu, Y.; Abd El-Aty, A.; Chen, D.; Chen, G. Experimental Investigation of Novel Impact Hydroforming Technology on Sheet Metal Formability. J. Phys. Conf. Ser. 2018, 1063, 012173. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, Y.; Xu, Y.; Abd El-Aty, A.; Chen, D. Effect of Impact Hydroforming Loads on the Formability of AA5A06 Sheet Metal. IOP Conf. Ser. Mater. Sci. Eng. 2018, 418, 012114. [Google Scholar] [CrossRef]
- Cao, L.; Liao, B.; Wu, X.; Li, C.; Huang, G.; Cheng, N. Hot Deformation Behavior and Microstructure Characterization of an Al-Cu-Li-Mg-Ag Alloy. Crystals 2020, 10, 416. [Google Scholar] [CrossRef]
- Zheng, K.; Politis, D.J.; Wang, L.; Lin, J. A review on forming techniques for manufacturing lightweight complex—Shaped aluminium panel components. Int. J. Lightweight Mater. Manuf. 2018, 1, 55–80. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, X.-M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Abd El-Aty, A.; Xu, Y.; Ha, S.; Zhang, S. Computational homogenization of tensile deformation behaviors of a third generation Al-Li alloy 2060-T8 using crystal plasticity finite element method. Mater. Sci. Eng. A 2018, 731, 583–594. [Google Scholar] [CrossRef]
- Abd El-Aty, A.; Ha, S.; Zhang, S.; Xu, Y. Prediction of tensile deformation behavior of Al-Li alloy 2060- T8 by computational homogenization-based crystal plasticity finite element method. J. Phys. Conf. Ser. 2018, 1063, 012058. [Google Scholar] [CrossRef]
- Abd El-Aty, A.; Xu, Y.; Zhang, S.H.; Guo, X.; Tao, J.; Lee, M.G. Phenomenological-based constitutive modelling of warm deformation behavior of high-Strength lightweight AL-Li alloy sheets. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1238, 012017. [Google Scholar] [CrossRef]
- Ou, L.; Zheng, Z.; Nie, Y.; Jian, H. Hot deformation behavior of 2060 alloy. J. Alloys Compd. 2015, 648, 681–689. [Google Scholar] [CrossRef]
- Gao, H.; Weng, T.; Liu, J.; Li, C.; Li, Z.; Wang, L. Hot stamping of an Al-Li alloy: A feasibility study. Manuf. Rev. 2016, 9, 9–15. [Google Scholar] [CrossRef]
- Liang, H.; Nan, Y.; Ning, Y.; Li, H.; Zhang, J.; Shi, Z.; Guo, H. Correlation between strain-rate sensitivity and dynamic softening behavior during hot processing. J. Alloys Compd. 2013, 632, 478–485. [Google Scholar] [CrossRef]
- Bijish, B.; Lindgren, L. Dislocation density based model for plastic deformation and globularization of Ti-6Al-4V. Int. J. Plast. 2013, 50, 94–108. [Google Scholar]
- Elkhodary, K.I.; Bakr, M.A. Single crystal plasticity with bend–twist modes. J. Mech. Phys. Solids 2015, 79, 44–66. [Google Scholar] [CrossRef]
- Pandey, A.; Khan, A.S.; Kim, E.-Y.; Choi, S.-H.; Gnäupel-Herold, T. Experimental and numerical investigations of yield surface, texture, and deformation mechanisms in AA5754 over low to high temperatures and strain rates. Int. J. Plast. 2012, 41, 165–188. [Google Scholar] [CrossRef]
- Abedrabbo, N.; Pourboghrat, F.; Carsley, J. Forming of AA5182-O and AA5754-O at elevated temperatures using coupled thermo-mechanical finite element models. Int. J. Plast. 2007, 23, 841–875. [Google Scholar] [CrossRef]
- Clayton, J. Dynamic plasticity and fracture in high density polycrystals: Constitutive modeling and numerical simulation. J. Mech. Phys. Solids 2005, 53, 261–301. [Google Scholar] [CrossRef]
- Cheong, K.-S.; Busso, E.P. Discrete dislocation density modelling of single phase FCC polycrystal aggregates. Acta Mater. 2004, 52, 5665–5675. [Google Scholar] [CrossRef]
- Asaro, R.; Needleman, A. Texture development and strain hardening in rate dependent polycrystals. Acta Metall. 1985, 33, 923–953. [Google Scholar] [CrossRef]
- Ha, S.; Jang, J.H.; Kim, K.T. Finite element implementation of dislocation-density-based crystal plasticity model and its application to pure aluminum crystalline materials. Int. J. Mech. Sci. 2017, 120, 249–262. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. An analysis of non-uniform and localized deformation in ductile single crystals. Acta Metall. 1982, 30, 1087–1119. [Google Scholar] [CrossRef]
- Kocks, U.F.; Argon, A.S.; Ashby, M.F. Thermodynamics and Kinetics of Slip. In Progress in Materials Science; Chalmers, B., Christian, J.W., Massalski, T.B., Eds.; Pergamon Press: Oxford, UK, 1975. [Google Scholar]
- Kocks, U.; Mecking, H. Physics and phenomenology of strain hardening: The FCC case. Prog. Mater. Sci. 2003, 48, 171–273. [Google Scholar] [CrossRef]
- Essmann, U.; Mughrabi, H. Annihilation of dislocations during tensile and cyclic deformation and limits of dislocation densities. Philos. Mag. A 1979, 40, 731–756. [Google Scholar] [CrossRef]
- Nix, W.D.; Gibeling, J.C.; Hughes, D.A. Time-dependent deformation of metals. Metall. Trans. A 1985, 16, 2215–2226. [Google Scholar] [CrossRef]
- Alankar, A.; Mastorakos, I.N.; Field, D.P. A dislocation-density-based 3D crystal plasticity model for pure aluminum. Acta Mater. 2009, 57, 5936–5946. [Google Scholar] [CrossRef]
- Arsenlis, A.; Parks, D.M. Modeling the evolution of crystallographic dislocation density in crystal plasticity. J. Mech. Phys. Solids 2002, 50, 1979–2009. [Google Scholar] [CrossRef]
- Vattré, A.; Devincre, B.; Feyel, F.; Gatti, R.; Groh, S.; Jamond, O.; Roos, A. Modelling crystal plasticity by 3D dislocation dynamics and the finite element method: The Discrete-Continuous Model revisited. J. Mech. Phys. Solids 2008, 59, 398–422. [Google Scholar] [CrossRef]
- Zhou, C.; Biner, S.B.; LeSar, R. Discrete dislocation dynamics simulations of plasticity at small scales. Acta Mater. 2010, 58, 1565–1577. [Google Scholar] [CrossRef]
- Devincre, B.; Hoc, T.; Kubin, L. Dislocation Mean Free Paths and Strain Hardening of Crystals. Science 2008, 320, 1745–1748. [Google Scholar] [CrossRef] [PubMed]
- Bouvier, S.; Gardey, B.; Haddadi, H.; Teodosiu, C. Characterization of the strain-induced plastic anisotropy of rolled sheets by using sequences of simple shear and uniaxial tensile tests. J. Mater. Process. Technol. 2006, 174, 115–126. [Google Scholar] [CrossRef]
- Franciosi, P.; Bevellers, M.; Zaoui, A. Latent hardening in copper and aluminum single crystals. Acta Metall. 1980, 28, 273–283. [Google Scholar] [CrossRef]
- Quey, R.; Dawson, P.R.; Barbe, F. Large-scale 3D random polycrystals for the finite element method: Generation, meshing and remeshing. Comput. Methods Appl. Mech. Eng. 2011, 200, 1729–1745. [Google Scholar] [CrossRef]
- Hazanov, S.; Huet, C. Order relationships for boundary conditions effect in heterogeneous bodies smaller than the representative volume. J. Mech. Phys. Solids 1994, 42, 1995–2011. [Google Scholar] [CrossRef]
- Rokni, M.R.; Zarei-Hanzaki, A.; Roostaei, A.A.; Abolhasani, A. Constitutive base analysis of a 7075 aluminum alloy during hot compression testing. Mater. Des. 2011, 32, 4955–4960. [Google Scholar] [CrossRef]
- Huang, C.-Q.; Deng, J.; Wang, S.-X.; Liu, L.-L. A physical-based constitutive model to describe the strain-hardening and dynamic recovery behaviors of 5754 aluminum alloy. Mater. Sci. Eng. A 2017, 699, 106–113. [Google Scholar] [CrossRef]
- Xiao, W.; Wang, B.; Wu, Y.; Yang, X. Constitutive modeling of flow behavior and microstructure evolution of AA7075 in hot tensile deformation. Mater. Sci. Eng. A 2018, 712, 704–713. [Google Scholar] [CrossRef]
- He, A.; Xie, G.; Zhang, H.; Wang, X. A comparative study on Johnson–Cook, modified Johnson–Cook and Arrhenius-type constitutive models to predict the high temperature flow stress in 20CrMo alloy steel. Mater. Des. 2013, 52, 677–685. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Duan, J.; Liu, J. A modified Johnson Cook model for elevated temperature flow behavior of T24 steel. Mater. Sci. Eng. A 2013, 577, 138–146. [Google Scholar] [CrossRef]
- Srinivasulu, S.; Jain, A. A comparative analysis of training methods for artificial neural network rainfall–runoff models. Appl. Soft Comput. 2006, 6, 295–306. [Google Scholar] [CrossRef]



| Value | R | ARRE (%) | RMSE (MPa) | NMBE (%) |
|---|---|---|---|---|
| /s | 0.992 | 3.37 | 6.14 | 0.186 |
| /s | 0.988 | 4.22 | 6.48 | 0.192 |
| /s | 0.982 | 4.46 | 6.95 | 0.199 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd El-Aty, A.; Ha, S.; Xu, Y.; Hou, Y.; Zhang, S.-H.; Alzahrani, B.; Ali, A.; Ahmed, M.M.Z. Coupling Computational Homogenization with Crystal Plasticity Modelling for Predicting the Warm Deformation Behaviour of AA2060-T8 Al-Li Alloy. Materials 2023, 16, 4069. https://doi.org/10.3390/ma16114069
Abd El-Aty A, Ha S, Xu Y, Hou Y, Zhang S-H, Alzahrani B, Ali A, Ahmed MMZ. Coupling Computational Homogenization with Crystal Plasticity Modelling for Predicting the Warm Deformation Behaviour of AA2060-T8 Al-Li Alloy. Materials. 2023; 16(11):4069. https://doi.org/10.3390/ma16114069
Chicago/Turabian StyleAbd El-Aty, Ali, Sangyul Ha, Yong Xu, Yong Hou, Shi-Hong Zhang, Bandar Alzahrani, Alamry Ali, and Mohamed M. Z. Ahmed. 2023. "Coupling Computational Homogenization with Crystal Plasticity Modelling for Predicting the Warm Deformation Behaviour of AA2060-T8 Al-Li Alloy" Materials 16, no. 11: 4069. https://doi.org/10.3390/ma16114069







