Modelling the Flow Behaviour of Al Alloy Sheets at Elevated Temperatures Using a Modified Zerilli–Armstrong Model and Phenomenological-Based Constitutive Models
Abstract
:1. Introduction
2. Experimental Procedures
3. Result and Discussion
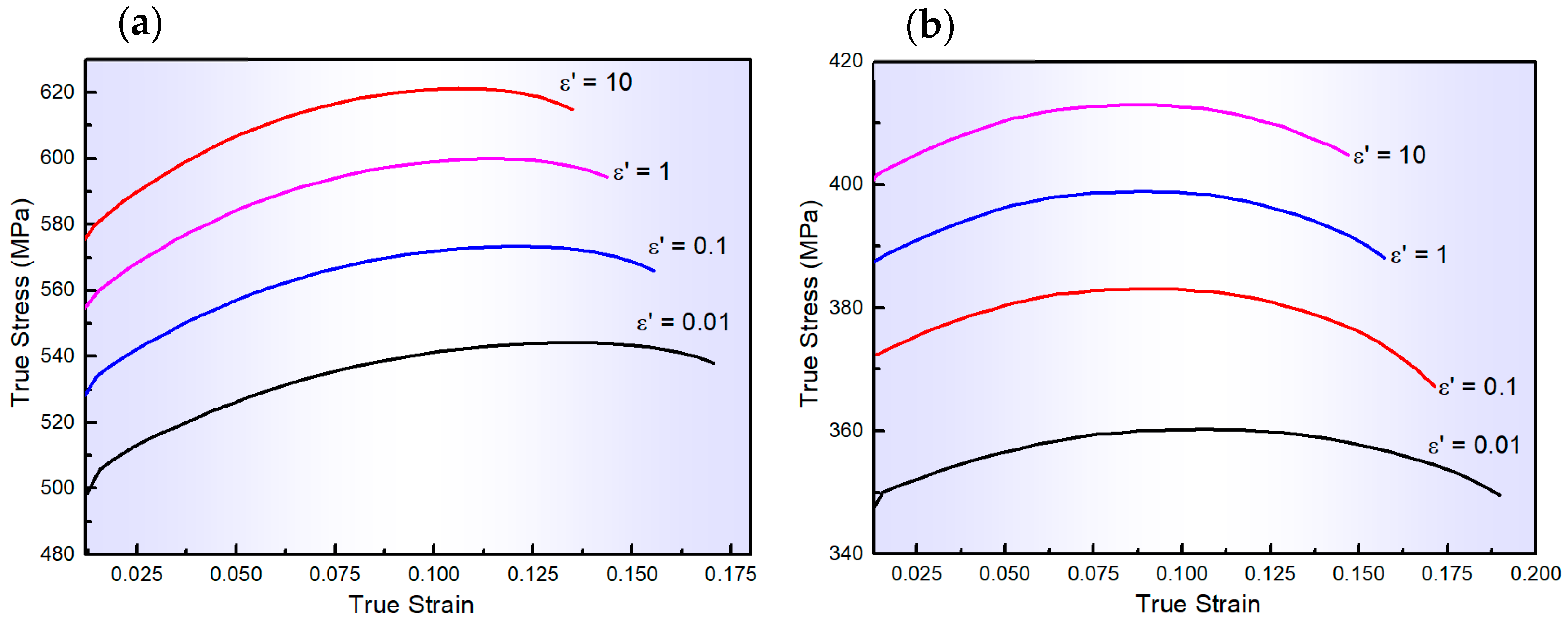
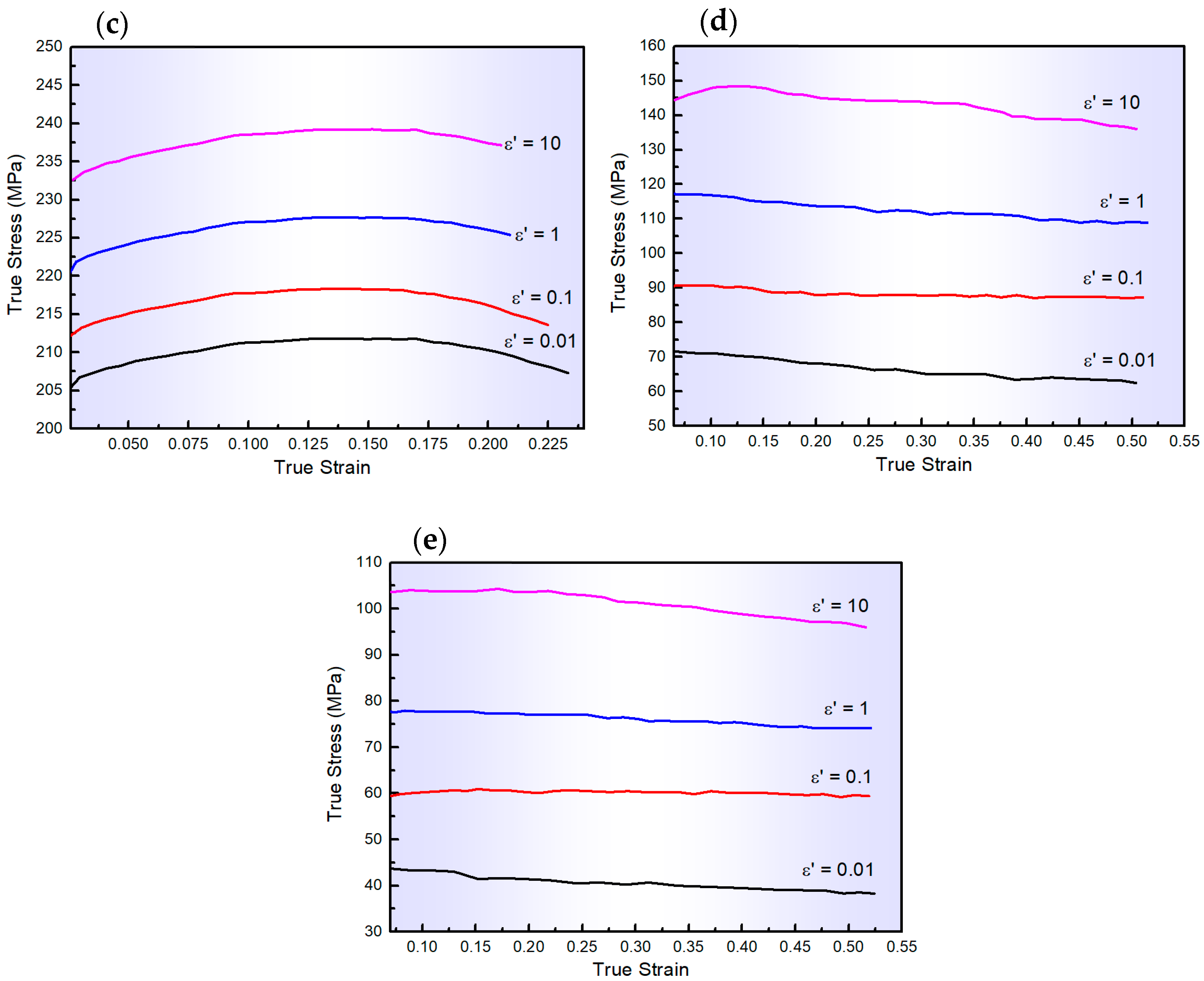
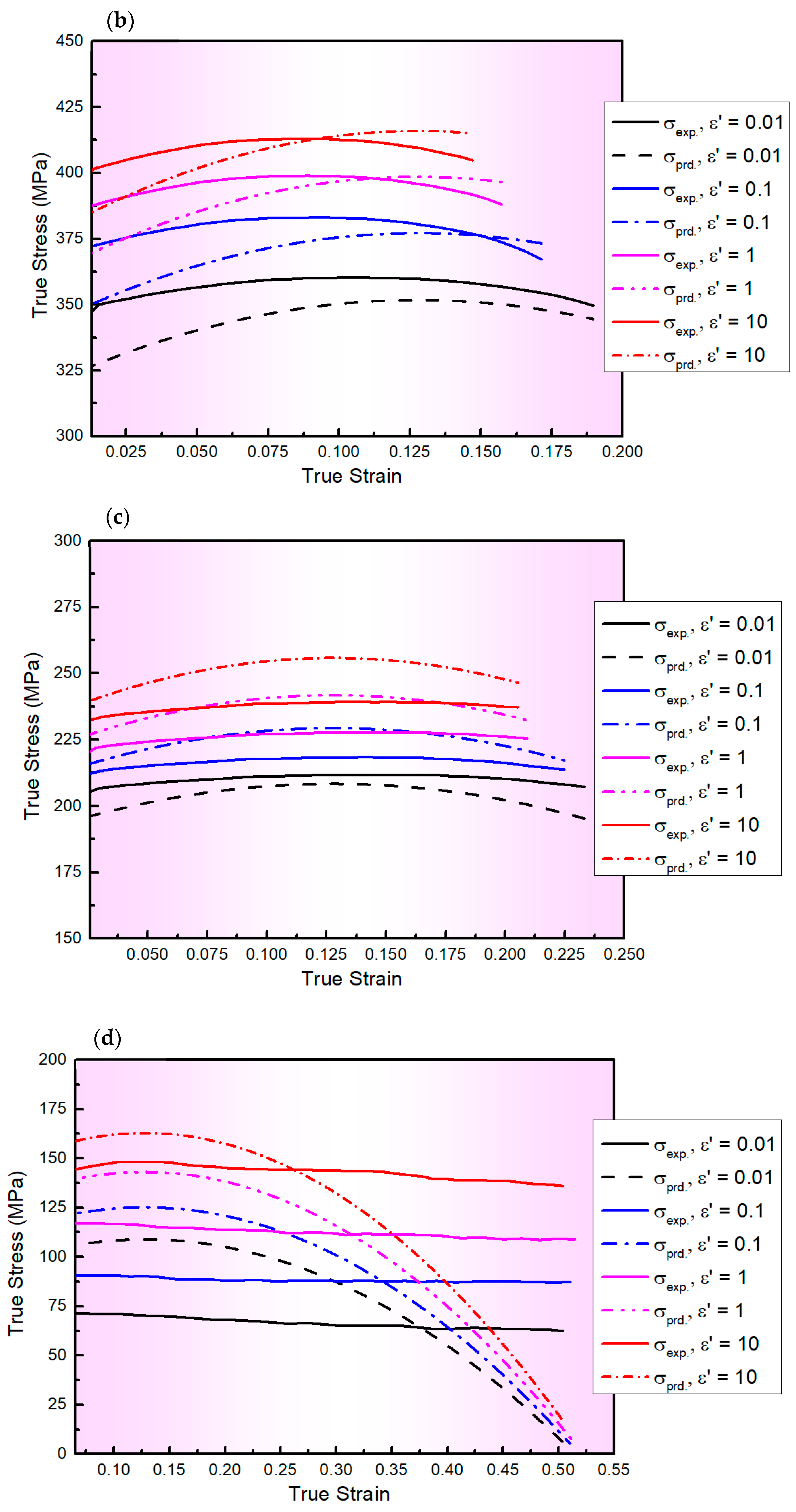
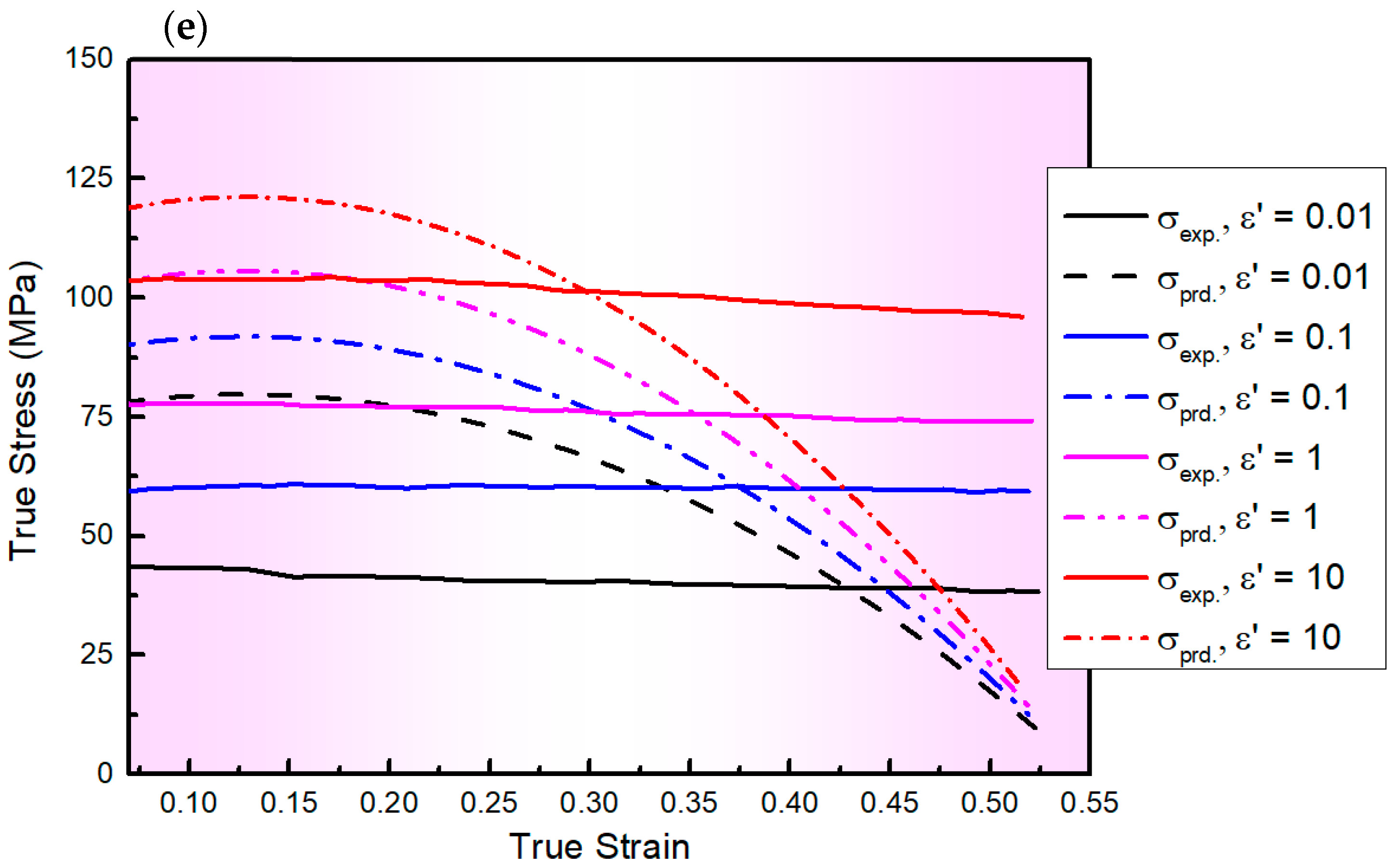
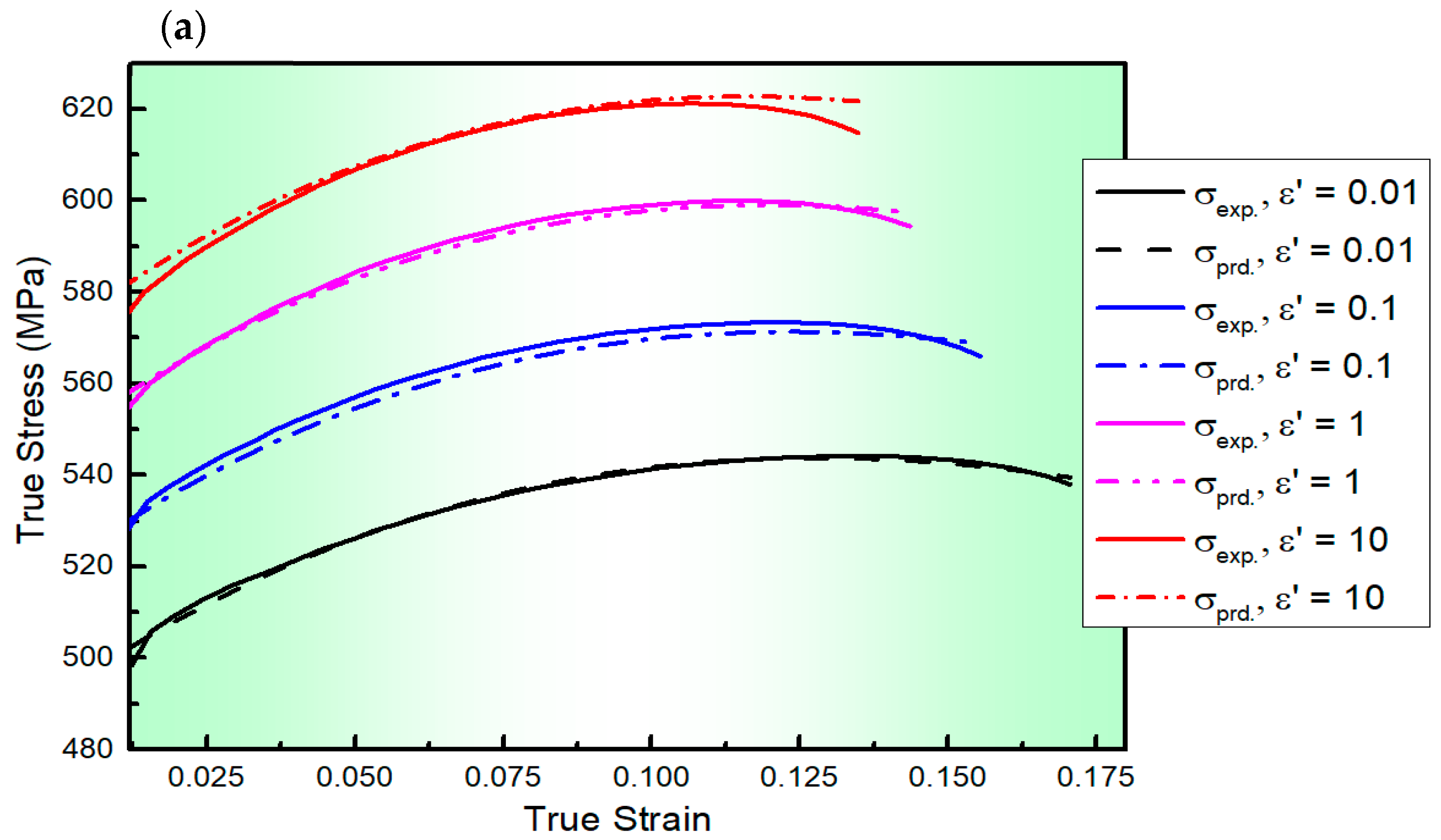
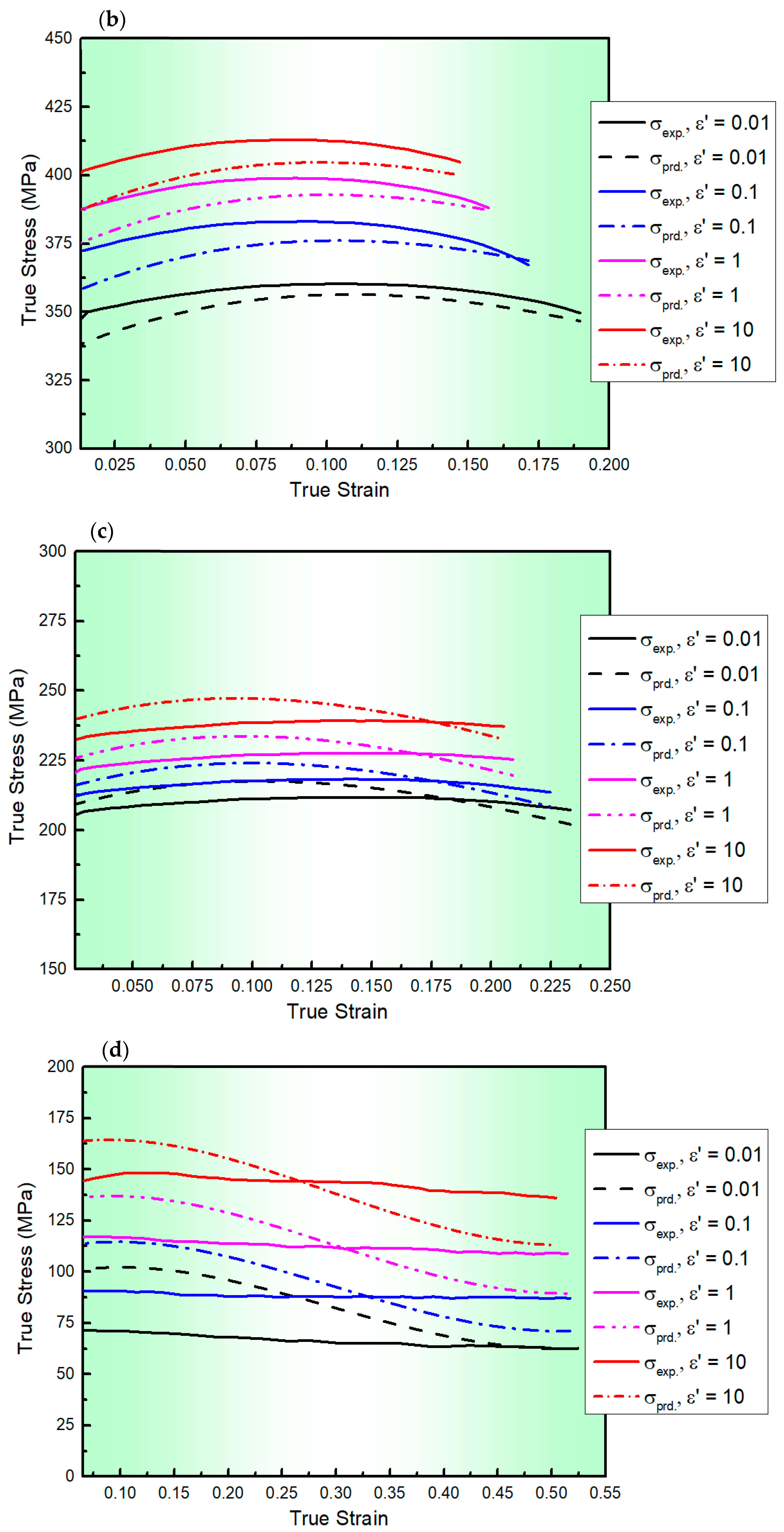
3.1. Flow Behaviour
3.2. Constitutive Modelling
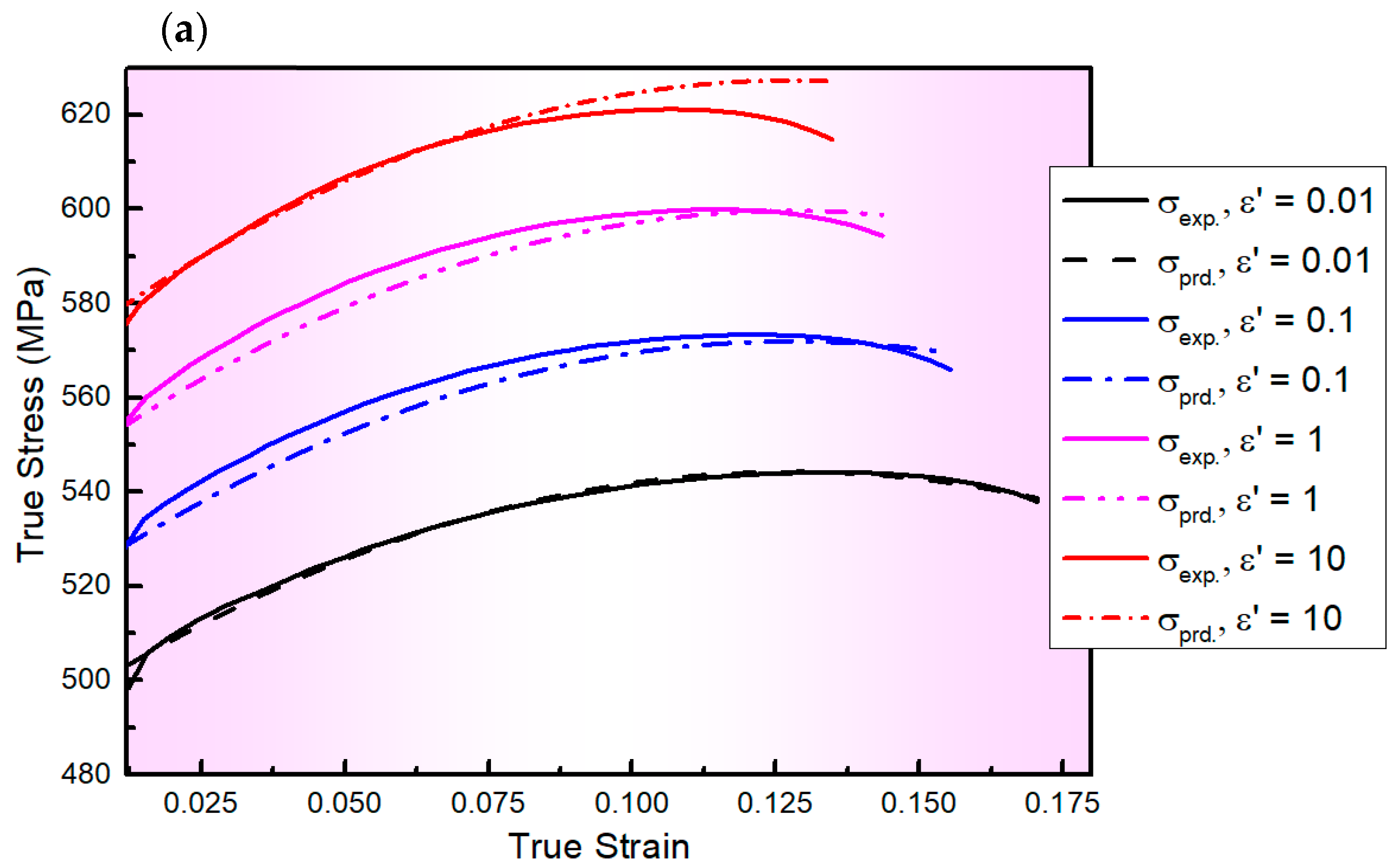
3.2.1. Modified ZA (MZA) Constitutive Model
3.2.2. Lin’s Modified Johnson–Cook Model (L-MJC)
3.2.3. Shokry’s Modified Johnson–Cook Model-1 (S1-MJC)
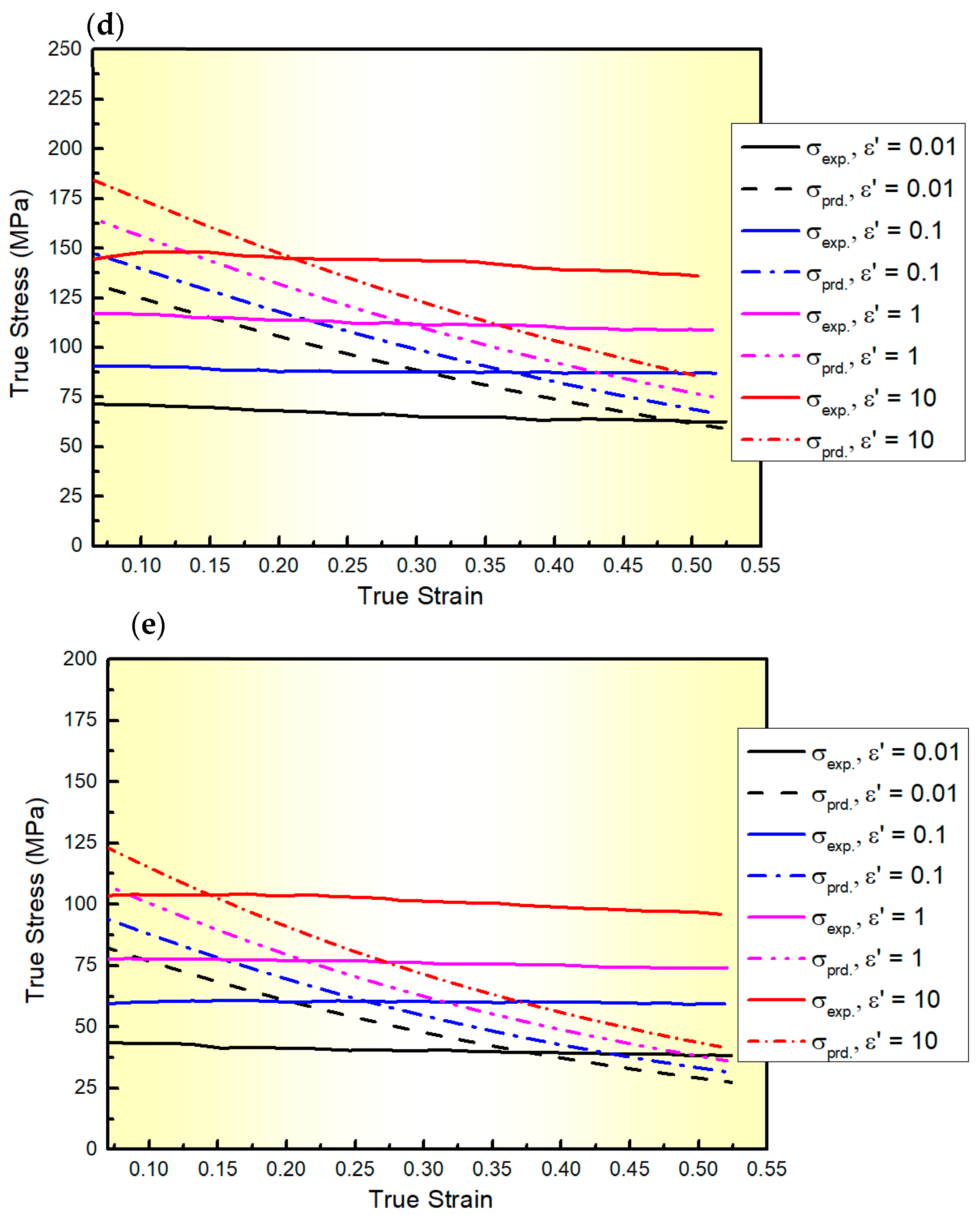
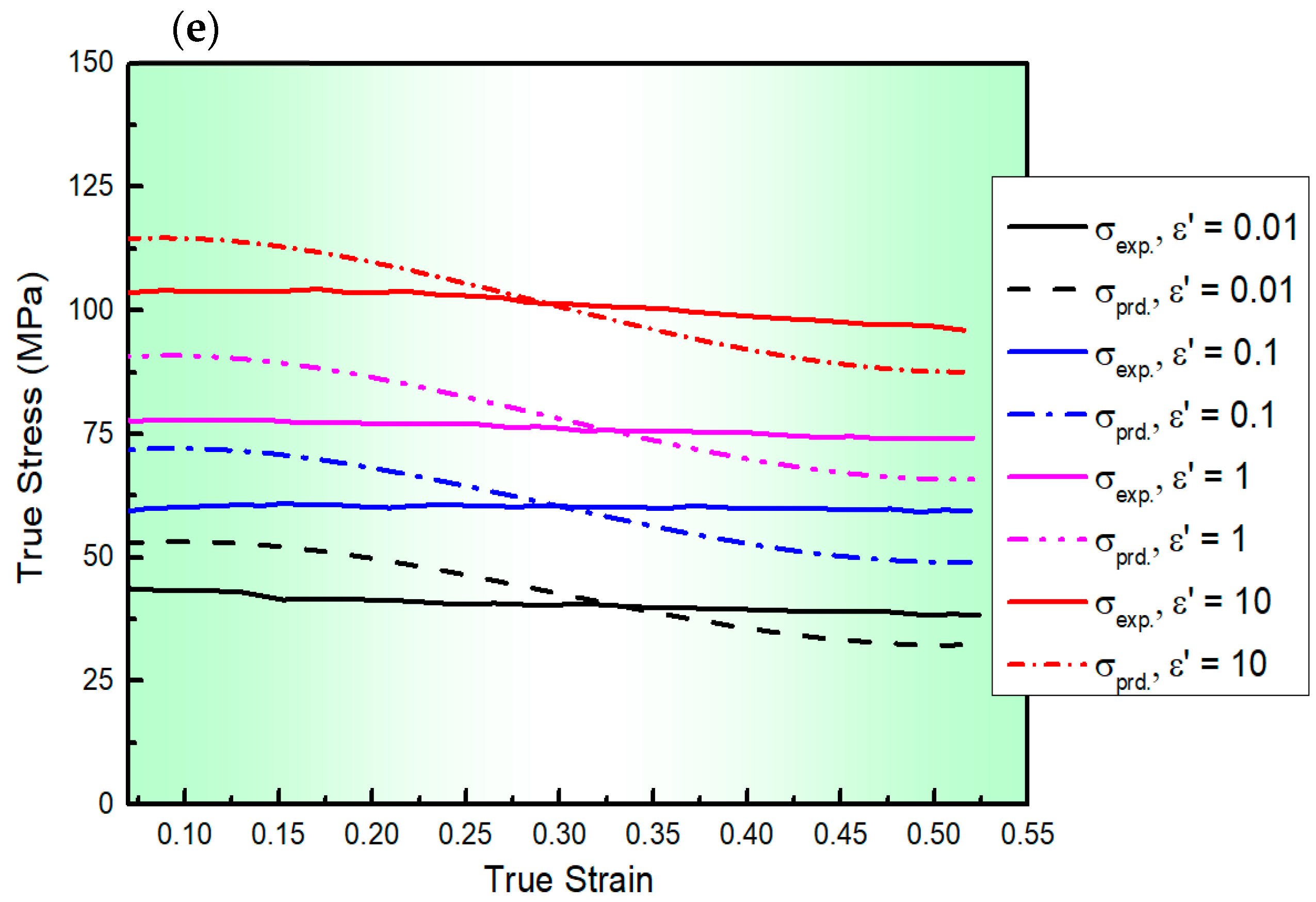
3.2.4. Shokry’s Modified Johnson–Cook Model-2 (S2-MJC)
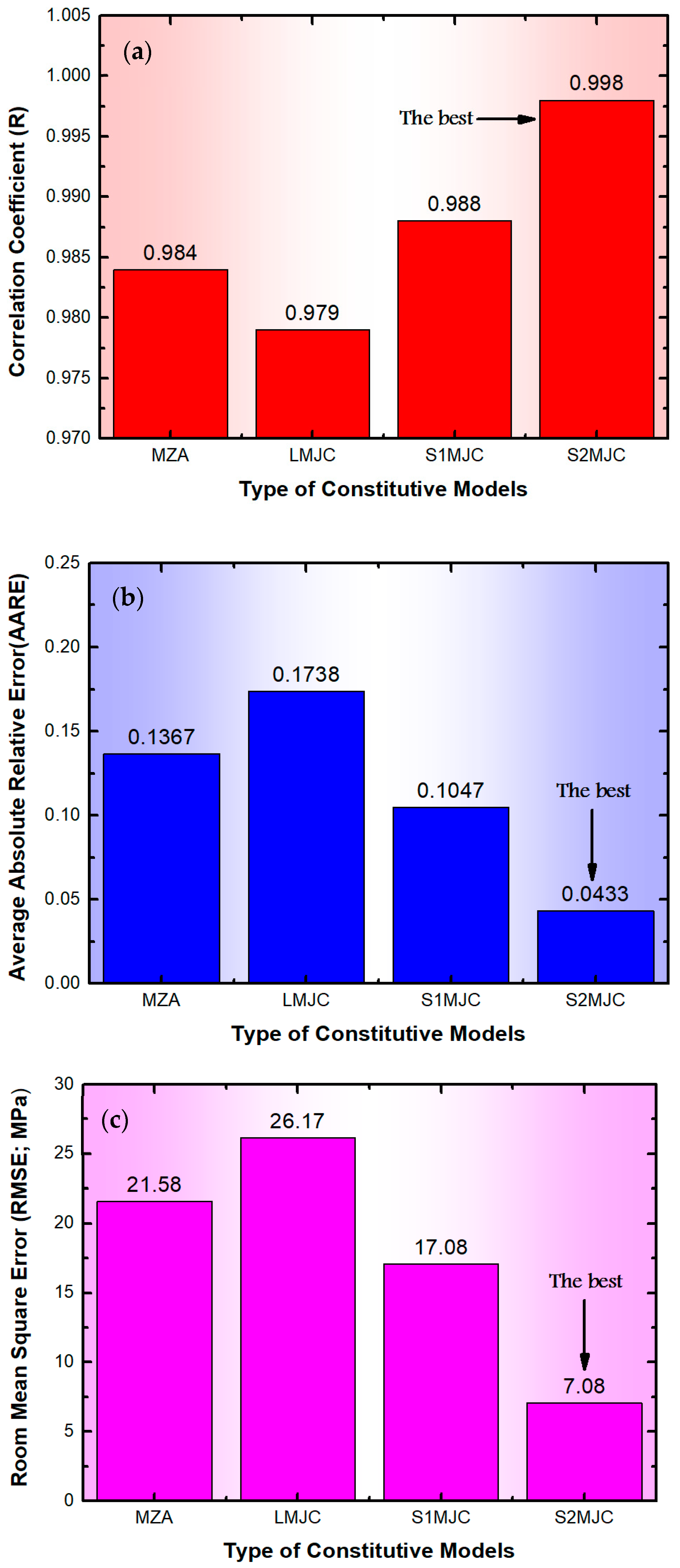
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abd El-Aty, A.; Xu, Y.; Guo, X.; Zhang, S.; Ma, Y.; Chen, D. Strengthening mechanisms, deformation behavior, and anisotropic mechanical properties of Al-Li alloys: A review. J. Adv. Res. 2018, 10, 49–67. [Google Scholar] [CrossRef] [PubMed]
- Khokhlatova, L.; Kolobnev, N.; Oglodkov, M.; Mikhaylov, E. Aluminum-lithium alloys for aircraft building. Metallurgist 2012, 56, 336–341. [Google Scholar] [CrossRef]
- Dong, F.; Huang, S.; Yi, Y.; He, H.; Huang, K.; Gao, S.; Jia, Y.; Yu, W. Effect of increased stretching deformation at cryogenic temperature on the precipitation behavior and mechanical properties of 2060 Al–Li alloy. Mater. Sci. Eng. A 2022, 834, 142585. [Google Scholar] [CrossRef]
- Dong, F.; Yi, Y.; Huang, S.; Wang, B.; He, H.; Huang, K.; Wang, C. Cryogenic formability and deformation behavior of 2060 Al–Li alloys with water-quenched and T4 aged temper. Mater. Sci. Eng. A 2021, 823, 141722. [Google Scholar] [CrossRef]
- Hou, Y.; Myung, D.; Park, J.K.; Min, J.; Lee, H.-R.; El-Aty, A.A.; Lee, M.-G. A Review of Characterization and Modelling Approaches for Sheet Metal Forming of Lightweight Metallic Materials. Materials 2023, 16, 836. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Luo, P.; Yue, G.; Hu, Y. Analysis of microstructure and high-temperature tensile properties of 2060 Al–Li alloy strengthened by laser shock peening. J. Alloys Compd. 2021, 860, 158539. [Google Scholar] [CrossRef]
- Liu, T.; Zhao, Y.; Kang, Y.; Zhan, X. Effect of micro morphology in different zones on mechanical properties of 2060 Al–Li alloy laser welded joints. J. Manuf. Process. 2020, 50, 336–344. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, K.; Song, Y.; Ali, R.A.; Chen, W.; Wang, X. Constitutive behavior and microstructural evolution of 2060 Al–Li alloy under high strain rate: Experiment and simulation. Mater. Sci. Eng. A 2022, 844, 143048. [Google Scholar] [CrossRef]
- Abd El-Aty, A.; Xu, Y.; Zhang, S.H.; Yan, M.; Guo, X.; Tao, J.; Hou, Y.; Lee, M.G. Dynamic Deformation Behaviour of Al–Li Alloys Under High Strain Rate Deformation. In NUMISHEET 2022; The Minerals, Metals & Materials Series; Inal, K., Levesque, J., Worswick, M., Butcher, C., Eds.; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Xia, L.; Zhang, S.-H.; Xu, Y.; Chen, S.; El-Aty, A.A.; Pokrovsky, A.I. Study of the ductility enhancement of 5A90 Al–Mg–Li alloy sheets with stress relaxation. Philos. Mag. 2021, 101, 2449–2472. [Google Scholar] [CrossRef]
- Cao, L.; Liao, B.; Wu, X.; Li, C.; Huang, G.; Cheng, N. Hot Deformation Behavior and Microstructure Characterization of an Al–Cu–Li–Mg–Ag Alloy. Crystals 2020, 10, 416. [Google Scholar] [CrossRef]
- Zheng, K.; Politis, D.; Wang, L.; Lin, J. A review on forming techniques for manufacturing lightweight complex-shaped aluminium panel components. Int. J. Light. Mater. Manuf. 2018, 1, 55–80. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, X. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Ou, L.; Zheng, Z.; Nie, Y.; Jian, H. Hot deformation behavior of 2060 alloy. J. Alloys Compd. 2015, 648, 681–689. [Google Scholar] [CrossRef]
- Gao, H.; Weng, T.; Liu, J.; Li, C.; Li, Z.; Wang, L. Hot stamping of an Al-Li alloy: A feasibility study. Manuf. Rev. 2016, 9, 9–15. [Google Scholar] [CrossRef]
- Liang, H.; Nan, Y.; Ning, Y.; Li, H.; Zhang, L.; Shi, Z.; Guo, H. Correlation between strain-rate sensitivity and dynamic softening behavior during hot processing. J. Alloys Compd. 2013, 632, 478–485. [Google Scholar] [CrossRef]
- Bijish, B.; Lindgren, L. Dislocation density based model for plastic deformation and globularization of Ti-6Al-4V. Int. J. Plast. 2013, 50, 94–108. [Google Scholar]
- Elkhodary, K.; Bakr, M. Single crystal plasticity with bend–twist modes. J. Mech. Phys. Solids 2015, 79, 44–66. [Google Scholar] [CrossRef]
- Pandey, A.; Khan, A.; Kim, E.; Choi, S.; Gnäupel-Herold, T. Experimental and numerical investigations of yield surface, texture, and deformation mechanisms in AA5754 over low to high temperatures and strain rates. Int. J. Plast. 2013, 41, 165–188. [Google Scholar] [CrossRef]
- Abedrabbo, N.; Pourboghrat, F.; Carsley, J. Forming of AA5182-O and AA5754-O at elevated temperatures using coupled thermo-mechanical finite element models. Int. J. Plast. 2007, 23, 841–875. [Google Scholar] [CrossRef]
- Clayton, D. Dynamic plasticity and fracture in high density polycrystals: Constitutive modeling and numerical simulation. J. Mech. Phys. Solids 2005, 53, 261–301. [Google Scholar] [CrossRef]
- Cheong, K.S.; Busso, E.P. Discrete dislocation density modelling of single phase FCC polycrystal aggregates. Acta Mater. 2004, 52, 5665–5675. [Google Scholar] [CrossRef]
- Asaro RNeedleman, A. Texture development and strain hardening in rate dependent polycrystals. Acta Metall. 1985, 33, 923–953. [Google Scholar] [CrossRef]
- Laasraoui, A.; Jonas, J.J. Prediction of Steel Flow Stresses at High Temperatures and Strain Rates. Metall. Trans. A 1991, 22, 1545–1558. [Google Scholar] [CrossRef]
- Chen, B.; Tian, X.; Li, X.; Lu, C. Hot deformation behavior and processing maps of 2099 Al-Li alloy. J. Mater. Eng. Perform. 2014, 23, 1929–1935. [Google Scholar] [CrossRef]
- Zheng, X.; Luo, A.A.; KSachdev, J.D.A.; Ding, W. Plastic flow behavior of a high-strength magnesium alloy NZ30K. Mater. Sci. Eng. A 2012, 532, 616–622. [Google Scholar] [CrossRef]
- Meng, Q.; Bai, C.; Xu, D. Flow behavior and processing map for hot deformation of ATI425 titanium alloy. J. Mater. Sci. Technol. 2018, 34, 679–688. [Google Scholar] [CrossRef]
- Abd El-Aty, A.; Zhang, S.-H.; Xu, Y.; Ha, S. Deformation behavior and anisotropic response of 2060 Al-Cu-Li alloy: Experimental investigation and computational homogenization-based crystal plasticity modeling. J. Mater. Res. Technol. 2019, 8, 1235–1249. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Shi, H.M.A.J.S. Constitutive equations for high temperature flow stress of aluminium alloys. Mater. Sci. Technol. 1997, 13, 210–216. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.; Zhong, J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel. Comput. Mater. Sci. 2008, 42, 470–477. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Bhaduri, A.K.; Venugopal, S.; Sivaprasad, P.V. Analysis and mathematical modelling of elevated temperature flow behaviour of austenitic stainless steels. Mater. Sci. Eng. A 2011, 528, 1937–1943. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Borah, U.; Bhaduri, A.K.; Sivaprasad, P.V. A thermo-viscoplastic constitutive model to predict elevated-temperature flow behaviour in a titanium-modified austenitic stainless steel. Mater. Sci. Eng. A 2009, 526, 1–6. [Google Scholar] [CrossRef]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Bhaduri, A.K. A comparative study on Johnson Cook, modified Zerilli–Armstrong and Arrhenius-type constitutive models to predict elevated temperature flow behaviour in modified 9Cr–1Mo steel. Comput. Mater. Sci. 2009, 47, 568–576. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Bhaduri, A.K. Constitutive analysis to predict high-temperature flow stress in modified 9Cre1Mo (P91) steel. Mater. Des. 2010, 31, 981–984. [Google Scholar] [CrossRef]
- Shokry, A.; Gowid, S.; Youssef, S.S. Modeling the flow behavior of Haynes 214 superalloy during hot deformation using mathematical and artificial intelligence-based models. Mater. Today Commun. 2022, 33, 104326. [Google Scholar] [CrossRef]
- Shokry, A.; Gowid, S.; Mulki, H.; Kharmanda, G. On the Prediction of the Flow Behavior of Metals and Alloys at a Wide Range of Temperatures and Strain Rates Using Johnson–Cook and Modified Johnson–Cook-Based Models: A Review. Materials 2023, 16, 1574. [Google Scholar] [CrossRef]
- Yaich, M.; Gavrus, A. New phenomenological material constitutive models for the description of the Ti6Al4V titanium alloy behavior under static and dynamic loadings. Proc. Manuf. 2020, 47, 1496–1503. [Google Scholar] [CrossRef]
- Ma, L.; Wan, M.; Li, W.; Shao, J.; Bai, X.; Zhang, J. Superplastic deformation mechanical behavior and constitutive modelling of a near-a titanium alloy TNW700 sheet. Mater. Sci. Eng. A Struct. Mater. Propert. Microstruct. Process. 2021, 817, 141419. [Google Scholar] [CrossRef]
- Shrot, A.; Beaker, M. Determination of Johnson-Cook parameters from machining simulations. Comput. Mater. Sci. 2012, 52, 298e–304. [Google Scholar] [CrossRef]
- Qiao, L.; Zhu, J. Constitutive modeling of hot deformation behavior of AlCrFeNi multi-component alloy. Vacuum 2022, 201, 111059. [Google Scholar] [CrossRef]
- Wang, H.; Qin, G.; Li, C. A modified Arrhenius constitutive model of 2219-O aluminum alloy based on hot compression with simulation verification. J. Mater. Res. Technol. 2022, 19, 3302–3320. [Google Scholar] [CrossRef]
- Jia, W.; Xu, S.; Le, Q.; Fu, L.; Ma, L.; Tang, Y. Modified Fields-Backofen model for constitutive behavior of as-cast AZ31B magnesium alloy during hot deformation. Mater. Des. 2016, 106, 120–132. [Google Scholar] [CrossRef]
- Shen, J.; Hu, L.; Sun, Y.; Wan, Z.; Feng, X.; Ning, Y. A comparative study on artificial neural network, phenomenological-based constitutive and modified fields-backofen models to predict flow stress in Ti-4Al-3V-2Mo-2Fe alloy. J. Mater. Eng. Perform. 2019, 28, 4302–4315. [Google Scholar] [CrossRef]
- Seshacharyulu, K.; Mahalle, G.; Kotkunde, N.; Singh, S.K.; Balu Naik, B. High temperatures deformation and formability behavior of DP590 steel: Mechanical characterization and modeling. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 472. [Google Scholar] [CrossRef]
- Mahalle, G.; Salunke, O.; Kotkunde, N.; Kumar Gupta, A.; Singh, S.K. Study of Khan-Huang-liang (KHL) anisotropic deformation model for deep drawing behaviour of inconel 718 alloy. IOP Conf. Ser. Mater. Sci. Eng. 2020, 967, 12054. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data formetals subjected to large strains, high strain rates and hightemperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.-M.; Liu, G. A modified Johnson–Cook model for tensile behaviors of typical high-strength alloy steel. Mater. Sci. Eng. A 2010, 527, 6980–6986. [Google Scholar] [CrossRef]
- Shokry, A. A modified Johnson–Cook model for flow behavior of alloy 800H at intermediate strain rates and high temperatures. J. Mater. Eng. Perform. 2017, 26, 5723–5730. [Google Scholar] [CrossRef]
- Shokry, A.; Gowid, S.; Kharmanda, G. An improved generic Johnson-Cook model for the flow prediction of different categories of alloys at elevated temperatures and dynamic loading conditions. Mater. Today Commun. 2021, 27, 102296. [Google Scholar] [CrossRef]
- Kumar, S.; Karmakar, A.; Nath, S.K. Construction of hot deformation processing maps for 9Cr-1Mo steel through conventional and ANN approach, Mater. Today Commun. 2021, 26, 101903. [Google Scholar]
- Pan, C.; Cheng, C.; Abd El-Aty, A.; Wang, J.; Tao, J.; Liu, C.; Guo, X.; Hu, S. Predicting the wrinkling in AA5052 seamless tubes manufactured by free bending forming technology. J. Manuf. Process. 2023, 101, 1065–1079. [Google Scholar] [CrossRef]
- Cheng, Z.; Abd El-Aty, A.; Zhang, R.; Cheng, C.; Guo, X.; Tao, J. Finite element modeling and experimental investigation on manufacturing TA18 alloy pipes via hot free bending forming technology: Forming characteristics and process optimization. J. Mater. Res. Technol. 2024, 29, 5225–5240. [Google Scholar] [CrossRef]



| 498 | 125.34 | 0.51 | 0.0042 | 0.0066 | 0.0184 | 0.0001 |
| 494.13 | 784.69 | −3069.85 | 0.0221 | −0.0048 | 0.0001 |
| 492.31 | 883.74 | −4376.80 | 4798.92 | 0.0244 | −0.0189 | 0.5717 | −0.1791 |
| 492.31 | 883.74 | −4376.8 | 4798.92 | 0.0245 | −0.0013 | 0.0001 | 0.0471 |
| −0.0188 | 0.0018 | −0.4575 | 0.1516 | −0.0145 | −1.1437 | 0.0565 | −0.0062 |
| m010 | m011 | m012 | m020 | m021 | m022 | m100 | m101 |
| −8.3062 | −0.4676 | 0.0633 | 47.2185 | −9.5081 | 0.6546 | −3.2713 | −0.6143 |
| 0.0571 | 10.8928 | 6.2511 | −0.5799 | −96.990 | 24.966 | −1.7706 | 0.8372 |
| 2.3817 | −0.2075 | 1.4364 | −11.601 | 1.0106 | 61.103 | −15.1629 | 1.0568 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd El-Aty, A.; Xu, Y.; Hou, Y.; Zhang, S.-H.; Ha, S.; Xia, L.; Alzahrani, B.; Ali, A.; Ahmed, M.M.Z.; Shokry, A. Modelling the Flow Behaviour of Al Alloy Sheets at Elevated Temperatures Using a Modified Zerilli–Armstrong Model and Phenomenological-Based Constitutive Models. Materials 2024, 17, 1584. https://doi.org/10.3390/ma17071584
Abd El-Aty A, Xu Y, Hou Y, Zhang S-H, Ha S, Xia L, Alzahrani B, Ali A, Ahmed MMZ, Shokry A. Modelling the Flow Behaviour of Al Alloy Sheets at Elevated Temperatures Using a Modified Zerilli–Armstrong Model and Phenomenological-Based Constitutive Models. Materials. 2024; 17(7):1584. https://doi.org/10.3390/ma17071584
Chicago/Turabian StyleAbd El-Aty, Ali, Yong Xu, Yong Hou, Shi-Hong Zhang, Sangyul Ha, Liangliang Xia, Bandar Alzahrani, Alamry Ali, Mohamed M. Z. Ahmed, and Abdallah Shokry. 2024. "Modelling the Flow Behaviour of Al Alloy Sheets at Elevated Temperatures Using a Modified Zerilli–Armstrong Model and Phenomenological-Based Constitutive Models" Materials 17, no. 7: 1584. https://doi.org/10.3390/ma17071584









