An Improved Method for Deriving the Heat Source Model for FCAW of 9% Nickel Steel for Cryogenic Tanks
Abstract
:1. Introduction
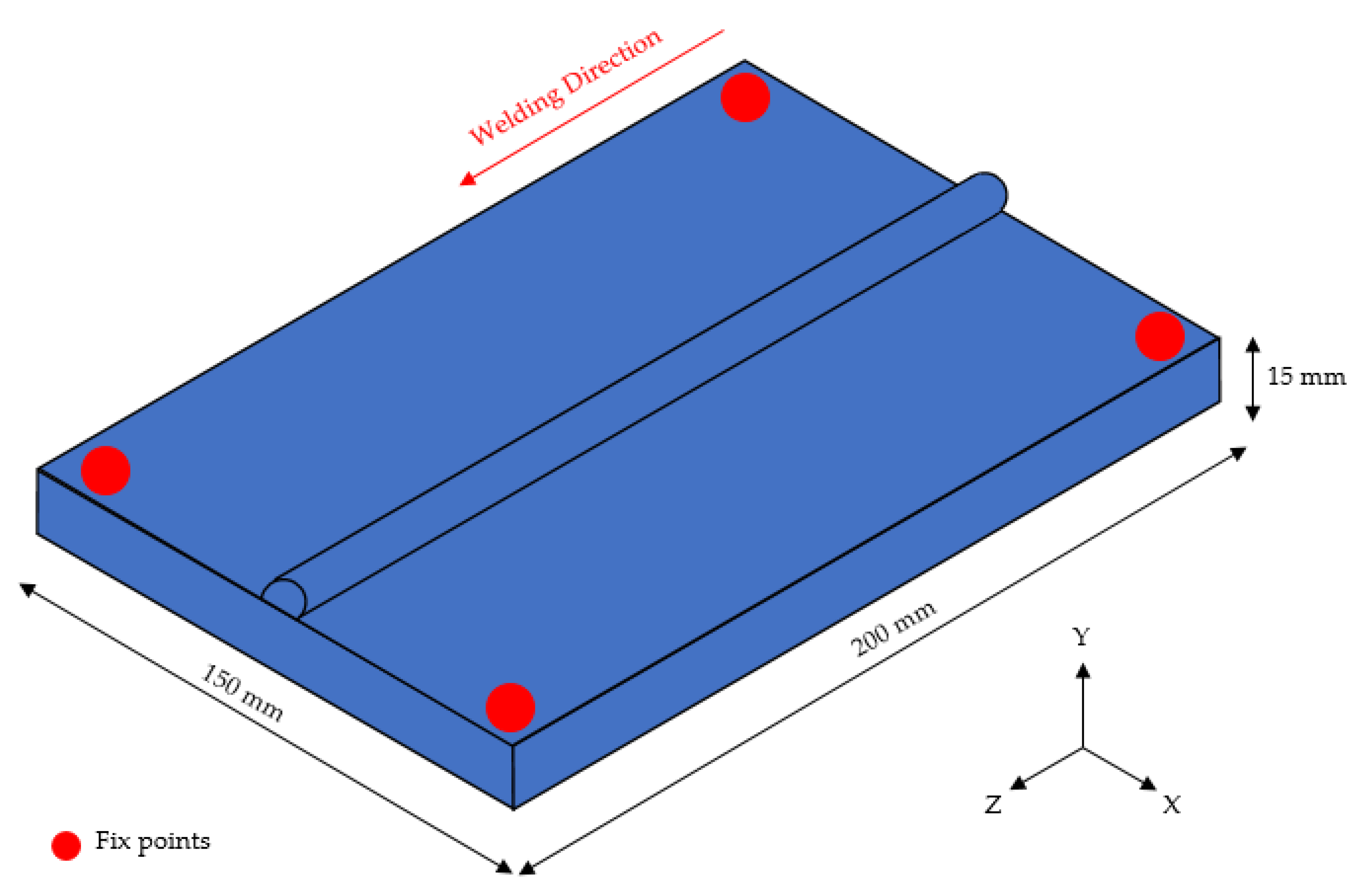
2. Welding Experiments and Results
2.1. Welding Materials and Conditions
2.2. Cross-Section Analysis Results
3. Deriving the Heat Source Model
3.1. Process for Deriving the Heat Source
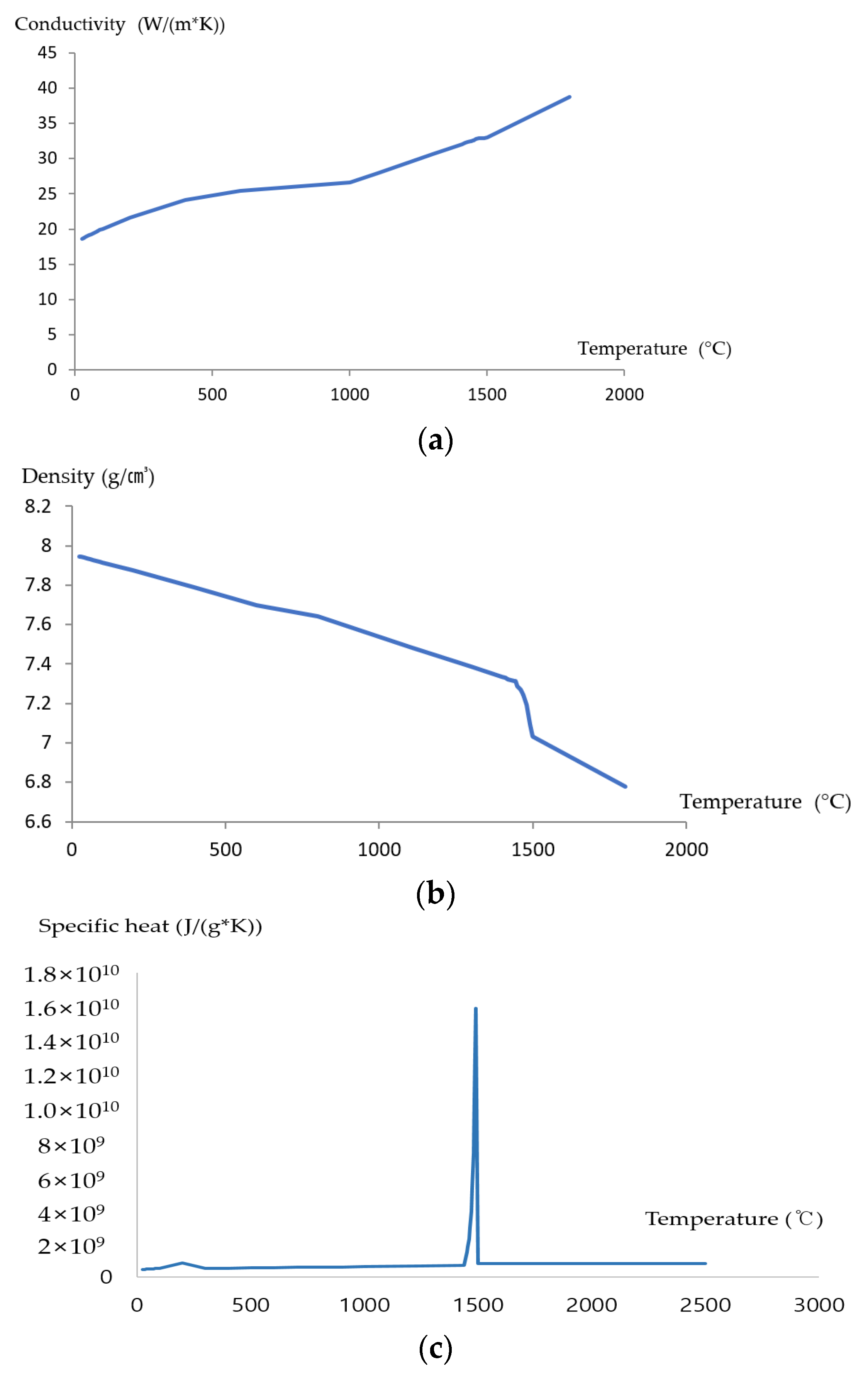
3.2. Simplifying the Heat Transfer Analysis Model
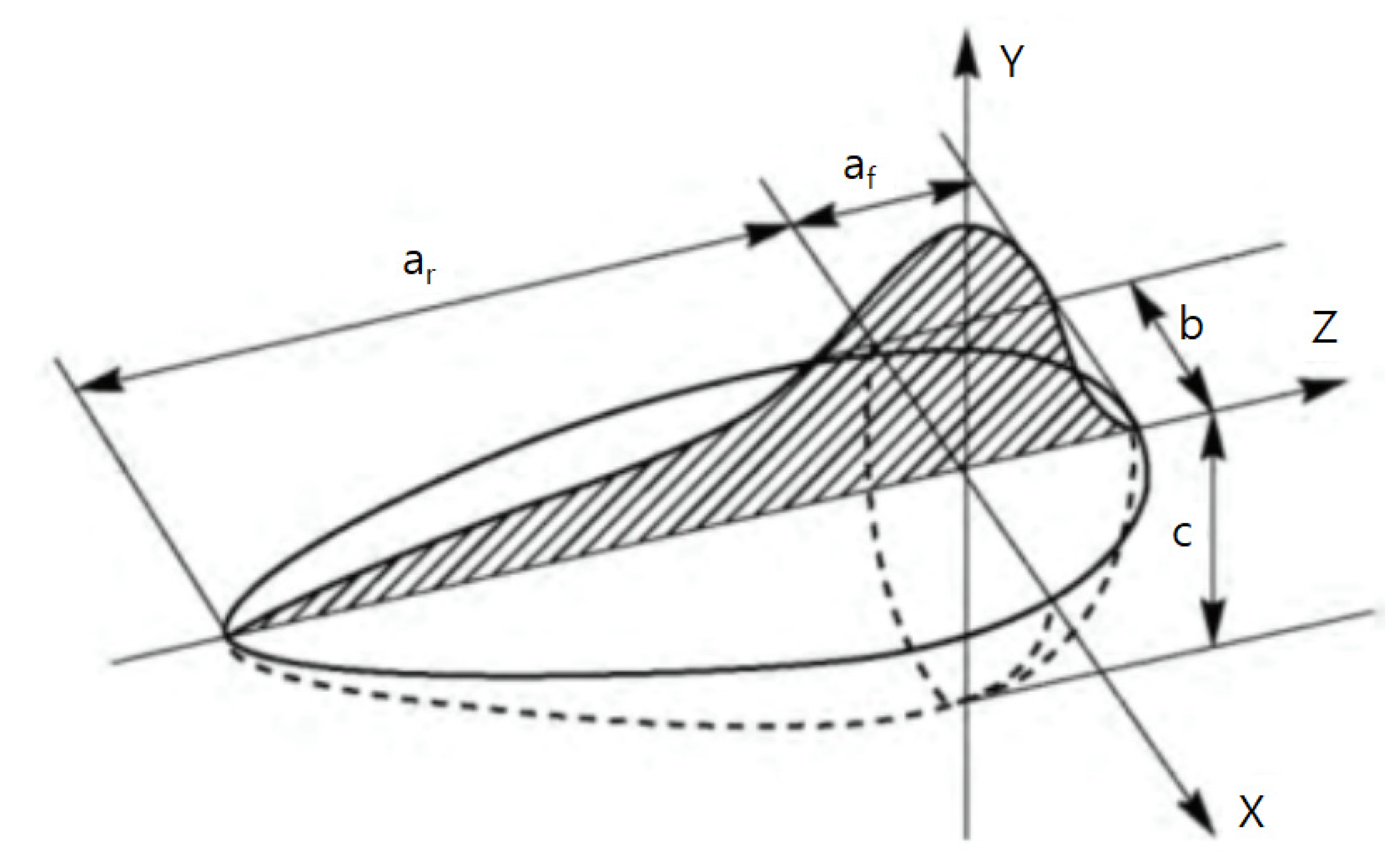
3.3. Goldak Model Heat Source
4. Optimization Algorithm
4.1. Software
4.2. Algorithm Process
4.3. Limiting Parameter Temperature Range
4.4. Setting Variables and Ranges
5. Results and Analysis
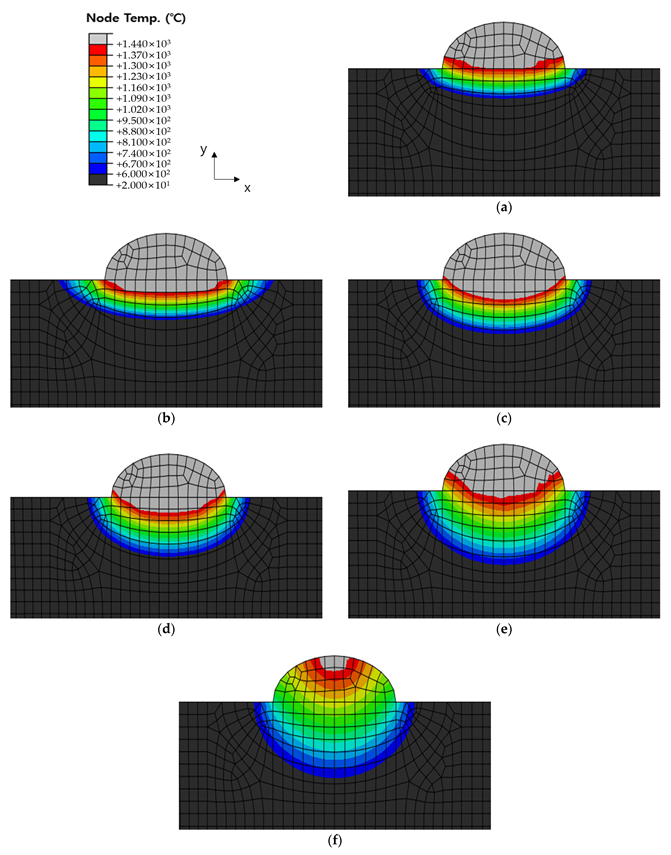
5.1. Deriving the Heat Source Parameters and Heat Transfer Analysis Results
5.2. Heat Transfer Analysis Results by Welding Conditions
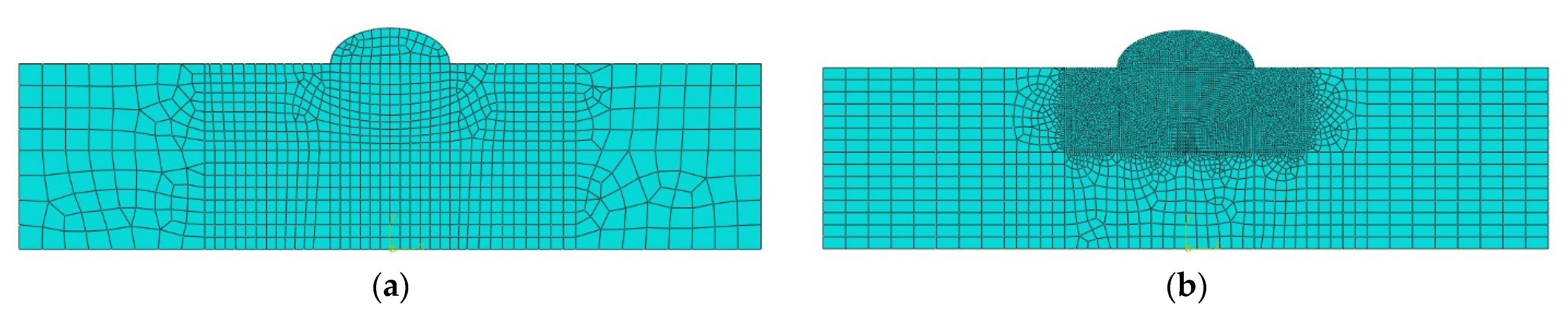
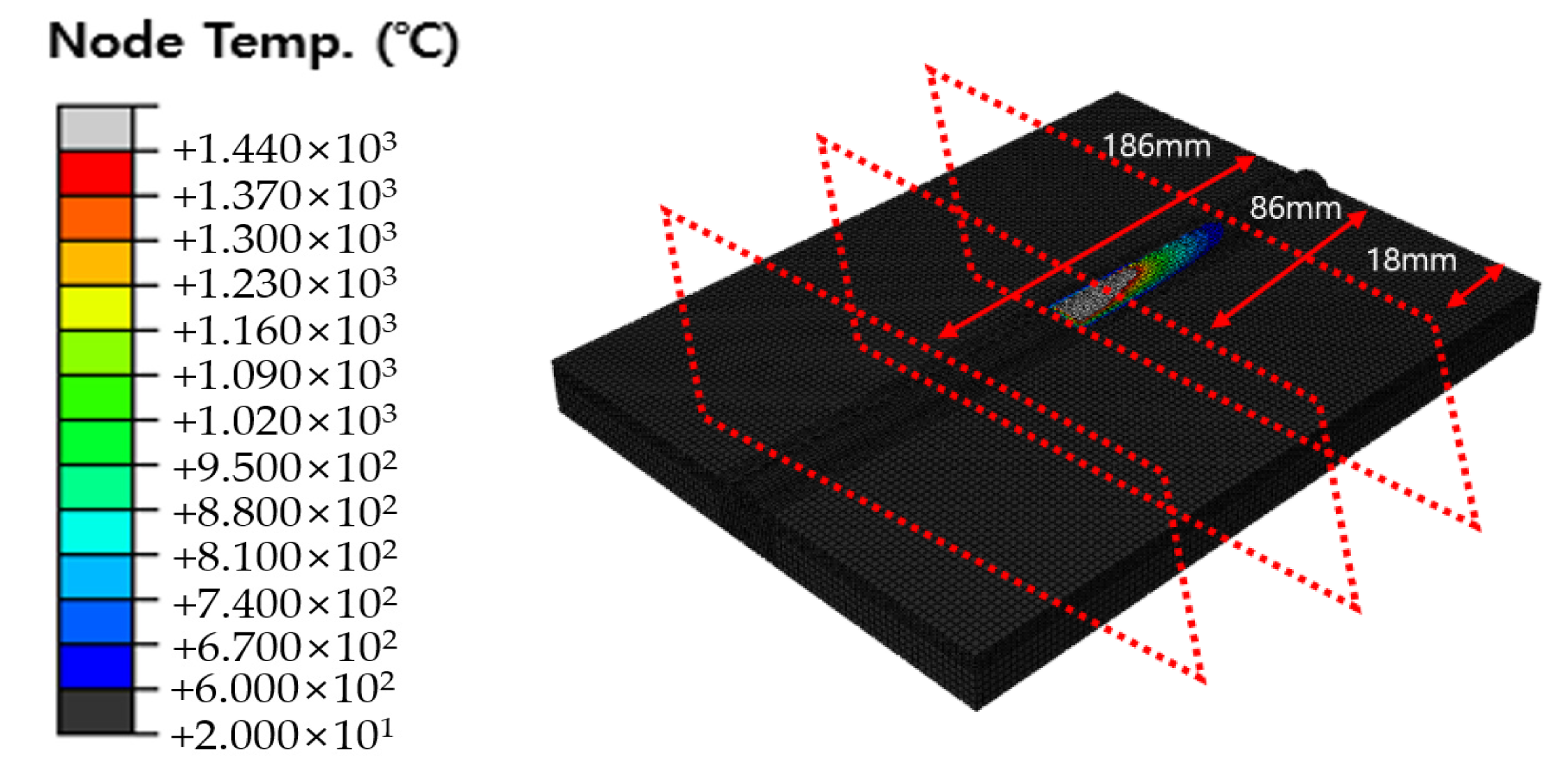
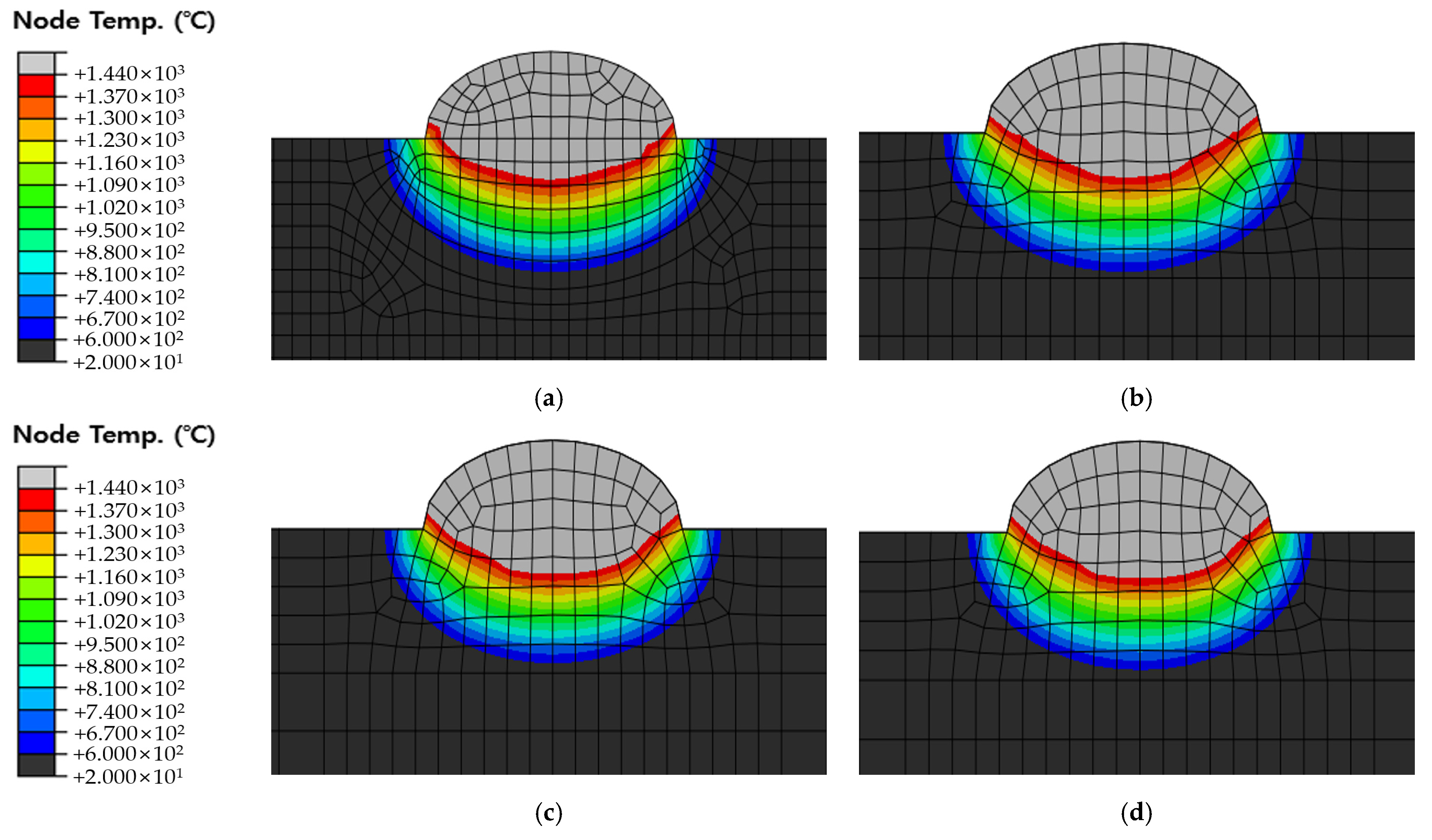
5.3. Comparing the Heat Transfer Results between the Original Dimension Model and the Simplified Model
6. Conclusions
- (1)
- The heat transfer analysis results show that the optimal parameters of the Goldak model derived by the optimization algorithm satisfied all temperature constraints.
- (2)
- The model applied in the previous study was simplified to speed up the analysis process, which increased the analysis speed by about 70%.
- (3)
- A heat source model that melts the entire weld bead was derived through the temperature constraints of the weld point, and a consistent HAZ area was simulated through a new objective function.
- (4)
- By comparing the HAZ width and HAZ depth of the simplified model with the actual weld cross-sections, the HAZ width and depth exhibited maximum differences of 4.81% and 14.73%, respectively.
- (5)
- By comparing the heat transfer analysis results between the simplified model and the original dimension model, the HAZ width and depth showed maximum differences of 13.49% and 12.75%, respectively.
- (6)
- This study applied a simplified model based on the HAZ size to rapidly derive optimal heat source parameters and identify the weld geometry through heat transfer analysis, which was considered to save time.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, M.; Kim, J.; Pyo, C.; Son, J.; Kim, J. Research for the Optimal Flux-Cored Arc Welding Process of 9% Nickel Steel Using Multi Object Optimization with Solidification Crack Susceptibility. Materials 2021, 14, 1659. [Google Scholar] [CrossRef] [PubMed]
- Park, D.-H.; Yi, M.-S.; Lee, J.-M. A Study on Welding-induced Temperature Distribution and Deformation of IMO Type C LNG Fuel Tank Support Structures. J. Weld. Join. 2022, 40, 118–132. [Google Scholar] [CrossRef]
- Mohd Noor, C.W.; Noor, M.M.; Mamat, R. Biodiesel as alternative fuel for marine diesel engine applications: A review. Renew. Sustain. Energy Rev. 2018, 94, 127–142. [Google Scholar] [CrossRef]
- Solakivi, T.; Laari, S.; Kiiski, T.; Töyli, J.; Ojala, L. How shipowners have adapted to sulphur regulations—Evidence from Finnish seaborne trade. Case Stud. Transp. Policy 2019, 7, 338–345. [Google Scholar] [CrossRef]
- Vierth, I.; Karlsson, R.; Mellin, A. Effects of More Stringent Sulphur Requirements for Sea Transports. Transp. Res. Procedia 2015, 8, 125–135. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, D.; Caglayan, O.; Jenkinson, I.; Bonsall, S.; Wang, J.; Huang, M.; Yan, X. Selection of techniques for reducing shipping NOx and SOx emissions. Transp. Res. Part D Transp. Environ. 2012, 17, 478–486. [Google Scholar] [CrossRef]
- Gu, Y.; Wallace, S.W. Scrubber: A potentially overestimated compliance method for the Emission Control Areas: The importance of involving a ship’s sailing pattern in the evaluation. Transp. Res. Part D Transp. Environ. 2017, 55, 51–66. [Google Scholar] [CrossRef]
- Hwang, S.; Jeong, B.; Jung, K.; Kim, M.; Zhou, P. Life Cycle Assessment of LNG Fueled Vessel in Domestic Services. J. Mar. Sci. Eng. 2019, 7, 359. [Google Scholar] [CrossRef]
- Burel, F.; Taccani, R.; Zuliani, N. Improving sustainability of maritime transport through utilization of Liquefied Natural Gas (LNG) for propulsion. Energy 2013, 57, 412–420. [Google Scholar] [CrossRef]
- Lee, D.; Kim, K.H.; Choi, I.; Gil Lee, D. Pressure-resisting capability of the knot area of the primary barrier for a LNG containment system. Ocean Eng. 2015, 95, 128–133. [Google Scholar] [CrossRef]
- Jo, Y.; Shin, K.; Hwang, S. Development of dynamic simulation model of LNG tank and its operational strategy. Energy 2021, 223, 120060. [Google Scholar] [CrossRef]
- Wang, S. The Adoption of Liquefied Natural Gas as a Ship Fuel: A Systematic Review of Perspectives and Challenges. Transp. Rev. 2014, 34, 749–774. [Google Scholar] [CrossRef]
- Kumar, S.; Kwon, H.-T.; Choi, K.-H.; Lim, W.; Cho, J.H.; Tak, K.; Moon, I. LNG: An eco-friendly cryogenic fuel for sustainable development. Appl. Energy 2011, 88, 4264–4273. [Google Scholar] [CrossRef]
- Bernatik, A.; Senovsky, P.; Pitt, M. LNG as a potential alternative fuel—Safety and security of storage facilities. J. Loss Prev. Process Ind. 2011, 24, 19–24. [Google Scholar] [CrossRef]
- Park, T.-U.; Jung, D.-H.; Park, J.-H.; Kim, J.-H.; Han, I.-W. Changes in the Mechanical Properties and Microstructure of High Manganese Steel by High Heat Input Welding and General Welding Processes. J. Weld. Join. 2022, 40, 33–39. [Google Scholar] [CrossRef]
- Park, T.-U.; Jeong, Y.-C.; Im, H.-D.; Choi, C.; Kil, W. Development and Evaluation of Stainless Steel-Base Flux-Cored Wires for 9% Nickel Steel. J. Weld. Join. 2022, 40, 367–376. [Google Scholar] [CrossRef]
- Pyo, C.-M. Experimental Study According to the Type of Shielding Gas using Fiber Laser Welding of 9% Nickel Steel. J. Korean Soc. Mech. Technol. 2021, 23, 702–707. [Google Scholar] [CrossRef]
- Park, J.-H.; Kim, Y.-H.; Baek, H.-J.; Cho, S.-M. A study on process development of super-TIG welding for 9% nickel steel with Alloy 625. J. Manuf. Process. 2019, 40, 140–148. [Google Scholar] [CrossRef]
- Xu, T.; Shi, Y.; Jiang, Z.; Wu, L.; Ma, Y.; Wang, Z. Improvement of cryogenic toughness for 9% Ni steel keyhole TIG butt-welded joints with a Ni interlayer. Mater. Sci. Eng. A 2022, 835, 142661. [Google Scholar] [CrossRef]
- Gook, S.; Krieger, S.; Gumenyuk, A.; El-Batahgy, A.; Rethmeier, M. Notch impact toughness of laser beam welded thick sheets of cryogenic nickel alloyed steel X8Ni9. Procedia CIRP 2020, 94, 627–631. [Google Scholar] [CrossRef]
- Kim, J. A Study on FCAW Butt Welds of 9% Nickel Steel Materials for Vessel Cryogenic Tank Part II: Mechanical Properties Study of Welding Bead. J. Korean Soc. Mech. Technol. 2021, 23, 426–431. [Google Scholar] [CrossRef]
- Mu, W.; Li, Y.; Cai, Y.; Wang, M. Cryogenic fracture toughness of 9%Ni steel flux cored arc welds. J. Mater. Process. Technol. 2018, 252, 804–812. [Google Scholar] [CrossRef]
- Park, M.; Kim, J.; Pyo, C.; Kim, J.; Chun, K. A Study on the Weldment Hardening Discrimination Procedure and Improvement of Flux Cored Arc Welding Process of ASTM A553-1 (9% Nickel Steel) Material Using Bead Geometry Distribution. Metals 2021, 11, 1282. [Google Scholar] [CrossRef]
- Moshtaghi, M.; Loder, B.; Safyari, M.; Willidal, T.; Hojo, T.; Mori, G. Hydrogen trapping and desorption affected by ferrite grain boundary types in shielded metal and flux-cored arc weldments with Ni addition. Int. J. Hydrogen Energy 2022, 47, 20676–20683. [Google Scholar] [CrossRef]
- Kim, Y.-K.; Kim, J.-H. Welding Residual Stress and Strength of Thick 9% Nickel Steel Plate. J. Korean Soc. Power Syst. Eng. 2014, 18, 85–90. [Google Scholar] [CrossRef]
- Manurung, Y.H.P.; Lidam, R.N.; Rahim, M.R.; Zakaria, M.Y.; Redza, M.R.; Sulaiman, M.S.; Tham, G.; Abas, S.K. Welding distortion analysis of multipass joint combination with different sequences using 3D FEM and experiment. Int. J. Press. Vessel. Pip. 2013, 111–112, 89–98. [Google Scholar] [CrossRef]
- Deng, D.; Murakawa, H. FEM prediction of buckling distortion induced by welding in thin plate panel structures. Comput. Mater. Sci. 2008, 43, 591–607. [Google Scholar] [CrossRef]
- García-García, V.; Mejía, I.; Reyes-Calderón, F. Experimental and FEM study of Ti-containing TWIP steel weldability. J. Mater. Process. Technol. 2018, 261, 107–122. [Google Scholar] [CrossRef]
- Pyo, C.-M. Research for Estimation of Heat Source Model Parameters with Simplified FE Model & Global Optimization Algorithm Part I. Application of Adaptive Simulated Annealing. J. Korean Soc. Mech. Technol. 2020, 22, 484–491. [Google Scholar] [CrossRef]
- Park, M.; Kim, J.; Pyo, C. A Study on Heat Input Control and a Quality Evaluation Algorithm to Prevent Toughness Deterioration of the Heat-Affected Zone in the Fiber Laser Welding Process of ASTM A553-1 (9% Nickel Steel) Material. Metals 2022, 12, 1195. [Google Scholar] [CrossRef]
- Obeid, O.; Leslie, A.J.; Olabi, A.G. Influence of girth welding material on thermal and residual stress fields in welded lined pipes. Int. J. Press. Vessel. Pip. 2022, 200, 104777. [Google Scholar] [CrossRef]
- Attar, M.A.; Ghoreishi, M.; Beiranvand, Z.M. Prediction of weld geometry, temperature contour and strain distribution in disk laser welding of dissimilar joining between copper & 304 stainless steel. Optik 2020, 219, 165288. [Google Scholar] [CrossRef]
- Pankaj, P.; Sawarkar, P.S.; Tiwari, A.; Biswas, P.; Pal, S. Three dimensional FE thermal analysis for friction stir welding of low carbon steel. Mater. Today Proc. 2020, 41, 902–907. [Google Scholar] [CrossRef]
- Hammad, A.; Churiaque, C.; Sánchez-Amaya, J.M.; Abdel-Nasser, Y. Experimental and numerical investigation of hybrid laser arc welding process and the influence of welding sequence on the manufacture of stiffened flat panels. J. Manuf. Process. 2020, 61, 527–538. [Google Scholar] [CrossRef]
- Ling, Y.; Ni, J.; Antonissen, J.; Ben Hamouda, H.; Voorde, J.V.; Wahab, M.A. Numerical prediction of microstructure and hardness for low carbon steel wire Arc additive manufacturing components. Simul. Model. Pract. Theory 2023, 122, 102664. [Google Scholar] [CrossRef]
- Hu, L.; Li, X.; Luo, W.; Li, S.; Deng, D. Residual stress and deformation in UHS quenched steel butt-welded joint. Int. J. Mech. Sci. 2023, 245, 108099. [Google Scholar] [CrossRef]
- Li, X.; Hu, L.; Deng, D. Influence of contact behavior on welding distortion and residual stress in a thin-plate butt-welded joint performed by partial-length welding. Thin-Walled Struct. 2022, 176, 109302. [Google Scholar] [CrossRef]
- Luo, W.; Guo, X.; Dai, J.; Rao, T. Hull optimization of an underwater vehicle based on dynamic surrogate model. Ocean Eng. 2021, 230, 109050. [Google Scholar] [CrossRef]
- Farias, R.; Teixeira, P.; Vilarinho, L. Variable profile heat source models for numerical simulations of arc welding processes. Int. J. Therm. Sci. 2022, 179, 107593. [Google Scholar] [CrossRef]
- Farias, R.; Teixeira, P.; Vilarinho, L. An efficient computational approach for heat source optimization in numerical simulations of arc welding processes. J. Constr. Steel Res. 2020, 176, 106382. [Google Scholar] [CrossRef]
- Pyo, C.; Jeong, S.-M.; Kim, J.; Park, M.; Shin, J.; Kim, Y.; Son, J.; Kim, J.-H.; Kim, M.-H. A Study on the Enhanced Process of Elaborate Heat Source Model Parameters for Flux Core Arc Welding of 9% Nickel Steel for Cryogenic Storage Tank. J. Mar. Sci. Eng. 2022, 10, 1810. [Google Scholar] [CrossRef]
- Wang, H.; Hou, Y.; Xiong, Y. Research on multi-interval coupling optimization of vessel speed for energy efficiency. Ocean Eng. 2022, 257, 111559. [Google Scholar] [CrossRef]
- Pyo, C.-M. A Study for Heat Source Model for Fiber Laser Welding with Global Optimization Algorithm Part I. Verification of Multi Layered Heat Source Model. J. Korean Soc. Mech. Technol. 2021, 23, 137–144. [Google Scholar] [CrossRef]
- Hahn, Y.; Cofer, J. Design Study of Dovetail Geometries of Turbine Blades Using Abaqus and Isight; Volume 7: Structures and Dynamics, Parts A and B. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; pp. 11–20. [Google Scholar]
- He, K.; Tole, K.; Ni, F.; Yuan, Y.; Liao, L. Adaptive large neighborhood search for solving the circle bin packing problem. Comput. Oper. Res. 2020, 127, 105140. [Google Scholar] [CrossRef]
- Hifi, M.; Paschos, V.T.; Zissimopoulos, V. A simulated annealing approach for the circular cutting problem. Eur. J. Oper. Res. 2004, 159, 430–448. [Google Scholar] [CrossRef]
- Geng, X.; Chen, Z.; Yang, W.; Shi, D.; Zhao, K. Solving the traveling salesman problem based on an adaptive simulated annealing algorithm with greedy search. Appl. Soft Comput. 2011, 11, 3680–3689. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Jeong, H.-M. Principles of Intelligent Information Systems for the 21st Century; 21cbook: Paju City, Republic of Korea, 1997; pp. 354–375. ISBN 978-898-700-116-6. [Google Scholar]
- Navid, M.; Soheil, G.; Behzad, A.; Izman, S.; Hamidreza, G.; Norizah, R.; Shukur, H.; Amran, A.; Sehun, R. A novel systematic numerical approach on determination of heat source parameters in welding process. J. Mater. Res. Technol. 2022, 18, 4427–4444. [Google Scholar] [CrossRef]








| C | Si | Mn | S | P | Ni | Fe | |
|---|---|---|---|---|---|---|---|
| Parent material | 0.05 | 0.67 | 0.004 | 0.003 | 0.25 | 9.02 | Bal. |
| Welding consumables | 0.02 | 0.02 | 0.1 | 0.001 | 0.001 | 69.8 | Bal. |
| Yield Strength (MPa) | Tensile Strength (MPa) | Elongation (%) | Hardness (HV) |
|---|---|---|---|
| 651.6 | 701.1 | 26.6 | 243 |
| Case | Current (A) | Voltage (V) | Welding Speed (m/min) | Shielding Gas (L/min) |
|---|---|---|---|---|
| Case 1 | 150 | 25 | 0.4 | 18 |
| Case 2 | 160 | 25 | 0.4 | 18 |
| Case 3 | 170 | 25 | 0.4 | 18 |
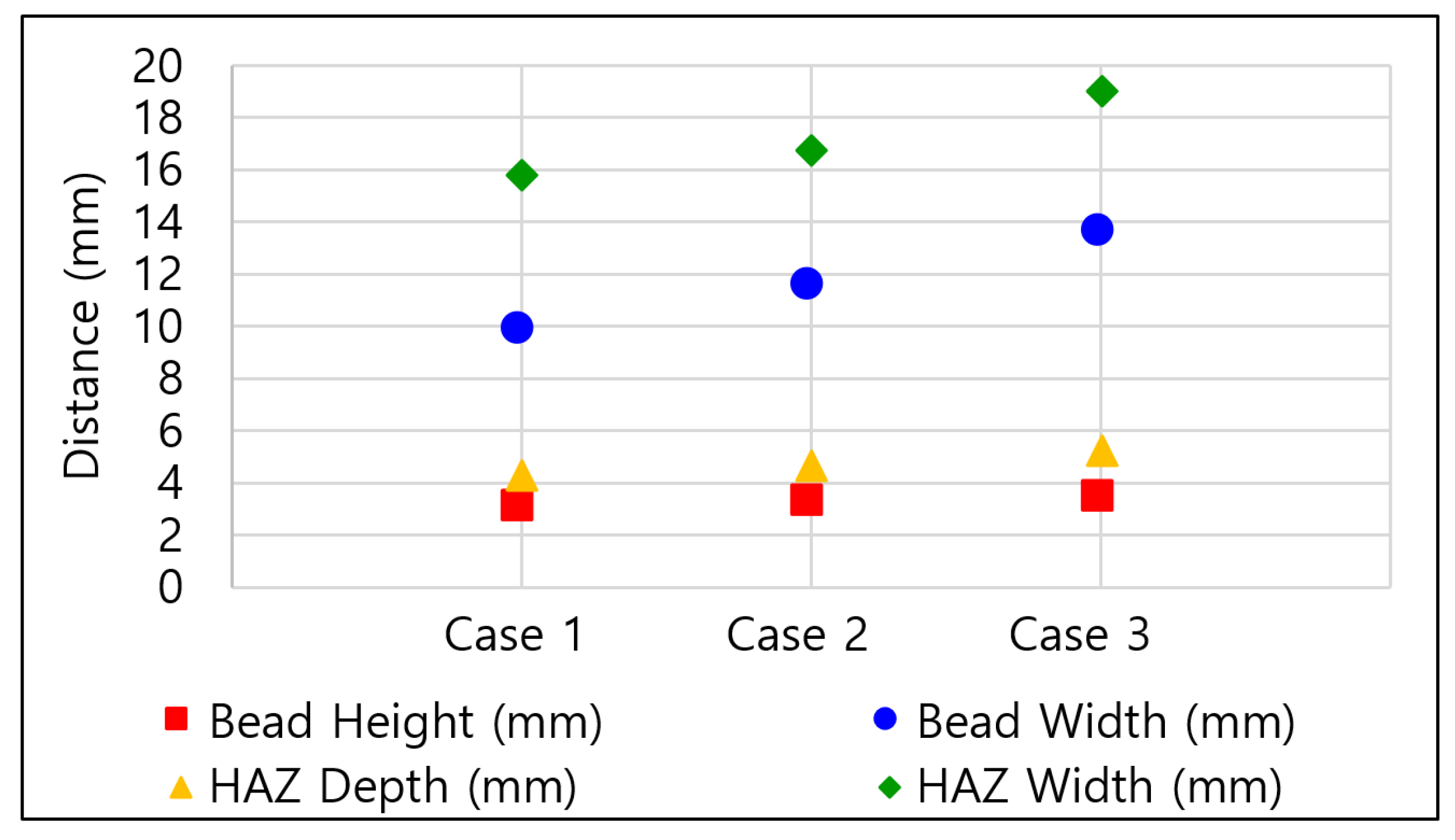
| Case | Bead Height (mm) | Bead Width (mm) | HAZ Depth (mm) | HAZ Width (mm) |
|---|---|---|---|---|
| Case 1 | 2.90 | 9.68 | 4.14 | 15.74 |
| Case 2 | 3.09 | 11.35 | 4.66 | 16.64 |
| Case 3 | 3.29 | 13.48 | 5.23 | 18.92 |
| Variable | Lower Bound | Upper Bound |
|---|---|---|
| μ (W/W) | 0.78 | 0.82 |
| af (mm) | 1.0 | 15.0 |
| ar/af (mm/mm) | 1.5 | 7.0 |
| b (mm) | 1.0 | 20.0 |
| c (mm) | 1.0 | 15.0 |
| L (Distance to Heat Source, mm) | ||
|---|---|---|
| Lower Bound | Upper Bound | |
| Case 1 | 0 | 2.90 |
| Case 2 | 0 | 3.09 |
| Case 3 | 0 | 3.29 |
| Variable | Value | ||
|---|---|---|---|
| Case 1 | Case 2 | Case 3 | |
| μ (W/W) | 0.82 | 0.81 | 0.82 |
| af (mm) | 2.96 | 1.84 | 7.72 |
| ar/af (mm) | 5.79 | 6.56 | 7 |
| b (mm) | 13.92 | 19.62 | 11.26 |
| c (mm) | 4.64 | 1.84 | 1.00 |
| L (mm) | 2.09 | 3.09 | 3.29 |
| Temperature (°C) | Value | ||
|---|---|---|---|
| Case 1 | Case 2 | Case 3 | |
| P1 | 546.83 | 522.86 | 266.03 |
| P2 | 413.66 | 389.53 | 407.15 |
| P3 | 419.67 | 391.85 | 458.52 |
| Q1 | 877.38 | 684.56 | 643.07 |
| Q2 | 787.20 | 830.43 | 821.43 |
| Q3 | 876.75 | 909.68 | 994.34 |
| M1 | 1450.84 | 1701.07 | 1474.87 |
| M2 | 2117.31 | 2692.81 | 3302.30 |
| T1 | 705.26 | 596.45 | 425.85 |
| T2 | 586.05 | 586.16 | 592.86 |
| T3 | 618.90 | 612.57 | 691.02 |
| Value | HAZ Width | HAZ Depth | ||||
|---|---|---|---|---|---|---|
| FEM (mm) | Experiment (mm) | Difference (%) | FEM (mm) | Experiment (mm) | Difference (%) | |
| Case 1 | 16.05 | 15.74 | 1.96 | 4.75 | 4.14 | 14.73 |
| Case 2 | 15.84 | 16.64 | 4.81 | 5.20 | 4.66 | 11.59 |
| Case 3 | 18.50 | 18.92 | 2.22 | 5.77 | 5.23 | 10.33 |
| Value | Variables | |||||
|---|---|---|---|---|---|---|
| Simplified Model (mm) | Original Dimension Model (mm) | Difference (%) | ||||
| 18 mm | 86 mm | 186 mm | ||||
| HAZ Width | Case 1 | 13.83 | 12.25 | 12.28 | 12.39 | 11.01 |
| Case 2 | 14.70 | 12.60 | 12.71 | 12.84 | 13.49 | |
| Case 3 | 16.89 | 14.62 | 14.70 | 14.95 | 12.63 | |
| HAZ Depth | Case 1 | 4.42 | 3.80 | 3.87 | 3.90 | 12.75 |
| Case 2 | 4.68 | 4.09 | 4.11 | 4.16 | 11.97 | |
| Case 3 | 5.70 | 5.05 | 5.18 | 5.24 | 9.53 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Kim, J.; Park, H.; Hong, S.; Pyo, C.; Park, G. An Improved Method for Deriving the Heat Source Model for FCAW of 9% Nickel Steel for Cryogenic Tanks. Materials 2023, 16, 6647. https://doi.org/10.3390/ma16206647
Kim Y, Kim J, Park H, Hong S, Pyo C, Park G. An Improved Method for Deriving the Heat Source Model for FCAW of 9% Nickel Steel for Cryogenic Tanks. Materials. 2023; 16(20):6647. https://doi.org/10.3390/ma16206647
Chicago/Turabian StyleKim, Younghyun, Jaewoong Kim, Hyeongsam Park, Sungbin Hong, Changmin Pyo, and Gyuhae Park. 2023. "An Improved Method for Deriving the Heat Source Model for FCAW of 9% Nickel Steel for Cryogenic Tanks" Materials 16, no. 20: 6647. https://doi.org/10.3390/ma16206647







