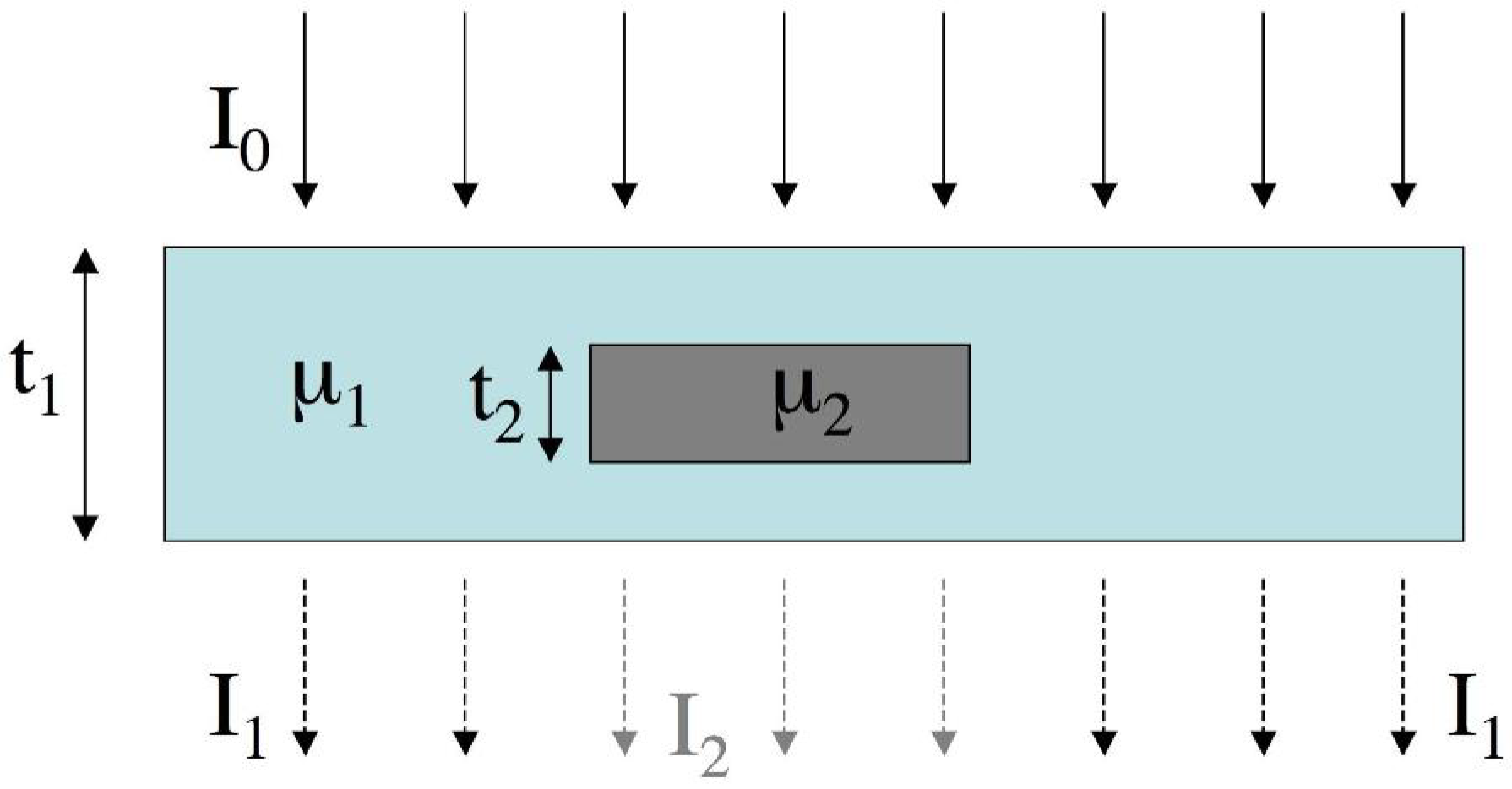
Alongside attenuation, which is the combination of x-ray absorption and scattering at angles sufficiently large to remove the x-rays from the primary beam, other phenomena take place when x-rays transverse a material. These phenomena, which are linked to the phase changes that x-rays undergo when crossing an object, are normally discarded in conventional x-ray imaging. In order to understand the nature of these phenomena, it is important to remember that, although in the “attenuation” picture x-rays are basically treated like particles, they are actually electromagnetic waves. Waves take different speeds when they travel through different materials, and, as a consequence, waves which were initially in phase may not be when they exit a given detail. The basic principle of XPCi is to exploit these phenomena to generate image contrast.
Attenuation-based methods only deal with changes in intensity, which, as discussed above, can be insufficient to generate adequate contrast in a number of situations. Changes of phase, unconsidered by conventional approaches, can however generate intense image contrast, as they can result in interference effects: waves with different phases interfere with each other constructively and destructively, creating strong intensity minima and maxima. In other words, even if the overall energy transported by the wave is not changed (e.g., in the case of negligible attenuation and therefore of no intensity variation), the spatial distribution of energy can change substantially, leading to intense minima and maxima in the detected signal. These can reveal features of the samples that created them.
The difference from unity of the real part,
δ, is responsible for the phase shift that the x-ray wavefront undergoes when crossing an object. Despite being several order of magnitudes greater than
β for most materials in the x-ray energy range [
5], in conventional x-ray imaging methods
δ is completely unconsidered. The fact that
δ >>
β, however, means that a much higher image contrast can be obtained if changes in
δ are properly exploited.
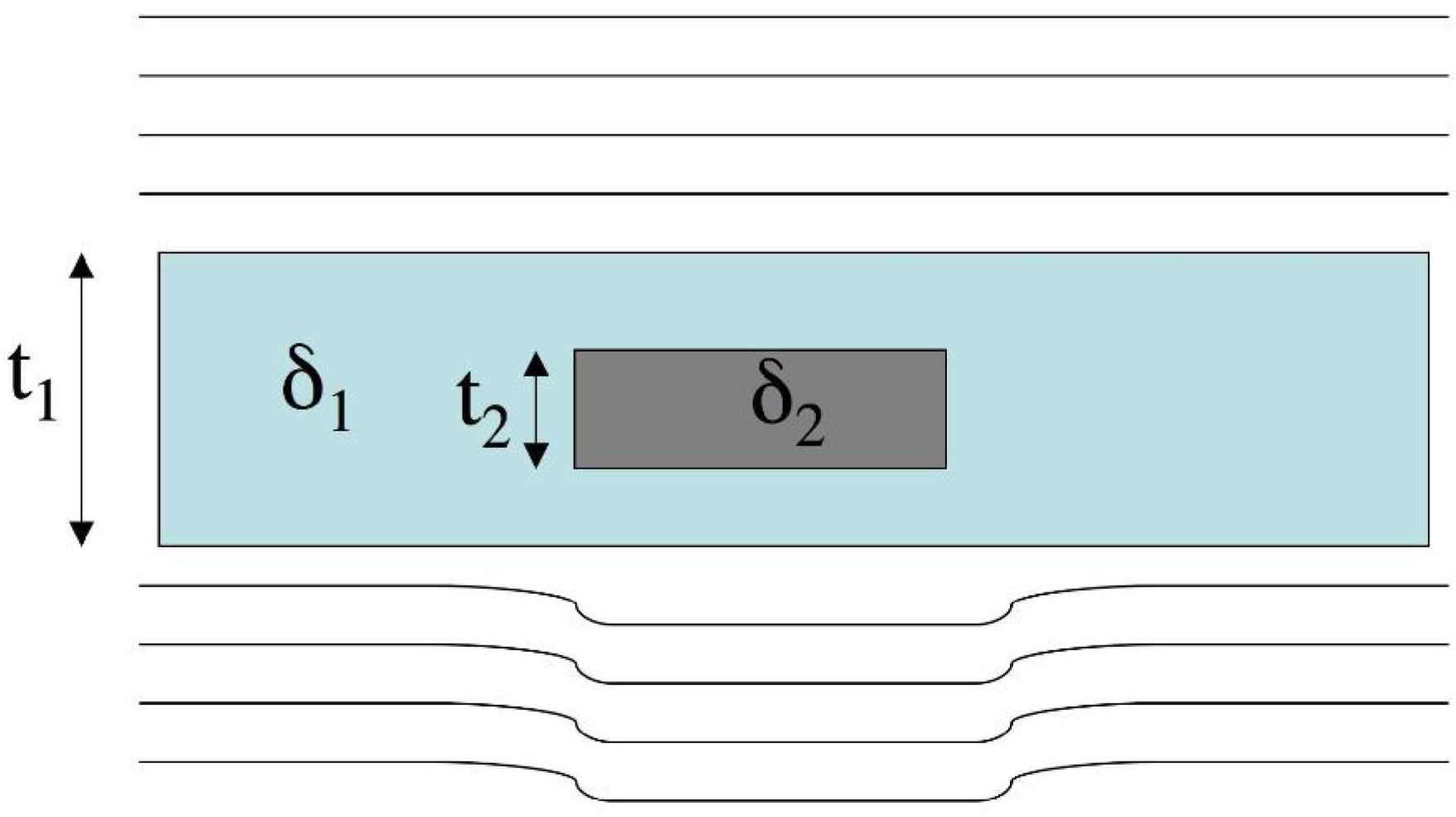
Figure 2 replicates the scheme of
Figure 1, but this time with the x-rays seen as waves. For simplicity’s sake, let us neglect variations in
β (as it can be done in cases where
Catt is small), and characterize the background and the detail by means of their
δ value. For simplicity’s sake, a plane wave impinging on the sample is considered, but the use of a spherical wave would not change the essence of what is discussed below: it would only change the shape of the wavefront and introduce a degree of magnification, as discussed by Wilkins
et al. [
6]. The case in which the presence of the detail advances the wavefront is represented (as it would happen by placing an homogeneous object in air, for example), but even when the opposite happens the substance of what is discussed below does not change.
It should be noted that the overall x-ray intensity might not have been changed at all by the presence of the object (this would be the case for a “pure” phase object, i.e., with β1 = β2 = 0 and both δ1 and δ2 ≠ 0), or a decrease in the overall intensity might have occurred, but the x-ray intensity in the shadow of the detail and outside is the same (β1 = β2 ≠ 0), and therefore Catt = 0. In both these cases, the object would be invisible to conventional, attenuation-based x-ray imaging, but could be detected by XPCi thanks to the wavefront distortion resulting from having δ1 ≠ δ2. Likewise, also in cases where there is a moderate but non-zero attenuation contrast (β1 and β2 slightly different), the difference between δ1 and δ2 can be used to enhance the detail visibility. The next section will present ways to translate this wavefront distortion into image contrast.
Figure 2.
Working principle of phase contrast imaging. An initially perfectly plane wavefront, with all waves “in phase”, becomes distorted because waves have a higher speed inside the detail than outside (see text).
2.1. Different Approaches to XPCi
The simplest implementation of XPCi is free-space propagation (FSP). By allowing the x-rays enough space to propagate beyond the sample, the anticipated (or delayed) and non-anticipated (or non-delayed) portions of the wavefront will interfere with each other, resulting in the generation of an interference pattern [
7]
i.e., a series of positive and negative peaks in the detected x-ray intensity. The problem with this approach is that, for a detectable interference pattern to be produced, the x-ray source must exhibit a high degree of spatial coherence,
i.e., the source size (the focal spot, for a conventional x-ray tube) must be small and/or seen from a long distance [
3]. This is summarized by the concept of projected source size
sp:
where s is the real source size (in the direction transverse to x-ray propagation), and
dsd and
dss are the sample-to-detector and the source-to-sample distances, respectively.
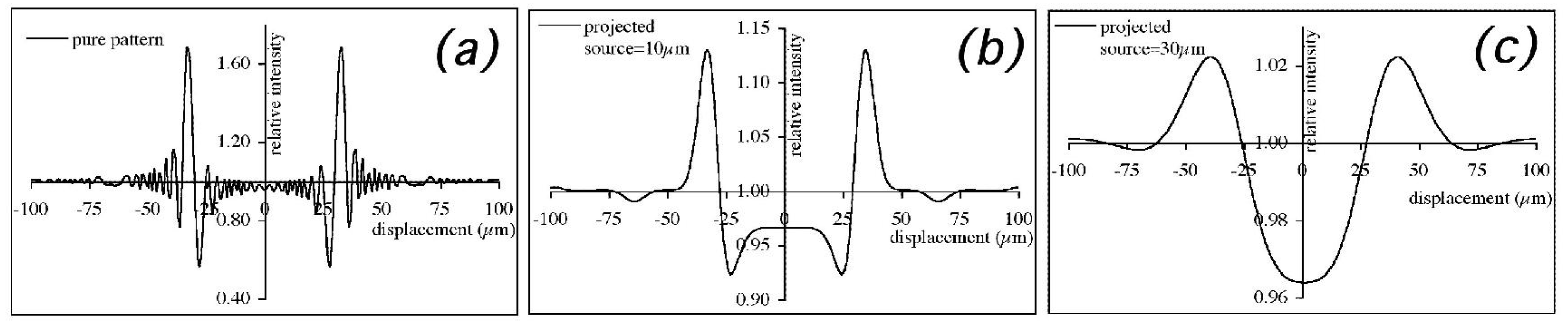
Figure 3.
The effect of an increasing projected source size s
p on the FSP phase contrast pattern. The pattern in (
a) was created by numerically solving the Fresnel/Kirchoff diffraction integral [
3] for a 50 µm thick polyethylene wire, and convolved with Gaussian distributions with a width of 10 and 30 µm to obtain plots (
b) and (
c), respectively.
Figure 3.
The effect of an increasing projected source size s
p on the FSP phase contrast pattern. The pattern in (
a) was created by numerically solving the Fresnel/Kirchoff diffraction integral [
3] for a 50 µm thick polyethylene wire, and convolved with Gaussian distributions with a width of 10 and 30 µm to obtain plots (
b) and (
c), respectively.
An example is provided in
Figure 3.
Figure 3(a) shows the “pure” FSP pattern that would be achieved with an ideal point source (practically never achievable in real cases), while
Figure 3(b,c) show the effect of a projected source size equal to 10 μm and 30 μm, respectively. The position of the highest peaks corresponds to the edges of the imaged detail. The important aspect to note is that the vertical scale has been drastically changed in order to accommodate the three plots in the same figure. It should also be noted that, given the substantial difference between the signals shown in
Figure 3 and attenuation-type signals, in this case it is convenient to introduce a “peak-to-peak” contrast:
where
Imax is the maximum intensity of the positive fringes,
Imin is the minimum intensity of the negative ones, and
Ibackground is the background intensity outside the imaged detail. The plots of
Figure 3 were normalized to
Ibackground, so that
CXPCi can be directly read-out on the vertical axis, leading to
CXPCi values equal to approximately 90%, 20% and 7% for the point source, the 10 μm projected source and the 30 μm projected source, respectively. This demonstrated the decrease of FSP phase contrast with the increase in the projected source size (and consequently also with the increase in the real source size).
As a consequence of this, FSP produces satisfying results only with synchrotron [
7,
8] or micro-focal x-ray sources [
6]. When
sp approaches values of the order of ~100 μm, XPCi-related image enhancement tend to vanish [
8], and therefore when conventional, non-microfocal sources are used, phase effects become very difficult to appreciate in the images [
9]. Alongside explaining why XPCi effects are not normally detected by conventional x-ray imaging systems (together with the fact that the detector is usually positioned immediately behind the sample, and the x-rays are not given enough space to propagate), this also explains why FSP-based XPCi cannot be directly translated into real-world applications requiring fast throughput. Synchrotrons are clearly out of the question, and the low power associated with micro-focal sources means that exposure times which could be as long as hours [
6] are required.
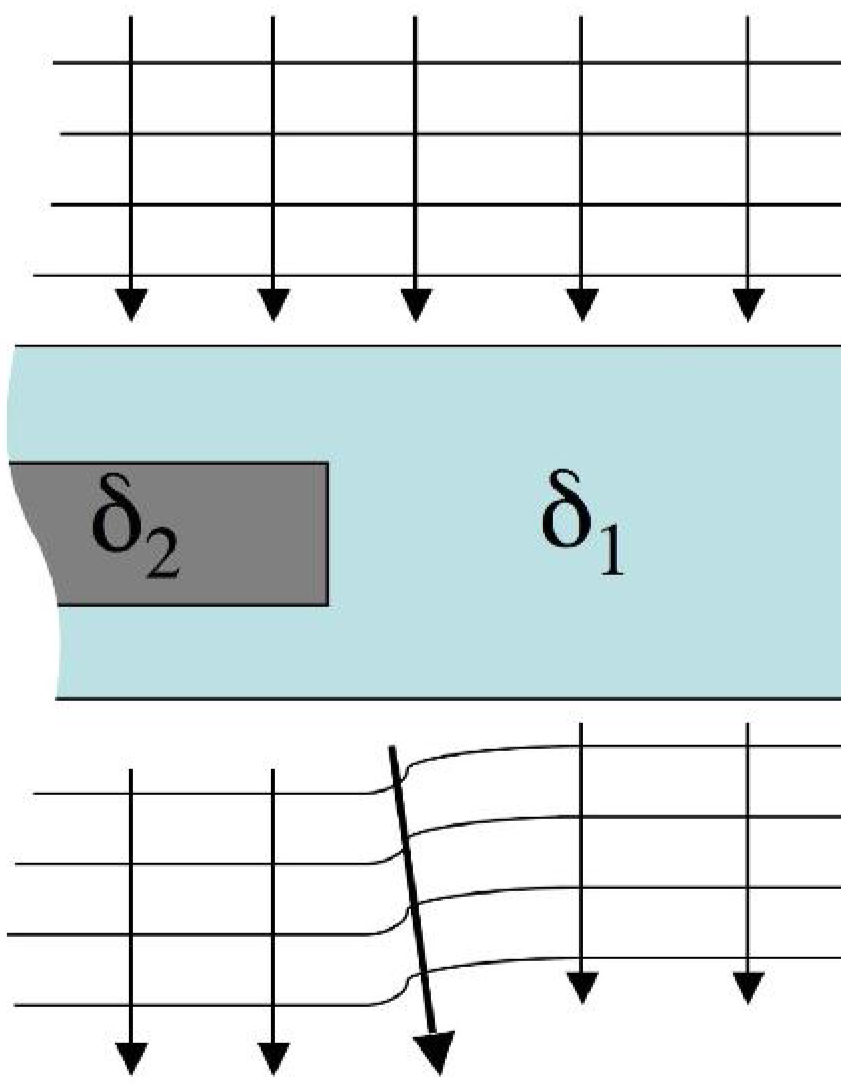
In order to enable such a translation, we followed a different approach to convert wavefront distortions into image contrast. This is schematized in
Figure 4, which shows a portion of the schematic shown in
Figure 2 in which the x-ray directions are highlighted by arrows. According to the ray-tracing approximation [
3], the direction of the x-rays is locally orthogonal to the wavefront. This means that, to a good approximation, the x-rays still travel in their original directions behind the bulk of the detail and outside it, but this is not the case in the vicinity of the detail edges, where the wavefront is most distorted (as underlined by the thick arrow under the detail in
Figure 4), resulting in a detectable difference in the x-ray direction. It should be noted that the effect has been highly exaggerated in the figure for clarity’s sake, and that those deviations are of the order of tens of microradians (~1/1,000 of a degree).
This is basically the phenomenon of x-ray refraction. The ray-tracing approximation enables calculating the deviation angle as:
where
z is the direction along which the x-rays are propagating. Φ is the total phase shift, calculated as the integral of
δ extended over the entire thickness of the imaged object along the
z direction, multiplied by 2
π/
λ (for a homogeneous object, the integral is simply
δ multiplied by the object thickness).
is the gradient operator where derivatives are performed along the transverse directions only. This means that the deviation angle depends on the spatial variations of
δ times the object thickness: the sharper these variations (e.g., at the edge of a detail), the larger the deviation of the x-rays transversing that region.
Figure 4.
Interpretation of wavefront distortions in terms of changes in the x-ray direction.
Figure 4.
Interpretation of wavefront distortions in terms of changes in the x-ray direction.
Therefore, by devising a method sensitive enough to detect these deviations in the x-ray direction, image contrast can be generated which arises at the interfaces between different materials. For what said above, the sharper are the transition between materials with different δ values, the easier is the detection of the effect or, equivalently, the stronger is the contrast that can be obtained with a system with a given angular sensitivity.
A very sensitive method is obtained by exploiting the reflectivity curves of perfect crystals [
10]. However, the use of perfect crystals requires the beam to be parallel and monochromatic, and therefore once again restricts the method to synchrotron radiation environments. In principle, crystals can be used with conventional sources, but they would automatically select the appropriate parallel and monochromatic components, which consist of only a small fraction of the total flux emitted by the source. This means that the source is used very inefficiently, and the exposure times are consequently long.
We have devised a different method, which achieves a comparable directional selectivity while employing a fully divergent, polychromatic beam generated by a conventional source [
11].
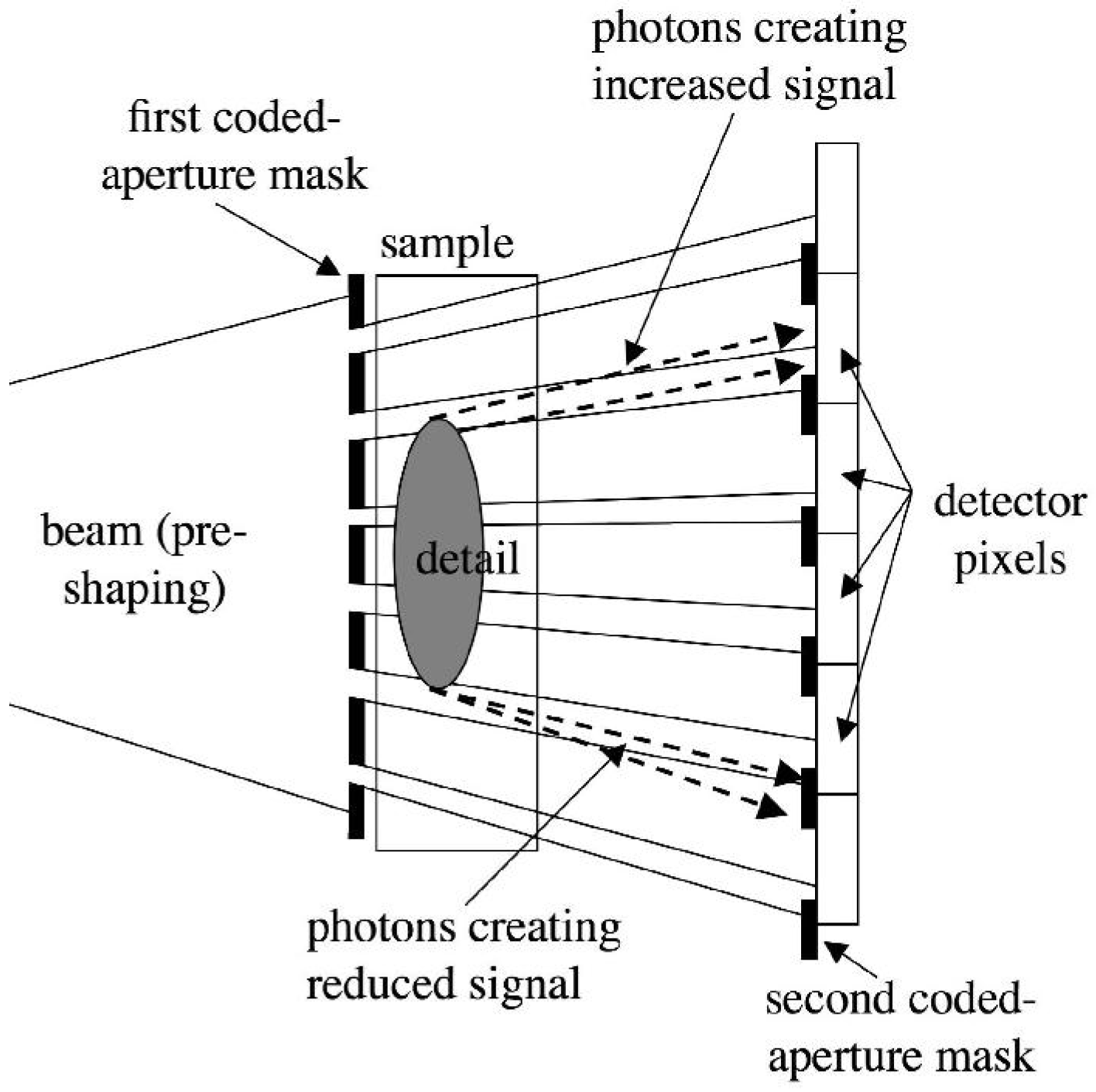
The method employs two sets of aperture masks. One is placed immediately before the imaged sample, and splits the beam into a plurality of individual beams. The second is placed in contact with the detector, and creates insensitive regions between adjacent pixels. The two masks are identical apart from a scaling factor which accounts for the beam divergence, and are positioned in such a way that each individual beam created by the first mask straddles the edge of one of the apertures in the second mask. This is schematized in
Figure 5.
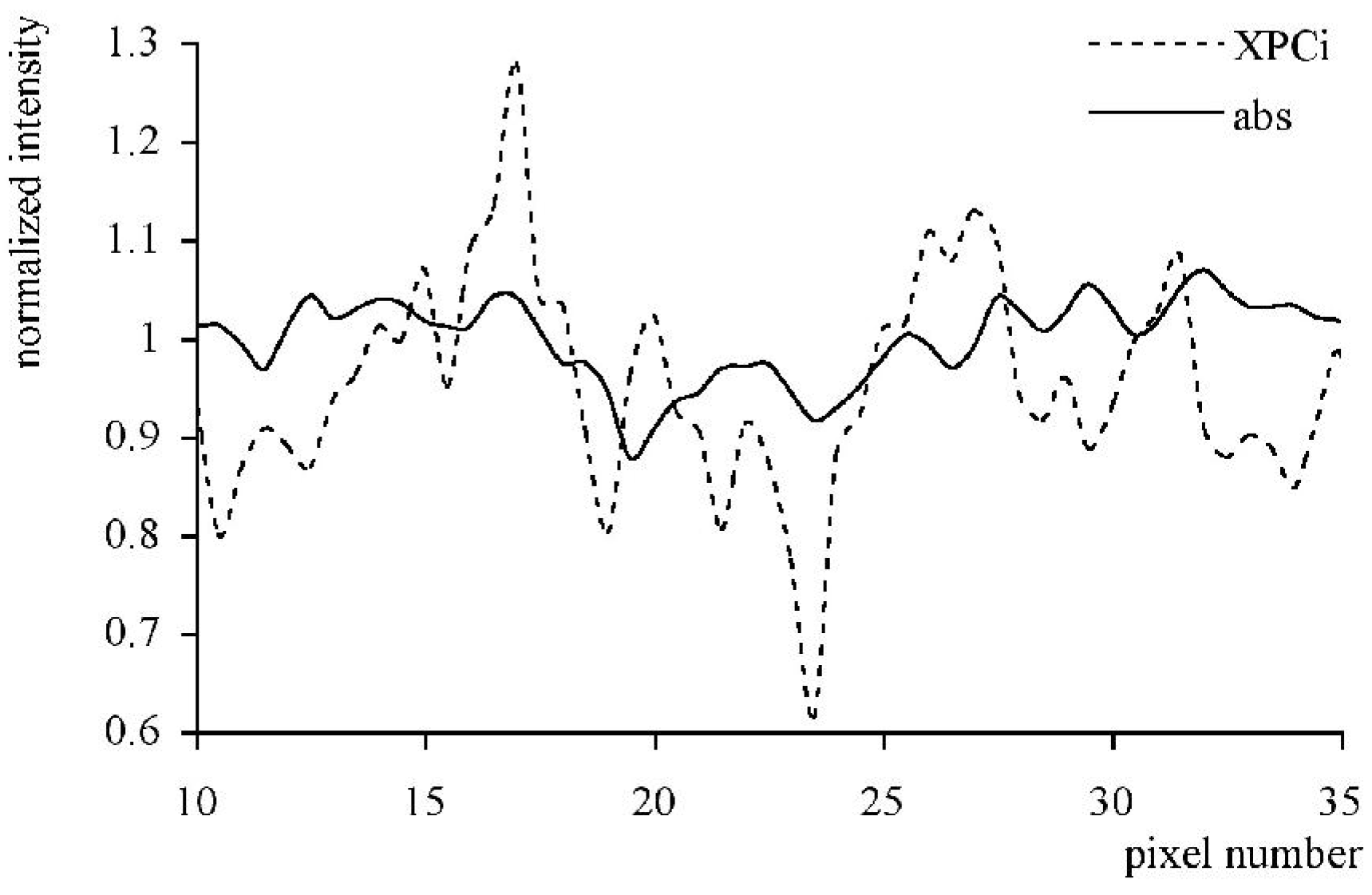
The fact that the beams created by the first mask fall on the edge between sensitive and insensitive regions of the detector (e.g., in absence of the sample, 50% of the x-rays in each beam would be detected), means that a very small deviation of these beams (or of parts of the beams) will generate a change in the number of x-rays detected by each pixel. An example of this is shown in
Figure 5. The upper edge of the detail inside the sample will deviate some x-rays upwards. As a consequence of this, x-rays which would, in absence of the sample, hit the solid parts of the detector mask, and therefore not be detected, are deviated into one of the mask apertures. Thus, they will reach the detector and be counted. This translates into an increase in the number of counts detected by the involved detector pixels, and therefore into a bright fringe appearing along the upper edge of the detail. The opposite occurs at the bottom edge of the detail. In this case, photons are sent downwards and deviated from one of the apertures (which they would have hit in absence of the sample) into the solid part of the mask. As a consequence, a reduction in the number of counts is observed in the corresponding pixels, and a dark fringe will appear along the lower border of the detail. Therefore, an x-ray transparent detail will become visible because of intense bright and dark fringes appearing along its edges. This produces images similar to those obtained using crystals [
12], but the use of an aperture mask instead of a crystal means that divergent and polychromatic beams, like those emitted by conventional x-ray sources, can be used. Some practical examples in which objects producing insufficient x-ray attenuation are detected because of these fringes will be shown below.
Figure 5.
Schematization of the coded-aperture XPCi method.
Figure 5.
Schematization of the coded-aperture XPCi method.
2.2. Experimental Set-up
A conventional, rotating anode tungsten source previously used in hospital work since the mid-eighties [
13] was used in this work. It features a source size of the order of 50 μm, about one order of magnitude larger than sources previously used in XPCi work outside synchrotrons. The Hamamatsu C9732DK passive-pixel CMOS flat panel (Hamamatsu, Japan) was used as detector device. The pre-sample and detector coded-aperture masks were built to the authors’ design by Creatv Microtech (Potomac, MD), and consisted of long parallel slits carved on a 150 μm thick gold mask electroplated on a graphite substrate. The area of the detector mask was 6 × 6 cm
2, while the pre-sample mask was scaled down to 4.8 × 4.8 cm
2 to account for the beam divergence, as the distances from the source to the pre-sample and detector masks were of 1.6 m and 2.0 m, respectively. The relatively small mask dimensions are due to the proof-of-concept nature of the present work, and it is possible to scale the system up to dimensions compatible with real baggage scanners. The aperture pitch was 100 μm in the detector mask, and scaled down to 80 μm in the sample mask again to account for the divergent nature of the beam. The parallel apertures were as long as the masks in one direction, and their number was sufficient to cover the masks completely along the other (
i.e., 6 cm/100 μm = 600 parallel apertures in total). In this case, the aperture dimension was 1/3 of the pitch for both masks. This was chosen in order to be able to experiment with dark field imaging approaches (
i.e., the condition in which the masks are arranged in such a way that they block off the primary beam completely) alongside the XPCi approach described above. In a dedicated system, a fill-factor of 50% would be chosen instead, in order to allow more photons through the mask thus reducing the exposure time. The masks were mounted on multiple-axis alignment stages consisting of Newport (Irvine, CA) Microcontrole translators and Kohzu (Kurigi, Japan) cradles. These were used first to align the apertures in the detector mask with the detector pixel columns, and then to align the pre-sample mask with the detector one. All the above components were mounted on a Melles-Griot (Albuquerque, NM) optical breadboard without vibration damping and/or insulation. This was done intentionally, to verify that a normal level of environmental vibrations could be accepted without excessively affecting image quality.
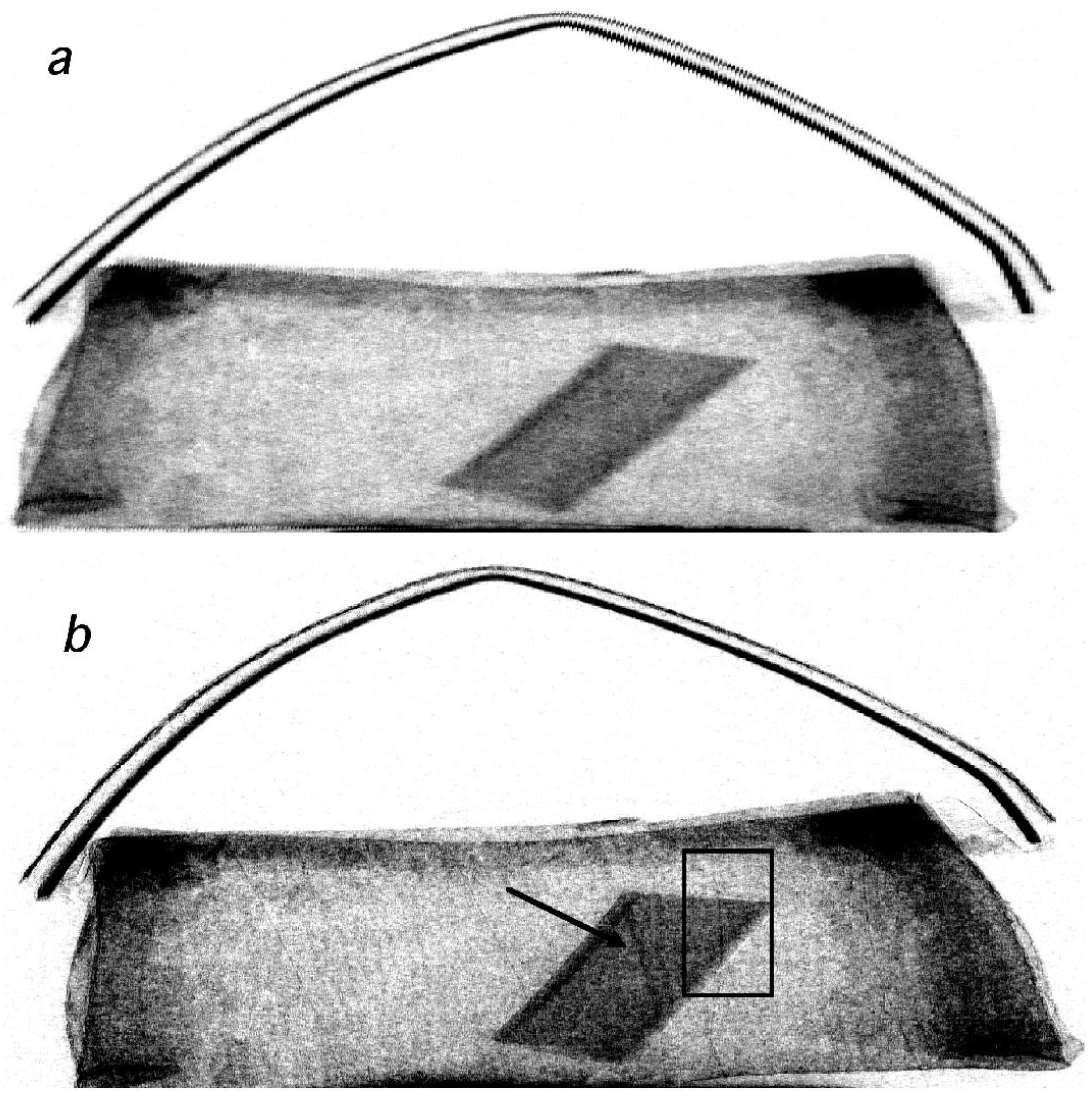
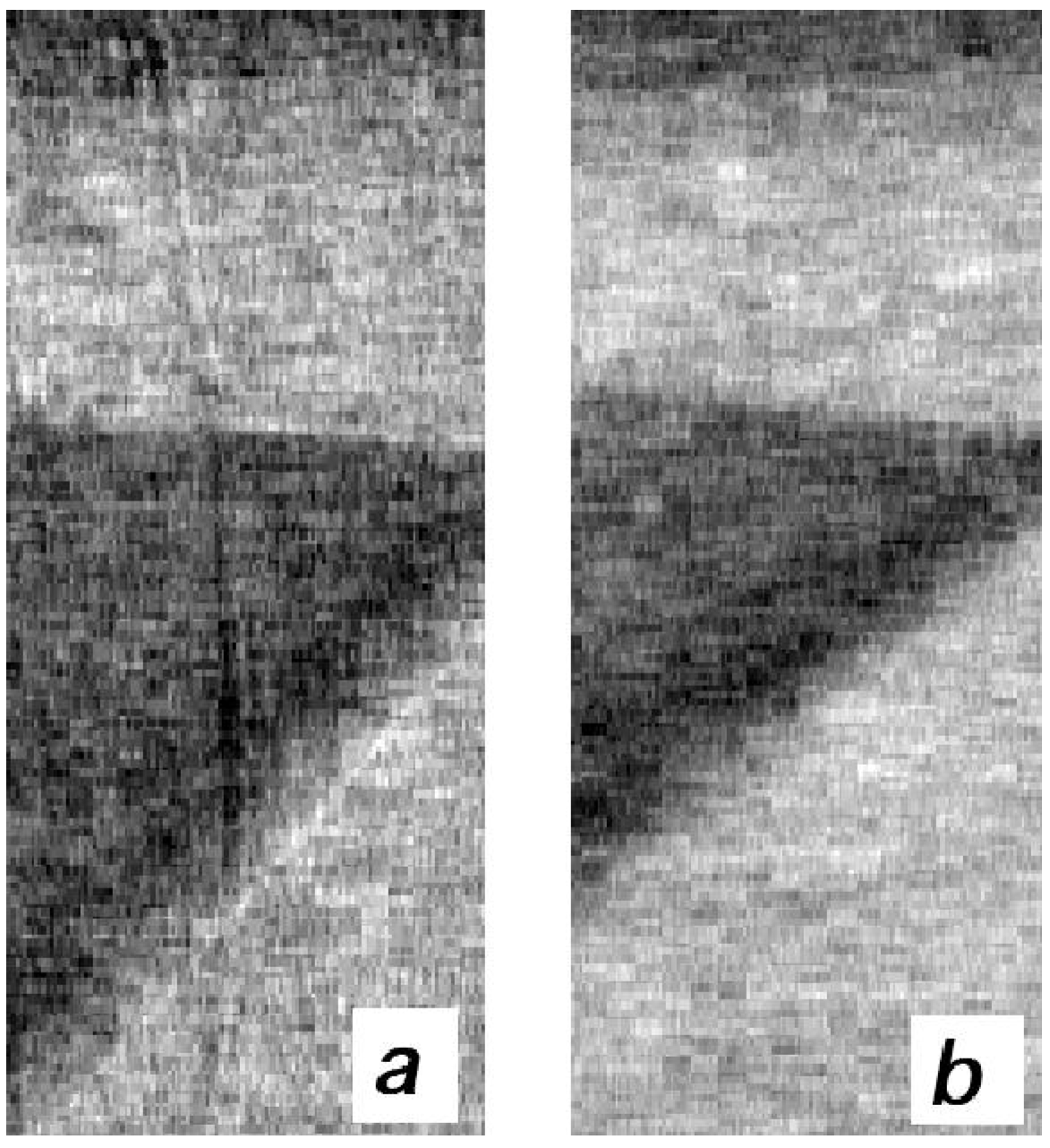
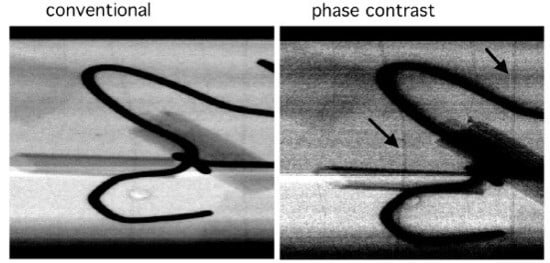
Two samples were built by hiding a small plastic cylinder, mimicking the explosive, and thin aluminum and polyethylene wires, mimicking detonator components in a toy wooden chest (see
Figure 6) and in a toy purse. Additional objects were progressively added to simulate increasingly cluttered conditions. Both samples were imaged both with the XPCi method described above and in the conventional attenuation modality. The latter was achieved by removing both coded-aperture masks, placing the sample in contact with the detector, and reducing the x-ray tube current to compensate for the x-rays stopped by the mask. This was done in order to have the same photon flux reaching the detector, and therefore the same x-ray statistics in the images (
i.e., the same noise level).
Figure 6.
One of the samples used in the proof-of-concept experiment.
Figure 6.
One of the samples used in the proof-of-concept experiment.