Atomistic Modeling of the Negative Thermal Expansion in δ- Plutonium Based on the Two-State Description
Abstract
:1. Introduction
2. Simulation Methods
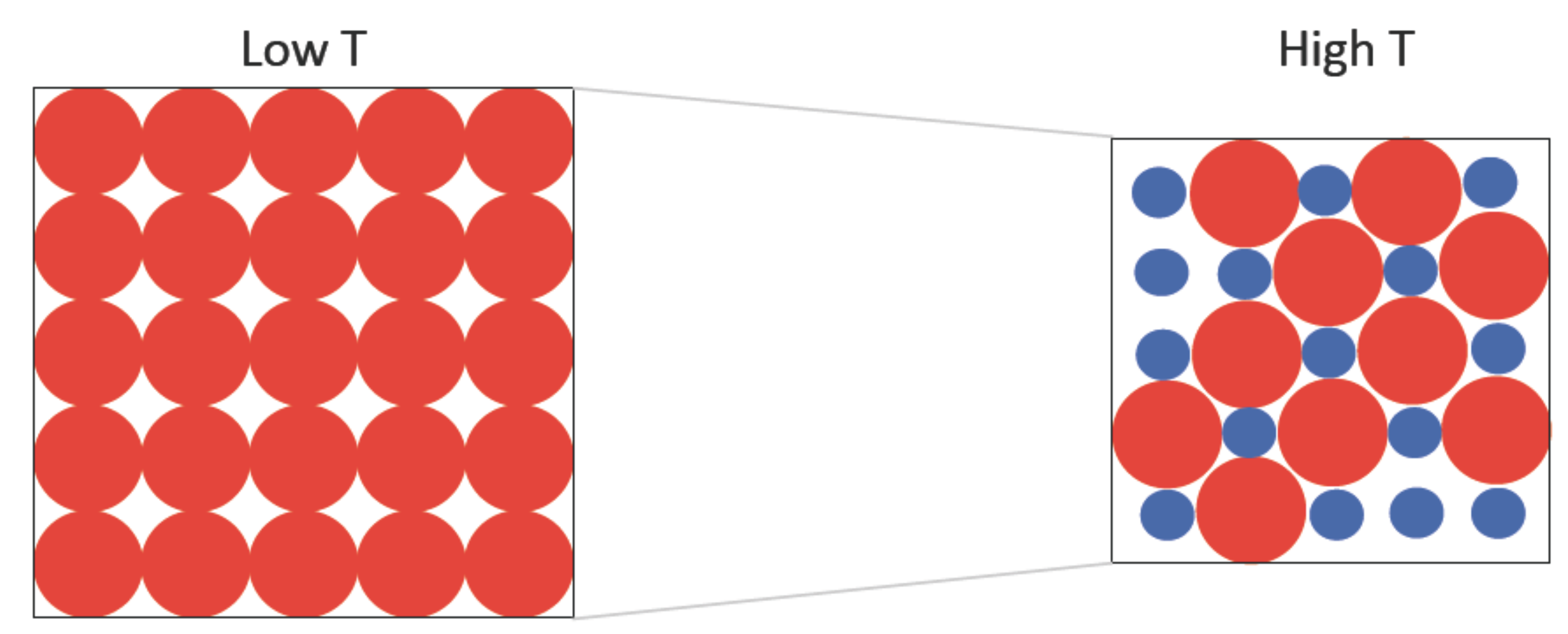
2.1. Two-State Model Description of Many-Body Interacting Systems

2.2. Computational Details
3. Simulation Results

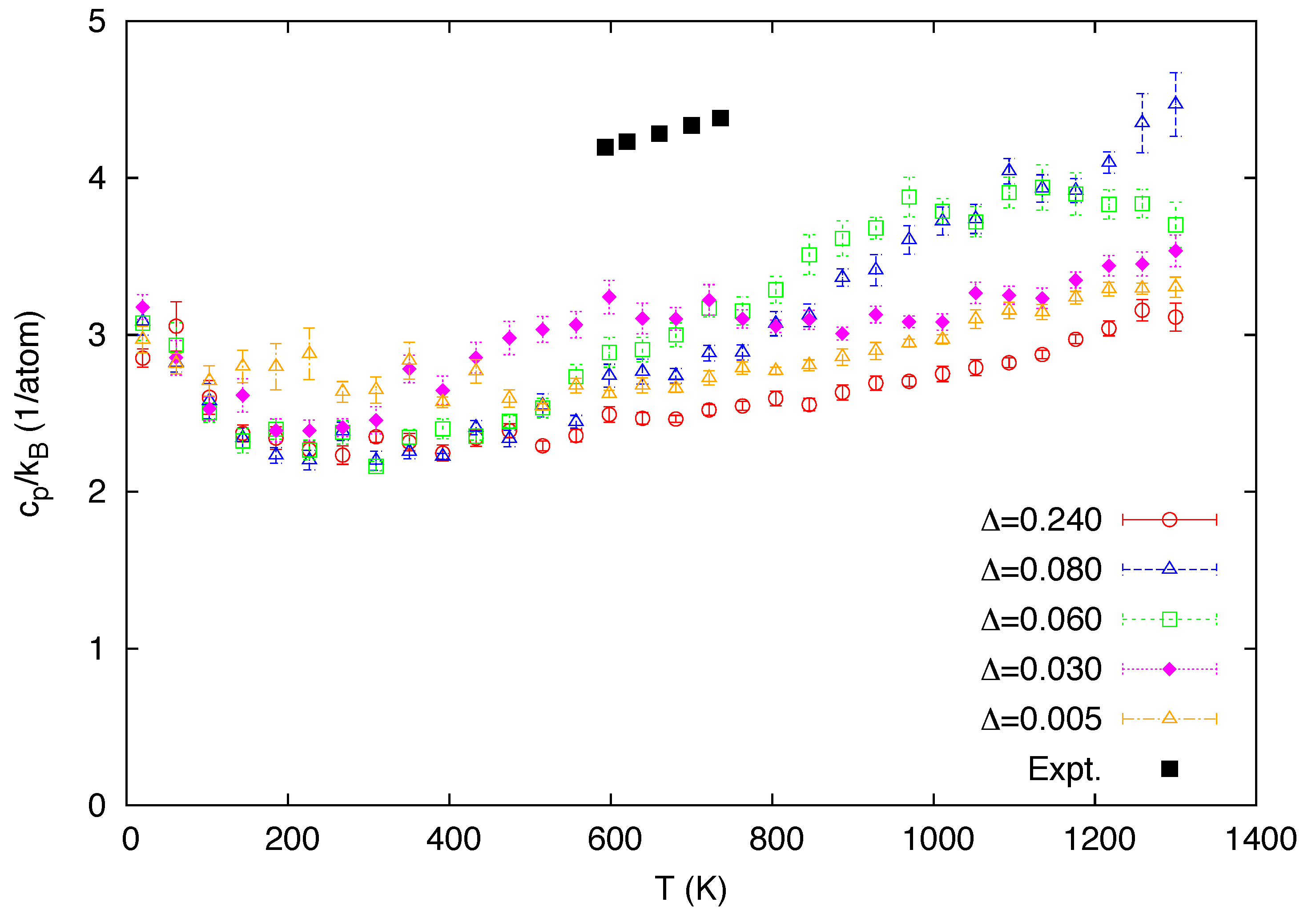
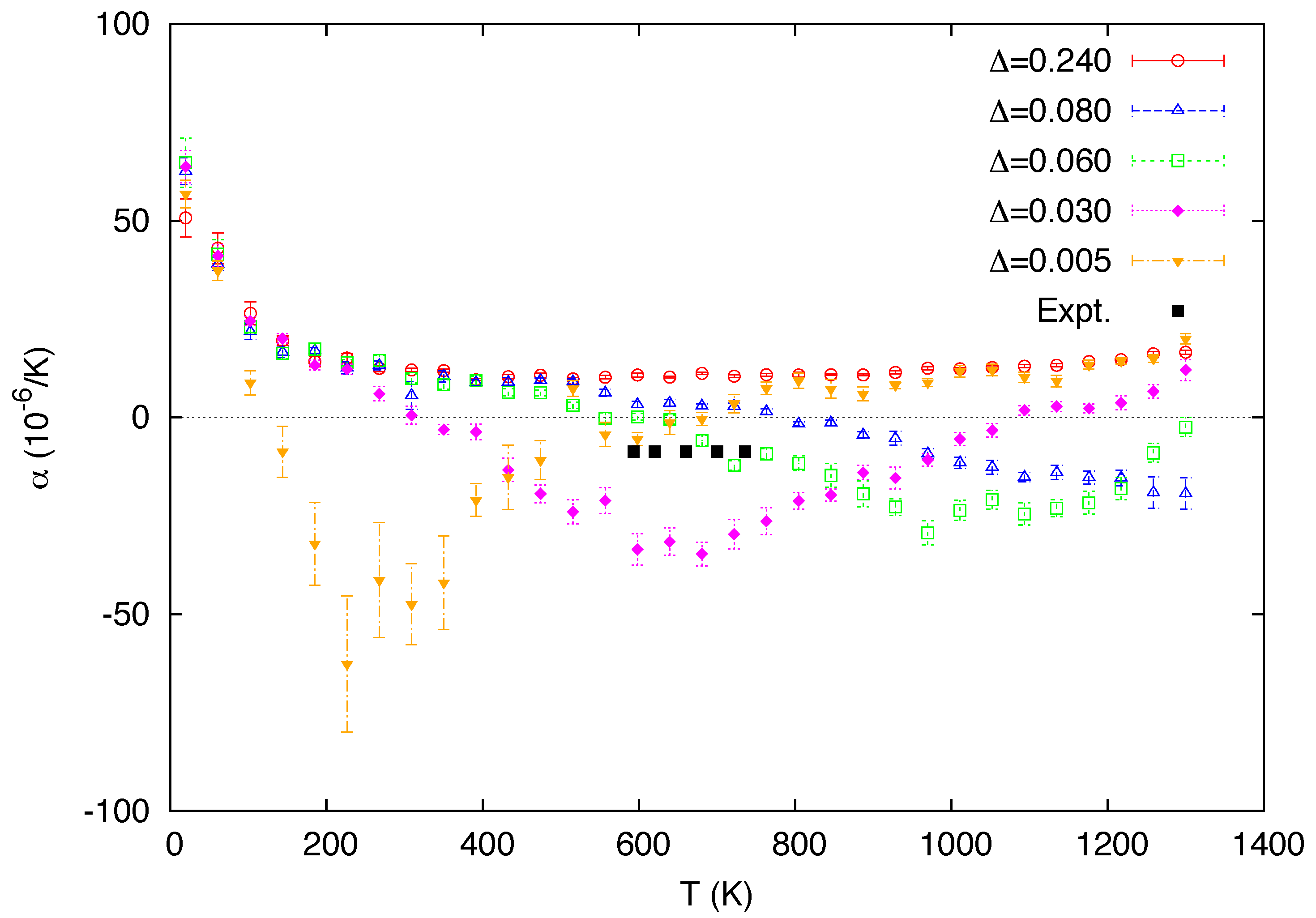
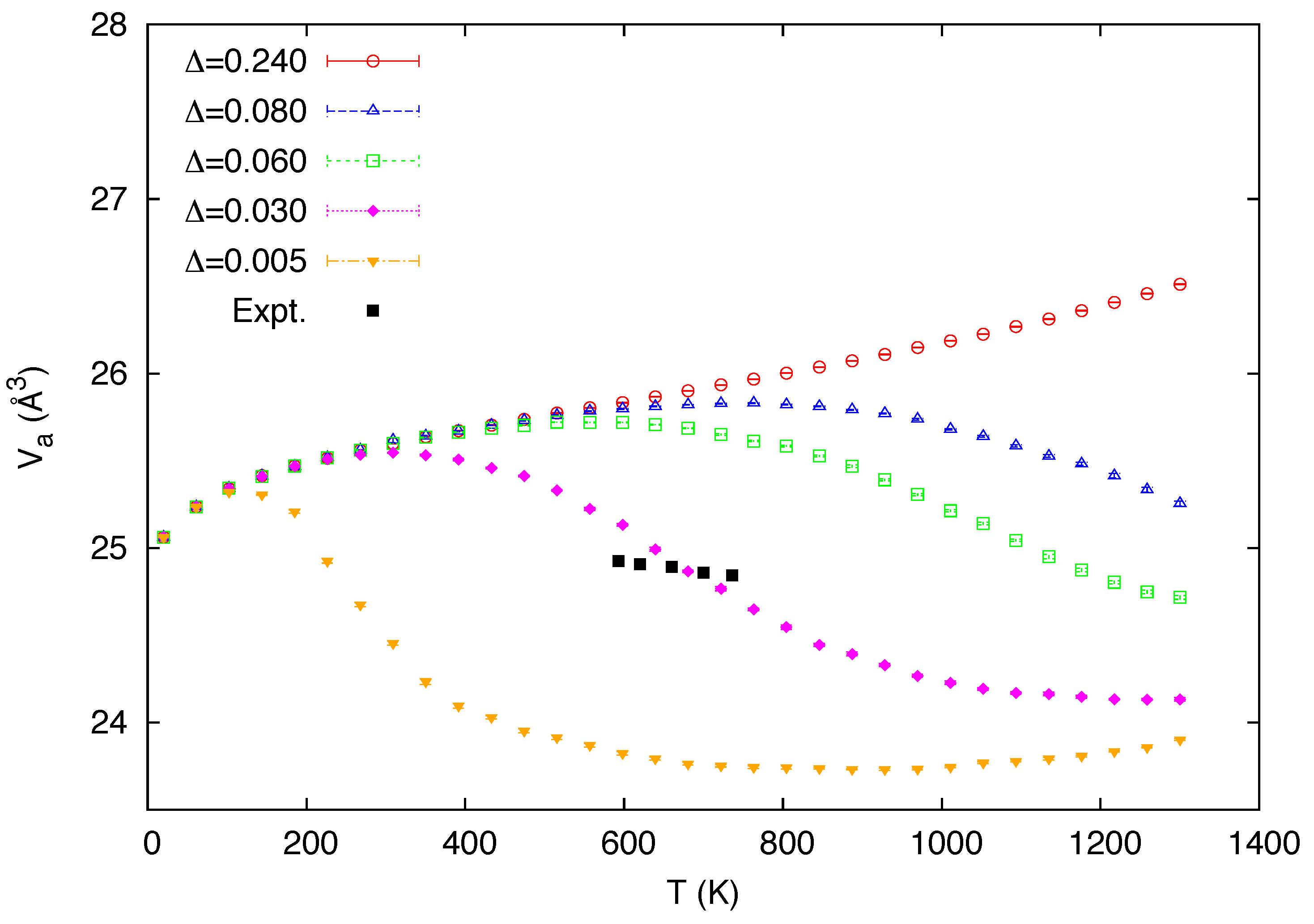
4. Conclusions
Acknowledgements
References
- Barron, T.H.K. On the thermal expansion of solids at low temperatures. Philos. Mag. 1955, 46, 720–734. [Google Scholar] [CrossRef]
- Giddy, A.P.; Dove, M.T.; Pawley, G.S.; Heine, V. The determination of rigid-unit modes as potential soft modes for displacive phase transitions in framework crystal structures. Acta Crystallogr. A 1993, 49, 697–703. [Google Scholar] [CrossRef]
- Barrera, G.D.; Bruno, J.A.O.; Barron, T.H.K.; Allan, N.L. Negative thermal expansion. J. Phys. Condens. Matter 2005, 17, R217–R252. [Google Scholar] [CrossRef]
- Cahn, R.W. An unusual Nobel prize. Notes Rec. R. Soc. 2005, 59, 145–153. [Google Scholar] [CrossRef]
- Wassermann, E.F. The Invar problem. J. Magn. Magn. Mater. 1991, 100, 346–362. [Google Scholar] [CrossRef]
- Weiss, R.J. Origin of invar effect. Proc. Phys. Soc. 1963, 82, 281–288. [Google Scholar] [CrossRef]
- Herper, H.C.; Hoffmann, E.; Entel, P. Ab initio full-potential study of the structural and magnetic phase stability of iron. Phys. Rev. B 1999, 60, 3839–3848. [Google Scholar] [CrossRef]
- Knöpfle, K.; Sandratskii, L.M.; Kübler, J. Spin spiral ground state of γ-iron. Phys. Rev. B 2000, 62, 5564–5569. [Google Scholar] [CrossRef]
- Kaufman, L.; Clougherty, E.V.; Weiss, R.J. The lattice stability of metals—III. Iron. Acta Met. 1963, 11, 323–335. [Google Scholar] [CrossRef]
- Blackburn, L.D.; Kaufman, L.; Cohen, M. Phase transitions in iron-ruthenium alloys under high pressure. Acta Met. 1965, 13, 533–541. [Google Scholar] [CrossRef]
- Acet, M.; Zähres, H.; Wassermann, E.F.; Pepperhoff, W. High-temperature moment-volume instability and anti-Invar of γ-Fe. Phys. Rev. B 1994, 49, 6012–6017. [Google Scholar] [CrossRef]
- Bendick, W.; Pepperhoff, W. On the α/γ phase stability of iron. Acta Met. 1982, 30, 679–684. [Google Scholar] [CrossRef]
- Pepperhoff, W.; Acet, M. Constitution of Magnetism of Iron and its Alloys; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Johansson, B. The α-γ transition in cerium is a Mott transition. Philos. Mag. 1974, 30, 469–482. [Google Scholar] [CrossRef]
- Smith, J.L.; Kmetko, E.A. Magnetism or monding: A nearly periodic table of transition elements. J. Less Common Met. 1983, 90, 83–88. [Google Scholar] [CrossRef]
- Eriksson, O.; Becker, J.N.; Balatsky, A.V.; Wills, J.M. Novel electronic configuration in ∂-Pu. J. Alloys Compd. 1999, 287, 1–5. [Google Scholar] [CrossRef]
- Olsen, C.E.; Comstock, A.L.; Sandenaw, T.A. Magnetic susceptibility of pure plutonium metal above 300 K. J. Nucl. Mater. 1992, 195. [Google Scholar] [CrossRef]
- Méot-Reymond, S.; Fournier, J.M. Localization of 5f electrons in δ-plutonium: Evidence for the Kondo effect. J. Alloys Compd. 1996, 232, 119–125. [Google Scholar] [CrossRef]
- Söderlind, P.; Landa, A.; Sadigh, B.; Vitos, L.; Ruban, A. First-principles elastic constants and phonons of δ-Pu. Phys. Rev. B 2004, 70, 144103:1–144103:5. [Google Scholar] [CrossRef]
- Lashley, J.C.; Lawson, A.; McQueeney, R.J.; Lander, G.H. Absence of magnetic moments in plutonium. Phys. Rev. B 2005, 72, 054416:1–054416:12. [Google Scholar] [CrossRef]
- McCall, S.K.; Fluss, M.J.; Chung, B.W.; McElfresh, M.W.; Jackson, D.D.; Chapline, G.F. Emergent magnetic moments produced by self-damage in plutonium. Proc. Natl. Acad. Sci. USA 2006, 103, 17179–17183. [Google Scholar] [CrossRef] [PubMed]
- Shim, J.H.; Haule, K.; Kotliar, G. Fluctuating valence in a correlated solid and the anomalous properties of δ-plutonium. Nature 2007, 446, 513–516. [Google Scholar] [CrossRef] [PubMed]
- Atta-Fynn, R.; Ray, A.K. Does hybrid density functional theory predict a non-magnetic ground state for δ-Pu? Europhys. Lett. 2009, 85, 27008:1–27008:24. [Google Scholar] [CrossRef]
- Solontsov, A.; Antropov, V.P. Effects of spin fluctuations and anomalous thermal expansion of δ-Pu. Phys. Rev. B 2010, 81, 214402:1–214402:5. [Google Scholar] [CrossRef]
- Lawson, A.C.; Roberts, J.A.; Martinez, B.; Richardson, J.W., Jr. Invar effect in Pu-Ga alloys. Philos. Mag. 2002, 82, 1837–1845. [Google Scholar] [CrossRef]
- Lawson, A.C.; Roberts, J.A.; Martinez, B.; Ramos, M.; Kotliar, G.; Trouw, F.W.; Fitzsimmons, M.R.; Hehlen, M.P.; Lashley, J.C.; Ledbetter, H.; McQueeney, R.J.; Migliori, A. Invar model for delta-phase Pu: Thermal expansion, elastic and magnetic properties. Philos. Mag. 2006, 86, 2713–2733. [Google Scholar] [CrossRef]
- Savrasov, S.Y.; Kotliar, G.; Abrahams, E. Correlated electrons in delta-plutonium within a dynamical mean-field picture. Nature 2001, 410, 793–795. [Google Scholar] [CrossRef] [PubMed]
- Albers, R.C.; Zhu, J.-X. Solid-state physics: Vacillating valence. Nature 2007, 446, 504–505. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.-X.; McMahan, A.K.; Jones, M.D.; Durakiewicz, T.; Joyce, J.J.; Wills, J.M.; Albers, R.C. Spectral properties of δ-plutonium: Sensitivity to 5f occupancy. Phys. Rev. B 2007, 76, 245118:1–245118:6. [Google Scholar] [CrossRef]
- Chen, S.P. Correlation-induced anomalies and extreme sensitivity in fcc Pu. Philos. Mag. 2009, 89, 1813–1822. [Google Scholar] [CrossRef]
- Baskes, M.I. Atomistic model of plutonium. Phys. Rev. B 2000, 62, 15532–15537. [Google Scholar] [CrossRef]
- Valone, S.M.; Baskes, M.I. Self-irradiation cascade simulations in plutonium metal: Model behavior at high energy. J. Comput.-Aided Mater. Des. 2007, 14, 357–365. [Google Scholar] [CrossRef]
- Kubota, A.; Wolfer, W.G.; Valone, S.M.; Baskes, M.I. Collision cascades in pure δ-plutonium. J. Comput.-Aided Mater. Des. 2007, 14, 367–378. [Google Scholar] [CrossRef]
- Baskes, M.I.; Hu, S.Y.; Valone, S.M.; Wang, G.F.; Lawson, A.C. Atomistic simulations of Ga atom ordering in Pu 5 at. % Ga alloys. J. Comput.-Aided Mater. Des. 2007, 14, 379–388. [Google Scholar] [CrossRef]
- Gruner, M.E.; Meyer, R.; Entel, P. Monte Carlo simulations of high-moment low-moment transitions in Invar alloys. Eur. Phys. J. B 1998, 2, 107–119. [Google Scholar] [CrossRef]
- Yokoyama, T.; Eguchi, K. Anharmonicity and quantum effects in thermal expansion of an invar alloy. Phys. Rev. Lett. 2011, 107, 065901:1–065901:4. [Google Scholar] [CrossRef] [PubMed]
- Baskes, M.I. Application of the Embedded-Atom Method to covalent materials: A semiempirical potential for silicon. Phys. Rev. Lett. 1987, 59, 2666–2669. [Google Scholar] [CrossRef] [PubMed]
- Baskes, M.I.; Nelson, J.S.; Wright, A.F. Semiempirical Modified Embedded-Atom Potentials for silicon and geranium. Phys. Rev. B 1989, 40, 6085–6100. [Google Scholar] [CrossRef]
- Baskes, M.I. Modified embedded-atom potentials for cubic materials and impurities. Phys. Rev. B 1992, 46, 2727–2742. [Google Scholar] [CrossRef]
- Ackland, G.J.; Reed, S.K. Two-band second moment model and an interatomic potential for caesium. Phys. Rev. B 2003, 67, 174108:1–174108:10. [Google Scholar] [CrossRef]
- Ackland, G.J. Two-band second moment model for transition metals and alloys. J. Nucl. Mater. 2006, 351, 20–27. [Google Scholar] [CrossRef]
- Lawson, A.C.; Goldstone, J.A.; Cort, B.; Martinez, R.J.; Vigil, F.A.; Zocco, T.G.; Richardson, J.W.; Mueller, M.H. Structure of ζ-phase plutonium-uranium. Acta Crystallogr. B 1996, 52, 32–37. [Google Scholar] [CrossRef]
- Kofke, D.A.; Glandt, E.D. Monte Carlo simulation of multicomponent equilibria in a semigrand canonical ensemble. Mol. Phys. 1988, 64, 1105–1131. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed.; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Foiles, S.M. Calculation of the surface segregation of alloys using the embedded atom method. In Surface Segregation Phenomena; Dowben, P.A., Miller, A., Eds.; CRC Press: Boca Raton, FL, USA, 1990; pp. 79–106. [Google Scholar]
- Lee, T.; Baskes, M.I.; Valone, S.M.; Doll, J.D. Atomistic modeling of thermodynamic equilibrium and polymorphism of iron. J. Phys. Condens. Matter 2012, 24, 225404. [Google Scholar] [CrossRef] [PubMed]
- Uberuaga, B.P.; Valone, S.M.; Baskes, M.I. Accelerated dynamics study of vacancy mobility in delta-plutonium. J. Alloys Compd. 2007, 444–445, 314–319. [Google Scholar] [CrossRef]
- Wallace, D.C. Electronic and phonon properties of six crystalline phases of Pu metal. Phys. Rev. B 1998, 58, 15433–15439. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: New York, NY, USA, 1987. [Google Scholar]
- Lawson, A.C.; Martinez, B.; Roberts, J.A.; Bennett, B.I.; Richardson, J.W. Melting of the light actinides. Philos. Mag. B 2000, 80, 53–59. [Google Scholar] [CrossRef]
- Lashley, J.C.; Singleton, J.; Migliori, A.; Betts, J.B.; Fisher, R.A.; Smith, J.L.; McQueeney, R.J. Experimental electronic heat capacities of α- and δ-plutonium: Heavy-fermion physics in an element. Phys. Rev. Lett. 2003, 91, 205901:1–205901:4. [Google Scholar] [CrossRef] [PubMed]
- Barron, T.H.K.; White, G.K. Heat Capacity and Thermal Expansion at Low Temperatures; Kluwer: New York, NY, USA, 1999. [Google Scholar]
- Söderlind, P.; Landa, A.; Klepeis, J.E.; Suzuki, Y.; Migliori, A. Elastic properties of Pu metal and Pu-Ga alloys. Phys. Rev. B 2010, 81, 224110:1–224110:9. [Google Scholar] [CrossRef]
- Lee, T.; Baskes, M.I.; Lawson, A.C.; Chen, S.P.; Valone, S.M. Atomistic modeling of thermodynamic equilibrium of plutonium and its alloys. 2012. to be submitted. [Google Scholar]
© 2012 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lee, T.; Baskes, M.I.; Lawson, A.C.; Chen, S.P.; Valone, S.M. Atomistic Modeling of the Negative Thermal Expansion in δ- Plutonium Based on the Two-State Description. Materials 2012, 5, 1040-1054. https://doi.org/10.3390/ma5061040
Lee T, Baskes MI, Lawson AC, Chen SP, Valone SM. Atomistic Modeling of the Negative Thermal Expansion in δ- Plutonium Based on the Two-State Description. Materials. 2012; 5(6):1040-1054. https://doi.org/10.3390/ma5061040
Chicago/Turabian StyleLee, Tongsik, Michael I. Baskes, A. C. Lawson, Shao Ping Chen, and Steven M. Valone. 2012. "Atomistic Modeling of the Negative Thermal Expansion in δ- Plutonium Based on the Two-State Description" Materials 5, no. 6: 1040-1054. https://doi.org/10.3390/ma5061040



