Truss Structure Optimization with Subset Simulation and Augmented Lagrangian Multiplier Method
Abstract
:1. Introduction
2. Subset Simulation Optimization (SSO)
2.1. Rationale of SSO
2.2. Implementation Procedure of SSO
- Initialization. Define the distributional parameters for the design vector and determine the level probability and the number of samples at a simulation level (i.e., ). Let , where INT[∙] is a function that rounds the number in the bracket down to the nearest integer. Set iteration counter .
- Monte Carlo simulation. Generate a set of random samples according to the truncated normal distribution.
- Selection. Calculate the objective function for the N random samples, and sort them in ascending order, i.e., . Obtain the first samples from the ascending sequence. Let the sample -quantile of the objective function be , and set , and then define the first intermediate event .
- Generation. Generate conditional samples using the MMH algorithm from the sample , and set .
- Selection. Repeat the same implementation as in Step 3.
- Convergence. If the convergence criterion is met, the optimization is terminated; otherwise, return to Step 4.
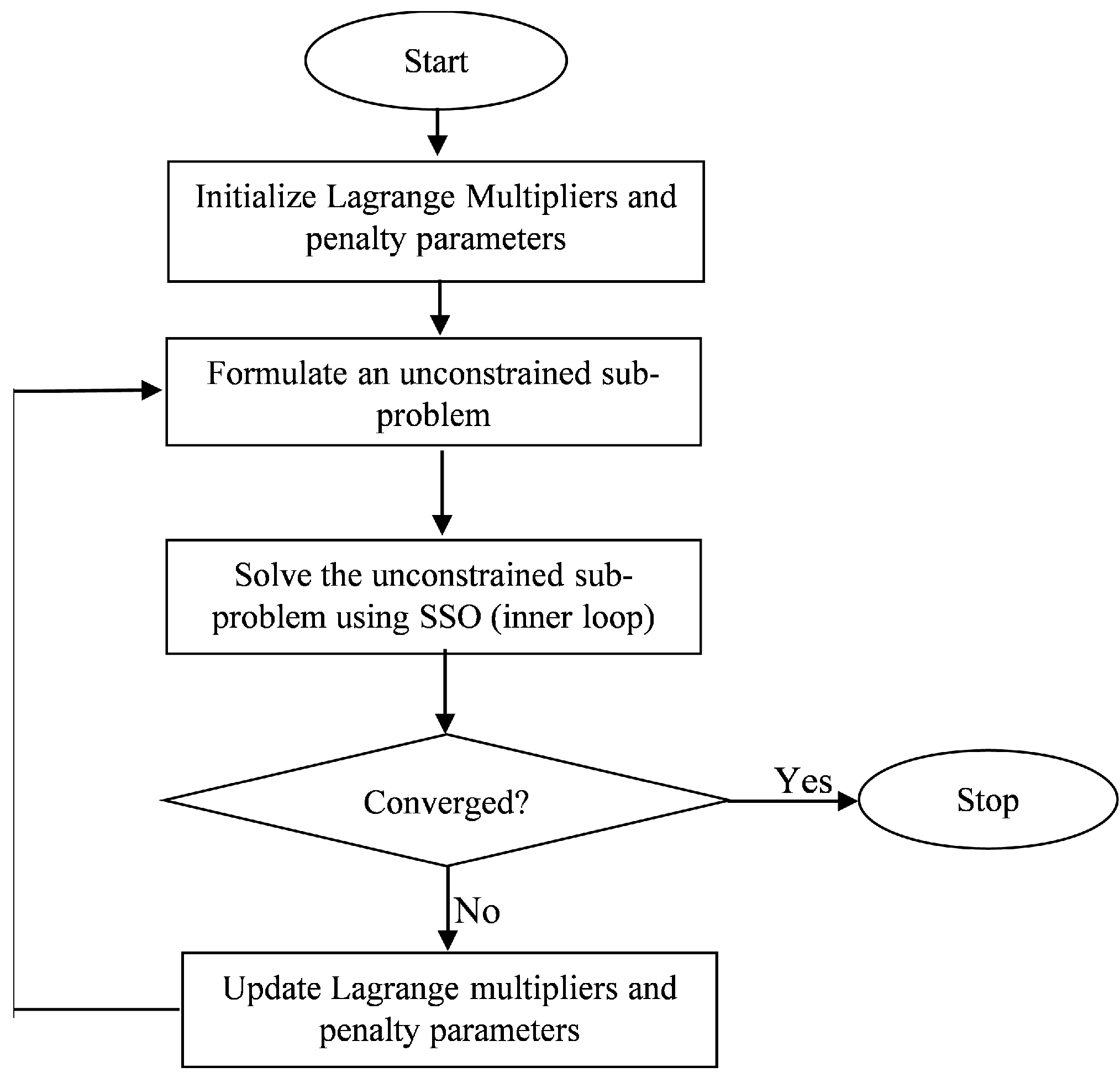
3. The Augmented Lagrangian Subset Simulation Optimization
3.1. The Augmented Lagrangian Multiplier Method
3.2. Initialization and Updating
3.3. Convergence Criterion for the Outer Loop
4. Test Problems and Optimization Results
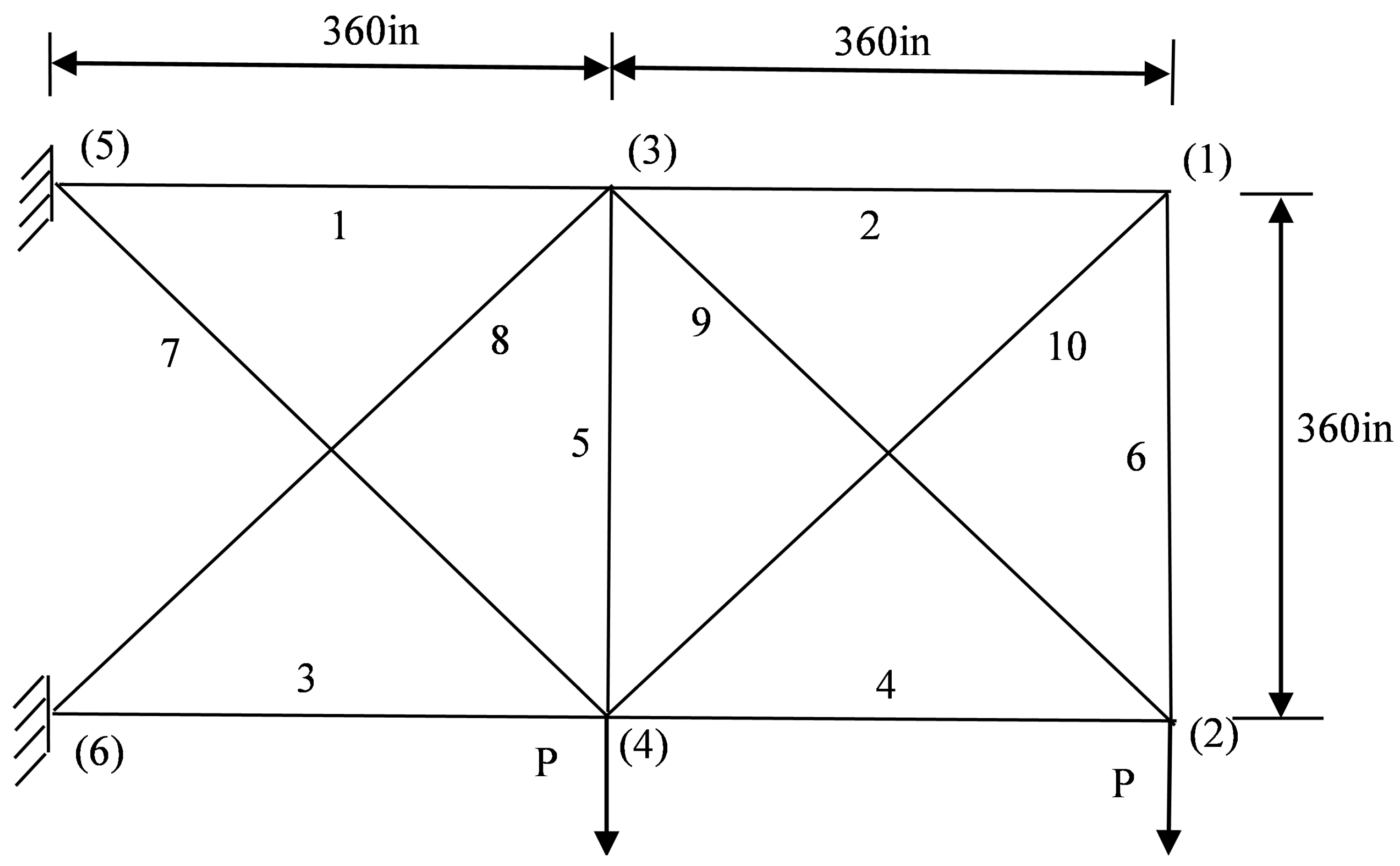
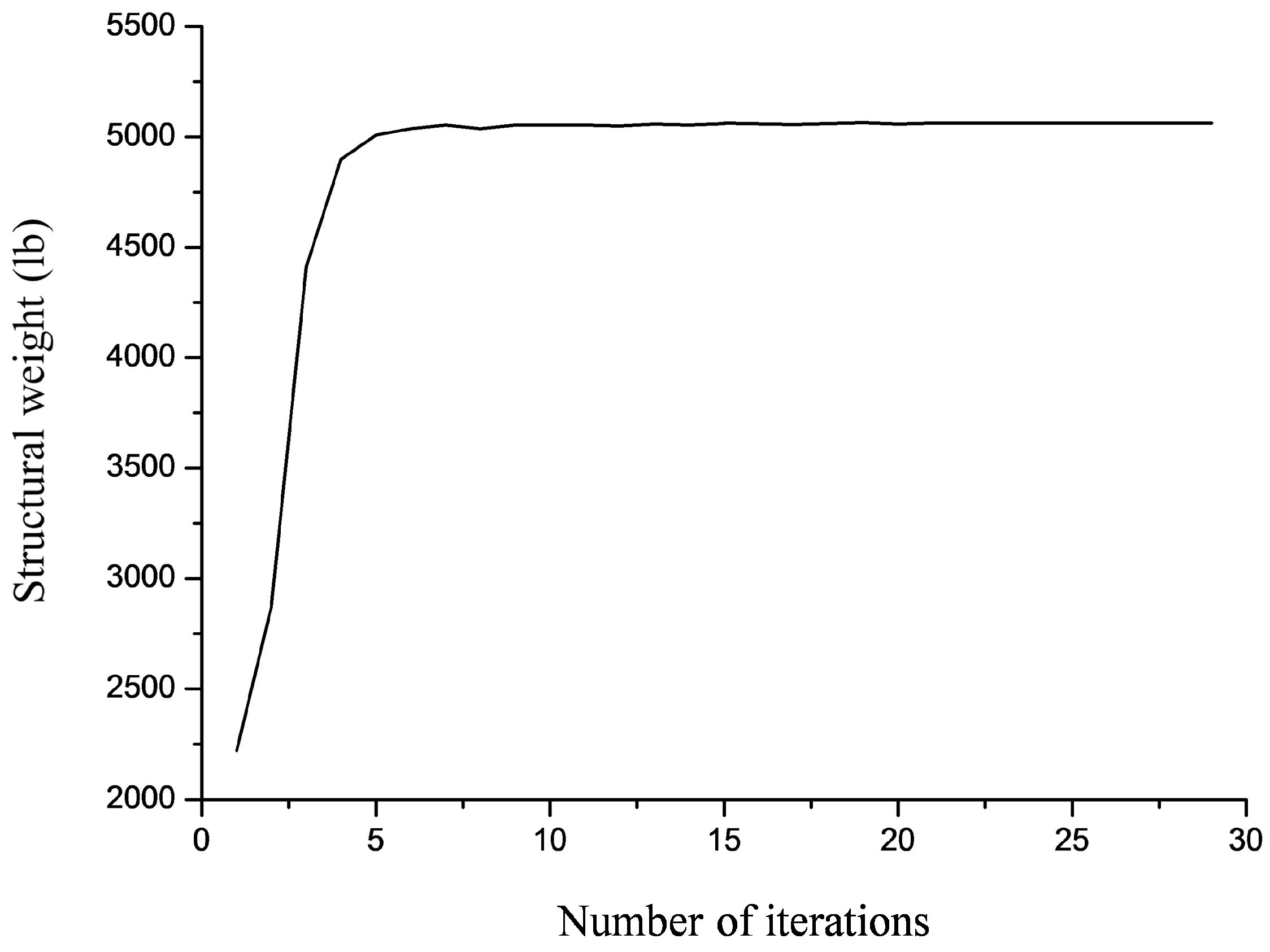
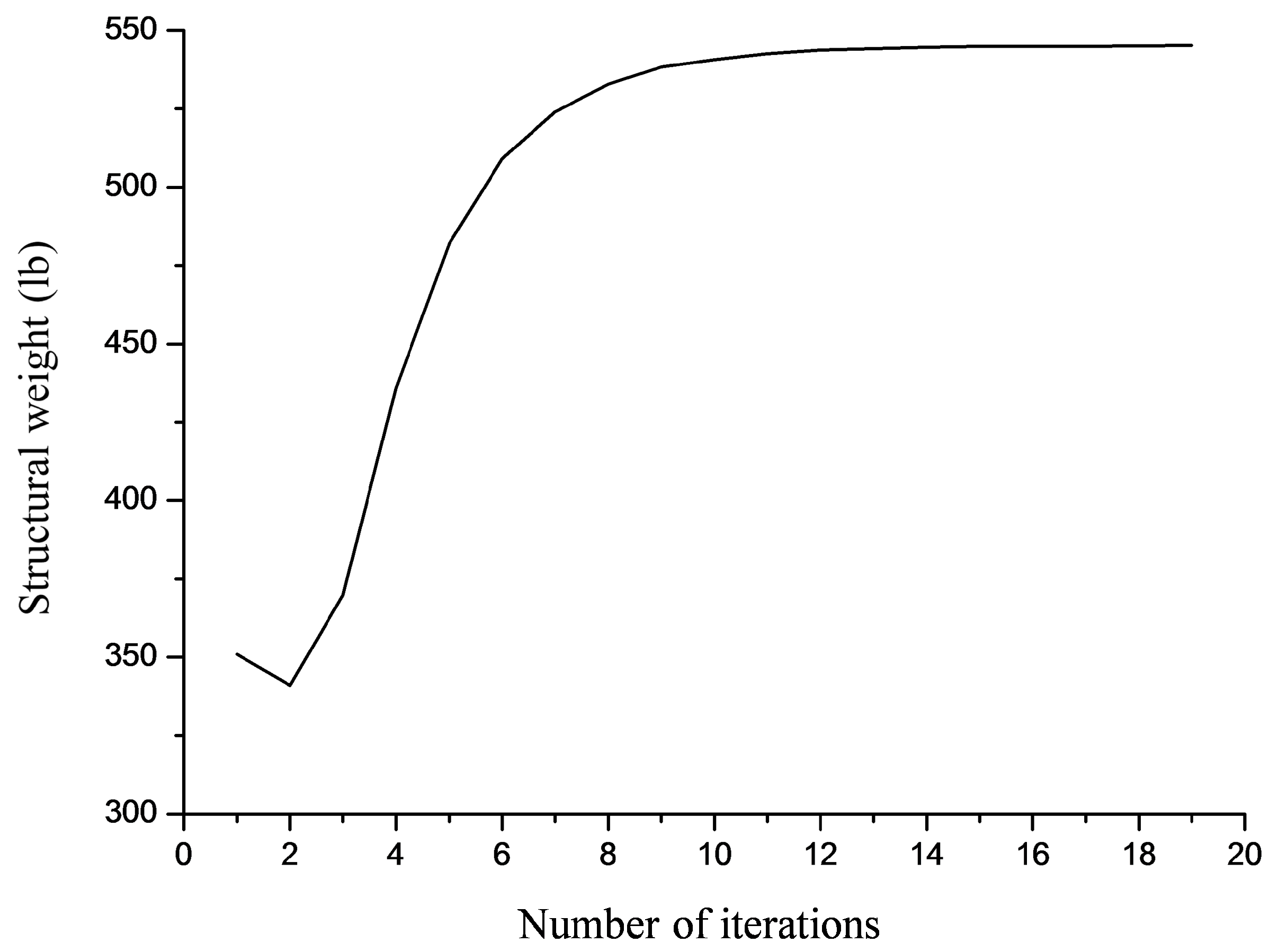
4.1. Planar 10-Bar Truss Structure
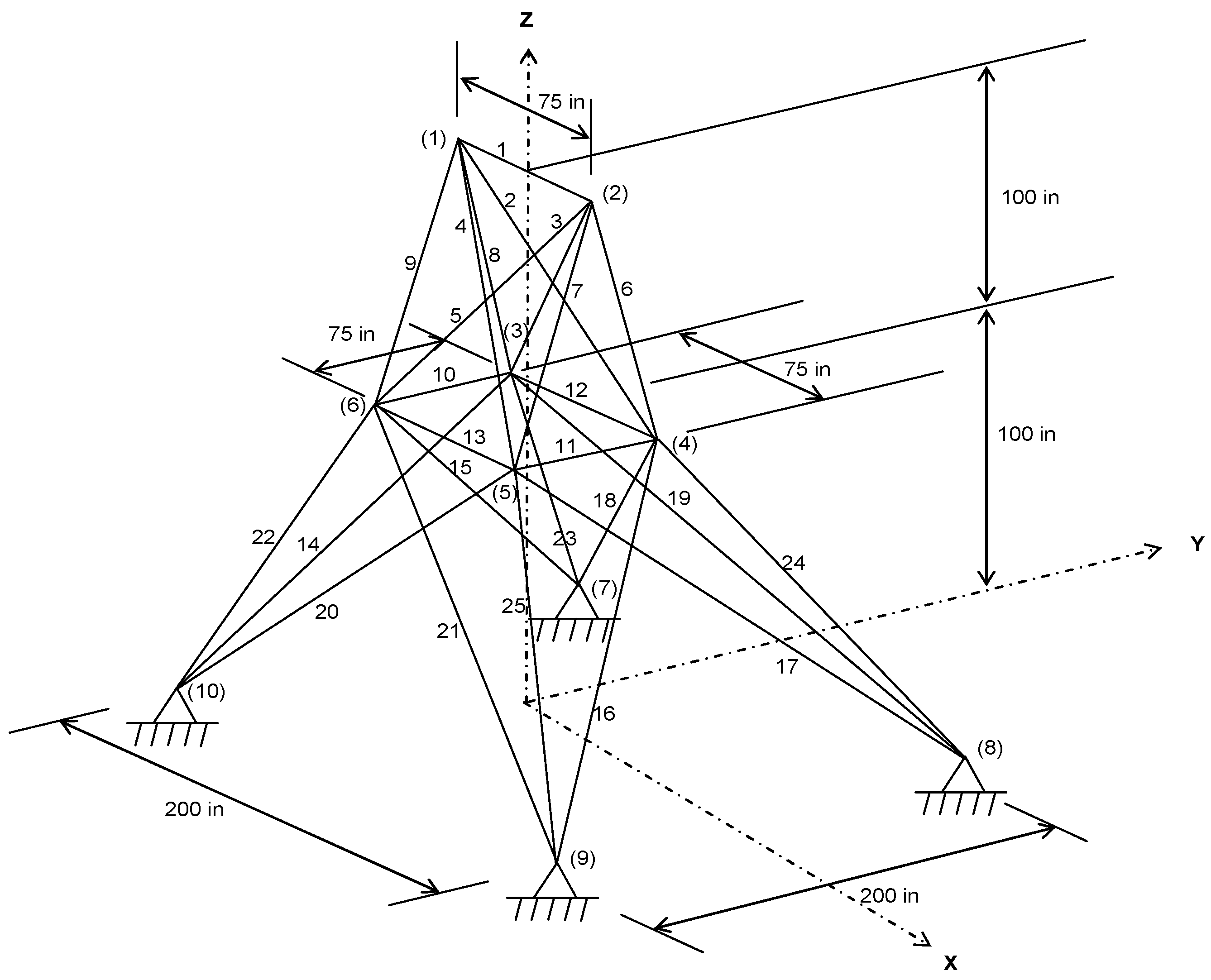
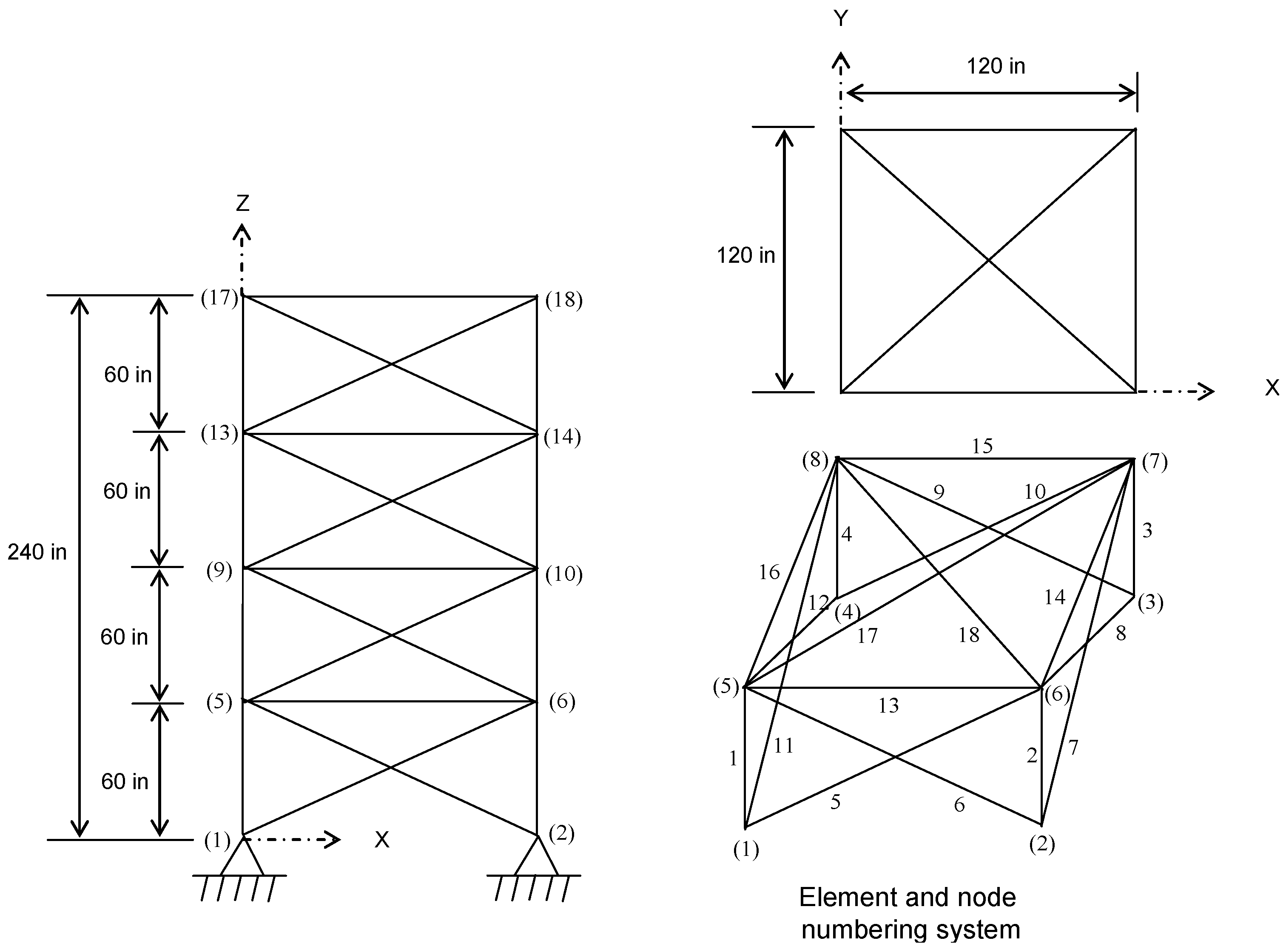
4.2. Spatial 25-Bar Truss Structure
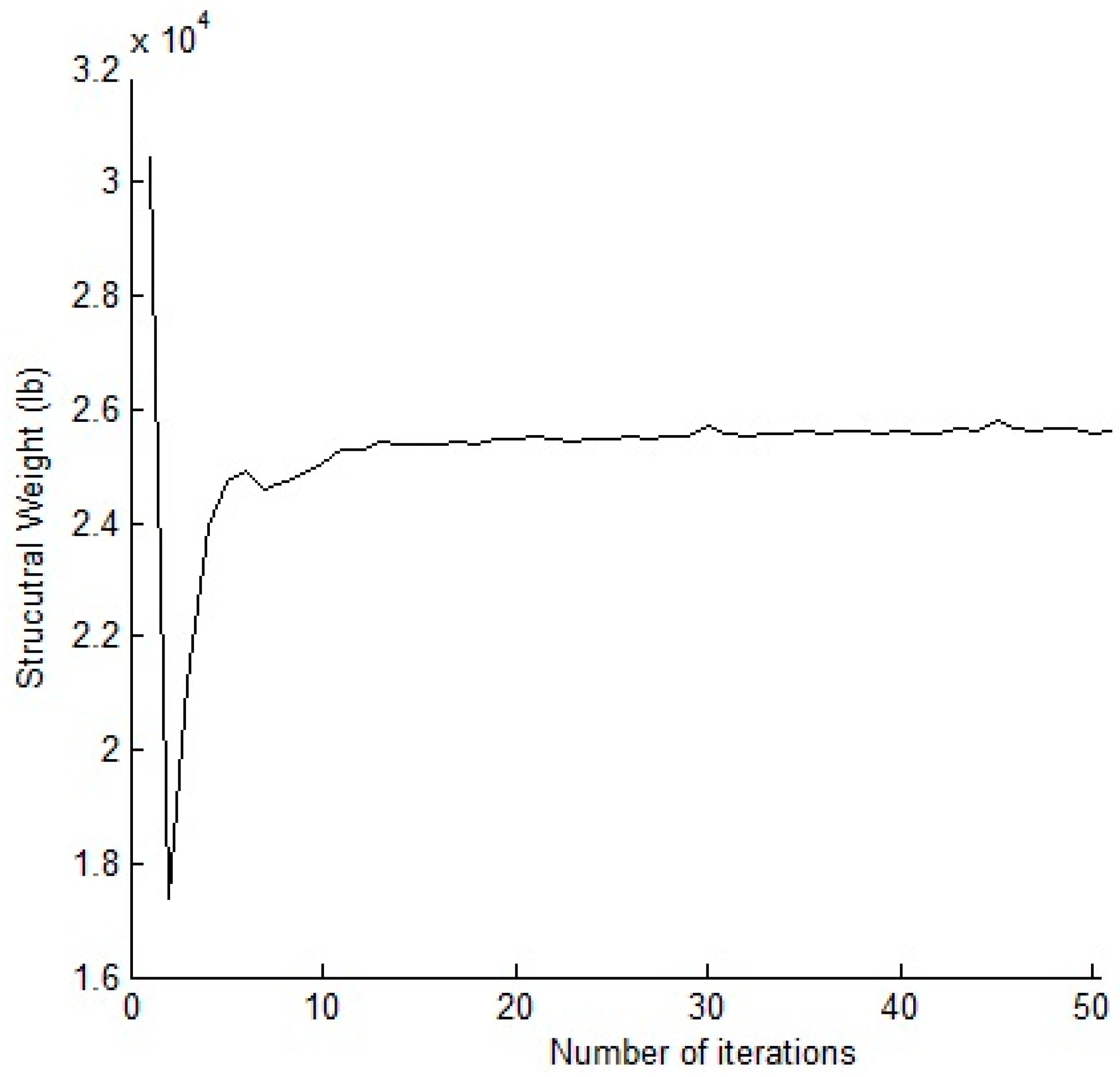
4.3. Spatial 72-Bar Truss Structure
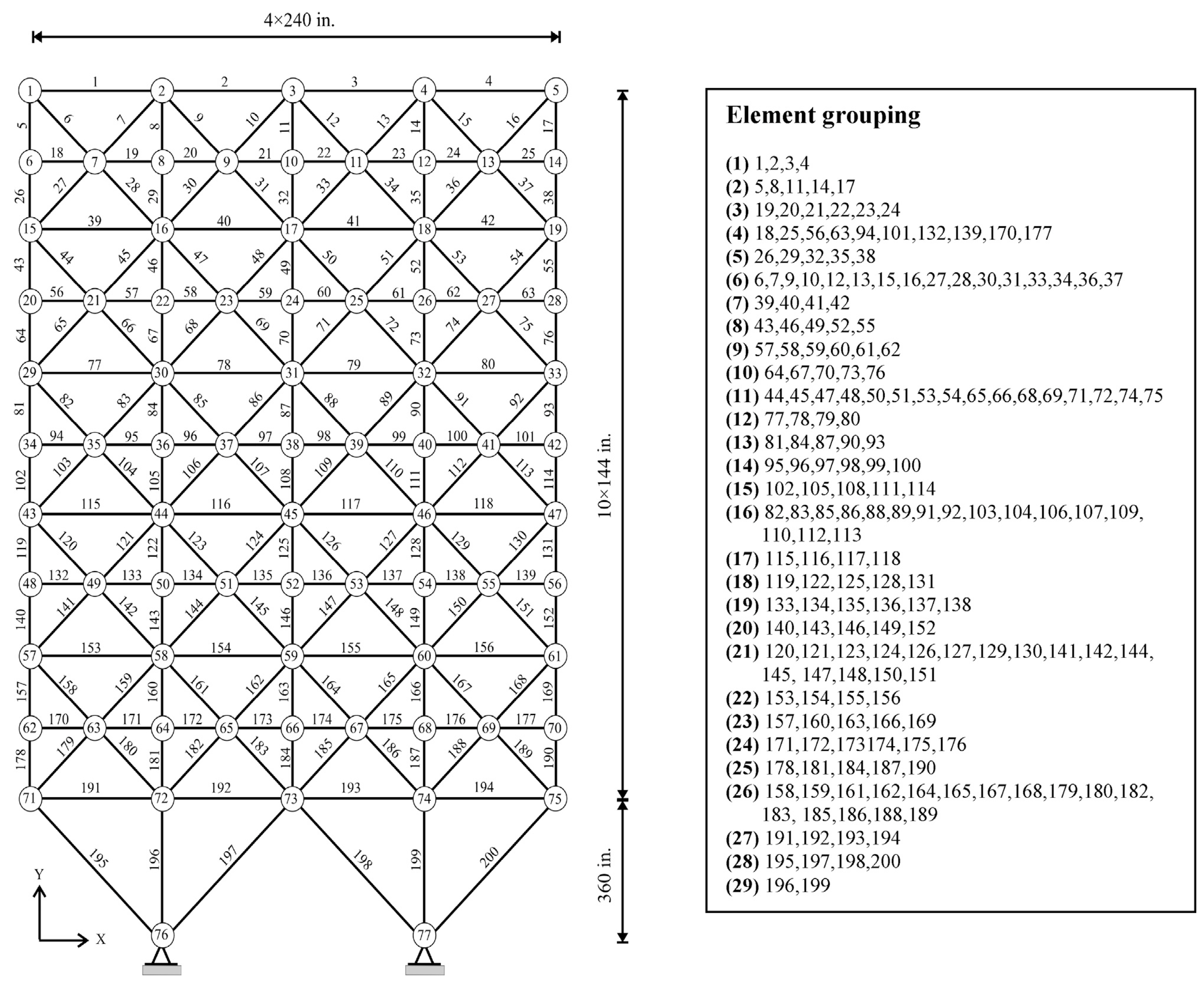
4.4. Planar 200-Bar Truss Structure
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Haftka, R.; Gurdal, Z. Elements of Structural Optimization, 3th ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Jones, D.R.; Perttunen, C.D.; Stuckman, B.E. Lipschitzian optimization without the Lipschitz constant. J. Opt. Theory Appl. 1993, 79, 157–181. [Google Scholar] [CrossRef]
- Mockus, J.; Paulavičius, R.; Rusakevičius, D.; Šešok, D.; Žilinskas, J. Application of Reduced-set Pareto-Lipschitzian Optimization to truss optimization. J. Glob. Opt. 2017, 67, 425–450. [Google Scholar] [CrossRef]
- Kvasov, D.E.; Sergeyev, Y.D. Deterministic approaches for solving practical black-box global optimization problems. Adv. Eng. Softw. 2015, 80 (Suppl. C), 58–66. [Google Scholar] [CrossRef]
- Kvasov, D.E.; Mukhametzhanov, M.S. Metaheuristic vs. deterministic global optimization algorithms: The univariate case. Appl. Math. Comput. 2018, 318, 245–259. [Google Scholar] [CrossRef]
- Adeli, H.; Kumar, S. Distributed genetic algorithm for structural optimization. J. Aerosp. Eng. 1995, 8, 156–163. [Google Scholar] [CrossRef]
- Kameshki, E.S.; Saka, M.P. Optimum geometry design of nonlinear braced domes using genetic algorithm. Comput. Struct. 2007, 85, 71–79. [Google Scholar] [CrossRef]
- Rajeev, S.; Krishnamoorthy, C.S. Discrete optimization of structures using genetic algorithms. J. Struct. Eng. 1992, 118, 1233–1250. [Google Scholar] [CrossRef]
- Wu, S.J.; Chow, P.T. Steady-state genetic algorithms for discrete optimization of trusses. Comput. Struct. 1995, 56, 979–991. [Google Scholar] [CrossRef]
- Saka, M.P. Optimum design of pitched roof steel frames with haunched rafters by genetic algorithm. Comput. Struct. 2003, 81, 1967–1978. [Google Scholar] [CrossRef]
- Erbatur, F.; Hasançebi, O.; Tütüncü, İ.; Kılıç, H. Optimal design of planar and space structures with genetic algorithms. Comput. Struct. 2000, 75, 209–224. [Google Scholar] [CrossRef]
- Galante, M. Structures optimization by a simple genetic algorithm. In Numerical Methods in Engineering and Applied Sciences; Centro Internacional de Métodos Numéricos en Ingeniería: Barcelona, Spain, 1992; pp. 862–870. [Google Scholar]
- Bennage, W.A.; Dhingra, A.K. Single and multiobjective structural optimization in discrete-continuous variables using simulated annealing. Int. J. Numer. Methods Eng. 1995, 38, 2753–2773. [Google Scholar] [CrossRef]
- Lamberti, L. An efficient simulated annealing algorithm for design optimization of truss structures. Comput. Struct. 2008, 86, 1936–1953. [Google Scholar] [CrossRef]
- Leite, J.P.B.; Topping, B.H.V. Parallel simulated annealing for structural optimization. Comput. Struct. 1999, 73, 545–564. [Google Scholar] [CrossRef]
- Camp, C.V.; Bichon, B.J. Design of Space Trusses Using Ant Colony Optimization. J. Struct. Eng. 2004, 130, 741–751. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. A particle swarm ant colony optimization for truss structures with discrete variables. J. Constr. Steel Res. 2009, 65, 1558–1568. [Google Scholar] [CrossRef]
- Kaveh, A.; Shojaee, S. Optimal design of skeletal structures using ant colony optimisation. Int. J. Numer. Methods Eng. 2007, 70, 563–581. [Google Scholar] [CrossRef]
- Kaveh, A.; Farahmand Azar, B.; Talatahari, S. Ant colony optimization for design of space trusses. Int. J. Space Struct. 2008, 23, 167–181. [Google Scholar] [CrossRef]
- Li, L.J.; Huang, Z.B.; Liu, F. A heuristic particle swarm optimization method for truss structures with discrete variables. Comput. Struct. 2009, 87, 435–443. [Google Scholar] [CrossRef]
- Li, L.J.; Huang, Z.B.; Liu, F.; Wu, Q.H. A heuristic particle swarm optimizer for optimization of pin connected structures. Comput. Struct. 2007, 85, 340–349. [Google Scholar] [CrossRef]
- Luh, G.C.; Lin, C.Y. Optimal design of truss-structures using particle swarm optimization. Comput. Struct. 2011, 89, 2221–2232. [Google Scholar] [CrossRef]
- Perez, R.E.; Behdinan, K. Particle swarm approach for structural design optimization. Comput. Struct. 2007, 85, 1579–1588. [Google Scholar] [CrossRef]
- Dong, Y.; Tang, J.; Xu, B.; Wang, D. An application of swarm optimization to nonlinear programming. Comput. Math. Appl. 2005, 49, 1655–1668. [Google Scholar] [CrossRef]
- Jansen, P.W.; Perez, R.E. Constrained structural design optimization via a parallel augmented Lagrangian particle swarm optimization approach. Comput. Struct. 2011, 89, 1352–1366. [Google Scholar] [CrossRef]
- Sedlaczek, K.; Eberhard, P. Using augmented Lagrangian particle swarm optimization for constrained problems in engineering. Struct. Multidiscip. Opt. 2006, 32, 277–286. [Google Scholar] [CrossRef]
- Talatahari, S.; Kheirollahi, M.; Farahmandpour, C.; Gandomi, A.H. A multi-stage particle swarm for optimum design of truss structures. Neural Comput. Appl. 2013, 23, 1297–1309. [Google Scholar] [CrossRef]
- Lee, K.S.; Geem, Z.W. A new structural optimization method based on the harmony search algorithm. Comput. Struct. 2004, 82, 781–798. [Google Scholar] [CrossRef]
- Lee, K.S.; Geem, Z.W.; Lee, S.H.; Bae, K.W. The harmony search heuristic algorithm for discrete structural optimization. Eng. Opt. 2005, 37, 663–684. [Google Scholar] [CrossRef]
- Saka, M. Optimum geometry design of geodesic domes using harmony search algorithm. Adv. Struct. Eng. 2007, 10, 595–606. [Google Scholar] [CrossRef]
- Degertekin, S.O. Improved harmony search algorithms for sizing optimization of truss structures. Comput. Struct. 2012, 92 (Suppl. C), 229–241. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. Optimal design of skeletal structures via the charged system search algorithm. Struct. Multidiscip. Opt. 2010, 41, 893–911. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. Size optimization of space trusses using Big Bang–Big Crunch algorithm. Comput. Struct. 2009, 87, 1129–1140. [Google Scholar] [CrossRef]
- Degertekin, S.O.; Hayalioglu, M.S. Sizing truss structures using teaching-learning-based optimization. Comput. Struct. 2013, 119 (Suppl. C), 177–188. [Google Scholar] [CrossRef]
- Camp, C.V.; Farshchin, M. Design of space trusses using modified teaching–learning based optimization. Eng. Struct. 2014, 62 (Suppl. C), 87–97. [Google Scholar] [CrossRef]
- Sonmez, M. Artificial Bee Colony algorithm for optimization of truss structures. Appl. Soft Comput. 2011, 11, 2406–2418. [Google Scholar] [CrossRef]
- Jalili, S.; Hosseinzadeh, Y. A Cultural Algorithm for Optimal Design of Truss Structures. Latin Am. J. Solids Struct. 2015, 12, 1721–1747. [Google Scholar] [CrossRef]
- Bekdaş, G.; Nigdeli, S.M.; Yang, X.-S. Sizing optimization of truss structures using flower pollination algorithm. Appl. Soft Comput. 2015, 37 (Suppl. C), 322–331. [Google Scholar] [CrossRef]
- Kaveh, A.; Bakhshpoori, T. A new metaheuristic for continuous structural optimization: Water evaporation optimization. Struct. Multidiscip. Opt. 2016, 54, 23–43. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. Particle swarm optimizer, ant colony strategy and harmony search scheme hybridized for optimization of truss structures. Comput. Struct. 2009, 87, 267–283. [Google Scholar] [CrossRef]
- Kaveh, A.; Bakhshpoori, T.; Afshari, E. An efficient hybrid Particle Swarm and Swallow Swarm Optimization algorithm. Comput. Struct. 2014, 143, 40–59. [Google Scholar] [CrossRef]
- Lamberti, L.; Pappalettere, C. Metaheuristic Design Optimization of Skeletal Structures: A Review. Comput. Technol. Rev. 2011, 4, 1–32. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Constrained Optimization and Lagrange Multiplier Methods; Athena Scientific: Belmont, TN, USA, 1996. [Google Scholar]
- Li, H.S. Subset simulation for unconstrained global optimization. Appl. Math. Model. 2011, 35, 5108–5120. [Google Scholar] [CrossRef]
- Li, H.S.; Au, S.K. Design optimization using Subset Simulation algorithm. Struct. Saf. 2010, 32, 384–392. [Google Scholar] [CrossRef]
- Li, H.S.; Ma, Y.Z. Discrete optimum design for truss structures by subset simulation algorithm. J. Aerosp. Eng. 2015, 28, 04014091. [Google Scholar] [CrossRef]
- Au, S.K.; Ching, J.; Beck, J.L. Application of subset simulation methods to reliability benchmark problems. Struct. Saf. 2007, 29, 183–193. [Google Scholar] [CrossRef]
- Au, S.K.; Beck, J.L. Estimation of small failure probabilities in high dimensions by subset simulation. Probab. Eng. Mech. 2001, 16, 263–277. [Google Scholar] [CrossRef]
- Coello, C.A.C. Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: A survey of the state of the art. Comput. Methods Appl. Mech. Eng. 2002, 191, 1245–1287. [Google Scholar] [CrossRef]
- Long, W.; Liang, X.; Huang, Y.; Chen, Y. A hybrid differential evolution augmented Lagrangian method for constrained numerical and engineering optimization. Comput.-Aided Des. 2013, 45, 1562–1574. [Google Scholar] [CrossRef]
- Au, S.K. Reliability-based design sensitivity by efficient simulation. Comput. Struct. 2005, 83, 1048–1061. [Google Scholar] [CrossRef]

| Design Variables | GA [12] | HPSO [21] | HS [28] | HPSACO [17] | PSO [23] | ALPSO [25] | HPSACO [40] | ABC-AP [36] | SAHS [31] | TLBO [34] | MSPSO [27] | HPSSO [41] | WEO [39] | ALSSO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 30.440 | 30.704 | 30.150 | 30.493 | 33.500 | 30.511 | 30.307 | 30.548 | 30.394 | 30.4286 | 30.5257 | 30.5838 | 30.5755 | 30.4397 |
| A2 | 0.100 | 0.100 | 0.102 | 0.100 | 0.100 | 0.100 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1001 | 0.1 | 0.1 | 0.1004 |
| A3 | 21.790 | 23.167 | 22.710 | 23.230 | 22.766 | 23.230 | 23.434 | 23.18 | 23.098 | 23.2436 | 23.225 | 23.15103 | 23.3368 | 23.1599 |
| A4 | 14.260 | 15.183 | 15.270 | 15.346 | 14.417 | 15.198 | 15.505 | 15.218 | 15.491 | 15.3677 | 15.4114 | 15.20566 | 15.1497 | 15.2446 |
| A5 | 0.100 | 0.100 | 0.102 | 0.100 | 0.100 | 0.100 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1001 | 0.1 | 0.1 | 0.1003 |
| A6 | 0.451 | 0.551 | 0.544 | 0.538 | 0.100 | 0.554 | 0.5241 | 0.551 | 0.529 | 0.5751 | 0.5583 | 0.548897 | 0.5276 | 0.5455 |
| A7 | 21.630 | 20.978 | 21.560 | 20.990 | 20.392 | 21.017 | 21.079 | 21.058 | 21.189 | 20.9665 | 20.9172 | 21.06437 | 20.9892 | 21.1123 |
| A8 | 7.628 | 7.460 | 7.541 | 7.451 | 7.534 | 7.452 | 7.4365 | 7.463 | 7.488 | 7.4404 | 7.4395 | 7.465322 | 7.4458 | 7.4660 |
| A9 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1000 |
| A10 | 21.360 | 21.508 | 21.458 | 21.458 | 20.467 | 21.554 | 21.229 | 21.501 | 21.342 | 21.533 | 21.5098 | 21.52935 | 21.5236 | 21.5191 |
| Weight (lb) | 4987.00 | 5060.92 | 5057.88 | 5058.43 | 5024.25 | 5060.85 | 5056.56 | 5060.88 | 5061.42 | 5060.96 | 5061.00 | 5060.86 | 5060.99 | 5060.885 |
| Method | N | Best | Mean | Worst | SD | NSA |
|---|---|---|---|---|---|---|
| ALSSO | 100 | 5060.931 | 5064.559 | 5079.894 | 3.363699 | 48,064 (44,710) |
| 200 | 5060.931 | 5062.391 | 5065.715 | 0.889472 | 94,540 (108,600) | |
| 500 | 5060.885 | 5061.713 | 5062.291 | 0.360457 | 247,828 (253,400) | |
| HPSACO [33] | 5056.56 | 5057.66 | 5061.12 | 1.42 | 10,650 | |
| ABC-AP [36] | 5060.88 | N/A | 5060.95 | N/A | 500,000 | |
| SAHS [31] | 5061.42 | 5061.95 | 5063.39 | 0.71 | 7081 | |
| TLBO [34] | 5060.96 | 5062.08 | 5063.23 | 0.79 | 16,872 | |
| MSPSO [27] | 5061.00 | 5064.46 | 5078.00 | 5.72 | N/A | |
| HPSSO [41] | 5060.86 | 5062.28 | 5076.90 | 4.325 | 14,118 | |
| WEO [39] | 5060.99 | 5062.09 | 5975.41 | 2.05 | 19,540 |
| Design Variables | Compressive Stress Limit (ksi) | Tensile Stress Limit (ksi) | |
|---|---|---|---|
| 1 | A1 | 35.092 | 40.0 |
| 2 | A2–A5 | 11.590 | 40.0 |
| 3 | A6–A9 | 17.305 | 40.0 |
| 4 | A10–A11 | 35.092 | 40.0 |
| 5 | A12–A13 | 35.092 | 40.0 |
| 6 | A14–A17 | 6.759 | 40.0 |
| 7 | A18–A21 | 6.957 | 40.0 |
| 8 | A22–A25 | 11.802 | 40.0 |
| Load Cases | Nodes | Loads | ||
|---|---|---|---|---|
| Px (kips) | Py (kips) | Pz (kips) | ||
| 1 | 1 | 0.0 | 20.0 | −5.0 |
| 2 | 0.0 | −20.0 | −5.0 | |
| 2 | 1 | 1.0 | 10.0 | −5.0 |
| 2 | 0.0 | 10.0 | −5.0 | |
| 3 | 0.5 | 0.0 | 0.0 | |
| 6 | 0.5 | 0.0 | 0.0 | |
| Design Variables | HS [28] | HPSO [21] | SSO [45] | PLOR [3] | ABC-AP [36] | SAHS [31] | TLBO [34] | MSPSO [27] | CA [37] | HPSSO [41] | TLBO [35] | FPA [38] | WEO [39] | ALSSO | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A1 | 0.047 | 0.010 | 0.010 | 0.010 | 0.011 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01001 |
| 2 | A2–A5 | 2.022 | 1.970 | 2.057 | 1.951 | 1.979 | 2.074 | 2.0712 | 1.9848 | 2.02064 | 1.9907 | 1.9878 | 1.8308 | 1.9184 | 1.983579 |
| 3 | A6–A9 | 2.950 | 3.016 | 2.892 | 3.025 | 3.003 | 2.961 | 2.957 | 2.9956 | 3.01733 | 2.9881 | 2.9914 | 3.1834 | 3.0023 | 2.998787 |
| 4 | A10–A11 | 0.010 | 0.010 | 0.010 | 0.010 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.0102 | 0.01 | 0.01 | 0.010008 |
| 5 | A12–A13 | 0.014 | 0.010 | 0.014 | 0.010 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.010005 |
| 6 | A14–A17 | 0.688 | 0.694 | 0.697 | 0.592 | 0.69 | 0.691 | 0.6891 | 0.6852 | 0.69383 | 0.6824 | 0.6828 | 0.7017 | 0.6827 | 0.683045 |
| 7 | A18–A21 | 1.657 | 1.681 | 1.666 | 1.706 | 1.679 | 1.617 | 1.6209 | 1.6778 | 1.63422 | 1.6764 | 1.6775 | 1.7266 | 1.6778 | 1.677394 |
| 8 | A22–A25 | 2.663 | 2.643 | 2.675 | 2.789 | 2.652 | 2.674 | 2.6768 | 2.6599 | 2.65277 | 2.6656 | 2.664 | 2.5713 | 2.6612 | 2.66077 |
| Weight (lb) | 544.38 | 545.19 | 545.37 | 546.80 | 545.193 | 545.12 | 545.09 | 545.172 | 545.05 | 545.164 | 545.175 | 545.159 | 545.166 | 545.1057 | |
| N | Best | Mean | Worst | SD | NSA | |
|---|---|---|---|---|---|---|
| ALSSO | 100 | 545.1241 | 545.2569 | 545.7793 | 0.135161 | 27,009 (23,170) |
| 200 | 545.1254 | 545.205 | 545.4292 | 0.067821 | 38,301 (32,580) | |
| 500 | 545.1057 | 545.185 | 545.2819 | 0.044924 | 86,490 (90,500) | |
| ABC-AP [36] | 545.19 | N/A | 545.28 | N/A | 300,000 | |
| SAHS [31] | 545.12 | 545.94 | 546.6 | 0.91 | 9051 | |
| TLBO [34] | 545.09 | 545.41 | 546.33 | 0.42 | 15,318 | |
| MSPSO [27] | 545.172 | 546.03 | 548.78 | 0.8 | 10,800 | |
| CA [37] | 545.05 | 545.93 | N/A | 1.55 | 9380 | |
| HPSSO [41] | 545.164 | 545.556 | 546.99 | 0.432 | 13,326 | |
| TLBO [35] | 545.175 | 545.483 | N/A | 0.306 | 12,199 | |
| FPA [38] | 545.159 | 545.73 | N/A | 0.59 | 8149 | |
| WEO [39] | 545.166 | 545.226 | 545.592 | 0.083 | 19,750 |
| Node | Case 1 (kips) | Case 2 (kips) | ||||
|---|---|---|---|---|---|---|
| Px | Py | Pz | Px | Py | Pz | |
| 17 | 5.0 | 5.0 | −5.0 | 0.0 | 0.0 | −5.0 |
| 18 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | −5.0 |
| 19 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | −5.0 |
| 20 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | −5.0 |
| Design Variables | GA [11] | ACO [16] | HS [28] | PSO [23] | ALPSO [25] | DIRECT-l [3] | BB-BC [33] | SAHS [27] | TLBO [34] | CA [37] | FPA [38] | ALSSO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1–A4 | 1.910 | 1.948 | 1.790 | 1.743 | 1.898 | 1.699 | 1.9042 | 1.86 | 1.8807 | 1.86093 | 1.8758 | 1.900283 |
| A5–A12 | 0.525 | 0.508 | 0.521 | 0.519 | 0.513 | 0.476 | 0.5162 | 0.521 | 0.5142 | 0.5093 | 0.516 | 0.511187 |
| A13–A16 | 0.122 | 0.101 | 0.100 | 0.100 | 0.100 | 0.100 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.100084 |
| A17–A18 | 0.103 | 0.102 | 0.100 | 0.100 | 0.100 | 0.100 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.100258 |
| A19–A22 | 1.310 | 1.303 | 1.229 | 1.308 | 1.258 | 1.371 | 1.2582 | 1.293 | 1.2711 | 1.26291 | 1.2993 | 1.268814 |
| A23–A30 | 0.498 | 0.511 | 0.522 | 0.519 | 0.513 | 0.547 | 0.5035 | 0.511 | 0.5151 | 0.50397 | 0.5246 | 0.510226 |
| A31–A34 | 0.100 | 0.101 | 0.100 | 0.100 | 0.100 | 0.100 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1001 | 0.100076 |
| A35–A36 | 0.103 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.100113 |
| A37–A40 | 0.535 | 0.561 | 0.517 | 0.514 | 0.520 | 0.618 | 0.5178 | 0.499 | 0.5317 | 0.52316 | 0.4971 | 0.519311 |
| A41–A48 | 0.535 | 0.492 | 0.504 | 0.546 | 0.518 | 0.476 | 0.5214 | 0.501 | 0.5134 | 0.52522 | 0.5089 | 0.516303 |
| A49–A52 | 0.103 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.1 | 0.1 | 0.1 | 0.10001 | 0.1 | 0.100062 |
| A53–A54 | 0.111 | 0.107 | 0.101 | 0.110 | 0.100 | 0.112 | 0.1007 | 0.1 | 0.1 | 0.10254 | 0.1 | 0.100502 |
| A55–A58 | 0.161 | 0.156 | 0.156 | 0.162 | 0.157 | 0.153 | 0.1566 | 0.168 | 0.1565 | 0.155962 | 0.1575 | 0.156389 |
| A59–A66 | 0.544 | 0.550 | 0.547 | 0.509 | 0.546 | 0.582 | 0.5421 | 0.584 | 0.5429 | 0.55349 | 0.5329 | 0.550278 |
| A67–A70 | 0.379 | 0.390 | 0.442 | 0.497 | 0.405 | 0.405 | 0.4132 | 0.433 | 0.4081 | 0.42026 | 0.4089 | 0.40533 |
| A71–A72 | 0.521 | 0.592 | 0.590 | 0.562 | 0.566 | 0.655 | 0.5756 | 0.52 | 0.5733 | 0.5615 | 0.5731 | 0.563667 |
| Weights (lb) | 383.12 | 380.24 | 379.27 | 381.91 | 379.61 | 382.34 | 379.66 | 380.62 | 379.632 | 379.69 | 379.095 | 379.59 |
| N | Best | Mean | Worst | SD | NSA | |
|---|---|---|---|---|---|---|
| ALSSO | 100 | 379.7376 | 380.1562 | 382.8799 | 0.60467 | 62,292 (77,020) |
| 200 | 379.6001 | 379.7373 | 380.0177 | 0.100794 | 131,819 (115,840) | |
| 500 | 379.5922 | 379.7058 | 379.981 | 0.103908 | 260,928 (307,700) | |
| BBBC [33] | 379.66 | 381.85 | N/A | 1.201 | 13,200 | |
| SAHS [31] | 380.62 | 382.85 | 383.89 | 1.38 | 13,742 | |
| TLBO [34] | 379.632 | 380.20 | 380.83 | 0.41 | 21,542 | |
| CA [37] | 379.69 | 380.86 | N/A | 1.8507 | 18,460 | |
| FPA [38] | 379.095 | 379.534 | N/A | 0.272 | 9029 |
| Element Group | HPSACO [40] | ABC-AP [36] | SAHB [31] | TLBO [34] | HPSSO [41] | FPA [38] | WEO [39] | ALSSO |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.1033 | 0.1039 | 0.1540 | 0.1460 | 0.1213 | 0.1425 | 0.1144 | 0.132626 |
| 2 | 0.9184 | 0.9463 | 0.9410 | 0.9410 | 0.9426 | 0.9637 | 0.9443 | 1.004183 |
| 3 | 0.1202 | 0.1037 | 0.1000 | 0.1000 | 0.1220 | 0.1005 | 0.1310 | 0.100772 |
| 4 | 0.1009 | 0.1126 | 0.1000 | 0.1010 | 0.1000 | 0.1000 | 0.1016 | 0.104438 |
| 5 | 1.8664 | 1.9520 | 1.9420 | 1.9410 | 2.0143 | 1.9514 | 2.0353 | 1.969623 |
| 6 | 0.2826 | 0.293 | 0.3010 | 0.2960 | 0.2800 | 0.2957 | 0.3126 | 0.285843 |
| 7 | 0.1000 | 0.1064 | 0.1000 | 0.1000 | 0.1589 | 0.1156 | 0.1679 | 0.145089 |
| 8 | 2.9683 | 3.1249 | 3.1080 | 3.1210 | 3.0666 | 3.1133 | 3.1541 | 3.136798 |
| 9 | 0.1000 | 0.1077 | 0.1000 | 0.1000 | 0.1002 | 0.1006 | 0.1003 | 0.120883 |
| 10 | 3.9456 | 4.1286 | 4.1060 | 4.1730 | 4.0418 | 4.1100 | 4.1005 | 4.124644 |
| 11 | 0.3742 | 0.4250 | 0.4090 | 0.4010 | 0.4142 | 0.4165 | 0.4350 | 0.438346 |
| 12 | 0.4501 | 0.1046 | 0.1910 | 0.1810 | 0.4852 | 0.1843 | 0.1148 | 0.163695 |
| 13 | 4.9603 | 5.4803 | 5.4280 | 5.4230 | 5.4196 | 5.4567 | 5.3823 | 5.514607 |
| 14 | 1.0738 | 0.1060 | 0.1000 | 0.1000 | 0.1000 | 0.1000 | 0.1607 | 0.148495 |
| 15 | 5.9785 | 6.4853 | 6.4270 | 6.4220 | 6.3749 | 6.4559 | 6.4152 | 6.415737 |
| 16 | 0.7863 | 0.5600 | 0.5810 | 0.5710 | 0.6813 | 0.5800 | 0.5629 | 0.592158 |
| 17 | 0.7374 | 0.1825 | 0.1510 | 0.1560 | 0.1576 | 0.1547 | 0.4010 | 0.186473 |
| 18 | 7.3809 | 8.0445 | 7.9730 | 7.9580 | 8.1447 | 8.0132 | 7.9735 | 8.037395 |
| 19 | 0.6674 | 0.1026 | 0.1000 | 0.1000 | 0.1000 | 0.1000 | 0.1092 | 0.130935 |
| 20 | 8.3000 | 9.0334 | 8.9740 | 8.9580 | 9.0920 | 9.0135 | 9.0155 | 9.017311 |
| 21 | 1.1967 | 0.7844 | 0.7190 | 0.7200 | 0.7462 | 0.7391 | 0.8628 | 0.780634 |
| 22 | 1.0000 | 0.7506 | 0.4220 | 0.4780 | 0.2114 | 0.7870 | 0.2220 | 0.312574 |
| 23 | 10.8262 | 11.3057 | 10.8920 | 10.8970 | 10.9587 | 11.1795 | 11.0254 | 11.03076 |
| 24 | 0.1000 | 0.2208 | 0.1000 | 0.1000 | 0.1000 | 0.1462 | 0.1397 | 0.112562 |
| 25 | 11.6976 | 12.2730 | 11.8870 | 11.8970 | 11.9832 | 12.1799 | 12.0340 | 12.00723 |
| 26 | 1.3880 | 1.4055 | 1.0400 | 1.0800 | 0.9241 | 1.3424 | 1.0043 | 1.017312 |
| 27 | 4.9523 | 5.1600 | 6.6460 | 6.4620 | 6.7676 | 5.4844 | 6.5762 | 6.458830 |
| 28 | 8.8000 | 9.9930 | 10.8040 | 10.7990 | 10.9639 | 10.1372 | 10.7265 | 10.66930 |
| 29 | 14.6645 | 14.70144 | 13.8700 | 13.9220 | 13.8186 | 14.5262 | 13.9666 | 13.96069 |
| Best weight (lb) | 25,156.5 | 25,533.79 | 25,491.9 | 25,488.15 | 25,698.85 | 25,521.81 | 25,674.83 | 25,569.98 |
| N | Best | Mean | Worst | SD | NSA | |
|---|---|---|---|---|---|---|
| ALSSO | 100 | 25,722.22 | 25,938.99 | 26,743.77 | 303.5379 | 89,655 (88,080) |
| 200 | 25,617.50 | 25,694.73 | 25,842.59 | 57.9310 | 181,068 (173,280) | |
| 500 | 25,569.98 | 25,624.89 | 25,696.47 | 32.3777 | 453,465 (447,600) | |
| HPSACO [40] | 25,156.5 | 25,786.2 | 26,421.6 | 830.5 | 9800 | |
| ABC-AP [36] | 25,533.79 | N/A | N/A | N/A | 1,450,000 | |
| SAHB [31] | 25,491.90 | 25,610.20 | 25,799.30 | 141.85 | 14,185 | |
| TLBO [34] | 25,488.15 | 25,533.14 | 25,563.05 | 27.44 | 28,059 | |
| HPSSO [41] | 25,698.85 | 28,386.72 | N/A | 2403 | 14,406 | |
| FPA [38] | 25,521.81 | 25,543.51 | N/A | 18.13 | 10,685 | |
| WEO [39] | 25,674.83 | 26,613.45 | N/A | 702.80 | 19,410 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, F.; Dong, Q.-Y.; Li, H.-S. Truss Structure Optimization with Subset Simulation and Augmented Lagrangian Multiplier Method. Algorithms 2017, 10, 128. https://doi.org/10.3390/a10040128
Du F, Dong Q-Y, Li H-S. Truss Structure Optimization with Subset Simulation and Augmented Lagrangian Multiplier Method. Algorithms. 2017; 10(4):128. https://doi.org/10.3390/a10040128
Chicago/Turabian StyleDu, Feng, Qiao-Yue Dong, and Hong-Shuang Li. 2017. "Truss Structure Optimization with Subset Simulation and Augmented Lagrangian Multiplier Method" Algorithms 10, no. 4: 128. https://doi.org/10.3390/a10040128




