Advances in Artificial Neural Networks – Methodological Development and Application
Abstract
:1. Introduction
2. History of ANN Development
3. ANN Architectures and Training Algorithms
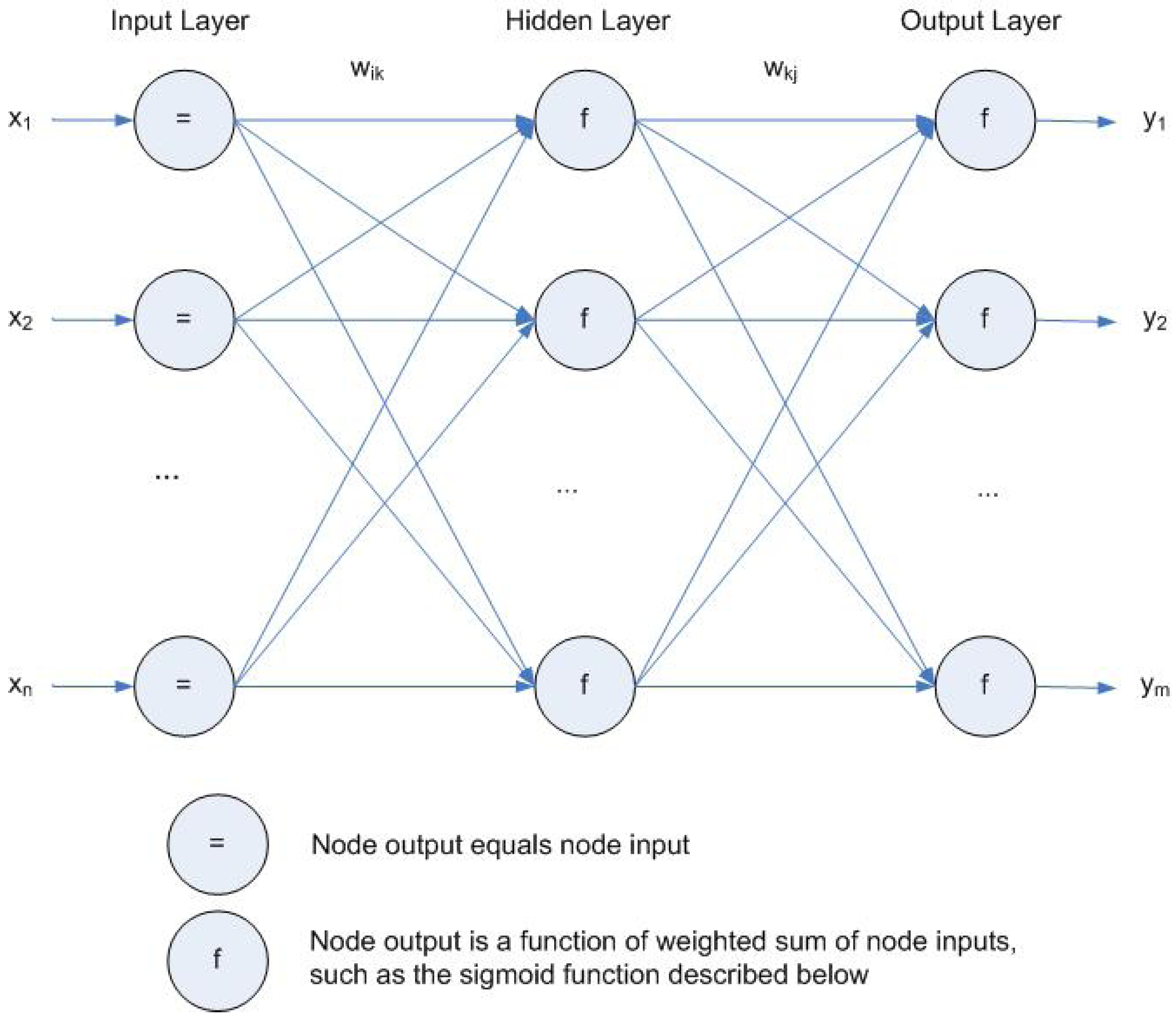
3.1. MLP and BP
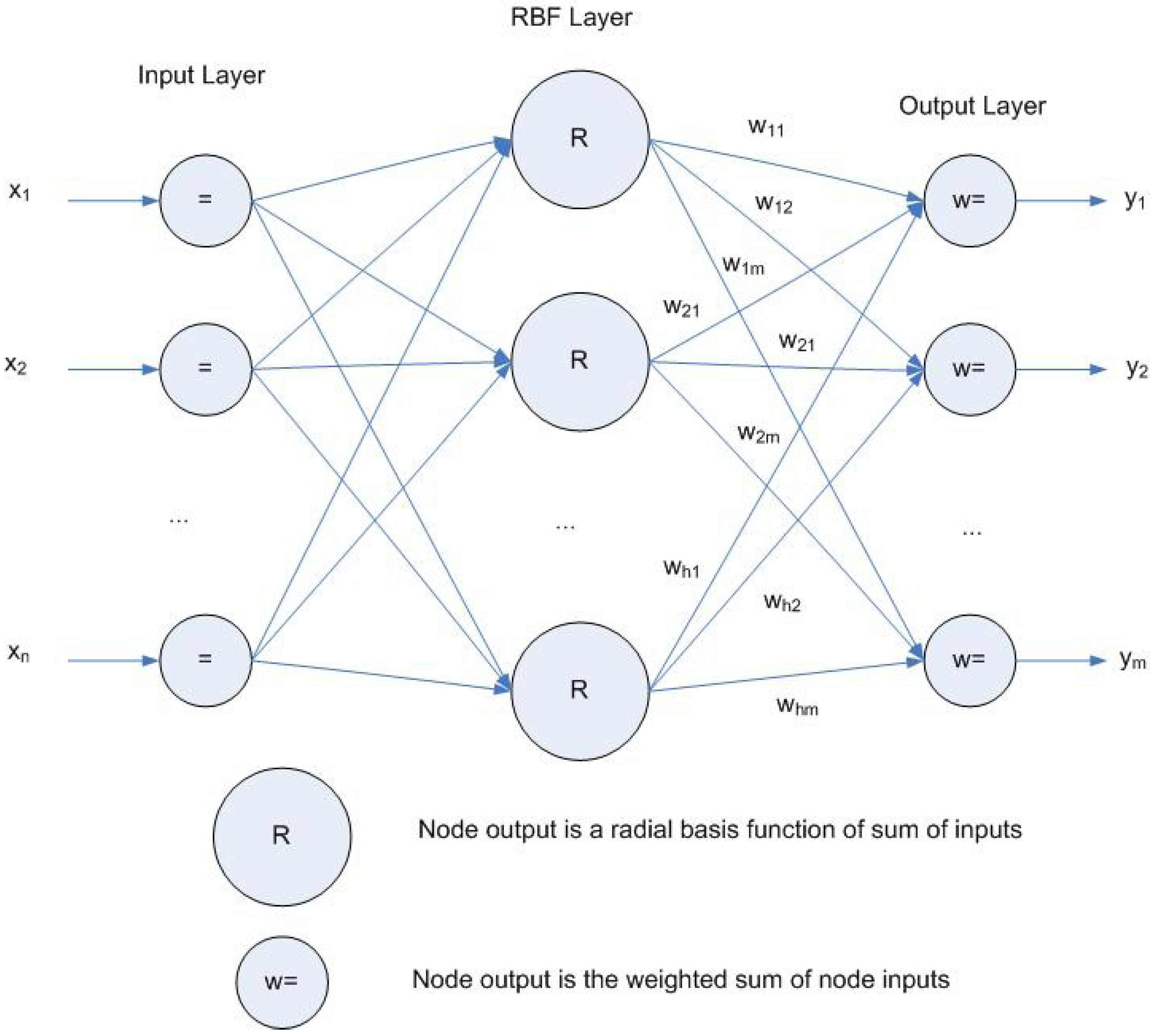
3.2. Radial Basis Function Network
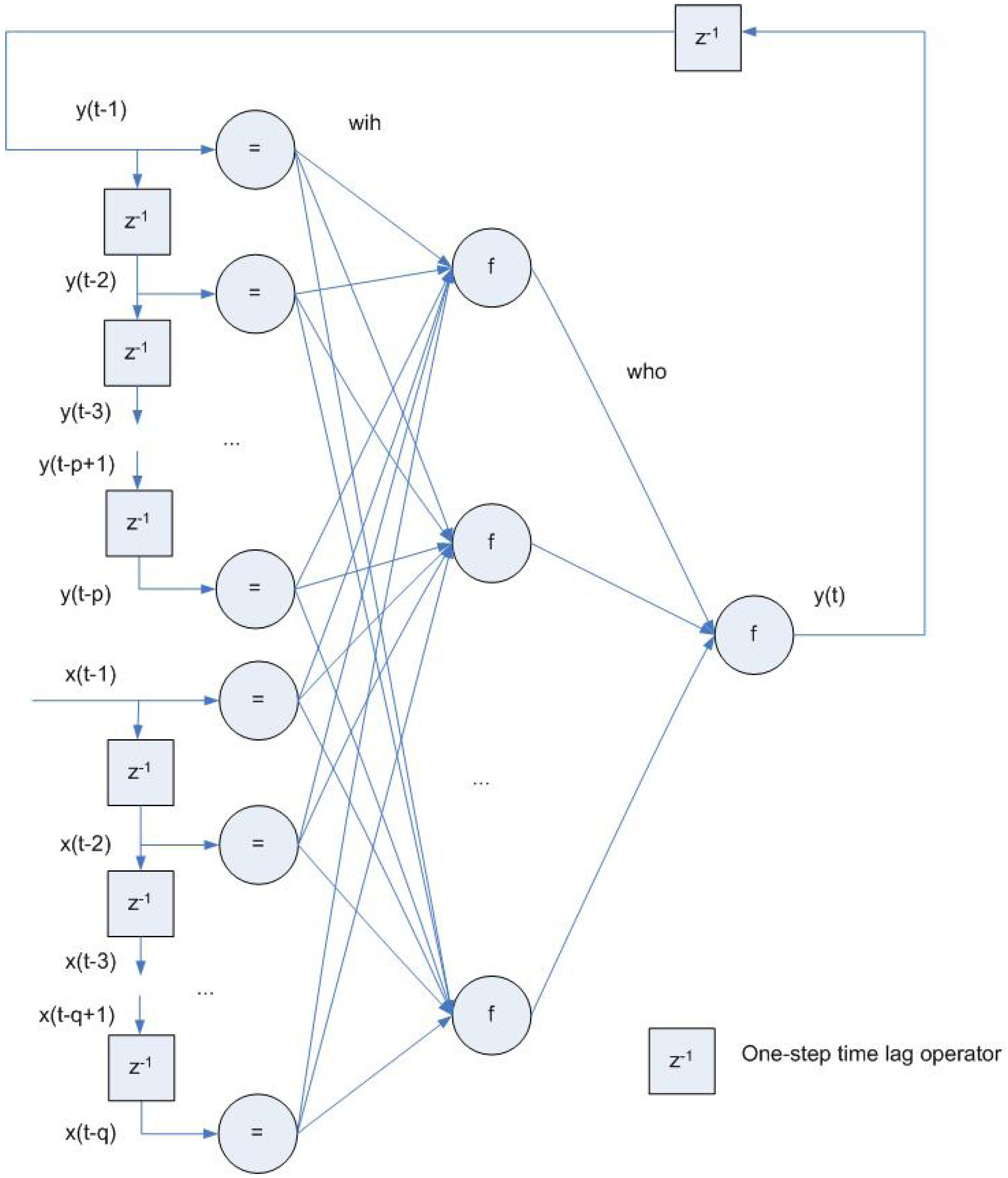
3.3. Recurrent and Feedback Networks
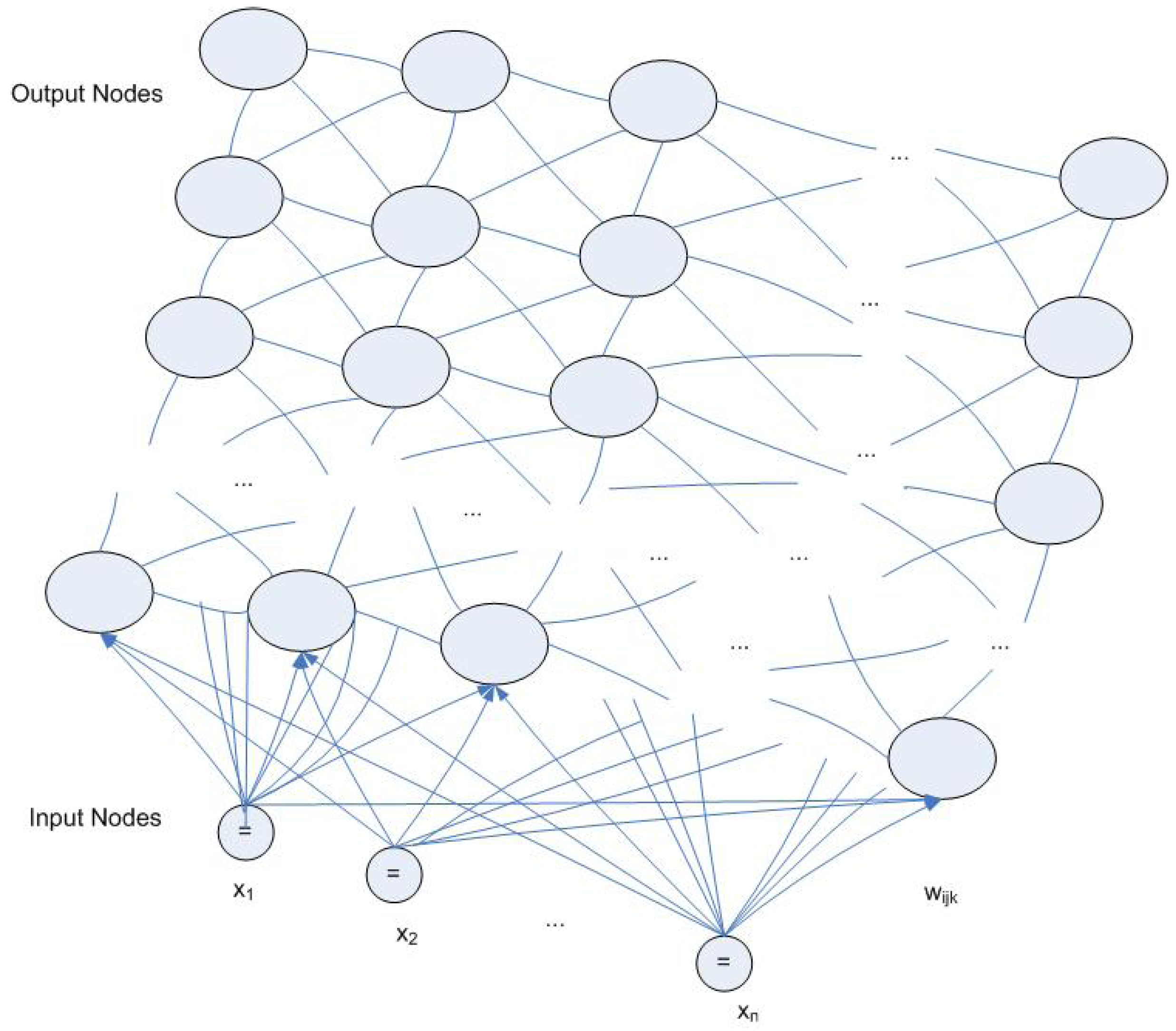
3.4. Kohonen SOM Network and Unsupervised Training
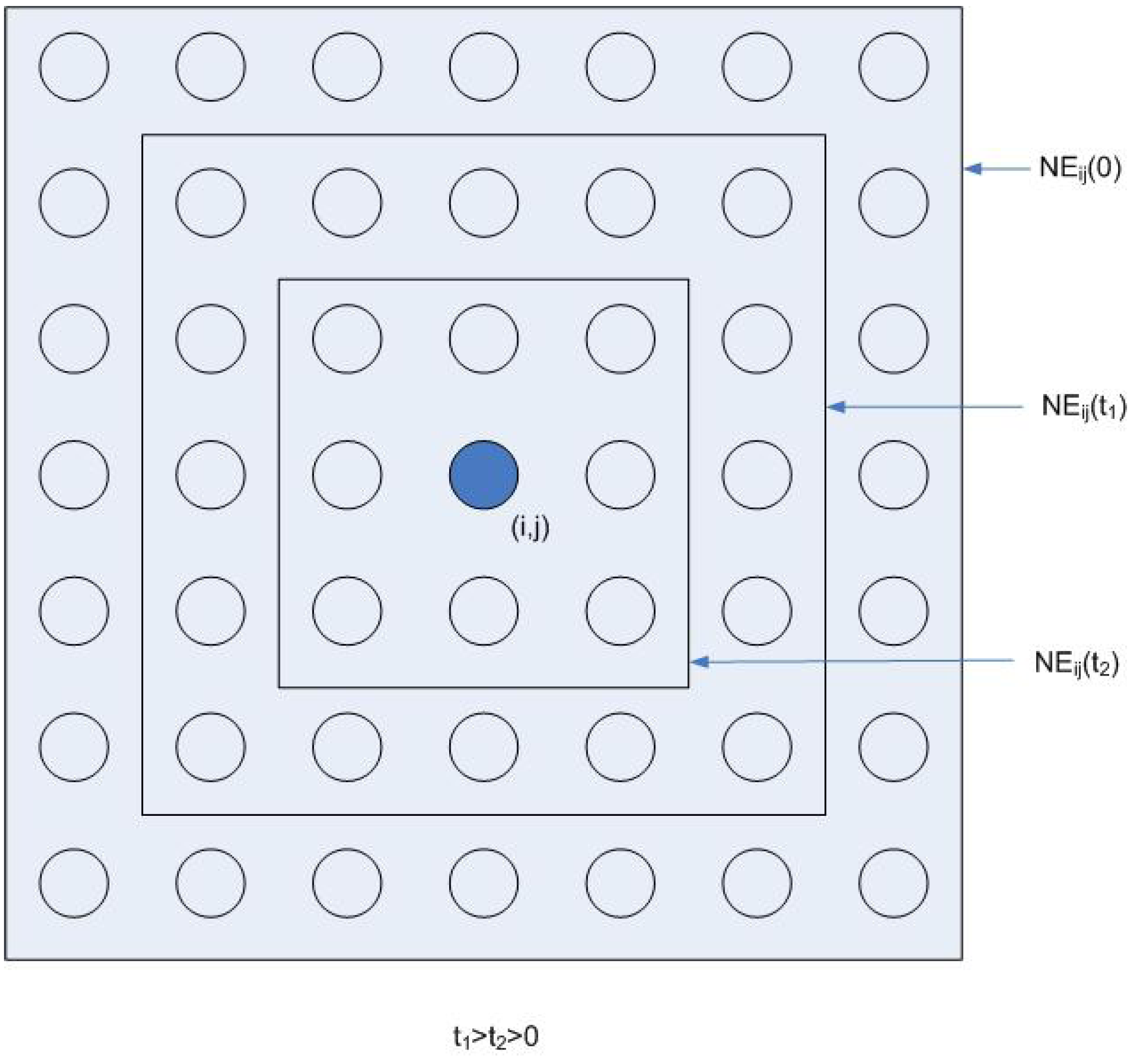
4. Advanced Development of ANNs
4.1. Standard BP Enhancement
4.2. Network Generalization

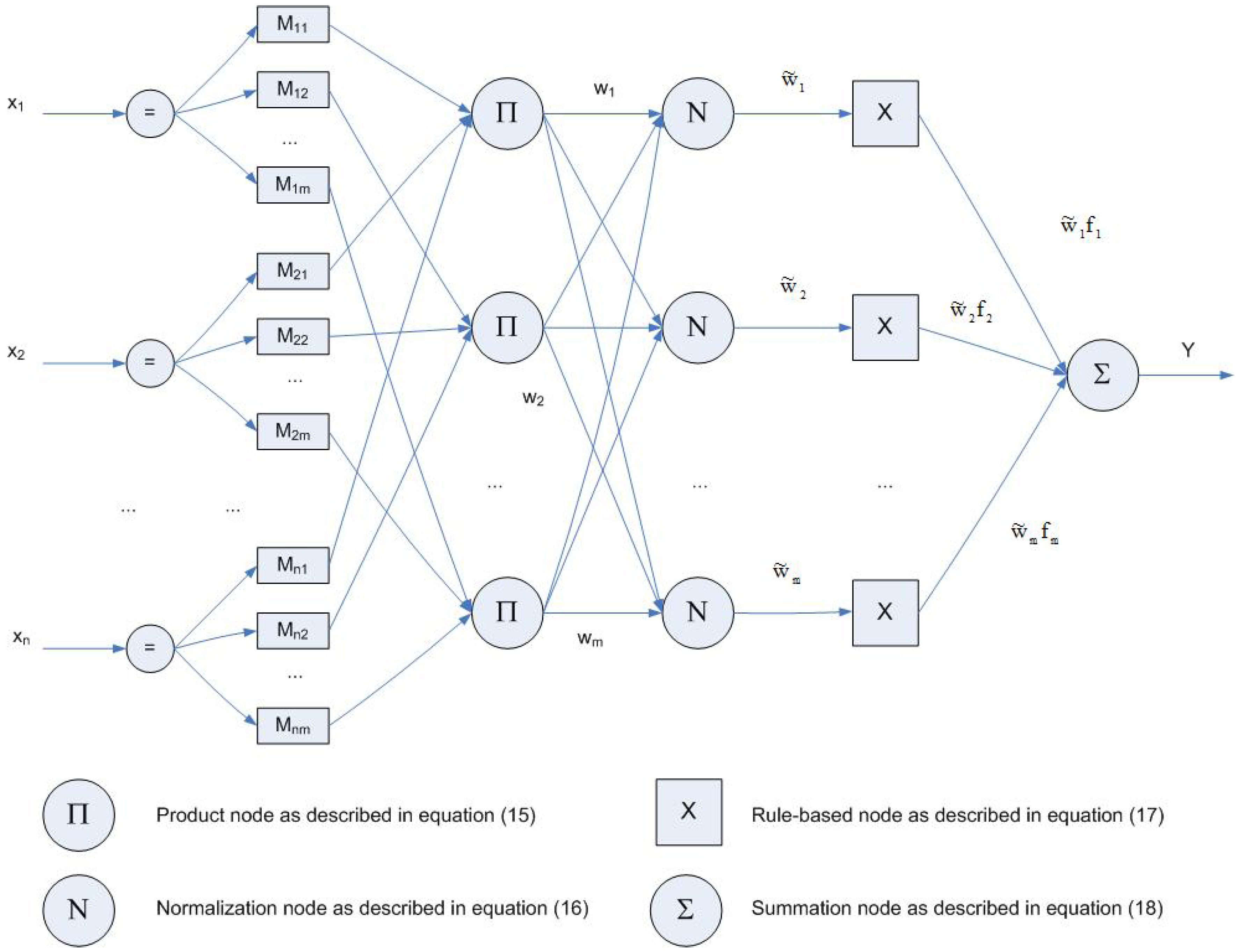
4.3. Neuro-Fuzzy Systems
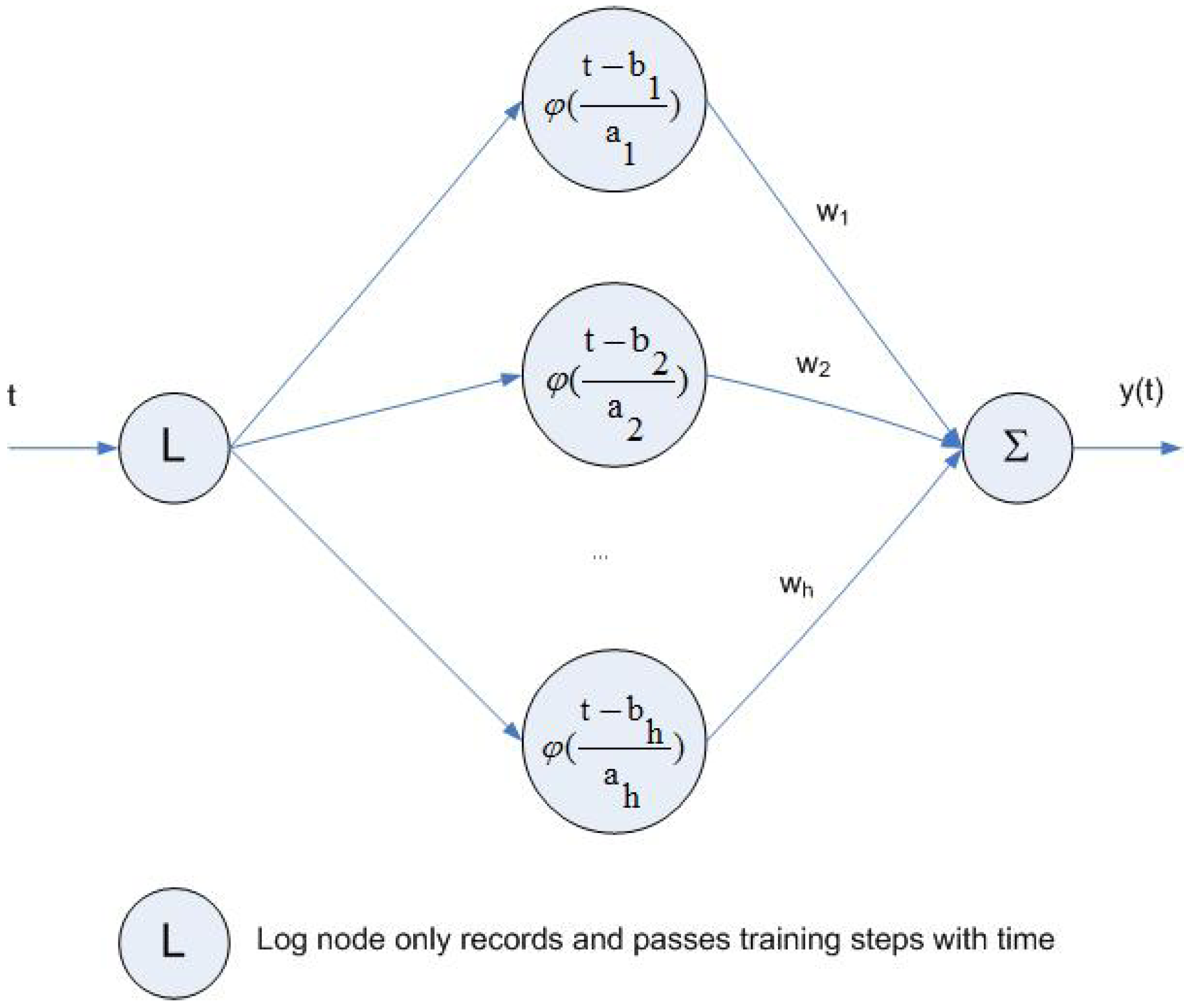
4.4. Wavelet-Based Neural Networks
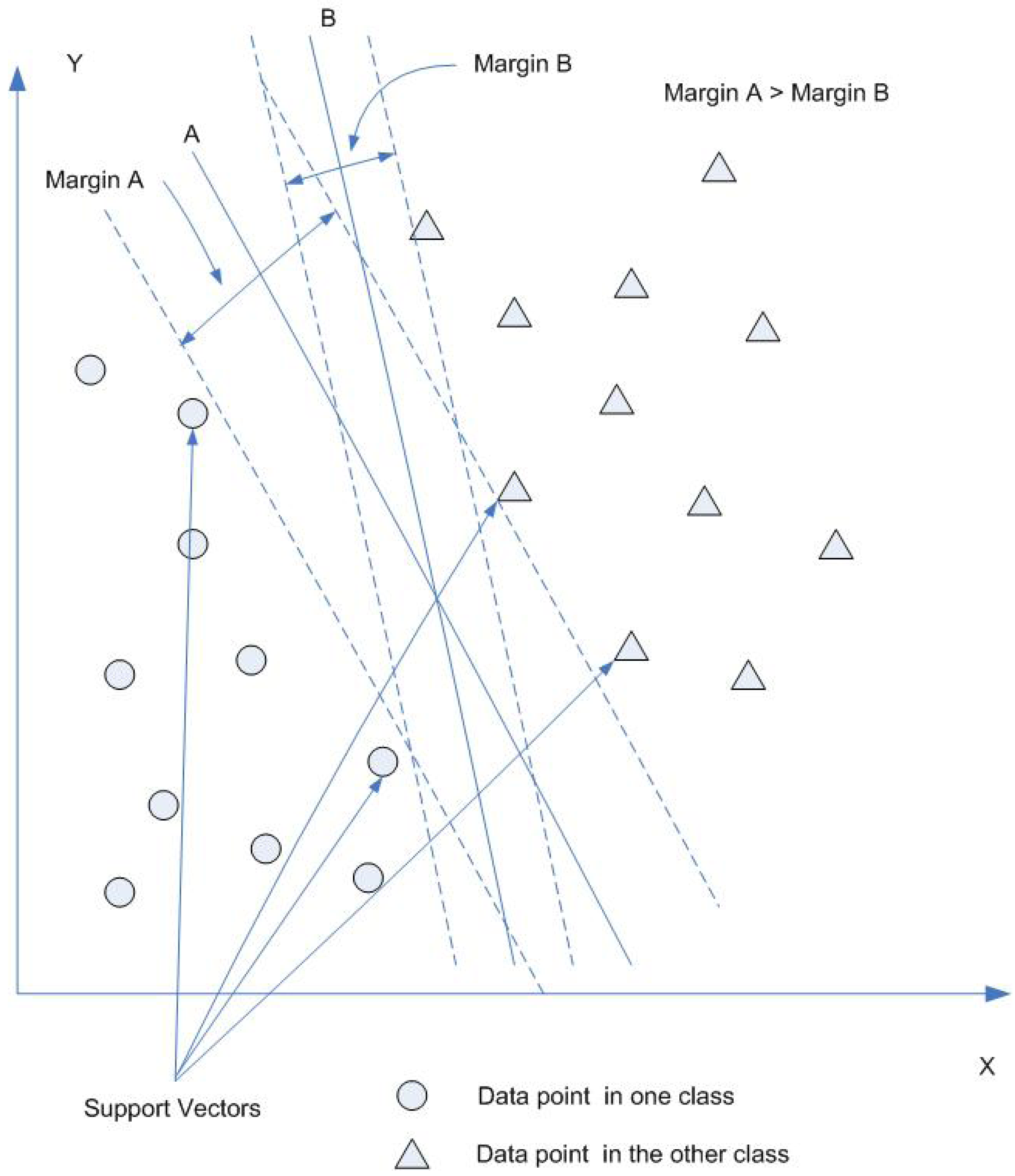
4.5. SVMs
5. Limitations of ANNs
- Black boxANNs are black box in nature. Therefore, if the problem is to find the output response to the input such as system identification [96], ANNs can be a good fit. However, if the problem is to specifically identify causal relationship between input and output, ANNs have only limited ability to do it compared with conventional statistical methods.
- Long computing timeANN training needs to iteratively determine network structure and update connection weights. This is a time-consuming process. With a typical personal computer or work station, the BP algorithm will take a lot of memory and may take hours, days and even longer before the network converges to the optimal point with minimum mean square error. Conventional statistical regression with the same set of data, on the contrary, may generate results in seconds using the same computer.
- OverfittingWith too much training time, too many hidden nodes, or too large training data set, the network will overfit the data and have a poor generalization, i.e. high accuracy for training data set but poor interpolation of testing data. This is an important issue being investigated in ANN research and applications as described above.
6. ANN Applications in Agricultural and Biological Engineering
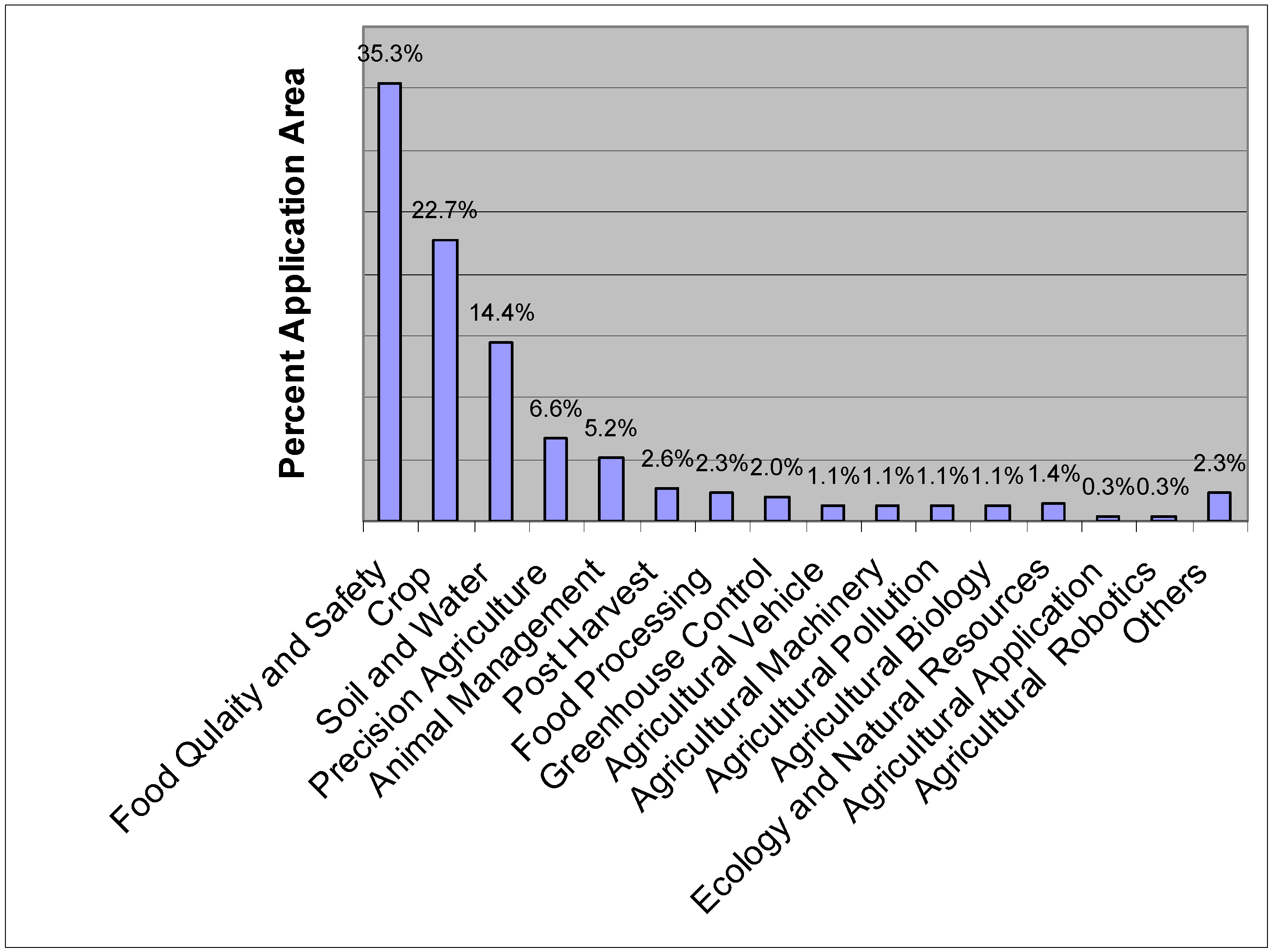
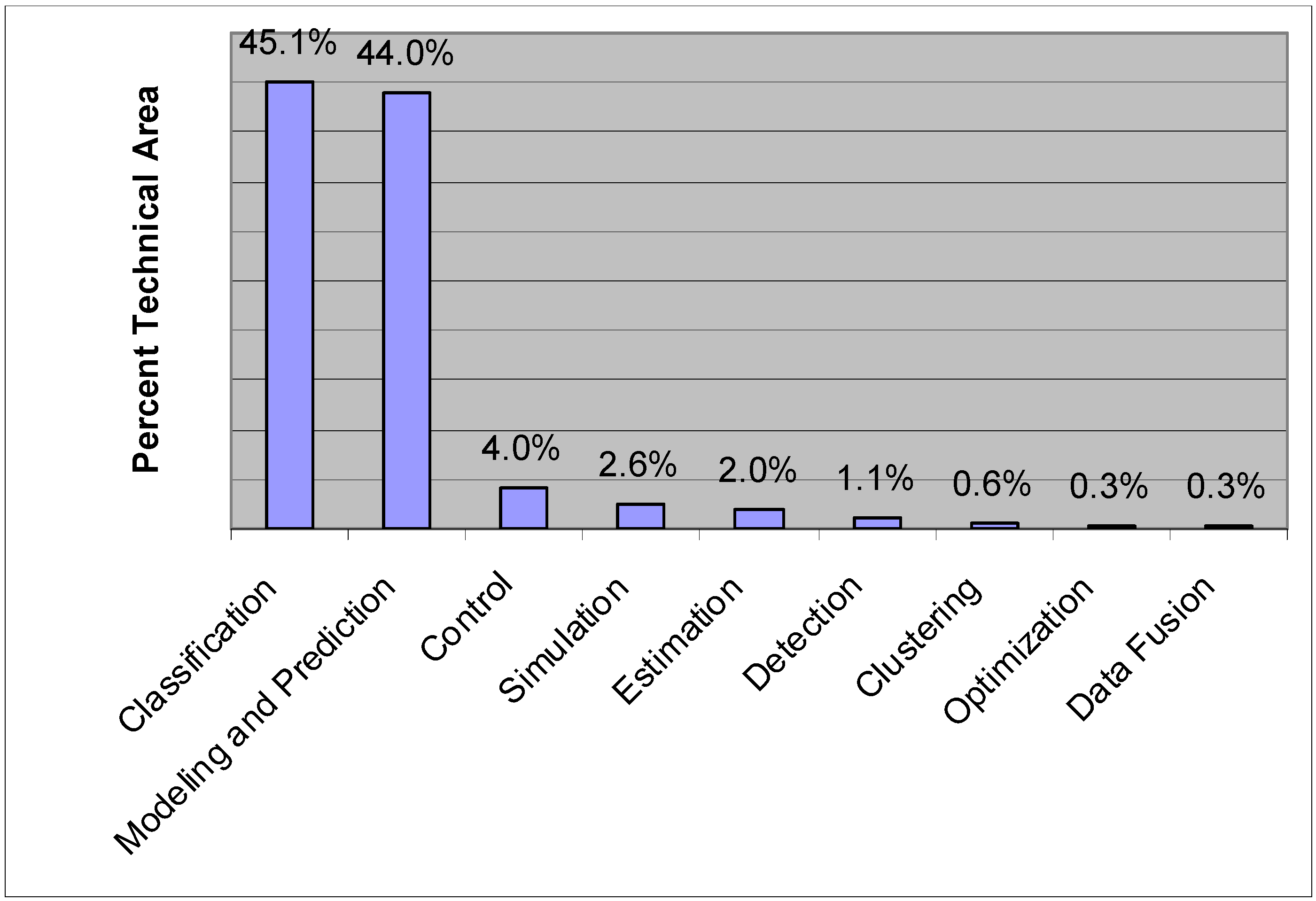
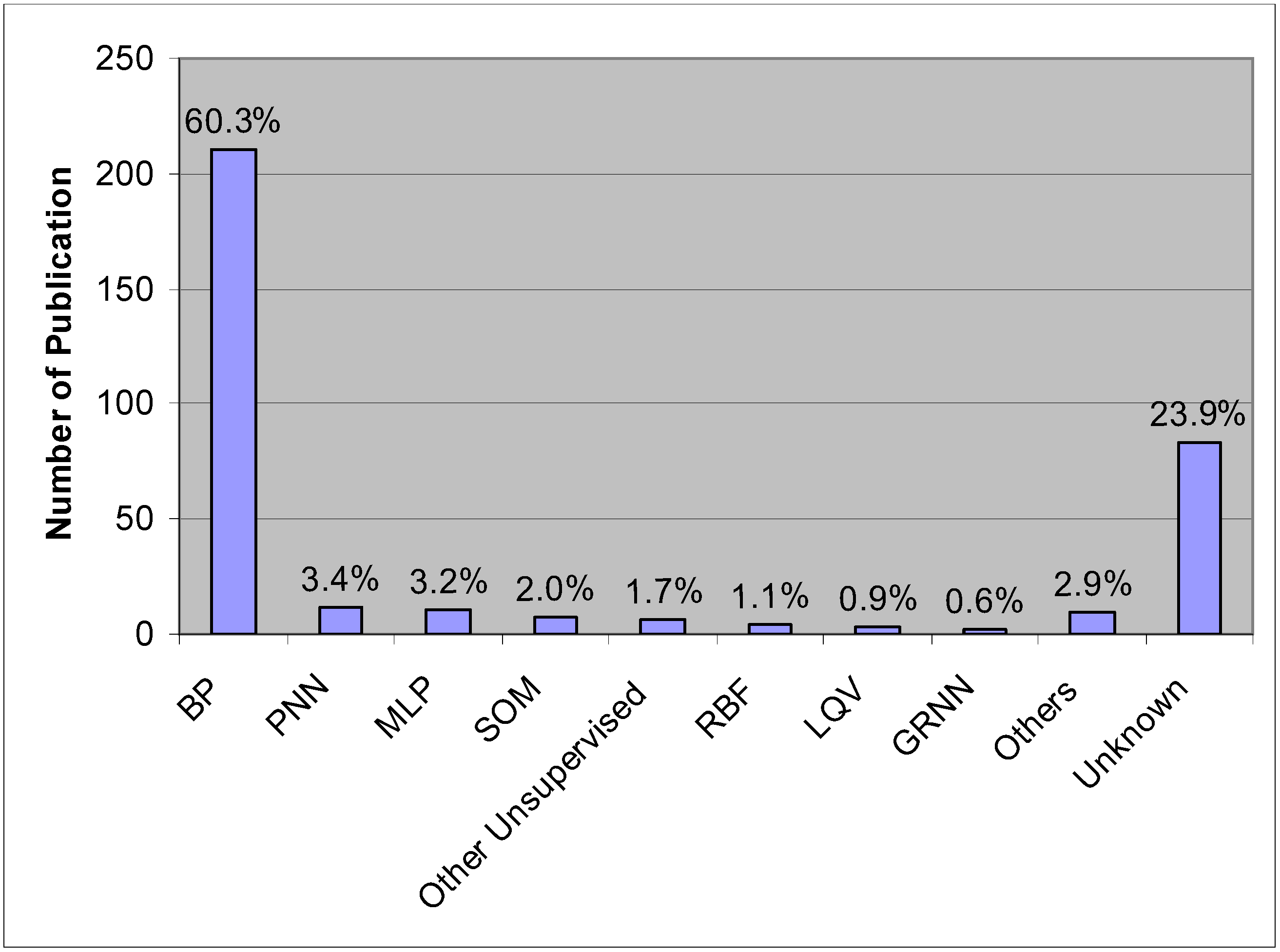
| Year | Author | Fusion Type | Application Area |
|---|---|---|---|
| 1992 | Linko et al. [109] | ANN modeling for fuzzy control | Extrusion control |
| 1997 | Kim and Cho [110] | ANN modeling plus fuzzy control simulation | Bread baking process control |
| 1997 | Morimoto et al. [111] | ANN modeling plus GA parameter optimization for fuzzy control | Fruit storage control |
| 2001 | Odhiambo et al. [112] | Conceptual and structural fusion of fuzzy logic and ANN | ET model optimization |
| 2003 | Andriyas et al. [118] | FCM clustering for RBF training | Prediction of the performance of vegetative filter strips |
| 2003 | Chtioui et al. [113] | SOM with FCM clustering | Color image segmentation of edible beans |
| 2003 | Lee et al. [119] | ANFIS modeling | Prediction of multiple soil properties |
| 2003 | Neto et al. [120] | ANFIS classification | Adaptive image segmentation for weed detection |
| 2004 | Odhiambo et al. [115] | Fuzzy-Neural Netwok unsupervised classification | Classification of soils |
| 2004 | Meyer et al. [114] | ANFIS classification | Classification of uniform plant, soil, and residue color images |
| 2004 | Goel et al. [121] | Fuzzy c-means clustering for RBF training | Prediction of sediment and phosphorous movement through vegetative filter strips |
| 2006 | Hancock and Zhang [115] | ANFIS classification | Hydraulic vane pump health classification |
| 2007 | Xiang and Tian [117] | ANN modeling plus ANFIS training of fuzzy logic controller | Outdoor automatic camera parameter control |

| Year | Author | Application Method | Application Area |
|---|---|---|---|
| 2003 | Fletcher and Kong [136] | SVM classification | Classifying feature vectors and decide whether each pixel in hyperspectral fluorescence images of poultry carcasses falls in normal or skin tumor categories |
| 2004 | Brudzewski et al. [134] | SVM neural network classification | Classification of milk by an electronic nose |
| 2004 | Tian et al. [135] | SVM classification | Classification for recognition of plant disease |
| 2005 | Pardo and Sberveglieri [132] | SVM with RBF kernel of RBF | Classification of electronic nose data |
| 2005 | Pierna et al. [133] | SVM classification | Classification of modified starches by Fourier transform infrared spectroscopy |
| 2006 | Chen et al. [129] | SVM classification | Identification of tea varieties by computer vision |
| 2006 | Karimi et al. [127] | SVM classification | Classification for weed and nitrogen stress detection in corn |
| 2006 | Onaran et al. [131] | SVM classification | Detection of underdeveloped hazenuts from fully developed nuts by impact acoustics |
| 2006 | Pierna et al. [128] | SVM classification | Discrimination of screening of compound feeds using NIR hyperspectral data |
| 2006 | Wang and Paliwal [130] | Least-Squares SVM classification | Discrimination of wheat classes with NIR spectroscopy |
| 2007 | Jiang et al. [125] | Gaussian kernel based SVM classification | Black walnut shell and meat classification using hyperspectral fluorescence imaging |
| 2007 | Oommen et al. [137] | SVM modeling and prediction | Simulation of daily, weekly, and monthly runoff and sediment yield fron a watershed |
| 2007 | Zhang et al. [126] | Multi-class SVM with kernel of RBF neural network | Classification to differentiate individual fungal infected and healthy wheat kernels. |
| 2008 | Fu et al. [138] | Least-Squares SVM modeling and prediction | Quantification of vitamin C content in kiwifruit using NIR spectroscopy |
| 2008 | Khot et al. [124] | SVM classification | Classification of meat with small data set |
| 2008 | Kovacs et al. [139] | SVM modeling and prediction | Prediction of different concentration classes of instant coffee with electronic tongue measurements |
| 2008 | Peng and Wang [140] | Least-Squares SVM modeling and prediction | Prediction of pork meat total viable bacteria count with hyperspectral imaging |
| 2008 | Sun et al. [106] | SVM modeling and prediction | On-line assessing internal quality of pears using visible/NIR transmission |
| 2008 | Trebar and Steele [123] | SVM classification | Classification of forest data cover types |
| 2008 | Yu et al. [9] | Least-Squares SVM modeling and prediction | Rice wine composition prediction by visible/NIR spectroscopy |
| 2009 | Deng et al. [122] | SVM classification | classification of intact and cracked eggs |
7. Conclusion and Future Directions
Acknowledgements
References
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning internal representations by error propagation. In Parallel Distributed Processing: Explorations in the Microstructures of Cognition; Rumelhart, D.E., McClelland, J.L., Eds.; MIT Press: Cambridge, MA, USA, 1986; Vol. I, pp. 318–362. [Google Scholar]
- Rumelhart, D.E.; McClelland, J.L. Parallel Distributed Processing: Explorations in the Microstructures of Cognition; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Kavuri, S.N.; Venkatasubramanian, V. Solving the hidden node problem in networks with ellipsoidal unitsand related issues. In Proceedings of International Joint Conference on Neural Networks, Baltimore, MA, USA, June 7-11, 1992; Vol. I, pp. 775–780.
- Su, H.; McAvoy, T.J.; Werbos, P.J. Long-term predictions of chemical processes using recurrent neural networks: a parallel training approach. Ind. Eng. Chem. Res. 1992, 31, 1338–1352. [Google Scholar] [CrossRef]
- Jou, I.C.; You, S.S.; Chang, L.W. Analysis of hidden nodes for multi-layer perceptron neural networks. Patt. Recog. 1994, 27, 859–864. [Google Scholar] [CrossRef]
- Sietsma, J.; Dow, R.J.F. Neural net pruning: why and how. In Proceedings of IEEE Int. Conf. Neural Networks, San Diego, CA, USA, July 24-27, 1988; Vol. I, pp. 325–333.
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- McClelland, J.L.; Rumelhart, D.E. Explorations in parallel distributed processing: A handbook of models, programs, and exercises; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Yu, X.; Loh, N.K.; Miller, W.C. A new acceleration technique for the backpropagation algorithm. In Proceedings of IEEE International Conference on Neural Networks, San Diego, CA, USA, March 28 – April 1, 1993; Vol. III, pp. 1157–1161.
- Gerke, M.; Hoyer, H. 1997. Fuzzy backpropagation training of neural networks. In Computational Intelligence Theory and Applications; Reusch, B., Ed.; Springer: Berlin, Germany, 1997; pp. 416–427. [Google Scholar]
- Jeenbekov, A.A.; Sarybaeva, A.A. Conditions of convergence of back-propagation learning algorithm. In Proceedings of SPIE on Optoelectronic and Hybrid Optical/Digital Systems for Image and Signal Processing, Bellingham, WA, USA, 2000; Vol. 4148, pp. 12–18.
- Wang, X.G.; Tang, Z.; Tamura, H.; Ishii, M.; Sun, W.D. An improved backpropagation algorithm to avoid the local minima problem. Neurocomputing 2004, 56, 455–460. [Google Scholar] [CrossRef]
- Bi, W.; Wang, X.; Tang, Z.; Tamura, H. Avoiding the local minima problem in backpropagation algorithm with modified error function. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2005, E88-A, 3645–3653. [Google Scholar] [CrossRef]
- Otair, M.A.; Salameh, W.A. Speeding up back-propagation neural networks. In Proceedings of the 2005 Informing Science and IT Education Joint Conference, Flagstaff, AZ, USA, June 16-19, 2005; pp. 167–173.
- Burke, L. Assessing a neural net. PC AI. 1993, 7, 20–24. [Google Scholar]
- Finnoff, W.; Hergert, F.; Zimmermann, H.G. Improving model selection by nonconvergent methods. Neural Netw. 1993, 6, 771–783. [Google Scholar] [CrossRef]
- Wang, J.H.; Jiang, J.H.; Yu, R.Q. Robust back propagation algorithm as a chemometric tool to prevent the overfitting to outliers. Chemom. Intell. Lab. Syst. 1996, 34, 109–115. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Mather, P.M. Assessing artificial neural network pruning algorithms. In Proceedings of the 24th Annual Conference and Exhibition of the Remote Sensing Society, Cardiff, South Glamorgan, UK, September 9-11, 1998; pp. 603–609.
- Kavzoglu, T.; Vieira, C.A.O. An analysis of artificial neural network pruning algorithms in relation to land cover classification accuracy. In Proceedings of the Remote Sensing Society Student Conference, Oxford, UK, April 23, 1998; pp. 53–58.
- Caruana, R.; Lawrence, S.; Giles, C.L. Overfitting in neural networks: backpropagation, conjugate gradient, and early stopping. In Proceedings of Neural Information Processing Systems Conference, Denver, CO, USA, November 28-30, 2000; pp. 402–408.
- Lawrence, S.; Giles, C.L. Overfitting and neural networks: conjugate gradient and backpropagation. In Proceedings of International Joint Conference on Neural Networks, Como, Italy, July 24-27, 2000; pp. 114–119.
- Takagi, T.; Hayashi, I. NN–driven fuzzy reasoning. IJAR 1991, 5, 191–212. [Google Scholar] [CrossRef]
- Horikawa, S.; Furuhashi, T.; Uchikawa, Y. On fuzzy modelling using fuzzy neural networks with back propagation algorithm. IEEE Trans. Neural Netw. 1992, 3, 801–806. [Google Scholar] [CrossRef]
- Nie, J.; Linkens, D. Neural network–based approximate reasoning: Principles and implementation. Int. J. Contr. 1992, 56, 399–413. [Google Scholar] [CrossRef]
- Simpson, P.K.; Jahns, G. Fuzzy min–max neural networks for function approximation. In Proceedings of IEEE International Conference on Neural Networks, San Francisco, CA, USA, March 28 – April 21, 1993; Vol. 3, pp. 1967–1972.
- Mitra, S.; Pal, S.K. Logical operation based fuzzy MLP for classification and rule generation. Neural Netw. 1994, 7, 353–373. [Google Scholar] [CrossRef]
- Jang, R.J.S.; Sun, C.T. Neuro–fuzzy modelling and control. Proc. IEEE 1995, 83, 378–406. [Google Scholar] [CrossRef]
- Cristea, P.; Tuduce, R.; Cristea, A. Time series prediction with wavelet neural networks. In Proceedings of IEEE Neural Network Applications in Electrical Engineering, Belgrade, Yugoslavia, September 25-27, 2000; pp. 5–10.
- Shashidhara, H.L.; Lohani, S.; Gadre, V.M. Function learning wavelet neural networks. In Proceedings of IEEE International Conference on Industrial Technology, Goa, India, January 19-22, 2000; Vol. II, pp. 335–340.
- Ho, D.W.C.; Zhang, P.A.; Xu, J. Fuzzy wavelet networks for function learning. IEEE Trans. on Fuzzy Syst. 2001, 9, 200–211. [Google Scholar] [CrossRef]
- Zhou, B.; Shi, A.; Cai, F.; Zhang, Y. Wavelet neural networks for nonlinear time series analysis. Lecture Notes Comput. Sci. 2004, 3174, 430–435. [Google Scholar]
- Burges, C.J.C. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Disc. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Cristianini, N.; Taylor, J.S. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Whittaker, A. D.; Park, B.P.; McCauley, J.D.; Huang, Y. Ultrasonic signal classification for beef quality grading through neural networks. In Proceedings of Automated Agriculture for the 21st Century, Chicago, IL, USA, December 10-14, 1991; pp. 116–125.
- Zhang, Q.; Litchfield, J.B. Advanced process controls: Applications of adaptive, fuzzy and neural control to the food industry. In Food Processing Automation; ASAE: St. Joseph, MI, USA, 1992; Vol. II, pp. 169–176. [Google Scholar]
- Eerikäinen, T.; Linko, P.; Linko, S.; Siimes, T.; Zhu, Y.H. Fuzzy logic and neural networks applications in food science and technology. Trends Food Sci. Technol. 1993, 4, 237–242. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W.H. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Hebb, D.O. The organization of behavior; Wiley: New York, NY, USA, 1949. [Google Scholar]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psycho. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef]
- Widrow, B.; Hoff, M.E. Adaptive switching circuits. In WESCON Convention Record; Institute of Radio Engineers: New York, NY, USA, 1960; Vol. VI, pp. 96–104. [Google Scholar]
- Minsky, M.; Papert, S.A. Perceptrons: An Introduction to Computational Geometry; MIT Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Grossberg, S. Adaptive pattern classification and universal recoding, 1: Parallel development and coding of neural feature detectors. Biol. Cybernetics 1976, 23, 187–202. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. In Proceedings of the National Academy of Sciences of the USA; National Academy of Sciences: Washington, DC, USA, 1982; Vol. 79, 8, pp. 2554–2558. [Google Scholar]
- Werbos, P.J. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. In Doctoral Dissertation; Applied Mathematics, Harvard University: Boston, MA, USA, 1974. [Google Scholar]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybernetics 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Broomhead, D.S.; Lowe, D. Multivariable functional interpolation and adaptive networks. Comp. Syst. 1988, 2, 321–355. [Google Scholar]
- Powell, M.J.D. Restart procedures for the conjugate gradient method. Math. Program. 1977, 12, 241–254. [Google Scholar] [CrossRef]
- Dong, C.X.; Yang, S.Q.; Rao, X.; Tang, J.L. An algorithm of estimating the generalization performance of RBF-SVM. In Proceedings of 5th International Conference on Computational Intelligence and Multimedia Applications, Xian, Shanxi, China, September 27-30, 2003; pp. 61–66.
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Cybenko, G.V. Approximation by superpositions of a sigmoidal function. Math. Contr. Signal. Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hammer, H.; Gersmann, K. A note on the universal approximation capability of support vector machines. Neural Process. Lett. 2003, 17, 43–53. [Google Scholar] [CrossRef]
- Lennox, B.; Montague, G.A.; Frith, A.M.; Gent, C.; Bevan, V. Industrial application of neural networks – an investigation. J. Process Contr. 2001, 11, 497–507. [Google Scholar] [CrossRef]
- Hussain, B.; Kabuka, M.R. A novel feature recognition neural network and its application to character recognition. IEEE Trans. Patt. Anal. Mach. Intell. 1998, 6, 98–106. [Google Scholar] [CrossRef]
- Ma, L.; Khorasani, K. Facial expression recognition using constructive feedforward neural networks. IEEE Trans. Syst. Man Cybernetics B 2004, 34, 1588–95. [Google Scholar] [CrossRef]
- Piramuthu, S. Financial credit-risk evaluation with neural and neurofuzzy systems. Eur. J. Operat. Res. 1999, 112, 310–321. [Google Scholar] [CrossRef]
- Barson, P.; Field, S.; Davey, N.; McAskie, G.; Frank, G. The detection of fraud in mobile phone networks. Neural Netw. World 1996, 6, 477–484. [Google Scholar]
- Ghosh, S.; Reilly, D.L. Credit card fraud detection with a neural-network. In Proceedings of the 27th Annual Hawaii International Conference on System Science, Maui, HI , USA, January 4-7, 1994; Vol. III, pp. 621–630.
- Braun, H.; Lai, L.L. A neural network linking process for insurance claims. In Proceedings of 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, Guangdong, China, August 18-21, 2005; Vol. I, pp. 399–404.
- Fu, T.C.; Cheung, T.L.; Chung, F.L.; Ng, C.M. An innovative use of historical data for neural network based stock prediction. In Proceedings of Joint Conference on Information Sciences, Kaohsiung, Taiwan, October 8-11, 2006.
- Hartigan, J.A.; Wong, M.A. A k-means clustering algorithm. Appl. Statistics 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Zhu, Y.; He, Y. Short-term load forecasting model using fuzzy c means based radial basis function network. In Proceedings of 6th International Conference on Intelligence Systems Design and Applications, Jinan, China, October 16-18, 2006; Vol. I, pp. 579–582.
- Jordan, M.I. Attractor dynamics and parallelism in a connectionist sequential machine. In Proceedings of 8th Annual Conference of Cognitive Science Society, Amherst, MA, USA, August 15-17, 1986; pp. 531–546.
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Pham, D.T.; Liu, X. Neural Networks for Identification, Prediction and Control; Springer-Verlag: London, UK, 1995. [Google Scholar]
- Yun, L.; Haubler, A. Artificial evolution of neural networks and its application to feedback control. Artif. Intell. Eng. 1996, 10, 143–152. [Google Scholar]
- Pham, D.T.; Karaboga, D. Training Elman and Jordan networks for system identification using genetic algorithms. Artif. Intell. Eng. 1999, 13, 107–117. [Google Scholar] [CrossRef]
- Pham, D.T.; Liu, X. Dynamic system identification using partially recurrent neural networks. J. Syst. Eng. 1992, 2, 90–97. [Google Scholar]
- Pham, D.T.; Liu, X. Training of Elman networks and dynamic system modeling. Int. J. Syst. Sci. 1996, 27, 221–226. [Google Scholar] [CrossRef]
- Ku, C.C.; Lee, K.Y. Diagonal recurrent neural networks for dynamic systems control. IEEE Trans. Neural Netw. 1995, 6, 144–156. [Google Scholar]
- Huang, Y.; Whittaker, A.D.; Lacey, R.E. Neural network prediction modeling for a continuous snack food frying process. Trans. ASAE 1998, 41, 1511–1517. [Google Scholar] [CrossRef]
- Pineda, F.J. Recurrent backpropagation and the dynamical approach to adaptive neural computation. Neural Comput. 1989, 1, 167–172. [Google Scholar] [CrossRef]
- William, R.J.; Zipser, D.A. A learning algorithm for continually running fully recurrent neural networks. Neural Comput. 1989, 1, 270–280. [Google Scholar] [CrossRef]
- Pearlmutter, A.B. Dynamic recurrent neural networks; Technical Report CMU-CS-90-196; Carnegie Mellon University: Pittsburgh, PA, USA, 1990. [Google Scholar]
- Huang, Y. Sanck food frying process input-output modeling and control through artificial neural networks. Ph.D. Dissertation, Texas A&M University, College Station, TX, USA, 1995. [Google Scholar]
- Huang, Y.; Lacey, R.E.; Whittaker, A.D. Neural network prediction modeling based on ultrasonic elastograms for meat quality evaluation. Trans. ASAE 1998, 41, 1173–1179. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks A Comprehensive Foundation, 2nd Edition ed; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer-Verlag New York, Inc.: Secaucus, NJ, USA, 2006. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Contr. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Simpson, P.K. Fuzzy min-max neural networks – part 2: clustering. IEEE Trans. Fuzzy Syst. 1992, 1, 32–45. [Google Scholar] [CrossRef]
- Jang, J.S.R. ANFIS: adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybernetics 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Daubechies, I. Orthonormal bases of compactly supported wavelets. Comm. Pure Appl. Math. 1988, 41, 909–996. [Google Scholar] [CrossRef]
- Mallat, S. A theory of multiresolution signal decomposition: The wavelet representation. IEEE Trans. Patt. Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Percival, D.B.; Walden, A.T. Wavelet Methods for Time Series Analysis; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer-Verlag: London, UK, 1995. [Google Scholar]
- Rychetsky, M.; Ortmann, S.; Glesner, M. Support vector approaches for engine knock detection. In Proceedings of International Joint Conference on Neural Networks (IJCNN 99), Washington, DC, USA, July 10-16, 1999; Vol. II, pp. 969–974.
- Müller, K.R.; Smola, A.; Rätsch, G.; Schölkopf, B.; Kohlmorgen, J.; Vapnik, V. Using support vector machines for time series prediction. In Advances in Kernel Methods; Schölkopf, B., Burges, C.J.C., Smola, A.J., Eds.; MIT Press: Cambridge, MA, USA, 1999; pp. 242–253. [Google Scholar]
- Iplikci, S. Dynamic reconstruction of chaotic systems from inter-spike intervals using least squares support vector machines. Phys. D. 2006, 216, 282–293. [Google Scholar] [CrossRef]
- Lee, Y.J.; Mangasarian, O.L.; Wolberg, W.H. Breast cancer survival and chemotherapy: a support vector machine analysis. In DIMACS Series in Discrete Mathematics and Theoretical Computer Science; American Mathematical Society: Providence, RI, USA, 2000; Vol. 55, pp. 1–10. [Google Scholar]
- Kim, K.I.; Jung, K; Park, S.H.; Kim, H.J. Support vector machines for texture classification. IEEE Trans. Patt. Anal. Mach. Intell. 2002, 24, 1542–1550. [Google Scholar] [Green Version]
- Hidalgo, H.; Sosa, S.; Gómez-Treviño, E. Application of the kernel method to the inverse geosounding problem. Neural Netw. 2003, 16, 349–353. [Google Scholar] [CrossRef]
- Pal, M. Support vector machines-based modelling of seismic liquefaction potential. Int. J. Num. Anal. Meth. Geomech. 2006, 30, 983–996. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J. Learning with Kernels; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Rangwala, H.; Karypis, G. Profile-based direct kernels for remote homology detection and fold recognition. Bioinformatics 2005, 21, 4239–4247. [Google Scholar]
- Iplikci, S. Support vector machines-based generalized predictive control. Int. J. Rob. Nonl. Contr. 2006, 16, 843–862. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Ljung, L. Perspectives on system identification; Division of Automatic Control, Linköpings Universitet: Linköping, Sweden, 2008. [Google Scholar]
- Hsu, C.W.; Lin, C.J. A comparison of methods for multi-class support vector machines. IEEE Trans. Neural Netw. 2002, 13, 415–425. [Google Scholar]
- Thai, C.N.; Shewfelt, R.L. Modeling sensory color quality of tomato and peach: neural networks and statistical regression. Trans. ASAE 1991, 34, 950–955. [Google Scholar] [CrossRef]
- Tani, A.; Murase, H.; Kiyota, M.; Honami, N. Growth simulation of alfalfa cuttings in vitro by Kalman filter neural network. Acta Horticul. 1992, 319, 671–676. [Google Scholar]
- Yang, Q. Classification of apple surface features using machine vision and neural networks. Comput. Electron. Agric. 1993, 9, 1–12. [Google Scholar] [CrossRef]
- Liao, K.; Paulsen, M.R.; Reid, J.F. Corn kernel breakage classification by machine vision using a neural network classifier. Trans. ASAE 1993, 36, 1949–1953. [Google Scholar] [CrossRef]
- Deck, S.H.; Morrow, C.T.; Heinemann, P.H.; Sommer III, H.J. Comparison of a neural network and traditional classifier for machine vision inspection of potatoes. Appl. Eng. Agric. 1995, 11, 319–326. [Google Scholar] [CrossRef]
- Khazaei, J.; Naghavi, M.R.; Jahansouz, M.R.; Salimi-Khorshidi, G. Yield estimation and clustering of chickpea genotypes using soft computing techniques. Agron. J. 2008, 100, 1077–1087. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J. Identification of stored-grain age using electronic nose by ANN. Appl. Eng. Agric. 2008, 24, 227–231. [Google Scholar] [CrossRef]
- Sun, G.; Hoff, S.J.; Zelle, B.C.; Nelson, M.A. Development and comparison of backpropagation and generalized regression neural network models to predict diurnal and seasonal gas and PM10 concentrations and emissions from swine buildings. Trans. ASABE 2008, 51, 685–694. [Google Scholar] [CrossRef]
- Ondimu, S.N.; Murase, H. Comparison of plant water stress detection ability of color and gray-level texture in sunagoke moss. Trans. ASABE 2008, 51, 1111–1120. [Google Scholar] [CrossRef]
- Wu, D.; Feng, L.; Zhang, C.; He, Y. Early detection of botrytis cinerea on eggplant leaves based on visible and near-infrared spectroscopy. Trans. ASABE 2008, 51, 1133–1139. [Google Scholar] [CrossRef]
- Linko, P.; Zhu, Y.H.; Linko, S. Application of neural network modeling in fuzzy extrusion control. Food Bioprod. process. 1992, 70, 131–137. [Google Scholar]
- Kim, S.; Cho, I. Neural network modeling and fuzzy control simulation for bread-baking process. Trans. ASAE 1997, 40, 671–676. [Google Scholar] [CrossRef]
- Morimoto, T.; Suzuki, J.; Hashimoto, Y. Optimization of a fuzzy controller for fruit storage using neural networks and genetic algorithms. Eng. Appl. Artif. Intell. 1997, 10, 453–461. [Google Scholar] [CrossRef]
- Odhiambo, L.O.; Yoder, R.E.; Yoder, D.C.; Hines, J.W. Optimization of fuzzy evapotranspiration model through neural training with input-output examples. Trans. ASAE 2001, 44, 1625–1633. [Google Scholar] [CrossRef]
- Chtioui, Y.; Panigrahi, S.; Backer, L.F. Self-organizing map combined with a fuzzy clustering for color image segmentation of edible beans. Trans. ASAE 2003, 46, 831–838. [Google Scholar] [CrossRef]
- Meyer, G.E.; Hindman, T.W.; Jones, D.D.; Mortensen, D.A. Digital camera operation and fuzzy logic classification of uniform plant, soil, and residue color images. Appl. Eng. Agric. 2004, 20, 519–529. [Google Scholar] [CrossRef]
- Odhiambo, L.O.; Freeland, R.S.; Yoder, R.E.; Hines, J.W. Investigation of a fuzzy-neural network application in classification of soils using ground-penetrating radar imagery. Appl. Eng. Agric. 2004, 20, 109–117. [Google Scholar] [CrossRef]
- Hancock, K.M.; Zhang, Q. A hybrid approach to hydraulic vane pump condition monitoring and fault detection. Trans. ASABE 2006, 49, 1203–1211. [Google Scholar] [CrossRef]
- Xiang, H.; Tian, L.F. Artificial intelligence controller for automatic multispectral camera parameter adjustment. Trans. ASABE 2007, 50, 1873–1881. [Google Scholar] [CrossRef]
- Andriyas, S.; Negi, S.C.; Rudra, R.P.; Yang, S.X. Modelling total suspended solids in vegetative filter strips using artificial neural networks; ASAE: St. Joseph, MI., USA, 2003; ASAE number: 032079. [Google Scholar]
- Lee, K.H; Zhang, N.; Das, S. Comparing adaptive neuro-fuzzy inference system (ANFIS) to partial least-squares (PLS) method for simultaneous prediction of multiple soil properties; ASAE: St. Joseph, MI., USA, 2003; ASAE paper number: 033144. [Google Scholar]
- Neto, J.C.; Meyer, G.E.; Jones, D.D.; Surkan, A.J. Adaptive image segmentation using a fuzzy neural network and genetic algorithm for weed detection; ASAE: St. Joseph, MI., USA, 2003; ASAE paper number: 033088. [Google Scholar]
- Goel, P.K.; Andriyas, S.; Rudra, R.P.; Negi, S.C. Modeling sediment and phosphorous movement through vegetative filter strips using artificial neural networks and GRAPH; ASAE: St. Joseph, MI., USA, 2004; ASAE paper number: 042263. [Google Scholar]
- Deng, X.; Wang, Q.; Wu, L.; Gao, H.; Wen, Y.; Wang, S. Eggshell crack detection by acoustic impulse response and support vector machine. African J. Agric. Res. 2009, 4, 40–48. [Google Scholar]
- Trebar, M.; Steele, N. Application of distributed SVM architectures in classifying forest data cover types. Comput. Electron. Agric. 2008, 63, 119–130. [Google Scholar] [CrossRef]
- Khot, L.R.; Panigrahi, S.; Woznica, S. Neural-network-based classification of meat: evaluation of techniques to overcome small dataset problems. Biol. Eng. 2008, 1, 127–143. [Google Scholar] [CrossRef]
- Jiang, L.; Zhu, B.; Rao, X.; Berney, G.; Tao, Y. Discrimination of black walnut shell and pulp in hyperspectral fluorescence Imagery using Gaussian kernel function approach. J. Food Eng. 2007, 81, 108–117. [Google Scholar] [CrossRef]
- Zhang, H.; Paliwal, J.; Jayas, D.S.; White, N.D.G. Classification of fungal infected wheat kernels using near-infrared reflectance hyperspectral imaging and support vector machine. Trans. ASABE 2007, 50, 1779–1785. [Google Scholar] [CrossRef]
- Karimi, Y.; Prasher, S.O.; Patel, R.M.; Kim, S.H. Application of support vector machine technology for weed and nitrogen stress detection in corn. Comput. Electron. Agric. 2006, 51, 99–109. [Google Scholar] [CrossRef]
- Pierna, J.A.F.; Baeten, V.; Dardenne, P. Screening of compound feeds using NIR hyperspectral data. Chemom. Intell. Lab. Syst. 2006, 84, 114–118. [Google Scholar] [CrossRef]
- Chen, Q.; Zhao, J.; Cai, J.; Wang, X. Study on identification of tea using computer vision based on support vector machine. Chinese J. Sci. Instrum. 2006, 27, 1704–1706. [Google Scholar]
- Wang, W.; Paliwal, J. Spectral data compression and analyses techniques to discriminate wheat classes. Trans. ASABE 2006, 49, 1607–1612. [Google Scholar] [CrossRef]
- Onaran, I.; Pearson, T.C.; Yardimci, Y.; Cetin, A.E. Detection of underdeveloped hazelnuts from fully developed nuts by impact acoustics. Trans. ASABE 2006, 49, 1971–1976. [Google Scholar] [CrossRef]
- Pardo, M.; Sberveglieri, G. Classification of electronic nose data with support vector machines. Sens. Actuat. B 2005, 107, 730–737. [Google Scholar] [CrossRef]
- Pierna, J.A.F.; Volery, P.; Besson, R.; Baeten, V.; Dardenne, P. Classification of modified starches by Fourier transform infrared spectroscopy using support vector machines. J. Agric. Food Chem. 2005, 53, 6581–6585. [Google Scholar] [CrossRef]
- Brudzewski, K.; Osowski, S.; Markiewicz, T. Classification of milk by means of an electronic nose and SVM neural network. Sens. Actuat. B 2004, 98, 291–298. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, C.; Li, C. Study on plant disease recognition using support vector machine and chromaticity moments. Trans. Chinese Soc. Agric. Mach. 2004, 35, 95–98. [Google Scholar]
- Fletcher, J.T.; Kong, S.G. Principal component analysis for poultry tumor inspection using hyperspectral fluorescence imaging. In Proceedings of the International Joint Conference on Neural Networks, Portland, Oregon, USA, July 20-24, 2003; Vol. I, pp. 149–153.
- Oommen, T.; Misra, D.; Agarwal, A.; Mishra, S.K. Analysis and application of support vector machine based simulation for runoff and sediment yield; ASABE: St. Joseph, MI., USA, 2007; ASABE paper number: 073019. [Google Scholar]
- Fu, X.; Ying, Y.; Xu, H.; Yu, H. Support vector machines and near infrared spectroscopy for quantification of vitamin C content in kiwifruit; ASABE: St. Joseph, MI., USA, 2008; ASABE number: 085204. [Google Scholar]
- Kovacs, Z.; Kantor, D.B.; Fekete, A. Comparison of quantitative determination techniques with electronic tongue measurements; ASABE: St. Joseph, MI., USA, 2008; ASABE paper number: 084879. [Google Scholar]
- Peng, Y.; Wang, W. Prediction of pork meat total viable bacteria count using hyperspectral imaging system and support vector machines. In Proceedings of the Food Processing Automation Conference, Providence, RI, USA, June 28-29, 2008. CD-ROM.
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Huang, Y. Advances in Artificial Neural Networks – Methodological Development and Application. Algorithms 2009, 2, 973-1007. https://doi.org/10.3390/algor2030973
Huang Y. Advances in Artificial Neural Networks – Methodological Development and Application. Algorithms. 2009; 2(3):973-1007. https://doi.org/10.3390/algor2030973
Chicago/Turabian StyleHuang, Yanbo. 2009. "Advances in Artificial Neural Networks – Methodological Development and Application" Algorithms 2, no. 3: 973-1007. https://doi.org/10.3390/algor2030973




