Reconstruction of Seasonal Kinetics in Conifer Radial Growth from Daily Meteorological Conditions, Tree-Ring Width, and Radial Size of Tracheids
Abstract
1. Introduction
2. Materials and Methods
2.1. General Scheme of Analysis
2.2. Sampling Sites Description
2.3. Long-Term Tree-Ring Width Chronology Development
2.4. Seasonal Growth Observations
2.5. Measurement of Tracheidograms
2.6. Simulation of Tree-Ring Width Chronologies and Calculations of Seasonal General Growth Rate
2.7. Usage of Band Model
2.8. Description of Cell Expansion Kinetics
3. Results
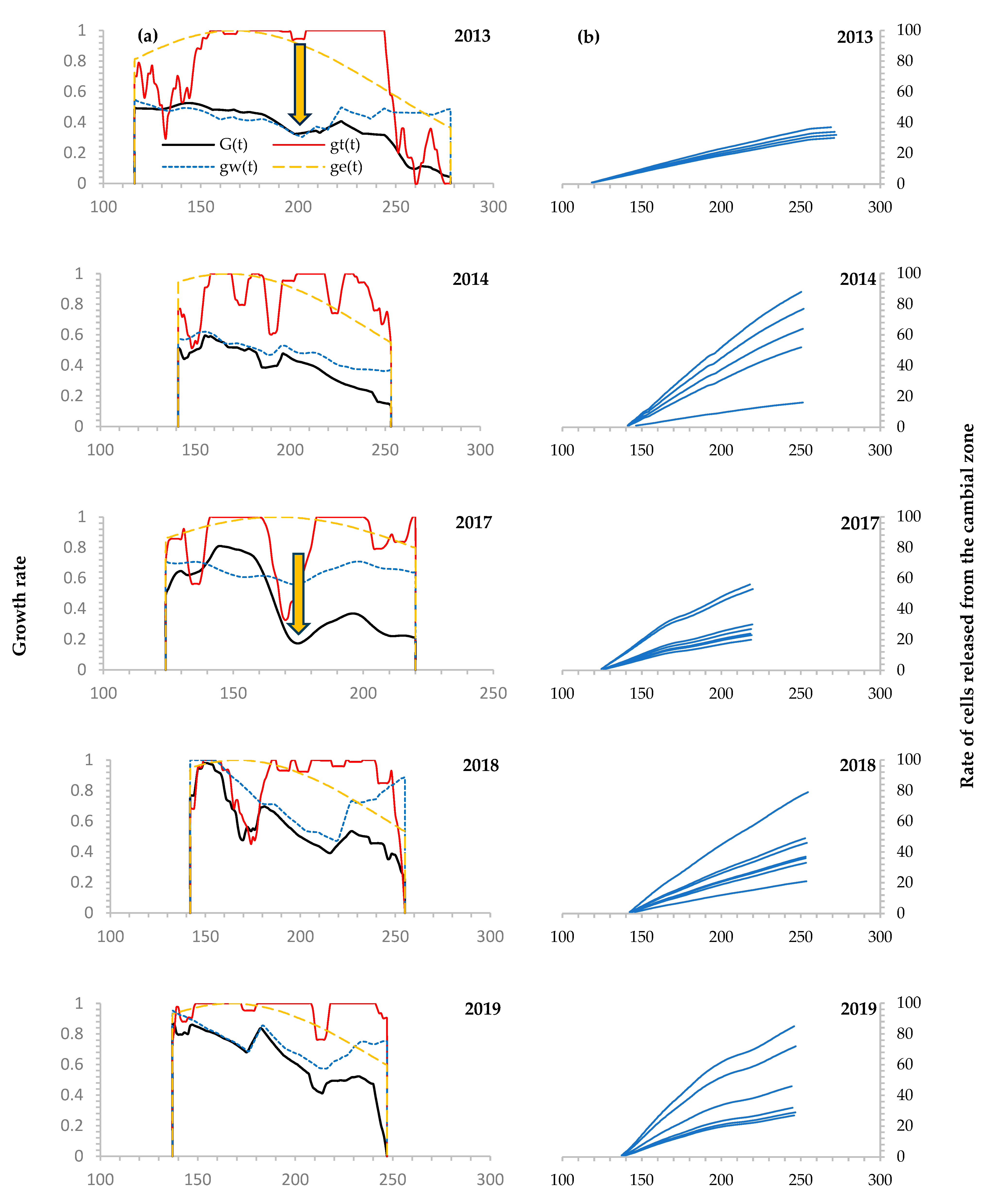
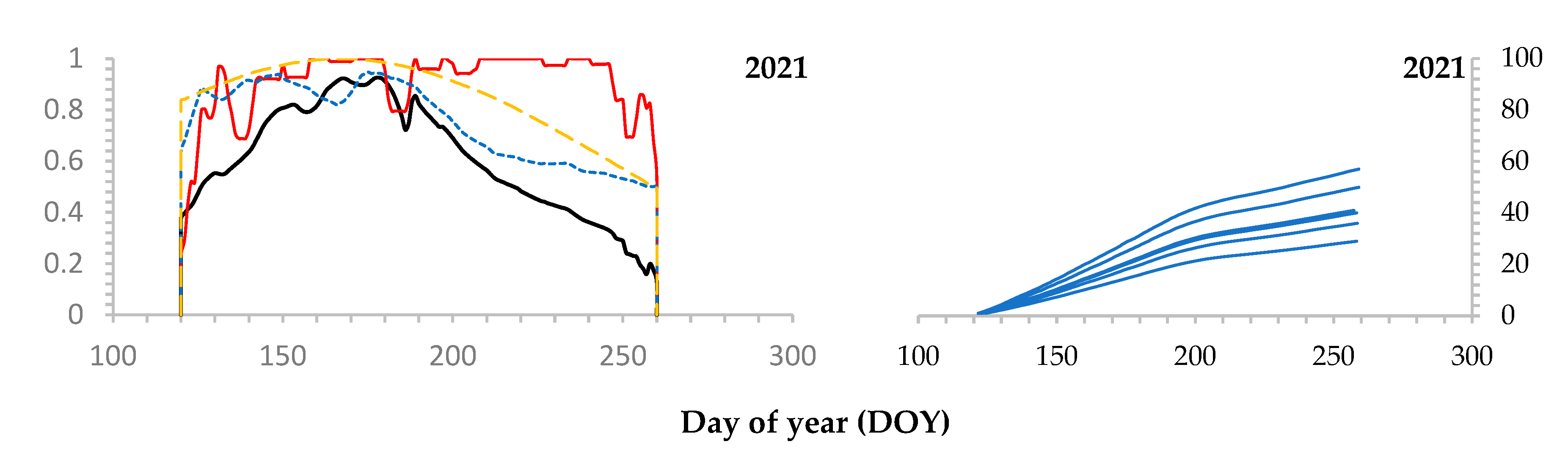
3.1. Fitting of VS-Model Parameters for Chronologies and Calculation of Seasonal Growth Rate
3.2. Band-Model: Absolute Production of Tracheids and Dates of Tracheid Transition from Cambium to Expansion Zone
- For growth rings of different widths (and different numbers of tracheids in radial cell rows), we were able to calculate the seasonal kinetics of growth in terms of the number of cells in the ring.
- For each tracheid in the cell row, we determined the date of its production by the cambial zone (i.e., the date of transition to the expansion zone).
- The inverse relationship between the number of produced cells and the main parameter of the Band-model (β) is clearly evident.
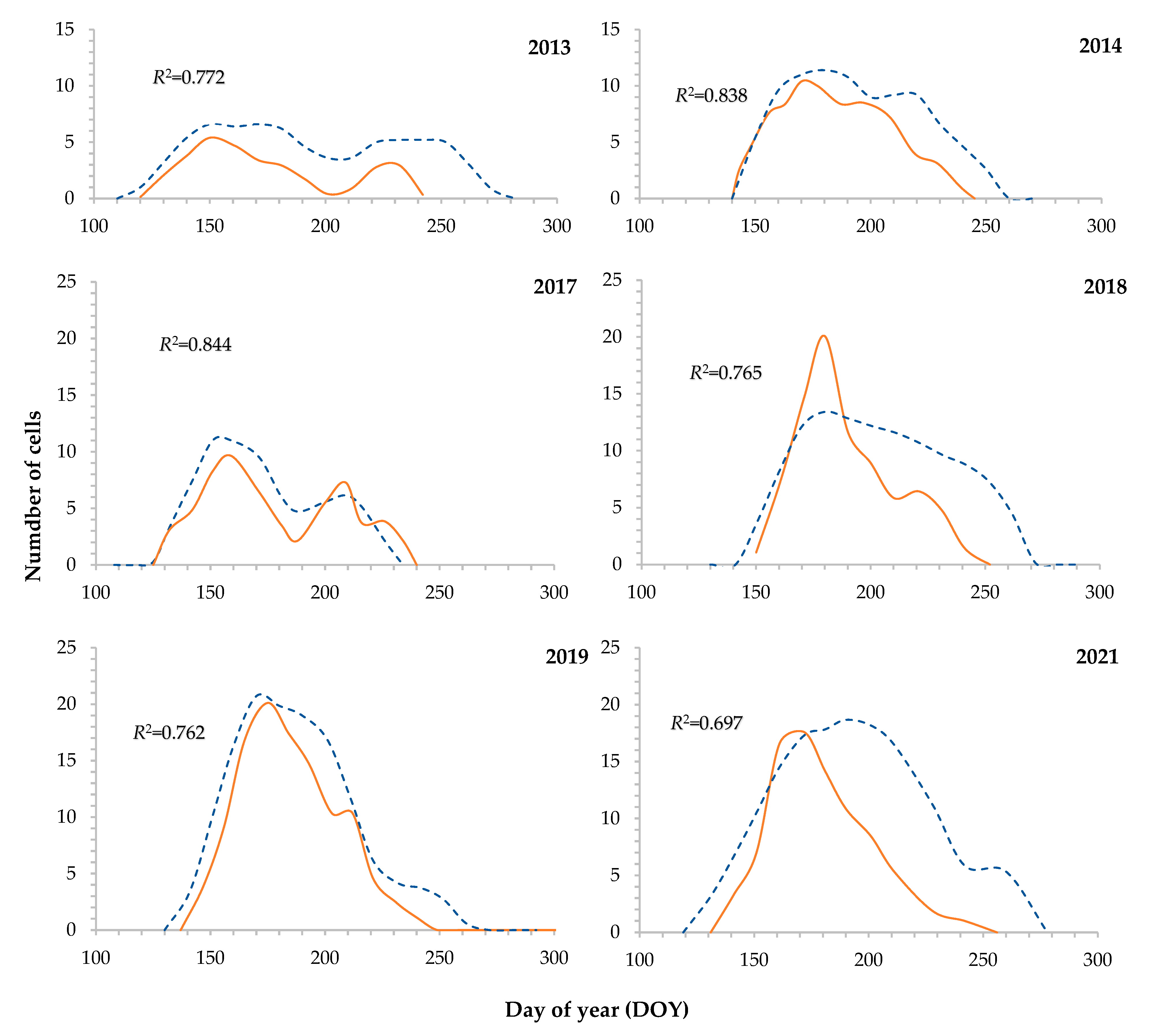
3.3. Cell Production Kinetics
3.4. Analysis of Tree-Ring Tracheidograms at the End of the Growth Season
3.5. Seasonal Curves of the Number of Cells in the Expansion Zone
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vaganov, E.A.; Shashkin, A.V.; Sviderskaya, I.V.; Vysotskaya, L.G. Histometric Analysis of Woody Plants Growth; Nauka: Novosibirsk, Russia, 1985; 102p. (In Russian) [Google Scholar]
- Vaganov, E.A.; Hughes, M.K.; Shashkin, A.V. Growth Dynamics of Conifer Tree Rings: Images of Past and Future Environments; Springer: Berlin/Heidelberg, Germany, 2006; 358p. [Google Scholar] [CrossRef]
- Rathgeber, C.B.K.; Cuny, H.E.; Fonti, P. Biological basis of tree-ring formation: A crash course. Front. Plant Sci. 2016, 7, 734. [Google Scholar] [CrossRef]
- Rathgeber, C.B.K.; Perez-de-Lis, G.; Fernandez-de-Una, L.; Fonti, P.; Rossi, S.; Treydte, K.; Gessler, A.; Deslaurier, A.; Fonti, M.; Ponton, S. Anatomical, developmental and physiological bases of tree-ring formation in relation to environmental factors. In Stable Isotopes in Tree Rings: Inferring Physiological, Climatic and Environmental Responses; Siegwolf, R.T.W., Brooks, J.R., Roden, J., Saurer, M., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 61–99. [Google Scholar] [CrossRef]
- Ziaco, E.; Biondi, F.B.; Heinrich, I. Wood cellular dendroclimatology: Testing view proxies in Great Basin bristlecone pine. Front. Plant Sci. 2016, 7, 1602. [Google Scholar] [CrossRef]
- Babushkina, E.A.; Sitnikov, G.A.; Upadhyay, K.K.; Zhirnova, D.F.; Zelenov, G.K.; Vaganov, E.A.; Belokopytova, L.V. Seasonal growth of pine tree rings: Comparison of direct observations and simulation. Forests 2022, 13, 1978. [Google Scholar] [CrossRef]
- Begum, S.; Nakaba, S.; Yamagishi, Y.; Oribe, Y.; Funada, R. Regulation of cambial activity in relation to environmental conditions: Understanding the role of temperature in wood formation of trees. Physiol. Plant. 2012, 147, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Begum, S.; Kudo, K.; Rahman, M.H.; Nakaba, S.; Yamagishi, Y.; Nabeshima, E.; Nugroho, W.D.; Oribe, Y.; Kitin, P.; Jin, H.-O.; et al. Climate change and the regulation of wood formation in trees by temperature. Trees 2018, 32, 3–15. [Google Scholar] [CrossRef]
- Babushkina, E.A.; Belokopytova, L.V.; Zhirnova, D.F.; Vaganov, E.A. Siberian spruce tree ring anatomy: Imprint of development processes and their high-temporal environmental regulation. Dendrochronologia 2019, 53, 114–124. [Google Scholar] [CrossRef]
- Belokopytova, L.V.; Babushkina, E.A.; Zhirnova, D.F.; Panyushkina, I.P.; Vaganov, E.A. Pine and larch tracheids capture seasonal variations of climatic signal at moisture-limited sites. Trees 2019, 33, 227–242. [Google Scholar] [CrossRef]
- De Micco, V.; Carrer, M.; Rathgeber, C.B.K.; Camarero, J.; Voltas, J.; Cherubini, P.; Battipaglia, G. From xylogenesis to tree rings: Wood traits to investigate tree response to environmental changes. IAWA J. 2019, 40, 155–182. [Google Scholar] [CrossRef]
- Butto, V.; Deslaurier, A.; Rossi, S.; Rozenberg, P.; Shishov, V.; Morin, H. The role of plant hormones in tree-ring formation. Trees 2020, 34, 315–335. [Google Scholar] [CrossRef]
- Deleuze, C.; Houllier, F. A simple process-based xylem growth model for describing wood microdensitometric profiles. J. Theor. Biol. 1998, 193, 99–113. [Google Scholar] [CrossRef]
- Cuny, H.E.; Rathgeber, C.B.K.; Frank, D.; Fonti, P.; Fournier, M. Kinetics of tracheid development explain conifer tree-ring structure. New Phytol. 2014, 203, 1231–1241. [Google Scholar] [CrossRef]
- Drew, D.M.; Downes, G. A model of stem growth and wood formation in Pinus radiata. Trees 2015, 29, 1395–1413. [Google Scholar] [CrossRef]
- Hartmann, F.P.K.; Rathgeber, C.B.; Fournier, M.; Moulia, B. Modelling wood formation and structure: Power and limits of a morphogenetic gradient in controlling xylem cell proliferation and growth. Ann. For. Sci. 2017, 74, 14. [Google Scholar] [CrossRef]
- Hartmann, F.P.; Rathgeber, C.B.K.; Badel, E.; Fournier, M.; Moulia, B. Modelling the spatial crosstalk between two biochemical signals explains wood formation dynamics and tree-ring structure. J. Exp. Bot. 2021, 72, 1727–1737. [Google Scholar] [CrossRef] [PubMed]
- Cartenì, F.; Deslauriers, A.; Rossi, S.; Morin, H.; De Micco, V.; Mazzoleni, S.; Giannino, F. The physiological mechanisms behind the earlywood-to-latewood transition: A process-based modeling approach. Front. Plant Sci. 2018, 9, 1053. [Google Scholar] [CrossRef] [PubMed]
- Tychkov, I.I.; Sviderskaya, I.V.; Babushkina, E.A.; Popkova, M.I.; Vaganov, E.A.; Shishov, V.V. How can the parameterization of a process-based model help us understand real tree-ring growth? Trees 2019, 33, 345–357. [Google Scholar] [CrossRef]
- Cabon, A.; Peters, R.L.; Fonti, P.; Martínez-Vilalta, J.; Cáceres, M.D. Temperature and water potential co-limit stem cambial activity along a steep elevational gradient. New Phytol. 2020, 226, 1325–1340. [Google Scholar] [CrossRef] [PubMed]
- Eckes-Shepard, A.H.; Ljungqvist, F.C.; Drew, D.M.; Rathgeber, C.B.K.; Friend, A.D. Wood formation modeling—A research review and future perspectives. Front. Plant Sci. 2022, 13, 837648. [Google Scholar] [CrossRef]
- Shishov, V.V.; Tychkov, I.I.; Anchukaitis, K.J.; Zelenov, G.K.; Vaganov, E.A. A band model of cambium development: Opportunities and prospects. Forests 2021, 12, 1361. [Google Scholar] [CrossRef]
- Seo, J.W.; Smiljanić, M.; Wilmking, M. Optimizing cell-anatomical chronologies of Scots pine by stepwise increasing the number of radial tracheid rows included—Case study based on three Scandinavian sites. Dendrochronologia 2014, 32, 205–209. [Google Scholar] [CrossRef]
- Shishov, V.V.; Tychkov, I.I.; Popkova, M.I.; Ilyin, V.A.; Bryukhanova, M.V.; Kirdyanov, A.V. VS-Oscilloscope: A new tool to parameterize tree radial growth based on climate conditions. Dendrochronologia 2016, 39, 42–50. [Google Scholar] [CrossRef]
- Anchukaitis, K.J.; Evans, M.N.; Hughes, M.K.; Vaganov, E.A. An interpreted language implementation of the Vaganov-Shashkin tree-ring proxy system model. Dendrochronologia 2020, 60, 125677. [Google Scholar] [CrossRef]
- Fonti, M.V.; Babushkina, E.A.; Zhirnova, D.F.; Vaganov, E.A. Xylogenesis of Scots pine in an uneven-aged stand of the Minusinsk Depression (Southern Siberia). J. Sib. Fed. Univ. Biol. 2020, 13, 197–207. [Google Scholar] [CrossRef]
- Cook, E.R.; Kairiukstis, L.A. (Eds.) Methods of Dendrochronology: Applications in the Environmental Sciences; Kluwer Acad. Publ.: Dordrecht, The Netherlands, 1990. [Google Scholar] [CrossRef]
- Rinn, F. TSAP-Win: Time Series Analysis and Presentation for Dendrochronology and Related Applications: User Reference; RINNTECH: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 69–78. [Google Scholar]
- Cook, E.R.; Krusic, P.J. Program ARSTAN: A Tree-Ring Standardization Program Based on Detrending and Autoregressive Time Series Modeling, with Interactive Graphics; Lamont-Doherty Earth Observatory, Columbia University: Palisades, NY, USA, 2005. [Google Scholar]
- Vysotskaya, L.G.; Vaganov, E.A. Components of the variability of radial cell size in tree-rings of conifers. IAWA Bull. 1989, 10, 417–428. [Google Scholar] [CrossRef]
- Vaganov, E.A.; Ivanov, V.B.; Vysotskaya, L.G. Histometric analysis of cell size variability in the meristem of corn root. Tsytologya 1991, 33, 50–59. (In Russian) [Google Scholar]
- Rossi, S.; Deslauriers, A.; Griçar, J.; Seo, J.W.; Rathgeber, C.B.; Anfodillo, T.; Morin, H.; Levanic, T.; Oven, P.; Jalkanen, R. Critical temperatures for xylogenesis in conifers of cold climates. Glob. Ecol. Biogeogr. 2008, 17, 696–707. [Google Scholar] [CrossRef]
- Russell, M.B.; Weiskittel, A.R.; Kershaw, J.A., Jr. Assessing model performance in forecasting long-term individual tree diameter versus basal area increment for the primary Acadian tree species. Can. J. For. Res. 2011, 41, 2267–2275. [Google Scholar] [CrossRef]
- Deslaurier, A.; Morin, H.; Begin, Y. Cellular phenology of annual ring formation of Abies balsamea in the Quebec boreal forest (Canada). Can. J. For. Res. 2003, 33, 190–200. [Google Scholar] [CrossRef]
- Cabon, A.; Fernandez-de-Una, L.; Gea-Izquierdo, G.; Meinzer, F.C.; Woodruff, D.R.; Martinez-Vilalta, J.; De Caceres, M. Water potential control of turgor-driven tracheid enlargement in Scots pine at its xeric distribution edge. New Phytol. 2020, 225, 209–221. [Google Scholar] [CrossRef]
- Peters, R.L.; Steppe, K.; Cuny, H.E.; De Pauw, D.J.W.; Frank, D.C.; Schaub, M.; Rathgeber, C.B.K.; Cabon, A.; Fonti, P. Turgor—A limiting factor for radial growth in mature conifers along an elevational gradient. New Phytol. 2021, 229, 213–229. [Google Scholar] [CrossRef]
- Vaganov, E.A. The tracheidogram method in tree-ring analysis and its application. In Methods of Dendrochronology: Applications in the Environmental Sciences; Cook, E., Kairiukstis, L., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990; pp. 63–75. [Google Scholar]
- Vaganov, E.A.; Anchukaitis, K.J.; Evans, M. How well understood are the processes that create dendroclimatic records? A mechanistic model of the climatic control on conifer tree-ring growth dynamics. In Dendroclimatology: Progress and Prospects; Hughes, M.K., Swetnam, T.W., Diaz, H.F., Eds.; Springer: Dordrecht, Germany, 2011; pp. 37–75. [Google Scholar] [CrossRef]
- Ziaco, E.; Truettner, C.; Biondi, F.; Bullock, S. Moisture-driven xylogenesis in Pinus ponderosa from a Mojave desert mountain reveals high phenological plasticity. Plant Cell Environ. 2018, 41, 823–836. [Google Scholar] [CrossRef] [PubMed]
- Cuny, H.E.; Rathgeber, C.B.; Frank, D.; Fonti, P.; Mäkinen, H.; Prislan, P.; Rossi, S.; Martinez del Castillo, E.; Campelo, F.; Vavrčík, H.; et al. Woody biomass production lags stem-girth increase by over one month in coniferous forests. Nat. Plants 2015, 1, 15160. [Google Scholar] [CrossRef] [PubMed]
- Anchukaitis, K.J.; Evans, M.N.; Kaplan, A.; Vaganov, E.A.; Hughes, M.K.; Grissino-Mayer, H.D.; Cane, M.A. Forward modeling of regional scale tree-ring patterns in the southeastern United States and recent influence of summer drought. Geophys. Res. Lett. 2006, 33, L04705. [Google Scholar] [CrossRef]
- Osakabe, Y.; Kajita, S.; Osakabe, K. Genetic engineering of woody plants: Current and future targets in a stressful environment. Physiol. Plant 2011, 142, 105–117. [Google Scholar] [CrossRef] [PubMed]
- Zharkov, M.S.; Huang, J.G.; Yang, B.; Babushkina, E.A.; Belokopytova, L.V.; Vaganov, E.A.; Zhirnova, D.F.; Ilyin, V.A.; Popkova, M.A.; Shishov, V.V. Tracheidograms classification as a new potential proxy in high-resolution dendroclimatic reconstruction. Forests 2022, 13, 970. [Google Scholar] [CrossRef]
- Perez-de-Lis, G.; Rathgeber, C.B.; Fernández-de-Uña, L.; Ponton, S. Cutting tree rings into time slices: How intra-annual dynamics of wood formation help decipher the space-for-time conversion. New Phytol. 2022, 233, 1520–1534. [Google Scholar] [CrossRef] [PubMed]
- Wimmer, R. Wood anatomical features in tree-rings as indicators of environmental change. Dendrochronologia 2002, 20, 21–36. [Google Scholar] [CrossRef]
- Brauning, A.; De Ridder, M.; Zafirov, N.; García-González, I.; Dimitrov, D.P.; Gärtner, H. Tree-ring features: Indicators of extreme event impacts. IAWA J. 2016, 37, 206–231. [Google Scholar] [CrossRef]
- Fritts, H.C. Dendroclimatology and dendroecology. Quat. Res. 1971, 1, 419–449. [Google Scholar] [CrossRef]
- Prislan, P.; Gricar, J.; de Luis, M.; Novak, K.; Martinez del Castello, E.; Schmitt, U.; Koch, G.; Strus, J.; Mrak, P.; Znidaric, M.T.; et al. Annual cambial rhythm in Pinus halepensis and Pinus sylvestris as indicator for climatic adaptation. Front. Plant Sci. 2016, 7, 1923. [Google Scholar] [CrossRef] [PubMed]
- Carrer, M.; Castagneri, D.; Prendin, A.L.; Petit, G.; von Arx, G. Retrospective analysis of wood anatomical traits reveals a recent extension in tree cambial activity in two high-elevation conifers. Front. Plant. Sci. 2017, 8, 737. [Google Scholar] [CrossRef] [PubMed]
- Barlow, P.W.; Lück, J. Repetitive cellular patterns in the secondary phloem of conifer and dicot trees, and a hypothesis for their development. Plant Biosyst. Int. J. Deal. Asp. Plant Biol. 2005, 139, 164–179. [Google Scholar] [CrossRef]
- Tumajer, J.; Buras, A.; Camarero, J.J.; Carrer, M.; Shetti, R.; Wilmking, M.; Altman, J.; Sangüesa-Barreda, G.; Lehejček, J. Growing faster, longer or both? Modelling plastic response of Juniperus communis growth phenology to climate change. Glob. Ecol. Biogeogr. 2021, 30, 2229–2244. [Google Scholar] [CrossRef]
- Noyer, E.; Stojanovic, M.; Horacek, P.; Perez-de-Lis, G. Toward a better understanding of angiosperm xylogenesis: A new method for a cellular approach. New Phytol. 2023, 239, 792–805. [Google Scholar] [CrossRef]




| Year | Equation |
|---|---|
| 2013 | N = 92.6·exp(−1.096·β) |
| 2014 | N = 106.4·exp(−1.37·β) |
| 2017 | N = 77.0·exp(−0.97·β) |
| 2018 | N = 108.0·exp(−1.22·β) |
| 2019 | N = 105.1·exp(−1.11·β) |
| 2021 | N = 104.3·exp(−1.31·β) |
| Total | N = 95.0·exp(−1.1·β) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zelenov, G.K.; Belokopytova, L.V.; Babushkina, E.A.; Zhirnova, D.F.; Yang, B.; Peng, X.; Liu, J.; Sitnikov, G.A.; Vaganov, E.A. Reconstruction of Seasonal Kinetics in Conifer Radial Growth from Daily Meteorological Conditions, Tree-Ring Width, and Radial Size of Tracheids. Forests 2024, 15, 249. https://doi.org/10.3390/f15020249
Zelenov GK, Belokopytova LV, Babushkina EA, Zhirnova DF, Yang B, Peng X, Liu J, Sitnikov GA, Vaganov EA. Reconstruction of Seasonal Kinetics in Conifer Radial Growth from Daily Meteorological Conditions, Tree-Ring Width, and Radial Size of Tracheids. Forests. 2024; 15(2):249. https://doi.org/10.3390/f15020249
Chicago/Turabian StyleZelenov, Grigory K., Liliana V. Belokopytova, Elena A. Babushkina, Dina F. Zhirnova, Bao Yang, Xiaomei Peng, Jingjing Liu, Gleb A. Sitnikov, and Eugene A. Vaganov. 2024. "Reconstruction of Seasonal Kinetics in Conifer Radial Growth from Daily Meteorological Conditions, Tree-Ring Width, and Radial Size of Tracheids" Forests 15, no. 2: 249. https://doi.org/10.3390/f15020249
APA StyleZelenov, G. K., Belokopytova, L. V., Babushkina, E. A., Zhirnova, D. F., Yang, B., Peng, X., Liu, J., Sitnikov, G. A., & Vaganov, E. A. (2024). Reconstruction of Seasonal Kinetics in Conifer Radial Growth from Daily Meteorological Conditions, Tree-Ring Width, and Radial Size of Tracheids. Forests, 15(2), 249. https://doi.org/10.3390/f15020249










