1. Introduction
In the past few years, the Fourth Generation (4G) of mobile telecommunication has been significantly changing and improving our lives. Meanwhile, the exponentially increasing rate requirements throw down the gauntlet to the latest standard for the mobile telecommunication. Nowadays, research interest has already been drawn on the the Fifth Generation (5G) of mobile telecommunication which can achieve substantially higher throughput than 4G. Massive multiple-input multiple-output (MIMO) and DEVICE-to-device (D2D) communication are two promising candidate technologies of 5G. Massive MIMO employing a few hundreds of antennas at the BS can achieve a higher data rate through focusing the energy into a narrow beam towards the receiver. D2D is another emerging technology to meet the high-rate data requirements due to the short-range direct transmission without going through the base station (BS).
1.1. Related Works
Compared with the traditional MIMO system, the large-scale antennas can bring in the higher spectrum efficiency (SE) and energy efficiency (EE) [
1,
2,
3]. Lower capacity bounds for linear detection are derived from the uplink massive MIMO systems [
3]. Conjugate and Zero-Forcing precoders are compare in terms of SE and EE for the downlink of massive MIMO systems [
4]. Nguyen et al. compared massive MIMO and small cells in terms of user-average SE by using stochastic geometry theory [
5]. Masini et al. analyzed MC-CDMA systems adopting an adaptive detection technique based on threshold orthogonality restoring combining [
6,
7]. Wen et al. derived the asymptotic sum-rate of the multiuser (MU) MIMO uplink channel in the large-system regime [
8].
D2D underlaying cellular network (CN) is regarded as a means to increase the data rate, and decrease the load of CNs [
9,
10]. However, the coexistence of the D2D and the CN causes the mutual interference. To combat the interference from the D2D to the CN, Doppler et al. proposed a mechanism to limit the maximum transmit power of the D2D transmitter [
11]. However, the interference from the CN to the D2D link is not considered. In [
12], the cellular user equipments (CUEs) are scheduled for the communication if they are not in the interference-limited area so as not to generate harmful interference to the D2D receiver. Bazzi et al. analyzed the performance of D2D enabling V2V Beaconing [
13]. Palombara et al. developed a framework for design and analysis of relay-assisted diversity communications accounting [
14].
The combination of massive MIMO and D2D is investigated in [
15,
16,
17]. Lin et al. adopt the partial zero-forcing receiving technique to cancel the uplink interference from the nearby CUEs and D2D links, and investigate the spectral efficiency with both the perfect and imperfect channel state information (CSI) [
15]. The precoding and power allocation are jointly optimized for D2D underlaying massive MIMO multicasting networks [
16]. Shalmashi et al. derived average sum rate and EE for massive MIMO system with D2D links underlay [
17].
1.2. Motivation and Contribution
To guarantee a required achievable rate, with perfect CSI available, Ngo et al. show that the transmit power of the CUEs can be made inversely proportional to the number of antennas in the uplink of massive MIMO systems [
3]. Inspired by this fact, we limit the maximum transmit power of the CUEs to suppress the interference from the CN to the D2D, and then guarantee the CN performance with the aid of large-scale antennas.
In this paper, we consider an uplink massive MIMO system with D2D underlay. The main contributions of this work are summarized as:
The probability density function of the signal-to-interference-plus-noise ratio (SINR) at the CUEs is approximated in closed-form.
The outage probabilities and the achievable rates of the massive MIMO system and the D2D link are derived in closed-form.
Constrained by the SE of the D2D link and CUEs, the EE of the massive MIMO system is maximized by jointly optimizing the transmit power of CUEs and the number of BS antennas.
2. System Model
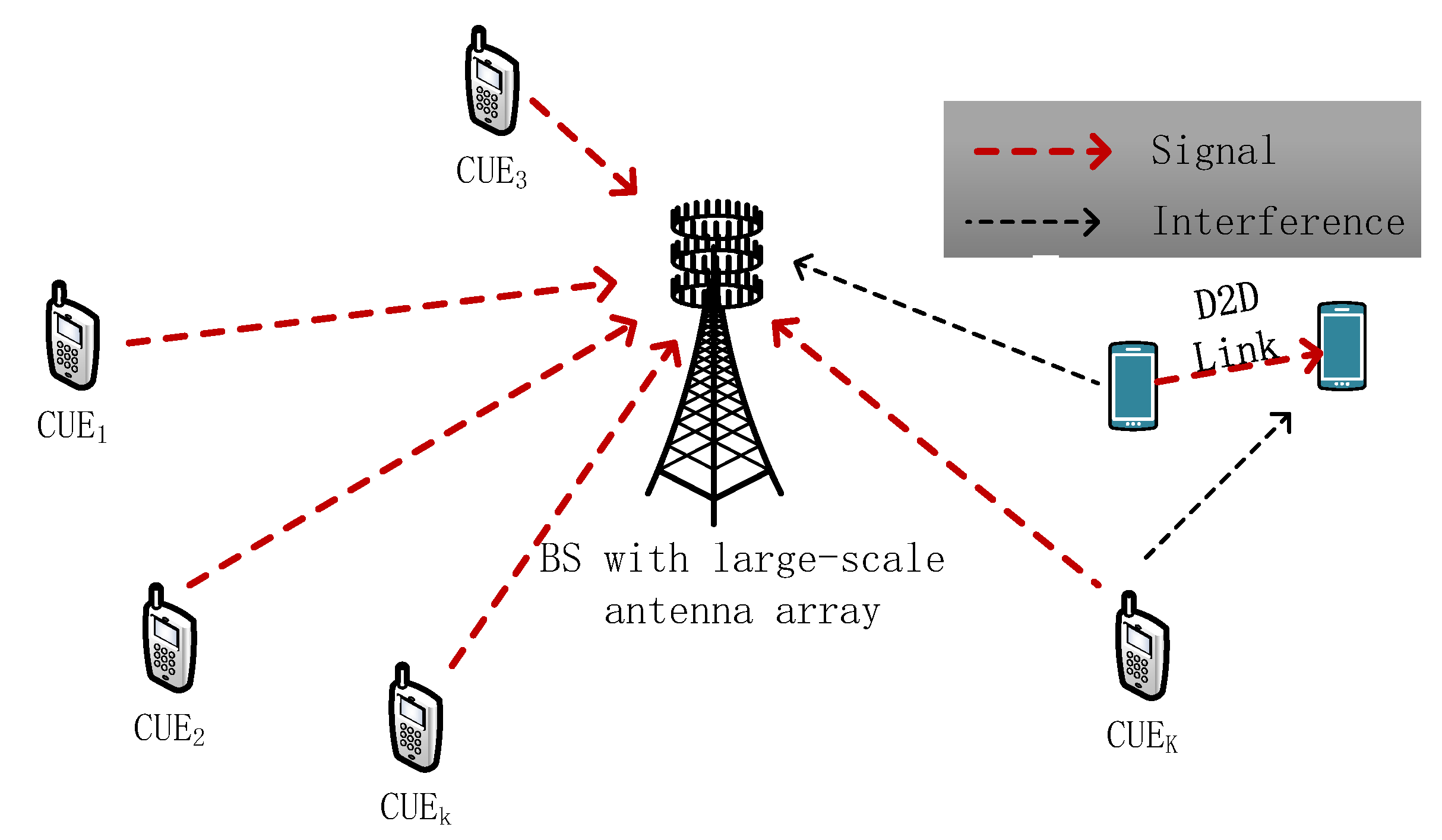
We consider a massive MIMO system with a D2D link underlay as shown in
Figure 1, which consists of a BS with
N antennas,
K CUEs, and one D2D link. Each CUE or D2D user is equipped with a single omnidirectional antenna. The CUEs transmit signal to the BS using the same time-frequency resource as the D2D link.
Let denote the channel vector from the k-th CUE to the BS, where and represent the large-scale fading (path-loss) and the small-scale fading, respectively. Similarly, denotes the channel vector from the D2D transmitter to the BS. and represent the channel fading from the k-th CUE and the D2D transmitter to the D2D receiver, respectively.
Similarly to [
3], the channel vectors from the CUEs to the BS are assumed to be available at the BS, and the maximum ratio combining (MRC) technique is adopted for the data reception. The detected signal of the
k-th CUE after the linear processing can be given as
where
and
represent the transmit powers of the CUEs and the D2D transmitter, respectively.
is an additive white Gaussian noise (AGWN) vector at the BS. In addition,
and
denote respectively the normalized signal sent by the D2D transmitter and the
k-th CUE, i.e.,
. The SINR at the
k-th CUE is denoted as
and given as
where
and
. The average achievable rate of the
k-th CUE is
The received signal at the D2D receiver can be given as
where
is the AGWN at the D2D receiver. The SINR at the D2D receiver is
where
and
. The average achievable rate of the D2D link is
The energy consumption of the massive MIMO system in a normalized time block is
where
and
represent the circuit power consumption per RF chain and the basic power consumption of the system, respectively. The EE of the massive MIMO system defined as the ratio between the sum-rate and the energy consumption is given as
3. Spectrum Efficiency Analysis
In this section, we propose the approximate probability density function (PDF) of the SINR, based on which, we analyze the outage probabilities and the achievable rates for both the D2D and the CUEs by considering the mutual interference between the two systems.
3.1. Outage Probability and Achievable Rate of CUEs
Theorem 1. The PDF of can be accurately approximated aswhereand is the gamma function. Given a target SINR
, we can obtain the outage probability of the
k-th CUE according to (A1) and (A2) as,
where
and
is the upper incomplete gamma function.
Theorem 2. The achievable rate of the k-th CUE can be approximated aswhere and . To make the analysis trackable, we also derive the simple lower bound using Jensen’s inequality, i.e.,
where
. Note that the achievable rates scales quickly with the number of transmit antennas, and can be made arbitrarily large when
N grows without bound.
3.2. Outage Probability and Achievable Rate of the D2D Link
Proposition 1. Given the target SINR for the D2D link, the outage probability of the D2D link can be obtained aswhere Proposition 2. The average achievable rate of the D2D link can be approximated aswhere 3.3. Power Management for CUEs
With the increase of , the SE of the CN can be improved, while the SE of the D2D link is degraded, and vice visa. So, it is interesting to strike a balance between the CN and the D2D link through the power management for the CUEs. The spectrum performance of the D2D link can be improved effectively by decreasing especially in the high signal-to-noise ratio (SNR) regime. However, the power management of has limited influence on the CN.
Proposition 3. When , approaches the lower bound , while approaches the upper bound given aswhereand . Proof. Let
. Similarly to
,
. With the increase of
,
approaches the following upper bound
where the last step is obtained using ([
18] Equation (4.352.1)). After calculating
similarly to Theorem 1, we can conclude the proof. ☐
4. Energy Efficiency Optimization
From the last section, we can see that the power management plays a critical role in the SE of the D2D link, while the number of antennas severely influence the SE of the CUEs. The EE with the unit bps/Hz/W is another important metric that should be considered for the green communications. In this section, we aim to maximize the EE
constrained by the SEs of the CUEs and the D2D link. To make the optimization problem trackable, we maximized the lower bound of the EE that is
. The optimization problem can be formulated as
C1 specifies the outage probability and the minimum data rate requirements of the D2D link. C2 specifies the SINR constraints of the CUEs.
is a predefined threshold that can guarantee the system operates in the massive MIMO scenario.
To guarantee the performance of the D2D link, the transmit power of CUEs
should be limited to less than
, where
is the solution of the equation
. So, the constraint C1 can be transformed into
. Owing to
, given a value of
, the optimization problem
can be reformulated as
.
where
Theorem 3. The optimal number of antennas for the optimization problem P2 is obtained as is given aswhere W is the lambert W function defined as , , and is the one of the two closest integer around that can maximize . Proof. The objective function can be written as
We can conclude the proof according to the quasi-concavity of
w.r.t.
N. ☐
It can be seen from Theorem 3 that the optimal N can be obtained in closed-form once is fixed. So the optimal solution of can be obtained by a one-dimensional search w.r.t. in the interval of .
5. Numerical and Simulation Results
In this section, the Monte Carlo simulations are performed over
independent trials. We verify the tightness of our analysis and show the optimal number of antennas obtained by our closed-form expression for a given
. The large-scale fading (path-loss) at distance
d is set as
[
19]. The distance between the D2D users is set as 10 m. Without loss of generality,
CUEs and the D2D link are uniformly placed in a circle of radius 200 m around the BS. The other parameter settings are detailed in
Table 1.
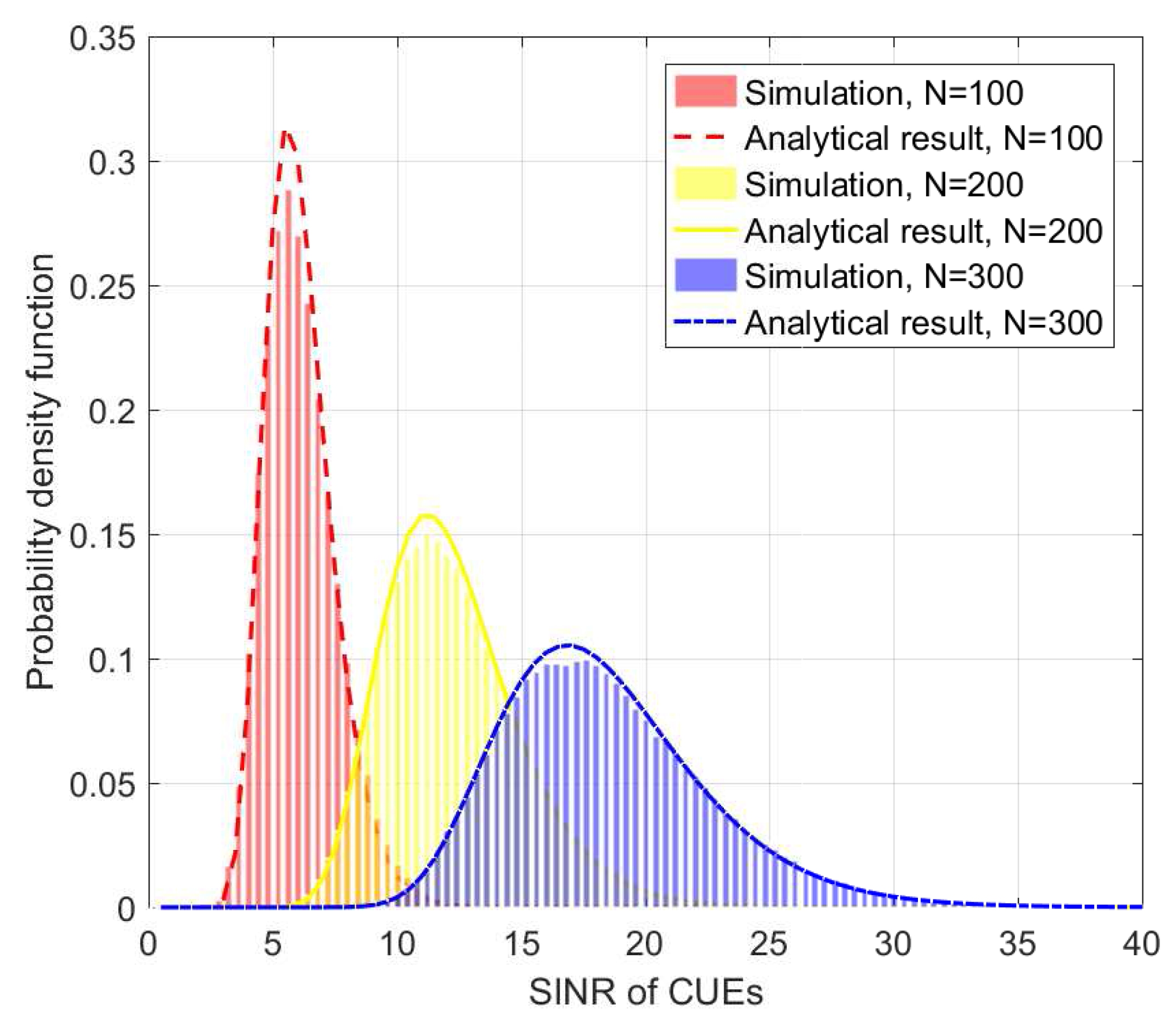
Figure 2 shows the PDF
obtained by our closed-form approximation and the simulations with
mW for different number of antennas. A good match can be observed between our closed-form approximation and the simulations.
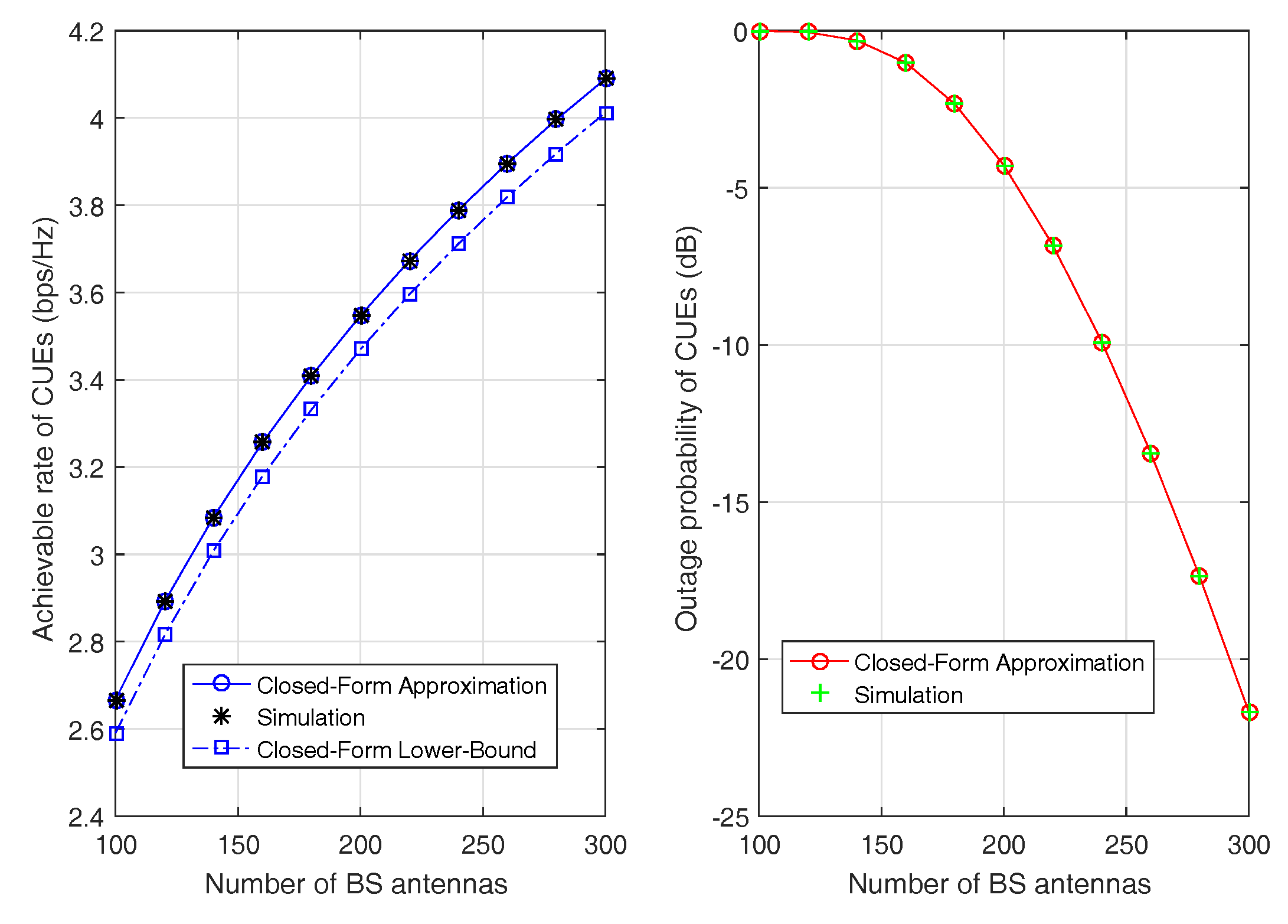
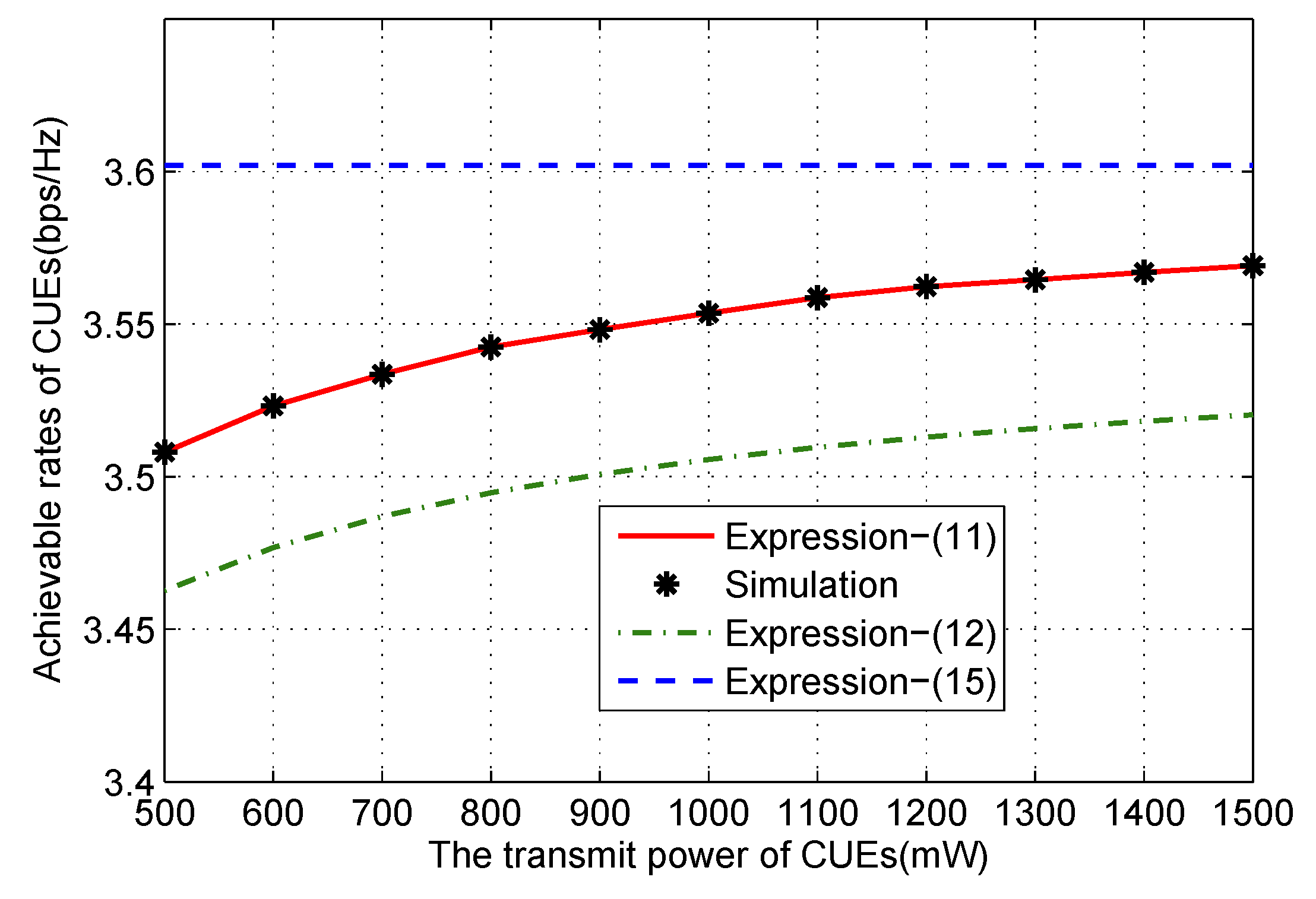
Figure 3 plots the achievable rate and the outage probability of CUEs versus the number of antennas. It reveals that the analytical results agree reasonably well with the simulation results. With the increase of the number of BS antennas, the achievable rate can be significantly improved. In addition, the derived lower bound rate is close to the real value. To evaluate the impact of
on the performance of massive MIMO system, the achievable rate of CUEs is shown in
Figure 4. The achievable rate gets larger and approaches the upper bound with the increase of
. It can be seen that increasing the transmit power imposes less impacts compared with increasing the number of antennas.
We have
mW by solving
. Then, the optimal solution of P1 can be obtained by a one-dimensional search w.r.t.
from 0 to 1100 mW.
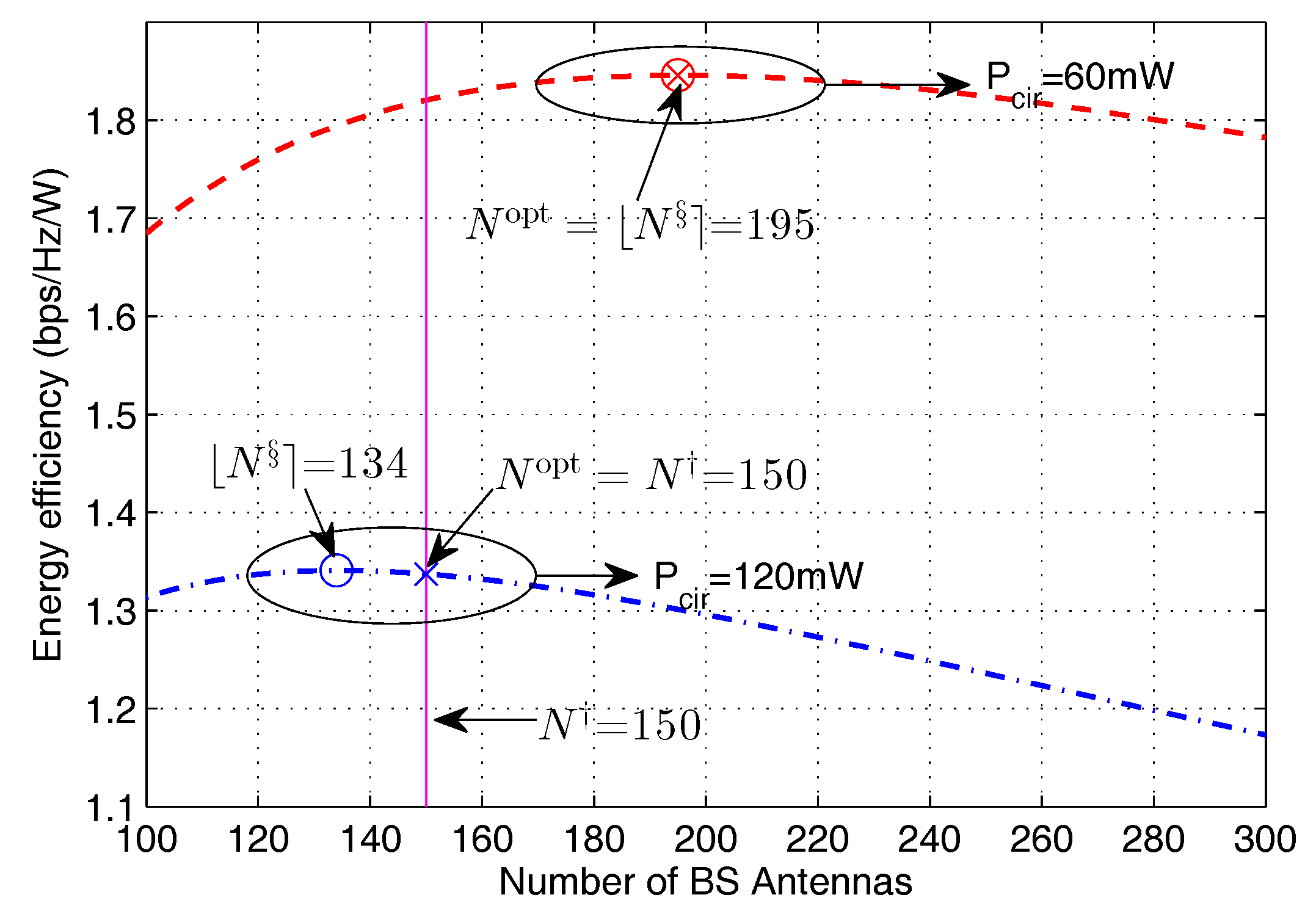
Figure 5. plots the EE for different number of BS antennas and different
for a given
mW. From the plot, we can see that the analytical result is the same as the result obtained by the exhaustive search. As expected, the optimal number of antennas gets smaller with the increase of
.
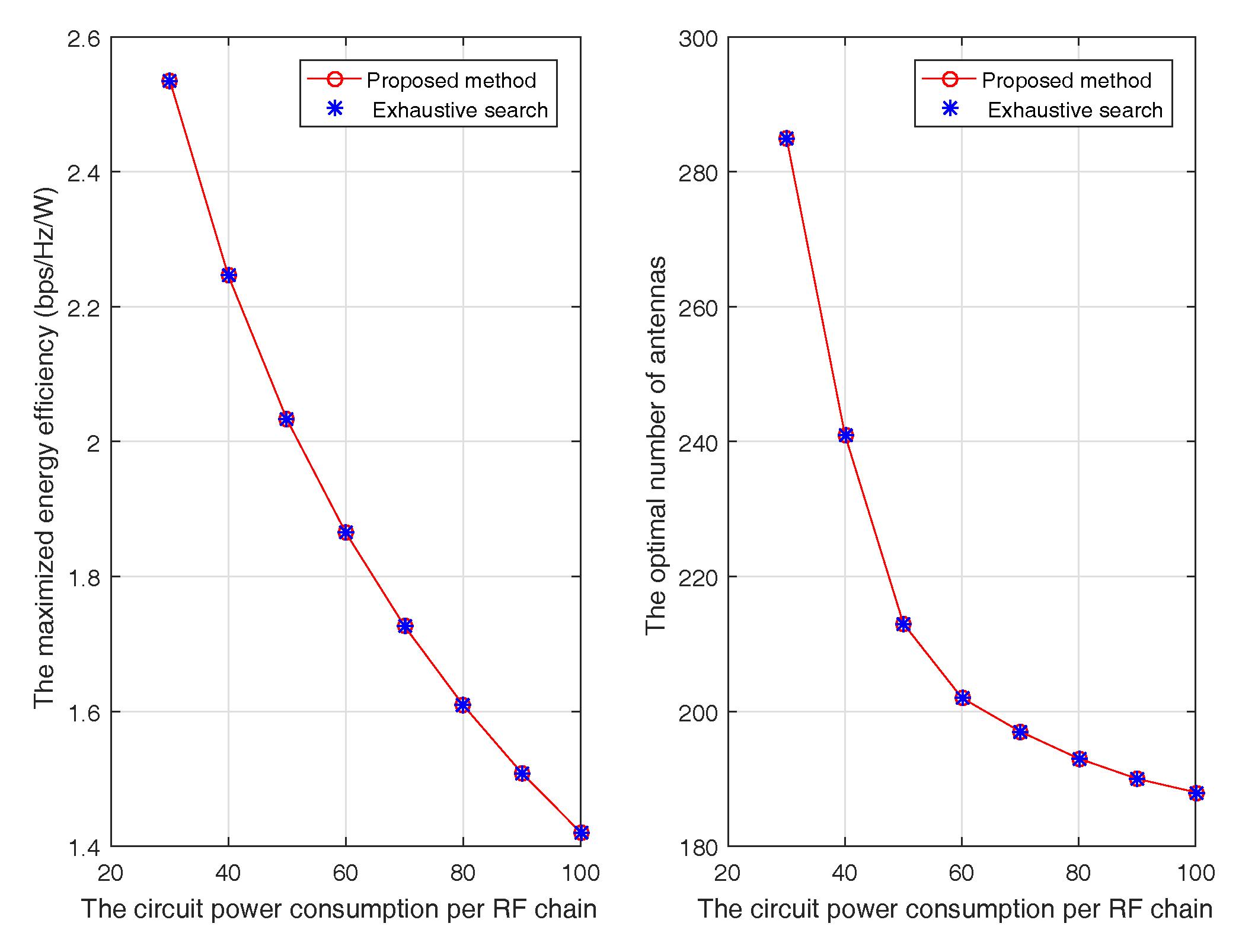
Figure 6 compares the maximized EE and the optimal number of antennas obtained by our proposed method and the exhaustive search. As expected, our proposed method achieves the same performance as the optimal exhaustive search with higher complexity.
6. Conclusions
We have derived the accurate closed-form expressions of the outage probability and average achievable rate for a heterogeneous network consisting of an uplink massive MIMO and a D2D link. The influence of the power of CUEs is investigated for the D2D and the CUEs. Constrained by the performance of the D2D link and CUEs, the EE of the massive MIMO system is maximized by jointly optimizing the number of BS antennas and the transmit power of CUEs. Meanwhile, the optimization problem is solved by a one-dimensional search with low complexity. Numerical results show the tightness of our closed-form expressions and reveal the impacts of various parameter settings. In particular, it is interesting to study some extensions of this work similarly to [
21,
22,
23].