Sustainability Index Evaluation of the Rainwater Harvesting System in Six US Urban Cities
Abstract
:1. Introduction
2. Materials and Methods
2.1. Analytical Approach
2.2. Physical Model Approach
2.3. Rainfall Data
2.4. Evaluation of Performance Indices
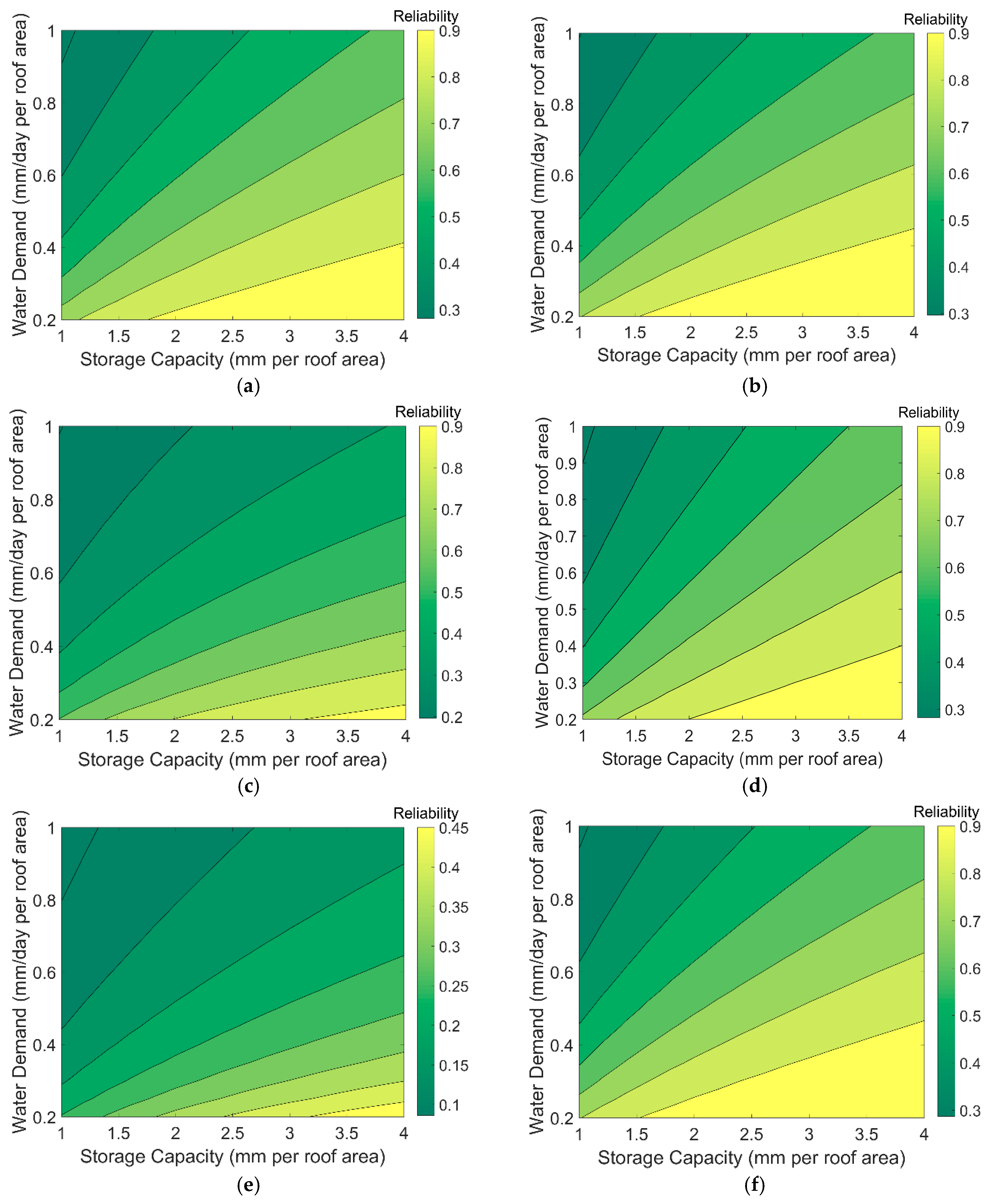
2.4.1. Evaluation of Reliability
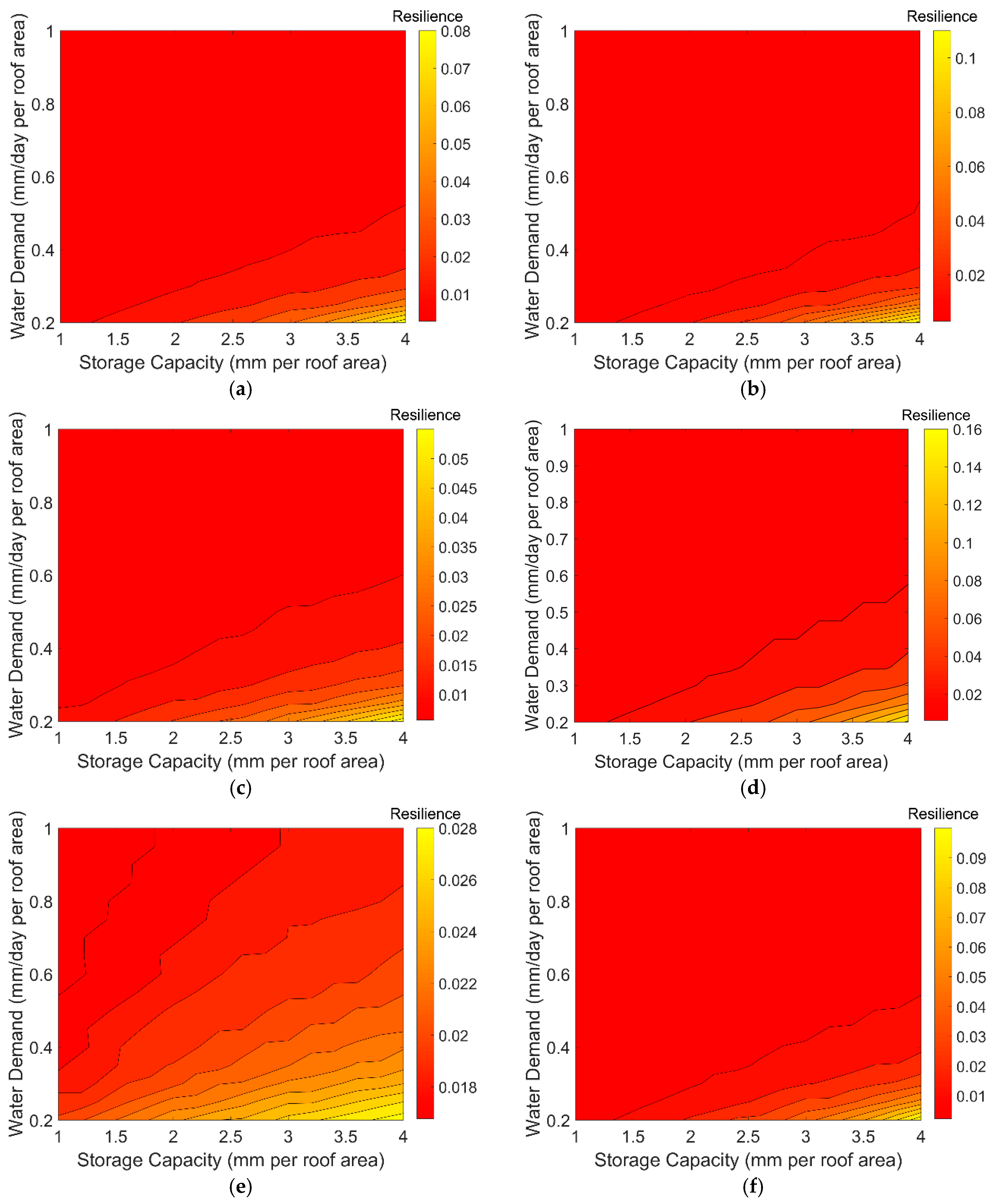
2.4.2. Evaluation of Resilience
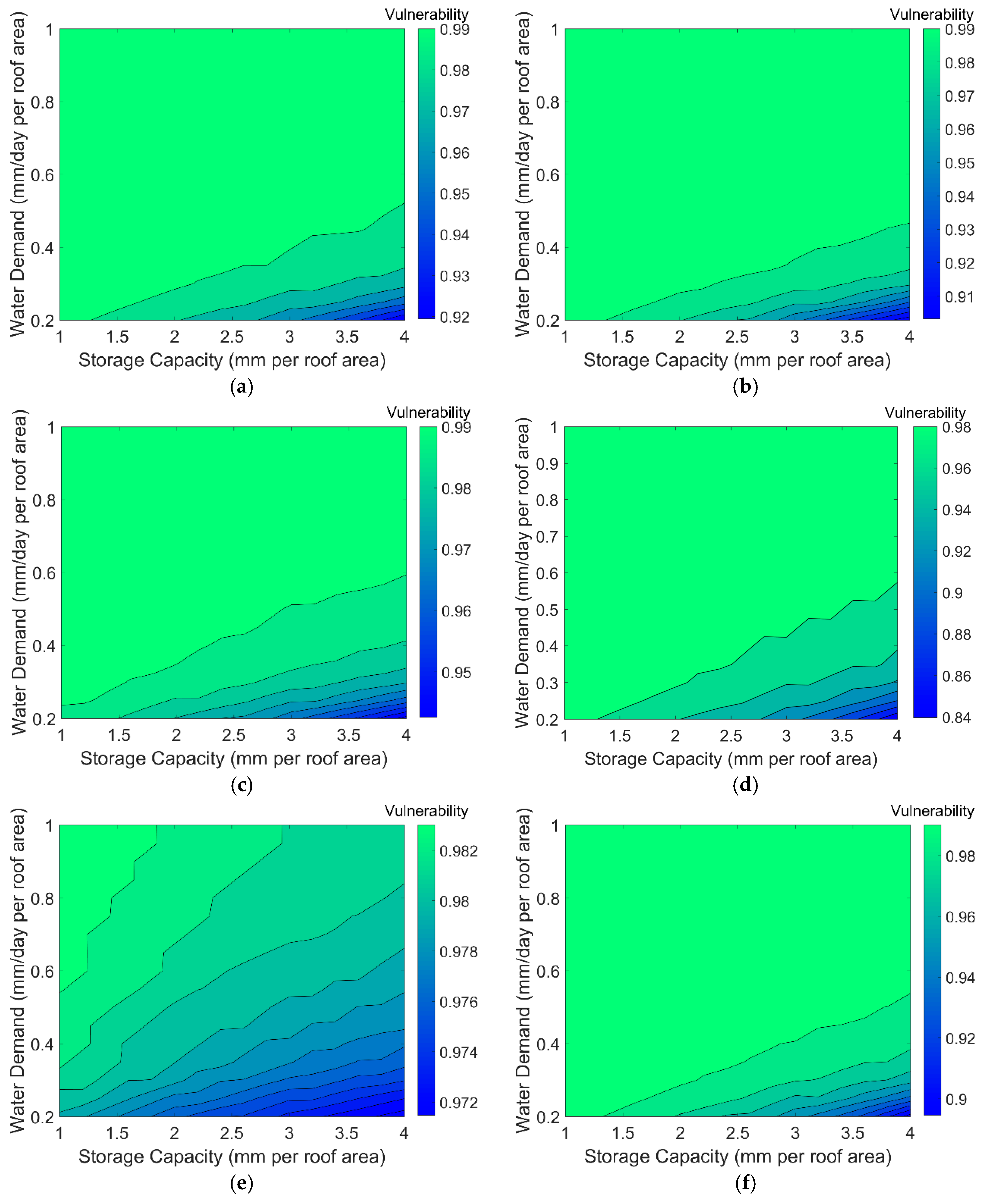
2.4.3. Evaluation of Vulnerability
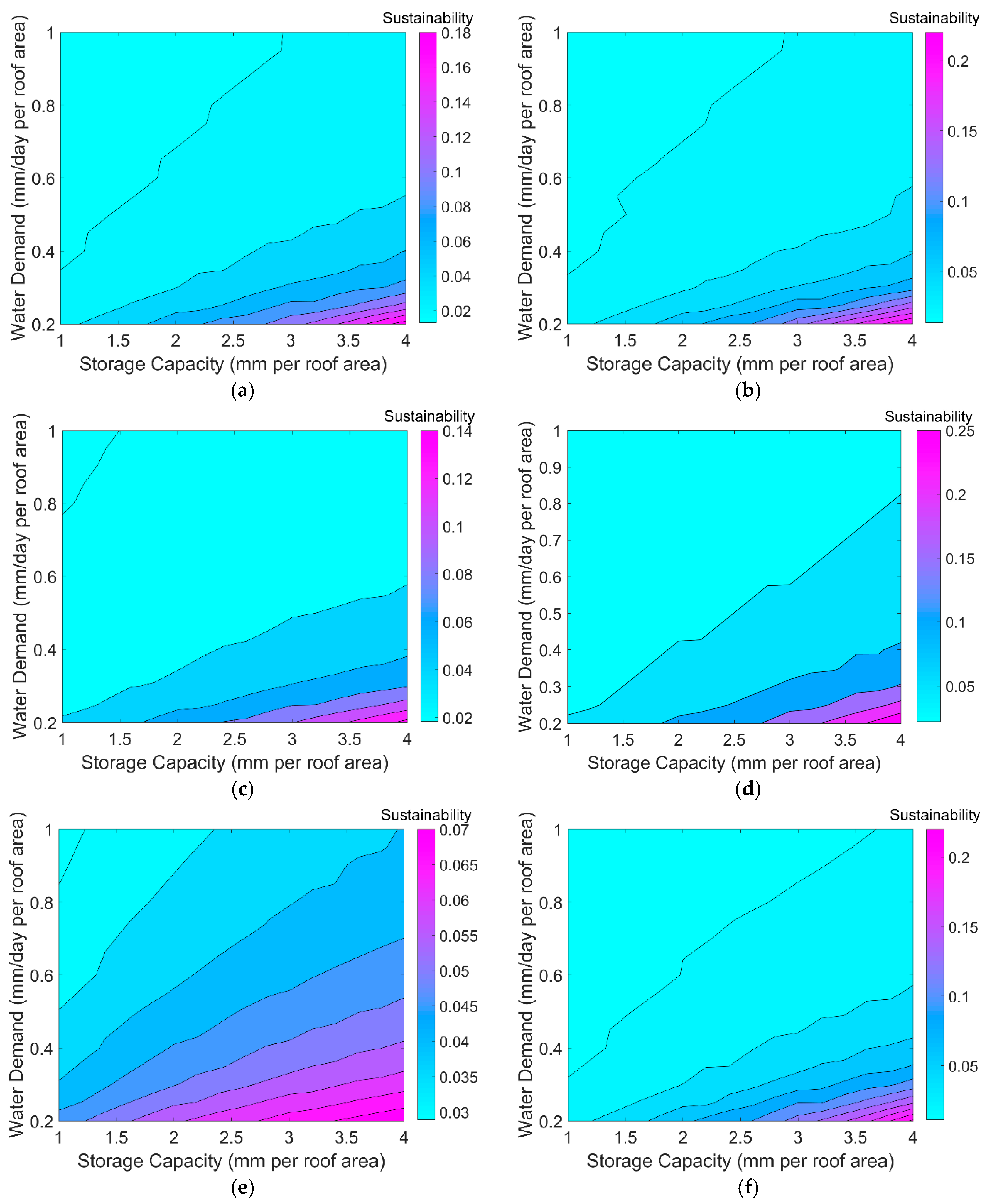
2.4.4. Evaluation of Sustainability
3. Results
3.1. Verification of Modified SS STORM Model
3.2. Evaluation of RWHS Sustainability
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Albrechtsen, H.-J. Microbiological investigations of rainwater and graywater collected for toilet flushing. Water Sci. Technol. 2002, 46, 311–316. [Google Scholar] [PubMed]
- Hilten, R.N.; Lawrence, T.M.; Tollner, E.W. Modeling stormwater runoff from green roofs with hydrus-1d. J. Hydrol. 2008, 358, 288–293. [Google Scholar] [CrossRef]
- Petrucci, G.; Deroubaix, J.-F.; De Gouvello, B.; Deutsch, J.-C.; Bompard, P.; Tassin, B. Rainwater harvesting to control stormwater runoff in suburban areas. An experimental case-study. Urban Water J. 2012, 9, 45–55. [Google Scholar] [CrossRef] [Green Version]
- Sazakli, E.; Alexopoulos, A.; Leotsinidis, M. Rainwater harvesting, quality assessment and utilization in kefalonia island, greece. Water Res. 2007, 41, 2039–2047. [Google Scholar] [CrossRef] [PubMed]
- Villarreal, E.L.; Dixon, A. Analysis of a rainwater collection system for domestic water supply in ringdansen, norrköping, sweden. Build. Environ. 2005, 40, 1174–1184. [Google Scholar] [CrossRef]
- Woltersdorf, L.; Jokisch, A.; Kluge, T. Benefits of rainwater harvesting for gardening and implications for future policy in namibia. Water Policy 2014, 16, 124–143. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, D.; Chen, L.; Ashbolt, S. Potential for rainwater use in high-rise buildings in Australian cities. J. Environ. Manag. 2009, 91, 222–226. [Google Scholar] [CrossRef] [PubMed]
- Basinger, M.; Montalto, F.; Lall, U. A rainwater harvesting system reliability model based on nonparametric stochastic rainfall generator. J. Hydrol. 2010, 392, 105–118. [Google Scholar] [CrossRef]
- Fewkes, A.; Butler, D. Simulating the performance of rainwater collection and reuse systems using behavioural models. Build. Serv. Eng. Res. Technol. 2000, 21, 99–106. [Google Scholar] [CrossRef]
- Ghisi, E.; Montibeller, A.; Schmidt, R.W. Potential for potable water savings by using rainwater: An analysis over 62 cities in southern Brazil. Build. Environ. 2006, 41, 204–210. [Google Scholar] [CrossRef]
- Guo, Y.P.; Baetz, B.W. Sizing of rainwater storage units for green building applications. J. Hydrol. Eng. 2007, 12, 197–205. [Google Scholar] [CrossRef]
- Jenkins, D.; Pearson, F. Feasibility of Rainwater Collection Systems in California. Contribution-California; California Water Resources Center, University of California: Oakland, CA, USA, 1978. [Google Scholar]
- Mitchell, V.G. How important is the selection of computational analysis method to the accuracy of rainwater tank behaviour modelling? Hydrol. Process. 2007, 21, 2850–2861. [Google Scholar] [CrossRef]
- Seo, Y.; Choi, N.J.; Park, D. Effect of connecting rain barrels on the storage size reduction. Hydrol. Process. 2012, 26, 3538–3551. [Google Scholar] [CrossRef]
- Hanson, L.; Vogel, R. Generalized storage-reliability-yield relationships for rainwater harvesting systems. Environ. Res. Lett. 2014, 9, 303–327. [Google Scholar] [CrossRef]
- Sample, D.J.; Liu, J. Optimizing rainwater harvesting systems for the dual purposes of water supply and runoff capture. J. Clean. Prod. 2014, 75, 174–194. [Google Scholar] [CrossRef]
- Hashimoto, T.; Stedinger, J.R.; Loucks, D.P. Reliability, resiliency, and vulnerability criteria for water resource system performance evaluation. Water Resour. Res. 1982, 18, 14–20. [Google Scholar] [CrossRef]
- Kjeldsen, T.R.; Rosbjerg, D. Choice of reliability, resilience and vulnerability estimators for risk assessments of water resources systems. Hydrol. Sci. J. 2004, 49, 755–767. [Google Scholar] [CrossRef]
- McMahon, T.A.; Adeloye, A.J.; Zhou, S.L. Understanding performance measures of reservoirs. J. Hydrol. 2006, 324, 359–382. [Google Scholar] [CrossRef]
- Sandoval-Solis, S.; McKinney, D.C.; Loucks, D.P. Sustainability index for water resources planning and management. J. Water Resour. Plan. Manag. 2011, 137, 381–390. [Google Scholar] [CrossRef]
- Moy, W.S.; Cohon, J.L.; ReVelle, C.S. A programming model for analysis of the reliability, resilience, and vulnerability of a water supply reservoir. Water Resour. Res. 1986, 22, 489–498. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Kindler, J. Multiple Criteria for Evaluation of Reliability Aspects of Water Resource Systems; IAHS Publication: Wallingford, UK, 1995; pp. 217–224. [Google Scholar]
- Asefa, T.; Adams, A.; Kajtezovic-Blankenship, I. A tale of integrated regional water supply planning: Meshing socio-economic, policy, governance, and sustainability desires together. J. Hydrol. 2014, 519, 2632–2641. [Google Scholar] [CrossRef]
- US EPA. Methodology for Analysis of Detention Basins for Control of Urban Runoff Quality; The Office of Water, and Nationwide Urban Runoff Program: Washington, DC, USA, 1986.
- Adams, B.; Papa, F. Urban Stormwater Management Planning with Analytical Probabilistic Models; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Lee, J.G.; Heaney, J.P.; Lai, F.H. Optimization of integrated urban wet-weather control strategies. J. Water Resour. Plan. Manag. 2005, 131, 307–315. [Google Scholar] [CrossRef]
- World Health Organization (WHO). Summary and Policy Implications Vision 2030: The Resilience of Water Supply and Sanitation in the Face of Climate Change; World Health Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Loucks, D.P. Quantifying trends in system sustainability. Hydrol. Sci. J. 1997, 42, 513–530. [Google Scholar] [CrossRef]
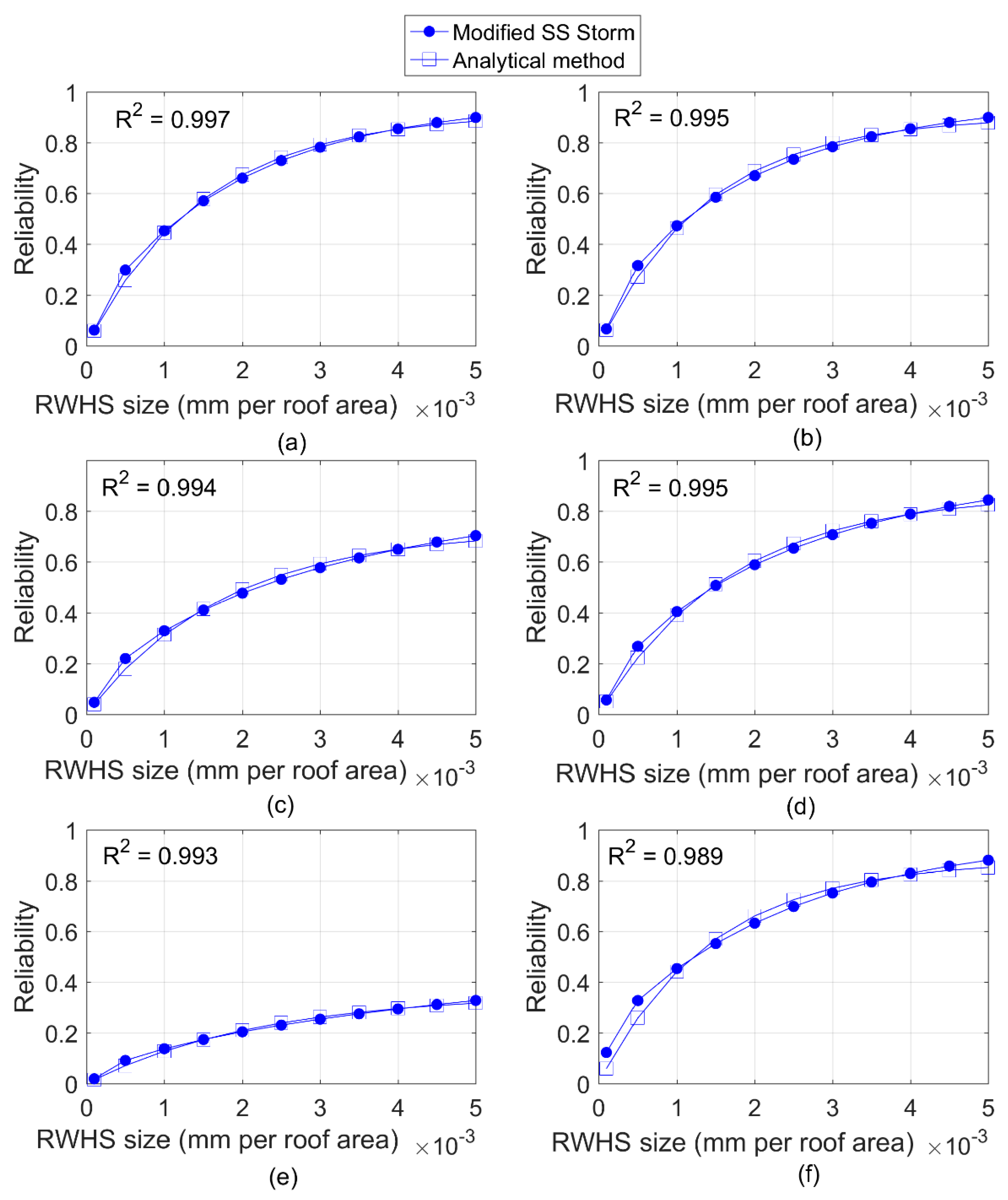
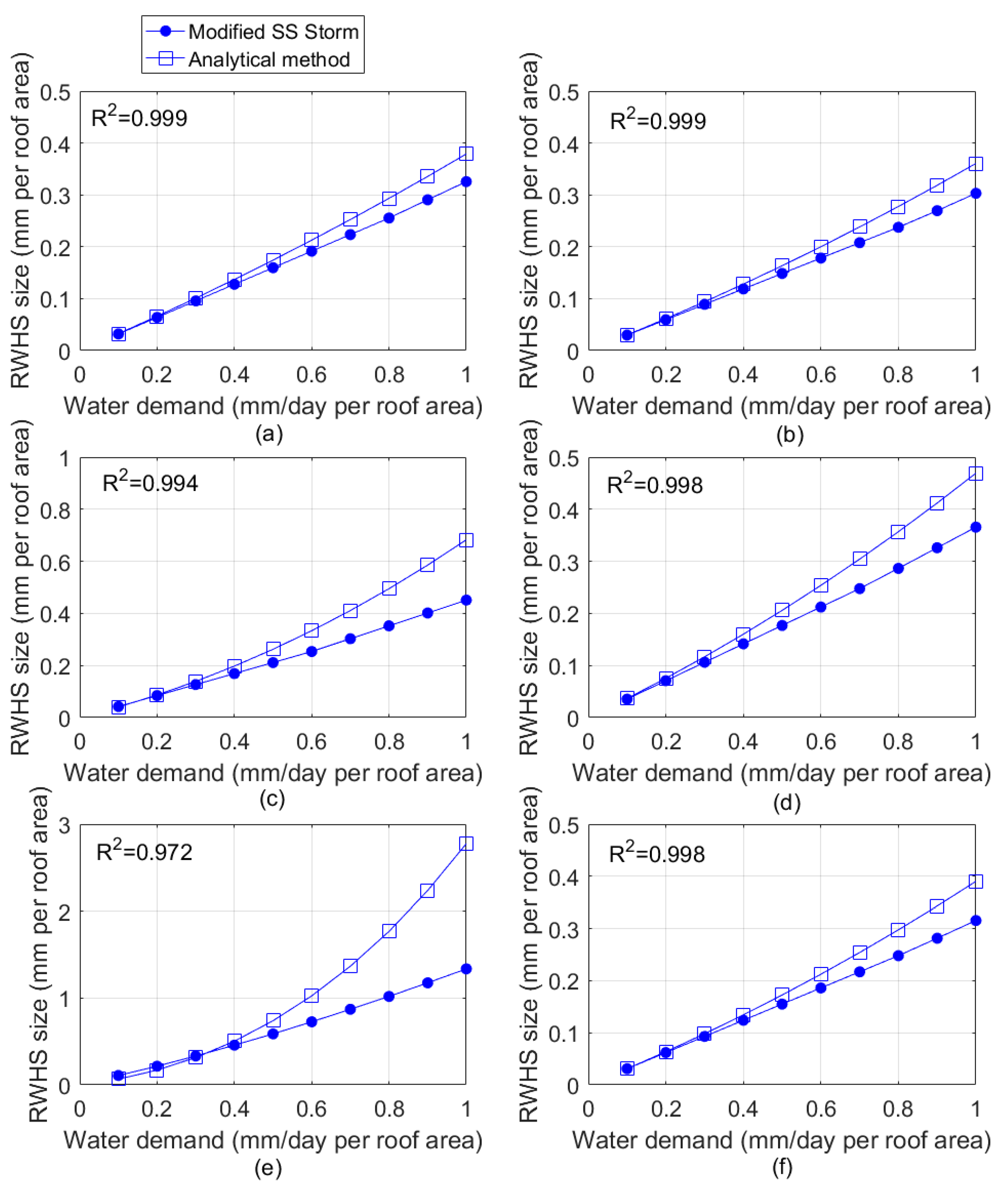
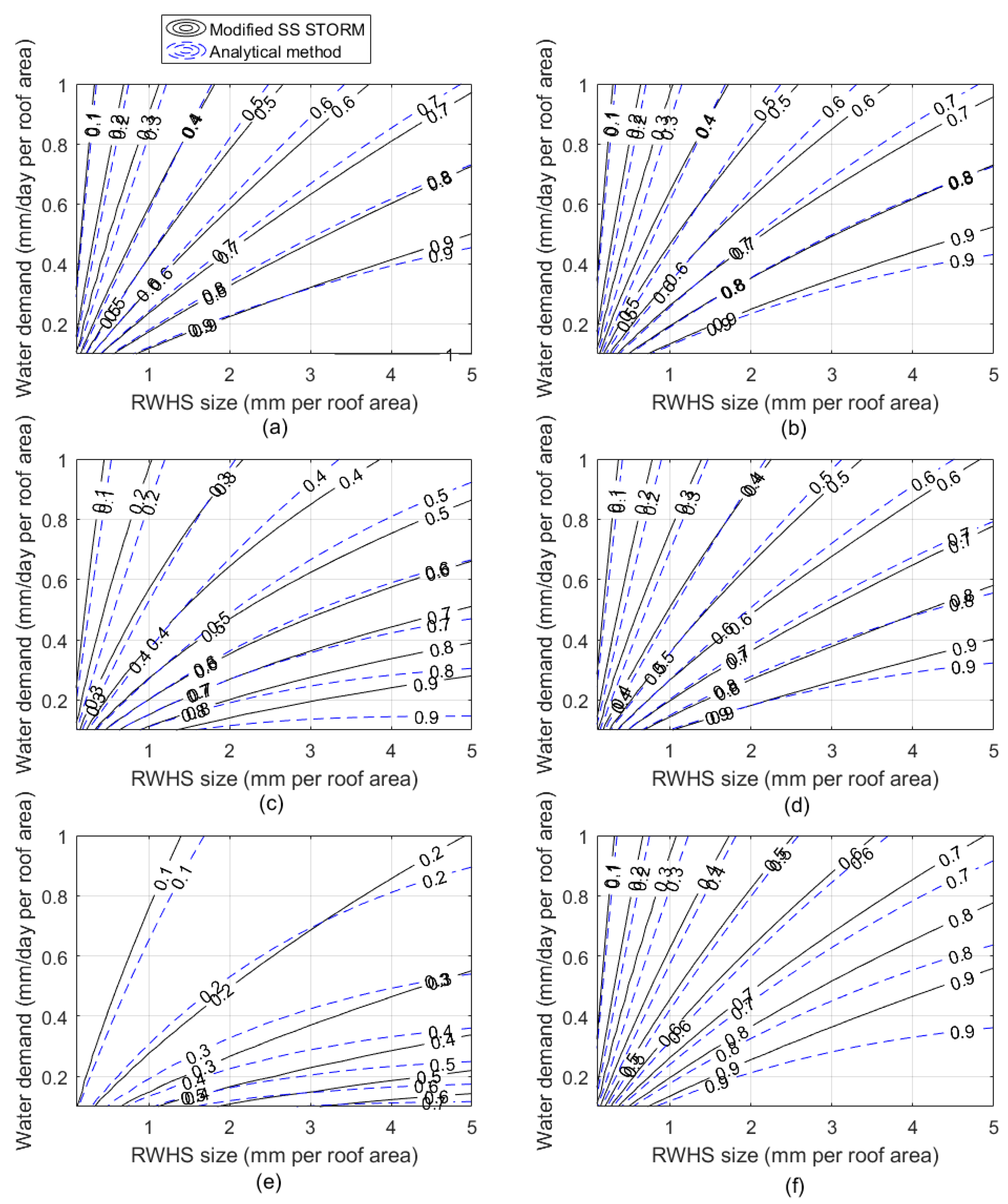
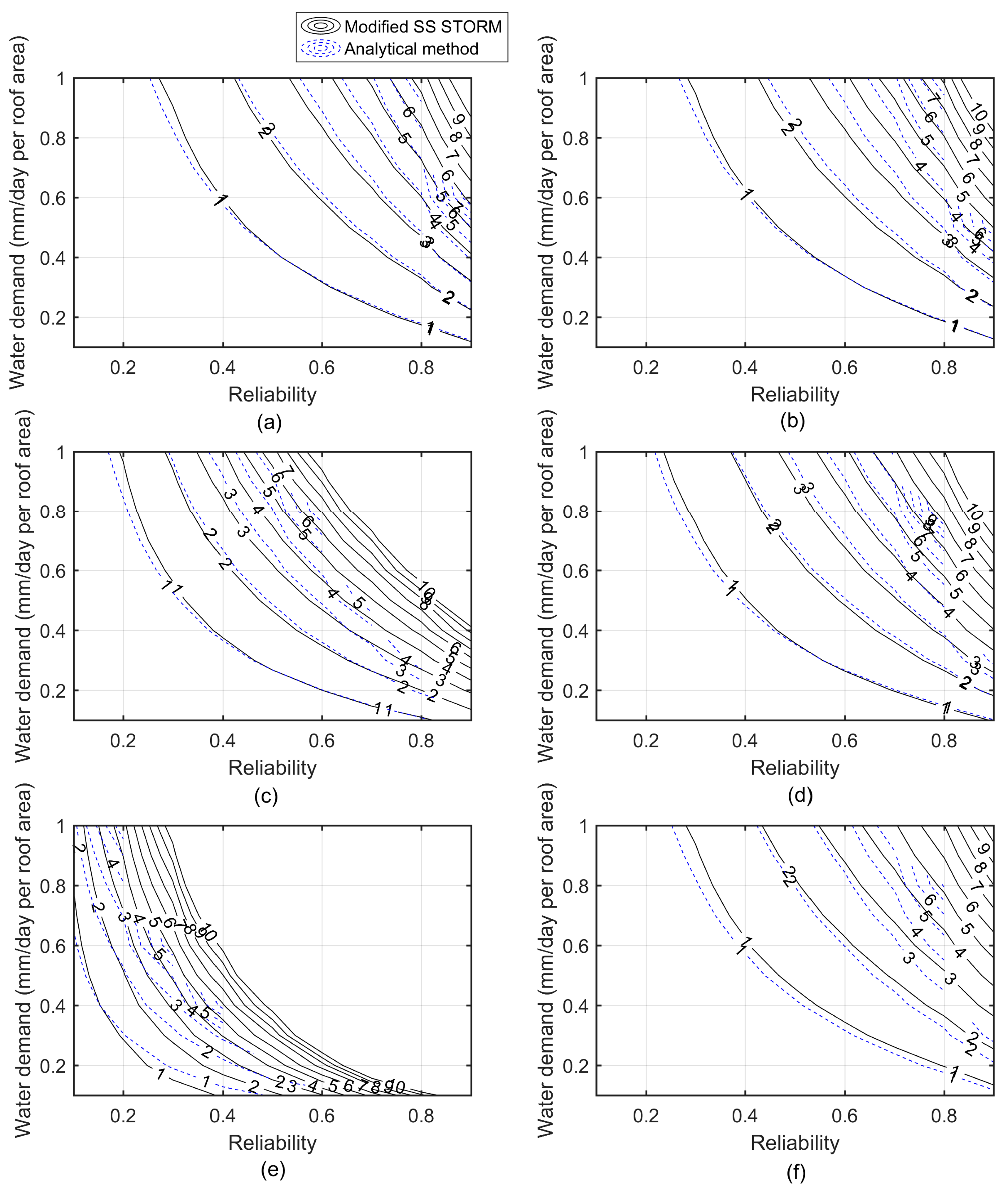
| Features | The Modified SS STORM | The Analytical Method [11] |
|---|---|---|
| Calculation Procedure | Does not need the parameter estimations | Needs to estimate , from rainfall data |
| rainfall data use | It is necessary | It is not necessary |
| Calculation limitation | Sometimes occur | Does not occur |
| Features | Atlanta | Chicago | Denver | Houston | Los Angeles | New York |
|---|---|---|---|---|---|---|
| COOP ID | 090451 | 111549 | 052220 | 414300 | 045114 | 305803 |
| Station Name | Atlanta Hartsfield International Airport | Chicago O’Hare International Airport | Denver Stapleton | Houston International Airport | Los Angeles International Airport | JFK International Airport |
| Latitude | 33.6301 | 41.995 | 39.7633 | 29.98 | 33.938 | 40.6386 |
| Longitude | −84.4418 | −87.9336 | −104.8694 | −95.36 | −118.3888 | −73.7622 |
| Period | 1 January 1971~31 December 2010 | 1 January 1971~31 December 2010 | 1 January 1971~31 December 2010 | 1 January 1971~31 December 2010 | 1 January 1971~31 December 2010 | 1 January 1971~31 December 2010 |
| (days) | 3.939 | 2.690 | 5.944 | 4.052 | 11.303 | 3.824 |
| () | 0.017 | 0.013 | 0.010 | 0.015 | 0.010 | 0.014 |
| Average annual precipitation () | 1262 | 937 | 396 | 1239 | 378 | 1087 |
| Parameters | Atlanta | Chicago | Denver | Houston | Los Angeles | New York |
|---|---|---|---|---|---|---|
| c | 0.050 | 0.028 | 0.051 | 0.044 | 0.037 | 0.049 |
| d | 0.321 | 0.194 | 0.070 | 0.199 | 0.036 | 0.172 |
| (days) | 0.013 | 0.010 | 0.009 | 0.011 | 0.003 | 0.013 |
| () | 19.4 | 15.1 | 6.8 | 13.6 | 3.7 | 12.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, D.; Um, M.-J. Sustainability Index Evaluation of the Rainwater Harvesting System in Six US Urban Cities. Sustainability 2018, 10, 280. https://doi.org/10.3390/su10010280
Park D, Um M-J. Sustainability Index Evaluation of the Rainwater Harvesting System in Six US Urban Cities. Sustainability. 2018; 10(1):280. https://doi.org/10.3390/su10010280
Chicago/Turabian StylePark, Daeryong, and Myoung-Jin Um. 2018. "Sustainability Index Evaluation of the Rainwater Harvesting System in Six US Urban Cities" Sustainability 10, no. 1: 280. https://doi.org/10.3390/su10010280
APA StylePark, D., & Um, M.-J. (2018). Sustainability Index Evaluation of the Rainwater Harvesting System in Six US Urban Cities. Sustainability, 10(1), 280. https://doi.org/10.3390/su10010280






