Determination of Initial Stiffness of Timber–Steel Composite (TSC) Beams Based on Experiment and Simulation Modeling
Abstract
:1. Introduction
2. Methodology
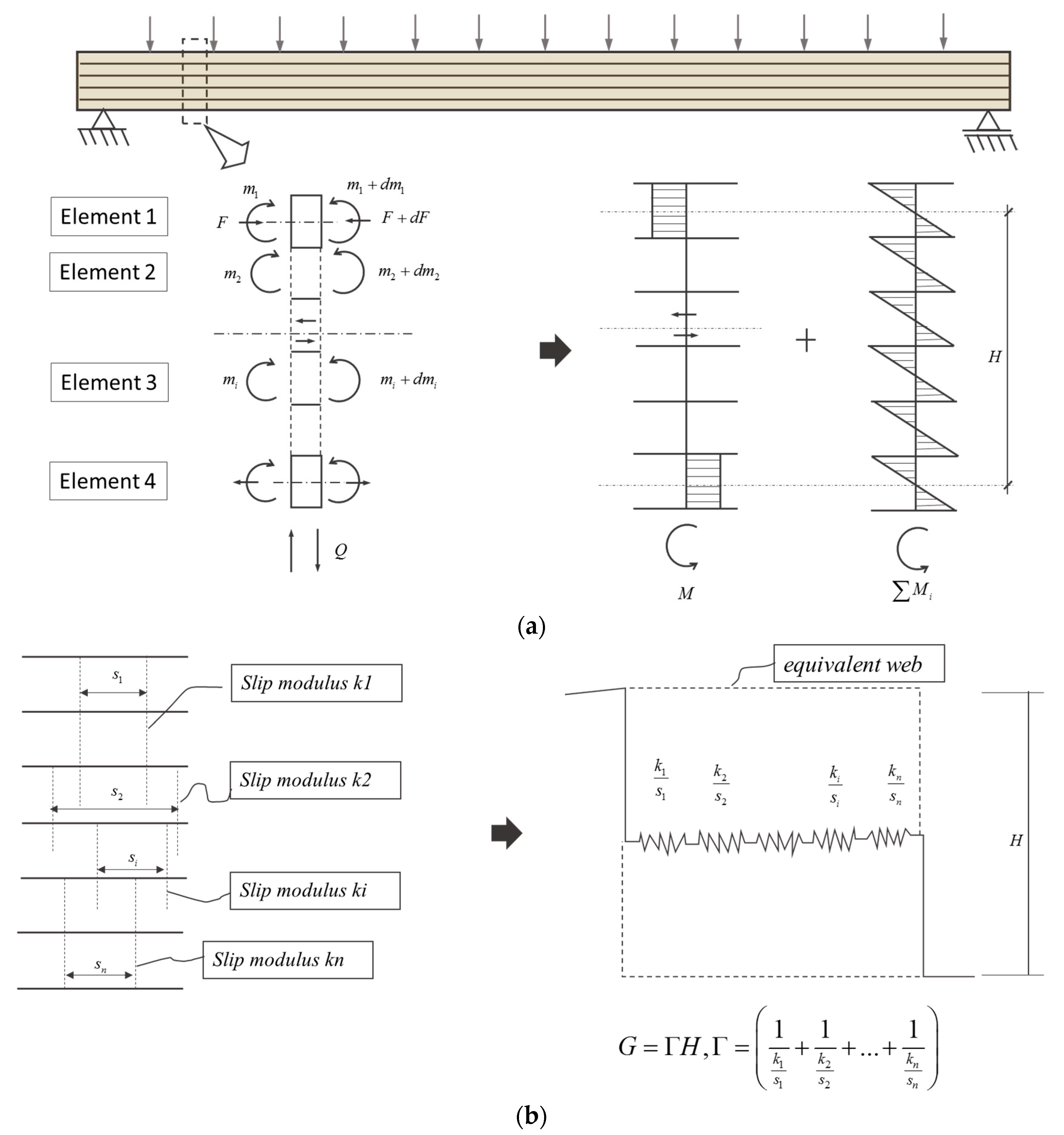
2.1. Introduction to Modeling of the Timber I-Shape Composite
- E: Young’s modulus (N/mm2).
- G: Shear modulus per unit of equivalent web (N/mm).
- Afc: Cross sectional of flange under compressive force (mm2).
- Aft: Cross sectional of flange under tensile force (mm2).
- H: Center to center height of the upper and lower flanges (mm).
- : Sum of flexural rigidity of the chord members of timber I-shaped composite (N mm2).
- Mt: Bending moment caused by external force (N mm).
- M: Bending moment when parts of components are ignored (N mm).
- mi: Bending moment at each individual component of timber I-shaped composite (N mm).
- : Joint stiffness per unit between upper and lower flanges (N/mm2).
- si: Spacing of fasteners (mm).
- ki: Slip modulus of individual fastener (N/mm).
- : Deflection at the middle of beam (mm).
- L: Span (mm).
- Ccl: Increase rate of rigidity subject to continuous load.
2.2. The Proposed Modeling of TSC Beam
- Es: Young’s modulus of steel (N/mm2);
- As: Cross sectional of steel (mm2);
- Aw: Cross-sectional of wood (mm2);
- Is: Moment of inertia of steel (mm4);
- Iw: Moment of inertia of wood (mm4).
- Es: Young’s modulus of steel (N/mm2).
- G: Shear stiffness per unit of web (N/mm).
- Asfc: Cross section of steel flange under compressive force (mm2).
- Awft: Cross section of wooden flange under tensile force (mm2).
- H: Center to center height of the upper and lower flanges (mm).
- : Sum of flexural rigidity of the chord members (Nmm2).
- Is and Iw: Moment of inertia of steel and wood, respectively.
- Kser: Slip modulus (N/mm);
- ρm: Mean density of wood (kg/m3);
- d or dc: diameter of fastener (mm).
3. Materials and Experiment
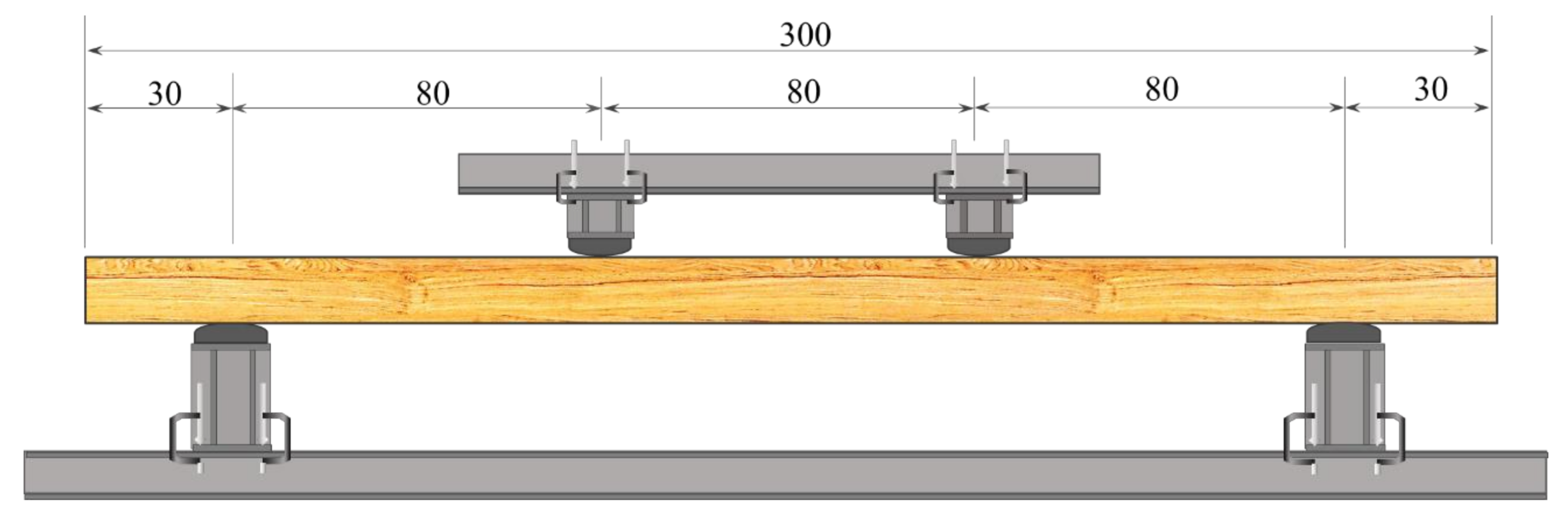
3.1. Materials
3.2. Experiment
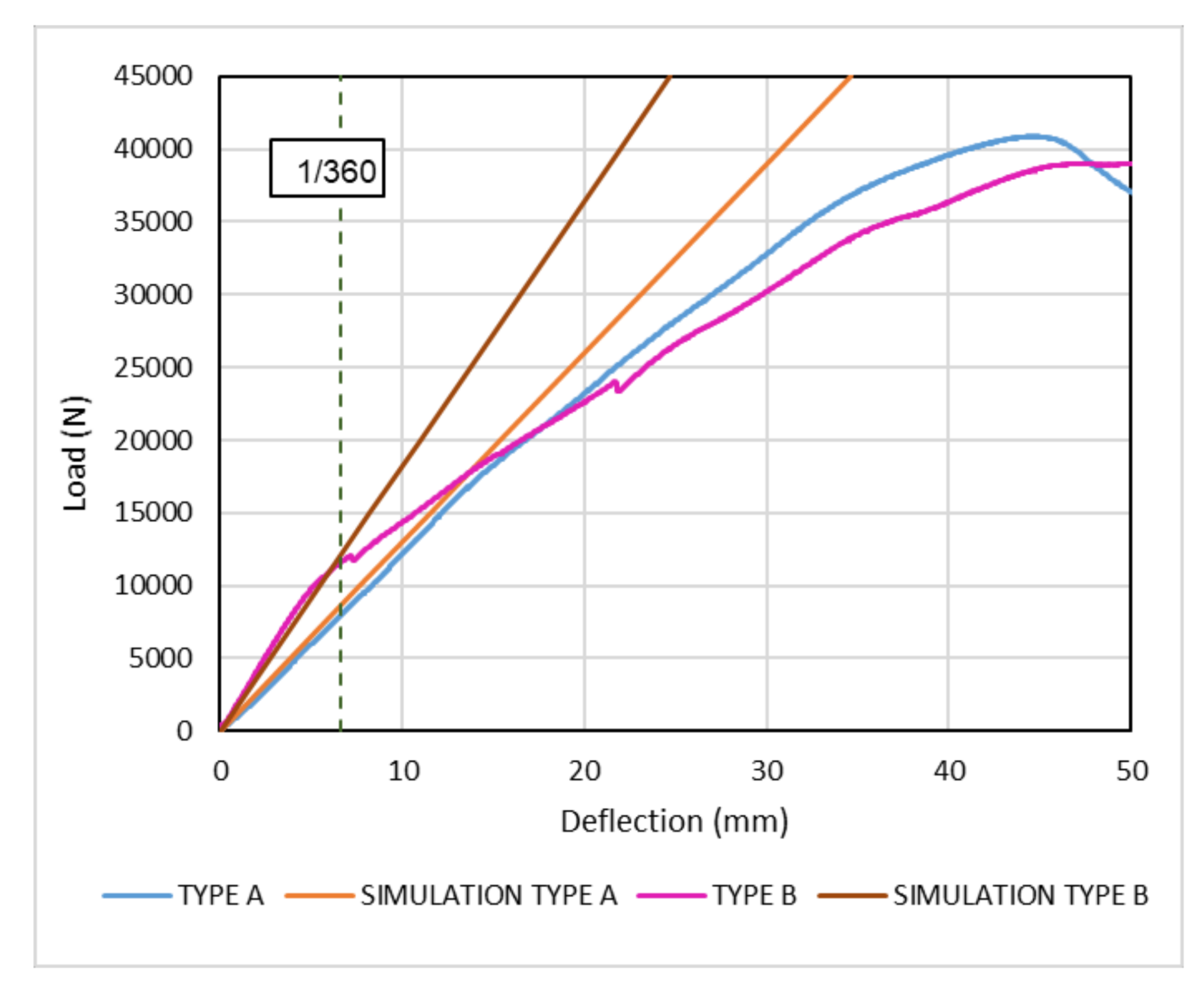
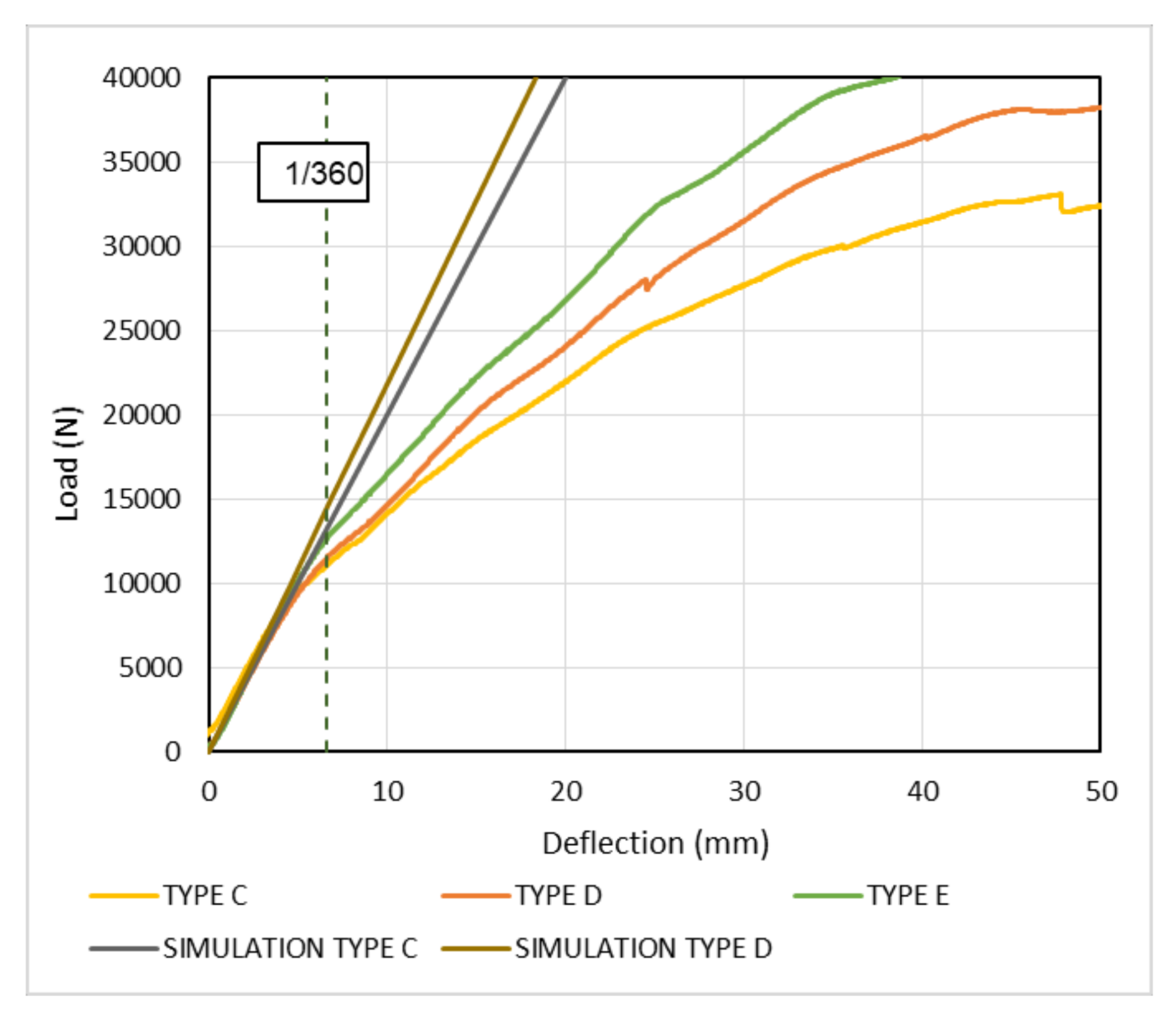
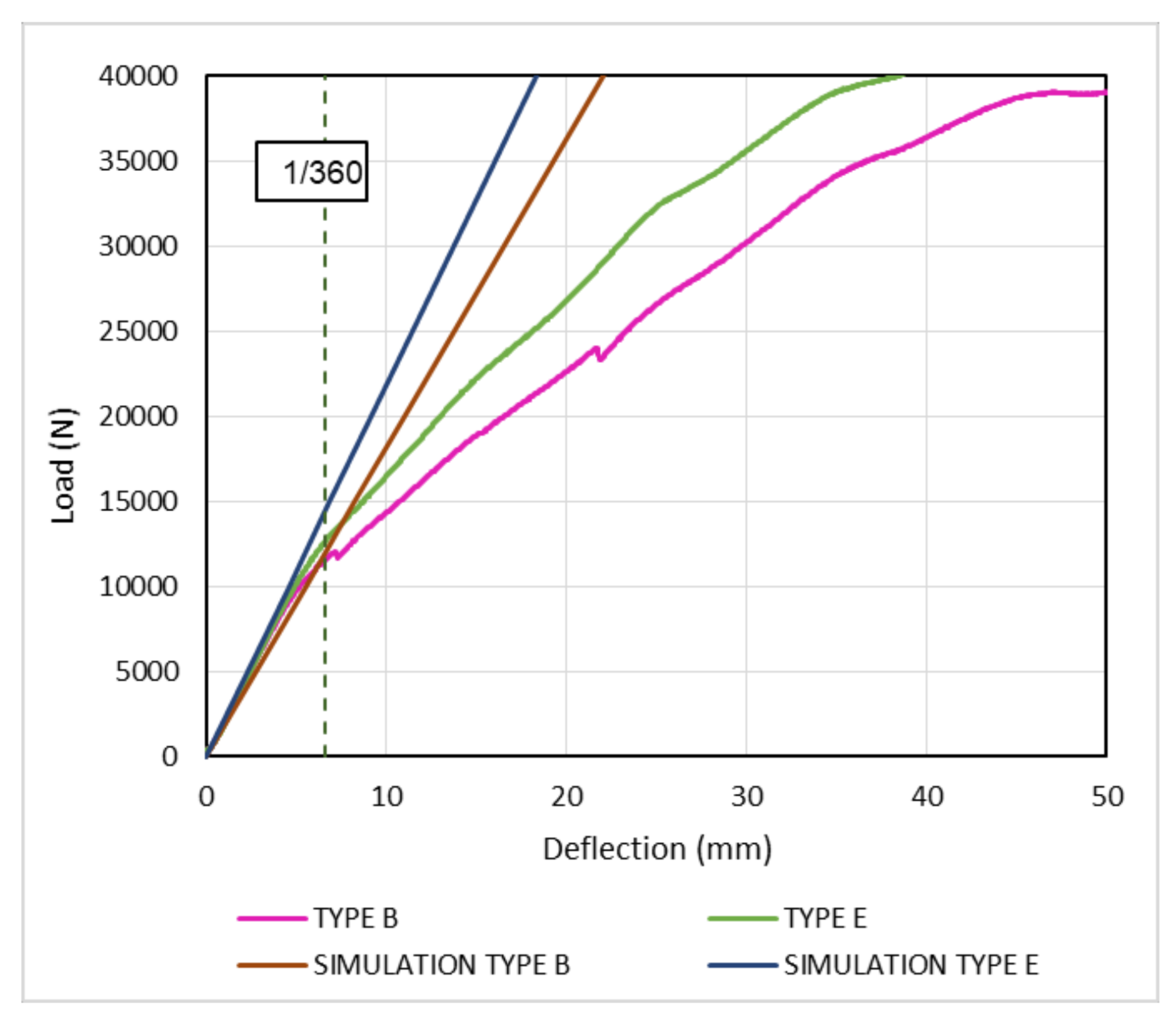
4. Results
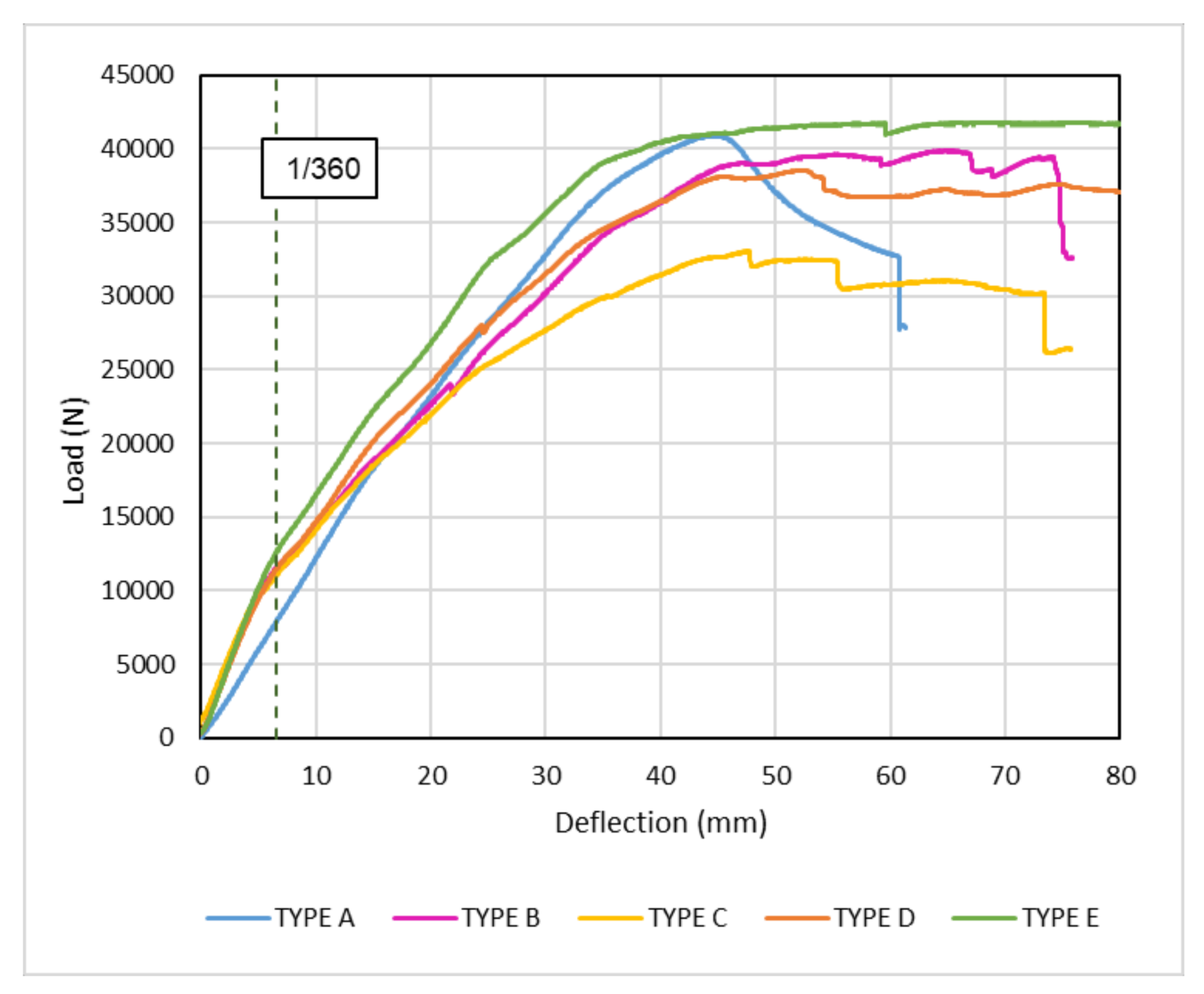
4.1. Experimental Results
4.2. Failure Mechanism
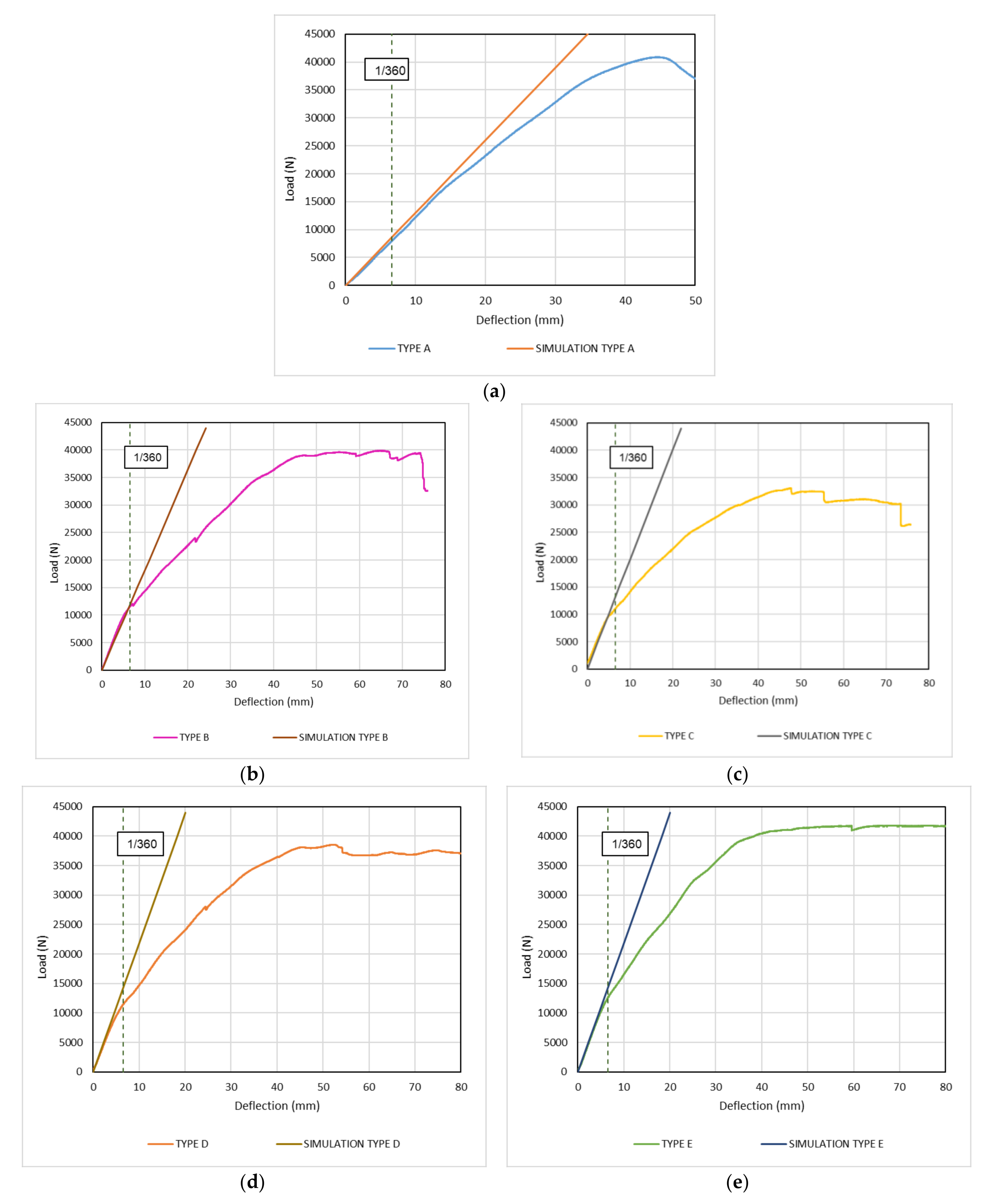
4.3. Comparison of Experimental and Simulation Results
5. Discussion
5.1. Shape Factor of Steel Members
5.2. Influence of Dowel Connection and Fasteners
5.3. Future Applications and Improvements
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nagamura, H.; Kirino, Y.; Koshihara, M. A study of five storied timber based hybrid building for practical use (Part 1 Summary of M-Building). In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Architectural Institute of Japan: Tokyo, Japan, 2005. [Google Scholar]
- Kirino, Y.; Nagamura, H.; Koshihara, M. A study of five storied timber based hybrid building for practical use (Part 2 Summary of Structure). In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Architectural Institute of Japan: Tokyo, Japan, 2005. [Google Scholar]
- Koshihara, M.; Nagamura, H.; Isoda, H.; Kirino, Y. A study of five storied timber based hybrid building for practical use (Part 3 Properties of structural elements). In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Architectural Institute of Japan: Tokyo, Japan, 2005. [Google Scholar]
- Jerzy, J.; Tomasz, P.N. Solid timber beams strengthened with steel plates—Experimental studies. Constr. Build. Mater. 2014, 63, 81–88. [Google Scholar]
- Franke, S.; Franke, B.; Harte, M.A. Failure modes and reinforcement techniques for timber beams—State of the art. Constr. Build. Mater. 2015, 97, 2–13. [Google Scholar] [CrossRef]
- Winter, W.; Tavoussi, K.; Pixner, T.; Parada, F.R. Timber-steel-hybrid beams for multi-storey buildings. In Proceedings of the World Conference on Timber Engineering, Auckland, New Zealand, 15–19 July 2012; pp. 41–48. [Google Scholar]
- Tsai, M.T. Field Investigation of Retrofitting and Adaptive Reuse of Historic Wooden Buildings in Taiwan. J. Asian Archit. Build. Eng. 2017, 16, 387–394. [Google Scholar] [CrossRef]
- Construction and Planning Agency. Design and Construction Specifications of Wood Construction for Buildings; Construction and Planning Agency: Taipei, Taiwan, 2011. [Google Scholar]
- Girhammar, U.A. A simplified analysis method for composite beams with interlayer slip. Int. J. Mech. Sci. 2009, 51, 515–530. [Google Scholar] [CrossRef]
- Hassanieh, A.; Valipour, H.R.; Bradford, M.A. Experimental and analytical behavior of steel-timber composite connections. Constr. Build. Mater. 2016, 118, 63–75. [Google Scholar] [CrossRef]
- Jumaat, M.Z.; Murty, B. Yield load prediction of nailed timber joints using nail diameter and timber specific gravity. Wood Sci. Technol. 2004, 38, 599–615. [Google Scholar] [CrossRef]
- Sawata, K.; Yasumura, M. Estimation of yield and ultimate strengths of bolted timber joints by nonlinear analysis and yield theory. J. Wood Sci. 2003, 49, 383–391. [Google Scholar] [CrossRef]
- Foschi, R.O. Load-Slip Characteristics of Nails. Wood Sci. 1974, 17, 69–77. [Google Scholar]
- Foschi, R.O.; Bonac, T. Load-Slip Characteristics for Connections with Common Nails. Wood Sci. 1977, 9, 118–123. [Google Scholar]
- Kawasaki, M.; Nanami, N.; Yasumura, M. Estimating single shear capacity of screwed timber joints by yield theory. J. Struct. Constr. Eng. AIJ 2008, 73, 1797–1804. [Google Scholar] [CrossRef]
- Sweedan, A.M.I.; Rojob, H.N.; El-Sawy, K.M. Mechanically-fastened hybrid composites for flexural strengthening of steel beams. Thin-Walled Struct. 2014, 85, 250–261. [Google Scholar] [CrossRef]
- Hassanieh, A. Modelling of steel-timber composite connections: Validation of finite element model and parametric study. Eng. Struct. 2017, 138, 35–49. [Google Scholar] [CrossRef]
- Kreuzinger, H. Mechanically jointed beams and columns. Timber Engineering Step 1; Centrum Hout: Westeinde, The Netherlands, 1995; Volume B11, pp. 1–8. [Google Scholar]
- Ceccotti, A. Timber-concrete composite structures. Timber Engineering Step 2; Centrum Hout: Westeinde, The Netherlands, 1995; Volume E13, pp. 1–12. [Google Scholar]
- Fernandez-Cabo, J.L.; Fernandez-Lavandera, J.; Diez-Barra, R.; Avila-Jalvo, J.M. Timber composite beams with a discrete connection system. Proc. Inst. Civ. Eng. 2013, 166, 57–72. [Google Scholar] [CrossRef]
- Bajzecerová, V. Bending Stiffness of CLT-Concrete Composite Members—Comparison of Simplified Calculation Methods. Procedia Eng. 2017, 190, 15–20. [Google Scholar] [CrossRef]
- Kobayashi, K.; Inayama, M.; Ando, N. New estimation method on stiffness and strength of single shear screw joints with structural panels. J. Struct. Constr. Eng. AIJ 2007, 622, 121–128. [Google Scholar] [CrossRef]
- Fukuyama, H. Proposal of analytical models of wooden dowel shear joint single shear joint with slender-type round dowels. J. Struct. Constr. Eng. AIJ 2007, 622, 129–136. [Google Scholar] [CrossRef]
- Fukuyama, H. Calculation model and yield process of single shear joint with wood dowel of various slendernesses. J. Struct. Constr. Eng. AIJ 2008, 73, 803–810. [Google Scholar] [CrossRef]
- Noguchi, M.; Komatsu, K. A new method for estimating stiffness and strength in bolted timber-to-timber joints and its verification by experiments (II): Bolted cross-lapped beam to column joints. J. Wood Sci. 2004, 50, 391–399. [Google Scholar] [CrossRef]
- Kamachi, K.; Inayama, M.; Inoue, M. Design method for the built-up beams. J. Struct. Constr. Eng. AIJ 2009, 74, 601–700. [Google Scholar] [CrossRef]
- Japan Architecture Society. Design Manual of Engineering Timber Joints; Japan Architecture Society: Tokyo, Japan, 2009. [Google Scholar]
- European Committee for Standardization. Eurocode 5: Design of Timber Structure; BSI: Brussels, Belgium, 1994. [Google Scholar]
- Yang, J.C.; Lee, C.H.; Chiu, C.M. Genetic Variation of Wood Density in Luanta Fir Tested In Central Taiwan. Wood Fiber Sci. 2001, 33, 486–491. [Google Scholar]
- Ragheb, W.F. Local buckling of welded steel I-beams considering flange–web interaction. Thin-Walled Struct. 2015, 97, 241–249. [Google Scholar] [CrossRef]
- Alpe, A. Determination of Screw and Nail Withdrawal Resistance of Some Important Wood Species. Int. J. Mol. Sci. 2008, 9, 626–637. [Google Scholar]
- Bues, C.T.; Schulz, H.; Eichenseer, F. Investigation of the Pull-out Resistance of Nails and Screws in Pine Wood. Holz Roh Werkst. 1987, 45, 514. [Google Scholar]




 | 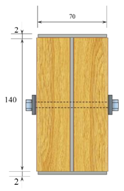 |  | 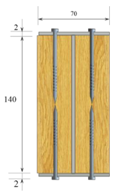 |  |
|---|---|---|---|---|
| TYPE A | TYPE B | TYPE C | TYPE D | TYPE E |
| Steel plate with dowel connection | I-shaped steel with dowel connection | I-shaped steel with nails fastened | I-shaped steel with screws fastened | I-shaped steel with dowel connection and screws fastened |
| Types of Coefficients | Type A | Type B | Type C | Type D | Type E |
|---|---|---|---|---|---|
| Slip modulus Kser (N/mm) | - | - | 1.57 | 3.1 | 3.1 |
| Joint stiffness (N/mm2) | - | - | 5.2 | 10.3 | 10.3 |
| Shear modulus G (N/rad) | - | - | 738 | 1642 | 1642 |
| (Nmm2) | 32.4 × 1010 | 52.5 × 1010 | 52.5 × 1010 | 52.5 × 1010 | 52.5 × 1010 |
| Parameter coefficient K | - | 0.80 | 0.80 | 0.80 | 0.80 |
| Parameter coefficient λ (mm−1) | - | 0.12 × 10−3 | 0.5 × 10−3 | 0.71 × 10−3 | 1.0 × 10−3 |
| Increased rate Ccl | - | 1 | 1.1 | 1.2 | 1.2 |
| Initial Stiffness (N/mm) | 1317 | 1882 | 2005 | 2187 | 2187 |
| Type of Specimens | Initial Stiffness (N/mm) | Strength at Deflection 1/360 of the Span (N) | Ratio of Difference (Ls-Le)/Le | |
|---|---|---|---|---|
| Simulation Value Ls | Experimental Value Le | |||
| Type A | 1317 | 8779 | 8070 | 0.09 |
| Type B | 1882 | 12,545 | 12,072 | 0.04 |
| Type C | 2005 | 13,365 | 10,203 | 0.24 |
| Type D | 2187 | 14,578 | 11,602 | 0.26 |
| Type E | 2187 | 14,578 | 13,442 | 0.10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, M.-T.; Le, T.D.H. Determination of Initial Stiffness of Timber–Steel Composite (TSC) Beams Based on Experiment and Simulation Modeling. Sustainability 2018, 10, 1220. https://doi.org/10.3390/su10041220
Tsai M-T, Le TDH. Determination of Initial Stiffness of Timber–Steel Composite (TSC) Beams Based on Experiment and Simulation Modeling. Sustainability. 2018; 10(4):1220. https://doi.org/10.3390/su10041220
Chicago/Turabian StyleTsai, Meng-Ting, and Truong Di Ha Le. 2018. "Determination of Initial Stiffness of Timber–Steel Composite (TSC) Beams Based on Experiment and Simulation Modeling" Sustainability 10, no. 4: 1220. https://doi.org/10.3390/su10041220
APA StyleTsai, M.-T., & Le, T. D. H. (2018). Determination of Initial Stiffness of Timber–Steel Composite (TSC) Beams Based on Experiment and Simulation Modeling. Sustainability, 10(4), 1220. https://doi.org/10.3390/su10041220




