An Improved Two-Step Floating Catchment Area Method for Evaluating Spatial Accessibility to Urban Emergency Shelters
Abstract
1. Introduction
2. An Improved 2SFCA Method Evaluating Shelter Accessibility
2.1. Optimizing the Assumptions in the Method
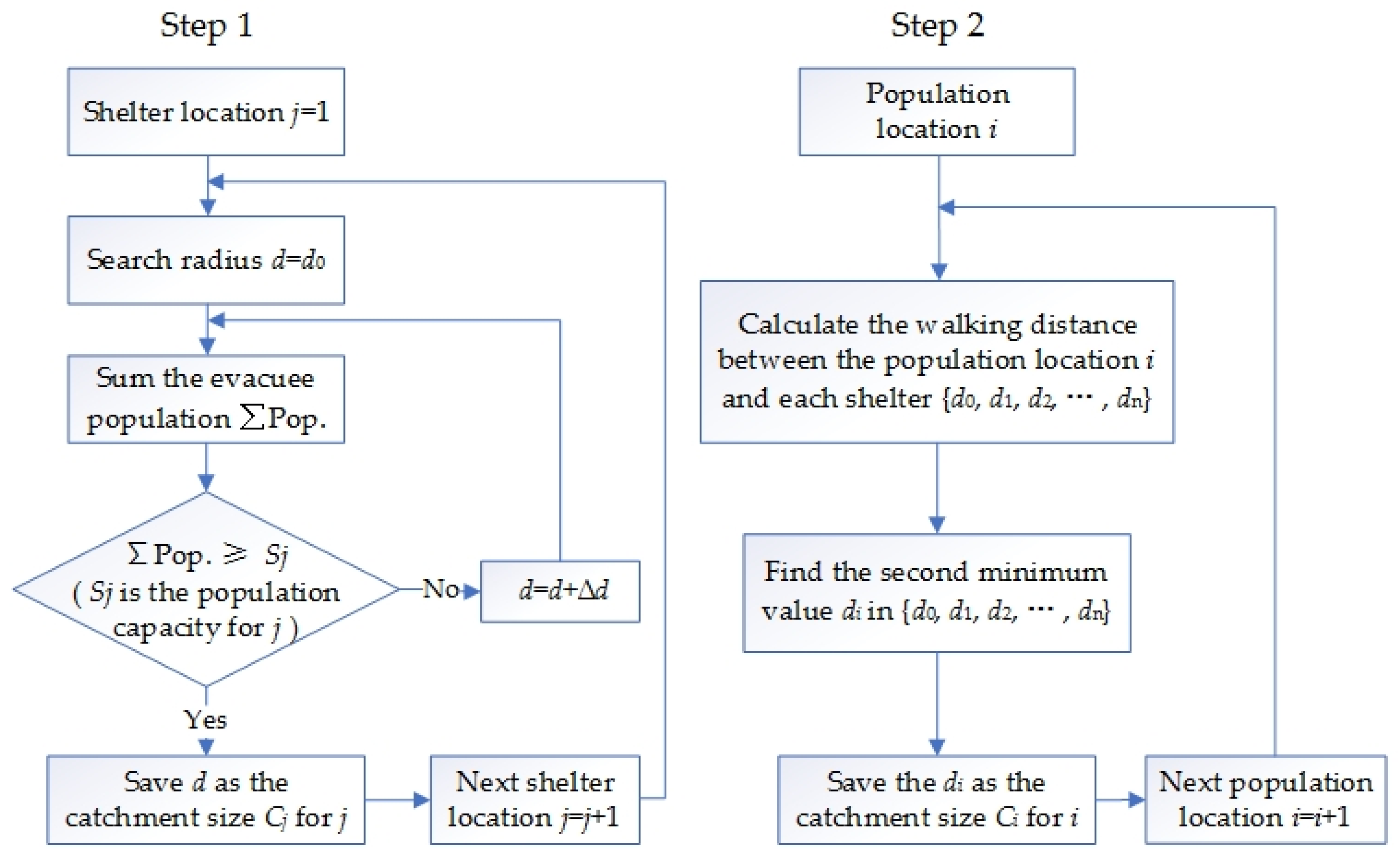
2.2. Optimization of the Proposed Method
2.3. Parameters Settings and Calculations
3. Case Study
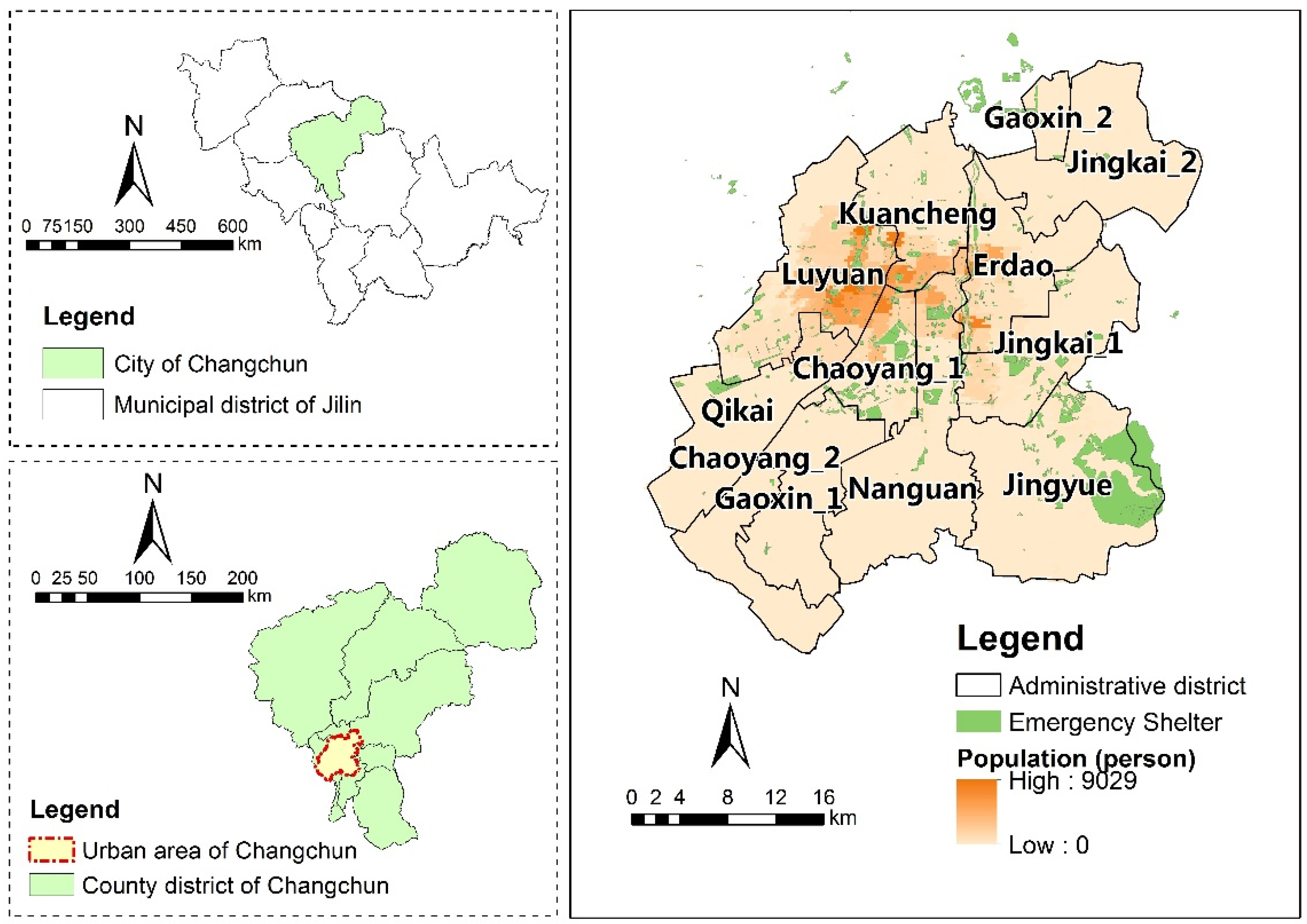
3.1. Study Area
3.2. Study Datasets
4. Results
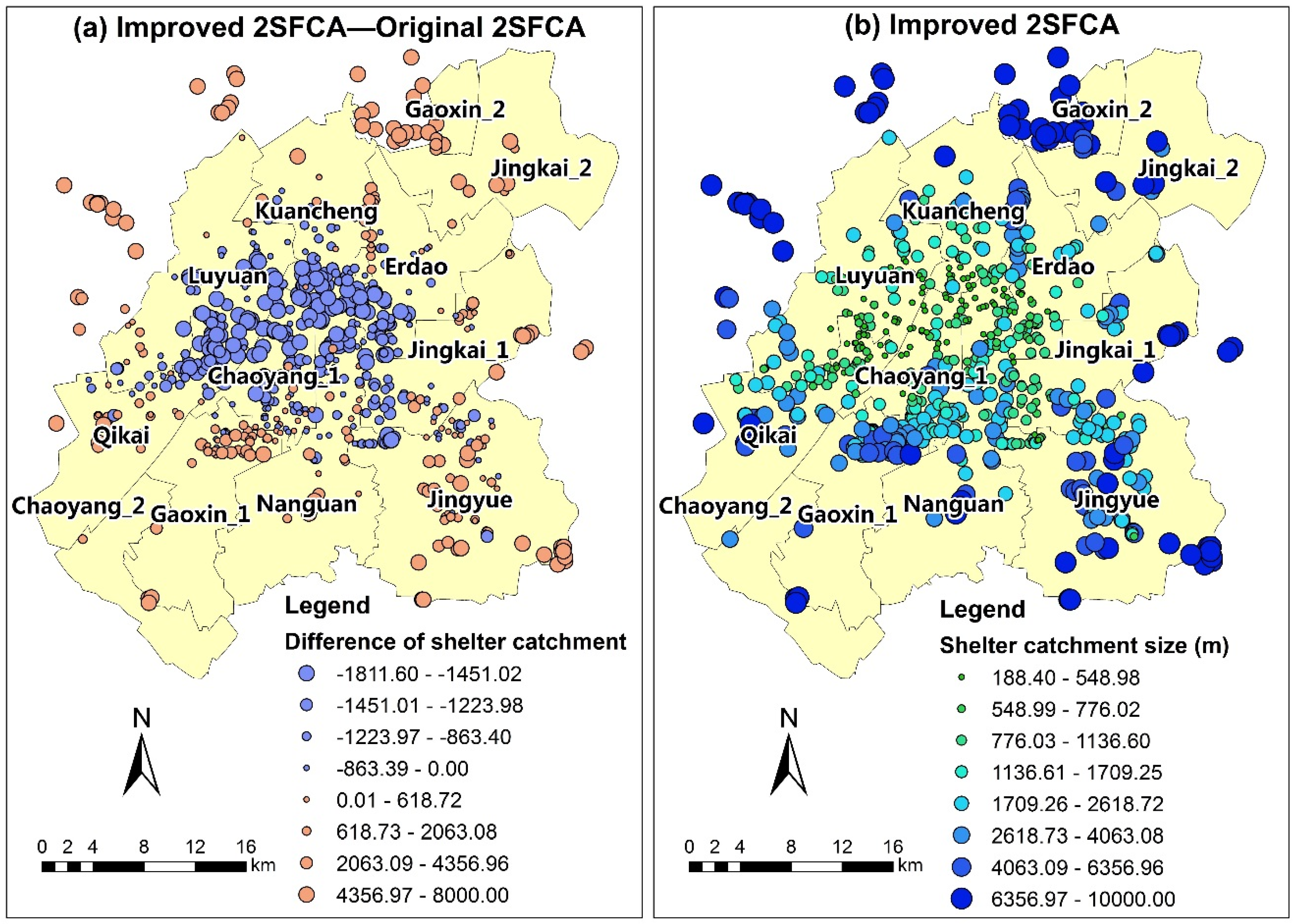
4.1. Results of Catchment Sizes
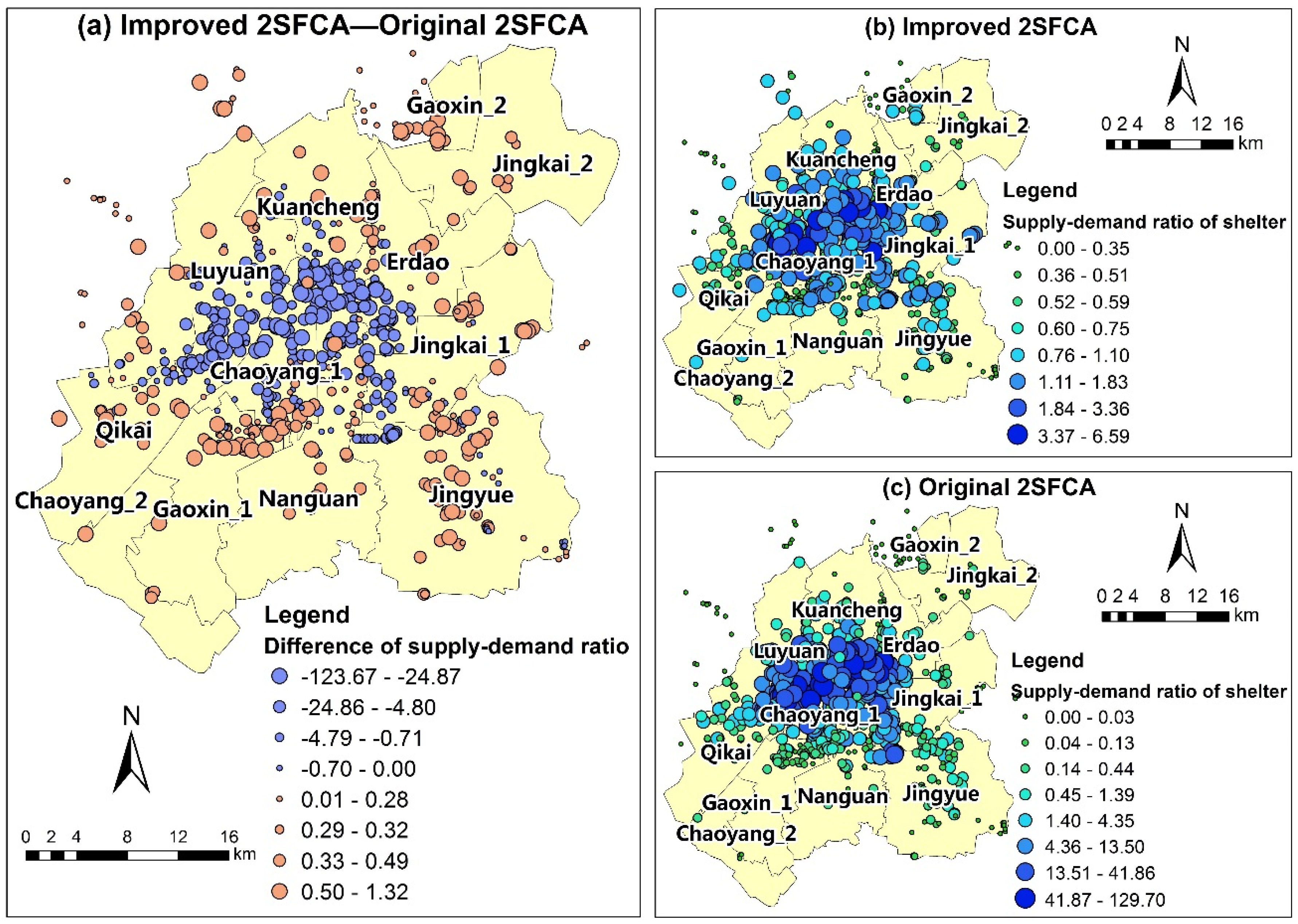
4.2. Results of Shelter Supply-Demand Ratios
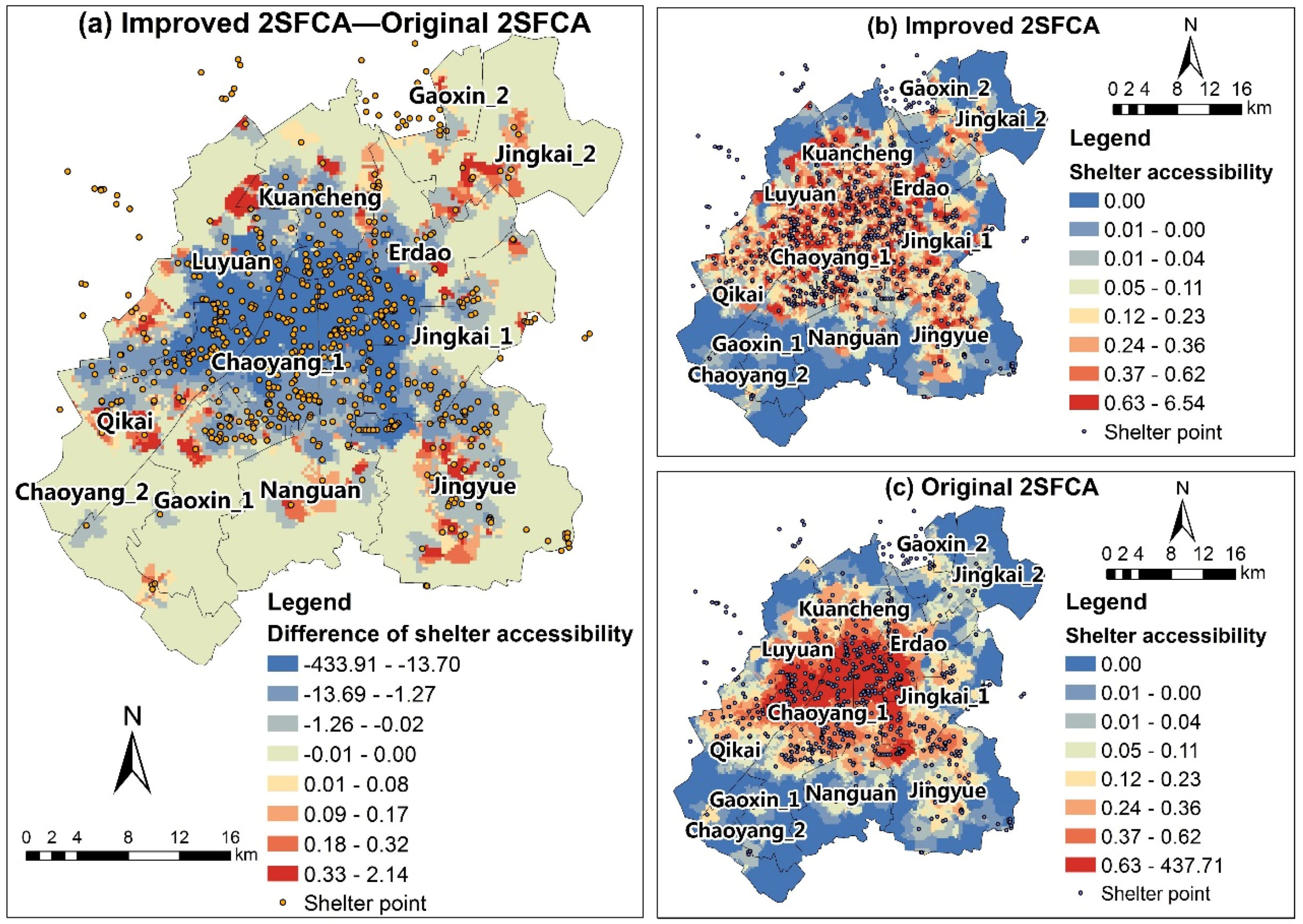
4.3. Results of Shelter Accessibility
5. Discussion
5.1. Strengths of the Improved 2SFCA Method
5.2. Possibilities for Prospective Research
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Park, S.J.; Kim, D.W.; Kim, J.H.; Chung, J.H.; Lee, J.S. Future disaster scenario using big data: A case study of extreme cold wave. Int. J. Des. Nat. Ecodyn. 2016, 11, 362–369. [Google Scholar] [CrossRef]
- Waugh, W.L. Shelter from the storm: Repairing the national emergency management system after hurricane Katrina. Ann. Am. Acad. Political Soc. Sci. 2006, 604, 288–332. [Google Scholar] [CrossRef]
- Nath, R.; Shannon, H.; Kabali, C.; Oremus, M. Investigating the key indicators for evaluating post-disaster shelter. Disasters 2016, 41, 606. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Li, H.; Sun, Y.; Huang, R.; Hu, Q.; Wang, J.; Gao, F. Planning emergency shelters for urban disaster resilience: An integrated location-allocation modeling approach. Sustainability 2017, 9, 2098. [Google Scholar] [CrossRef]
- Quarantelli, E.L. Patterns of sheltering and housing in US disasters. Disaster Prev. Manag. Int. J. 1995, 4, 43–53. [Google Scholar] [CrossRef]
- Soltani, A.; Ardalan, A.; Darvishi Boloorani, A.; Haghdoost, A.; Hosseinzadeh-Attar, M.J. Site selection criteria for sheltering after earthquakes: A systematic review. PLoS Curr. 2014, 6. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Design of Disasters Mitigation Emergency Congregate Shelter; Architecture & Building Press: Beijing, China, 2015. (In Chinese)
- Yang, N.; Chen, S.; Hu, W.; Wu, Z.; Yi, C. Spatial Distribution Balance Analysis of Hospitals in Wuhan. Int. J. Environ. Res. Public Health 2016, 13, 971. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Wang, Z.; Li, Z.; Tang, Z. An assessment of urban park access in Shanghai: Implications for the social equity in urban China. Landsc. Urban Plan. 2017, 157, 383–393. [Google Scholar] [CrossRef]
- Zhang, M. Exploring the relationship between urban form and nonwork travel through time use analysis. Landsc. Urban Plan. 2005, 73, 244–261. [Google Scholar] [CrossRef]
- Gregory, D.; Johnston, R.; Pratt, G.; Watts, M.J.; Whatmore, S. The Dcitionary of Human Geography, 5th ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2009; p. 152. ISBN 9781405132886. [Google Scholar]
- Unal, M.; Uslu, C. GIS-Based Accessibility Analysis of Urban Emergency Shelters: The Case of Adana City. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 95–101. [Google Scholar] [CrossRef]
- Rigolon, A. A complex landscape of inequity in access to urban parks: A literature review. Landsc. Urban Plan. 2016, 153, 160–169. [Google Scholar] [CrossRef]
- Wang, F.H. Measurement, optimization, and impact of health care accessibility: A methodological review. Ann. Assoc. Am. Geogr. 2012, 102, 1104–1112. [Google Scholar] [CrossRef] [PubMed]
- Kwan, M.P. Space-time and integral measures of individual accessibility: A comparative analysis using a point-based framework. Geogr. Anal. 1998, 30, 191–216. [Google Scholar] [CrossRef]
- Talen, E. Neighborhoods as service providers: A methodology for evaluating pedestrian access. Environ. Plan. B Plan. Des. 2003, 30, 181–200. [Google Scholar] [CrossRef]
- Tao, Z.; Cheng, Y. Research Progress of the Two-Step Floating Catchment Area Method and Extensions. Prog. Geogr. 2016, 35, 589–599. (In Chinese) [Google Scholar] [CrossRef]
- Nicholls, S. Measuring the accessibility and equity of public parks: A case study using GIS. Manag. Leis. 2001, 6, 201–219. [Google Scholar] [CrossRef]
- Vaughan, K.B.; Kaczynski, A.T.; Wilhelm, S.S.A.; Besenyi, G.M.; Bergstrom, R.; Heinrich, K.M. Exploring the distribution of park availability, features, and quality across Kansas city, Missouri by income and race/ethnicity: An environmental justice investigation. Ann. Behav. Med. 2013, 45 (Suppl. 1), S28–S38. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Xiu, C.; Cheng, L.; Wang, N. Evaluation on spatial structure and rationality of city parks based on goal of disaster prevention: An application of proximal area method in Changchun, China. Chin. J. Appl. Ecol. 2016, 27, 3641–3648. (In Chinese) [Google Scholar] [CrossRef]
- Smoyer-Tomic, K.E.; Hewko, J.N.; Hodgson, M.J. Spatial accessibility and equity of playgrounds in edmonton, canada. Can. Geogr. 2010, 48, 287–302. [Google Scholar] [CrossRef]
- Yu, K.; Duan, T.; Li, D.; Peng, J. Landscape accessibility as a measurement of the function of urban green system. Plan. Stud. 1999, 23, 8–11. (In Chinese) [Google Scholar]
- Gu, Z.; Xu, W.; Yuan, Y.; Zhou, H.; Ge, Y. Evaluation of Disaster Shelter Planning in Rural Areas: A Case Study of Xiaoyudong Town in Sichuan Province. J. Catastrophol. 2011, 26, 115–119. (In Chinese) [Google Scholar] [CrossRef]
- Miyake, K.K.; Maroko, A.R.; Grady, K.L.; Maantay, J.A.; Arno, P.S. Not Just a Walk in the Park: Methodological Improvements for Determining Environmental Justice Implications of Park Access in New York City for the Promotion of Physical Activity. Cities Environ. 2010, 3, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Wang, F. Measures of spatial accessibility to health care in a GIS environment: Synthesis and a case study in the Chicago region. Environ. Plan. B Urban Anal. City Sci. 2003, 30, 865–884. [Google Scholar] [CrossRef]
- Suárez-Vega, R.; Santos-Peñate, D.R.; Dorta-González, P.; Rodríguez-Díaz, M. A multi-criteria GIS based procedure to solve a network competitive location problem. Appl. Geogr. 2011, 31, 282–291. [Google Scholar] [CrossRef]
- McGrail, M.R.; Humphreys, J.S. Measuring spatial accessibility to primary care in rural areas: Improving the effectiveness of the two-step floating catchment area method. Appl. Geogr. 2009, 29, 533–541. [Google Scholar] [CrossRef]
- Dony, C.C.; Delmelle, E.M.; Delmelle, E.C. Re-conceptualizing accessibility to parks in multi-modal cities: A variable-width floating catchment area (VFCA) method. Landsc. Urban Plan. 2015, 143, 90–99. [Google Scholar] [CrossRef]
- Kocatepe, A.; Ulak, M.B.; Ozguven, E.E.; Horner, M.W.; Arghandeh, R. Socioeconomic characteristics and crash injury exposure: A case study in Florida using two-step floating catchment area method. Appl. Geogr. 2017, 87, 207–221. [Google Scholar] [CrossRef]
- Tao, Z.; Cheng, Y.; Dai, T.; Rosenberg, M.W. Spatial optimization of residential care facility locations in Beijing, china: Maximum equity in accessibility. Int. J. Health Geogr. 2014, 13, 33. [Google Scholar] [CrossRef] [PubMed]
- Dai, D. Racial/ethnic and socioeconomic disparities in urban green space accessibility: Where to intervene? Landsc. Urban Plan. 2011, 102, 234–244. [Google Scholar] [CrossRef]
- Wan, N.; Zou, B.; Sternberg, T. A three-step floating catchment area method for analyzing spatial access to health services. Int. J. Geogr. Inf. Sci. 2012, 26, 1073–1089. [Google Scholar] [CrossRef]
- Luo, J. Integrating the Huff Model and Floating Catchment Area Methods to Analyze Spatial Access to Healthcare Services. Trans. GIS 2014, 18, 436–448. [Google Scholar] [CrossRef]
- Fransen, K.; Neutens, T.; De Maeyer, P.; Deruyter, G. A commuter-based two-step floating catchment area method for measuring spatial accessibility of daycare centers. Health Place 2015, 32, 65–73. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Whippo, T. Variable catchment sizes for the two-step floating catchment area (2SFCA) method. Health Place 2012, 18, 789–795. [Google Scholar] [CrossRef] [PubMed]
- Jamtsho, S.; Corner, R.; Dewan, A. Spatio-Temporal Analysis of Spatial Accessibility to Primary Health Care in Bhutan. ISPRS Int. J. Geo-Inf. 2015, 4, 1584–1604. [Google Scholar] [CrossRef]
- Zhou, A.; Zhang, J.; Zhang, Y.; Fu, X. Study on the Emergency Shelter Accessibility and Distribution in Beijing Based on the GIS. Bull. Surv. Mapp. 2016, 1, 111–114. (In Chinese) [Google Scholar] [CrossRef]
- Tang, B.; Wang, D.; Song, Y.; Qiu, J.; Yan, Y.; Zhang, Z. Research on the emergency shelter accessibility in urban communities. J. Risk Anal. Crisis Response 2017, 7, 230. [Google Scholar] [CrossRef]
- Li, M.; Yang, L.; Wei, Y. Improved Gaussian Based 2-Step Floating Catchment Area Method: A Case Study of Green Space Accessibility in Shanghai. Prog. Geogr. 2016, 35, 990–996. (In Chinese) [Google Scholar] [CrossRef]
- Wu, H.; Liu, L.; Yu, Y.; Peng, Z. Evaluation and Planning of Urban Green Space Distribution Based on Mobile Phone Data and Two-Step Floating Catchment Area Method. Sustainability 2018, 10, 214. [Google Scholar] [CrossRef]
- Zhou, A.; Zhang, J.; Fu, X. Research on the Spatial Distribution of the Urban-Emergency Shelter in Beijing Downtown Areas. J. Saf. Environ. 2014, 14, 151–156. (In Chinese) [Google Scholar] [CrossRef]
- Luo, W.; Qi, Y. An enhanced two-step floating catchment area (E2SFCA) method for measuring spatial accessibility to primary care physicians. Health Place 2009, 15, 1100–1107. [Google Scholar] [CrossRef] [PubMed]
- McGrail, M.R.; Humphreys, J.S. Measuring spatial accessibility to primary health care services: Utilising dynamic catchment sizes. Appl. Geogr. 2014, 54, 182–188. [Google Scholar] [CrossRef]
- Ni, J.; Wang, J.; Rui, Y.; Qian, T.; Wang, J. An Enhanced Variable Two-Step Floating Catchment Area Method for Measuring Spatial Accessibility to Residential Care Facilities in Nanjing. Int. J. Environ. Res. Public Health 2015, 12, 14490–14504. [Google Scholar] [CrossRef] [PubMed]
- Zhou, A.; Zhang, J.; Du, S.; He, D.; Fu, X. Spatial Accessibility of Emergency Shelters in Beijing Based on Improved Two-Step Floating Catchment Area Method. Sci. Surv. Mapp. 2017, 42, 88–92. (In Chinese) [Google Scholar] [CrossRef]
- McGrail, M.R. Spatial accessibility of primary health care utilising the two step floating catchment area method: An assessment of recent improvements. Int. J. Health Geogr. 2012, 25, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Li, Q. Modeling road network vulnerability for evacuees and first responders in no-notice evacuation. J. Adv. Transp. 2017, 2017, 1–12. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standard for Urban Planning on Earthquake Resistance and Hazardous Prevention; Architecture & Building Press: Beijing, China, 2015. (In Chinese)
- Chen, Z.; Chen, X.; Li, Q.; Chen, J. The temporal hierarchy of shelters: A hierarchical location model for earthquake-shelter planning. Int. J. Geogr. Inf. Sci. 2013, 27, 1612–1630. [Google Scholar] [CrossRef]
- European Commission, Joint Research Centre (JRC). Columbia University, Center for International Earth Science Information Network—CIESIN (2015): GHS Population Grid, Derived from GPW4, Multitemporal (1975, 1990, 2000, 2015); European Commission, Joint Research Centre (JRC): Brussels, Belgium, 2015. [Google Scholar]
- The Planning Outline of Earthquake and Emergency Shelter (Outdoor) in Beijing. Available online: http://www.bjghw.gov.cn/web/static/articles/catalog_30000/article_ff80808122dedb360122eeb648c50046/ff80808122dedb360122eeb648c50046.html (accessed on 20 December 2017). (In Chinese)
- Allan, D.P. Catchments of general practice in different countries—A literature review. Int. J. Health Geogr. 2014, 13, 32. [Google Scholar] [CrossRef] [PubMed]


| Accessibility Measurement | Definition |
|---|---|
| Container | The number of facilities within a given spatial unit (e.g., census tract, political district, or municipal boundary) [18]. |
| Coverage | The number of facilities within a certain distance from a demand point (it is sometimes described as the cumulative opportunity method) [19,20]. |
| Minimum distance | The distance between a demand point and the nearest facility [21]. |
| Travel cost | The average distance (cost) between a demand point and all related facilities [22,23]. |
| Gravity Model | An index computed by sum of facilities (weighted by their size or other properties) and adjusted by the effect of distance decay [16,25]. |
| Level of Emergency Shelter | Effective Shelter Area 1 (hm2) | Per-Capita Effective Shelter Area (m2/person) |
|---|---|---|
| Emergency Evacuation and Embarkation Shelter | <0.2 | 0.5 |
| Resident Emergency Congregate Shelter (short-term) | 0.2~1.0 | 2.0 |
| Resident Emergency Congregate Shelter (mid-term) | 1.0~5.0 | 3.0 |
| Resident Emergency Congregate Shelter (long-term) | 5.0~20.0 | 4.5 |
| Central Emergency Congregate Shelter | ≥20.0 | ≥5.0 |
| Method | Minimum | Maximum | Average | Standard Deviation | Variable Coefficient |
|---|---|---|---|---|---|
| Improved 2SFCA | 0 | 6.545 | 0.195 | 0.361 | 185.128% |
| Original 2SFCA | 0 | 437.713 | 14.282 | 15.197 | 106.407% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Tong, Z.; Liu, X.; Li, X.; Lin, P.; Wang, T. An Improved Two-Step Floating Catchment Area Method for Evaluating Spatial Accessibility to Urban Emergency Shelters. Sustainability 2018, 10, 2180. https://doi.org/10.3390/su10072180
Zhu X, Tong Z, Liu X, Li X, Lin P, Wang T. An Improved Two-Step Floating Catchment Area Method for Evaluating Spatial Accessibility to Urban Emergency Shelters. Sustainability. 2018; 10(7):2180. https://doi.org/10.3390/su10072180
Chicago/Turabian StyleZhu, Xiaomeng, Zhijun Tong, Xingpeng Liu, Xiangqian Li, Pengda Lin, and Tong Wang. 2018. "An Improved Two-Step Floating Catchment Area Method for Evaluating Spatial Accessibility to Urban Emergency Shelters" Sustainability 10, no. 7: 2180. https://doi.org/10.3390/su10072180
APA StyleZhu, X., Tong, Z., Liu, X., Li, X., Lin, P., & Wang, T. (2018). An Improved Two-Step Floating Catchment Area Method for Evaluating Spatial Accessibility to Urban Emergency Shelters. Sustainability, 10(7), 2180. https://doi.org/10.3390/su10072180






