Characteristics of Pressure Stimulated Current and Damage Evolution of Granite under Progressive Uniaxial Loading
Abstract
:1. Introduction
2. Material and Method
2.1. Specimen Preparation
2.2. System and Equipment
2.3. Experimental Procedures and Schemes
3. Results and Analysis
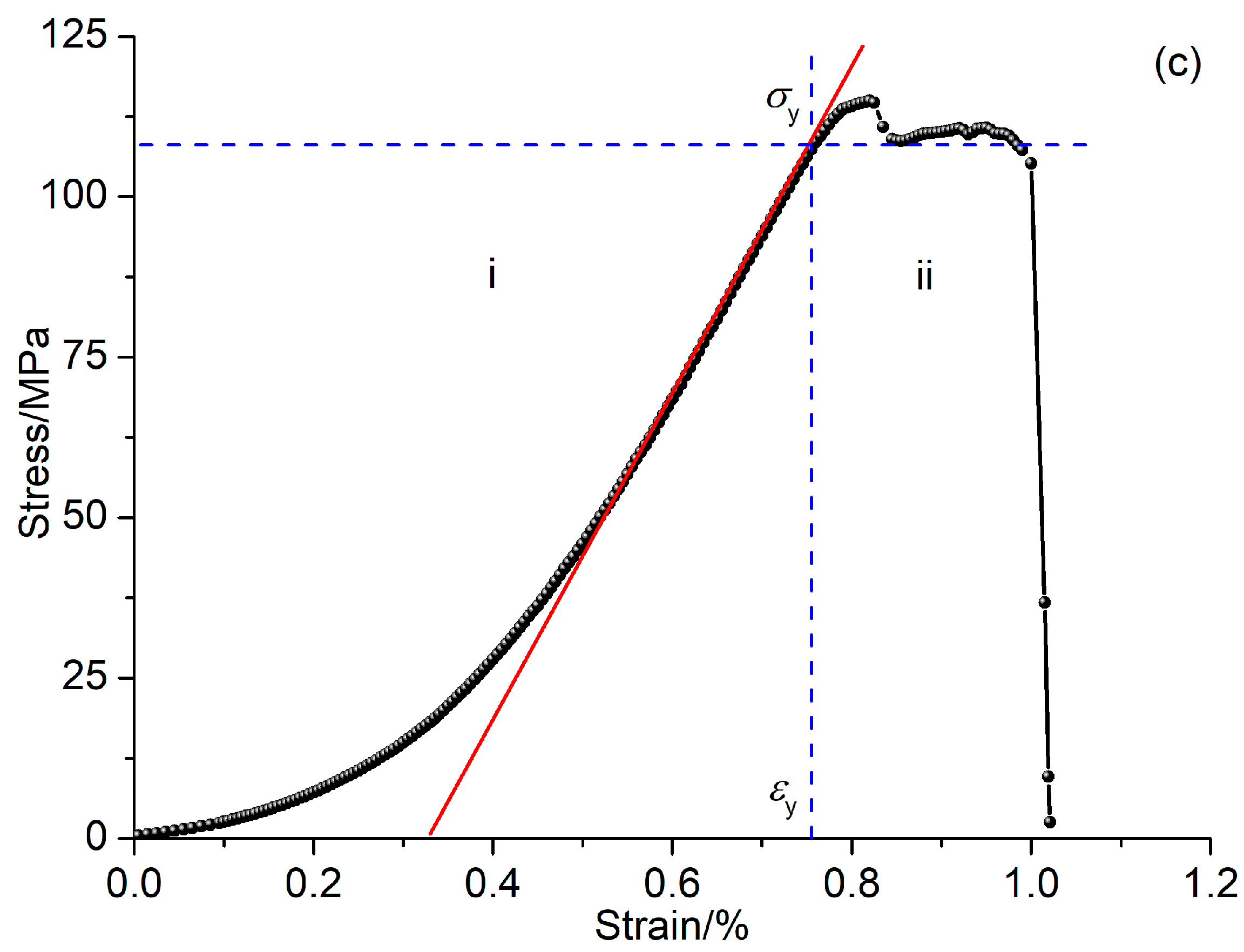
3.1. PSC Response Characteristics
3.2. Damage Evolution of Granite Analyzed by PSC
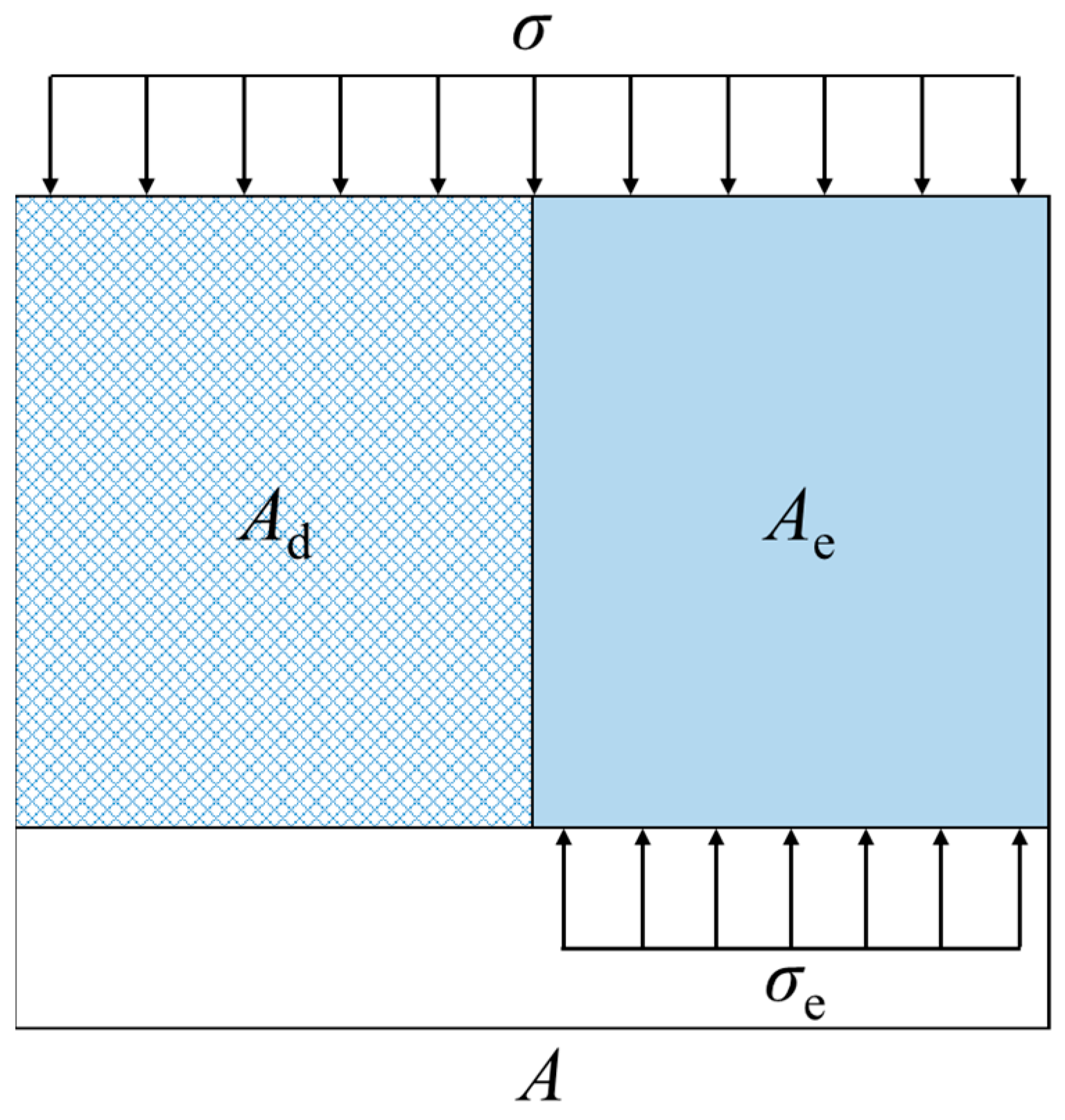
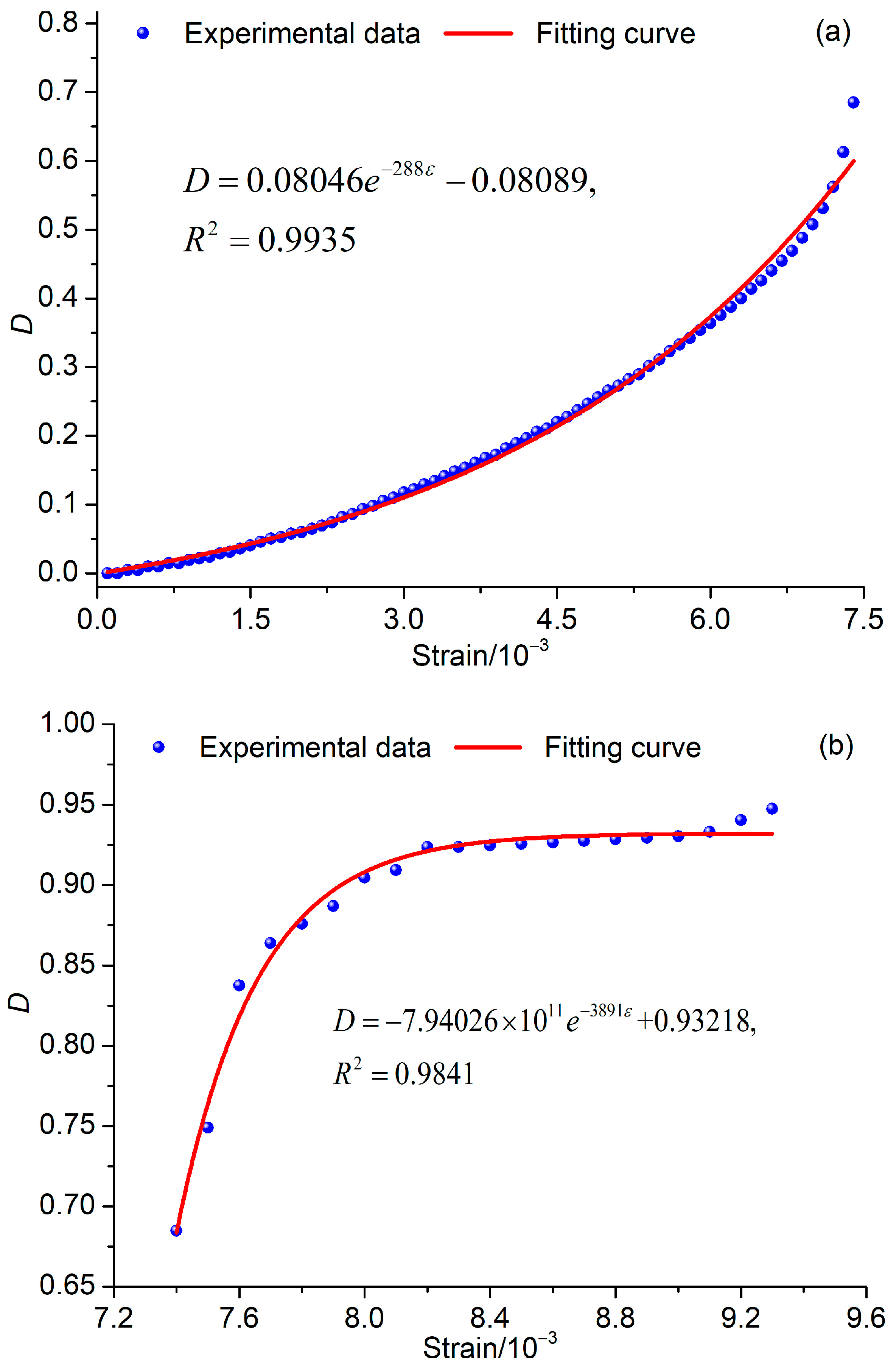
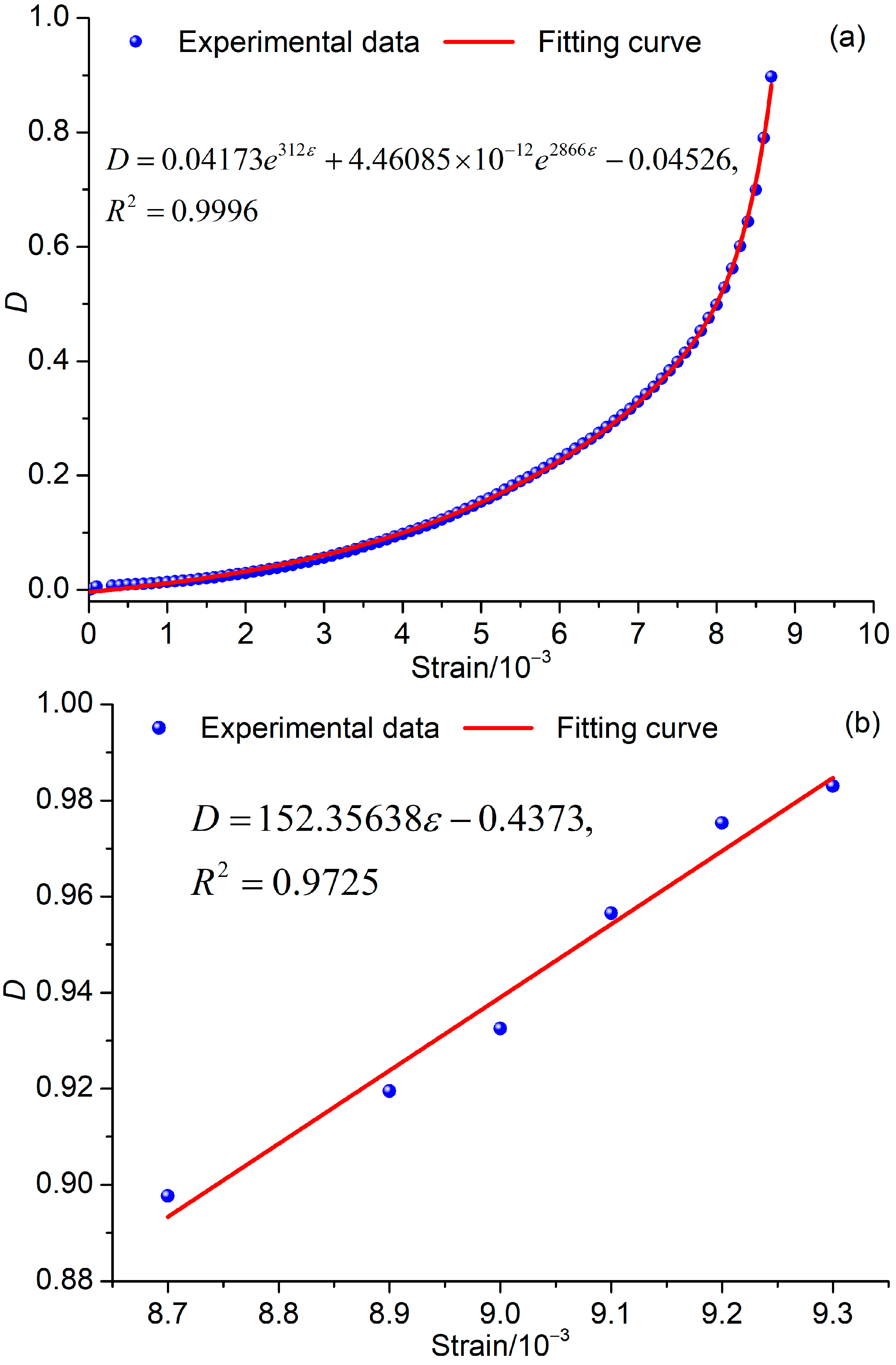
3.2.1. Analytical Expression of Damage Variable
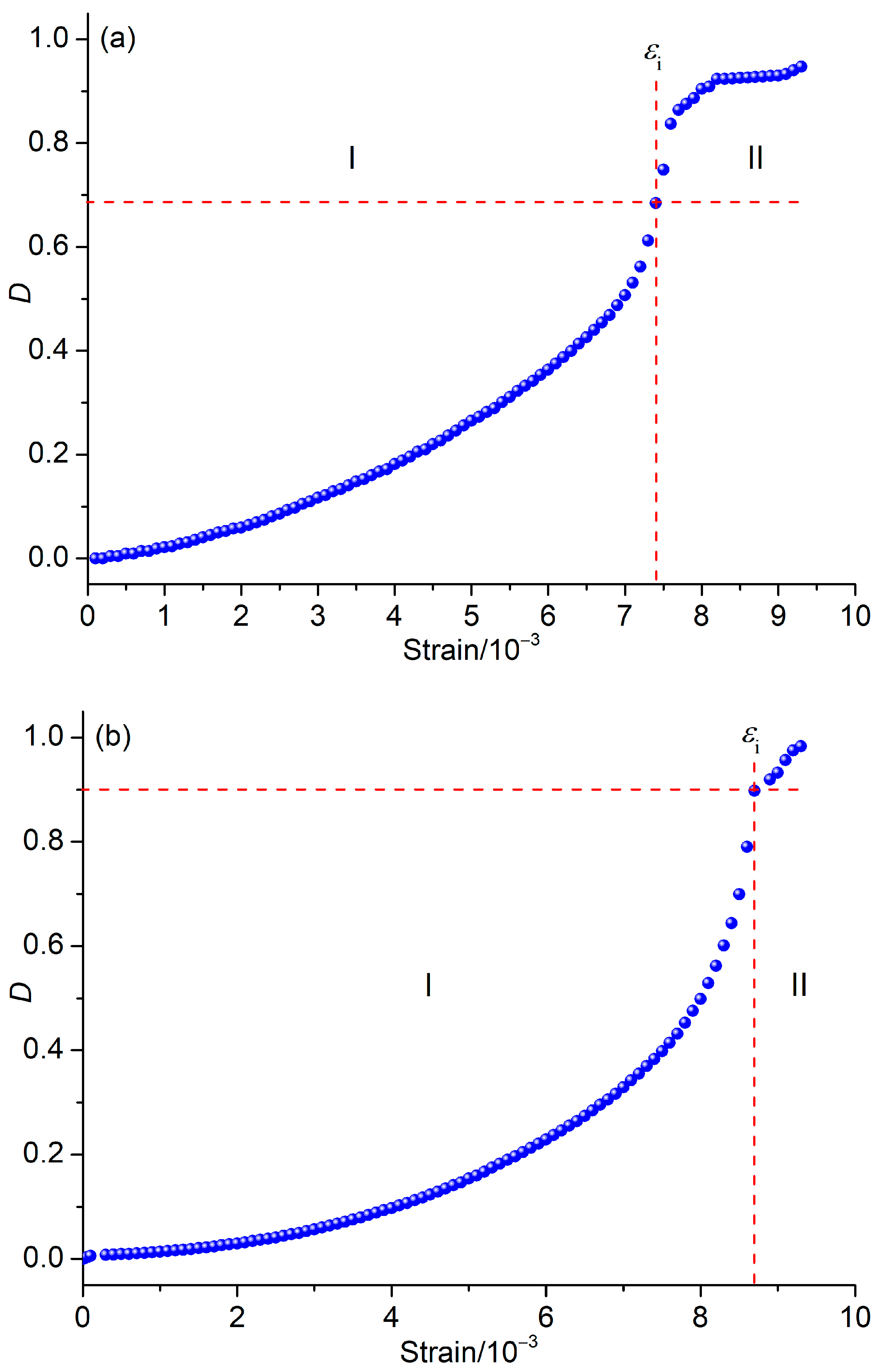
3.2.2. Damage Evolution Law of Granite
3.2.3. Damage Constitutive Model for Granite
4. Discussion
4.1. Mechanism of PSCs from Granite during Damage
4.2. Application of PSC in Rockburst Prediction
5. Conclusions
- (1)
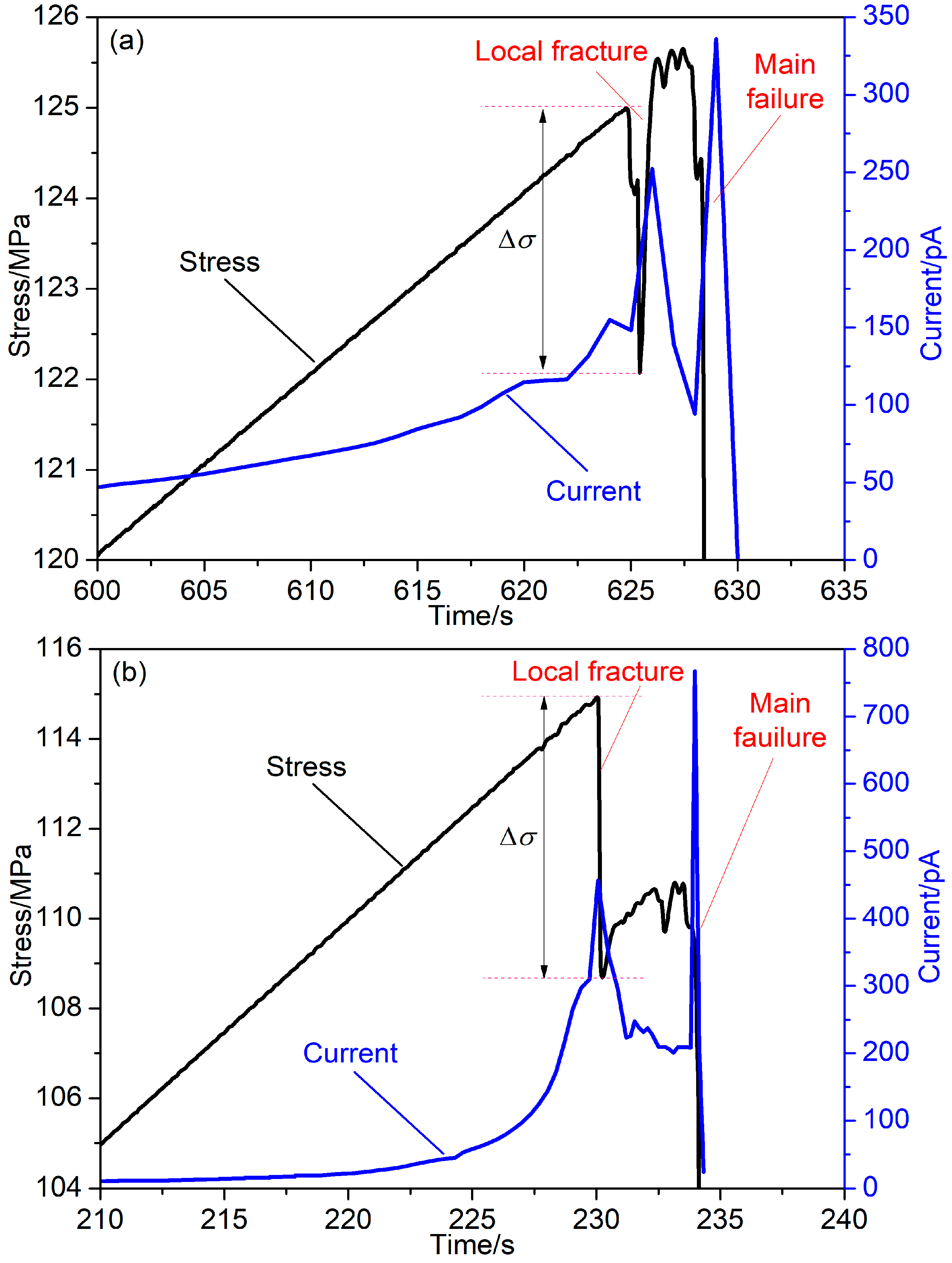
- PSC can be generated from granite during deformation, and its variation effectively reflects the different deformation stages of the rock. During the compaction and elastic deformation stages, PSC shows a gradual increase with stress. However, after the deformation enters the plastic stage, PSC exhibits an accelerated increase in response to stress.
- (2)
- PSC exhibits precursory behavior prior to granite failure. A stress drop is accompanied by a sudden and significant increase in PSC, which then decays rapidly. The growth rate and amplitude of the PSC associated with the main fracture are greater compared to those observed during a local fracture. Following the occurrence of the main failure, PSC experiences a sudden drop to pre-loading levels. In the case of a local fracture, PSC decreases slightly and continues to vibrate at a high value. The fluctuation following an abnormal increase in PSC during the accelerated increase process can serve as a precursor to rock failure.
- (3)
- The cumulative charge calculated based on PSC effectively reflects the damage process of granite samples. The stress–strain curve obtained using a theoretical constitutive model, established according to the defined damage variable based on cumulative charge, is in good agreement with the experimental results. This indicates that the damage variable defined by cumulative charge accurately reflects the damage evolution process of granite.
- (4)
- The carriers of PSC in rocks are primarily electrons, and their distribution follows the tip effect, with charge enrichment towards the crack tip. The generation mechanism of weak currents during rock damage involves the transfer, accumulation, and release of free charges. During the deformation process, currents are stimulated due to charge diffusion resulting from density differences. When a fracture occurs, currents are stimulated by the rapid release of accumulated charges.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kaiser, P.K.; McCreath, D.R.; Tannant, D.D. Canadian Rockburst Support Handbook; Geomechanics Research Centre, Laurentian University: Sudbury, ON, Canada, 1996; p. 314. [Google Scholar]
- Li, X.B.; Zhou, J.; Wang, S.F.; Liu, B. Review and practice of deep mining for solid mineral resources speed. Chin. J. Nonferrous Met. 2017, 27, 1236–1262. [Google Scholar]
- Li, D.X.; Wang, E.Y.; Kong, X.G.; Ali, M.; Wang, D.M. Mechanical behaviors and acoustic emission fractal characteristics of coal specimens with a pre-existing flaw of various inclinations under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2019, 116, 38–51. [Google Scholar] [CrossRef]
- Feng, G.L.; Feng, X.T.; Xiao, Y.X.; Yao, Z.B.; Hu, L.; Niu, W.J.; Li, T. Characteristic microseismicity during the development process of intermittent rockburst in a deep railway tunnel. Int. J. Rock Mech. Min. Sci. 2019, 124, 104135. [Google Scholar] [CrossRef]
- Keneti, A.; Sainsbury, B.A. Review of published rockburst events and their contributing factors. Eng. Geol. 2018, 246, 361–373. [Google Scholar] [CrossRef]
- Li, C.C. Principles and methods of rock support for rockburst control. J. Rock Mech. Geotech. 2021, 13, 46–59. [Google Scholar] [CrossRef]
- Luo, S.; Gong, F.Q. Evaluation of energy storage and release potentials of highly stressed rock pillar from rockburst control perspectives. Int. J. Rock Mech. Min. Sci. 2023, 163, 105324. [Google Scholar] [CrossRef]
- Vallianatos, F.; Tzanis, A. Electric current generation associated with the deformation rate of a solid: Preseismic and coseismic signals. Phys. Chem. Earth 1998, 23, 933–939. [Google Scholar] [CrossRef]
- Vallianatos, F.; Triantis, D.; Tzanis, A.; Anastasiadis, C.; Stavrakas, I. Electric earthquake precursors: From laboratory results to field observations. Phys. Chem. Earth 2004, 29, 339–351. [Google Scholar] [CrossRef]
- Stavrakas, I.; Anastasiadis, C.; Triantis, D.; Vallianatos, F. Piezo stimulated currents in marble samples: Precursory and concurrent-with-failure signals. Nat. Hazards Earth Syst. Sci. 2003, 3, 243–247. [Google Scholar] [CrossRef]
- Triantis, D.; Stavrakas, I.; Anastasiadis, C.; Kyriazopoulos, A.; Vallianatos, F. An analysis of pressure stimulated currents (PSC), in marble samples under mechanical stress. Phys. Chem. Earth 2006, 31, 234–239. [Google Scholar] [CrossRef]
- Freund, F.T.; Takeuchi, A.; Lau, B.W. Electric currents streaming out of stressed igneous rocks—A step towards understanding pre-earthquake low frequency EM emissions. Phys. Chem. Earth 2006, 31, 389–396. [Google Scholar] [CrossRef]
- Li, D.X.; Wang, E.Y.; Li, Z.H.; Ju, Y.Q.; Wang, D.M.; Wang, X.Y. Experimental investigations of pressure stimulated currents from stressed sandstone used as precursors to rock fracture. Int. J. Rock Mech. Min. Sci. 2021, 145, 104841. [Google Scholar] [CrossRef]
- Kyriazopoulos, A.; Anastasiadis, C.; Triantis, D.; Brown, C.J. Non-destructive evaluation of cement-based materials from pressure-stimulated electrical emission—Preliminary results. Constr. Build. Mater. 2011, 25, 1980–1990. [Google Scholar]
- Takeuchi, A.; Lau, B.W.S.; Freund, F.T. Current and surface potential induced by stress-activated positive holes in igneous rocks. Phys. Chem. Earth 2006, 31, 240–247. [Google Scholar] [CrossRef]
- Scoville, J.; Sornette, J.; Freund, F.T. Paradox of peroxy defects and positive holes in rocks Part II: Outflow of electric currents from stressed rocks. J. Asian Earth Sci. 2015, 114, 338–351. [Google Scholar] [CrossRef]
- Freund, F.; Ouillon, G.; Scoville, J.; Sornette, D. Earthquake precursors in the light of peroxy defects theory: Critical review of systematic observations. Eur. Phys. J. Spec. Top. 2021, 230, 7–46. [Google Scholar]
- Li, D.X.; Wang, E.Y.; Feng, X.J.; Wang, D.M.; Zhang, X.; Ju, Y.Q. Weak current induced by coal deformation and fracture and its response to mine seismicity in a deep underground coal mine. Eng. Geol. 2023, 315, 107018. [Google Scholar] [CrossRef]
- Li, M.; Lin, Z.J.; Shi, S.L.; Wang, D.M.; Lu, Y.; Li, H.; Ye, Q.; Zhang, X.N. Experimental research on influence mechanism of loading rates on rock pressure stimulated currents. Int. J. Min. Sci. Technol. 2023, 33, 243–250. [Google Scholar] [CrossRef]
- Triantis, D.; Stavrakas, I.; Kyriazopoulos, A.; Hloupis, G.; Agioutantis, Z. Pressure stimulated electrical emissions from cement mortar used as failure predictors. Int. J. Fract. 2012, 175, 53–61. [Google Scholar] [CrossRef]
- Vallianatos, F.; Triantis, D. A non-extensive view of the Pressure Stimulated Current relaxation during repeated abrupt uniaxial load-unload in rock samples. Europhys. Lett. 2013, 104, 68002. [Google Scholar] [CrossRef]
- Stergiopoulos, C.; Stavrakas, I.; Triantis, D.; Vallianatos, F.; Stonham, J. Predicting fracture of mortar beams under three-point bending using non-extensive statistical modeling of electric emissions. Phys. A 2015, 419, 603–611. [Google Scholar]
- Stavrakas, I.; Kourkoulis, S.; Triantis, D. Damage evolution in marble under uniaxial compression monitored by pressure stimulated currents and acoustic emissions. Fract. Struct. Integr. 2019, 13, 573–583. [Google Scholar] [CrossRef]
- Triantis, D.; Pasiou, E.D.; Stavrakas, I.; Kourkoulis, S.K. Hidden affinities between electric and acoustic activities in brittle materials at near-fracture load levels. Rock Mech. Rock Eng. 2022, 55, 1325–1342. [Google Scholar]
- Loukidis, A.; Tzagkarakis, D.; Kyriazopoulos, A.; Stavrakas, I.; Triantis, D. Correlation of acoustic emissions with electrical signals in the vicinity of fracture in cement mortars subjected to uniaxial compressive loading. Appl. Sci. 2023, 13, 365. [Google Scholar] [CrossRef]
- Li, D.X.; Wang, E.Y.; Ju, Y.Q.; Wang, D.M. Laboratory investigations of a new method using pressure stimulated currents to monitor concentrated stress variations in coal. Nat. Resour. Res. 2021, 30, 707–724. [Google Scholar] [CrossRef]
- Kachanov, M. Effective elastic properties of cracked solids: Critical review of some basic concepts. Appl. Mech. Rev. 1992, 45, 304–335. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. A comparative study of damage variables in continuum damage mechanics. Int. J. Damage Mech. 2009, 18, 315–340. [Google Scholar] [CrossRef]
- Xiao, J.Q.; Ding, D.X.; Jiang, F.L.; Xu, G. Fatigue damage variable and evolution of rock subjected to cyclic loading. Int. J. Rock. Mech. Min. Sci. 2010, 47, 461–468. [Google Scholar] [CrossRef]
- Gong, F.Q.; Zhang, P.L.; Xu, L. Damage constitutive model of brittle rock under uniaxial compression based on linear energy dissipation law. Int. J. Rock. Mech. Min. Sci. 2022, 160, 105273. [Google Scholar] [CrossRef]
- Lemaitre, J. How to use damage mechanics. Nucl. Eng. Des. 1984, 80, 233–245. [Google Scholar] [CrossRef]
- Jin, F.N.; Jiang, M.R.; Gao, X.L. Defining damage variable based on energy dissipation. Chin. J. Rock Mech. Eng. 2004, 23, 1976–1980. [Google Scholar]
- Liu, B.X.; Huang, J.L.; Wang, Z.Y.; Liu, L. Study on damage evolution and acoustic emission character of coal-rock under uniaxial compression. Chin. J. Rock Mech. Eng. 2009, 28, 3234–3238. [Google Scholar]
- Li, S.C.; Xu, X.J.; Liu, Z.Y.; Yang, W.M.; Liu, B.; Zhang, X.; Wang, Z.C.; Nie, L.C.; Li, J.L.; Xu, L. Electrical resistivity and acoustic emission response characteristics and damage evolution of sandstone during whole process of uniaxial compression. Chin. J. Rock Mech. Eng. 2014, 33, 14–23. [Google Scholar] [CrossRef]
- Barton, N. Suggested methods for the quantitative description of discontinuities in rock masses. International Society for Rock Mechanics. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 319–368. [Google Scholar]
- Fischer-Cripps, A.C. The Electronics Companion; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Freund, F.T. Pre-earthquake signals: Underlying physical processes. J. Asian Earth Sci. 2011, 41, 383–400. [Google Scholar]
- Kong, X.G.; He, D.; Liu, X.F.; Wang, E.Y.; Li, S.G.; Liu, T.; Ji, P.F.; Deng, D.Y.; Yang, S.R. Strain characteristics and energy dissipation laws of gas-bearing coal during impact fracture process. Energy 2022, 242, 123028. [Google Scholar] [CrossRef]
- Qiu, L.M.; Zhu, Y.; Song, D.Z.; He, X.Q.; Wang, W.X.; Liu, Y.; Xiao, Y.Z.; Wei, M.H.; Yin, S.; Liu, Q. Study on the nonlinear characteristics of EMR and AE during coal splitting tests. Minerals 2022, 12, 108. [Google Scholar] [CrossRef]



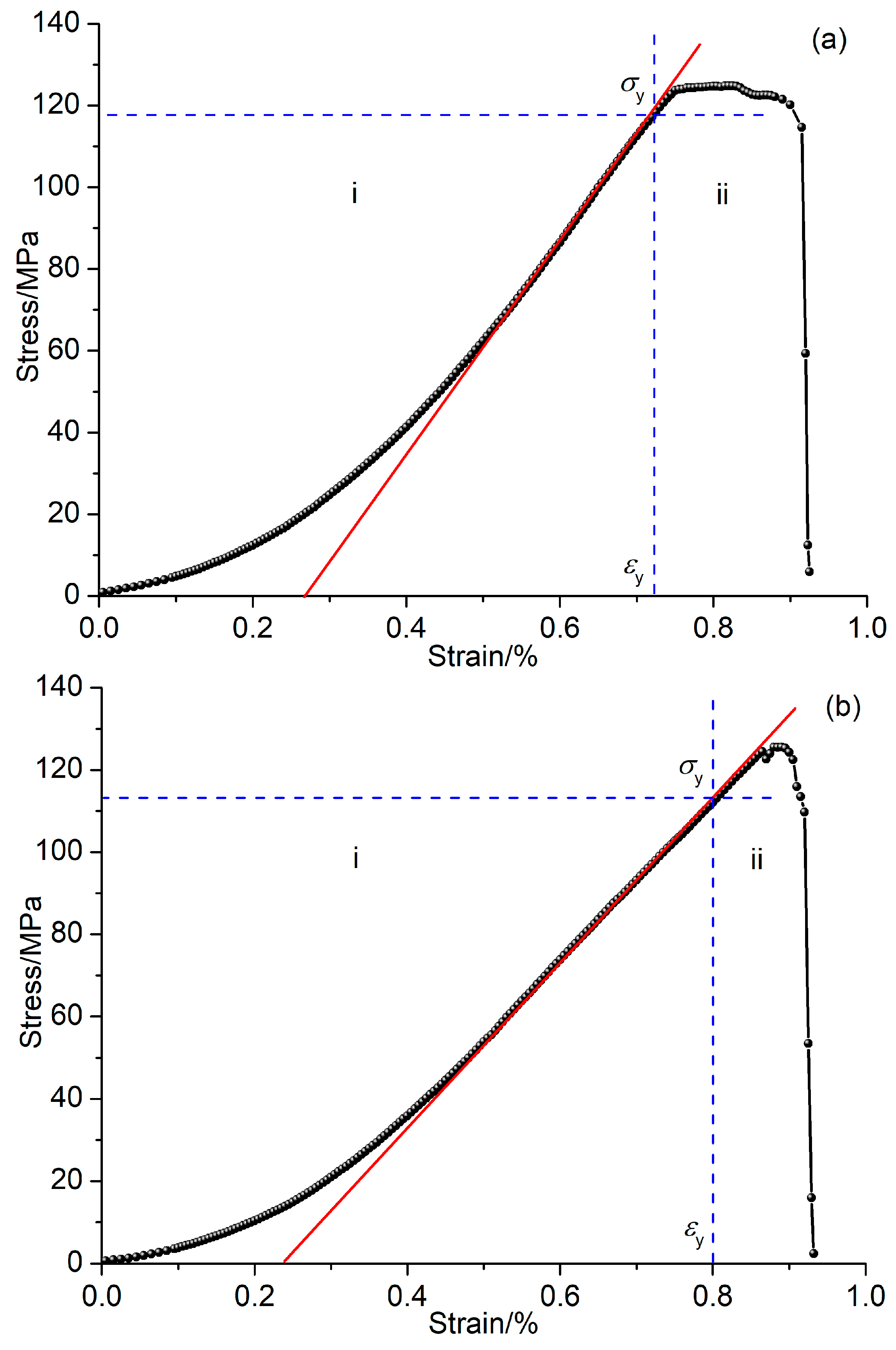



| Specimen | σca/MPa | σy/MPa | εy/% |
|---|---|---|---|
| GLS01 | 117.2 | 116.4 | 0.720 |
| GLS02 | 112.9 | 113.1 | 0.852 |
| GLS03 | 107.5 | 108.2 | 0.755 |
| Specimen | σf/MPa | σr/MPa | Du/s | Q0/pC | εi |
|---|---|---|---|---|---|
| GLS01 | 124.9 | 5.96 | 0.952 | 7309.5 | 0.0074 |
| GLS02 | 125.6 | 2.09 | 0.983 | 8815.6 | 0.0087 |
| Specimen | εpt | εpe | Δεp | ε0 |
|---|---|---|---|---|
| GLS01 | 0.00660 | 0.00885 | 0.00225 | 0.00220 |
| GLS02 | 0.00695 | 0.00960 | 0.00265 | 0.00330 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Wang, E.; Yue, J.; Li, M.; Li, L.; Wang, D.; Liang, W. Characteristics of Pressure Stimulated Current and Damage Evolution of Granite under Progressive Uniaxial Loading. Sustainability 2023, 15, 14526. https://doi.org/10.3390/su151914526
Li D, Wang E, Yue J, Li M, Li L, Wang D, Liang W. Characteristics of Pressure Stimulated Current and Damage Evolution of Granite under Progressive Uniaxial Loading. Sustainability. 2023; 15(19):14526. https://doi.org/10.3390/su151914526
Chicago/Turabian StyleLi, Dexing, Enyuan Wang, Jianhua Yue, Manman Li, Li Li, Dongming Wang, and Wei Liang. 2023. "Characteristics of Pressure Stimulated Current and Damage Evolution of Granite under Progressive Uniaxial Loading" Sustainability 15, no. 19: 14526. https://doi.org/10.3390/su151914526
APA StyleLi, D., Wang, E., Yue, J., Li, M., Li, L., Wang, D., & Liang, W. (2023). Characteristics of Pressure Stimulated Current and Damage Evolution of Granite under Progressive Uniaxial Loading. Sustainability, 15(19), 14526. https://doi.org/10.3390/su151914526







