Review of State Estimation and Remaining Useful Life Prediction Methods for Lithium–Ion Batteries
Abstract
:1. Introduction
2. SOC Estimation Method
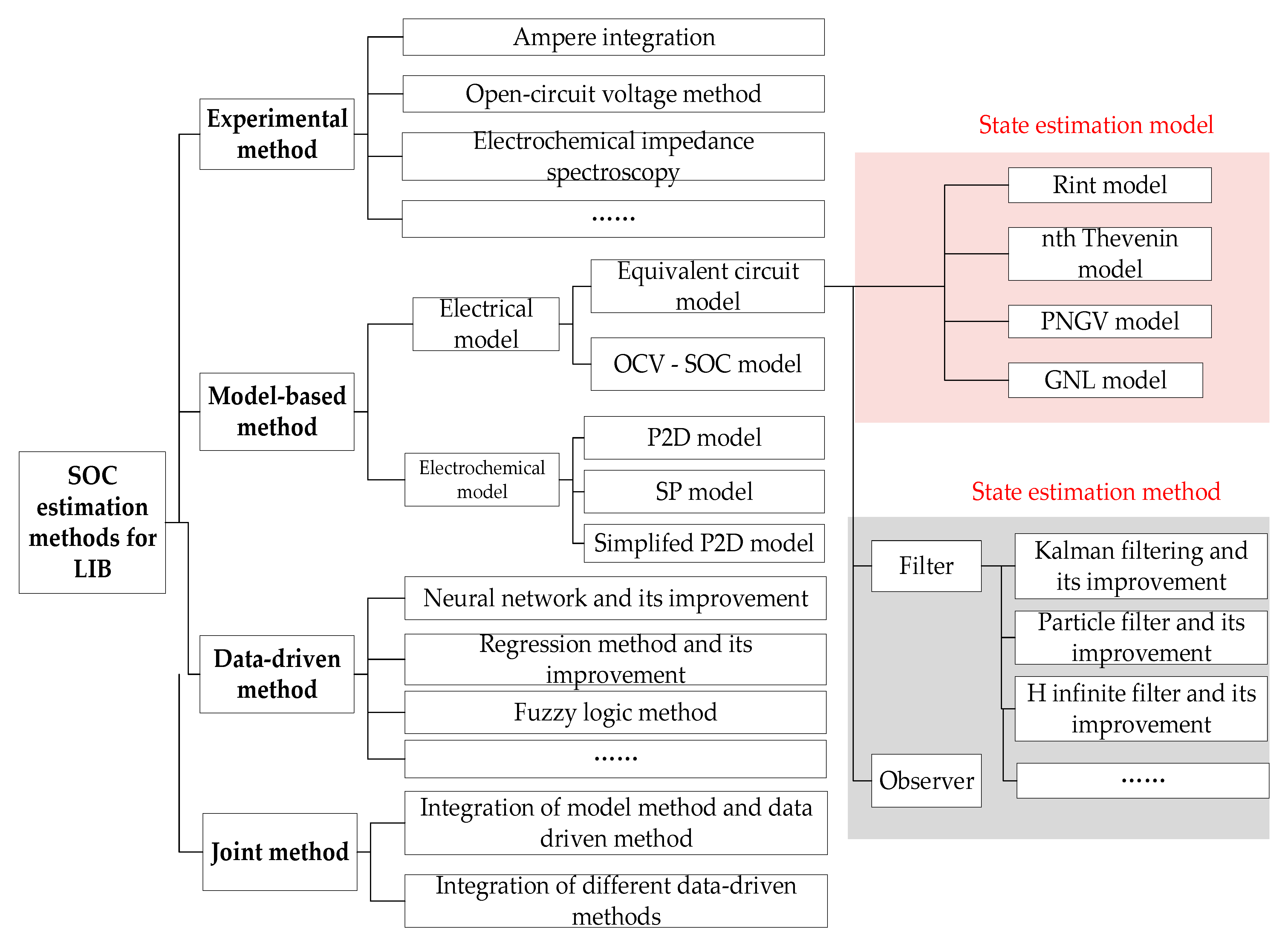
2.1. Classification of SOC Estimation Methods
2.2. The Experimental SOC Estimation Method
2.2.1. Ampere Integration
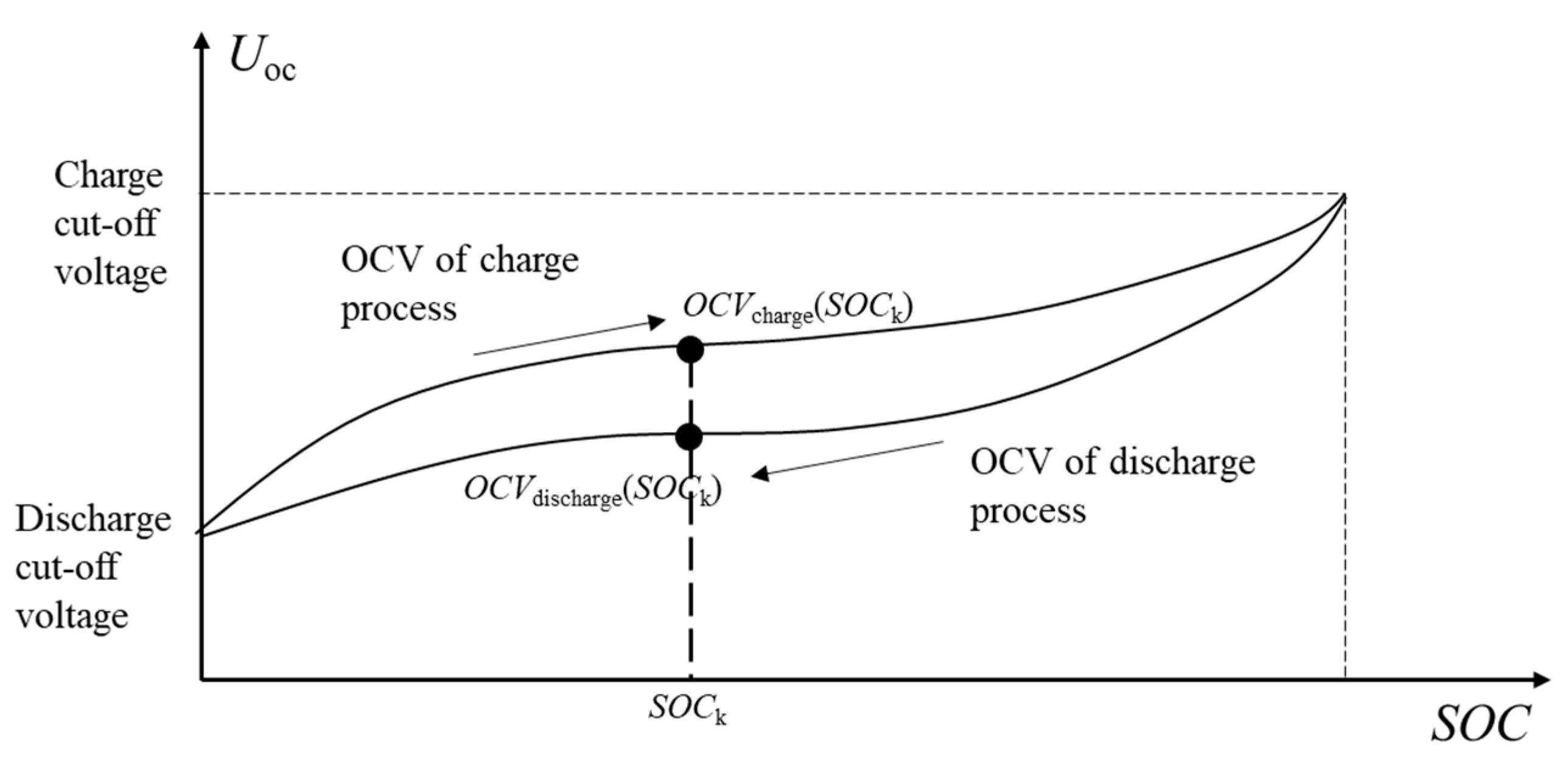
2.2.2. The Open-Circuit Voltage-Based Method
2.2.3. Other Methods
2.3. The Model Method
2.3.1. SOC Estimation Method Based on the Electrical Model
2.3.2. SOC Estimation Method Based on the Electrochemical Model
2.4. Data-Driven Methods
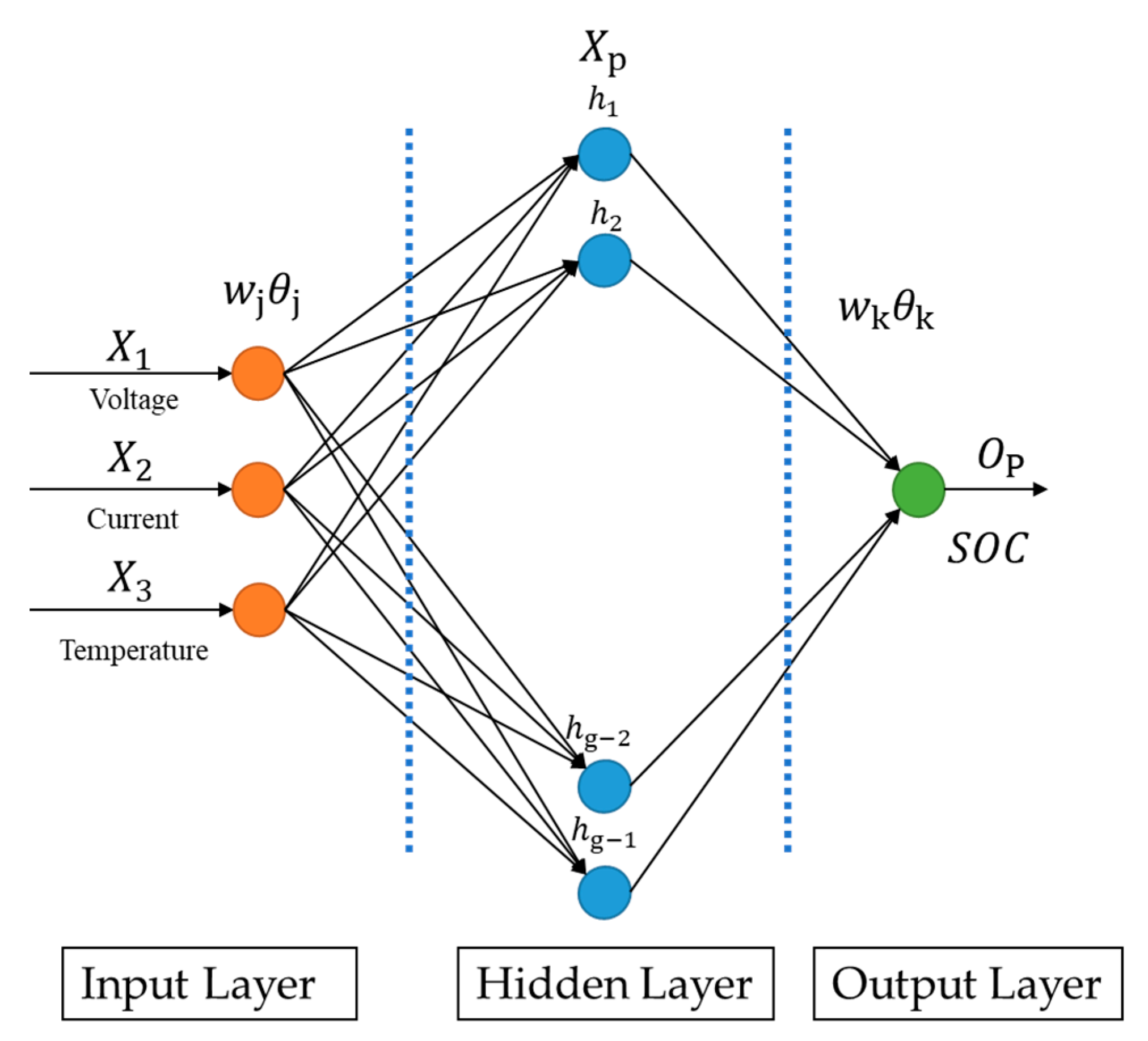
2.4.1. Neural Networks and their Improvement Method
2.4.2. The Regression Analysis Method and Its Improvement
2.5. The Joint Method
3. RUL Prediction Method
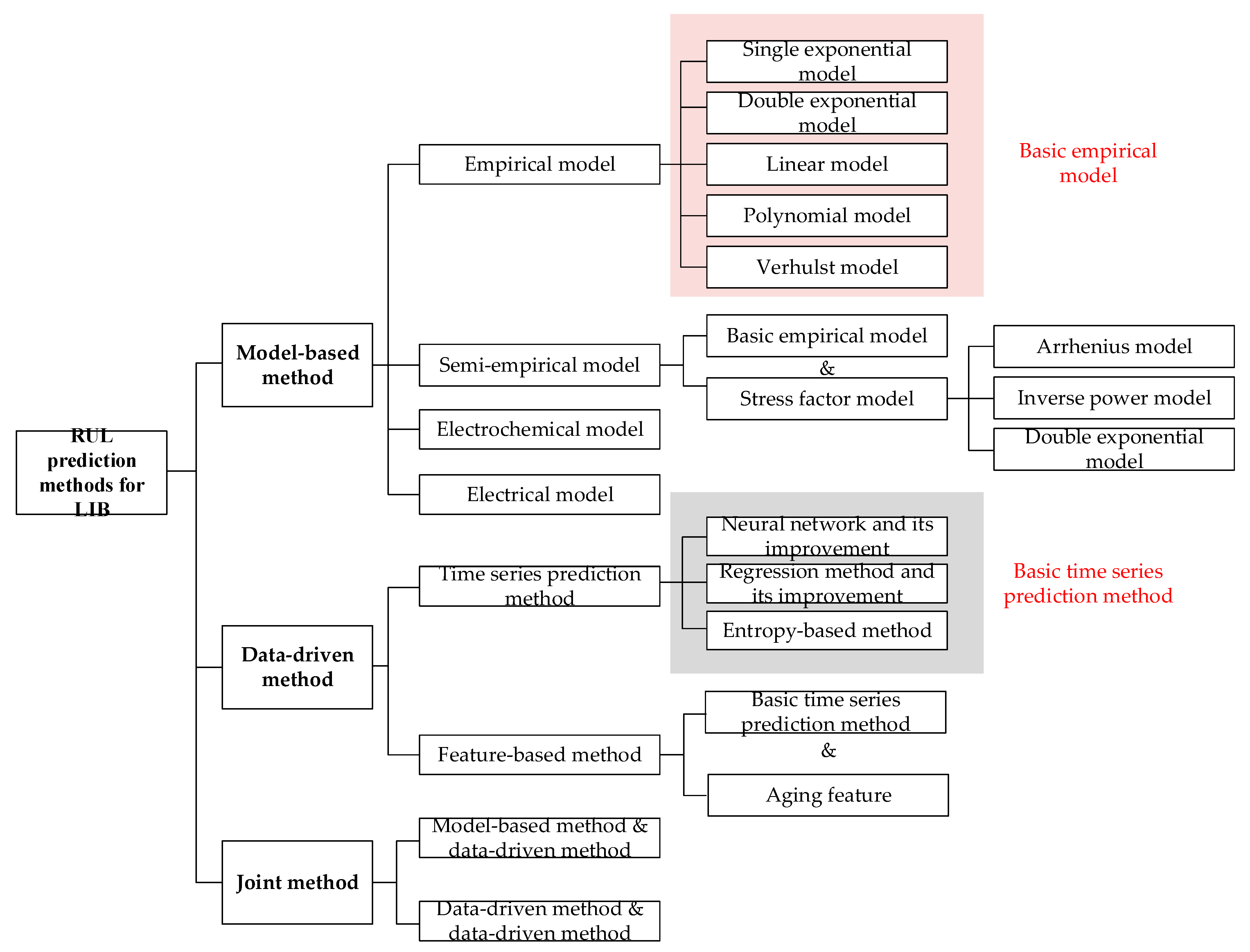
3.1. Classification of RUL Prediction Methods
3.2. The Model-Based Method
3.2.1. Empirical Model
3.2.2. The Semi-Empirical Model
3.2.3. The Electrical Model
3.2.4. The Electrochemical Model
3.3. The Data-Driven Method
3.3.1. The Time Series Prediction Method
- (1)
- Low accuracy for local capacity variation;
- (2)
- Not applicable to predict the RUL in the battery’s entire life cycle due to different degradation characteristics in each aging period;
- (3)
- High dependence on the training set and data quality;
- (4)
- Problem of overfitting.
3.3.2. The Feature-Based Method
3.4. The Joint Method
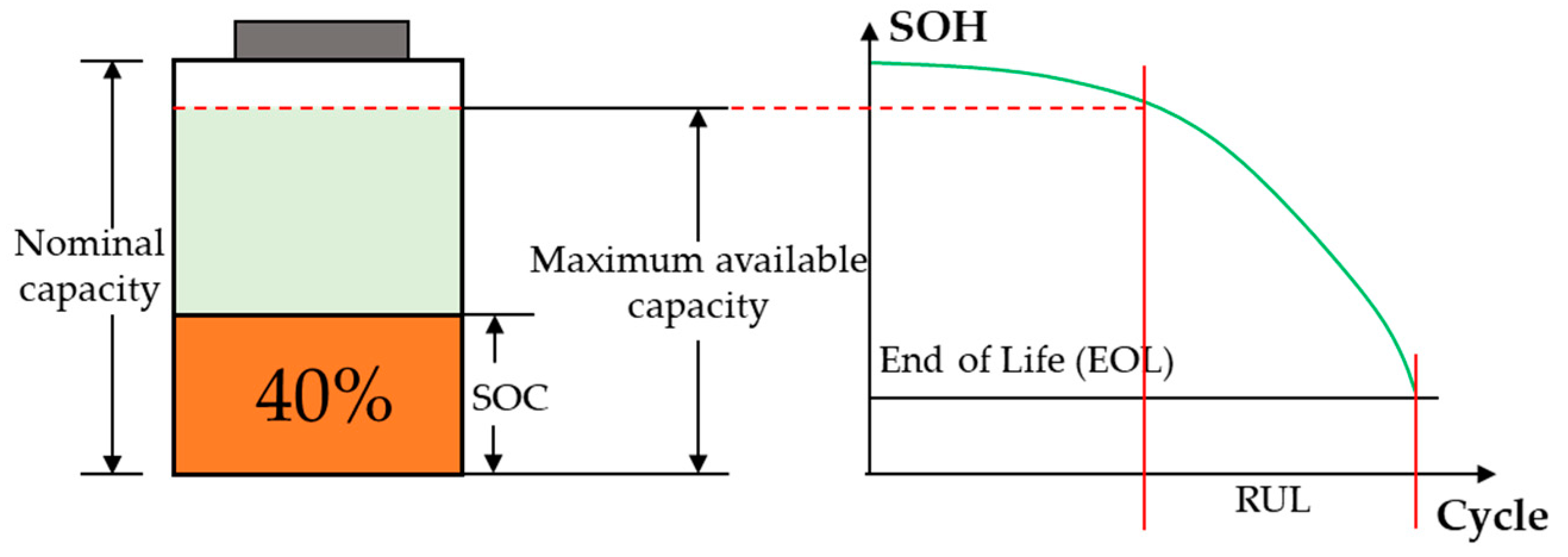
4. Conclusions
- (1)
- The balance between calculation time and accuracy is difficult to reach. Due to the limitations in the number of computations required, most algorithms are not suitable for online application. In addition, since batteries are usually integrated as modules, calculations multiply in the real world which makes real-time application a challenge;
- (2)
- There are only relevant studies on single batteries at present; however, factors such as the inconsistency of batteries in battery strings in large-scale lithium battery systems such as in an energy storage power station, will cause the original method to no longer be applicable. At present, there is little research on the state estimation and RUL prediction methods of battery packs.
- (1)
- Develop the pack-level, cluster-level, system-level battery equivalent model to reduce the amount of calculation required for state evaluation and RUL prediction;
- (2)
- Enhance state estimation and RUL prediction methods with joint algorithms to compensate for weaknesses and improve the algorithm’s capacity for generalization;
- (3)
- Establish a multi-physical field coupling model for lithium–ion batteries to improve the accuracy of battery status assessment and RUL prediction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sarmah, S.B.; Kalita, P.; Garg, A.; Niu, X.-D.; Zhang, X.-W.; Peng, X.; Bhattacharjee, D. A Review of State of Health Estimation of Energy Storage Systems: Challenges and Possible Solutions for Futuristic Applications of Li-Ion Battery Packs in Electric Vehicles. J. Electrochem. Energy Convers. Storage 2019, 16, 040801. [Google Scholar] [CrossRef] [Green Version]
- Hasib, S.A.; Islam, S.; Chakrabortty, R.K.; Ryan, M.J.; Saha, D.K.; Ahamed, H.; Moyeen, S.I.; Das, S.K.; Ali, F.; Islam, R.; et al. A Comprehensive Review of Available Battery Datasets, RUL Prediction Approaches, and Advanced Battery Management. IEEE Access 2021, 9, 86166–86193. [Google Scholar] [CrossRef]
- Elmahallawy, M.; Elfouly, T.; Alouani, A.; Massoud, A.M. A Comprehensive Review of Lithium-Ion Batteries Modeling, and State of Health and Remaining Useful Lifetime Prediction. IEEE Access 2022, 10, 119040–119070. [Google Scholar] [CrossRef]
- Su, N.K.H.; Juwono, F.H.; Wong, W.K.; Chew, I.M. Review on Machine Learning Methods for Remaining Useful Lifetime Prediction of Lithium-ion Batteries. In Proceedings of the 2022 International Conference on Green Energy, Computing and Sustainable Technology (GECOST), Miri Sarawak, Malaysia, 26–28 October 2022; pp. 286–292. [Google Scholar] [CrossRef]
- Wang, Y.; Zuo, X. State of Charge Estimation Methods and Application Scenarios of Lithium-Ion Batteries. Power Syst. Autom. 2022, 32-1180/TP, 1–15. Available online: http://kns.cnki.net/kcms/detail/32.1180.TP.20220331.1418.002.html (accessed on 14 April 2022).
- He, L.; Hu, M.; Shi, Q.; Ye, W. A staged state of charge estimation algorithm for lithium-ion batteries. Power Electron. Technol. 2020, 54, 8–11. [Google Scholar]
- Wu, L.; Pang, H.; Jin, J.; Geng, Y.; Liu, K. A Review of State of Charge Estimation Methods for Lithium Ion Batteries Based on Electrochemical Models. J. Electr. Technol. 2022, 37, 1703–1725. [Google Scholar] [CrossRef]
- Wu, C.; Hu, W.; Meng, J.; Liu, Z.; Cheng, D. State of Charge Estimation of Lithium Ion Battery Based on Maximum Correlation Entropy Extended Kalman Filter Algorithm. J. Electr. Technol. 2021, 36, 5165–5175. [Google Scholar] [CrossRef]
- Li, C.; Xiao, F.; Fan, Y.; Yang, G.; Tang, X. State of Charge Estimation of Lithium Ion Battery Based on Gated Cyclic Unit Neural Network and Huber-M Estimation Robust Kalman Filter Fusion Method. J. Electr. Technol. 2020, 35, 2051–2062. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, C.; Zhang, S.; Dai, M.; Xiao, W.; Chen, X. Summary of fusing algorithm research in estimation for state of charge of battery. Sichuan Electr. Power Technol. 2021, 44, 43–46. [Google Scholar]
- Li, Z.; Lu, L.; Ouyang, M. Comparison of Methods to Improve the Accuracy of Battery SOC Estimation by Ampere Hour Integration. J. Tsinghua Univ. 2010, 50, 1293–1296. [Google Scholar]
- Luo, Y.; Qi, P.; Huang, H.; Wang, J.; Wang, Y.; Li, P. Research on Estimation Method of Ampere Hour Integration SOC Based on Capacity Correction. Automot. Eng. 2020, 42, 681–687. [Google Scholar]
- Li, K.; Zhao, L.; Zhao, B.; Ke, H.; Li, J. Stream Ampere Hour Integral SOC Estimation Method Based on Frequent Item Statistics. J. Chongqing Univ. Sci. Technol. 2022, 36, 19–27. [Google Scholar]
- Guo, B.; Zhang, P.; Wang, W.; Wang, F. Study on SOC Estimation of Lithium Iron Phosphate Battery Based on OCV–SOC Curve Cluster. Power Technol. 2019, 43, 1125–1128. [Google Scholar]
- Huang, K.; Guo, Y.; Li, Z. State of Charge Estimation of Power Lithium Ion Batteries. Power Technol. 2018, 42, 1398–1401. [Google Scholar]
- Blanke, H.; Bohlen, O.; Buller, S.; De Doncker, R.W.; Fricke, B.; Hammouche, A.; Linzen, D.; Thele, M.; Sauer, D.U. Impedance Measurements on Lead-acid Batteries for State-of-charge, State-of-health and Cranking Capability Prognosis in Electric and Hybrid Electric Vehicles. J. Power Sources 2005, 144, 418–425. [Google Scholar] [CrossRef]
- Zenati, A.; Desprez, P.; Razik, H.; Rael, S. Impedance Measurements Combined with the Fuzzy Logic Methodology to Assess the SOC and SOH of Lithium-ion Cells. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference (VPPC), Lille, France, 1–3 September 2010. [Google Scholar]
- Zeng, Q.; Zhang, X.; Fan, X. Discussion on Estimation Method of SOC of Electric Vehicle Power Battery. Electr. Meas. Instrum. 2014, 51, 76–84. [Google Scholar]
- Available online: https://www.zhihu.com/question/434952446/answer/1628793249 (accessed on 15 December 2020).
- Li, J.; Xiao, Y. Overview of Modeling Status of Lithium Ion Battery. Energy Storage Sci. Technol. 2022, 11, 697–703. [Google Scholar]
- Wu, X.; Zhang, X. Parameter Identification of Second Order RC Equivalent Circuit Model of Lithium Battery. J. Nanjing Univ. 2020, 56, 754–761. [Google Scholar]
- Park, J.H.; Kim, H.G.; Nho, E.C.; Chun, T.-W. Power conditioning system for a grid connected PV power generation using a Quasi-Z-source inverter. IEEE J. Power Electron. 2010, 10, 79–84. [Google Scholar] [CrossRef] [Green Version]
- Mao, H.; Wan, G.; Wang, L.; Zhang, Q. Estimation of Battery SOC Based on Modified Kalman Filter Algorithm. Power Technol. 2014, 38, 298–302. [Google Scholar]
- Pang, H.; Guo, L.; Wu, L.; Min, J.; Liu, K. Improved Bipolarization Model of Lithium Ion Battery Considering the Effect of Ambient Temperature and Its State of Charge Estimation. J. Electr. Technol. 2021, 36, 2178–2189. [Google Scholar]
- Hu, X. SOC Estimation and Implementation of Power Lithium Battery Based on Traceless Kalman Filter. Master’s Thesis, Central South University, Changsha, China, 2014. [Google Scholar]
- Sun, D.; Chen, X. State of Charge Estimation of Lithium Battery Based on Discrete Sliding Mode Observer. Chin. J. Electr. Eng. 2015, 35, 185–191. [Google Scholar] [CrossRef]
- Fei, Y.; Xie, C.; Tang, Z.; Zeng, C.; Quan, S. State Estimation of Lithium Battery Based on Square Root Unscented Kalman Filter. Chin. J. Electr. Eng. 2017, 37, 4514–4520+4593. [Google Scholar] [CrossRef]
- Wang, Y.; Li, L.; Ding, Q.; Liu, J.; Chen, P. Lithium-ion battery SOC estimation based on an improved adaptive extended Kalman filter. In Proceedings of the 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 1–4 August 2021; pp. 417–421. [Google Scholar] [CrossRef]
- Schwunk, S.; Armbruster, N.; Straub, S.; Kehl, J.; Vetter, M. Particle filter for state of charge and state of health estimation forlithium-iron phosphate batteries. J. Power Sources 2013, 239, 705–710. [Google Scholar] [CrossRef]
- Xie, C.; Fei, Y.; Zeng, C.; Fang, W. State Estimation of Vehicle Lithium Ion Battery Based on Traceless Particle Filter. J. Electr. Technol. 2018, 33, 3958–3964. [Google Scholar] [CrossRef]
- Chen, X.; Sun, D.; Chen, X. Modeling and Robust State of Charge Estimation of Lithium Ion Batteries. J. Electr. Technol. 2015, 30, 141–147. [Google Scholar]
- Liu, C.Z.; Zhu, Q.; Li, L. A state of charge estimation method based on H-infinity observer for switched systems of lithium-ion nickel-manganese-cobalt batteries. IEEE Trans. Ind. Electron. 2017, 64, 8128–8137. [Google Scholar] [CrossRef]
- Chen, C.; Xiong, R.; Shen, W. A lithium-ion battery-in-the-loop approach to test and validate multiscale dual H infinity filters for state-of-charge and capacity estimation. IEEE Trans. Power Electron. 2018, 33, 332–342. [Google Scholar] [CrossRef]
- Da, Y.; Wan, Y.; He, W. An Adaptive Central Difference H-infinity Filter Based SOC Estimation for Lithium-ion Batteries with Measurement Noise. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 1402–1407. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, L.; Hu, X.S. H-infinity-based nonlinear observer design for state of charge estimation of lithium-ion battery with polynomial parameters. IEEE Trans. Veh. Technol. 2017, 12, 10853–10865. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Han, X.; Lu, L.; Li, J. Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles. J. Power Sources 2018, 377, 161–188. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, X. A Method for SOC Estimation of Lithium Battery Based on Improved Discrete Sliding Mode Observer. Ind. Control Comput. 2018, 31, 67–68. [Google Scholar]
- He, H.; Xiong, R. State of Charge Estimation of Lithium-Ion Power Battery Based on Sliding Mode Observer. J. Jilin Univ. 2011, 41, 623–628. [Google Scholar] [CrossRef]
- Du, J. Research on Estimation Algorithm of State of Charge and Health of Lithium Ion Battery Based on Sliding Mode Observer. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2018. [Google Scholar]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Li, Z. Study on Electrochemical Modeling and Aging State Identification of Lithium-Ion Power Battery. Master’s Thesis, Beijing University of Technology, Beijing, China, 2018. [Google Scholar] [CrossRef]
- Ahmed, R.; Sayed, M.E.; Arasaratnam, I.; Tjong, J.; Habibi, S. Reduced-Order Electrochemical Model Parameters Identification and State of Charge Estimation for Healthy and Aged Li-Ion Batteries—Part II: Aged Battery Model and State of Charge Estimation. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 678–690. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef] [Green Version]
- Hussein, A.A. Capacity fade estimation in electric vehicles Li-ion batteries using artificial neural networks. IEEE Energy Convers. Congr. Expo. 2013, 51, 677–681. [Google Scholar] [CrossRef]
- Moura, S.J.; Argomedo, F.B.; Klein, R.; Mirtabatabaei, A.; Krstic, M. Battery State Estimation for a Single Particle Model with Electrolyte Dynamics. IEEE Trans. Control Syst. Technol. 2017, 25, 453–468. [Google Scholar] [CrossRef]
- Schmidt, A.P.; Bitzer, M.; Imre, Á.W.; Guzzella, L. Experiment-driven electrochemical modeling and systematic parameterization for a lithium-ion battery cell. J. Power Sources 2010, 195, 5071–5080. [Google Scholar] [CrossRef]
- Yin, A.; Zhang, W.; Zhao, H.; Jiang, H. Study on SOC Prediction of Lithium Iron Phosphate Battery Based on Neural Network. J. Electron. Meas. Instrum. 2011, 25, 433–437. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.; Ayob, A. Neural Network Approach for Estimating State of Charge of Lithium-Ion Battery Using Backtracking Search Algorithm. IEEE Access 2018, 6, 10069–10079. [Google Scholar] [CrossRef]
- Zahid, T.; Xu, K.; Li, W.; Li, C.; Li, H. State of charge estimation for electric vehicle power battery using advanced machine learning algorithm under diversified drive cycles. Energy 2018, 162, 871–882. [Google Scholar] [CrossRef]
- Cai, X.; Li, B.; Wang, H.; Nie, L. Study on SOC Estimation of Power Battery Based on Neural Network Model. Electrom. Eng. 2015, 32, 128–132. [Google Scholar]
- Xu, S.; Liu, Y.; Zhou, F. Research Progress of SOC Estimation of Lithium Ion Battery Based on RNN. Power Technol. 2021, 45, 263–269. [Google Scholar]
- Ming, T.; Zhao, J.; Wang, X.; Wang, K. SOC Estimation of Lithium Battery under High Pulse Rate Based on Improved LSTM. Power Syst. Prot. Control 2021, 49, 144–150. [Google Scholar]
- Xu, C.Y.; Shen, J.Z.; Du, X.; Zhang, F. An intrusion detection system using a deep neural network with gated recurrent units. IEEE Access 2018, 6, 48697–48707. [Google Scholar] [CrossRef]
- Zheng, Y.; Wen, H.; Han, F.; Yang, X.; Zhang, J. Study on SOC Estimation of Power Battery Based on LSTM Neural Network. Comput. Appl. Softw. 2020, 37, 78–81. [Google Scholar]
- Wu, H.; Fan, Y.; Huang, H.; Fang, L.; Liu, J.; Chen, W.; Li, Z. SOC Estimation Method of Lithium-ion Batteries Based on Relaxation Effect and GRU-RNN. In Proceedings of the 2022 IEEE 9th International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, China, 20–22 September 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Han, Y. Wide Temperature SOC Estimation of Lithium Ion Battery Based on Gated Cyclic Unit Neural Network. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2021. [Google Scholar] [CrossRef]
- Zhu, Y.; He, W.; Li, J.; Li, Y.; Li, P. SOC Estimation of Lithium Battery Based on Bi LSTM/Bi GRU Cyclic Neural Network. Energy Storage Sci. Technol. 2021, 10, 1163–1176. [Google Scholar] [CrossRef]
- Xiao, B.; Liu, Y.; Xiao, B. Accurate State-of-Charge Estimation Approach for Lithium-Ion Batteries by Gated Recurrent Unit with Ensemble Optimizer. IEEE Access 2019, 7, 54192–54202. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, B.; Huang, X.; Hou, C. Estimation of Lithium Battery SOC Based on SVM. Power Technol. 2016, 40, 287–290. [Google Scholar]
- Kecman, V. Support Vector Machines–An Introduction; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–47. [Google Scholar]
- Anton, J.C.A.; Nieto, P.J.G.; Viejo, C.B.; Vilan, J.A.V. Support Vector Machines Used to Estimate the Battery State of Charge. IEEE Trans. Power Electron. 2013, 28, 5919–5926. [Google Scholar] [CrossRef]
- Dang, X.; Yan, L.; Jiang, H.; Wu, X.; Zhang, X. Research on SOC estimation Method of Power Battery Based on Online LS-SVM. Power Technol. 2017, 41, 752–756. [Google Scholar]
- Pao, Y.; Feng, C.; Ren, X.; Zhang, J.; Ma, C.; Shao, W. On-line Transient Stability Fault Screening Based on Support Vector Machine. Power Syst. Autom. 2019, 43, 52–58. [Google Scholar]
- Song, X.; Yang, F.; Wang, D.; Tsui, K.L. Combined CNN-LSTM Network for State-of-Charge Estimation of Lithium-Ion Batteries. IEEE Access 2019, 7, 88894–88902. [Google Scholar] [CrossRef]
- Li, R.; Chen, Y. SOC Estimation of Power Lithium Ion Battery Based on AFFDRLS-AHIF. J. Beijing Jiaotong Univ. 2020, 44, 129–135. [Google Scholar]
- Zhang, S. A new method for lithium-ion battery’s SOH estimation and RUL prediction. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 2693–2697. [Google Scholar] [CrossRef]
- Saha, B.; Kai, G.; Christophersen, J. Comparison of prognostic algorithms for estimating remaining useful life of batteries. Trans. Inst. Meas. Control 2009, 31, 293–308. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, W.; Su, Y.; Jiang, K.; Huang, H. Review of methods for predicting residual life of lithium ion batteries. Chin. J. Power Sources 2021, 45, 678–682. [Google Scholar]
- Zhang, C.; Zhao, S.; He, Y. An Integrated Method of the Future Capacity and RUL Prediction for Lithium-Ion Battery Pack. IEEE Trans. Veh.Technol. 2022, 71, 2601–2613. [Google Scholar] [CrossRef]
- Zhang, L.; Mu, Z.; Sun, C. Remaining Useful Life Prediction for Lithium-Ion Batteries Based on Exponential Model and Particle Filter. IEEE Access 2018, 6, 17729–17740. [Google Scholar] [CrossRef]
- Cheng, L.; Wan, Y.; Zhou, Y.; Gao, D.W. Operational Reliability Modeling and Assessment of Battery Energy Storage Based on Lithium-ion Battery Lifetime Degradation. J. Mod. Power Syst. Clean Energy 2022, 10, 1738–1749. [Google Scholar] [CrossRef]
- Xue, Y.; Zhou, H.; Luo, Y.; Lam, J. Battery Degradation Modelling and Prediction with Combination of Machine Learning and Semi-empirical Methods. In Proceedings of the 2022 12th International Conference on Power, Energy and Electrical Engineering (CPEEE), Shiga, Japan, 25–27 February 2022; pp. 78–85. [Google Scholar] [CrossRef]
- Rathore, K. An Empirical Capacity Degradation Modeling and Prognostics of Remaining Useful Life of Li-ion Battery using Unscented Kalman Filter. In Proceedings of the 2018 8th IEEE India International Conference on Power Electronics (IICPE), Jaipur, India, 13–15 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zhu, Q.; Yu, X.; Wu, Q.; Xu, Y.; Chen, F.; Huang, R. Semi-empirical Degradation Model of Lithium-ion Battery with High Energy Density. Energy Storage Sci. Technol. 2022, 11, 2324–2331. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?doi=10.19799/j.cnki.2095-4239.2021.0725 (accessed on 17 March 2022). [CrossRef]
- Jônatas, M.; Pedro, T.J.; Carlos, A. Optimisation of an electric bus charging strategy considering a semi-empirical battery degradation model and weather conditions. In Proceedings of the 2022 11th International Conference on Control, Automation and Information Sciences (ICCAIS), Hanoi, Vietnam, 21–24 November 2022; pp. 298–303. [Google Scholar] [CrossRef]
- Li, K.; Zhou, P.; Lu, Y.; Han, X.; Li, X.; Zheng, Y. Battery life estimation based on cloud data for electric vehicles. J. Power Sources 2020, 468, 228192. [Google Scholar] [CrossRef]
- Chen, D.; Meng, J.; Huang, H.; Wu, J.; Liu, P.; Lu, J.; Liu, T. An empirical-data hybrid driven approach for remaining useful lifeprediction of lithium-ion batteries considering capacity diving. Energy 2022, 245, 123222. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Wang, Z. State of health estimation for Li-ion battery via partial incremental capacity analysis based on support vector regression. Energy 2020, 203, 117852. [Google Scholar] [CrossRef]
- Saurabh, S.; Darius, R.; Valentin, R.; Flynn, D.; Michael, P. Battery Stress Factor Ranking for Accelerated Degradation Test Planning Using Machine Learning. Energies 2021, 14, 723. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, X.; Gu, W.; Wei, X.; Sun, Z. A Semi-Empirical Capacity Degradation Model of EV Li-Ion Batteries Based on Eyring Equation. In Proceedings of the 2013 IEEE Vehicle Power and Propulsion Conference (VPPC), Beijing, China, 15–18 October 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, L.; Pan, C.; Liu, L.; Cheng, Y.; Zhao, X. On-board state of health estimation of LiFePO4 battery pack through differential voltage analysis. Appl. Energy 2016, 168, 465–472. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Source 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Preetpal, S.; Che, C.; Cher, T.; Shyh-Chin, H. Semi-Empirical Capacity Fading Model for SoH Estimation of Li-Ion Batteries. Appl. Sci. 2019, 9, 3012. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Lu, L.; Ouyang, M.; Xiao, Y. Modeling the capacity degradation of LiFePO4/graphite batteries based on stress coupling analysis. J. Power Source 2011, 196, 9757–9766. [Google Scholar] [CrossRef]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of lithium-ion battery degradation for cell life assessment. IEEE Trans. Smart Grid 2018, 9, 1131–1140. [Google Scholar] [CrossRef]
- Miao, Q.; Xie, L.; Cui, H.; Liang, W.; Pecht, M. Remaining useful life prediction of lithium-ion battery with unscented particle filter technique. Microelectron. Reliab. 2013, 53, 805–810. [Google Scholar] [CrossRef]
- Jiao, R.; Peng, K.; Dong, J. Remaining useful life prediction of Lithium-ion batteries based on conditional variational autoencodersparticle filter. IEEE Trans. Instrum. Meas. 2020, 69, 8831–8843. [Google Scholar] [CrossRef]
- Edge, J.S.; O’Kane, S.; Prosser, R.; Kirkaldy, N.D.; Patel, A.N.; Hales, A.; Ghosh, A.; Ai, W.; Chen, J.; Yang, J.; et al. Lithium ion battery degradation: What you need to know. Phys. Chem. Chem. Phys. 2021, 23, 8200–8221. [Google Scholar] [CrossRef] [PubMed]
- Chiodo, E.; De Falco, P.; Di Noia, L.P. Probabilistic Modeling of Li-Ion Battery Remaining Useful Life. IEEE Trans. Ind. Appl. 2022, 58, 5214–5226. [Google Scholar] [CrossRef]
- Wu, Y.; Li, W.; Wang, Y.; Zhang, K. Remaining Useful Life Prediction of Lithium-Ion Batteries Using Neural Network and Bat-Based Particle Filter. IEEE Access 2019, 7, 54843–54854. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, M. Lithium-ion batteries remaining useful life prediction based on a mixture of empirical mode decomposition and ARIMA model. Microelectron. Reliab. 2016, 65, 265–273. [Google Scholar] [CrossRef]
- Li, D.; Yang, L. Remaining useful life prediction of lithium battery using convolutional neural network with optimized parameters. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020; pp. 840–844. [Google Scholar] [CrossRef]
- Williard, N.; He, W.; Osterman, M.; Pecht, M. Comparative analysis of features for determining state of health in lithium-ion batteries. Int. J. Progn. Health Manag. 2013, 4, 1–7. [Google Scholar] [CrossRef]
- Ma, Q.; Wang, Y.; Yang, W.; Tao, B.; Zheng, Y. A Novel Health Index for Battery RUL Degradation Modeling and Prognostics. In Proceedings of the 2019 IEEE 8th Data Driven Control and Learning Systems Conference (DDCLS), Dali, China, 24–27 May 2019; pp. 1077–1081. [Google Scholar] [CrossRef]
- Jia, J.; Liang, J.; Shi, Y.; Wen, J.; Pang, X.; Zeng, J. SOH and RUL Prediction of Lithium-Ion Batteries Based on Gaussian Process Regression with Indirect Health Indicators. Energies 2020, 13, 375. [Google Scholar] [CrossRef] [Green Version]
- Ren, L.; Zhao, L.; Hong, S.; Zhao, S.; Wang, H.; Zhang, L. Remaining Useful Life Prediction for Lithium-Ion Battery: A Deep Learning Approach. IEEE Access 2018, 6, 50587–50598. [Google Scholar] [CrossRef]
- Goyal, H.; Kikuchi, A.; Ueda, S.; Honkura, K.; Kawaji, J. Novel Multiple Parameter Optimization for Improving Accuracy of Battery Ageing Model and Lifetime Prediction. In Proceedings of the IECON 2022–48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, L.; Chen, J.; Wang, H.; Wang, Y.; An, J.; Yang, R.; Pan, H. Remaining Useful Life Prediction of Battery Using a Novel Indicator and Framework With Fractional Grey Model and Unscented Particle Filter. IEEE Trans. Power Electron. 2020, 35, 5850–5859. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, J.; Liao, H.; Peng, Y.; Peng, X. A Health Indicator Extraction and Optimization Framework for Lithium-Ion Battery Degradation Modeling and Prognostics. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 915–928. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Lithium-Ion Battery Remaining Useful Life Prediction With Box–Cox Transformation and Monte Carlo Simulation. IEEE Trans. Ind. Electron. 2019, 66, 1585–1597. [Google Scholar] [CrossRef]
- Huang, Z.; Zhou, X.; Gao, D.; Zhang, X.; Jiang, F.; Chen, B.; Yang, Y.; Wu, M.; Peng, J. A Novel Label-Free Supervision Learning Method for Lithium-ion Battery RUL Prediction. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 3150–3156. [Google Scholar] [CrossRef]
- Karmawijaya, M.I.; Haq, I.N.; Leksono, E.; Widyotriatmo, A. Development of Remaining Useful Life (RUL) Prediction of Lithium-ion Battery Using Genetic Algorithm-Deep Learning Neural Network (GADNN) Hybrid Model. In Proceedings of the 2022 7th International Conference on Electric Vehicular Technology (ICEVT), Bali, Indonesia, 14–16 September 2022; pp. 13–19. [Google Scholar] [CrossRef]
- Xu, J.; Zhen, A.; Cai, Z.; Wang, P.; Gao, K.; Jiang, D. State of Health Diagnosis and Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Multi-Feature Data and Mechanism Fusion. IEEE Access 2021, 9, 85431–85441. [Google Scholar] [CrossRef]
- Zhu, J.; Tan, T.; Wu, L.; Yuan, H. RUL Prediction of Lithium-Ion Battery Based on Improved DGWO-ELM Method in a Random Discharge Rates Environment. IEEE Access 2019, 7, 125176–125187. [Google Scholar] [CrossRef]
- Jiantao, Q.; Feng, L.; Yuxiang, M.; Jiaming, F. A Neural-Network-based Method for RUL Prediction and SOH Monitoring of Lithium-Ion Battery. IEEE Access 2019, 7, 87178–87191. [Google Scholar] [CrossRef]



| Classification | Configuration | Description | Advantage | Disadvantage | |
|---|---|---|---|---|---|
| Electrical model | Rint model | 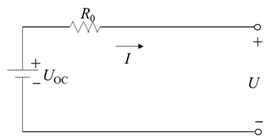 | An ideal voltage source is connected to a resistor in series. | The model is simple, and the parameter measurement is easy. | It cannot reflect the dynamic characteristics of the battery and has low accuracy with a small range of applications. |
| Thevenin model | 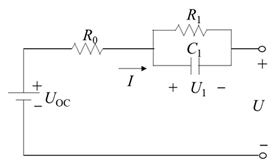 | The n-order Thevenin equivalent circuit model is based on the Rint model; n RC circuits are connected in series to represent the polarization phenomenon of the cell. | The RC loop is used to simulate the dynamic characteristics of batteries, and the higher the n, the higher the precision | The change in open-circuit voltage and the self-discharge caused by load current accumulated over time are not considered. The bigger the n, the more computation. | |
| PNGV model | 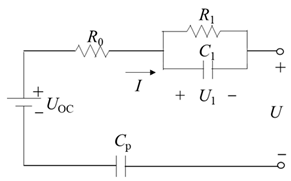 | Based on the 1st order Thevenin equivalent circuit model, capacitor Cp is added to describe the change in open-circuit voltage caused by load current over time. | The calculation burden is low; Compared with the 1st order Thevenin equivalent circuit model, the accuracy is higher. | It does not solve the battery self-discharge problem. | |
| GNL model | 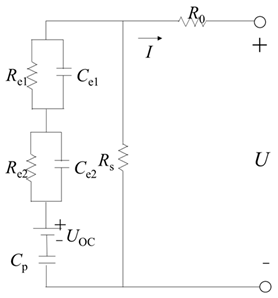 | The two RC loops represent concentration polarization and electrochemical polarization, respectively, and the structure is closer to the internal characteristics of the cell. | Compared with PNGV, the open circuit voltage change caused by load current over time is considered, and the battery self-discharge is considered; higher precision and wider applicability. | Compared with the PNGV model, the calculation is more complex with larger calculation burden. | |
| Open-circuit voltage SOC model | The battery terminal voltage is calculated with the relationship between OCV and SOC. | Simple calculation | Some parameters of the model do not have actual physical significance, and the accuracy is low. | ||
| Electrochemical model | P2D model | 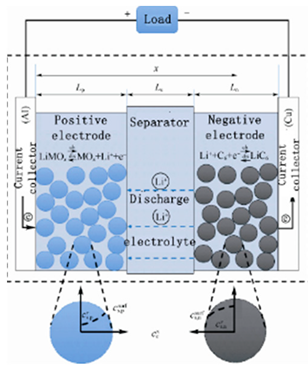 | The lithium–ion battery is equivalent to the structure of electrode (positive and negative electrode); diaphragm and electrolyte are composed of numerous spherical solid particles. | High accuracy and wide applicability | It is too complex and computationally intensive, and the analytical solution can be is difficult to obtain. |
| SP model |  | Two spherical particles are used to represent the positive and negative terminals of lithium ion batteries, respectively. | Simple structure and small amount of calculation | Under the condition of high rate charge and discharge, the assumption of the model is not valid, the calculation error is large and the application range is small. | |
| Simplify the P2D model | The PDE of the P2D model is simplified. | The calculation burden of the P2D model is greatly reduced. It is more accurate and applicable than the SP model. | Unable to solve the inherent problems of the P2D, it is difficult to apply online. | ||
| Classification | Method | Advantage | Disadvantage | |
|---|---|---|---|---|
| Experimental method | Ampere integration | Non-relative internal mechanism of the battery; simple | Easy to generate cumulative error, which requires high initial value and sensor precision | |
| OCV–SOC method | Non-relative to battery types; simple | The SOC cannot be calculated online in real time [5] | ||
| Model-based method | Basic model | Electrical model | Simple and practical | Poor accuracy |
| Electrochemical model | It reflects the internal characteristics of the battery | Complex and computationally intensive [5] | ||
| State estimation method | KF method | The convergence speed is fast, and the noise suppression ability is strong. Low sensitivity to initial value | The system noise is uncertain, which requires high accuracy of the model | |
| PF method | Strong robustness and low requirement for model accuracy | Prone to particle degradation Computationally intensive | ||
| Data-driven method | Neural network | No reliance on high-precision battery models | Easy to disappear gradient and fall into local optimization Computationally intensive Easy to overfit, poor generalization capability | |
| Regression analysis | It can achieve good results in high-dimensional pattern recognition, nonlinear regression and other problems | Only applicable to small data samples | ||
| Joint method | Model-based method and data-driven method | The accuracy and reliability of the estimation results are high | High complexity and computationally intensive [2] | |
| Data-driven method and data-driven method | ||||
| Classification | Health Factors |
|---|---|
| Voltage curve relavant | Constant voltage charging time [93], voltage increment in the same time interval [94], time consumed for certain voltage increments [95], dQ/dV [97], dV/dQ [97], maximum slope of voltage curve [95] |
| Current curve relavant | Constant current charging time [93], current increment in the same time interval [94], time consumed for certain current increments [96], area under current curve [95] |
| Temperature | Temperature increment in the same time interval [94], time consumed for certain temperature increments [95] |
| Other | Wavelet packet energy entropy [98] |
| Classification | Method | Advantage | Disadvantage |
|---|---|---|---|
| Model-based method | Empirical model | Low calculation burden [3] | Poor accuracy; not be able to consider influence of working conditions and the environment [2] |
| Semi-empirical model | Able to consider influence of working conditions and environment | Low accuracy; low robustness under dramatic working condition changes [1] | |
| Electrochemical model | Able to reveal the aging mechanism | Large calculation amounts due to too many parameters [3] | |
| Data-driven method | Time series prediction method | Does not require complex mathematical models | Large calculation amounts; overfitting; unable to reveal local RUL variation and highly dependent on training set and data quality |
| Feature-based method | Related to battery characteristics [4] Good accuracy for local RUL variation | Heavy calculation burden [2] | |
| Joint method | Model-based method and data-driven method | Relatively high reliability and accuracy [4] | Heavy calculation burden; high complexity [2] |
| Data-driven method and data-driven method |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Zhu, Y.; Zhang, B.; Liu, M.; Wang, J.; Liu, C.; Hao, X. Review of State Estimation and Remaining Useful Life Prediction Methods for Lithium–Ion Batteries. Sustainability 2023, 15, 5014. https://doi.org/10.3390/su15065014
Zhao J, Zhu Y, Zhang B, Liu M, Wang J, Liu C, Hao X. Review of State Estimation and Remaining Useful Life Prediction Methods for Lithium–Ion Batteries. Sustainability. 2023; 15(6):5014. https://doi.org/10.3390/su15065014
Chicago/Turabian StyleZhao, Jiahui, Yong Zhu, Bin Zhang, Mingyi Liu, Jianxing Wang, Chenghao Liu, and Xiaowei Hao. 2023. "Review of State Estimation and Remaining Useful Life Prediction Methods for Lithium–Ion Batteries" Sustainability 15, no. 6: 5014. https://doi.org/10.3390/su15065014





