High-Accuracy Positioning in Urban Environments Using Single-Frequency Multi-GNSS RTK/MEMS-IMU Integration
Abstract
:1. Introduction
2. Methods
2.1. Tightly-Coupled GPS/BDS/GLONASS RTK/INS Integration Model
2.1.1. INS Dynamic Model
2.1.2. Measurement Model
2.1.3. Single-Epoch Ambiguity Resolution with Inertial Aiding
2.2. Innovation-Based Outlier-Resistant Ambiguity Resolution and Kalman Filtering Strategy
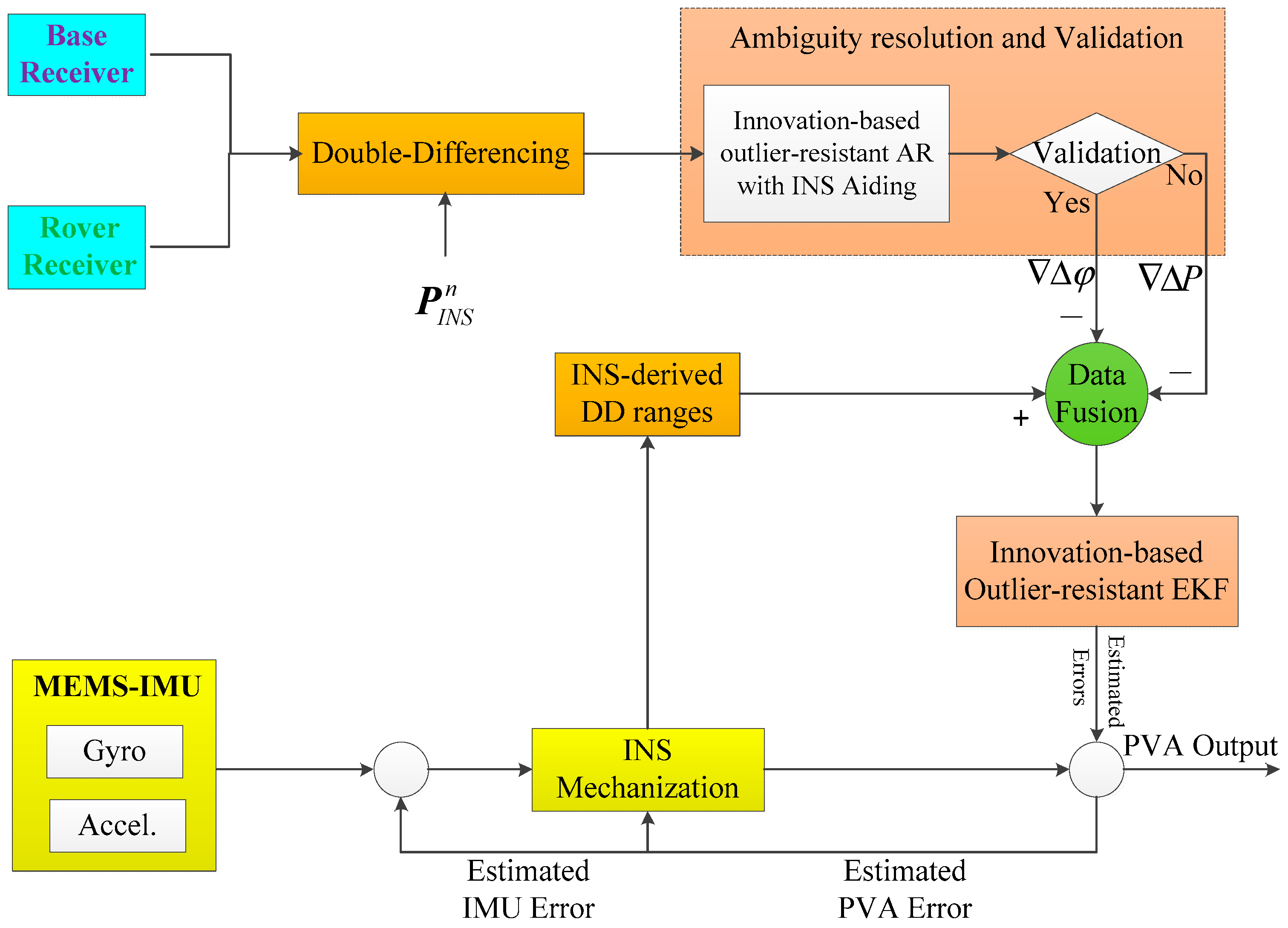
2.3. Overview of Multi-GNSS RTK/INS Tightly-Coupled Integration with Innovation-Based FDE
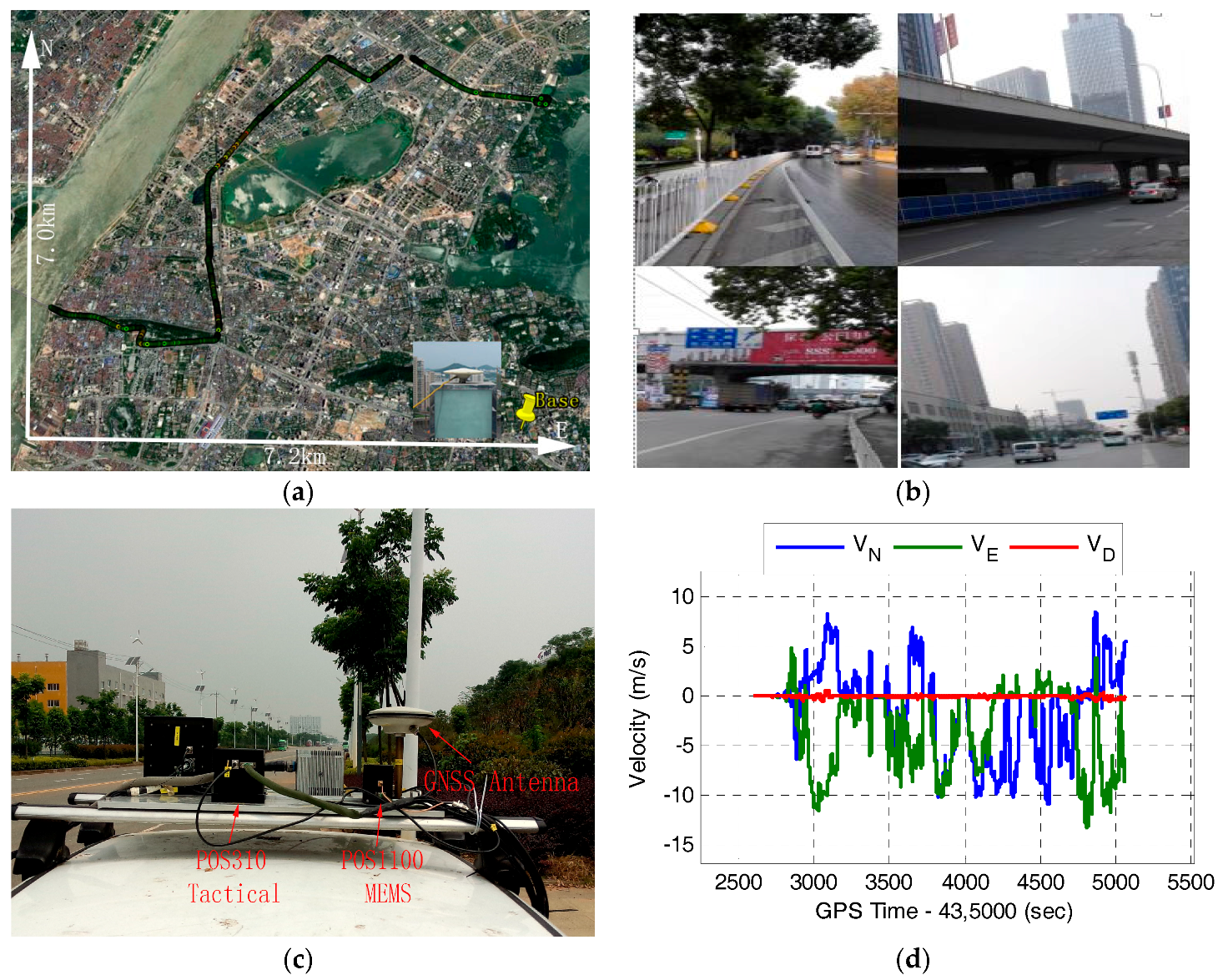
3. Field Test Description and Data Processing Strategy
4. Results and Discussion
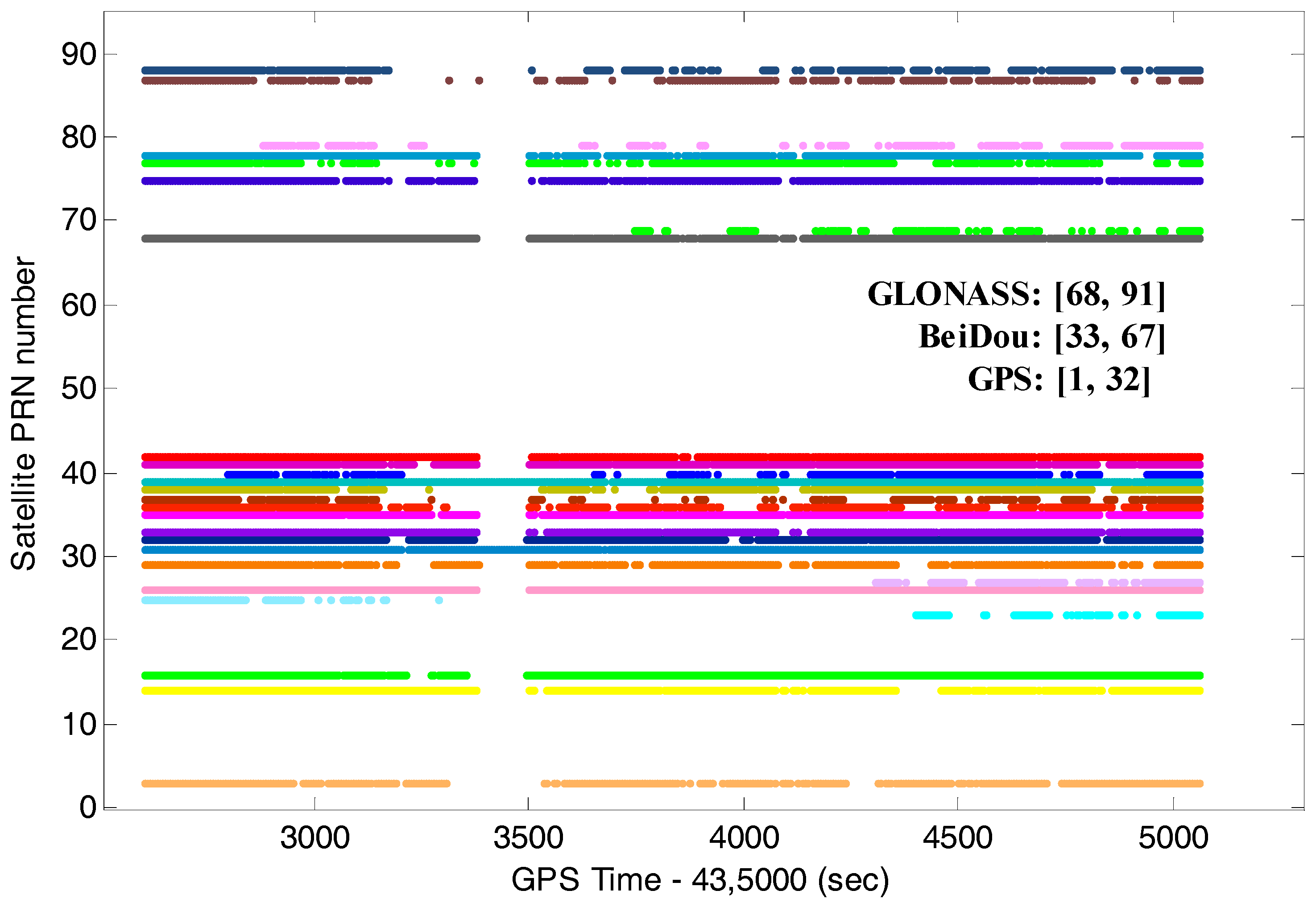
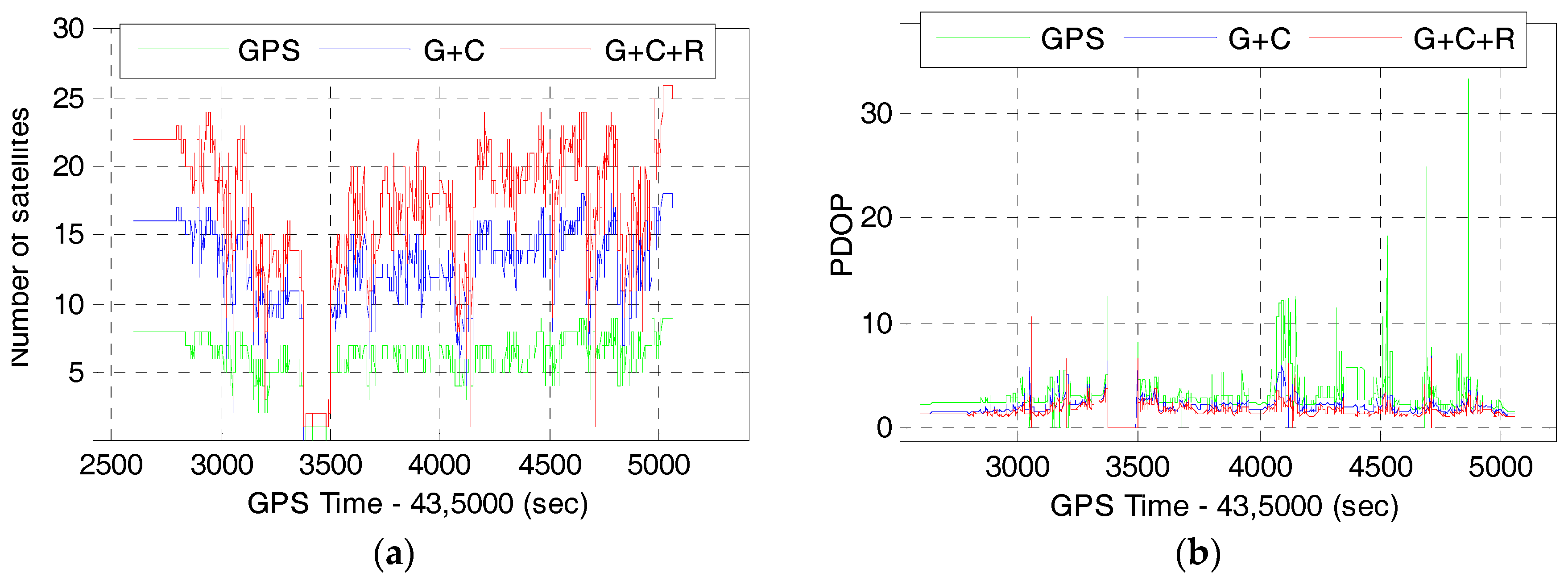
4.1. Satellite Availability
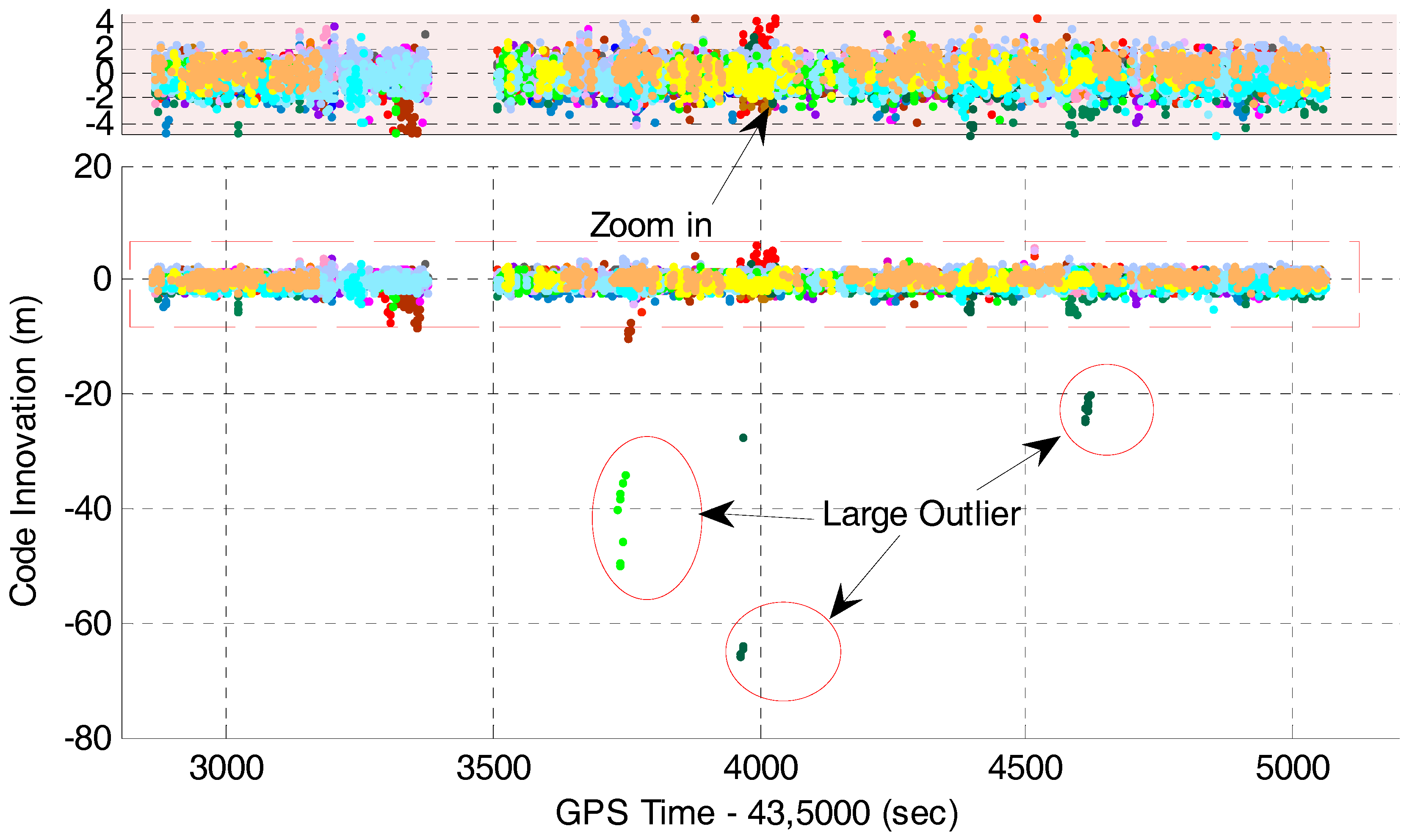
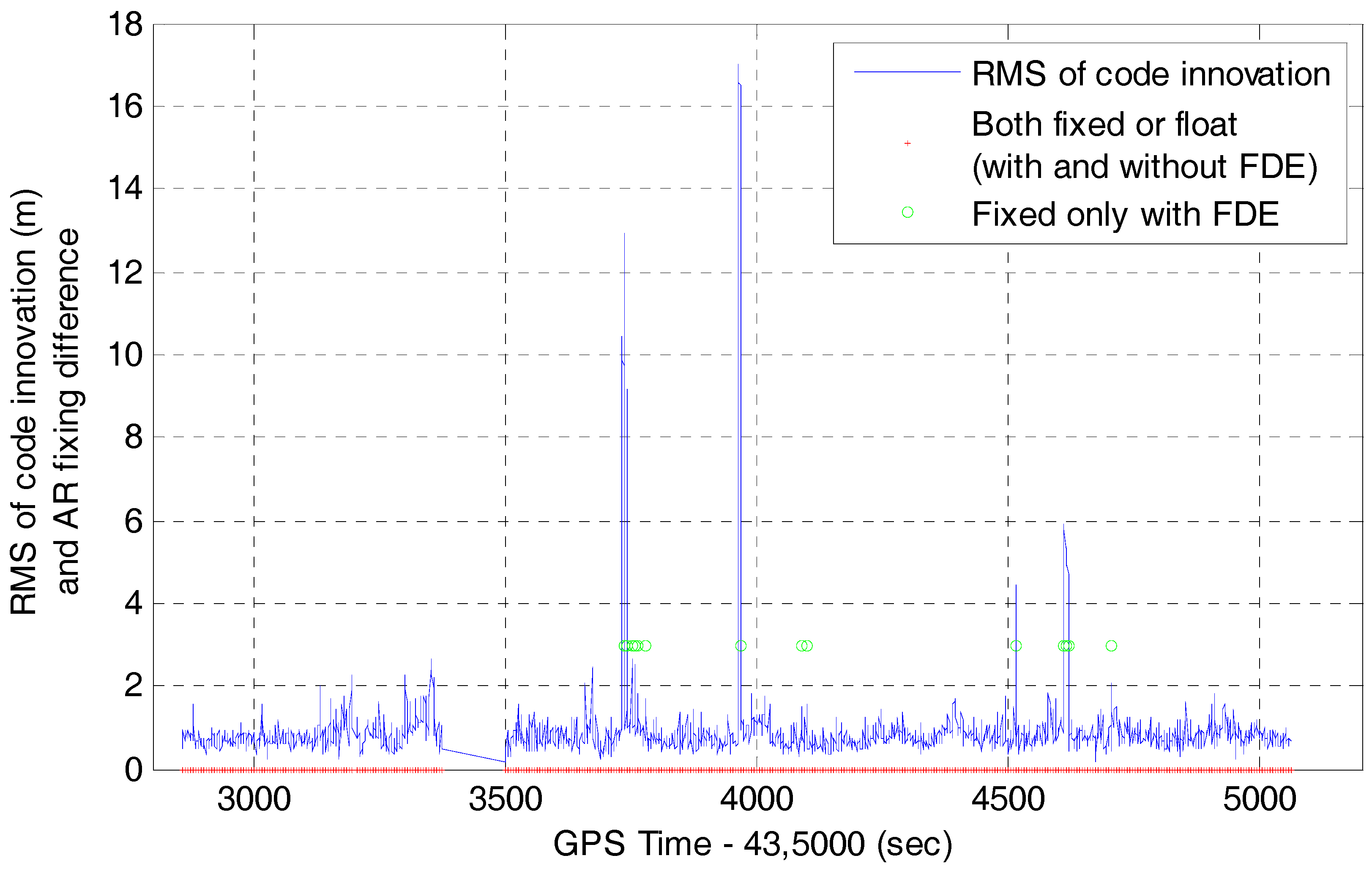
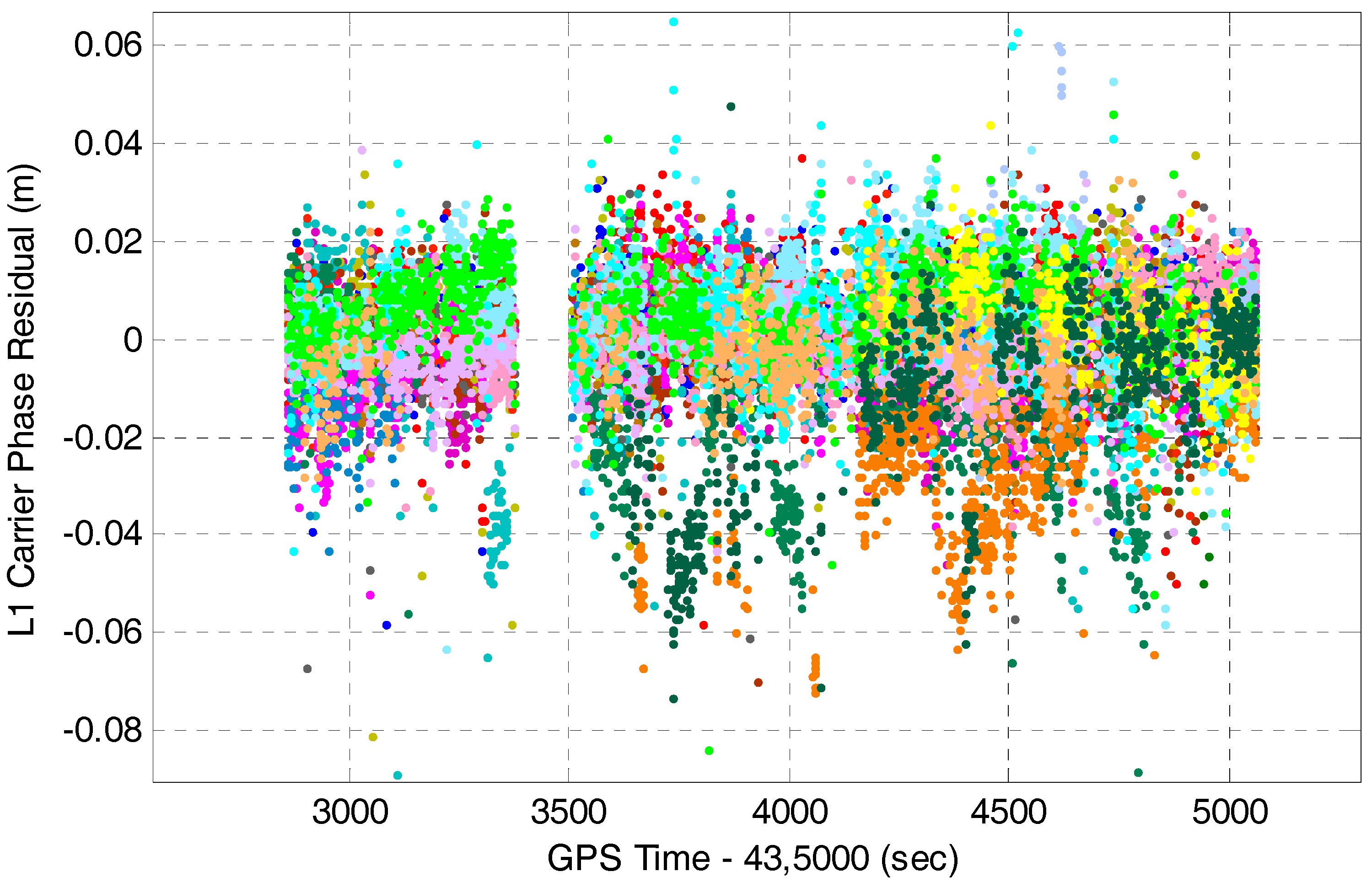
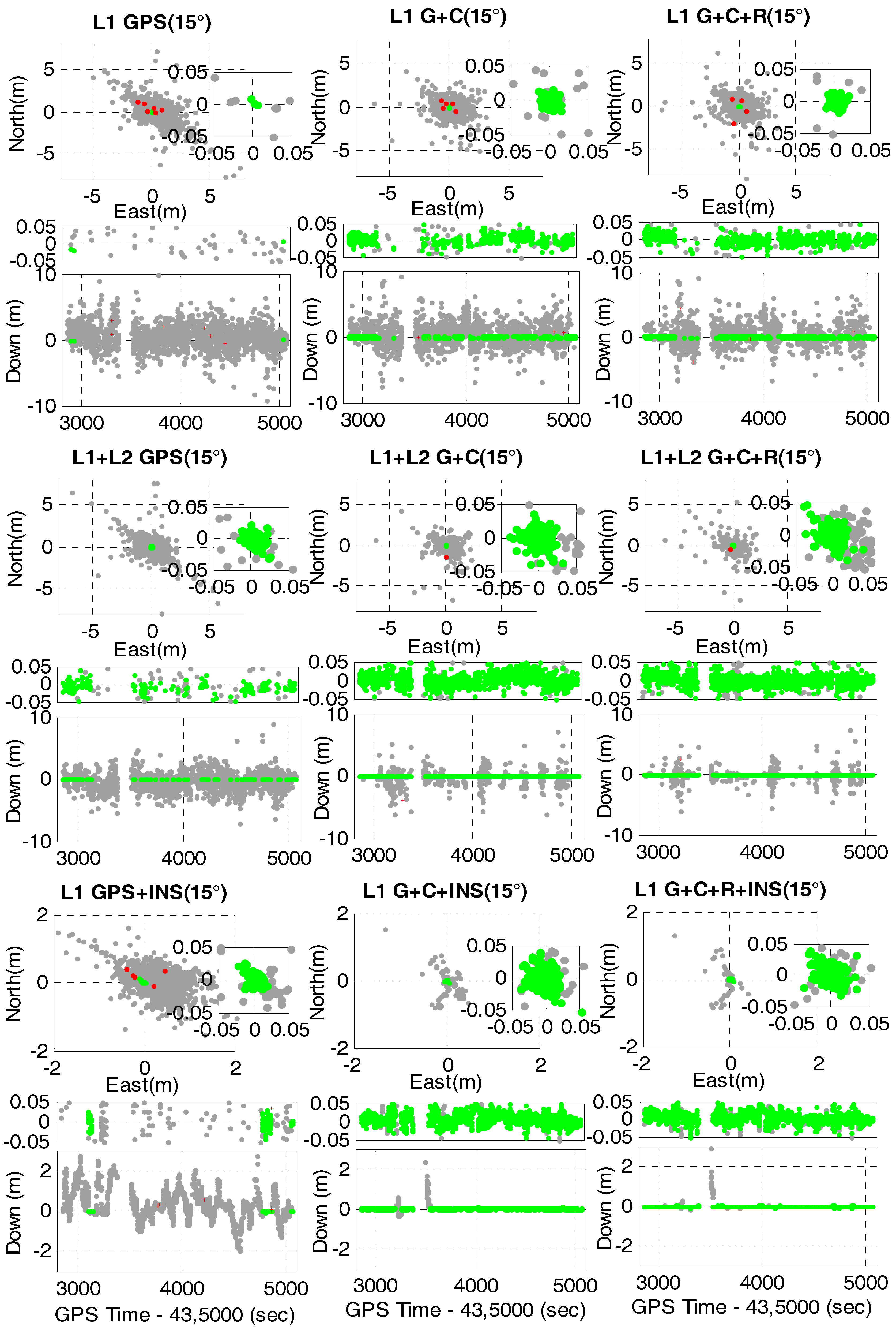
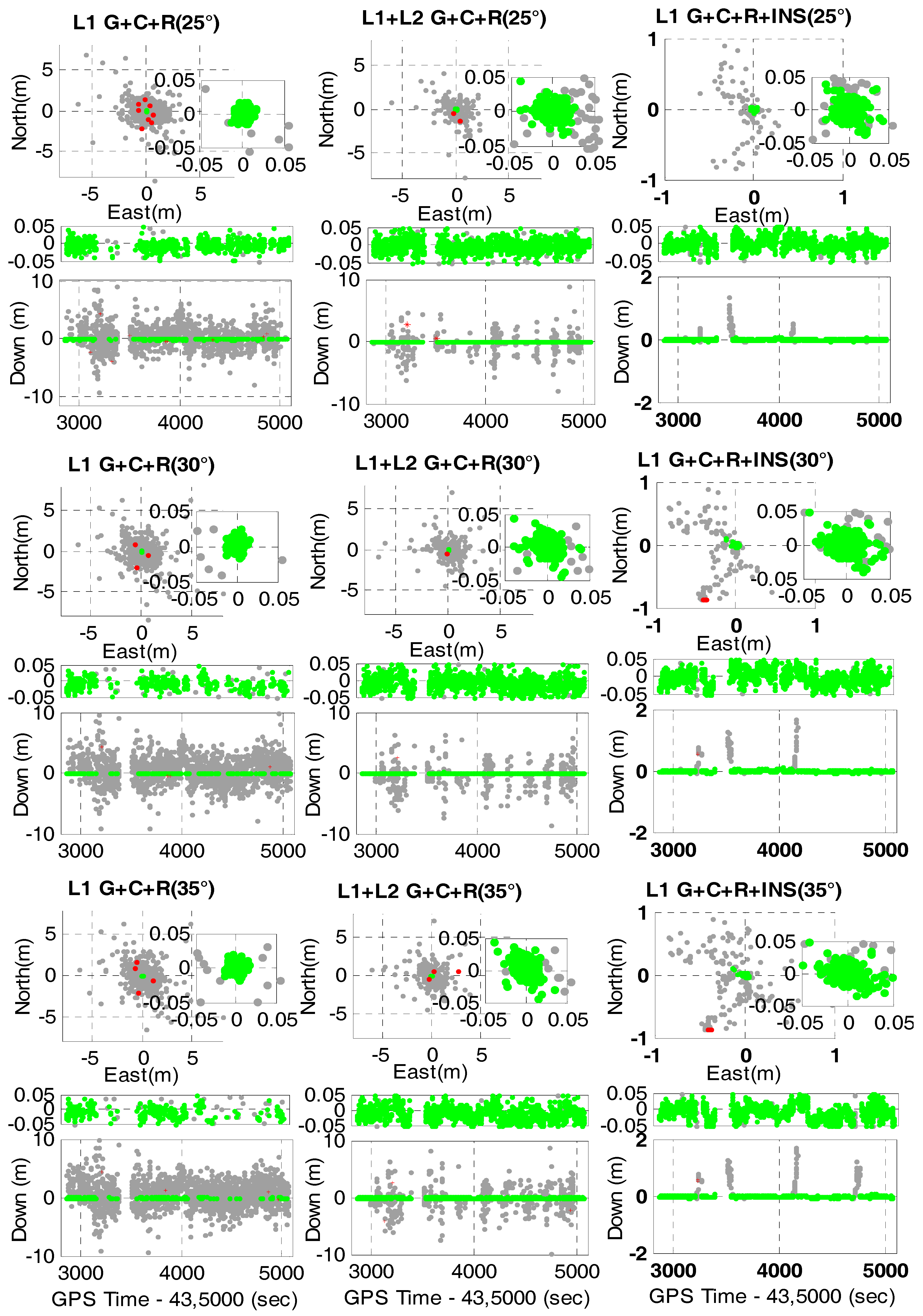
4.2. Multi-GNSS RTK/INS Integration with Innovation-Based FDE
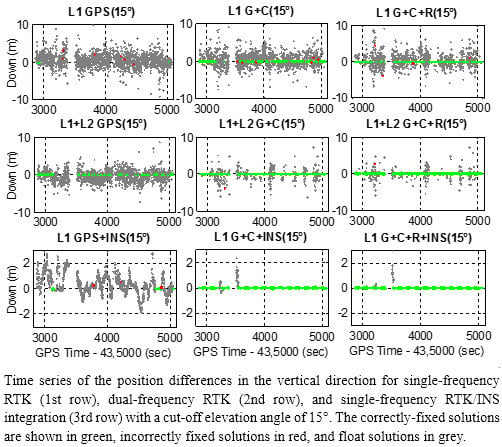
4.3. Single-Epoch Ambiguity Resolution and Positioning
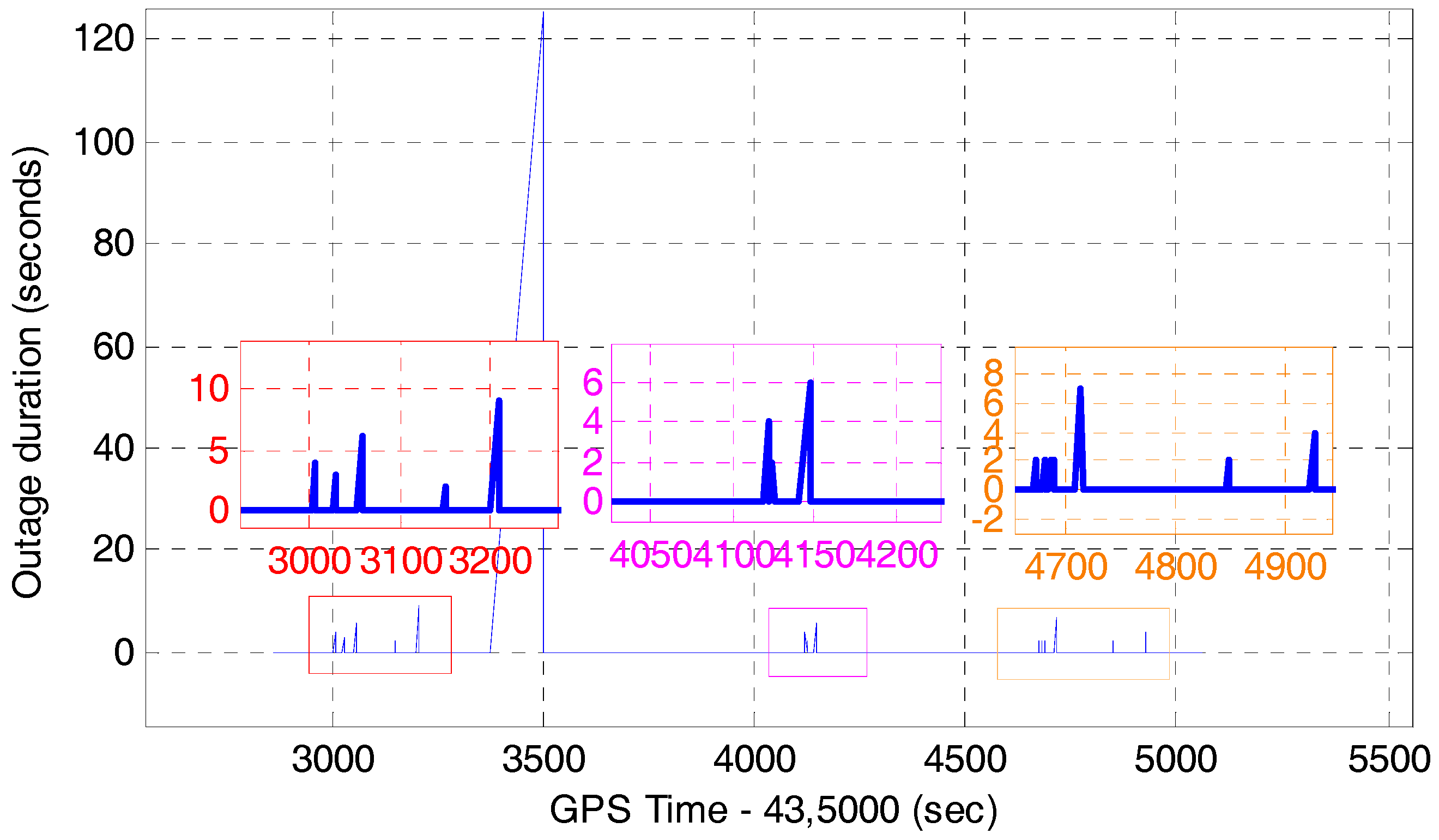
4.4. Position Drift Error for Multi-GNSS RTK/INS Integration after the End of GNSS Outages
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- He, H.; Li, J.; Yang, Y.; Xu, J.; Guo, H.; Wang, A. Performance assessment of single- and dual-frequency BeiDou/GPS single-epoch kinematic positioning. GPS Solut. 2014, 18, 393–403. [Google Scholar] [CrossRef]
- Ong, R.B.; Petovello, M.G.; Lachapelle, G. Assessment of GPS/GLONASS RTK under Various Operational Conditions. In Proceedings of the 22nd International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009; pp. 3297–3308. [Google Scholar]
- Carcanague, S.; Julien, O.; Vigneau, W.; Macabiau, C. Low-Cost Single-Frequency GPS/GLONASS RTK for Road Users. In Proceedings of the ION 2013 Pacific PNT Meeting, Honolulu, HI, USA, 23–25 April 2013; pp. 168–184. [Google Scholar]
- Montenbruck, O.; Steigenberger, P.; Khachikyan, R.; Weber, G.; Langley, R.B.; Mervart, L.; Hugentobler, U. IGS-MGEX: Preparing the ground for multi-constellation GNSS science. Inside GNSS 2014, 9, 42–49. [Google Scholar]
- Teunissen, P.J.G.; Odolinski, R.; Odijk, D. Instantaneous BeiDou+GPS RTK positioning with high cut-off elevation angles. J. Geod. 2013, 88, 335–350. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G. Low-cost, high-precision, single-frequency GPS–BDS RTK positioning. GPS Solut. 2017, 21, 1315–1330. [Google Scholar] [CrossRef]
- Li, T.; Zhang, H.; Niu, X.; Gao, Z. Tightly-Coupled Integration of Multi-GNSS Single-Frequency RTK and MEMS-IMU for Enhanced Positioning Performance. Sensors 2017, 17, 2462. [Google Scholar] [CrossRef] [PubMed]
- Odolinski, R.; Teunissen, P.J.G.; Odijk, D. Combined BDS, Galileo, QZSS and GPS single-frequency RTK. GPS Solut. 2014, 19, 151–163. [Google Scholar] [CrossRef]
- Wanninger, L.; Wallstab-Freitag, S. Combined Processing of GPS, GLONASS, and SBAS Code Phase and Carrier Phase Measurements. In Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 866–875. [Google Scholar]
- Sleewaegen, J.; Simsky, A.; De Wilde, W.; Boon, F.; Willems, T. Demystifying GLONASS inter-frequency carrier phase bias. Inside GNSS 2012, 7, 57–61. [Google Scholar]
- Wanninger, L. Carrier-phase inter-frequency biases of GLONASS receivers. J. Geod. 2012, 86, 139–148. [Google Scholar] [CrossRef]
- Tian, Y.; Ge, M.; Neitzel, F. Particle filter-based estimation of inter-frequency phase bias for real-time GLONASS integer ambiguity resolution. J. Geod. 2015, 89, 1145–1158. [Google Scholar] [CrossRef]
- Gao, Z.; Shen, W.; Zhang, H.; Ge, M.; Niu, X. Application of Helmert Variance Component Based Adaptive Kalman Filter in Multi-GNSS PPP/INS Tightly Coupled Integration. Remote Sens. 2016, 8, 553. [Google Scholar] [CrossRef]
- Grejner-Brzezinska, D.A.; Da, R.; Toth, C. GPS error modeling and OTF ambiguity resolution for high-accuracy GPS/INS integrated system. J. Geod. 1998, 72, 626–638. [Google Scholar] [CrossRef]
- Niu, X.; Zhang, Q.; Gong, L.; Liu, C.; Zhang, H.; Shi, C.; Wang, J.; Coleman, M. Development and evaluation of GNSS/INS data processing software for position and orientation systems. Surv. Rev. 2015, 47, 87–98. [Google Scholar] [CrossRef]
- Falco, G.; Einicke, G.A.; Malos, J.T.; Dovis, F. Performance Analysis of Constrained Loosely Coupled GPS/INS Integration Solutions. Sensors 2012, 12, 15983–16007. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Jiang, W. On-Board GNSS/IMU Assisted Feature Extraction and Matching for Oblique UAV Images. Remote Sens. 2017, 9, 813. [Google Scholar] [CrossRef]
- Hide, C.; Moore, T. GPS and Low Cost INS Integration for Positioning in the Urban Environment. In Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation, Long Beach, CA, USA, 13–16 September 2005; pp. 1007–1015. [Google Scholar]
- Godha, S.; Cannon, M.E. GPS/MEMS INS integrated system for navigation in urban areas. GPS Solut. 2007, 11, 193–203. [Google Scholar] [CrossRef]
- Chiang, K.-W.; Duong, T.; Liao, J.-K. The Performance Analysis of a Real-Time Integrated INS/GPS Vehicle Navigation System with Abnormal GPS Measurement Elimination. Sensors 2013, 13, 10599–10622. [Google Scholar] [CrossRef] [PubMed]
- Falco, G.; Gutiérrez, C.C.; Serna, E.P.; Zacchello, F.; Bories, S. Low-cost Real-time Tightly-Coupled GNSS/INS Navigation System Based on Carrier-phase Double- differences for UAV Applications. In Proceedings of the 27th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2014), Tampa, FL, USA, 8–12 September 2014; pp. 841–857. [Google Scholar]
- Eling, C.; Klingbeil, L.; Kuhlmann, H. Real-Time Single-Frequency GPS/MEMS-IMU Attitude Determination of Lightweight UAVs. Sensors 2015, 15, 26212–26235. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Chen, Y.; Farrell, J.A. High-Precision Vehicle Navigation in Urban Environments Using an MEM’s IMU and Single-Frequency GPS Receiver. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2854–2867. [Google Scholar] [CrossRef]
- Falco, G.; Pini, M.; Marucco, G. Loose and Tight GNSS/INS Integrations: Comparison of Performance Assessed in Real Urban Scenarios. Sensors 2017, 17, 255. [Google Scholar] [CrossRef] [PubMed]
- Dorn, M.; Filwarny, J.O.; Wieser, M. Inertially-aided RTK based on tightly-coupled integration using low-cost GNSS receivers. In Proceedings of the 2017 European Navigation Conference (ENC), Lausanne, Switzerland, 9–12 May 2017; pp. 186–197. [Google Scholar]
- Teunissen, P.J.G. Quality control in integrated navigation systems. In Proceedings of the IEEE Symposium on Position Location and Navigation. A Decade of Excellence in the Navigation Sciences, Las Vegas, NV, USA, 20–23 March 1990; pp. 158–165. [Google Scholar]
- Gillissen, I.; Elema, I.A. Test results of DIA: A real-time adaptive integrity monitoring procedure, used in an integrated navigation system. Int. Hydrogr. Rev. 1996, 73, 75–100. [Google Scholar]
- Clark, B.J.; Bevly, D.M. GPS/INS integration with fault detection and exclusion in shadowed environments. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008; pp. 1–8. [Google Scholar]
- Hewitson, S.; Wang, J. Extended receiver autonomous integrity monitoring (eRAIM) for GNSS/INS integration. J. Surv. Eng. 2007, 136, 13–22. [Google Scholar] [CrossRef]
- Benson, D.O. A Comparison of Two Approaches to Pure-Inertial and Doppler-Inertial Error Analysis. IEEE Trans. Aerosp. Electron. Syst. 1975, 4, 447–455. [Google Scholar] [CrossRef]
- Park, M. Error Analysis and Stochastic Modeling of MEMS Based Inertial Sensors for Land Vehicle Navigation Applications. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, April 2004. [Google Scholar]
- Petovello, M. GLONASS inter-frequency biases and ambiguity resolution. Inside GNSS 2009, 4, 24–28. [Google Scholar]
- Gendt, G.; Dick, G.; Reigber, C.H.; Tomassini, M.; Liu, Y.; Ramatschi, M. Demonstration of NRT GPS Water Vapor Monitoring for Numerical Weather Prediction in Germany. J. Meteorol. Soc. Jpn. 2003, 82, 360–370. [Google Scholar]
- Shin, E.-H. Estimation Techniques for Low-Cost Inertial Navigation. Ph.D. Thesis, The University of Calgary, Calgary, AB, Canada, May 2005. [Google Scholar]
- Scherzinger, B.M. Robust Positioning with Single Frequency Inertially Aided RTK. In Proceedings of the 2002 National Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 28–30 January 2002; pp. 911–917. [Google Scholar]
- Teunissen, P.J.G. The Least-Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Ji, S.; Chen, W.; Ding, X.; Chen, Y.; Zhao, C.; Hu, C. Ambiguity validation with combined ratio test and ellipsoidal integer aperture estimator. J. Geod. 2010, 84, 597–604. [Google Scholar] [CrossRef]
- Verhagen, S. On the Reliability of Integer Ambiguity Resolution. Navigation 2005, 52, 99–110. [Google Scholar] [CrossRef]
- Yang, Y.; Song, L.; Xu, T. Robust estimator for correlated observations based on bifactor equivalent weights. J. Geod. 2002, 76, 353–358. [Google Scholar] [CrossRef]
- Savage, P.G. Strapdown inertial navigation integration algorithm design part 1: Attitude algorithms. J. Guid. Control Dyn. 1998, 21, 19–28. [Google Scholar] [CrossRef]
- Savage, P.G. Strapdown inertial navigation integration algorithm design part 2: Velocity and position algorithms. J. Guid. Control Dyn. 1998, 21, 208–221. [Google Scholar] [CrossRef]
- Deng, C.; Tang, W.; Liu, J.; Shi, C. Reliable single-epoch ambiguity resolution for short baselines using combined GPS/BeiDou system. GPS Solut. 2013, 18, 375–386. [Google Scholar] [CrossRef]
- Gelb, A. Applied Optimal Estimation; MIT Press: Cambridge, MA, USA, 1974; pp. 160–165. [Google Scholar]

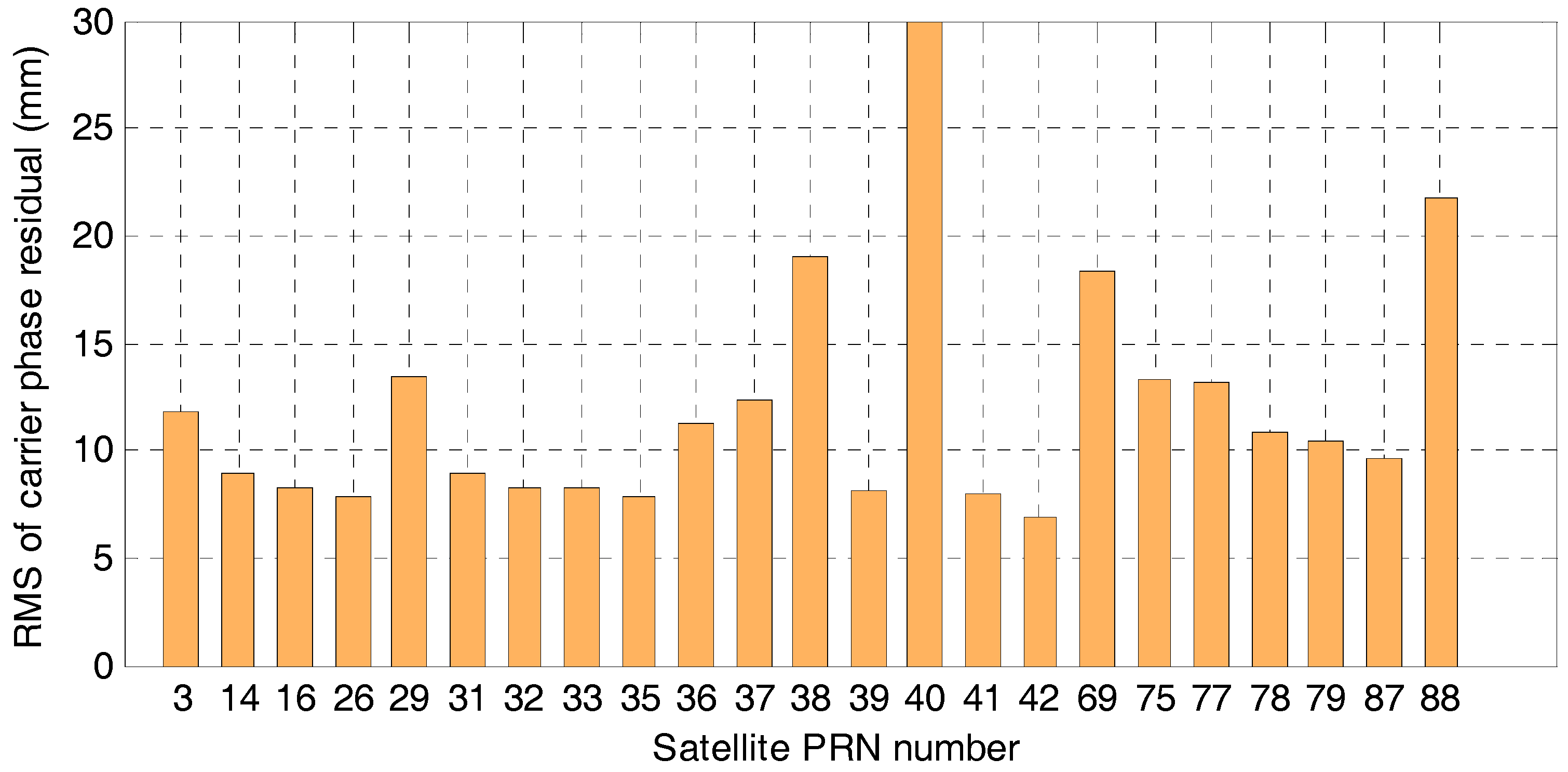
| IMU | Grade | Dimensions (mm) | Bias | Random Walk | ||
|---|---|---|---|---|---|---|
| Gyro. ( | Acce. (mGal) | Angular () | Velocity () | |||
| POS310 | Tactical | 151 × 120 × 101 | 0.5 | 300 | 0.05 | 0.10 |
| POS1100 | MEMS | 81.8 × 68 × 70 | 10.0 | 1500 | 0.33 | 0.18 |
| System | G | G + C | G + C + R | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PA | 85.5 | 91.8 | 92.4 | |||||||||
| RMS (cm) | N | E | D | FR | N | E | D | FR | N | E | D | FR |
| L1 RTK Fixed/Float | 0.35 | 0.45 | 1.58 | 0.1 | 1.27 | 2.21 | 2.09 | 25.1 | 0.35 | 0.38 | 1.13 | 44.7 |
| 105.9 | 97.2 | 179.0 | 74.42 | 76.27 | 180.9 | 83.54 | 86.67 | 188.9 | ||||
| L1 + L2 RTK Fixed/Float | 0.72 | 0.74 | 1.47 | 10.4 | 0.57 | 0.62 | 1.59 | 75.8 | 0.57 | 0.56 | 1.41 | 76.7 |
| 91.19 | 90.88 | 147.1 | 81.66 | 95.23 | 170.9 | 86.83 | 91.90 | 143.9 | ||||
| L1 + INS Fixed/Float | 1.60 | 1.60 | 1.45 | 5.8 | 0.55 | 0.65 | 1.79 | 86.1 | 0.53 | 0.57 | 1.50 | 86.1 |
| 58.40 | 34.94 | 85.61 | 23.54 | 37.35 | 53.61 | 16.44 | 27.78 | 44.81 | ||||
| Cut-off (°) | 25 | 30 | 35 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMS (cm) | N | E | D | FR | N | E | D | FR | N | E | D | FR |
| L1 RTK Fixed/Float | 0.35 | 0.44 | 1.33 | 36.1 | 0.41 | 0.52 | 1.95 | 20.3 | 0.46 | 0.54 | 2.07 | 14.7 |
| 78.44 | 88.31 | 206.3 | 81.30 | 87.39 | 223.9 | 81.14 | 87.75 | 226.4 | ||||
| L1 + L2 RTK Fixed/Float | 0.50 | 0.56 | 1.56 | 77.7 | 0.60 | 0.73 | 2.28 | 74.3 | 0.55 | 0.76 | 2.60 | 71.5 |
| 82.56 | 100.9 | 183.5 | 102.8 | 102.5 | 221.2 | 107.9 | 103.4 | 230.4 | ||||
| L1 + INS Fixed/Float | 0.54 | 0.62 | 1.75 | 86.2 | 0.76 | 0.78 | 2.51 | 84.7 | 0.78 | 0.77 | 2.37 | 82.2 |
| 20.35 | 32.28 | 43.03 | 35.47 | 50.04 | 67.94 | 36.00 | 47.65 | 67.59 | ||||
| Outage Items | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Duration (s) | 4 | 3 | 6 | 2 | 9 | 127 | 4 | 6 | 2 | 2 | 7 | 2 | 4 | |
| MAX (cm) | North | 0.4 | 1.2 | 5.6 | 1.9 | 0.9 | 523.5 | 1.9 | 5.8 | 7.1 | 6.8 | 6.7 | 1.5 | 3.2 |
| East | 6.2 | 0.4 | 9.3 | 1.7 | 15.3 | 1739.3 | 1.1 | 14.6 | 1.5 | 0.3 | 14.7 | 4.2 | 3.2 | |
| Down | 7.1 | 1.6 | 5.5 | 1.4 | 4.8 | 2817.3 | 6.9 | 1.1 | 2.3 | 8.7 | 1.4 | 1.4 | 1.7 | |
| 3D | 9.4 | 2.0 | 12.2 | 2.9 | 16.1 | 3352.1 | 7.2 | 15.7 | 7.6 | 11.0 | 16.2 | 4.7 | 4.8 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Zhang, H.; Gao, Z.; Chen, Q.; Niu, X. High-Accuracy Positioning in Urban Environments Using Single-Frequency Multi-GNSS RTK/MEMS-IMU Integration. Remote Sens. 2018, 10, 205. https://doi.org/10.3390/rs10020205
Li T, Zhang H, Gao Z, Chen Q, Niu X. High-Accuracy Positioning in Urban Environments Using Single-Frequency Multi-GNSS RTK/MEMS-IMU Integration. Remote Sensing. 2018; 10(2):205. https://doi.org/10.3390/rs10020205
Chicago/Turabian StyleLi, Tuan, Hongping Zhang, Zhouzheng Gao, Qijin Chen, and Xiaoji Niu. 2018. "High-Accuracy Positioning in Urban Environments Using Single-Frequency Multi-GNSS RTK/MEMS-IMU Integration" Remote Sensing 10, no. 2: 205. https://doi.org/10.3390/rs10020205
APA StyleLi, T., Zhang, H., Gao, Z., Chen, Q., & Niu, X. (2018). High-Accuracy Positioning in Urban Environments Using Single-Frequency Multi-GNSS RTK/MEMS-IMU Integration. Remote Sensing, 10(2), 205. https://doi.org/10.3390/rs10020205