Comparative Study of 2D Lattice Boltzmann Models for Simulating Seismic Waves
Abstract
:1. Introduction
2. Lattice Boltzmann Models
2.1. Basis Theory
2.2. 2D Discrete Velocity Models
2.3. TRT and MRT Collision Operators
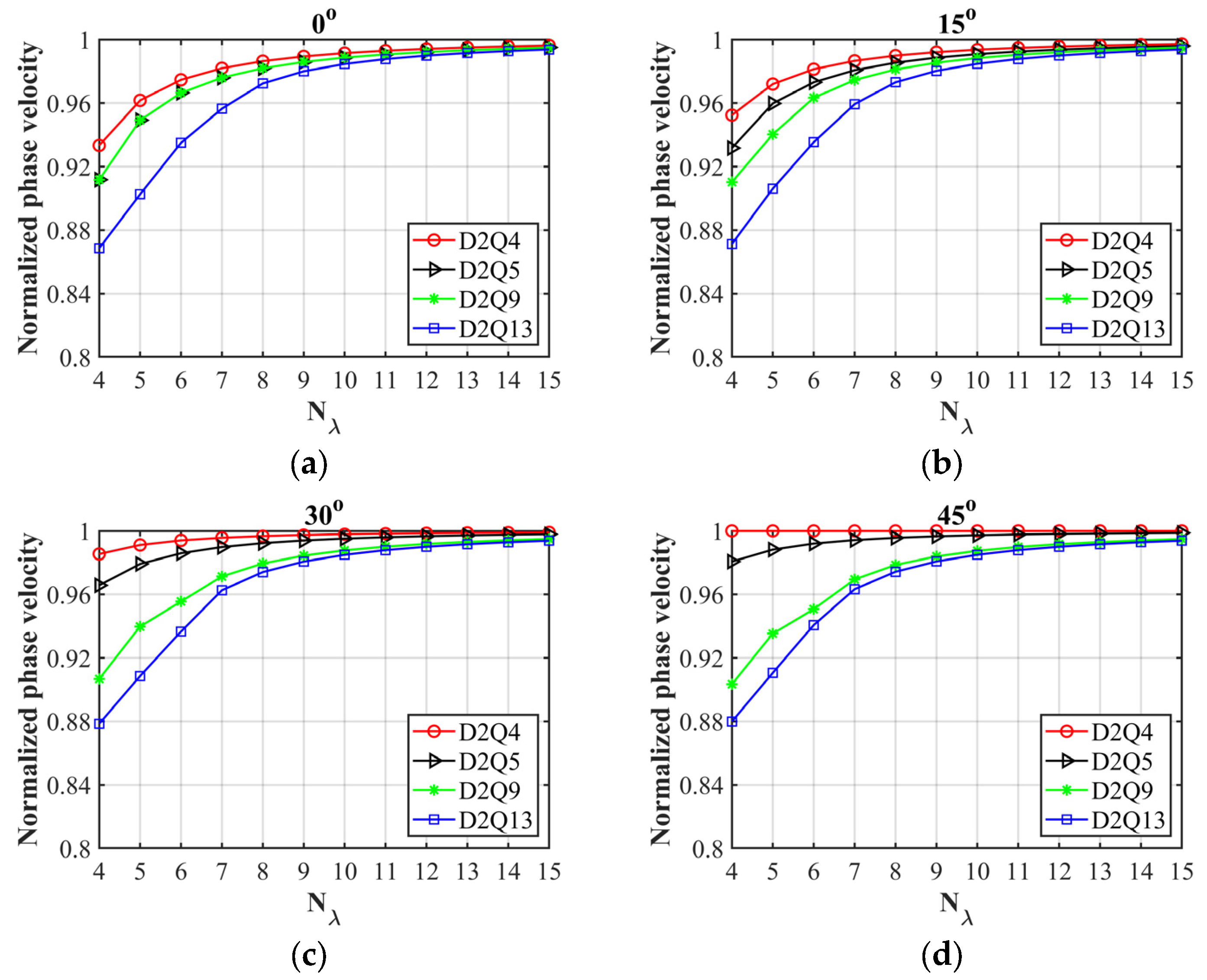
3. Numerical Dispersion and Stability Analysis
3.1. Numerical Dispersion Analysis
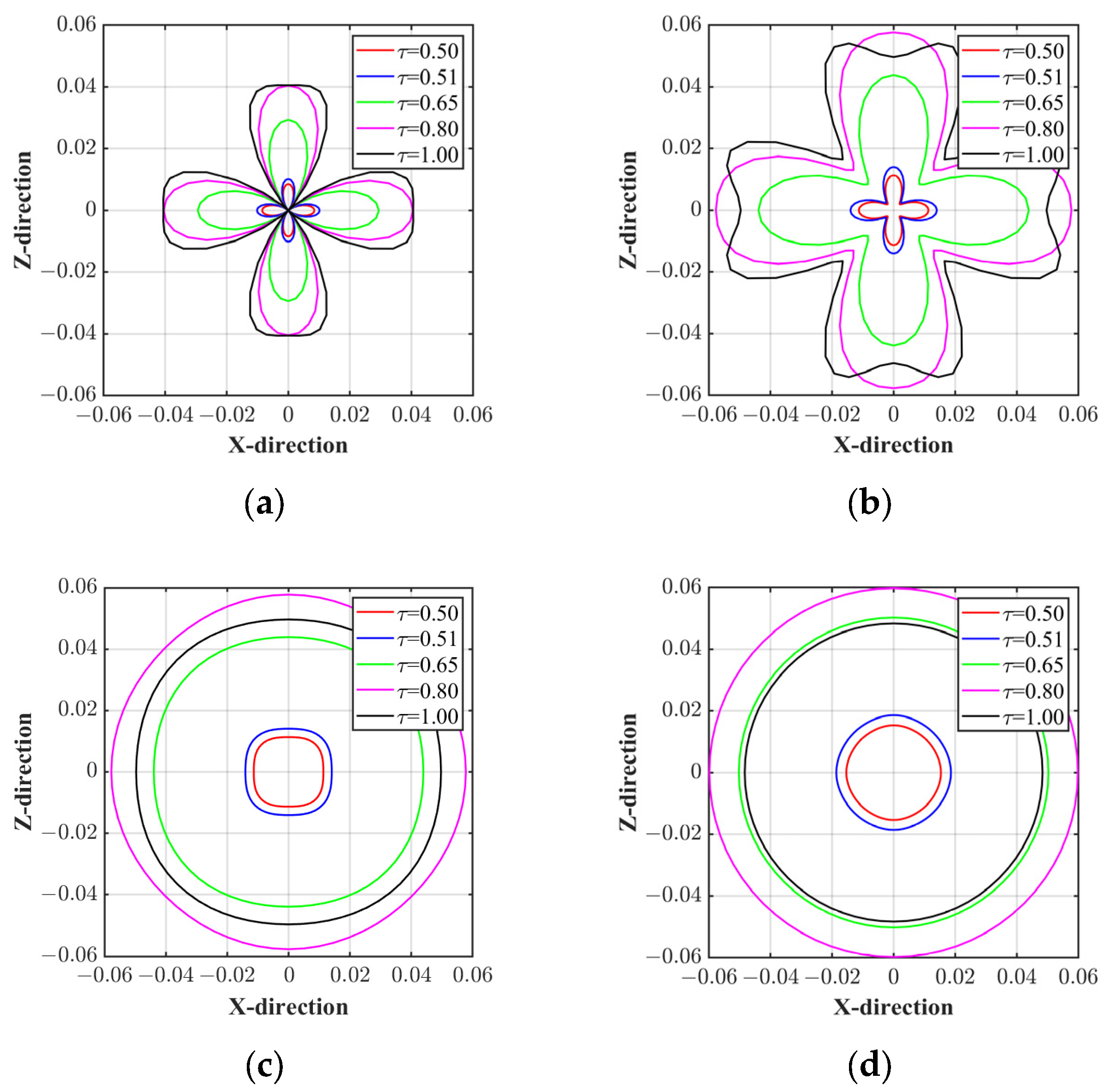
3.2. Stability Analysis
- (1)
- Influence of the relaxation time. Relaxation times are pivotal in determining LBM stability, particularly within the collision step of the LBM algorithm, where they dictate the system’s approach to equilibrium. Understanding their impact on LBM stability is vital for precise and efficient simulations. In LBM, each lattice node holds distribution functions representing particle populations moving in discrete directions. During collision, these functions adjust according to the relaxation times, influencing the system’s relaxation factor toward equilibrium. Choosing inappropriate relaxation times can result in numerical instability, yielding inaccurate or unrealistic simulation outcomes. This selection significantly influences the stability of seismic simulation, with shorter relaxation times necessitating smaller time steps due to higher associated wave speeds. Conversely, longer relaxation times permit larger time steps but may introduce artificial damping of seismic waves. Usually, the relaxation time is located in the range of (0.50, 2.00).
- (2)
- Influence of discrete velocity models. The discrete velocity set is a fundamental component of LBM and profoundly impacts both the stability and accuracy of simulations. It signifies the directions the particles move along the lattice grid during each time step and makes it pivotal for tailoring LBM to specific fluid flow scenarios. Selecting an appropriate set is critical for numerical stability, ensuring simulations generate physically meaningful results devoid of uncontrolled growth or oscillations in the flow field. The velocity set choice influences isotropy, ensuring accurate representation of wave behavior in all spatial directions. A well-balanced discrete velocity set preserves isotropy, minimizing numerical artifacts and maintaining stability. The discrete velocity model also affects stability, with models featuring more discrete velocities (e.g., D2Q13 model) demanding smaller time steps for stability and precise wave propagation representation, albeit at the potential cost of increased computational resources.
- (3)
- Influence of the collision operators. The collision operator, a critical element of LBM, significantly impacts the simulation’s stability by modeling particle interactions at lattice nodes. Its choice, particularly in terms of the relaxation time (τ) within the SRT model, a common LBM collision operator, plays a pivotal role. τ dictates the rate of distribution function convergence towards equilibrium, influencing numerical dissipation. Optimal τ selection is essential, as too small values may result in excessive dissipation and loss of fine-scale details, while overly large values can lead to instability with unphysical oscillations or divergence. Beyond the SRT model, advanced options like the TRT and MRT collision models provide flexibility by allowing distinct relaxation factors for various moments of distribution functions, potentially enhancing stability. Collision model selection depends on specific simulation needs and complexity. Careful consideration of these factors is necessary to design successful LBM simulations yielding reliable, physically meaningful results across diverse fluid flow and wave propagation scenarios.
4. Numerical Examples
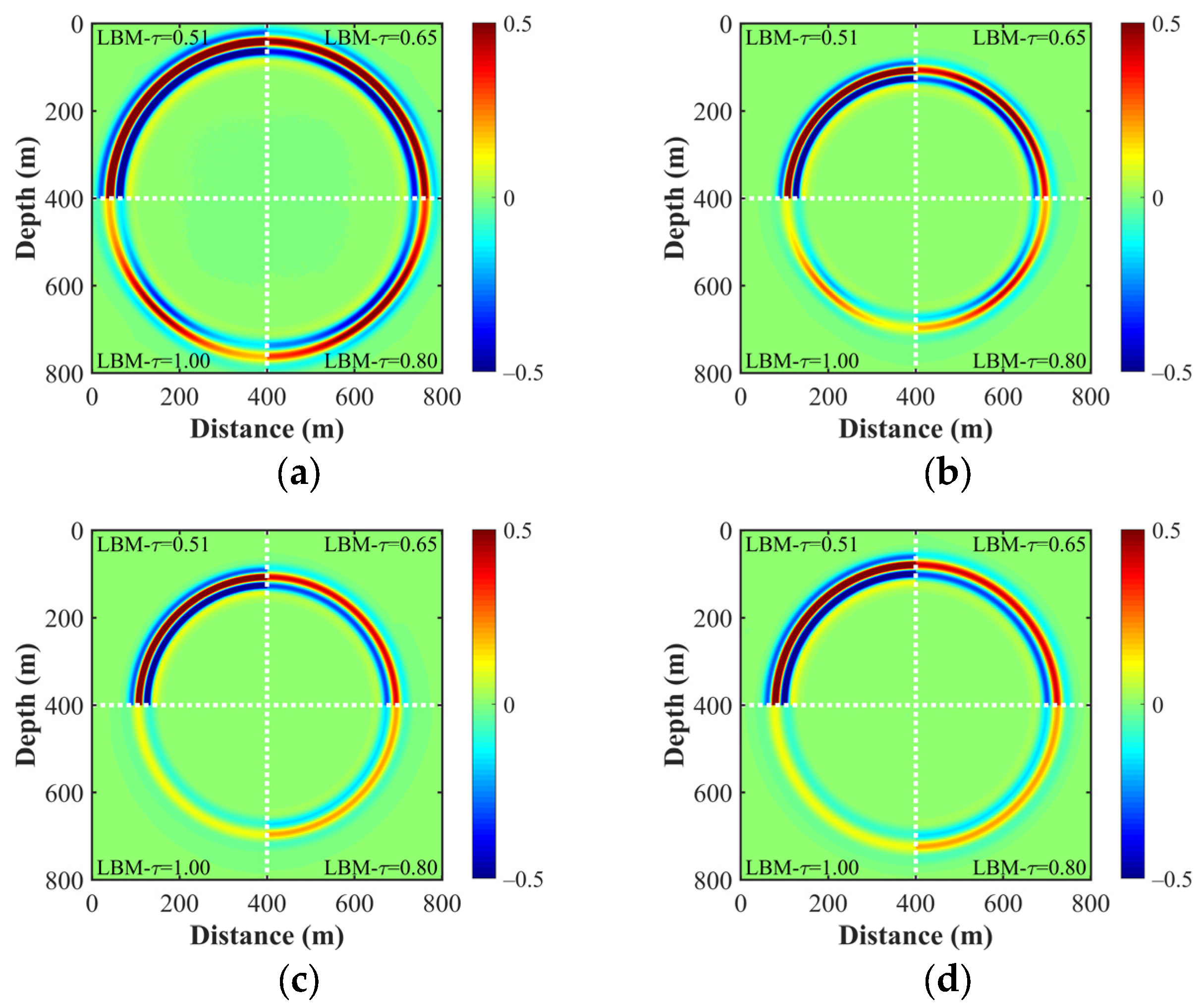
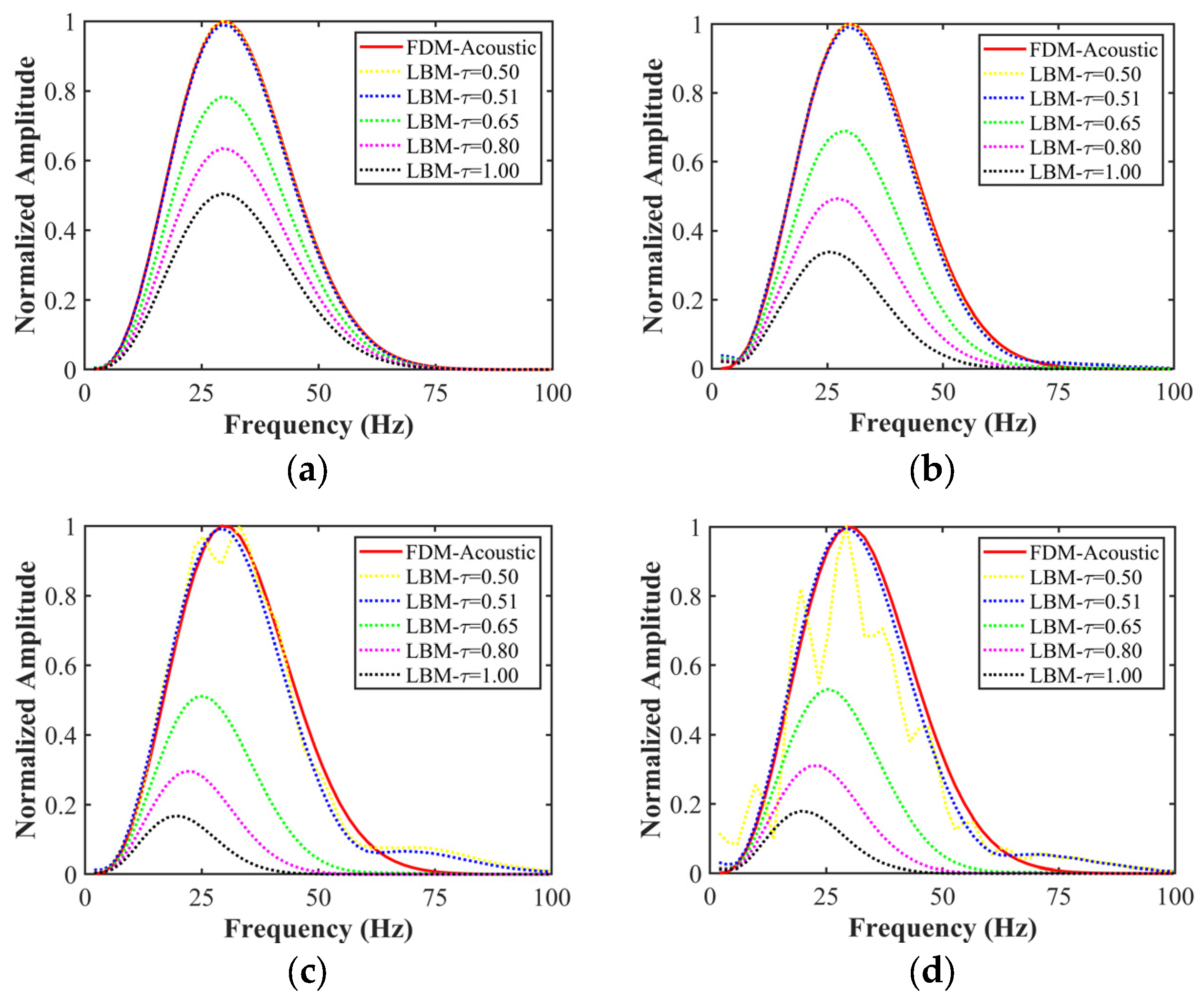
4.1. Comparative Tests of Different Relaxation Times and Discrete Velocity Models
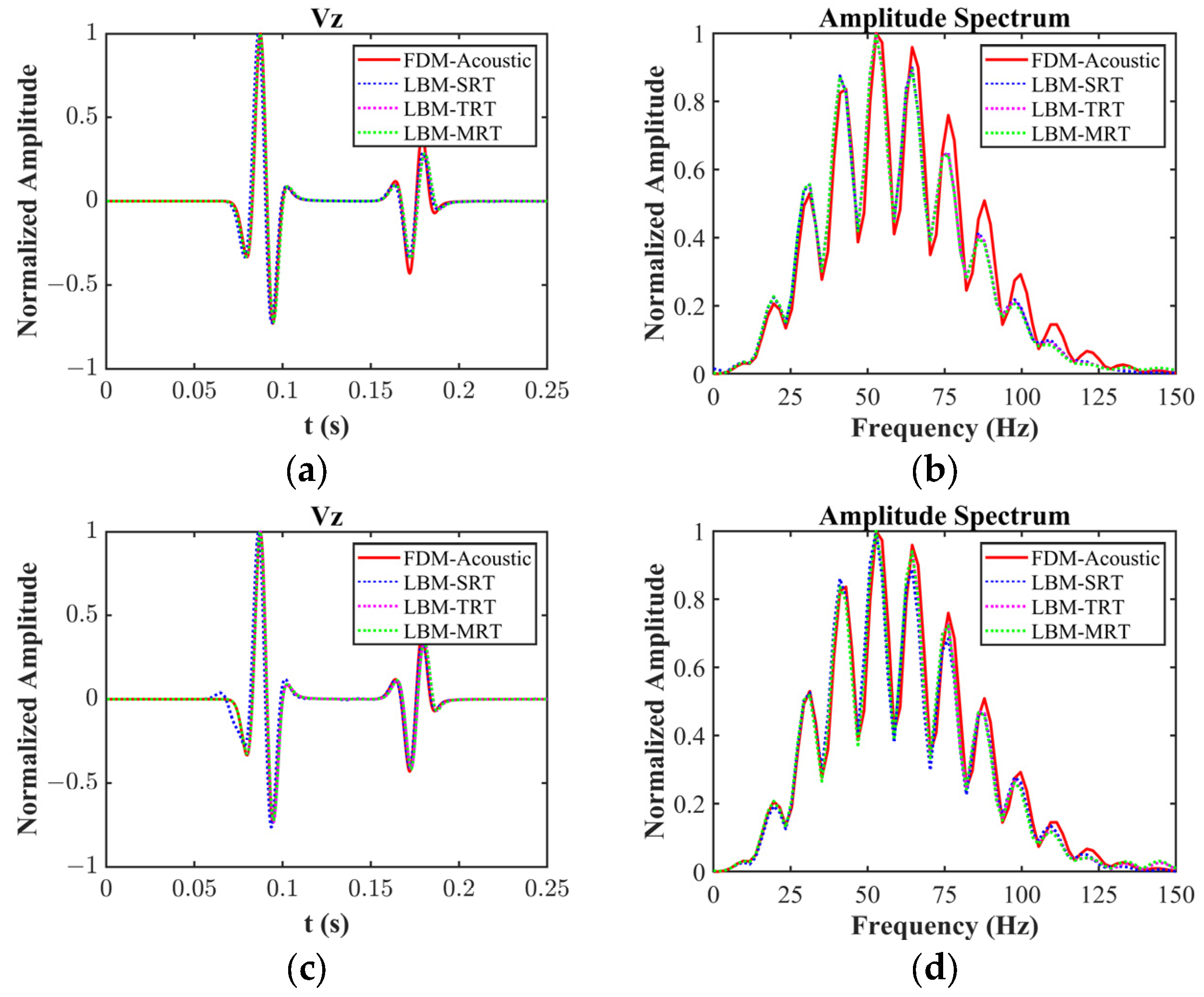
4.2. Comparative Tests of Different Collision Operators
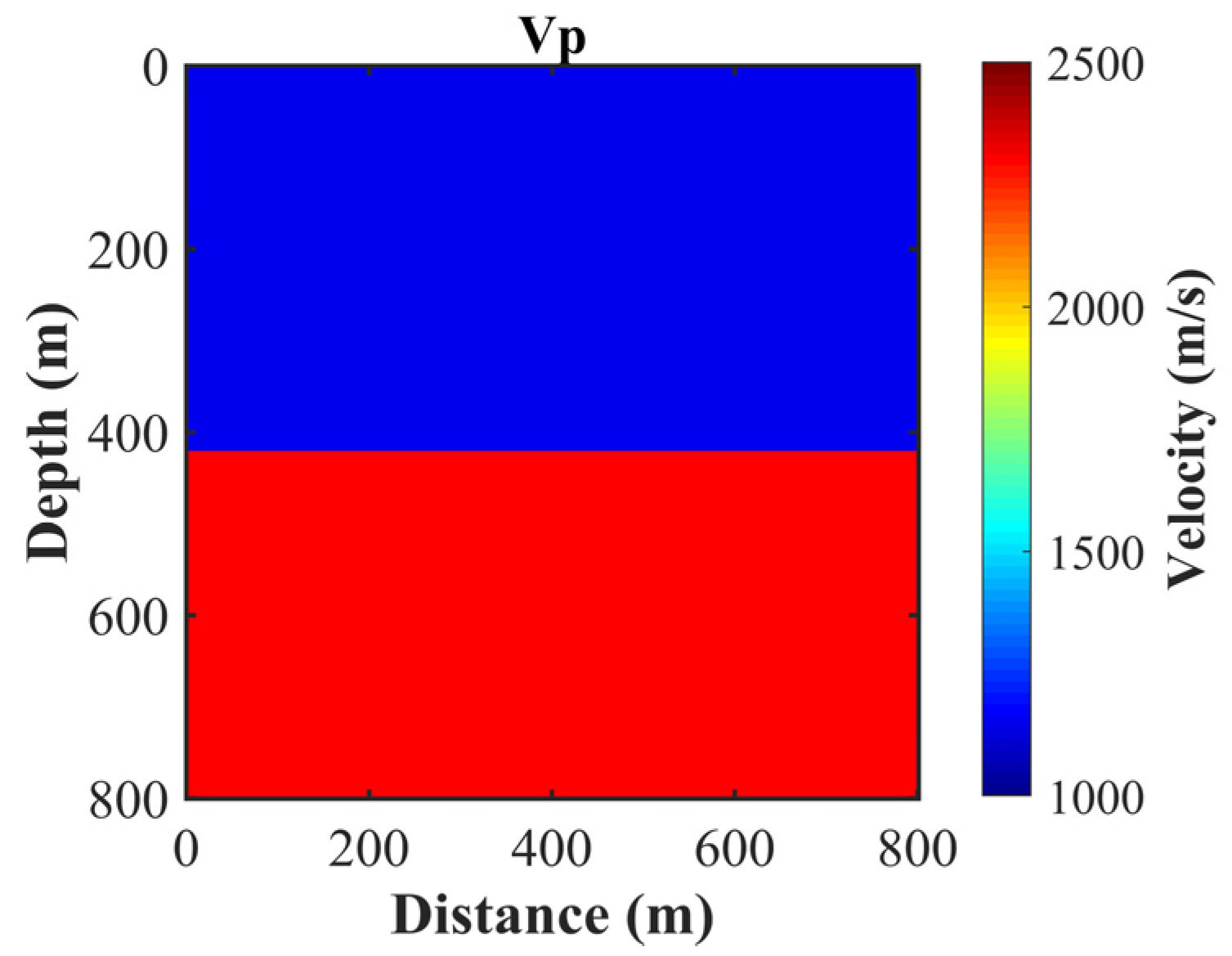
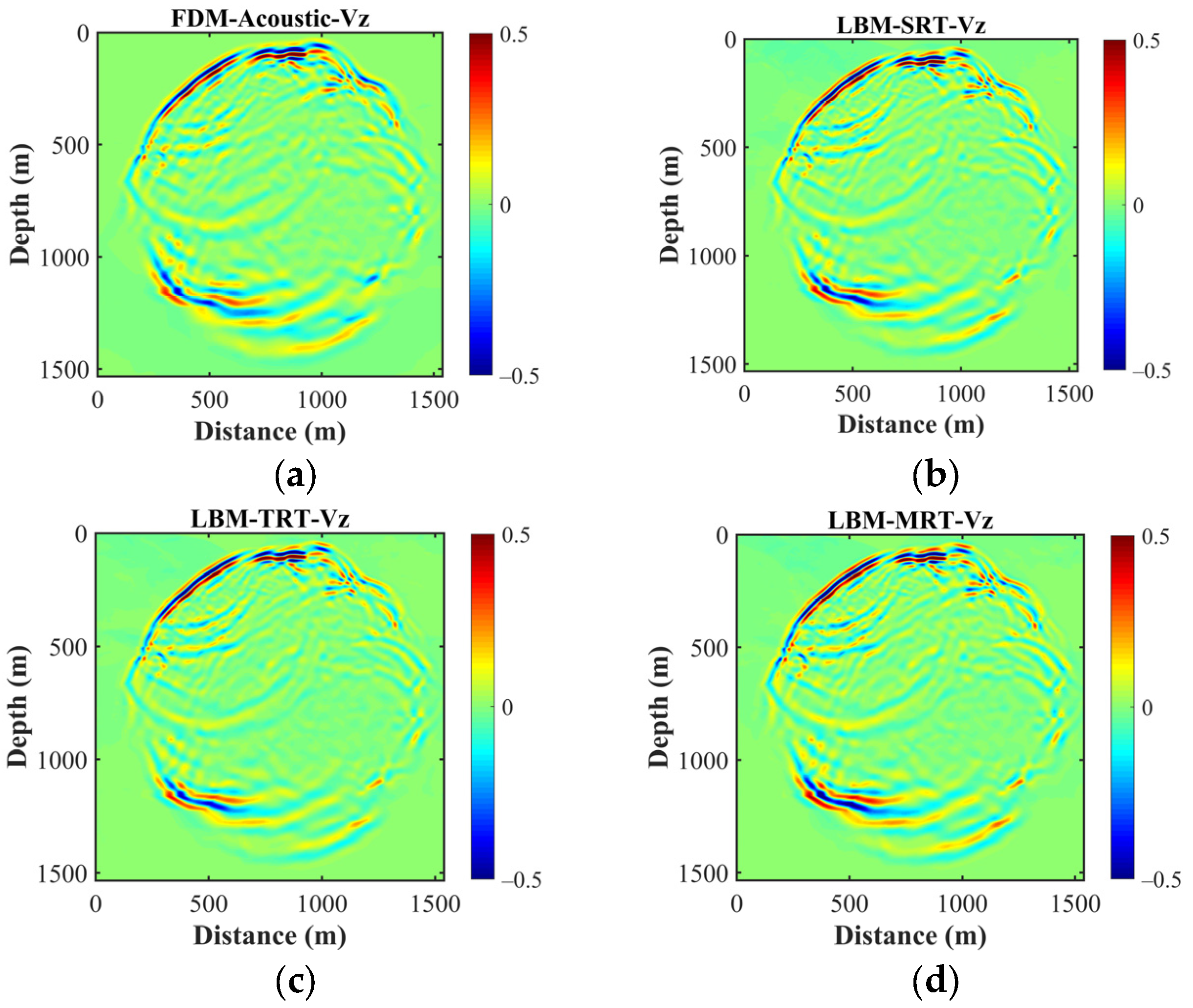
4.2.1. Two-Layer Model
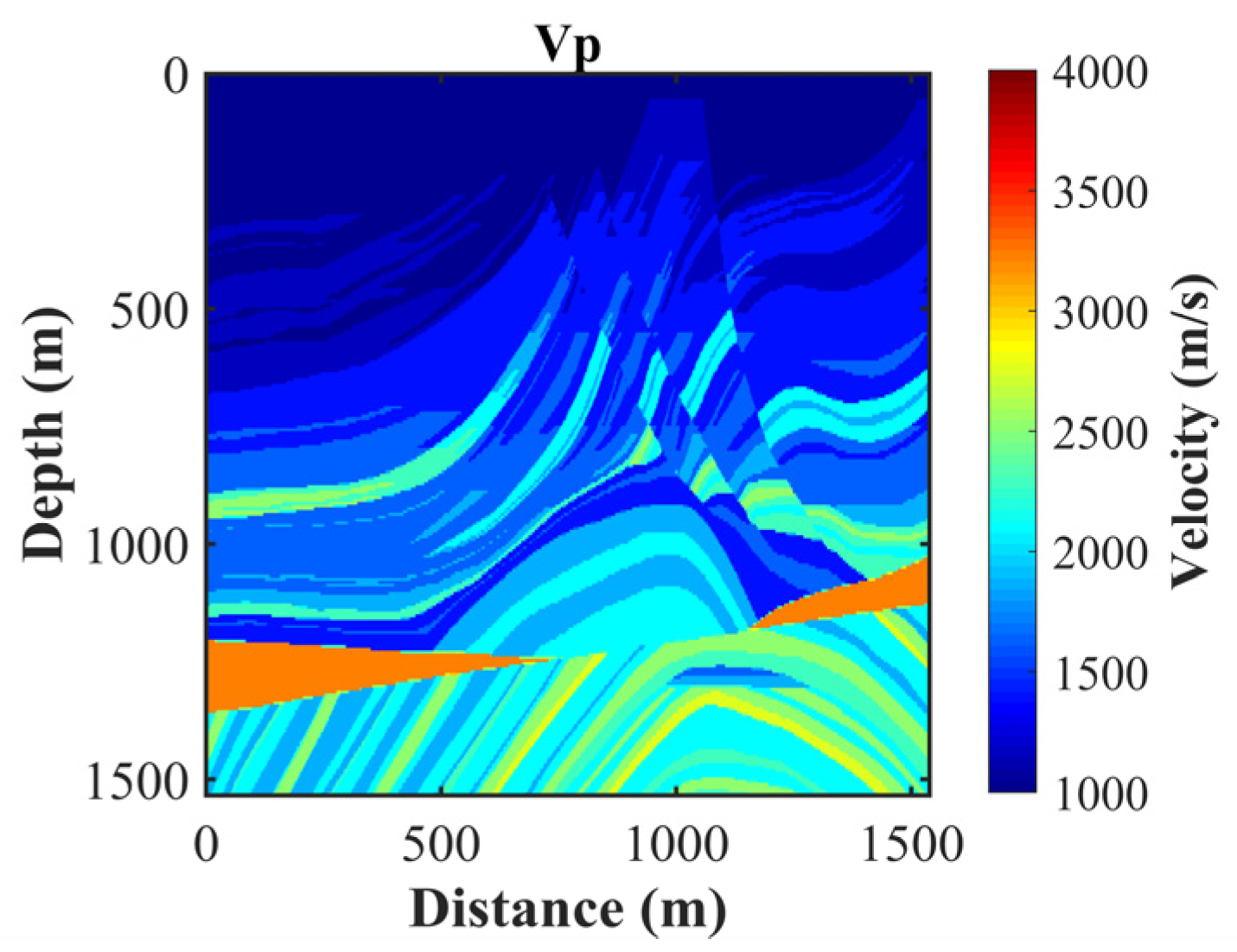
4.2.2. Modified Marmousi Model
5. Discussion
6. Conclusions
- (1)
- Relaxation time. We observed that the choice of relaxation time profoundly influences wave propagation speed. Small relaxation times (i.e., around 0.50) yield more fidelity seismic recording and higher wavefield energy, while larger relaxation times dampen wave propagation. The choice of a suitable relaxation time depends on the desired wave dynamics and the level of physical fidelity required in the simulation.
- (2)
- Discrete velocity models. Our analysis revealed that discrete velocity models with a larger number of velocities provide finer spatial resolution and more accurate wavefield representation. However, this comes at the cost of increased computational complexity. The trade-off between accuracy and computational efficiency must be carefully considered when choosing a discrete velocity model.
- (3)
- Collision operators. The collision operator plays a crucial role in dictating relaxation dynamics and consequently influences the wave propagation behavior. While the SRT model offers computational efficiency, it may not capture complex wave interactions accurately. The TRT and MRT models, with their ability to accommodate different relaxation factors, excel in representing non-equilibrium wave phenomena and anisotropic behaviors.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tarantola, A. Inversion of seismic reflection data in the acoustic approximation. Geophysics 1984, 49, 1259–1266. [Google Scholar] [CrossRef]
- Tarantola, A. A strategy for nonlinear elastic inversion of seismic reflection data. Geophysics 1986, 51, 1893–1903. [Google Scholar] [CrossRef]
- Virieux, J.; Operto, S. An overview of full-waveform inversion in exploration. Geophysics 2009, 74, WCC1–WCC26. [Google Scholar] [CrossRef]
- Aghamiry, H.S.; Gholami, A.; Operto, S. Compound regularization of full-waveform inversion for imaging piecewise media. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1192–1204. [Google Scholar] [CrossRef]
- Zhang, Q.C.; Mao, W.J.; Fang, J.W. Elastic full waveform inversion with source-independent crosstalk-free source-encoding algorithm. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2915–2927. [Google Scholar] [CrossRef]
- Hu, Y.; Fu, L.Y.; Li, Q.Q.; Deng, W.B.; Han, L.G. Frequency-wavenumber domain elastic full waveform inversion with a multistage phase correction. Remote Sens. 2022, 14, 5916. [Google Scholar] [CrossRef]
- Feng, D.S.; Li, B.C.; Cao, C.; Wang, X.; Li, D.B.; Chen, C. Multi-constrained seismic multi-parameter full waveform inversion based on projected quasi-Newton algorithm. Remote Sens. 2023, 15, 2416. [Google Scholar] [CrossRef]
- Baysal, E.; Kosloff, D.D.; Sherwood, J.W.C. Reverse time migration. Geophysics 1983, 48, 1514–1524. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; McMechan, G.A. Imaging conditions for prestack reverse-time migration. Geophysics 2008, 73, S81–S89. [Google Scholar] [CrossRef]
- Li, Q.Q.; Fu, L.Y.; Wei, W.; Sun, W.J.; Du, Q.Z.; Feng, Y.S. Stable and high-efficiency attenuation compensation in reverse-time migration using wavefield decomposition algorithm. IEEE Geosci. Remote Sens. 2019, 16, 1615–1619. [Google Scholar] [CrossRef]
- Li, Q.Q.; Fu, L.Y.; Wu, R.S.; Du, Q.Z. A novel wavefield-reconstruction algorithm for RTM in attenuating media. IEEE Geosci. Remote Sens. 2021, 18, 731–735. [Google Scholar] [CrossRef]
- Shen, R.Q.; Zhao, Y.H.; Hu, S.F.; Li, B.; Bi, W.D. Reverse-time migration imaging of ground-penetrating radar in NDT of reinforced concrete structures. Remote Sens. 2021, 13, 2020. [Google Scholar] [CrossRef]
- Wang, N.; Shi, Y.; Zhou, H. Accurately stable Q-compensated reverse-time migration scheme for heterogeneous viscoelastic media. Remote Sens. 2022, 14, 4782. [Google Scholar] [CrossRef]
- Fang, J.W.; Shi, Y.; Zhou, H. A high-precision elastic reverse-time migration for complex geologic structure imaging in applied geophysics. Remote Sens. 2022, 14, 3542. [Google Scholar] [CrossRef]
- Chen, S.Y.; Chen, H.D.; Martnez, D.; Matthaeus, W. Lattice Boltzmann model for simulation of magnetohydrodynamics. Phys. Rev. Lett. 1991, 67, 3776–3779. [Google Scholar] [CrossRef] [PubMed]
- Koelman, J.M.V.A. A simple lattice Boltzmann scheme for Navier-Stokes fluid flow. Europhys. Lett. 1991, 15, 603–607. [Google Scholar] [CrossRef]
- Qian, Y.H.; d’Humières, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Xiao, S. A lattice Boltzmann method for shock wave propagation in solids. Commun. Numer. Methods Eng. 2007, 23, 71–84. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Yan, G.W.; Shi, X.B. Lattice Boltzmann model for wave propagation. Phys. Rev. E 2009, 80, 026706. [Google Scholar] [CrossRef]
- Frantziskonis, G.N. Lattice Boltzmann method for multimode wave propagation in viscoelastic media and in elastic solids. Phys. Rev. E 2011, 283, 066703. [Google Scholar] [CrossRef]
- Viggen, E.M. The Lattice Boltzmann Method with Applications in Acoustics. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2009; pp. 1–95. [Google Scholar]
- Viggen, E.M. The Lattice Boltzmann Method: Fundamentals and Acoustics. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2014; pp. 1–233. [Google Scholar]
- Salomons, E.M.; Lohman, W.J.A.; Zhou, H. Simulation of sound waves using the lattice Boltzmann method for fluid flow: Benchmark cases for outdoor sound propagation. PLoS ONE 2016, 11, e0147206. [Google Scholar] [CrossRef]
- Jiang, C.T.; Zhou, H.; Xia, M.M.; Tang, J.X.; Zhang, M.K.; An, Y. Study on absorbing boundary conditions of viscous sponge layers based on lattice Boltzmann method. In Proceedings of the 82nd EAGE Annual Conference & Exhibition, Amsterdam, The Netherlands, 8–11 December 2020; pp. 1–5. [Google Scholar]
- Xia, M.M.; Wang, S.C.; Zhou, H.; Shan, X.W.; Chen, H.M.; Li, Q.Q.; Zhang, Q.C. Modelling viscoacoustic wave propagation with the lattice Boltzmann method. Sci. Rep. 2017, 7, 10169. [Google Scholar] [CrossRef] [PubMed]
- Xia, M.M.; Zhou, H.; Jiang, C.T.; Tang, J.X.; Wang, C.Y.; Yang, C.C. Viscoacoustic wave simulation with the lattice Boltzmann method. Geophysics 2022, 87, T403–T416. [Google Scholar] [CrossRef]
- Ginzburg, I. Equilibrium-type and link-type lattice Boltzmann models for generic advection and anisotropic-dispersion equation. Adv. Water Resour. 2005, 28, 1171–1195. [Google Scholar] [CrossRef]
- Servan-Camas, B.; Tsai, F.T.C. Lattice Boltzmann method with two relaxation times for advection–diffusion equation: Third order analysis and stability analysis. Adv. Water Resour. 2008, 31, 1113–1126. [Google Scholar] [CrossRef]
- Talon, L.; Bauer, D.; Gland, N.; Youssef, S.; Auradou, H.; Ginzburg, I. Assessment of the two relaxation time Lattice-Boltzmann scheme to simulate Stokes flow in porous media. Water Resour. Res. 2012, 48, W04526. [Google Scholar] [CrossRef]
- Vikhansky, A.; Ginzburg, I. Taylor dispersion in heterogeneous porous media: Extended method of moments, theory, and modelling with two-relaxation-times lattice Boltzmann scheme. Phys. Fluids 2014, 26, 22104. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, J.M.; Zhou, J.G. Lattice Boltzmann model using two relaxation times for shallow-water equations. J. Hydraul. Eng. 2016, 142, 06015017. [Google Scholar] [CrossRef]
- Zhao, W.F.; Wang, L.; Yong, W.A. On a two-relaxation-time D2Q9 lattice Boltzmann model for the Navier–Stokes equations. Physica A Stat. Mech. Appl. 2018, 492, 1570–1580. [Google Scholar] [CrossRef]
- Bhopalam, S.R.; Perumal, D.A.; Yadav, A.K. Computation of fluid flow in double sided cross-shaped lid-driven cavities using lattice Boltzmann method. Eur. J. Mech. B-Fluid 2018, 70, 46–72. [Google Scholar]
- Postma, B.; Silva, G. Force methods for the two-relaxation-times lattice Boltzmann. Phys. Rev. E 2020, 102, 063307. [Google Scholar] [CrossRef] [PubMed]
- D’Humières, D. Generalized lattice-Boltzmann equations, in Rarefied Gas Dynamics: Theory and Simulations. In Progress in Astronautics and Aeronautics; Shizgal, B.D., Weave, D.P., Eds.; AIAA: Washington, DC, USA, 1992; Volume 159, pp. 450–458. [Google Scholar]
- D’Humières, D. Multiple-relaxation-time lattice Boltzmann models in three dimensions. Philos. Trans. R. Soc. Lond. Ser. A 2002, 360, 437–451. [Google Scholar] [CrossRef] [PubMed]
- Fakhari, A.; Rahimian, M.H. Phase-field modeling by the method of lattice Boltzmann equations. Phys. Rev. E 2010, 81, 036707. [Google Scholar] [CrossRef]
- Zhao, Z.M.; Huang, P.; Li, Y.N.; Li, J.M. A lattice Boltzmann method for viscous free surface waves in two dimensions. Int. J. Numer. Methods Fluids 2013, 71, 223–248. [Google Scholar] [CrossRef]
- Wang, J.; Wang, D.; Lallemand, P.; Luo, L.S. Lattice Boltzmann simulations of thermal convective flows in two dimensions. Comput. Math. Appl. 2013, 65, 262–286. [Google Scholar] [CrossRef]
- Dhuri, D.B.; Hanasoge, S.M.; Perlekar, P.; Robertsson, J.O. Numerical analysis of the lattice Boltzmann method for simulation of linear acoustic waves. Phys. Rev. E 2017, 95, 043306. [Google Scholar] [CrossRef] [PubMed]
- Chai, Z.H.; Shi, B.C. Multiple-relaxation-time lattice Boltzmann method for the Navier-Stokes and nonlinear convection-diffusion equations: Modeling, analysis, and elements. Phys. Rev. E 2020, 102, 023306. [Google Scholar] [CrossRef]
- Benhamou, J.; Jami, M.; Mezrhab, A.; Henry, D.; Botton, V. Numerical simulation study of acoustic waves propagation and streaming using MRT-lattice Boltzmann method. Int. J. Comput. Methods Eng. Sci. Mech. 2023, 24, 62–75. [Google Scholar] [CrossRef]
- Jiang, C.T.; Zhou, H.; Xia, M.M.; Chen, H.M.; Tang, J.X. A joint absorbing boundary for the multiple-relaxation-time lattice Boltzmann method in seismic acoustic wavefield modeling. Pet. Sci. 2023, 20, 2113–2126. [Google Scholar] [CrossRef]
- Qian, Y.H.; Deng, Y.F. A lattice BGK model for viscoelastic media. Phys. Rev. 1997, 79, 2742–2745. [Google Scholar] [CrossRef]
- Buick, J.M.; Buckley, C.L.; Greated, C.A. Lattice Boltzmann BGK simulation of nonlinear sound waves: The development of a shock front. J. Phys. A Math. Gen. 2000, 33, 3917. [Google Scholar] [CrossRef]
- Xia, Y.X.; Qiu, X.; Qian, Y.H. Numerical simulation of two-dimensional turbulence based on immersed boundary lattice Boltzmann method. Comput. Fluids 2019, 195, 104321. [Google Scholar] [CrossRef]
- Ezzatneshan, E.; Salehi, A.; Vaseghnia, H. Study on forcing schemes in the thermal lattice Boltzmann method for simulation of natural convection flow problems. Heat Transfer 2021, 50, 7604–7631. [Google Scholar] [CrossRef]
- Luo, L.S.; Liao, W.; Chen, X.W.; Peng, Y.; Zhang, W. Numerics of the lattice Boltzmann method: Effects of collision models on the lattice Boltzmann simulations. Phys. Rev. E 2011, 83, 056710. [Google Scholar] [CrossRef]
- Lallemand, P.; Luo, L.S. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546–6562. [Google Scholar] [CrossRef]
- Aslan, E.; Taymaz, I.; Benim, A.C. Investigation of the lattice Boltzmann SRT and MRT stability for lid driven cavity flow. Int. J. Mater. Mech. Manuf. 2014, 2, 317–324. [Google Scholar]
- Haydock, D.; Yeomans, J.M. Lattice Boltzmann simulations of attenuation-driven acoustic streaming. J. Phys. A Math. Gen. 2003, 36, 5683–5694. [Google Scholar] [CrossRef]


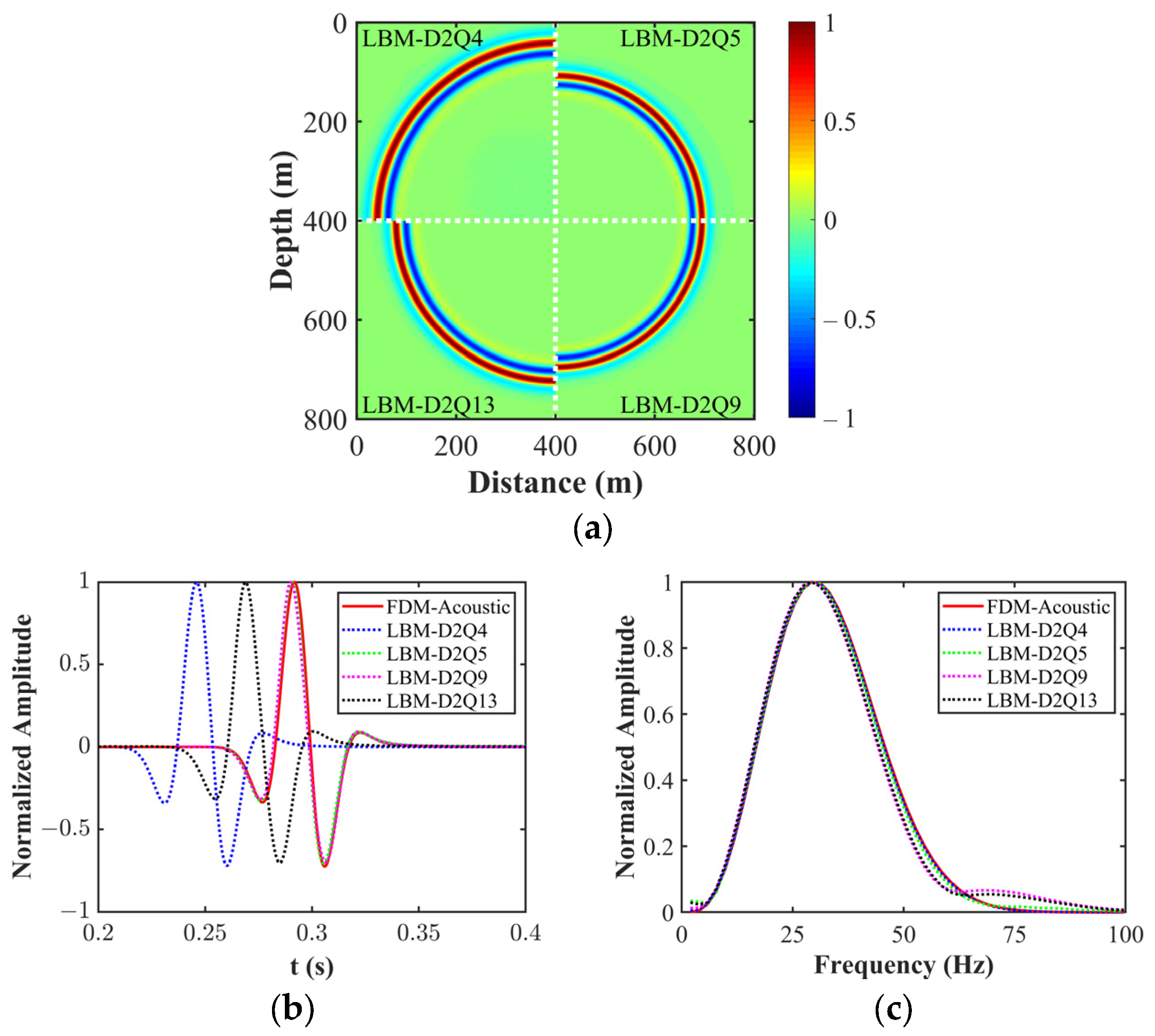

| Discrete Models | |||
|---|---|---|---|
| D2Q4 | 1/2 | ||
| D2Q5 | 1/3 | ||
| D2Q9 | 1/3 | ||
| D2Q13 | 2/5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, M.; Zhou, H.; Jiang, C.; Cui, J.; Zeng, Y.; Chen, H. Comparative Study of 2D Lattice Boltzmann Models for Simulating Seismic Waves. Remote Sens. 2024, 16, 285. https://doi.org/10.3390/rs16020285
Xia M, Zhou H, Jiang C, Cui J, Zeng Y, Chen H. Comparative Study of 2D Lattice Boltzmann Models for Simulating Seismic Waves. Remote Sensing. 2024; 16(2):285. https://doi.org/10.3390/rs16020285
Chicago/Turabian StyleXia, Muming, Hui Zhou, Chuntao Jiang, Jinming Cui, Yong Zeng, and Hanming Chen. 2024. "Comparative Study of 2D Lattice Boltzmann Models for Simulating Seismic Waves" Remote Sensing 16, no. 2: 285. https://doi.org/10.3390/rs16020285







