Evaluation of Satellite Rainfall Estimates for Drought and Flood Monitoring in Mozambique

Abstract

Satellite derived rainfall products are useful for drought and flood early warning and overcome the problem of sparse, unevenly distributed and erratic rain gauge observations, provided their accuracy is well known. Mozambique is highly vulnerable to extreme weather events such as major droughts and floods and thus, an understanding of the strengths and weaknesses of different rainfall products is valuable. Three dekadal (10-day) gridded satellite rainfall products (TAMSAT African Rainfall Climatology And Time-series (TARCAT) v2.0, Famine Early Warning System NETwork (FEWS NET) Rainfall Estimate (RFE) v2.0, and Climate Hazards Group InfraRed Precipitation with Stations (CHIRPS)) are compared to independent gauge data (2001–2012). This is done using pairwise comparison statistics to evaluate the performance in estimating rainfall amounts and categorical statistics to assess rain-detection capabilities. The analysis was performed for different rainfall categories, over the seasonal cycle and for regions dominated by different weather systems. Overall, satellite products overestimate low and underestimate high dekadal rainfall values. The RFE and CHIRPS products perform as good, generally outperforming TARCAT on the majority of statistical measures of skill. TARCAT detects best the relative frequency of rainfall events, while RFE underestimates and CHIRPS overestimates the rainfall events frequency. Differences in products performance disappear with higher rainfall and all products achieve better results during the wet season. During the cyclone season, CHIRPS shows the best results, while RFE outperforms the other products for lower dekadal rainfall. Products blending thermal infrared and passive microwave imagery perform better than infrared only products and particularly when meteorological patterns are more complex, such as over the coastal, central and south regions of Mozambique, where precipitation is influenced by frontal systems.

1. Introduction

Since African agriculture is predominantly rain fed, and many regions are affected by high rainfall variability in both space and time, there is a pressing need for accurate gridded rainfall products for different applications, such as agricultural monitoring and yield prediction in remote areas. Rain gauges have been the main source of rainfall data, but in many countries the rain gauge network is inadequate to produce reliable distributed rainfall maps. Although there are important limitations of the use of satellite imagery for rainfall estimation—none of the satellite sensors detect rainfall as such and the relationship between observations and precipitation is indirect—satellite derived rainfall estimates overcome the need for near real-time rain gauge observations, which are typically sparse, poorly spatially distributed, and reported sporadically, especially in Africa [1,2,3]. In recent decades, these full spatial coverage products have been crucial, particularly in drought, flood and famine early warning [3].

Algorithms to derive rainfall from satellite observations are either based on thermal infrared (TIR) bands, which measure cloud top temperature that can be used to identify convective rainfall in the Inter-Tropical Convergence Zone (ITCZ), or on passive microwave (PM) sensors. In the first case, cold cloud duration (CCD), or the length of time that a pixel temperature is below a certain threshold, is assumed to be linearly related with rainfall. Misidentification can occur because some cold clouds, such as cirrus, may not be associated with any rainfall, while warm cloud such as stratiform clouds can produce substantial amounts of rain [4]. This method is therefore less reliable in coastal monsoon areas, regions where mid-latitude weather systems dominate, or areas with high topography [5,6]. On the other hand, PM imagery can be used to assess atmospheric liquid water content and rainfall intensity as microwaves penetrate clouds and precipitation sized particles are the major source of attenuation at PM frequencies [4]. For PM algorithms, the two main challenges are warm orographic rains and very cold surfaces and ice over mountain-tops, which can be confused with precipitation. Additional drawbacks include the poorer spatial resolution and, more importantly, the poor temporal sampling of the PM sensors compared to TIR imagery, since PM sensors are carried on polar orbiting satellites. Although PM techniques generally seem to outperform TIR techniques for instantaneous rain areas and rates, for estimates over longer periods (e.g., monthly estimates) the TIR outperform PM algorithms [4].

In the last decades, many satellite based rainfall estimate products have been developed. Empirical algorithms, calibrated using rain gauge data, are used to derive rainfall rates from observed signals, but parameters can vary in space and time. Some of the algorithms are exclusively based on TIR data (e.g., [7]) from geostationary satellites such as Meteosat-8 and Geostationary Operational Environmental Satellite (GOES), while others are based only on microwave data (e.g., [8]) from the Special Sensor Microwave Imager (SSM/I), Tropical Rainfall Measuring Mission (TRMM), or the Advanced Microwave Sounding Unit (AMSU). Some products combine both TIR and PM imagery (e.g., [9]) and/or include ground-based rainfall observations (e.g., [10]) or numerical weather prediction (NWP) model information (e.g., [11]). Multi-sensor algorithms have been reported to reduce the inherent sampling errors of satellite estimates [12].

The adjustment of satellite estimates against gauge data allows reduction of the bias in the satellite precipitation estimates and yields higher accuracies [13], although this may not provide a complete solution because of the low availability of ground-based data for calibration and validation in Africa [1]. Most recent methods (e.g., [14]) perform calibration using real-time rain gauge data. These are made available through the Global Precipitation Climatology Project (GPCC) and are distributed through the Global Telecommunications System (GTS).

Users of satellite derived rainfall data need to evaluate how reliable the products are, in order to choose the most suitable product for their application. Although validation is necessary to have some level of confidence, with the exception of TAMSAT’s routine validation [3], few studies validate rainfall over the African continent due to the lack of appropriate dense rain gauge networks. Most evaluation studies cover the west African Sahel [10,13,15,16,17,18], some cover southern Africa [5,6] or East Africa [19,20]. Results from such studies show large differences in algorithm performance depending on location, topography, local climate and season [20], but algorithms that rely on local calibration usually show better performance (e.g., [13]), and satellite estimates give a more accurate representation of the rainfall compared to modeled products. In addition, the “best” product depends on the specific application: for operational agricultural monitoring focusing on drought impacts, the accuracy of low rainfall is essential; for hydrological purposes and flood forecasting it is key to accurately estimate high rainfalls.

The aim of this paper is to evaluate satellite derived rainfall products for the monitoring of both dry spells and high rainfall events in Mozambique, by comparing satellite products against rain gauge observations provided by the Mozambican meteorological institute. The study focuses on satellite derived rainfall data with a relatively high spatial and temporal resolution. Specific questions to be addressed are how the satellite data compare with the gauge data for different rainfall categories, over the seasonal cycle and over three distinct regions dominated by different weather systems.

2. Study Area

Mozambique is one of the poorest countries in the world, and development has been compromised in recent years by civil war and extreme climate events such as major droughts and floods [21]. The high incidence of flooding is firstly explained by the tropical cyclones that form in the Mozambique Channel: while relatively few of these actually make landfall [22], some get close enough to cause high winds and heavy rain. Secondly, nine major river systems that drain vast areas of southeastern Africa find their way to the ocean by crossing Mozambique [21]. The Mozambican economy is driven by the agricultural sector. Around 80 percent of Mozambique’s population works in agriculture and fisheries [23] and are therefore highly vulnerable to climate variability and extreme weather events. Accurate measurement of rainfall is therefore a high priority.

Mozambique is located on the southeast coast of the African continent and has a tropical climate characterized by a cool and dry winter season from April to September and a warm and rainy summer season from October to March [24]. Annual mean temperature and rainfall vary from north to south and from the coast to the highlands in the interior of the country. The weather system is dominated in the north by the ITCZ, and in the south by Antarctic Polar Fronts (APF) and Tropical Temperate Troughs (TTTs). The central region receives influences from both systems. TTT occurrence is positively related to La Niña and Southern Hemisphere planetary waves, while El Niño-Southern Oscillation (ENSO) appears to play a significant role in causing dry conditions over Mozambique [25]. The most significant natural hazards are severe droughts, such as those of 2002/3, 2003/4 and 2009/10, and devastating cyclones and floods, as in 2000 and 2001, in the central and southern provinces [21,26].

3. Data

3.1. Satellite Products

A brief description of the three gridded satellite rainfall products that are compared to gauge data in this study is given below and summarized in Table 1: (1) the TAMSAT African Rainfall Climatology and Time-series (TARCAT) v2.0; (2) the Famine Early Warning System NETwork (FEWS NET) RFE v2.0 product; and (3) the Climate Hazards Group InfraRed Precipitation with Stations (CHIRPS) dataset. From all three sources the dekadal products were used, whereby the first two dekads of each month are comprised of 10 days and the last dekad consists of 8 to 11 days.

(1)

TARCAT v2.0 is produced by TAMSAT (the Tropical Applications of Meteorology using SATellite data and ground-based observations) research group of the University of Reading and is based on Meteosat TIR CCD. The algorithm is locally calibrated using historical rain gauge records producing monthly and regional calibration parameters [2,3]. Data are available from 1983 onwards, and dekadal, monthly, and seasonal products at 0.0375° spatial resolution (~4 km) can be accessed in near-real time.

(2)

The FEWS NET RFE v2.0 product is implemented by NOAA’s Climate Prediction Center (CPC) and is a blended product based on CCD derived from Meteosat TIR, estimates from SSM/I and AMSU, and daily station rainfall data. Daily rainfall estimates are obtained using a two part merging process [27]: all satellite data are first combined using the maximum likelihood estimation method, then Global Telecommunications Station (GTS) station data are used to remove bias. Data over Africa are available from 2001 onwards and dekadal products at 8 km spatial resolution can be accessed in near-real time.

(3)

The CHIRPS dataset, developed by the U.S. Geological Survey (USGS) and the Climate Hazards Group at the University of California, Santa Barbara, is a blended product combining a pentadal precipitation climatology, quasi-global geostationary TIR satellite observations from the CPC and the National Climatic Data Center (NCDC) [28,29], atmospheric model rainfall fields from the NOAA Climate Forecast System version 2 (CFSv2) [30], and in situ precipitation observations. Pentadal rainfall estimates, created from satellite data based on CCD based on regression models calibrated using TRMM, are expressed as percent of normal and multiplied by the corresponding precipitation climatology. Next, stations are blended with this CHIRP data to produce CHIRPS. Quasi-global gridded products are available from 1981 to near-present at 0.05° spatial resolution (~5.3 km) and at pentadal, dekadal, and monthly temporal resolution [14,31]. New products are released approximately mid-month of the month following the observation.

The satellite derived rainfall products validated in this study have a relatively high spatial (<10 km) and temporal (dekad) resolution, are available for a relatively long time period and are widely used, with the exception of CHIRPS, which is a relatively new dataset. The temporal resolution of 10 days is a common period used for operational drought and famine monitoring. The areal averaged dekadal rainfall over Mozambique for 2001–2012, and the country-wide average of the mean 10-daily rainfall (2001–2012) for TARCAT, RFE, and CHIRPS (Figure 1) illustrate the differences between the datasets regarding peak rainfall, rainfall in the dry season, temporal and spatial variation.

Figure 1. Time series of country wide average dekadal rainfall (black line) ± 1 standard deviation (gray shading) 2001–2012 (left) and country wide average of the mean dekadal rainfall (averaged over 2001–2012) ± 1 standard deviation (right) for TAMSAT African Rainfall Climatology and Time-series (TARCAT), Rainfall Estimate (RFE), and Climate Hazards Group InfraRed Precipitation with Stations (CHIRPS).

Figure 1. Time series of country wide average dekadal rainfall (black line) ± 1 standard deviation (gray shading) 2001–2012 (left) and country wide average of the mean dekadal rainfall (averaged over 2001–2012) ± 1 standard deviation (right) for TAMSAT African Rainfall Climatology and Time-series (TARCAT), Rainfall Estimate (RFE), and Climate Hazards Group InfraRed Precipitation with Stations (CHIRPS).

Table 1. Summary of the three satellite products used.

Satellite Product	Temporal Coverage	Spatial Coverage	Spatial Resolution
TARCAT v2.0 1	1983–present	Africa 38° N–36° S, 19° W–52° E	0.0375° (~4 km)
FEWS NET RFE v2.0 2	2001–present	Africa 43.7° N–42.2° S, 23.5° W–63.4° E	8 km (~0.075°)
CHIRPS v1.8 3	1981–present	(near) global 50° N–50° S, 180° W–180° E	0.05° (~5.3 km)

Source: ¹ [32], ² [33], ³ [34].

Table 1. Summary of the three satellite products used.

Satellite Product	Temporal Coverage	Spatial Coverage	Spatial Resolution
TARCAT v2.0 1	1983–present	Africa 38° N–36° S, 19° W–52° E	0.0375° (~4 km)
FEWS NET RFE v2.0 2	2001–present	Africa 43.7° N–42.2° S, 23.5° W–63.4° E	8 km (~0.075°)
CHIRPS v1.8 3	1981–present	(near) global 50° N–50° S, 180° W–180° E	0.05° (~5.3 km)

Source: ¹ [32], ² [33], ³ [34].

3.2. Rain Gauge Data

Daily rain gauge observations from 26 stations (Figure 2, Table 2) from 1969 to present were obtained from the National Meteorological Institute (INAM). The daily rainfall data were accumulated to dekadal totals, when a complete dekadal data record was available. For the time period of 2001–2012, the number of complete dekadal observations per station varies between 111 and 411 with an average of 239 complete observations out of a total of 432 dekads.

Mean distance to the coastline is 100 km, and stations are located at an average elevation of 247 meters above sea level. Table 2 also lists the region the stations are located in: North (Cabo Delgado, Niassa and Nampula provinces), Central (Manica, Sofala, Tete, and Zambezia provinces), and South (Gaza, Inhambane, Maputo provinces and Maputo City).

Figure 2. Topographic map of Mozambique and location within Africa. Circles denote the location of 26 rain gauges, with symbol size indicating the number of complete dekadal observations per station (2001–2012).

Figure 2. Topographic map of Mozambique and location within Africa. Circles denote the location of 26 rain gauges, with symbol size indicating the number of complete dekadal observations per station (2001–2012).

Table 2. Overview of 26 rain gauges.

Station	Region 1	Latitude	Longitude	Elevation (m a.s.l.)	Distance to Coastline (km)	Number of Observations 2 (%)	Number Used in Validation 3
Angoche	N	16.23° S	39.90° E	61	0.1	47	18
Beira/Aeroporto	C	19.80° S	34.90° E	8	3.1	26	1
Changalane	S	26.30° S	32.18° E	100	52.7	49	33
Chimoio	C	19.11° S	33.46° E	732	161.6	59	4
Cuamba	N	14.82° S	36.53° E	606	316	60	28
Inhambane	S	23.87° S	35.38° E	14	0.1	41	11
Inharrime	S	24.48° S	35.02° E	43	17.3	65	280
Lichinga	N	13.30° S	35.23° E	137	563.7	31	10
Lumbo	N	15.03° S	40.67° E	10	1.4	60	26
Maniquenique	S	24.73° S	33.53° E	13	46.3	82	314
Manjacaze	S	24.72°S	33.88° E	65	36.2	26	97
Maputo/Observatorio	S	25.96° S	32.60° E	60	0.6	95	410
Marrupa	N	13.23° S	37.55° E	838	318.9	55	220
Massingir	S	25.88°S	32.15° E	100	45.2	83	320
Mocimboa da Praia	N	11.35°S	40.37° E	27	0.0	77	45
Montepuez	N	13.13° S	39.03° E	534	161.4	61	54
Nampula	N	15.10° S	39.28° E	438	134.4	29	16
Panda	S	24.05° S	34.72° E	150	69.2	57	25
Pemba	N	12.98° S	40.53° E	50	1.4	32	28
Quelimane	C	17.88° S	36.88° E	16	18.2	30	16
Sussundenga	C	19.33° S	33.23° E	620	171.7	81	311
Tete	C	16.17° S	33.47° E	149	417.6	50	30
Umbeluzi	S	26.05° S	32.38° E	12	23.1	81	349
Vila-Macia	S	25.03° S	33.10° E	56	34.6	80	305
Vilanculo	S	22.00° S	35.32° E	20	0.8	28	116
Xai-Xai	S	25.05° S	33.63° E	4	10.8	55	18

¹ N: North region, C: Central region, S: South region. ² Percentage of complete dekadal rain gauge observations (2001–2012). ³ Number of complete dekadal observations used in validation.

Table 2. Overview of 26 rain gauges.

Station	Region 1	Latitude	Longitude	Elevation (m a.s.l.)	Distance to Coastline (km)	Number of Observations 2 (%)	Number Used in Validation 3
Angoche	N	16.23° S	39.90° E	61	0.1	47	18
Beira/Aeroporto	C	19.80° S	34.90° E	8	3.1	26	1
Changalane	S	26.30° S	32.18° E	100	52.7	49	33
Chimoio	C	19.11° S	33.46° E	732	161.6	59	4
Cuamba	N	14.82° S	36.53° E	606	316	60	28
Inhambane	S	23.87° S	35.38° E	14	0.1	41	11
Inharrime	S	24.48° S	35.02° E	43	17.3	65	280
Lichinga	N	13.30° S	35.23° E	137	563.7	31	10
Lumbo	N	15.03° S	40.67° E	10	1.4	60	26
Maniquenique	S	24.73° S	33.53° E	13	46.3	82	314
Manjacaze	S	24.72°S	33.88° E	65	36.2	26	97
Maputo/Observatorio	S	25.96° S	32.60° E	60	0.6	95	410
Marrupa	N	13.23° S	37.55° E	838	318.9	55	220
Massingir	S	25.88°S	32.15° E	100	45.2	83	320
Mocimboa da Praia	N	11.35°S	40.37° E	27	0.0	77	45
Montepuez	N	13.13° S	39.03° E	534	161.4	61	54
Nampula	N	15.10° S	39.28° E	438	134.4	29	16
Panda	S	24.05° S	34.72° E	150	69.2	57	25
Pemba	N	12.98° S	40.53° E	50	1.4	32	28
Quelimane	C	17.88° S	36.88° E	16	18.2	30	16
Sussundenga	C	19.33° S	33.23° E	620	171.7	81	311
Tete	C	16.17° S	33.47° E	149	417.6	50	30
Umbeluzi	S	26.05° S	32.38° E	12	23.1	81	349
Vila-Macia	S	25.03° S	33.10° E	56	34.6	80	305
Vilanculo	S	22.00° S	35.32° E	20	0.8	28	116
Xai-Xai	S	25.05° S	33.63° E	4	10.8	55	18

¹ N: North region, C: Central region, S: South region. ² Percentage of complete dekadal rain gauge observations (2001–2012). ³ Number of complete dekadal observations used in validation.

4. Methods

4.1. Generation of an Independent Validation Dataset

Validation was done on the overlapping period (2001–2012). Since the satellite based rainfall products all are retrieved using rain gauge data, a separate validation dataset was generated that is independent of all products evaluated here. The rain gauge database was compared with the Global Summary of the Day (GSoD) product that is transmitted through GTS, in order to create one validation data set. The GSoD contains some data that were also used for producing TARCAT [2], and is the main data source for the RFE and CHIRPS products. Only dekads without any daily observations used in the calibration and/or merging phase of the different products were retained for the validation, resulting in 3085 dekadal observations over the 26 stations. We choose not to interpolate the gauge measurements into a gridded product, since the stations are too sparse and unevenly distributed, but rather to convert the point location of the rain gauges into polygons with 12 km diameter. These were rasterized according to the respective satellite products projection system and resolution, in order to extract satellite estimates for the TARCAT, RFE, and CHIRPS series for the gauge locations. The use of point data results in a demanding validation process; the variance of satellite estimates are fundamentally smoother in space and time as they represent spatial averages over grid cells, and some systematic differences between the point observations and pixel estimates are to be expected.

4.2. Validation Statistics

Two groups of statistics were used to evaluate the satellite products: pairwise comparison statistics that evaluate the performance of the satellite products in estimating the amount of rainfall, and categorical validation statistics that assess rain-detection capabilities [35]. In the first group, summarized in Table 3, the Pearson correlation coefficient (r) is used to evaluate how well the estimates corresponded to the observed values. The Mean Error (ME) and Relative Mean Absolute Error (RMAE) both estimate the average estimation error, respectively in millimeters and as fractions. The Nash-Sutcliffe Efficiency coefficient (Eff) shows the skill of the estimates relative to the gauge mean and varies from minus infinity to one: negative values mean that the gauge mean is a better estimate, zero means that the gauge mean is as good as the estimate, and 1 corresponds to a perfect match between gauge data and satellite based data. The Bias indicates how well the mean estimate and gauge mean correspond. Eff and Bias do not have units.

Table 3. Pairwise comparison statistics with G = gauge rainfall measurement, $\overline{G}$ = average gauge rainfall measurement, S = satellite rainfall estimate, $\overline{S}$ = average satellite rainfall estimate, and N = number of data pairs.

Name	Formula	Perfect Score
Pearson correlation coefficient	$r=\frac{{\displaystyle \sum }\left(G-\overline{G}\right)\left(S-\overline{S}\right)}{\sqrt{{\displaystyle \sum }{\left(G-\overline{G}\right)}^2}\sqrt{{\displaystyle \sum }{\left(S-\overline{S}\right)}^2}}$	1
Mean Error	$ME=1/N{\displaystyle \sum }\left(S-G\right)$	0
Relative mean absolute error	$RMAE=\left(1/N{\displaystyle \sum }|\left(S-G\right)|\right)/\left(\overline{G}\right)$	0
Nash-Sutcliffe Efficiency coefficient	$Eff=1-\left({\displaystyle \sum }{\left(S-G\right)}^2\right)/\left({\displaystyle \sum }{\left(G-\overline{G}\right)}^2\right)$	1
Bias	$Bias={\displaystyle \sum }S/{\displaystyle \sum }G$	1

Table 3. Pairwise comparison statistics with G = gauge rainfall measurement, $\overline{G}$ = average gauge rainfall measurement, S = satellite rainfall estimate, $\overline{S}$ = average satellite rainfall estimate, and N = number of data pairs.

Name	Formula	Perfect Score
Pearson correlation coefficient	$r=\frac{{\displaystyle \sum }\left(G-\overline{G}\right)\left(S-\overline{S}\right)}{\sqrt{{\displaystyle \sum }{\left(G-\overline{G}\right)}^2}\sqrt{{\displaystyle \sum }{\left(S-\overline{S}\right)}^2}}$	1
Mean Error	$ME=1/N{\displaystyle \sum }\left(S-G\right)$	0
Relative mean absolute error	$RMAE=\left(1/N{\displaystyle \sum }|\left(S-G\right)|\right)/\left(\overline{G}\right)$	0
Nash-Sutcliffe Efficiency coefficient	$Eff=1-\left({\displaystyle \sum }{\left(S-G\right)}^2\right)/\left({\displaystyle \sum }{\left(G-\overline{G}\right)}^2\right)$	1
Bias	$Bias={\displaystyle \sum }S/{\displaystyle \sum }G$	1

The second group of statistics is based on a contingency table, where A, B, C, and D represent hits, false alarms, misses, and correct negatives, respectively, with a rainfall threshold of 5 mm. The categorical validation statistics are summarized in Table 4. The Probability of Detection (POD) and False Alarm Ratio (FAR) respectively indicate what fraction of the observed events was correctly forecast and what fraction of the predicted events did not occur. The Equitable Threat Score (ETS) evaluates how well the satellite rain events correspond to the gauge events, accounting for hits due to chance. The Hansen and Kuipers discriminate (HK) shows how well the satellite estimates discriminate between rain and no-rain events, and the Heidke Skill Score (HSS) measures the accuracy of the estimates accounting for matches due to random chance. The Frequency Bias (FB), finally, expresses systematic differences between the frequency of rain events in gauge observations and satellite estimates.

Depending on the specific application, some statistics can be more useful than others to evaluate the satellite products. For drought monitoring, it is important not to overestimate rainfall amounts or rainfall events, and thus to avoid a ME > 0, high FAR or FB > 1. The opposite is true for hydrological purposes and flood forecasting, where underestimations need to be avoided, thus to avoid ME < 0, low POD or FB < 1. For more general purposes, the user should seek after products with high r, Eff, ETS, HSS and low RMAE.

Table 4. Categorical validation statistics with A = number of hits, B = number of false alarms, C = number of misses, and D = number of correct negatives.

Name	Formula	Perfect Score
obability of detection	$POD=A/\left(A+C\right)$	1
False alarm ratio	$FAR=B/\left(A+B\right)$	0
Equitable threat score	$ETS=\left(A-Ar\right)/\left(A+B+C-Ar\right)$ with hits that occur by chance: $Ar=\left(\left(A+C\right)\left(A+B\right)\right)/N$	1
Hansen and Kuipers discriminate	$HK=A/\left(A+C\right)-B/\left(B+D\right)$	1
Heidke Skill Score	$HSS=\left(2\left(AD-BC\right)\right)/\left(\left(A+C\right)\left(C+D\right)+\left(A+B\right)\left(B+D\right)\right)$	1
Frequency Bias	$FB=\left(A+B\right)/\left(A+C\right)$	1

Table 4. Categorical validation statistics with A = number of hits, B = number of false alarms, C = number of misses, and D = number of correct negatives.

Name	Formula	Perfect Score
obability of detection	$POD=A/\left(A+C\right)$	1
False alarm ratio	$FAR=B/\left(A+B\right)$	0
Equitable threat score	$ETS=\left(A-Ar\right)/\left(A+B+C-Ar\right)$ with hits that occur by chance: $Ar=\left(\left(A+C\right)\left(A+B\right)\right)/N$	1
Hansen and Kuipers discriminate	$HK=A/\left(A+C\right)-B/\left(B+D\right)$	1
Heidke Skill Score	$HSS=\left(2\left(AD-BC\right)\right)/\left(\left(A+C\right)\left(C+D\right)+\left(A+B\right)\left(B+D\right)\right)$	1
Frequency Bias	$FB=\left(A+B\right)/\left(A+C\right)$	1

5. Results and Discussion

5.1. Overall Comparison of Satellite Products

Figure 3 shows the mean (2001–2012) total annual rainfall and the mean (2001–2012) total rainfall over both the dry and wet seasons for TARCAT, RFE, and CHIRPS. While TARCAT and RFE show similar spatial patterns over land, CHIRPS has higher estimates for annual totals in the northern provinces, and lower estimates over the dry season in central and southern Mozambique. The CHIRPS product also seems to show the highest spatial detail—although its spatial resolution is not higher—while TARCAT shows the least spatial differentiation. The spatial detail arises from the high resolution climatology used to derive the CHIRPS precipitation.

Figure 3. Mean (2001–2012) (a) total annual rainfall, (b) total rainfall over the dry season (April–September) and (c) over the wet season (October–March) for TARCAT, RFE, and CHIRPS.

Figure 3. Mean (2001–2012) (a) total annual rainfall, (b) total rainfall over the dry season (April–September) and (c) over the wet season (October–March) for TARCAT, RFE, and CHIRPS.

5.2. Overall Validation

Plots in Figure 4 show the comparison of rain gauge data with satellite rainfall estimates for all dekads in the validation dataset. All three products show overestimation of low rainfall values and underestimation of high values. The overestimations of low rainfall values are highest for CHIRPS, where the regression line shows the highest intercept, while the underestimations are highest for TARCAT. This is confirmed by the cumulative density plots (CDP) in Figure 5. The CDP of the TARCAT product resembles the gauge plot the most for lower dekadal rainfall values (<15 mm), but the discrepancy for higher dekadal rainfall values is larger for TARCAT than for the RFE and CHIRPS products. TARCAT shows the highest underestimations for very high rainfall events. On the other hand, CHIRPS underestimates the frequency of 0 mm rainfall events while overestimating the frequency of low rainfall events (between 0 and 20 mm). This has implications for different applications: while TARCAT is designed as a reliable drought-monitoring product, CHIRPS might be more useful for flood monitoring.

The validation statistics over all stations are compared between the three satellite products in Table 5. All products underestimate rainfall with negative mean errors (ME). The CHIRPS product corresponds best to the rain gauge values (highest r), shows the smallest absolute ME, highest Eff, and POD, and best Bias. The RFE product shows the lowest RMAE, FAR, and highest ETS, HK, and HSS. TARCAT performs best for FB. Generally, CHIRPS shows the best results for pairwise comparison statistics and RFE performs better on the categorical validation statistics. TARCAT is outperformed by the other products, except for FB, indicating that TARCAT has a good prediction of the frequency of rainfall events. This can be explained by TARCAT’s temporally consistent climatology-based calibration and the large amount of local gauge observations that were used for local CCD-threshold tuning [2,3]. TARCAT and especially RFE show underpredicting of the frequency of rainfall events (FB < 1). CHIRPS shows the highest POD linked to a high FAR, resulting in FB > 1, thus overpredicting the number of rainfall events makes this product less useful for drought monitoring. This problem may arise from the specifics of the CHIRPS rainfall estimation procedure: once the IR CCD has been calculated, this value is translated into a precipitation estimate using regression coefficients derived from 0.25° TRMM precipitation fields. Using TRMM satellite estimates as “truth” allows for a rapid fit at global spatial scales, but may result in too much “drizzle” as the TRMM spatial scale is much larger than the point locations of rain gauges and correction of instantaneous rainfall rates for the sub-grid variability of rain/no-rain areas is relevant [36].

Figure 4. Comparison of rain gauge data with satellite products for all dekads (N = 3085) in the validation dataset. Dashed line indicates 1:1 correspondence and red line gives the linear regression best fit.

Figure 4. Comparison of rain gauge data with satellite products for all dekads (N = 3085) in the validation dataset. Dashed line indicates 1:1 correspondence and red line gives the linear regression best fit.

Figure 5. Comparison of cumulative density plots of the satellite products and the rain gauges.

Figure 5. Comparison of cumulative density plots of the satellite products and the rain gauges.

Table 5. Comparison of validation statistics for all stations for three satellite products. Values in bold denote the best result.

Dataset	N	r	ME	RMAE	Eff	Bias	POD	FAR	ETS	HK	HSS	FB
TARCAT	3085	0.57	−9.14	0.76	0.28	0.64	0.74	0.24	0.31	0.47	0.47	0.97
RFE	3085	0.62	−7.55	0.69	0.35	0.70	0.71	0.18	0.36	0.54	0.53	0.87
CHIRPS	3085	0.64	−3.21	0.71	0.41	0.87	0.89	0.29	0.32	0.47	0.48	1.26

Table 5. Comparison of validation statistics for all stations for three satellite products. Values in bold denote the best result.

Dataset	N	r	ME	RMAE	Eff	Bias	POD	FAR	ETS	HK	HSS	FB
TARCAT	3085	0.57	−9.14	0.76	0.28	0.64	0.74	0.24	0.31	0.47	0.47	0.97
RFE	3085	0.62	−7.55	0.69	0.35	0.70	0.71	0.18	0.36	0.54	0.53	0.87
CHIRPS	3085	0.64	−3.21	0.71	0.41	0.87	0.89	0.29	0.32	0.47	0.48	1.26

5.3. Results per Rainfall Category

Validation statistics were calculated for different rainfall categories based on the dekadal rain gauge data: <5 mm (N = 1433), 5–10 mm (N = 312), 10–20 mm (N = 355), 20–50 mm (N = 492), 50–100 mm (N = 288), and >100 mm (N = 205). Generally, with increasing rainfall the satellite products show larger absolute underestimations, lower RMAE, higher Eff, and lower Bias (Figure 6). Differences between products are largest for low rainfall, where RFE in general performs best and CHIRPS scores worse with higher RMAE, lower Eff, and higher Bias. This is important for detecting dry spells. For high rainfall, the products roughly show similar results, although the absolute ME of TARCAT is the largest, related to higher underestimations, making it less suitable for flood monitoring applications in this region.

Figure 6. Pairwise comparison statistics (ME, RMAE, Eff and Bias) of the satellite products compared to the independent validation dataset. Categories based on dekadal rain gauge observations. Grey dashed lines indicate perfect score.

Figure 6. Pairwise comparison statistics (ME, RMAE, Eff and Bias) of the satellite products compared to the independent validation dataset. Categories based on dekadal rain gauge observations. Grey dashed lines indicate perfect score.

5.4. Temporal Patterns

Figure 7 shows pairwise comparison statistics of the satellite products with the validation dataset for each month. For this purpose, the validation dataset was split up in 12 subsets, with N between 174 (June) and 305 (April). During the dry season (April-September), for all products r is lower, the RMAE is worse, Eff is lower, and Bias is higher. The opposite is true for the wet, main crop season (October–March), when satellite products show higher correspondence (r) with the rain gauge data, RMAE and Bias are lower, and Eff is higher. During the cyclone season (December–February), CHIRPS shows the best ME (lowest underestimations) and Eff. The same can be concluded over the entire seasonal cycle: it is mostly CHIRPS that has the best ME, Eff, and Bias.

Figure 7. Pairwise comparison statistics (r, ME, RMAE, Eff, and Bias) of the satellite products compared to the independent validation dataset for each month. The lower right graph shows number of observations in the validation dataset per month.

Figure 7. Pairwise comparison statistics (r, ME, RMAE, Eff, and Bias) of the satellite products compared to the independent validation dataset for each month. The lower right graph shows number of observations in the validation dataset per month.

The monthly categorical validation statistics (Figure 8) demonstrate very similar results between the different products for the wet season, when all satellite products perform best: in general, POD and ETS are higher, and FAR is lower. During the dry season, however, there is more differentiation between the products. CHIRPS shows the highest POD and a high FAR. TARCAT tends to underestimate rainfall events, but also has the lowest number of false alarms. This is not unexpected given the design of TARCAT as a drought monitoring dataset based on climatology-based calibration using the median (the most frequently occurring) rather than the mean rainfall event [2,3]. The ETS is lower for all products compared with the wet season, when RFE scores best and TARCAT achieves the lowest ETS from June to November.

Figure 8. Categorical validation statistics (POD, FAR, and ETS) of the satellite products compared to the independent validation dataset for each month.

Figure 8. Categorical validation statistics (POD, FAR, and ETS) of the satellite products compared to the independent validation dataset for each month.

5.5. Spatial Patterns

In order to investigate spatial patterns in the performance of satellite derived rainfall products, the validation dataset was split into coastal stations, located at less than 100 km from the coastline, and inland stations. Table 6 shows the validation statistics for both groups. For all statistics, except ME, Bias, and FB, the inland group performs better: for the inland stations dataset Pearson correlation coefficients range between 0.72 and 0.75, considerably higher than for the coastal stations (0.46 to 0.55). In addition, RMAE and Eff are better and the estimate of rainfall events is more accurate, as demonstrated by the substantially higher POD, ETS, HK, and HSS, and lower FAR. The better performance of satellite derived rainfall estimates at larger distances from the coast is related to the predominance of convective rainfall in these areas, in contrast to the frontal systems with warm cloud precipitation along the coastal region [37,38]. Note that none of the inland stations are located in the drier southern part of Mozambique.

For both groups, RFE and CHIRPS perform similarly, outperforming the TARCAT dataset. TARCAT scores better for FB, as was also concluded from the overall analysis. The differences in performance between the different products is however lower for the inland stations with a smaller range on r and most of the categorical validation statistics.

Table 6. Comparison of validation statistics for (a) coastal stations and (b) inland stations, for three satellite products. Underlined values denote the best result, values in bold the best result per subgroup.

Dataset	N	r	ME	RMAE	Eff	Bias	POD	FAR	ETS	HK	HSS	FB
(a)
TARCAT	2466	0.46	−7.18	0.82	0.18	0.67	0.73	0.27	0.27	0.42	0.42	1.00
RFE	2466	0.55	−5.85	0.74	0.22	0.73	0.70	0.20	0.33	0.50	0.50	0.87
CHIRPS	2466	0.55	−2.02	0.78	0.29	0.91	0.89	0.31	0.28	0.43	0.44	1.29
(b)
TARCAT	619	0.72	−16.97	0.62	0.39	0.57	0.78	0.11	0.48	0.66	0.65	0.87
RFE	619	0.75	−14.34	0.58	0.49	0.64	0.77	0.09	0.49	0.67	0.65	0.84
CHIRPS	619	0.75	−7.92	0.55	0.55	0.80	0.92	0.20	0.47	0.62	0.63	1.15

Table 6. Comparison of validation statistics for (a) coastal stations and (b) inland stations, for three satellite products. Underlined values denote the best result, values in bold the best result per subgroup.

Dataset	N	r	ME	RMAE	Eff	Bias	POD	FAR	ETS	HK	HSS	FB
(a)
TARCAT	2466	0.46	−7.18	0.82	0.18	0.67	0.73	0.27	0.27	0.42	0.42	1.00
RFE	2466	0.55	−5.85	0.74	0.22	0.73	0.70	0.20	0.33	0.50	0.50	0.87
CHIRPS	2466	0.55	−2.02	0.78	0.29	0.91	0.89	0.31	0.28	0.43	0.44	1.29
(b)
TARCAT	619	0.72	−16.97	0.62	0.39	0.57	0.78	0.11	0.48	0.66	0.65	0.87
RFE	619	0.75	−14.34	0.58	0.49	0.64	0.77	0.09	0.49	0.67	0.65	0.84
CHIRPS	619	0.75	−7.92	0.55	0.55	0.80	0.92	0.20	0.47	0.62	0.63	1.15

Performance of satellite products for the North, Central, and South regions is summarized in Table 7. For all statistics the satellite products perform better in the North region. Here, TARCAT outperforms the other products not only on FB, as in previous analyses, but also on ETS, HK, and HSS: in the ITCZ dominated North region, the TIR only based products performs better than or as well as the blended RFE and CHIRPS.

The South region shows the worst results for all products, which is also related to the fact that only coastal stations are found here. Although the ME shows relatively small underestimations, r and Eff are much lower and the RMAE is higher. In addition, the FAR is considerably higher. Both the RFE and CHIRPS products outperform TARCAT. The blended products, including PM algorithms, perform better than the TIR only based product in this region dominated by frontal systems.

The Central region shows results in-between the other two regions: r, RMAE, Eff, and FAR are as good as the North region, while ETS, HK, and HSS are as poor as the South region. The Central region shows the highest average underestimations. CHIRPS outperforms the other products in almost all statistics.

Table 7. Comparison of validation statistics for (a) North, (b) Central, and (c) South regions for the three satellite products considered here. Underlined values denote the best result, values in bold—the best result per subgroup.

Dataset	N	r	ME	RMAE	Eff	Bias	POD	FAR	ETS	HK	HSS	FB
(a)
TARCAT	445	0.75	−7.94	0.57	0.53	0.77	0.89	0.10	0.65	0.79	0.79	1.00
RFE	445	0.74	−5.92	0.54	0.52	0.83	0.84	0.08	0.61	0.76	0.76	0.91
CHIRPS	445	0.76	−1.47	0.54	0.57	0.96	0.96	0.19	0.57	0.72	0.72	1.20
(b)
TARCAT	362	0.70	−21.97	0.70	0.29	0.45	0.67	0.11	0.32	0.53	0.49	0.75
RFE	362	0.75	−18.43	0.66	0.44	0.54	0.67	0.10	0.34	0.55	0.51	0.74
CHIRPS	362	0.76	−12.36	0.59	0.52	0.69	0.88	0.21	0.35	0.50	0.52	1.11
(c)
TARCAT	2278	0.43	−7.34	0.84	0.15	0.65	0.72	0.28	0.25	0.40	0.40	1.01
RFE	2278	0.53	−6.14	0.75	0.21	0.71	0.70	0.21	0.32	0.49	0.49	0.88
CHIRPS	2278	0.53	−2.09	0.79	0.27	0.90	0.88	0.32	0.27	0.42	0.43	1.30

Table 7. Comparison of validation statistics for (a) North, (b) Central, and (c) South regions for the three satellite products considered here. Underlined values denote the best result, values in bold—the best result per subgroup.

Dataset	N	r	ME	RMAE	Eff	Bias	POD	FAR	ETS	HK	HSS	FB
(a)
TARCAT	445	0.75	−7.94	0.57	0.53	0.77	0.89	0.10	0.65	0.79	0.79	1.00
RFE	445	0.74	−5.92	0.54	0.52	0.83	0.84	0.08	0.61	0.76	0.76	0.91
CHIRPS	445	0.76	−1.47	0.54	0.57	0.96	0.96	0.19	0.57	0.72	0.72	1.20
(b)
TARCAT	362	0.70	−21.97	0.70	0.29	0.45	0.67	0.11	0.32	0.53	0.49	0.75
RFE	362	0.75	−18.43	0.66	0.44	0.54	0.67	0.10	0.34	0.55	0.51	0.74
CHIRPS	362	0.76	−12.36	0.59	0.52	0.69	0.88	0.21	0.35	0.50	0.52	1.11
(c)
TARCAT	2278	0.43	−7.34	0.84	0.15	0.65	0.72	0.28	0.25	0.40	0.40	1.01
RFE	2278	0.53	−6.14	0.75	0.21	0.71	0.70	0.21	0.32	0.49	0.49	0.88
CHIRPS	2278	0.53	−2.09	0.79	0.27	0.90	0.88	0.32	0.27	0.42	0.43	1.30

6. Conclusions

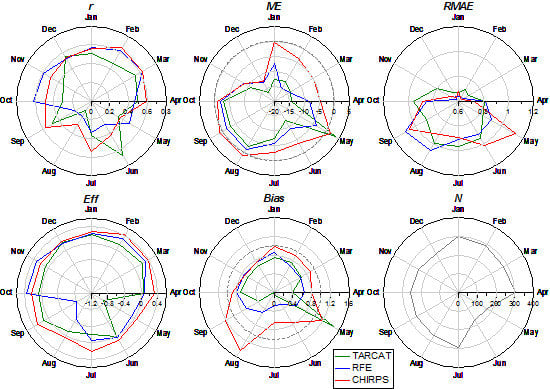
Three satellite-based rainfall datasets were evaluated against an independent rain gauge dataset provided by the Mozambican meteorological institute. The TARCAT, RFE, and CHIRPS products have a relatively high spatial and temporal resolution and these gridded rainfall products could be very beneficial for accurate drought and flood monitoring for agricultural applications and early warning of food insecurity, provided their accuracies, strengths and weaknesses are well understood. Rain gauges in Mozambique are sparse, poorly distributed, and often show gaps in the temporal record of observations. Satellite rainfall estimates, on the other hand, contain random errors and bias because of the indirect relation between observations and precipitation, inadequate sampling and algorithm imperfections [17]. The analysis focused on both pairwise comparison statistics that evaluate the performance of the satellite products in estimating the amount of rainfall, and categorical validation statistics that assess rain-detection capabilities.

Overall, satellite products show overestimation of lower dekadal rainfall values and underestimation of higher values. The products that combine TIR and PM imagery with GTS stations (RFE) or TIR imagery and GTS stations (CHIRPS), perform comparatively well and outperform the TARCAT product, which is based on TIR only. However, TARCAT shows the best relative frequency of rainfall events, related to the local tuning of the TARCAT algorithm. TARCAT performs best in detecting rainfall events at point spatial scales, as represented by stations, likely due to the large number of gauge observations that were used to generate the product [3]. RFE tends to underpredict the frequency of rainfall events, while CHIRPS tends to overpredict events and has the highest FAR, making this product less useful for drought monitoring. The CHIRPS algorithm depends on 0.25° TRMM training data, and this dependence may contribute to its tendency to overpredict, since averaging over larger areas increases the frequency of rainfall events.

For drought monitoring and estimation of the effect on agricultural production, users require datasets, in which low rainfall amounts are skillfully detected and not overestimated, while for flood monitoring high rainfall events need to be correctly estimated. Differences in performance between products disappear with higher dekadal rainfall and all products achieve better results during the wet season. Although underestimations of absolute values are larger, Eff increases and Bias decreases. CHIRPS shows the best results during the cyclone season (December-February). RFE outperforms the other products for lower dekadal rainfall, and seems the most useful product for dry spell assessments during the main crop season (October–March). Over the entire seasonal cycle, however, CHIRPS tends to outperform RFE and TARCAT.

Estimations of inland rainfall were also compared to coastal rainfall and differences between the satellite products were found to be lower at larger distances from the coast. In addition, for the North region dominated by the ITCZ all satellite products perform better compared with the Central and South region, which is dominated by frontal weather systems. The TIR-only based TARCAT product performs better or as good as the other products in the North. CHIRPS outperforms the other products in the Central region. Additionally, for regions dominated by convective rainfall a locally calibrated algorithm using only TIR could perform at least as well as more sophisticated algorithms making use of multiple data sources [20]. Our results confirm however that products blending TIR and PM imagery perform better when the situation is more complex, such as over the coastal, Central and South regions of Mozambique, where precipitation is influenced by frontal systems.

All three products evaluated here show both good qualities and relevant shortcomings when used for agro-climatic monitoring, early warning systems, and different hydrological applications. Further work could focus on rainfall anomalies and deviations from what is considered normal rainfall. The deeper historical record of the TIR-only estimates provides an important context for evaluating extremes and precipitation trends. Additionally, the performance of the different satellite products during specific, serious drought events or large floods in the recent past could be further investigated.