Investigation of Simultaneous Effects of Aerosol Properties and Aerosol Peak Height on the Air Mass Factors for Space-Borne NO₂ Retrievals

Abstract

We investigate the simultaneous effects of aerosol peak height (APH), aerosol properties, measurement geometry, and other factors on the air mass factor for NO₂ retrieval at sites with high NO₂ concentration. A comparison of the effects of high and low surface reflectance reveals that NO₂ air mass factor (AMF) values over a snowy surface (surface reflectance 0.8) are generally higher than those over a deciduous forest surface (surface reflectance 0.05). Under high aerosol optical depth (AOD) conditions, the aerosol shielding effect over a high-albedo surface is revealed to reduce the path-length of light at the surface, whereas high single scattering albedo (SSA) conditions (e.g., SSA = 0.95) lead to an increase in the aerosol albedo effect, which results in an increased AMF over areas with low surface reflectance. We also conducted an in-depth study of the APH effect on AMF. For an AOD of 0.1 and half width (HW) of 5 km, NO₂ AMF decreases by 29% from 1.36 to 0.96 as APH changes from 0 to 2 km. In the case of high-AOD conditions (0.9) and HW of 5 km, the NO₂ AMF decreases by 240% from 1.85 to 0.54 as APH changes from 0 to 2 km. The AMF variation due to error in the model input parameters (e.g., AOD, SSA, aerosol shape, and APH) is also examined. When APH is 0 km with an AOD of 0.4, SSA of 0.88, and surface reflectance of 0.05, a 30% error in AOD induces an AMF error of between 4.85% and −3.67%, an SSA error of 0.04 leads to NO₂ VCD errors of between 4.46% and −4.77%, and a 30% error in AOD induces an AMF error of between −9.53% and 8.35% with an APH of 3 km. In addition to AOD and SSA, APH is an important factor in calculating AMF, due to the 2 km error in APH under high-SZA conditions, which leads to an NO₂ VCD error of over 60%. Aerosol shape is also found to have a measureable effect on AMF under high-AOD and small relative azimuth angle (RAA) conditions. The diurnal effect of the NO₂ profile is also examined and discussed.

1. Introduction

Nitrogen dioxide (NO₂) plays a key role in the photochemistry of tropospheric and stratospheric ozone [1]. Tropospheric NO₂ is present in urban and industrialized areas because one of the major sources of tropospheric NO₂ is fossil fuel combustion [2] in addition to biomass burning, soil emission, and lightning [3]. Since the 1990s, NO₂ has been monitored on a global scale by several space-borne sensors: the Global Ozone Monitoring Experiment (GOME) instrument, the Scanning Imaging Spectrometer for Atmospheric Cartography (SCIAMACHY), the Ozone Monitoring Instrument (OMI) and the GOME-2 instrument. Furthermore, observations of diurnal variations in NO₂ will be possible with the launch of the Tropospheric Emission: Monitoring Pollution (TEMPO) instrument by the National Aeronautics and Space Administration (NASA) [4], the Sentinel-4 on board the Meteosat Third Generation Sounder (MTG-S) by the European Space Agency (ESA), and the Geostationary environment monitoring sensor (GEMS) on board the Geostationary Korean Multi-Purpose Satellite—2B (GEO-KOMPSAT 2B) by the National Institute of Environmental Research (NIER) of Korea. NO₂ is typically measured by satellite sensors using spectral fitting methods such as differential optical absorption spectroscopy (DOAS). NO₂ slant column density (SCD), which is the integral of the NO₂ concentration present over the path between a light source and the sensor, is usually first retrieved by the DOAS method. The NO₂ SCD is then converted into vertical column density (VCD) by dividing the SCD by the air mass factor (AMF), which is calculated using a radiative transfer model (RTM). However, questions remain about the accuracy of NO₂ retrieval using the DOAS method, especially in relation to NO₂ AMF errors arising from uncertainties in radiative transfer model input parameters such as the vertical distribution of NO₂ and aerosol particles, aerosol physical properties, surface reflectance, and cloud coverage, among other factors. Given the importance of AMF to the accuracy of NO₂ retrieval using the DOAS method, previous studies have investigated AMF sensitivity to the effects of aerosol and surface reflectance. Boersma et al. [5] report that in polluted regions, AMF errors in the OMI NO₂ column retrieval over the visible wavelength range (405–465 nm) are 20%, 20%, and 15%, which are induced by uncertainties in the NO₂ vertical profile, surface reflectance, and aerosol concentration, respectively. According to Valks et al. [6], AMF errors in the GOME-2 NO₂ column retrieval are 15%–50% in polluted regions. Boersma et al. [7] showed that uncertainties in model input parameters (e.g., cloud coverage, surface reflectivity, and a priori NO₂ vertical shape) result in reduced accuracy in NO₂ AMF calculations. In addition, Leitão et al. [2] carried out an AMF sensitivity study that considered the effects of the NO₂ vertical profile, boundary layer height, surface reflectance, AOD, and SSA on NO₂ AMF values. However, AMF values commonly change simultaneously with a variety of factors such as aerosol properties (aerosol peak height (APH), AOD, and SSA), surface reflectance, solar zenith angle (SZA), and viewing zenith angle (VZA), especially for high-temporal-resolution observations from geostationary orbit. Furthermore, AMF errors are much larger than the spectral fitting errors (~10%) that occur from NO2 cross section uncertainties, spectral calibration uncertainties, instrument noise such as dark current, etc. The details of spectral fitting error sources can be found in previous study [7,8]. Thus, the following analyses were carried out as part of the present study.

▪

An investigation of the simultaneous effects of aerosol peak height (APH), various aerosol properties (e.g., AOD, SSA, and aerosol shape), and geometric information on the AMF for NO₂ retrieval.

▪

A calculation of AMF for specific environmental conditions such as high surface reflectance (snow case) and high APH (Asian dust case).

▪

A quantification of the diurnal effect of the NO₂ vertical profile on AMF calculations for geostationary NO₂ measurements.

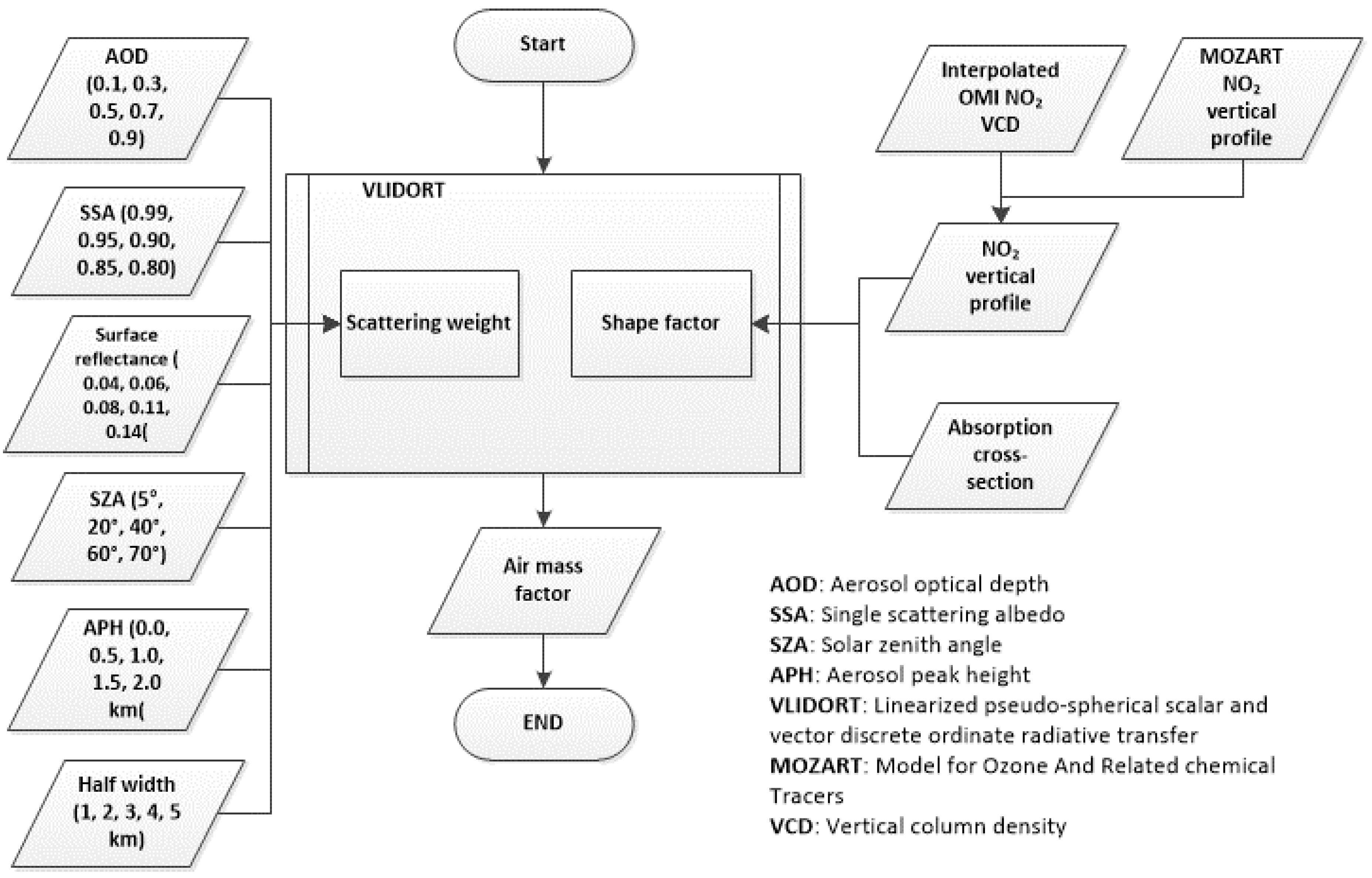
2. Methodology

The AMF definition is the ratio of the NO₂ slant column density (Ω_S) to the NO₂ vertical column density (Ω_V), and depends on the radiative transfer properties of the atmosphere such as aerosol, cloud, and NO₂ vertical distribution [9]. The equation of AMF is as follows:

$$AMF=\frac{{\Omega }_{\mathbf{S}}}{{\Omega }_{\mathbf{V}}}$$

(1)

AMF can be calculated using the scattering weight, ω’(z), and the shape factor S’_z(z) at each layer [9]. The scattering weight is the sensitivity of the backscattered spectrum to the abundance of the absorber at each layer, while the shape factor is a normalized vertical profile of number density [9]. AMF can be expressed in terms of the scattering weight and shape factor, as follows:

$$AMF=\mathit{AM}{\mathit{F}}_{\mathit{G}}{{\displaystyle \int }}_0^{\mathit{\infty }}{\mathit{\omega }}^{\prime }\left(\mathit{z}\right){{\mathit{S}}^{\prime }}_{\mathit{z}}\left(\mathit{z}\right)\mathit{d}\mathit{z}$$

(2)

$${\mathsf{\omega }}^{\prime }\left(\mathit{z}\right)=-\frac{1}{\mathit{A}\mathit{M}{\mathit{F}}_{\mathit{G}}}\frac{\partial \ln {\mathit{I}}_{\mathit{B}}}{\partial \mathit{\tau }}$$

(3)

$${S^{\prime }}_z\left(z\right)=\frac{\mathsf{\alpha }\left(z\right)n\left(z\right)}{{\int }_0^{\infty }\mathsf{\alpha }\left(z\right)n\left(z\right)dz}$$

(4)

$$\mathsf{\tau }=G+R+A$$

(5)

where AMF_G is the geometric AMF; I_B represents the backscattered intensity observed by the satellite instrument; τ is the optical thickness; α(z) and n(z) are the absorption cross-section (m²·molecules⁻¹) and number density (molecules·m⁻³), respectively; z denotes each vertical layer; G is the molecular (trace gas) absorption optical depth; R is the molecular (Rayleigh) scattering optical depth; and A is the aerosol extinction optical depth [10]. In addition to NO₂ column density, aerosol extinction vertical shape has an effect on NO₂ AMF, as the vertical shape influences the scattering weight at each layer. In this study, AMF was computed using linearized pseudo-spherical scalar and vector discrete ordinate radiative transfer (VLIDORT, version 2.6). A detailed description of VLIDORT and its utilization for AMF calculation is provided by [10]. In the present study, AMF was computed at 440 nm, as the spectral fitting is carried out over a wavelength interval of 430–450 nm where there exist four strong NO₂ absorption bands. Figure 1 presents a summary of the AMF computation. We calculated the scattering weight using AOD, SSA, surface reflectance, SZA, VZA, APH and HW, while the shape factor was calculated using the NO₂ vertical profile and absorption cross-section. A description of each input parameter follows.

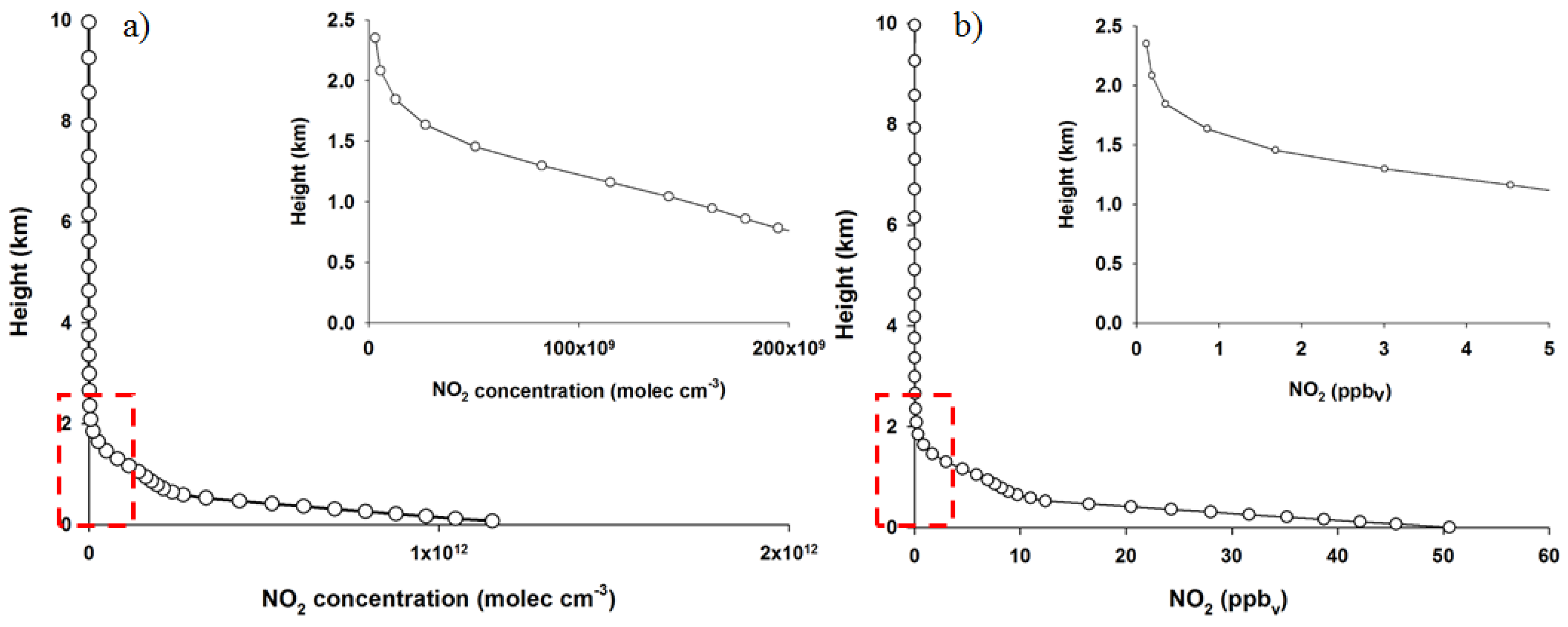
2.1. NO₂ Vertical Profile

Figure 2 shows NO₂ vertical profiles used as input data for the AMF calculation by: (a) concentration; and (b) mixing ratio. NO₂ vertical profiles obtained in Beijing during Dec 2011 from the Model for Ozone And Related chemical Tracers, version 4 (MOZART-4), and NO₂ vertical column densities (VCD) for the same month from OMNO2d of the Aura OMI Level-3 Global Gridded Total and Tropospheric NO₂ Data Product (0.25° × 0.25°) are used to generate a NO₂ vertical profile that represents the high-NO₂ site of this study. A detailed description of the emission inventory and chemistry used for the MOZART simulation can be found in [11]. The spatial resolution of the MOZART NO₂ vertical profile is 1.89° latitude × 2.5° longitude and it consists of 56 layers from the surface to ~2 hPa. We do not use the unadjusted NO₂ VMR profile from MOZART because the spatial resolution of MOZART is low, but instead calculate a NO₂ profile through comparison with the OMI NO₂ VCD. The comparison between the tropospheric NO₂ VCDs from MOZART and OMI is iterated until the MOZART tropospheric NO₂ column equals that of OMI by increasing or decreasing the MOZART NO₂ volume mixing ratio at all tropospheric layers by 0.2% per iteration. The shapes of the MOZART tropospheric NO₂ vertical profiles were not changed by this adjustment. Despite the low spatial resolution of MOZART stratospheric NO₂ measurements, stratospheric NO₂ vertical profiles from MOZART are used without adjustment to represent the stratospheric NO₂ in both polluted and background areas because NO₂ concentrations are lower and relatively stable in the stratosphere compared with those in the troposphere [12]. The NO₂ vertical shape in Beijing, a polluted area, is similar to that of an average urban profile used in a previous study [2] although the magnitude for the Beijing case is larger by a factor of two.

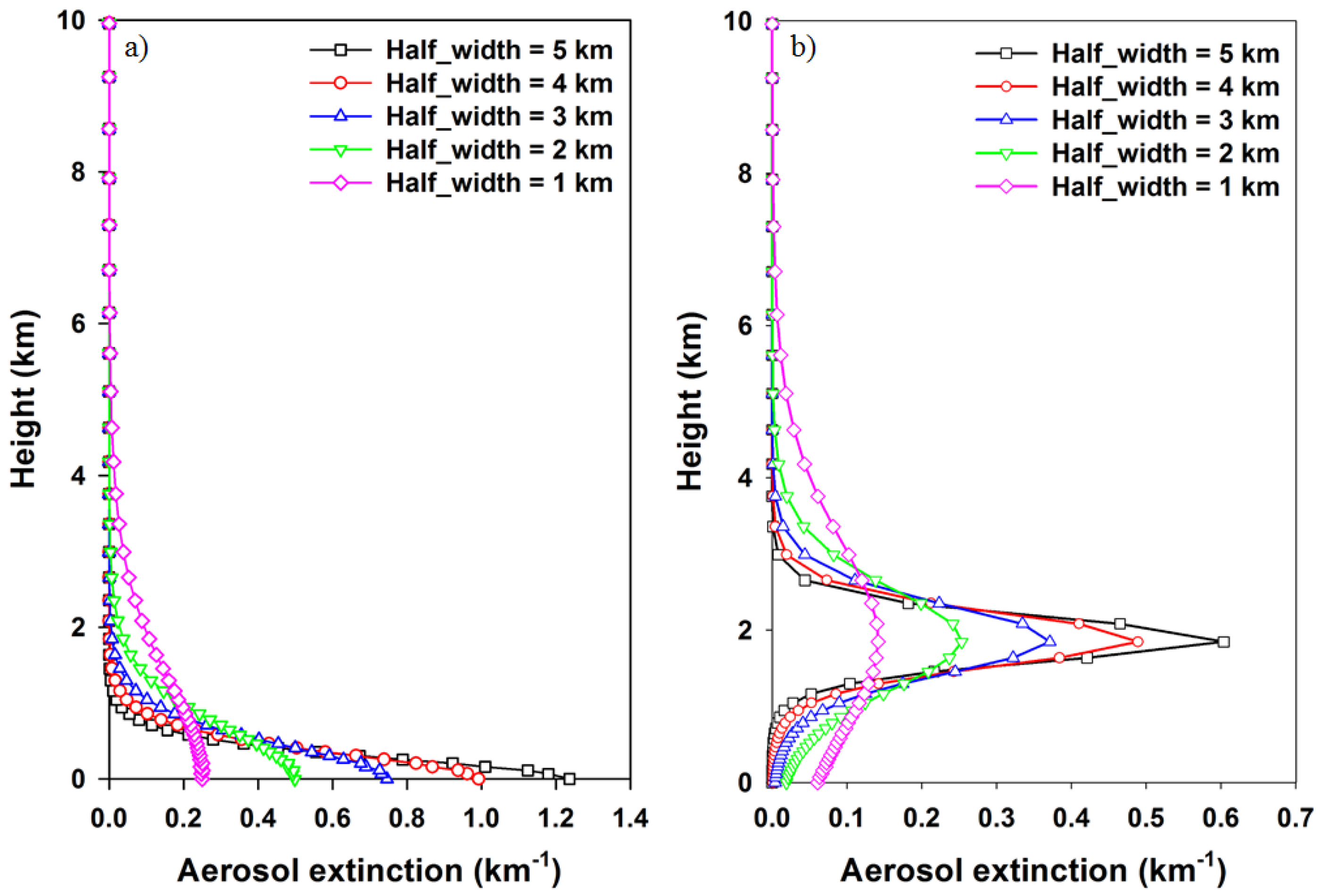
2.2. Aerosol Extinction Profile

To quantify the effects of APH on NO₂ AMF, we used a variety of parameters (AOD, APH, aerosol upper limit, and aerosol lower limit) to calculate the aerosol extinction coefficient profiles used as inputs for the AMF calculations. The aerosol vertical distribution is based on a Gaussian distribution function (GDF), as used by [13]. The equation of GDF is as follows:

$$\mathit{G}\mathit{D}\mathit{F}={{\displaystyle \int }}_{{\mathit{z}}_{\mathit{n}2}}^{{\mathit{z}}_{\mathit{n}1}}\mathit{W}\frac{{\mathit{e}}^{-\mathit{h}\left(\mathit{z}-{\mathit{z}}_{\mathit{p}}\right)}}{{\left[1+{\mathit{e}}^{-\mathit{h}\left(\mathit{z}-{\mathit{z}}_{\mathit{p}}\right)}\right]}^2}$$

(6)

$$\mathsf{\eta }= \frac{\mathit{l}\mathit{n} \left(3+\sqrt{8}\right)}{\mathit{h}}$$

(7)

where W is a normalization constant related to total aerosol loading; z_n1 and z_n2 is aerosol upper limit and lower limit, respectively; Z_p is the APH; and h is related to the Half width η [10].

In the present study, AOD, APH, and HW range from 0.1 to 0.9 at an interval of 0.2, from 0 to 2 km at an interval of 0.5 km, and from 1 to 5 km at an interval of 1 km, respectively. The upper and lower limits for aerosol height are set as 10 km and surface level, respectively. Twenty-five aerosol extinction coefficient profiles are used to account for normal aerosol cases, and 100 aerosol extinction coefficient profiles are used to account for dust events. Definitions of Gaussian loading, APH, and HW can be found in [10]. Although most aerosol particles exist near the surface, APH values of up to 2 km for Asian dust cases are used in accordance with previous investigations [14,15,16,17]. As aerosol scattering efficiency is known to influence AMF, five SSA values of 0.99, 0.95, 0.9, 0.85, and 0.8 were adopted. These five SSA values, which are commonly used in northeast Asia [18], were selected as model parameters because the scattering efficiency of aerosols also influence AMF. Figure 3 shows: (a) examples of aerosol extinction profiles under normal conditions with an AOD of 0.5, APH of 0 km, aerosol upper limit of 10 km, and aerosol lower limit of 0 km; and (b) those for an Asian dust case with the same AOD, aerosol upper and lower limits, but with APH of 2 km.

2.3. Setting of Aerosol Type

Because the AMF values for each aerosol type (smoke, dust, and sulfate) have similar patterns with small differences in magnitude, one type (smoke) was chosen for this study. However, we calculated each AMF for various aerosol shapes (spherical and cylinders) using the T-matrix in VLIDORT [19], given the effect of particle shape on the aerosol phase function [20]. Model input values, including fine- and coarse-mode radii and variance, refractive index, and fine-mode fraction for each aerosol type, can be found in [13].

2.4. Other Settings

SZA and VZA are important model input parameters for AMF because geometric AMF (AMF_G) is calculated as shown in Equation (6). Five SZA and VZA values (5°, 20°, 40°, 60°, and 70°) and seven Relative azimuth angle (RAA) values (0°, 30°, 60°, 90°, 120°, 150°, and 180°) were adopted for the present study. SZA and VZA values over 70° were not considered because NO₂ VCD retrieval is difficult in the case of a low signal-to-noise ratio.

$$AM{F}_{\mathit{G}}=\sec \mathit{S}\mathit{Z}\mathit{A}+\sec \mathit{V}\mathit{Z}\mathit{A}$$

(8)

AMF was calculated using surface reflectance from 0.4 to 0.14, which covers values typical of grassland, ocean, and deciduous forests in the UV-VIS range, because surface reflectance also has a major influence on AMF and varies with surface type.

3. Results

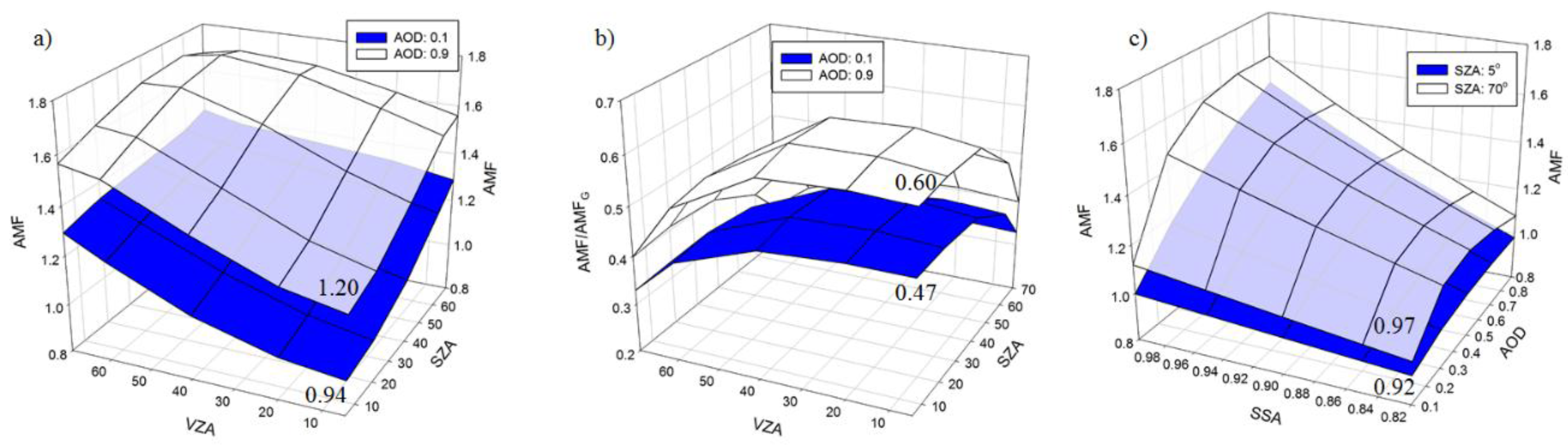
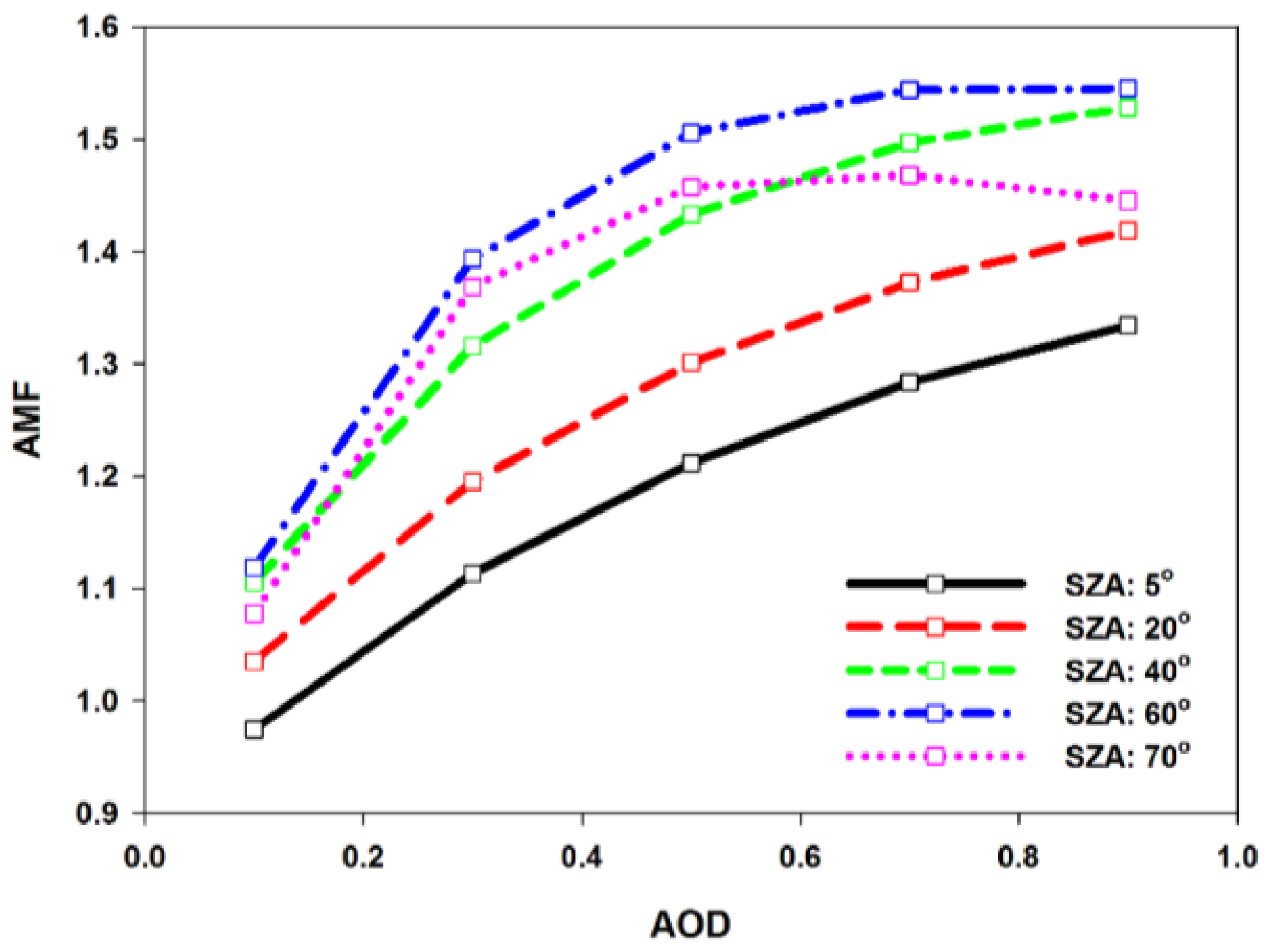
3.1. Influence of SZA and VZA

As shown in Figure 4a, SZA and VZA have a strong influence on the variations in NO₂ AMF compared with other parameters because the AMF_G in Equation (8) increases due to the increased light path between the sun and the satellite via the atmosphere under high-SZA and high-VZA conditions. In general, the pattern of the AMF changes with SZA and VZA in Figure 4 is similar to that in a previous study by [2]. AMF tends to increase when SZA and VZA increase, but decreases in polluted regions when SZA and VZA increase over 60° when AOD is high. This decreasing trend in NO₂ AMF when SZA and VZA are higher than 60° at AOD of 0.9 can be ascribed to a reduced path length due to fewer photons surviving Mie scattering to reach the satellite sensor than those at an AOD of 0.1. Figure 4b shows the ratio of AMF and AMF_G as a function of SZA and VZA at low and high AOD conditions. In this case, the ratio of AMF and AMF_G has low value at high SZA and VZA conditions due to the increase in the absorption light path. Figure 4c shows the AMF distribution with respect to AOD and SSA for two different SZA at high-NO₂ sites. Figure 4c shows similar results to those reported for an urban area in a previous study [2]. Notably, an increase in SSA always leads to an increase in AMF, and the rate of increase in AMF as a function of SSA is enhanced for high-AOD conditions, which can be attributed to the increase in the absorption light path. As shown in Figure 4c, for low-SZA conditions at the high-NO₂ site, the AMF tends to increase with increasing AOD with an APH of 0 km, whereas the AMF does not increase with increasing AOD at high SZA. Further details on the effects of SZA on NO₂ AMF for various AOD conditions are provided below and in Figure 5.

Figure 5 shows the variations in AMF caused by changes in SZA and AOD when aerosol is located near the surface (APH 0 km and HW 4 km) at the high-NO₂ site. AMF increases with increasing AOD at SZA lower than 60°, which implies that the absorption light path tends to increase with increasing aerosol loadings under low-SZA conditions. AMF increases by 37.11% and 38.40% at SZA of 5° and 60°, respectively, when AOD increases from 0.1 to 0.9. When SZA is 70°, the AMF increases with increasing AODs up to ~0.5. However, the AMF decreases by 2% (from 1.47 to 1.44) in the AOD range of 0.7 to 0.9. This decreasing trend in AMF may imply a shortened light path due to the lower probability of surviving photons, which are scattered further to reach the detector in the case of high-SZA conditions. Thus, when constructing a NO₂ AMF look-up table, it is helpful to construct the table at fine intervals of SZA and AOD to account for sudden changes in AMF.

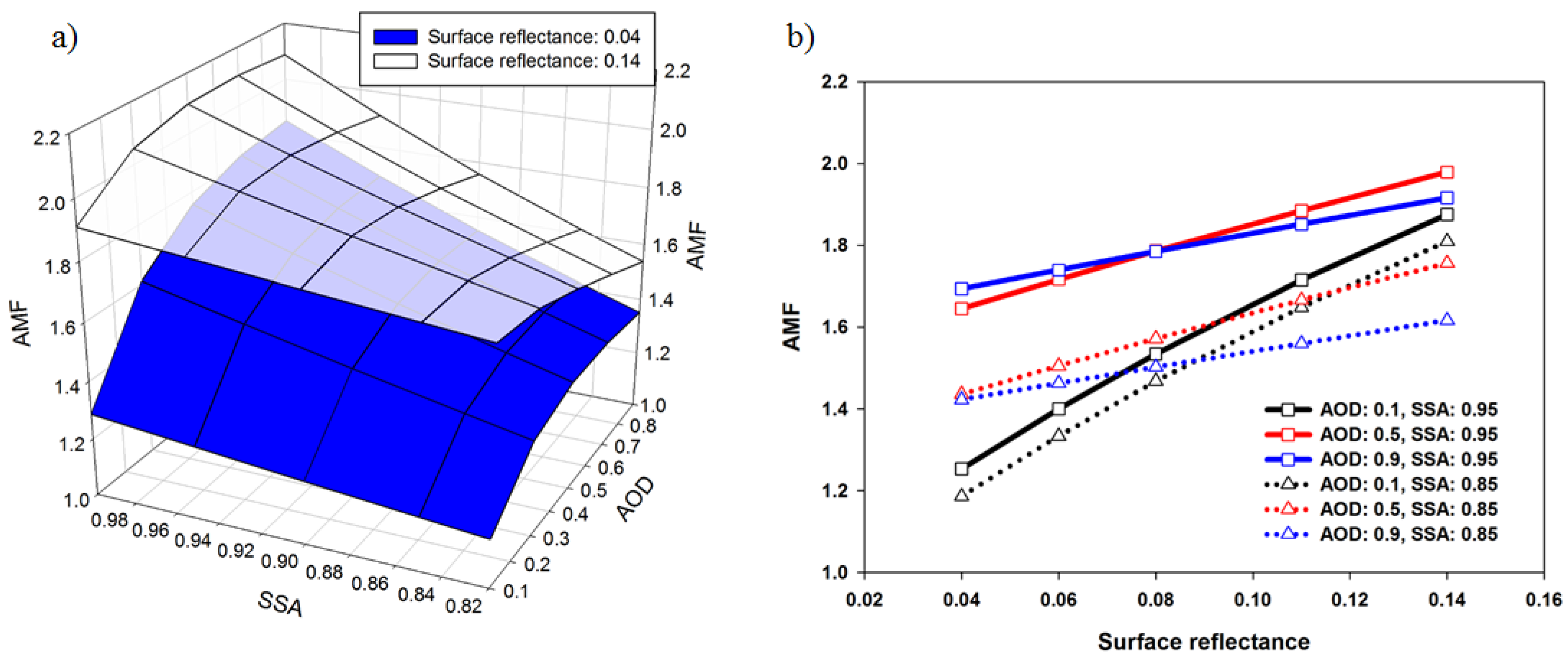
3.2. Influence of Surface Reflectance

Surface reflectance is an important factor in determining NO₂ AMF. Leitão et al. [2] reported that a change in surface reflectance from 0.01 to 0.1 can result in an increase in NO₂ AMF by ~90%. According to [21], the minimum Lambertian-equivalent reflectance values at 400 nm are 0.05, 0.06 and 0.07 for deciduous forests, grassland, and ocean, respectively. However, no previous study has investigated the effects of high surface reflectance under various AOD and SSA conditions on AMF where the Lambertian-equivalent reflectance values are as low as 0.5 and 0.8, such as on refreezing ice and fresh snow [22]. We compared the effect of high and low surface reflectance values on AMF for various AOD and SSA values, as shown in Figure 6a. The NO₂ AMF tends to increase with increasing surface reflectance at high-NO₂ site. The NO₂ AMF for an AOD of 0.1 and SSA of 0.95 increases by 49.6% (from 1.25 to 1.87) at the high-NO₂ site when the surface reflectance is 0.04 and 0.14, respectively. Figure 6b shows the variations in NO₂ AMF at high-NO₂ site as a function of surface reflectance under various AOD and SSA conditions. NO₂ AMF increases with increasing surface reflectance between 0.04 and 0.14. However, the increasing rate in NO₂ AMF as a function of surface reflectance decreases with increasing AOD values due to the increased aerosol shielding effect. In the case of AOD = 0.1 and SSA = 0.85, the NO₂ AMF increases by 38.66% (from 1.19 to 1.65) as surface reflectance changes from 0.04 to 0.14. In the case of AOD = 0.9 and SSA = 0.85, NO₂ AMF increases by 14.08% (from 1.69 to 1.92) when surface reflectance changes from 0.04 to 0.14. NO₂ AMF values under high-SSA conditions are always larger than those in the case of low SSA values, and the influence of SSA is much greater under high-AOD conditions.

We compared the effects of low and extremely high surface reflectance values on AMF under several AOD and SSA conditions, as shown in Figure 7. A surface reflectance of 0.8 corresponds to values for after 3–4 days of snowfall. NO₂ AMF values at a surface reflectance of 0.8 are much higher than those at a surface reflectance of 0.05. Furthermore, at a surface reflectance of 0.8, as AOD increases the AMF decreases despite an APH of 0 km, as the aerosol blocks reflectance from the surface. It is interesting to compare aerosol effects on AMF over low- and high-reflectance areas. Aerosol shielding effects over high-albedo surfaces act to reduce the light path-length on the surface, whereas high-SSA conditions (e.g., SSA = 0.95) lead to an increase in the aerosol albedo effect, which also results in increased AMF over areas with low surface reflectance. Figure 7 shows that NO₂ VCD can be significantly overestimated when using the wrong surface reflectance for AMF calculation over snow surfaces.

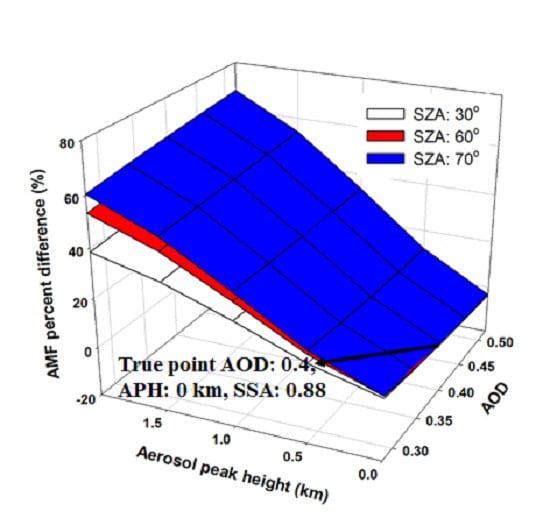
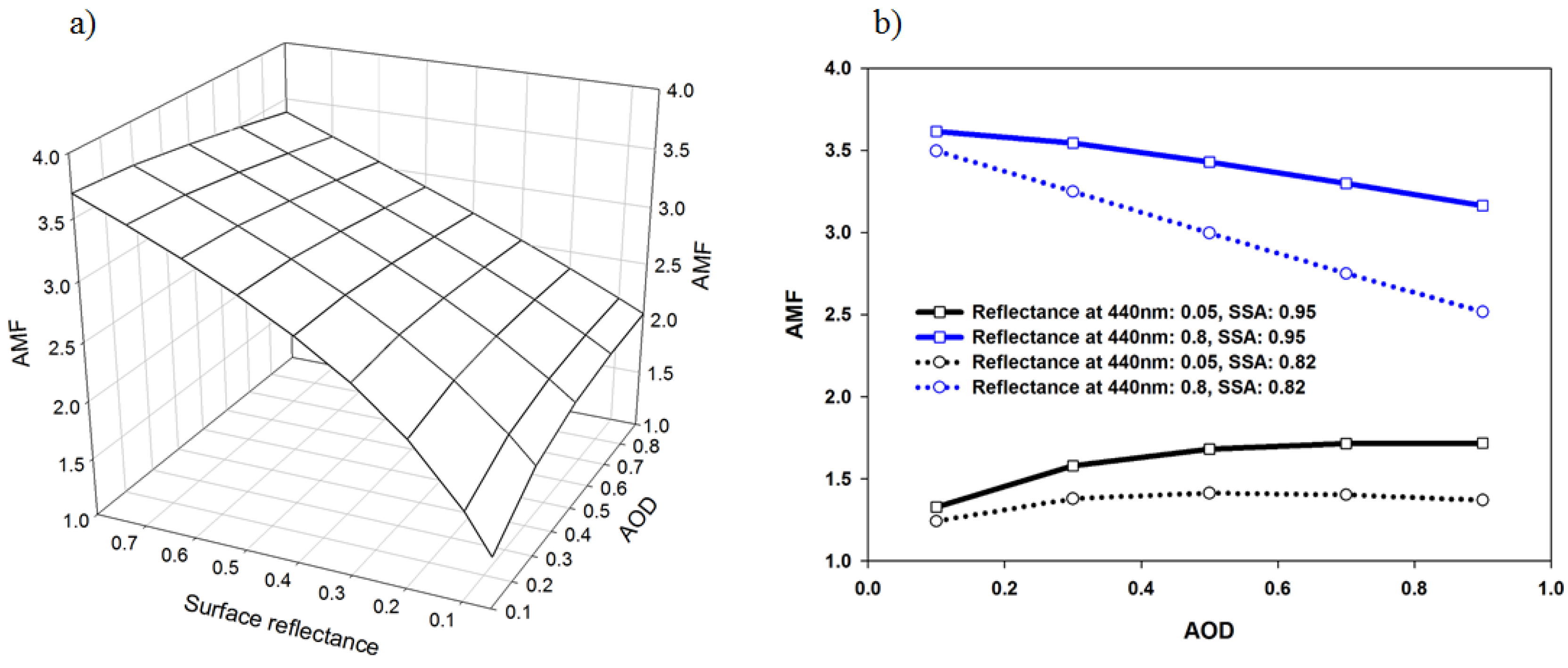
3.3. Influence of Aerosol Peak Height

Leitão et al. [2] investigated the effects of AOD, SSA and aerosol extinction profile on NO₂ AMF. However, they did not discuss the effect of APH on AMF in detail. The APH effect on NO₂ AMF has been studied comprehensively here, as APH may increase or decrease AMF depending on the properties of the aerosol layer. Figure 8a shows the change in NO₂ AMF as a function of AOD, APH and HW, which determine the aerosol vertical profile. When APH and HW are 0 and 5 km, respectively (Figure 3, black squares), the increase in AOD leads to an enhancement in NO₂ AMF due to the increased scattering probability within the NO₂ layer. Under these conditions of AMF enhancement, AOD changes from 0.1 to 0.9, which increases AMF by 36% from 1.36 to 1.85. The APH increase leads to decreased NO₂ AMF, which can be attributed to the shielding effect of the aerosol layer, as shown in Figure 3b. This shielding relates to the decreased sensitivity below the aerosol layer as more photons are scattered back to the satellite detector before they reach these low altitudes, as described by [2]. Under conditions of AOD = 0.1 and HW = 5 km, NO₂ AMF decreases by 29% (from 1.36 to 0.96) as APH changes from 0 to 2 km. Under conditions of high AOD (0.9) and a HW of 5 km, the NO₂ AMF decreases by 241% (from 1.85 to 0.54) as APH changes from 0 to 2 km. Therefore, the APH effect on NO₂ AMF is greater in the case of high-AOD conditions. However, as shown in Figure 8a, NO₂ AMF shows a smaller variation as a function of APH under low HW conditions (e.g., HW = 1 km (Figure 3, purple diamonds) compared with HW = 5 km (Figure 3, black squares)), as neither shielding nor albedo has a large effect on NO₂ AMF. We found that the increase in AOD leads to an increase in NO₂ AMF under low-APH conditions (0 and 0.5 km) due to the increased albedo effect of the aerosol layer. However, as shown in Figure 8b, as the increase in APH enhances the shielding effect of the aerosol layer, the NO₂ AMF decreases with increasing AOD above 1 km of APH. Figure 8c shows the change in NO₂ AMF as a function of AOD, APH, and SZA at the high-NO₂ site, and Figure 8d shows the change in NO₂ AMF as a function of SZA and APH at AOD = 0.3. The increase in AOD leads to increases in NO₂ AMF under low-APH conditions (APH = 0 and 0.5 km) but to decreases in NO₂ AMF under high-APH conditions (APH = 1.5 and 2 km), which implies that the shielding effect is enhanced with increased SZA at high APH. We examined the AMF sensitivity to simple rectangular aerosol distributions that reflect polluted environments where convection creates very homogeneous vertical aerosol distribution within the planter boundary layer. Figure 8e shows the change in NO₂ AMF as functions of AOD, surface reflectance, and aerosol upper limit. NO₂ AMFs are lower with aerosol upper limit of 5 km than those with aerosol upper limit of 1 km due to the aerosol shielding effect especially in high AOD conditions.

We additionally examined the APH effect on AMF under various AOD and SSA conditions. Figure 9a shows the NO₂ AMF variation due to changes in SSA, APH, and HW at AOD = 0.5; the effects of AOD, SSA, and APH on NO₂ AMF are shown in Figure 9b. NO₂ AMF decreases with decreasing SSA since the absorbing aerosol contributes to a decreased light path. When SSA changes from 0.99 to 0.82, and APH = 0 km and HW = 5 km, the NO₂ AMF decreases by 21.05% (from 1.90 to 1.50) in cases of APH = 0 km, but for HW = 1 km the AMF decreases only by 17.86% (from 1.12 to 0.92). The decrease in NO₂ AMF is greater at high HW than at low HW, which implies an enhancement of the shielding effect of the aerosol layer due to high HW. The AMF is reduced by 12.1% (from 0.57 to 0.50) when SSA is changed from 0.99 to 0.82 under conditions of AOD = 0.9 and APH = 2 km. Under the same AOD and SSA conditions, but with APH = 0 km, the AMF is reduced by 26.8% (from 1.87 to 1.37), which shows the higher sensitivity of AMF to the changes in SSA under low-APH conditions.

3.4. Diurnal Effects of NO₂ Profile

NO₂ concentrations in the planetary boundary layer show a diurnal variation, especially over fossil fuel source regions [1]; consequently, tropospheric NO₂ VCD obtained from OMI (overpass time: 13:30 local time) are generally different from those obtained from SCHIMACHY or GOME-2 (10:00 and 09:30 local time, respectively) on the same day due to differences in both NO₂ SCD and AMF [23]. The NO₂ AMF at noon generally shows an increase due to the change in NO₂ shape factor with the increase in mixing layer height. To investigate the change in AMF with diurnal variations in the NO₂ profile, NO₂ AMF was calculated using three NO₂ profiles obtained from the Goddard Earth Observing System-Chem Model (GEOS-Chem; [24]) for December 2006 at the peak times of NO₂ concentration (0700 LT and 2000 LT) and at noon (1300 LT) in Beijing. A detailed description of this approach, including the emission inventory used for the GEOS-Chem modeling, can be found in a previous study [25].

Figure 10 shows the normalized NO₂ shape factor for 0700, 1300, and 2000 LT, and the absolute percent difference error of calculated AMF using NO₂ profiles between 1300 and 0700 LT (white) and between 0700 and 2000 LT (blue). The AMF calculated using the NO₂ profile at 0700 LT is similar to that at 2000 LT (percent difference < 15%) due to a similar normalized NO₂ shape factor, whereas the AMF at 1300 LT shows a significant difference (percent difference > 63%) in AMF to that at 0700 LT (and 2000 LT) due to a normalized NO₂ shape factor as well as a mixing layer height that is significantly different. Of note, the AMF changes are large under high-AOD and high-APH conditions as the NO₂ profile changes diurnally. Therefore, in order to improve AMF calculation accuracy in geostationary satellite measurements such as GEMS, TEMPO, and Sentinel-4, it is important to account for the diurnal variation in NO₂ profiles, especially over high-NO₂ sites such as industrial regions, power plants, and megacities.

3.5. Influence of Aerosol Shape

To investigate the effect of aerosol shape on AMF, we calculated AMF for two types of aerosol shape (spherical and cylindrical) as a function of APH and RAA (Figure 11a), and as a function of APH and AOD (Figure 11b). Large AMF values are found for both spherical and cylindrical aerosol shapes at RAA of 0° and an APH of 0 km, whereas AMF has the smallest value at RAA of 160° due to a back-scattering phase function that is smaller than that in the forward direction [26]. The AMF difference between spheres and cylinders is ~14% at an APH of 0 km and RAA of 0°, is smaller under low-APH conditions, and becomes large at high AOD. For both spherical and cylindrical aerosols, the change in APH from 0 to 2 km leads to a significant change in AMF (spherical: ~180%; cylindrical: ~130%), especially under high-AOD and low-RAA conditions. The aerosol shape is also found to have a noticeable effect on AMF under high-AOD and small-RAA conditions.

3.6. Estimation of NO₂ AMF Errors

As discussed above, the accuracy of the input data for the RTM calculations (e.g., AOD, SSA, and APH) affects the AMF accuracy. Therefore, we quantified the AMF errors due to uncertainty in the input data. The AMF errors in this study are presented as the percent difference of AMF compared with the true AMF. Thus, aerosol data (AOD = 0.40; and SSA = 0.88) were averaged from Aerosol Robotic Network (AERONET) measurements in December 2011 in Beijing and used as the true aerosol data for the AMF calculations. An APH of 0 km was assumed as a true value for the AMF calculation. To calculate the AMF, the various input parameter values were set as follows. The range of SZA was set between 30° and 70°, which covers the typical SZA in Beijing. The range of AOD was set from 0.28 to 0.52 at an interval of 0.06, because the AOD retrieved in the near-UV wavelength of the OMI has a ±30% error compared with the AERONET AOD [27]. The range of SSA was set from 0.84 to 0.92 at an interval of 0.02, as the SSA retrieved by the OMI/Aura level-2 near-UV two-channel algorithm (OMAERUV) has a ±0.04 error compared with the AERONET SSA [18]. To calculate AMF, the NO₂ profile shown in Figure 2a is used as the input for the RTM calculations.

Figure 12a shows the percent difference in AMF calculated with various AOD and SSA values against the true AMF. As mentioned above, the true AMF values are obtained with AOD = 0.4 and SSA = 0.88, which are obtained by averaging AERONET data in Beijing for December 2011. The true AMF values are 1.64 and 0.79 in Figure 12a,b, respectively. In Figure 12a, where APH is 0 km and where AOD is 0.52, which is 30% smaller than the true AOD (0.4), the NO₂ AMF value is underestimated by 3.67% compared with the true AMF (1.64). However, when AOD is 0.28, which is 30% smaller than the true AOD, the NO₂ AMF value is overestimated by 4.85%. When SSA is 0.84, which is smaller than the true SSA of 0.88, the NO₂ AMF value is overestimated by 4.46% compared with the true AMF. However, when SSA is 0.92, the NO₂ AMF value is underestimated by 4.77%. As shown in Figure 12b where APH is 3 km, when using an AOD value that is 30% higher than the true AOD value, the NO₂ AMF is overestimated by 8.35% compared with the true AMF value (0.79). However, In Figure 12b, when using an AOD value that is 30% lower than true AOD value, the NO₂ AMF is underestimated by 9.53%. We found the effects of SSA on NO₂ AMF to be negligible for the case of high APH (3 km), as NO₂ AMF is overestimated by only 0.90% and underestimated by 0.93% when using SSA values of 0.84 and 0.92, respectively. The accuracy of AOD and SSA has an effect on the accuracy of NO₂ AMF when APH is 0 km. Under high-APH conditions (0.3 km), however, AOD is predicted to have more of an impact on AMF accuracy than is SSA.

As shown in Figure 13, we found that errors in APH information cause significant errors in the NO₂ AMF calculation. Under the condition of SZA = 70°, AOD = 0.4, and SSA = 0.8, an APH error of 2 km causes and error in AMF of ~70%. The magnitude of the error in the AMF calculations due to inaccurate APH information becomes larger with increasing SZA. If the wrong APH value is used for AMF calculations under high-SZA conditions (e.g., winter season, early morning, or late afternoon), significant errors in AMF as well as NO₂ VCD would be expected. AMF calculations may be particularly susceptible to errors associated with inaccurate APH information during long-range transported dust events when the APH is usually higher and/or aerosol vertical profiles are difficult to predict.

4. Discussion

The accuracy of NO₂ AMF is a key factor to retrieve NO₂ VCD from satellite measurement [2,7]. Several previous studies reported the NO₂ AMF error arising from uncertainties in RTM input parameters [5,28]. Leitao et al. [2] carried out a NO₂ AMF sensitivity study under various conditions such as aerosol vertical profiles, SSA, surface reflectance, and so on.

▪

The AMF variations due to the change in aerosol properties in low surface reflectance shows agreements with those reported in the previous study [2]. However, we, for the first time, found that at high surface reflectance conditions such as snowy surface, AMF decreases as AOD increases despite on APH of 0 km due to the aerosol shielding effect on the reflected radiance (Figure 7).

▪

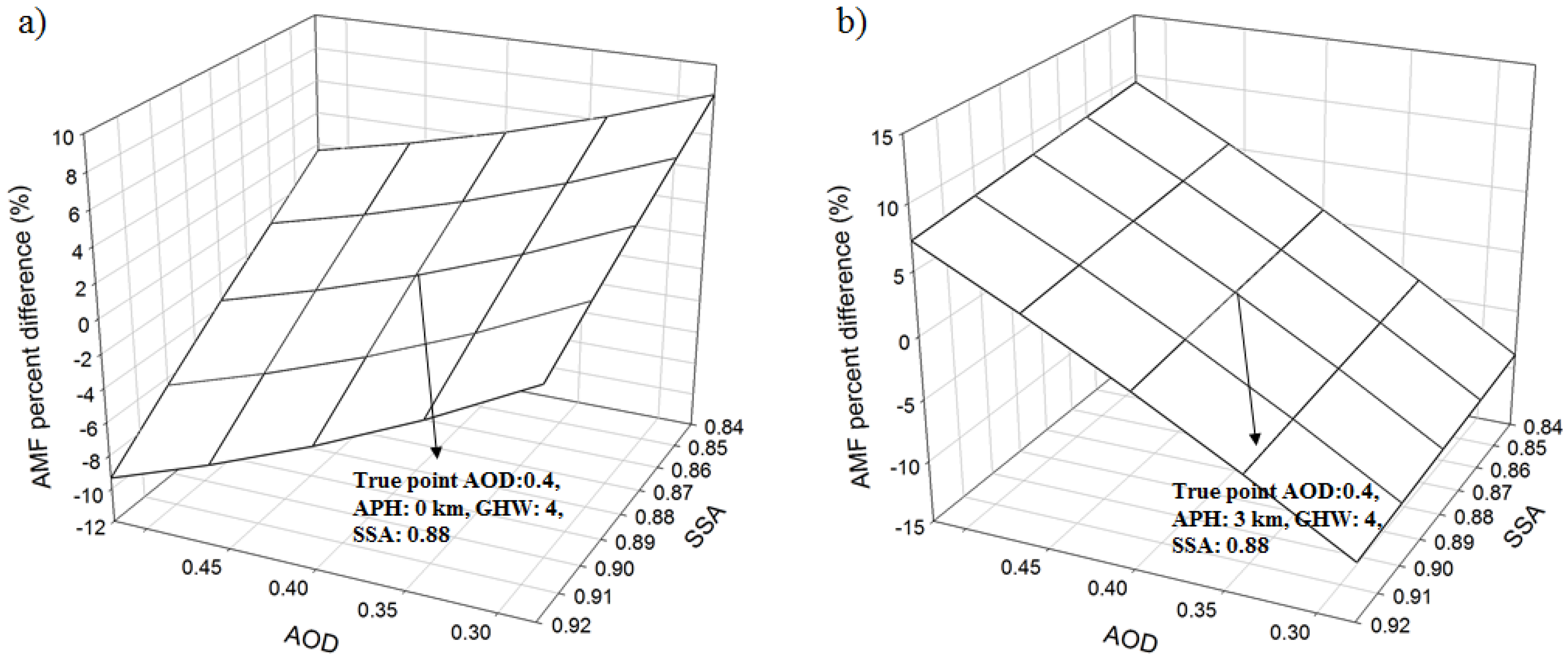
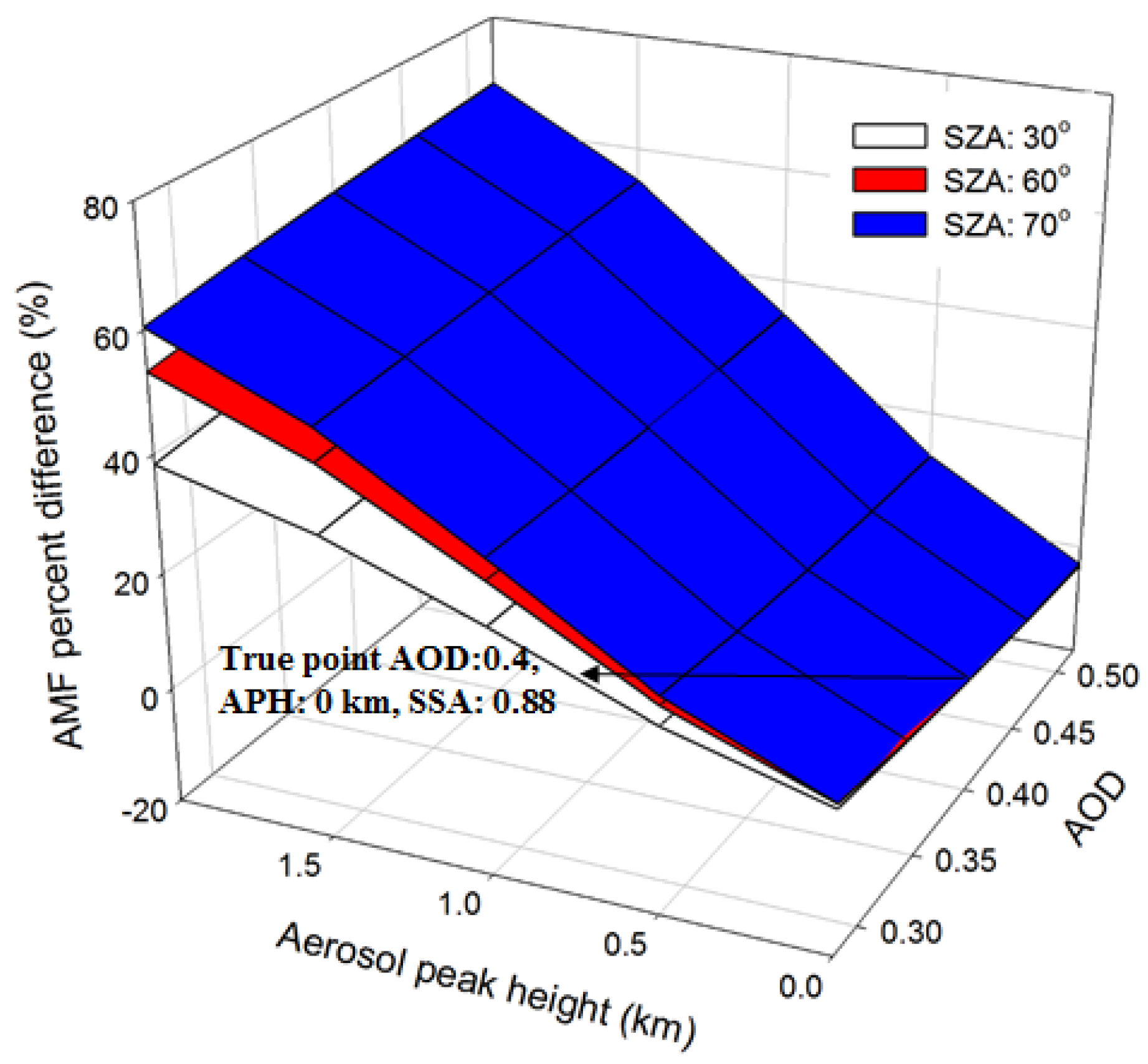
Leitão et al. [2] discussed the effects of APH on NO₂ AMF using several observed aerosol vertical profiles. It reported that aerosol profile, SSA and AOD contributes to the NO₂ AMF. However, we comprehensively examined the AMF variation using 125 aerosol vertical profile types simultaneously under various AOD, SSA, and aerosol shape and geometry conditions. Our study found that an increase in AOD at high altitude induces the decrease in NO₂ AMF due to aerosol shielding effect while the enhanced AOD at low altitude leads to the increased AMF due to aerosol albedo effect. Under conditions of high AOD (0.9) and a HW of 5 km, the NO₂ AMF decreases by 241% (from 1.85 to 0.54) as APH changes from 0 to 2 km at high-NO₂ site such as Beijing (Figure 8).

▪

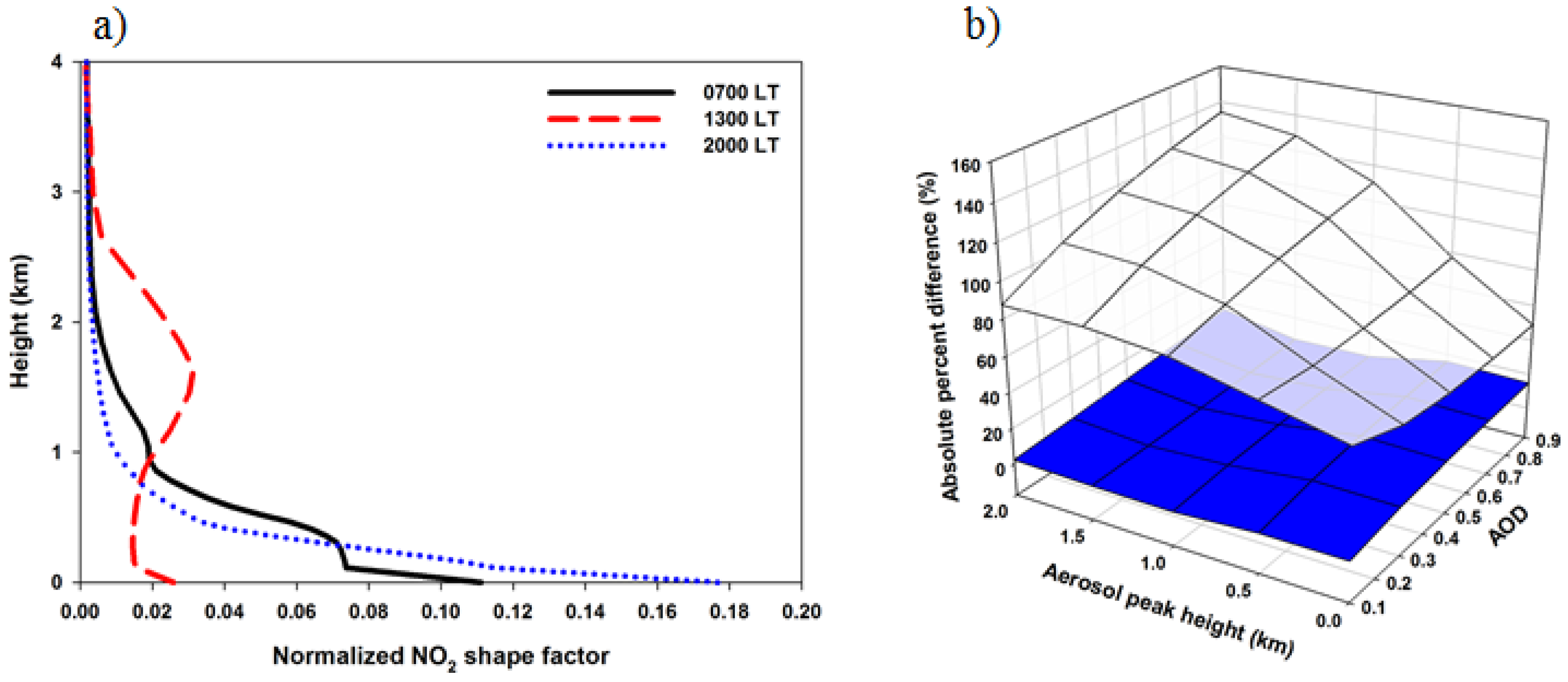
We also investigated the effect of diurnal variation in the NO₂ profile on NO₂ AMF, for future geostationary satellite measurements. The NO₂ AMF at 1300 LT shows a significant difference (percent difference > 63%) from that at 0700 LT due to the difference of NO₂ shape factors at high-NO₂ site (Figure 10).

▪

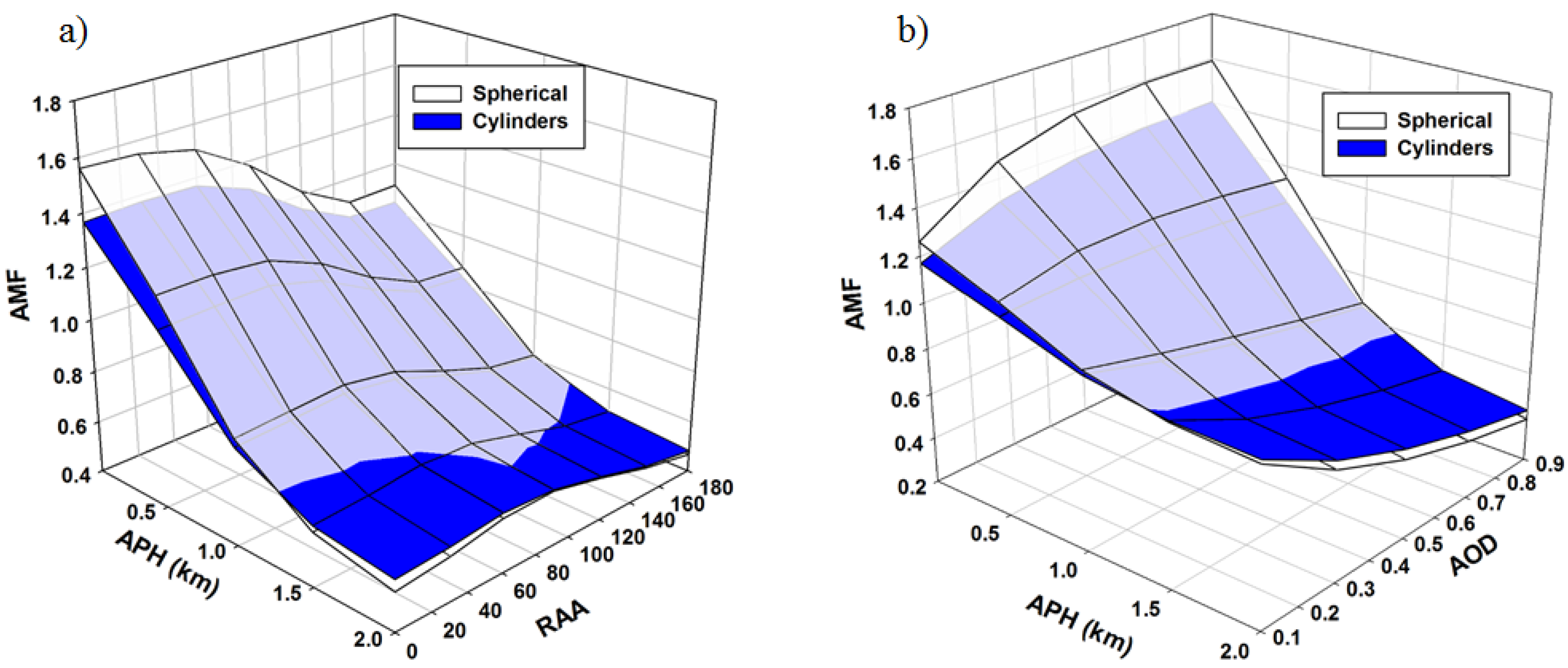
Lastly, we investigated the effect of aerosol shape on AMF, The AMF difference between spherical and non-spherical aerosol shape becomes large at the conditions of high AOD, low APH and RAA of 0° (Figure 11).

In this present study, we simultaneously investigated the effects of aerosol properties (AOD, SSA, APH, HW and aerosol shape), geometry information (SZA, VZA and RAA), surface reflectance and NO₂ vertical profile on NO₂ AMF. The results found in this present study show that it is important to use accurate aerosol extinction profiles and surface reflectance information along with other aerosol information under high-NO₂ conditions when constructing a NO₂ AMF look-up table or calculate NO₂ AMF in DOAS retrieval. In addition, it is important to account for the diurnal variation in NO₂ profiles for the geostationary satellite measurements especially over high-NO₂ sites such as industrial regions, power plants, and megacities.

In current NO₂ retrieval algorithms adopted for space-borne measurements, the aerosol information such as aerosol extinction profile and SSA are mostly obtained from chemical transfer model [6,23,29]. Especially, the aerosol vertical distribution information can be obtained from the high spectral resolution data of Oxygen A band from either Greenhouse Gases Observing Satellite (GOSAT) or Orbiting Carbon Observatory 2 (OCO-2). Furthermore, TROPOspheric Monitoring Instrument (TROPOMI), which will be launched in 2017, is planned to provide the aerosol layer height information using Oxygen A band. Such aerosol layer height information is expected to be helpful for an improvement on NO₂ AMF accuracy.

This study was conducted for the clear sky conditions. In the future, however, the sensitivity studies need to be carried out under cloud condition, since satellite measurements are frequently affected by cloud.

5. Summary and Conclusions

AMF errors are much larger than the spectral fitting errors generally induced for NO₂ VCD retrieval in the DOAS NO₂ algorithm. In this study, we examined the simultaneous effects of APH, various aerosol properties, and geometric information on AMF at sites with high concentrations of NO₂. Both geometric information and aerosol properties are important in calculating AMF at the high-NO₂ site. Over snowy surfaces (surface reflectance = 0.8), increases in AOD lead to AMF decreases, which is the opposite of the trend for surfaces without snow where increases in AOD lead to increased AMF.

When the APH is in the boundary layer where most NO₂ exists, an increase in AOD leads to an increase in AMF, whereas when the APH is high above the boundary layer, AMF decreases due to the shielding effects of aerosols. HW is also an important parameter in determining AMF. When estimating the effects of aerosol input data error on AMF calculations, AOD and SSA errors play a large role at low APH (APH = 0 km); however, we found that errors in SSA are negligible at high APH (APH = 3 km). We also found that inaccurate APH information causes significant errors in NO₂ AMF calculations. The aerosol shape is found to have an effect on AMF, especially under high-AOD and small-RAA conditions.