Equity versus Efficiency? Evidence from Three-Person Generosity Experiments
Abstract
:1. Introduction
2. Experimental design
2.1. The class of games
- Proposer X, whose exogenous agreement payoff is , chooses the pie size p from some interval with .
- Responder Y accepts or rejects proposer X’s choice of pie size p.
- Recipient Z can only reject what is assigned to him or not , rendering Z a dummy player.
- Y-games where Y earns with and , yielding the payoff for Z, and
- Z-games where Y earns with and , yielding the payoff for Z.
| a | ||
| b | ||
| c |
- in the interval in Y-games where due to one has for all and
- in the interval in Z-games where due to one has .
- either arbitrarily weak efficiency concerns3 implying the unambiguous play prediction , and
- or arbitrarily weak equity seeking4 with the unambiguous play prediction , , and for the symmetric b-variants of Y-games () and Z-games () due to .For the asymmetric a- and c-variants of Y- and Z-games with , partial inequity avoidance would suggest or to avoid unequal payoffs between X and Y or respectively X and Z. Furthermore, proposers in the asymmetric a- and c-variants may also consider the average respectively of the exogenously given payoffs and choose as in the symmetric b-variants.
- dummy Z, observing , chooses in Z-games and, in case of , in Y-games; Z will reject if is negative in Y-games, and will be indifferent if his share is 0, i.e., in case of or
- responder Y chooses in Y-games and, in case of , in Z-games; if in Z-games, a secondary concern of Y for efficiency suggests , whereas a secondary concern of Y for equity calls for ; if in Z-games, responder Y should reject ;
- proposer X, due to and , will select when secondarily caring for efficiency and in case of the b-variants and some in the asymmetric a- and c-variants of Table 1 when secondarily caring for equality.
2.2. Experimental protocol and hypotheses
3. Results
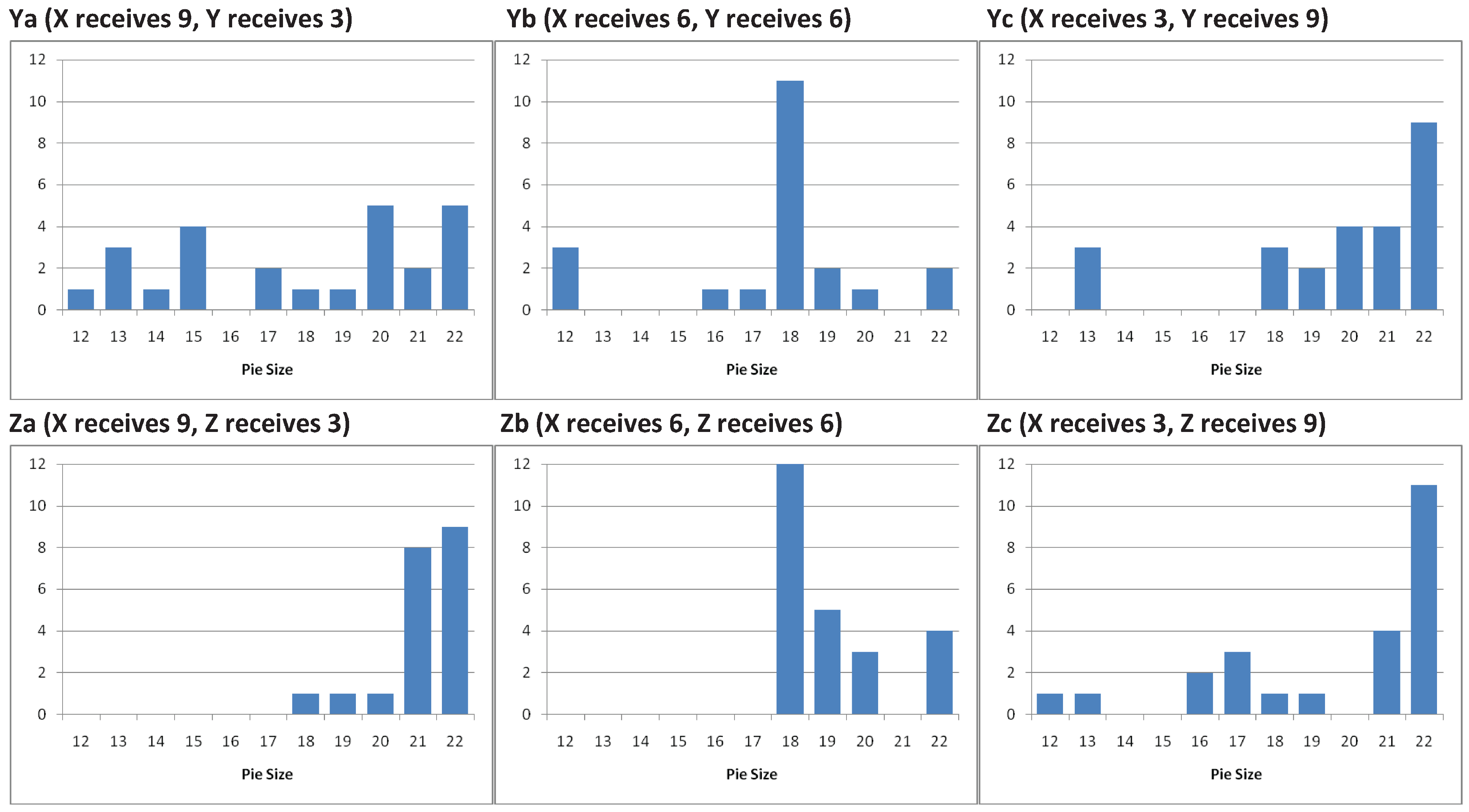
3.1. Structure of the data
| Role: | X | Y | Z | ||||||
| Lecture: | I | A | ∑ | I | A | ∑ | I | A | ∑ |
| Ya | 21 | 4 | 25 | 12 | 4 | 16 | 13 | 4 | 17 |
| Yb | 18 | 3 | 21 | 15 | 5 | 20 | 13 | 5 | 18 |
| Yc | 21 | 4 | 25 | 15 | 3 | 18 | 10 | 4 | 14 |
| Za | 17 | 3 | 20 | 10 | 4 | 14 | 12 | 3 | 15 |
| Zb | 21 | 3 | 24 | 10 | 4 | 14 | 6 | 5 | 11 |
| Zc | 19 | 5 | 24 | 14 | 4 | 18 | 14 | 4 | 18 |
| ∑ | 117 | 22 | 139 | 76 | 24 | 100 | 68 | 25 | 93 |
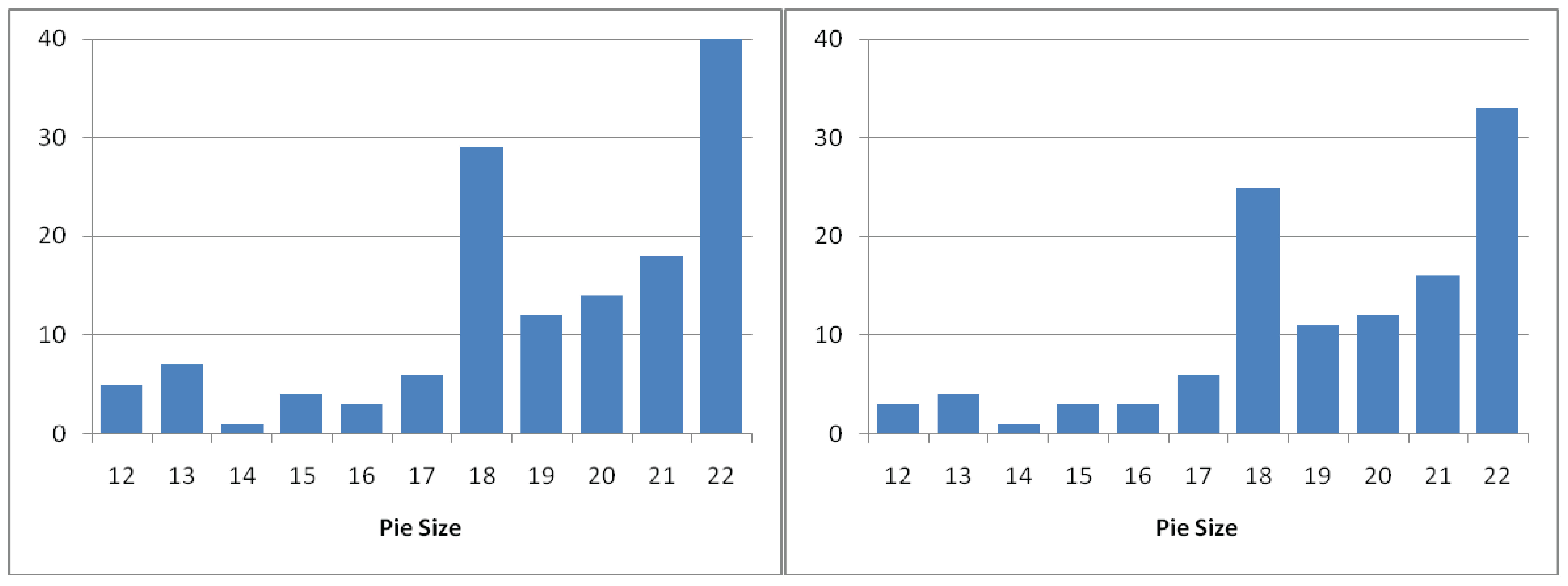
3.2. Proposer behavior
- either equity seeking by pie choice , corresponding to in Table 1,
- or efficiency minded, i.e., choose the maximal pie size .

3.3. Acceptance behavior
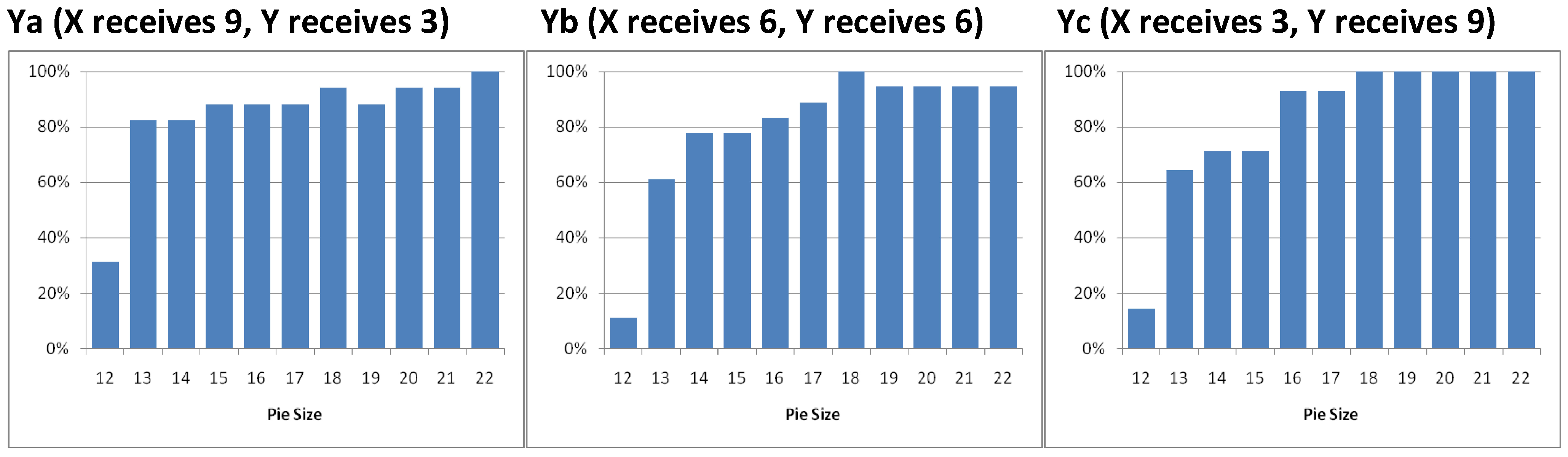
Conclusions
Acknowledgments
Appendix
Instructions for the Y-Game (a-, b-, and c-variants)
- the participant in role X receives a payoff of [a-variant: 9, b-variant: 6, c-variant: 3]
- the participant in role Y receives a payoff of [a-variant: 3, b-variant: 6, c-variant: 9]
- the participant in role Z receives a payoff of B - 12 on the condition that the participant in role Z accepts his amount.
- X chooses an integer amount B with .
- For every given amount B, Y has to decide whether he accepts the offer or not.
- For every given payoff Z will receive, Z has to decide whether he accepts or not.
- If Y accepts the decision of X and if Z also accepts his payoff, the payoffs for the following roles are
- ‒
- X: [a-variant: 9, b-variant: 6, c-variant: 3]
- ‒
- Y: [a-variant: 3, b-variant: 6, c-variant: 9]
- ‒
- Z: B - 12
- If Y accepts the decision of X, but Z rejects his payoff, the payoffs for the following roles are
- ‒
- X: [a-variant: 9, b-variant: 6, c-variant: 3]
- ‒
- Y: [a-variant: 3, b-variant: 6, c-variant: 9]
- ‒
- Z: 0
- If Y rejects the decision of X, then X, Y, and Z receive nothing (0).
Instructions for the Z-Game (a-, b-, and c-variants)
- the participant in role X receives a payoff of [a-variant: 9, b-variant: 6, c-variant: 3]
- the participant in role Y receives a payoff of B - 12
- the participant in role Z receives a payoff of [a-variant: 3, b-variant: 6, c-variant: 9] on the condition that the participant in role Z accepts his amount.
- X chooses an integer amount B with
- For every given amount B, Y has to decide whether he accepts the offer or not.
- Z has to decide whether he accepts his amount or not.
- If Y accepts the decision of X, and if Z also accepts his payoff, the payoffs for the following roles are
- ‒
- X: [a-variant: 9, b-variant: 6, c-variant: 3]
- ‒
- Y: B - 12
- ‒
- Z: [a-variant: 3, b-variant: 6, c-variant: 9]
- If Y accepts the decision of X, but Z rejects his payoff, the payoffs for the following roles are
- ‒
- X: [a-variant: 9, b-variant: . 6, c-variant: 3]
- ‒
- Y: B - 12
- ‒
- Z: 0
- If Y rejects the decision of X, then X, Y, and Z receive nothing (0).
References
- Binmore, K.; Shaked, A. Experimental Economics: Where Next? Rejoinder. Journal of Economic Behavior and Organization 2010, 73, 120–121. [Google Scholar] [CrossRef]
- Bolton, G. A Comparative Model of Bargaining: Theory and Evidence. American Economic Review 1991, 81, 1096–1136. [Google Scholar]
- Bolton, G.; Ockenfels, A. ERC: A Theory of Equity, Reciprocity, and Competition. American Economic Review 2000, 90, 166–193. [Google Scholar] [CrossRef]
- Engelmann, D.; Strobel, M. Inequality Aversion, Efficiency, and Maximin Preferences in Simple Distribution Experiments. American Economic Review 2004, 94, 857–869. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K. On Inequity Aversion: A Reply to Binmore and Shaked. Journal of Economic Behavior and Organization 2010, 73, 101–108. [Google Scholar] [CrossRef] [Green Version]
- Fehr, E.; Schmidt, K. A Theory of Fairness, Competition, and Cooperation. The Quarterly Journal of Economics 1999, 114, 817–868. [Google Scholar]
- Güth, W. The Generosity Game and its Use for Calibrating Linear Inequity Aversion. J. Socio-Econ. 2010, 39, 155–157. [Google Scholar] [CrossRef]
- Güth, W.; Levati, M. V.; Ploner, M. Making the World a Better Place: Experimental Evidence from the Generosity Game. Working paper series of the Max Planck Institute of Economics and Friedrich Schiller University of Jena. 2009; No. #2009-071. [Google Scholar]
- Güth, W.; Van Damme, E. Information, Strategic Behavior and Fairness in Ultimatum Bargaining - An Experimental Study. J. Math. Psychol. 1998, 42, 227–247. [Google Scholar] [CrossRef] [PubMed]
- Hackett, S. Incomplete Contracting: A Laboratory Experimental Analysis. Economic Inquiry 1993, 31, 274–297. [Google Scholar] [CrossRef]
- Hoffmann, E.; Spitzer, M. Entitlements, Rights, and Fairness: An Experimental Examination of Subjects’ Concepts of Distributive Justice. J. Legal Stud. 1985, 14, 259–298. [Google Scholar] [CrossRef]
- Homans, G.C. Social Behaviour: Its Elementary Forms; Routledge and Keegan Paul: London, UK, 1961. [Google Scholar]
- Königstein, M. Equity, Efficiency and Evolutionary Stability in Bargaining Games with Joint Production. Lecture Notes in Economics and Mathematical Systems; Springer: Berlin, Germany, 2000. [Google Scholar]
- Shapiro, E.G. Effects of future interaction reward allocation in dyads: equity or equality. J. Pers. Soc. Psychol. 1975, 32, 873–880. [Google Scholar] [CrossRef]
- 1.It seems questionable whether participants will invest “real effort” when anticipating that their (agreement) payoff is exogenously given.
- 2.One could independently auction off the player roles, meaning that players earn only what they receive in the game minus their role price as determined by the auction.
- 3.Actually, we could rely on lexicographical preferences, primarily for own (monetary) earnings and only secondarily for efficiency.
- 4.This means an equal payoff distribution is preferred over an unequal one when both yield the same payoff for the proposer.
- 5.Different colors were used for the instructions of the six different games in Table 1. After blocks of X-, Y-, and Z-participants were formed in the large lecture room, neighboring participants in the same block and thus with the same role type (X, Y, or Z) received the instructions, control questionnaires, and decision forms of different games to discourage any attempts to learn from others.
- 6.The results are similar if we separately look at the data from the Introductory I-lecture and the Advanced A-course; only the statistical significance is reduced (but is still significant on the level).
- 7.Again, the results do not change much if we separately look at the data from the Introductory I-lecture and the Advanced A-course.
- 8.Only one of 49 Z-participants, and actually one of the introductory course, rejected a payoff of ten. In the advanced course, only one participant decided to reject an amount equal to four or larger, virtually no one rejected an amount of eight or larger.
© 2010 by the authors; licensee MDPI, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Güth, W.; Pull, K.; Stadler, M.; Stribeck, A. Equity versus Efficiency? Evidence from Three-Person Generosity Experiments. Games 2010, 1, 89-102. https://doi.org/10.3390/g1020089
Güth W, Pull K, Stadler M, Stribeck A. Equity versus Efficiency? Evidence from Three-Person Generosity Experiments. Games. 2010; 1(2):89-102. https://doi.org/10.3390/g1020089
Chicago/Turabian StyleGüth, Werner, Kerstin Pull, Manfred Stadler, and Agnes Stribeck. 2010. "Equity versus Efficiency? Evidence from Three-Person Generosity Experiments" Games 1, no. 2: 89-102. https://doi.org/10.3390/g1020089




