Disproportionation of Rosin Driven by 4,4′-Thio-bis(3-Methyl-6-Tert-Butylphenol): Kinetic Model Discrimination
Abstract
:1. Introduction
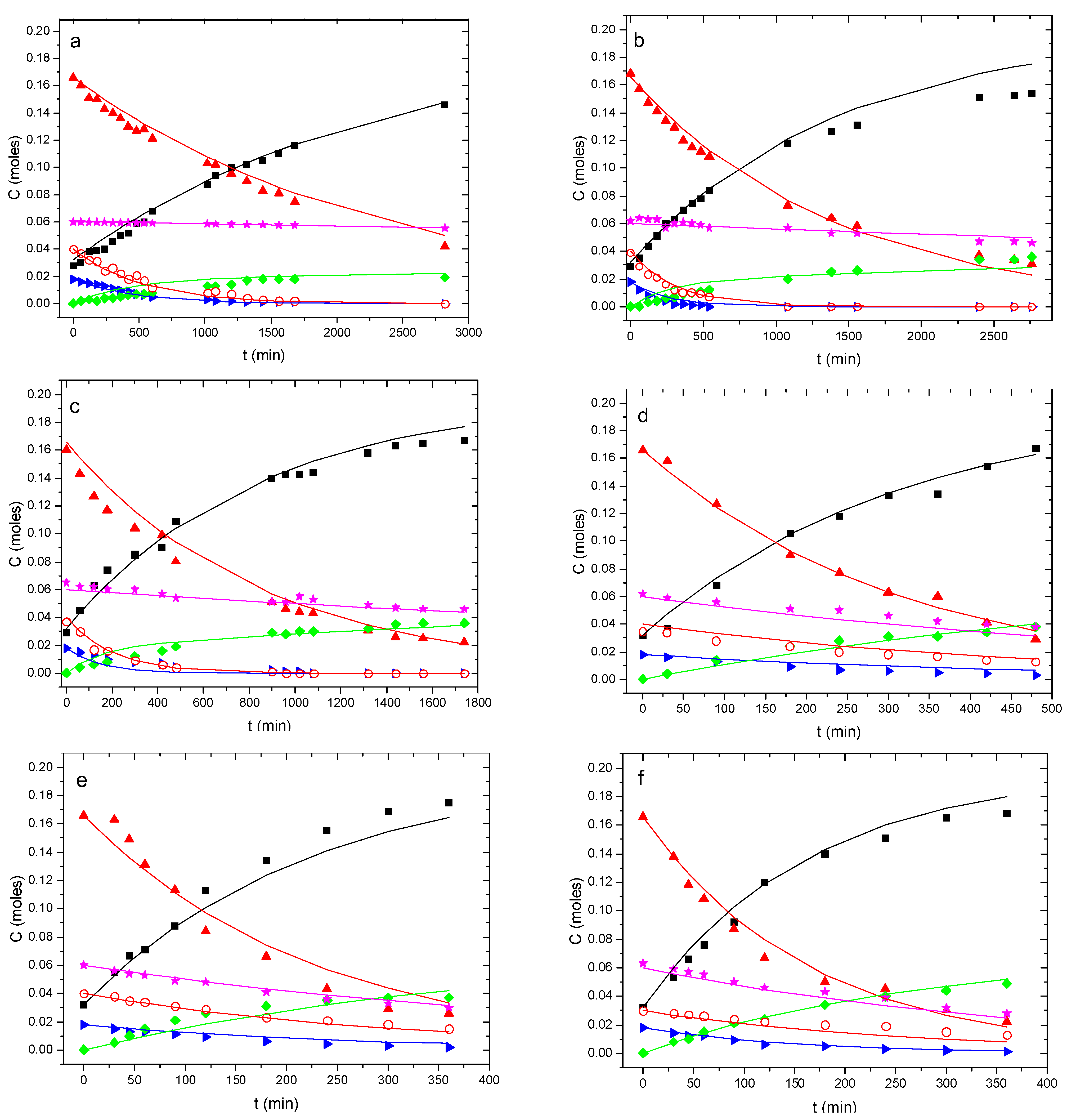
2. Results
Reaction Scheme and Kinetic Model Selection
3. Discussion
4. Conclusions
5. Materials and Methods
5.1. Materials
5.2. Disproportionation Reactions and Chemical Analysis
5.3. Kinetic Modeling and Simulation
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Soltes, E.J.; Zinkel, D.F. Chemistry of Rosin. Naval Stores: Production, Chemistry, and Utilization; Zinkel, D.F., Russell, J., Eds.; Pulp Chemical Association: New York, NY, USA, 1989. [Google Scholar]
- Kugler, S.; Ossowicz, P.; Malarczyk-Matusiak, K.; Wierzbicka, E. Advances in rosin-based chemicals: The latest recipes, applications and future trends. Molecules 2019, 24, 1651. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimnezhad-Khaljiri, H.; Ghadi, A. Recent advancement in synthesizing bio-epoxy nanocomposites using lignin, plant oils, saccharides, polyphenols, and natural rubbers: A review. Int. J. Biol. Macromol. 2023, 256, 128041. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Qiu, F.; Xie, H.; Chen, X.; Wu, C.; Chen, Y.; Liang, J.; Wang, L. Efficient catalytic hydrogenation of acrylic rosin over high-activity Pd/C catalyst under mild conditions. React. Kin. Mechan. Catal. 2024, 1–19. [Google Scholar] [CrossRef]
- Winnacker, M.; Rieger, B. Recent progress in sustainable polymers obtained from cyclic terpenes: Synthesis, properties, and application potential. ChemSusChem 2015, 8, 2455–2471. [Google Scholar] [CrossRef] [PubMed]
- Pertino, M.W.; Vega, C.; Rolón, M.; Coronel, C.; Rojas de Arias, A.; Schmeda-Hirschmann, G. Antiprotozoal activity of triazole derivatives of dehydroabietic acid and oleanolic acid. Molecules 2017, 22, 369. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, M.A.; Perez-Guaita, D.; Correa-Royero, J.; Zapata, B.; Agudelo, L.; Mesa-Arango, A.; Betancur-Galvis, L. Synthesis and biological evaluation of dehydroabietic acid derivatives. Eur. J. Med. Chem. 2010, 45, 811–816. [Google Scholar] [CrossRef] [PubMed]
- Gu, W.; Wu, R.; Qi, S.; Gu, C.; Si, F.; Chen, Z. Synthesis and antibacterial evaluation of new N-acylhydrazone derivatives from dehydroabietic acid. Molecules 2012, 17, 4634–4650. [Google Scholar] [CrossRef]
- Huang, X.C.; Wang, M.; Pan, Y.M.; Yao, G.Y.; Wang, H.S.; Tian, X.Y.; Qin, J.K.; Zhang, Y. Synthesis and antitumor activities of novel thiourea α-aminophosphonates from dehydroabietic acid. Eur. J. Med. Chem. 2013, 69, 508–520. [Google Scholar] [CrossRef]
- Hao, M.; Xu, J.; Wen, H.; Du, J.; Zhang, S.; Lv, M.; Xu, H. Recent advances on biological activities and structural modifications of dehydroabietic acid. Toxins 2022, 14, 632. [Google Scholar] [CrossRef]
- Halbrook, N.J.; Lawrence, R.V. The isolation of dehydroabietic acid from disproportionated rosin. J. Org. Chem. 1966, 31, 4246–4247. [Google Scholar] [CrossRef]
- Souto, J.C.; Yustos, P.; Ladero, M.; Garcia-Ochoa, F. Disproportionation of rosin on an industrial Pd/C catalyst: Reaction pathway and kinetic model discrimination. Bioresour. Technol. 2011, 102, 3504–3511. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Li, Y.; Zhang, J.; Zhang, H.; Wu, C.; Lin, J.; Zhou, J.; Fan, Y.; Murugadoss, V.; Guo, Z. Effects of pretreated carbon supports in Pd/C catalysts on rosin disproportionation catalytic performance. Chem. Eng. Sci. 2020, 216, 115588. [Google Scholar] [CrossRef]
- Song, Z.Q.; Zavarin, E.; Zinkel, D.F. On the palladium-on-charcoal disproportionate of rosin. J. Wood Chem. Technol. 1985, 5, 535–542. [Google Scholar] [CrossRef]
- Zhang, P.; Zhao, Z.; Bi, L.; Lu, Y.; Li, D. Review on colorless disproportionated rosin and its catalysts. J. Bioproc. Eng. Bioref. 2012, 1, 140–146. [Google Scholar] [CrossRef]
- Mitani, K.; Fujioka, M.; Uchida, A.; Kataoka, H. Analysis of abietic acid and dehydroabietic acid in food samples by in-tube solid-phase microextraction coupled with liquid chromatography–mass spectrometry. J. Chromatog. A 2007, 1146, 61–66. [Google Scholar] [CrossRef] [PubMed]
- Rezzi, S.; Bighelli, A.; Castola, V.; Casanova, J. Direct identification and quantitative determination of acidic and neutral diterpenes using 13 C-NMR spectroscopy: Application to the analysis of oleoresin of Pinus nigra. Appl. Spect. 2002, 56, 312–317. [Google Scholar] [CrossRef]
- Wang, L.; Chen, X.; Liang, J.; Chen, Y.; Pu, X.; Tong, Z. Kinetics of the catalytic isomerization and disproportionation of rosin over carbon-supported palladium. Chem. Eng. J. 2009, 152, 242–250. [Google Scholar] [CrossRef]
- Wang, L.; Chen, X.; Sun, W.; Liang, J.; Xu, X.; Tong, Z. Kinetic model for the catalytic disproportionation of pine oleoresin over Pd/C catalyst. Ind. Crops Prod. 2013, 49, 1–9. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, L.; Chen, X.; Wei, X.; Liang, J.; Li, W. Intrinsic kinetics study of rosin hydrogenation on a nickel catalyst supported on spent equilibrium catalyst. RSC Adv. 2017, 7, 25780–25788. [Google Scholar] [CrossRef]
- Hardhianti, M.P.W.; Rochmadi Azis, M.M. Kinetic studies of esterification of rosin and pentaerythritol. Processes 2021, 10, 39. [Google Scholar] [CrossRef]
- Meyerriecks, W. Organic fuels: Composition and formation enthalpy, part I, wood derivatives, related carbohydrates, exudates and rosin. J. Pyrotech. 1998, 8, 1–17. [Google Scholar]
- Dénès, F.; Beaufils, F.; Renaud, P. Thiophenol-mediated 1, 5-hydrogen transfer for the preparation of pyrrolizidines, indolizidines, and related compounds. Org. Lett. 2007, 9, 4375–4378. [Google Scholar] [CrossRef] [PubMed]
- House, W.T.; Orchin, M. A Study of the selenium dehydrogenation of guaiol and related compounds. Selenium as a hydrogen transfer agent. J. Am. Chem. Soc. 1960, 82, 639–642. [Google Scholar] [CrossRef]
- Beaufils, F.; Dénès, F.; Becattini, B.; Renaud, P.; Schenk, K. Thiophenol-mediated 1, 5-hydrogen atom abstraction: Easy access to mono-and bicyclic compounds. Adv. Synth. Catal. 2005, 347, 1587–1594. [Google Scholar] [CrossRef]
- Wei, X.; Ogata, E.; Zong, Z.; Zhou, S.; Qin, Z.; Liu, J.; Shen, K.; Li, H. Advances in the study of hydrogen transfer to model compounds for coal liquefaction. Fuel Proc. Technol. 2000, 62, 103–107. [Google Scholar] [CrossRef]
- Del Giacco, T.; Elisei, F.; Lanzalunga, O. Photoinduced hydrogen-and electron-transfer processes between chloranil and aryl alkyl sulfides in organic solvents. Steady-state and time-resolved studies. Phys. Chem. Phys. 2000, 2, 1701–1708. [Google Scholar] [CrossRef]
- Liu, P.; Liu, X.; Saburi, T.; Kubota, S.; Huang, P.; Wada, Y. Thermal stability evaluation of resin acids and rosin modified resins. ACS Omega 2020, 5, 29102–29109. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chen, H.; Yan, H.; Xu, Y.; Tang, J.; Wang, R.; Yan, M.; Dai, Y.; Huang, Y.; Liu, X. Thermal stability of levopimaric acid and its oxidation products. BMC Chem. 2023, 17, 118. [Google Scholar] [CrossRef] [PubMed]
- Esteban, J.; Fuente, E.; Blanco, A.; Ladero, M.; Garcia-Ochoa, F. Phenomenological Kinetic Model of the synthesis of glycerol carbonate assisted by focused beam reflectance measurements. Chem. Eng. J. 2015, 260, 434–443. [Google Scholar] [CrossRef]
- Cavanaugh, J.E.; Neath, A.A. The Akaike information criterion: Background, derivation, properties, application, interpretation, and refinements. Wiley Interdisc. Rev. Comput. Stat. 2019, 11, e1460. [Google Scholar] [CrossRef]
- Neath, A.A.; Cavanaugh, J.E. The Bayesian information criterion: Background, derivation, and applications. Wiley Interdisc. Rev. Comput. Stat. 2012, 4, 199–203. [Google Scholar] [CrossRef]



| Model | Reaction Scheme and Kinetic Equations |
|---|---|
| 1 | 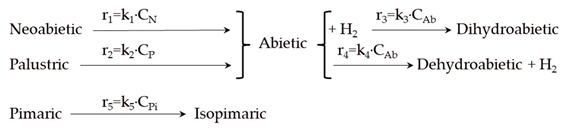 |
| 2 | 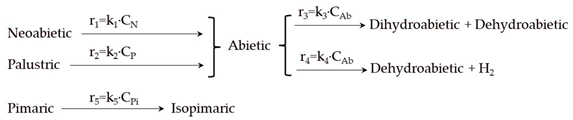 |
| 3 | 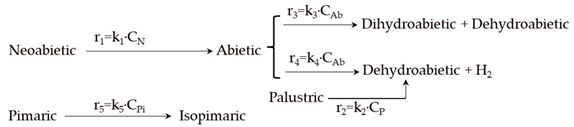 |
| 4 | 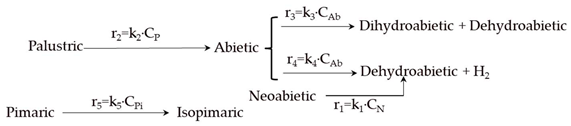 |
| 5 |  |
| Statistical Parameters | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 |
|---|---|---|---|---|---|
| SSR | 0.91 | 0.46 | 0.49 | 0.51 | 0.44 |
| F-value | 28,033 | 54,078 | 51,069 | 49,143 | 56,182 |
| AIC | −6.98 | −7.65 | −7.59 | −7.55 | −7.69 |
| BIC | −6.88 | −7.55 | −7.49 | −7.45 | −7.59 |
| VE (%) | 97.04 | 99.52 | 99.45 | 99.34 | 99.89 |
| Component | Selected Kinetic Equations | Parameters of the Model |
|---|---|---|
| Abietic acid | ||
| Dehydroabietic acid | ||
| Palustric acid | ||
| Neoabietic acid | ||
| Dihydroabietic acid | ||
| Pimaric acid |
| Run | T (°C) | % cat |
|---|---|---|
| 1 | 260 | 0 |
| 2 | 270 | 0 |
| 3 | 280 | 0 |
| 4 | 260 | 1 |
| 5 | 270 | 0.5 |
| 6 | 270 | 1 |
| 7 | 270 | 2 |
| 8 | 280 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souto, J.C.; Yustos, P.; Garcia-Ochoa, F.; Ladero, M. Disproportionation of Rosin Driven by 4,4′-Thio-bis(3-Methyl-6-Tert-Butylphenol): Kinetic Model Discrimination. Catalysts 2024, 14, 235. https://doi.org/10.3390/catal14040235
Souto JC, Yustos P, Garcia-Ochoa F, Ladero M. Disproportionation of Rosin Driven by 4,4′-Thio-bis(3-Methyl-6-Tert-Butylphenol): Kinetic Model Discrimination. Catalysts. 2024; 14(4):235. https://doi.org/10.3390/catal14040235
Chicago/Turabian StyleSouto, Juan C., Pedro Yustos, Felix Garcia-Ochoa, and Miguel Ladero. 2024. "Disproportionation of Rosin Driven by 4,4′-Thio-bis(3-Methyl-6-Tert-Butylphenol): Kinetic Model Discrimination" Catalysts 14, no. 4: 235. https://doi.org/10.3390/catal14040235




