Temperature Effect on the Deformation Behavior in Nanocrystalline Magnesium under Compression: An Atomistic Study
Abstract
:1. Introduction
2. Simulation Method
3. Results and Discussion
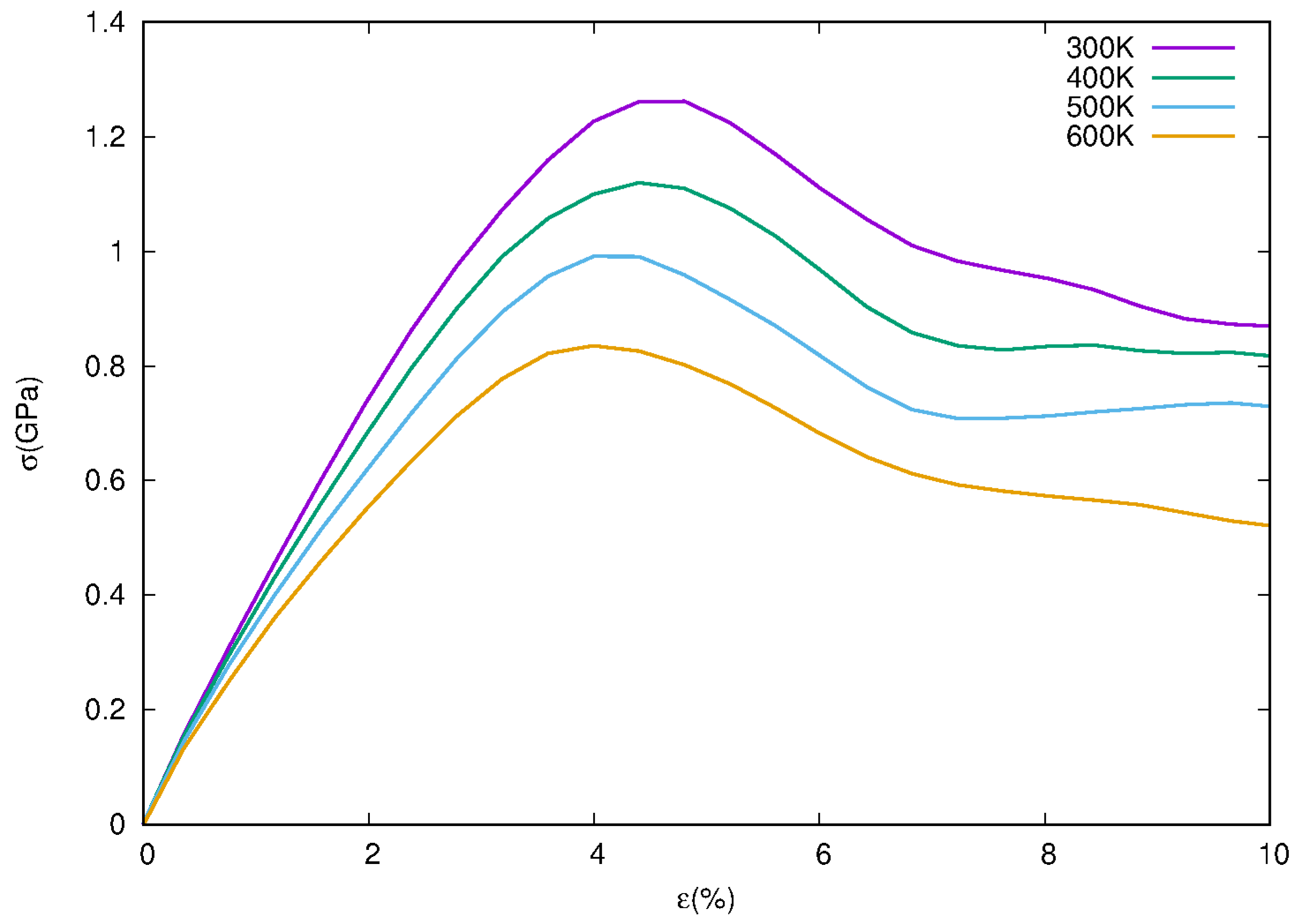
3.1. Stress–Strain Curves
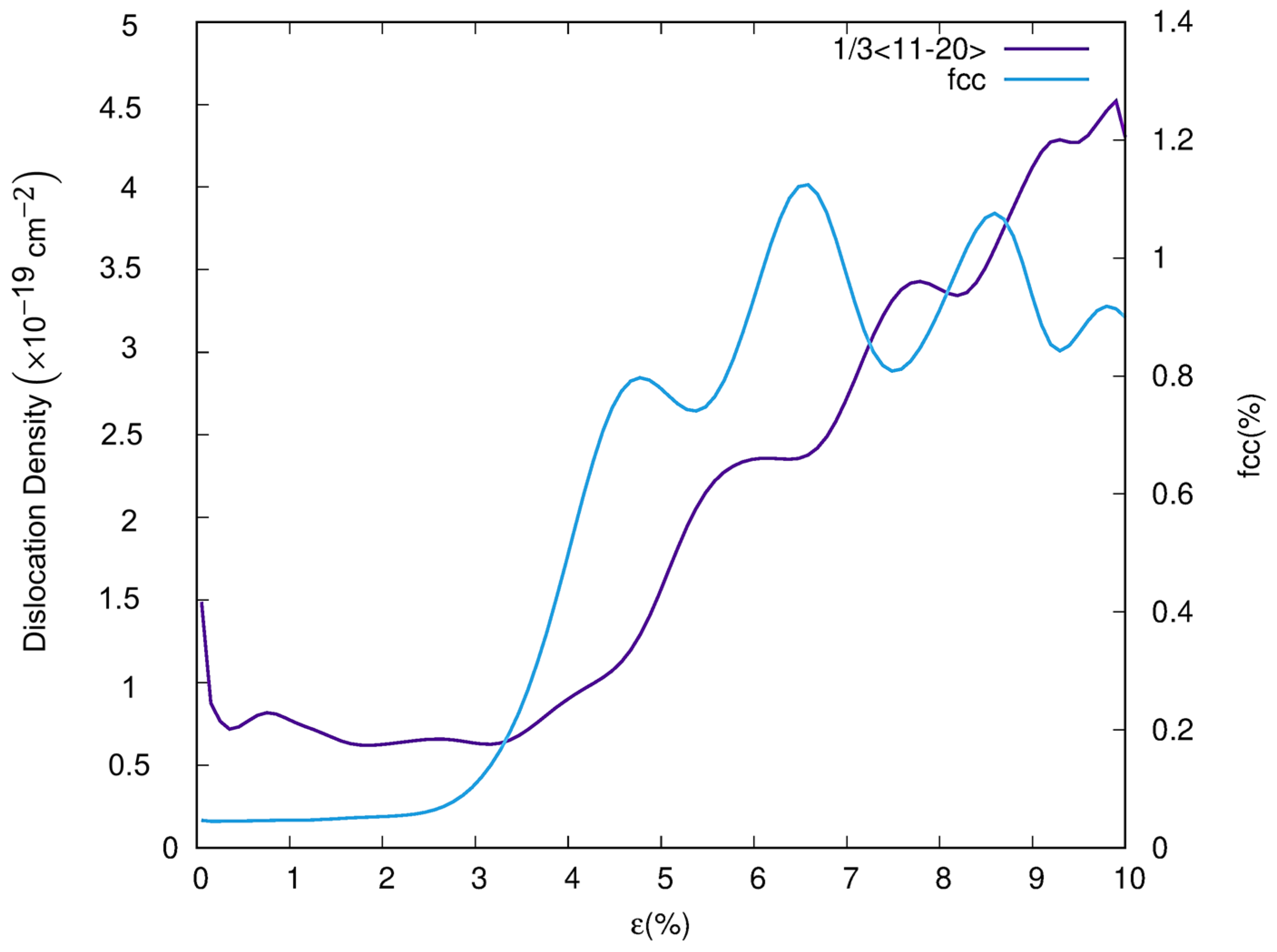
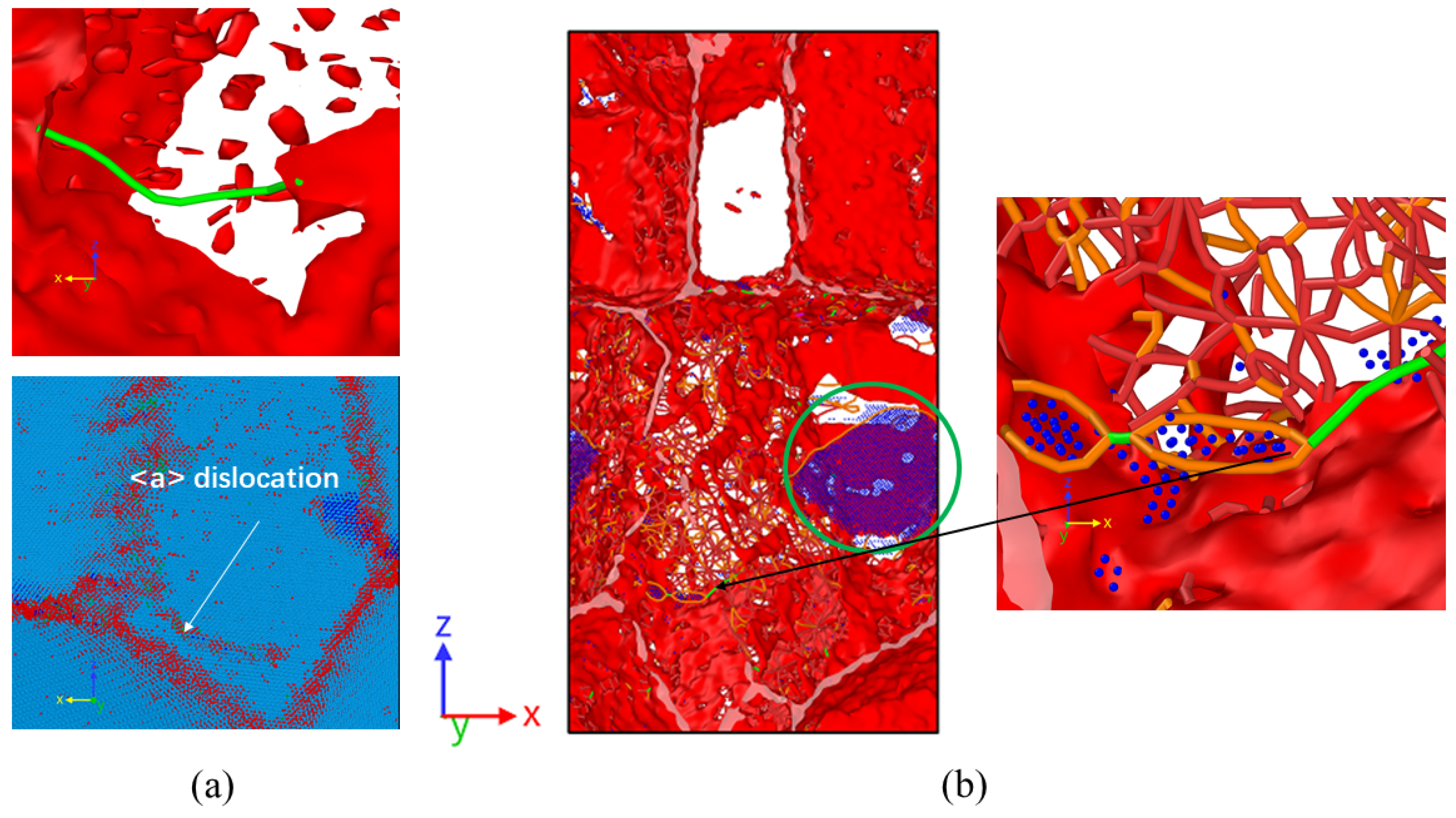
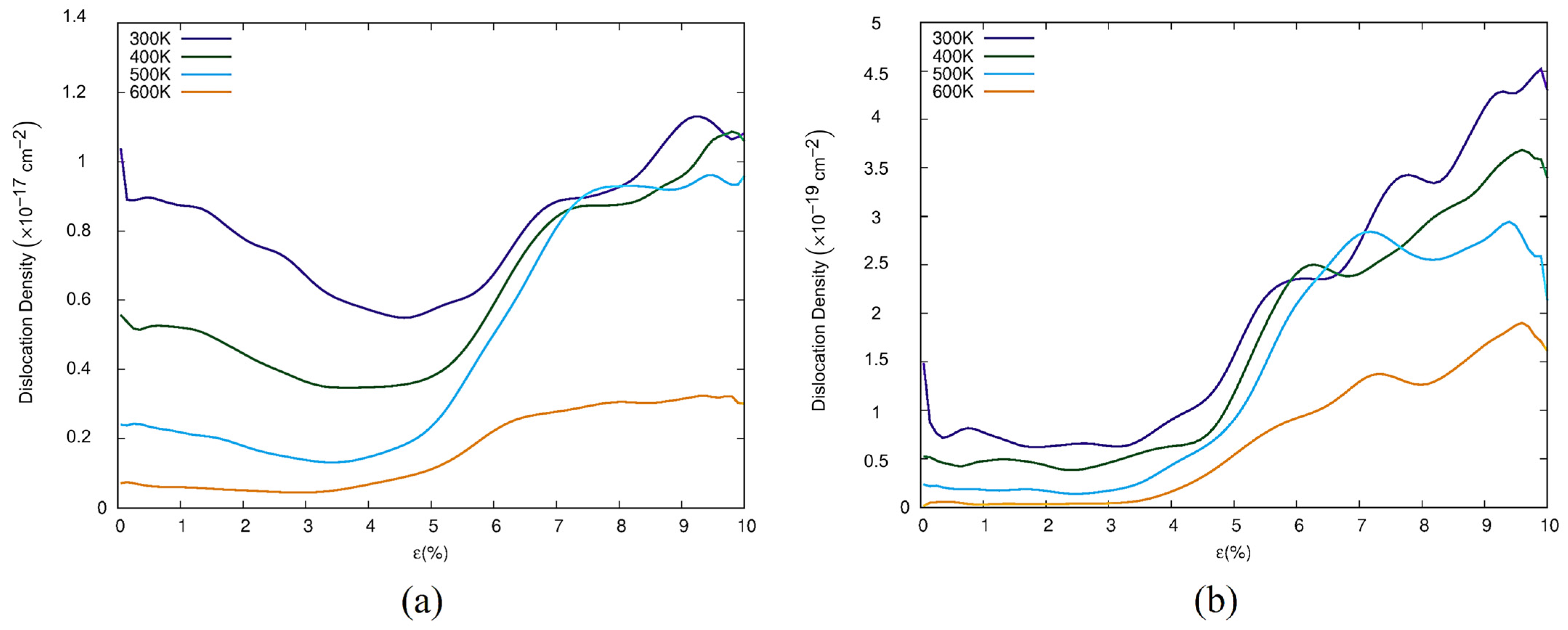
3.2. Dislocation and Twin Behavior
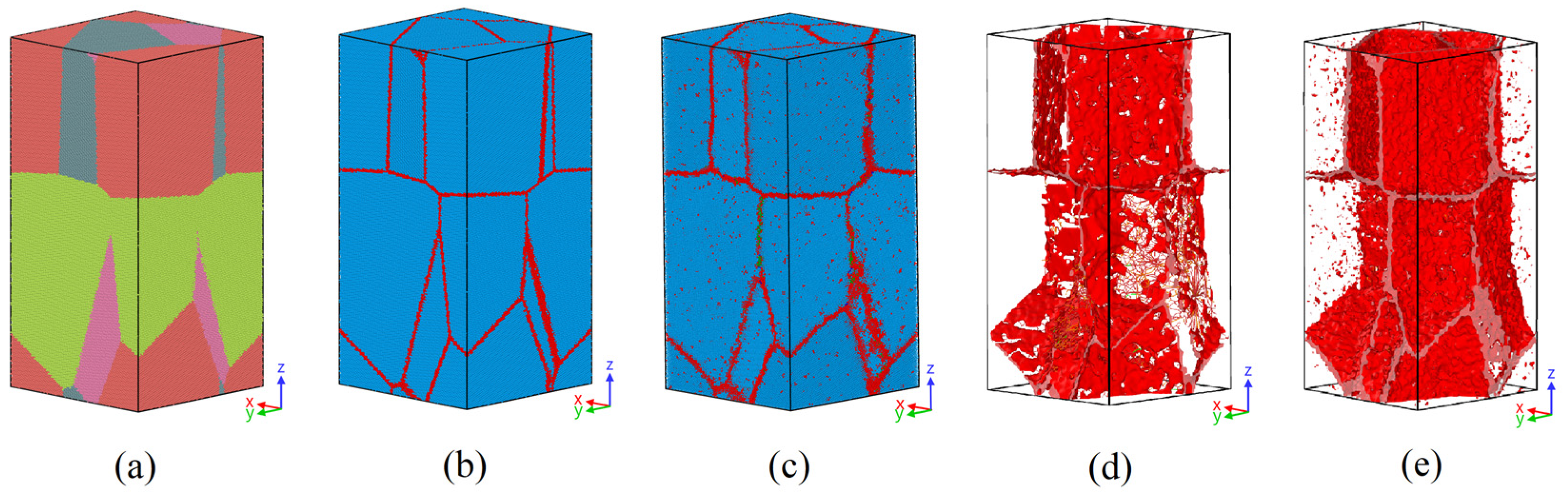
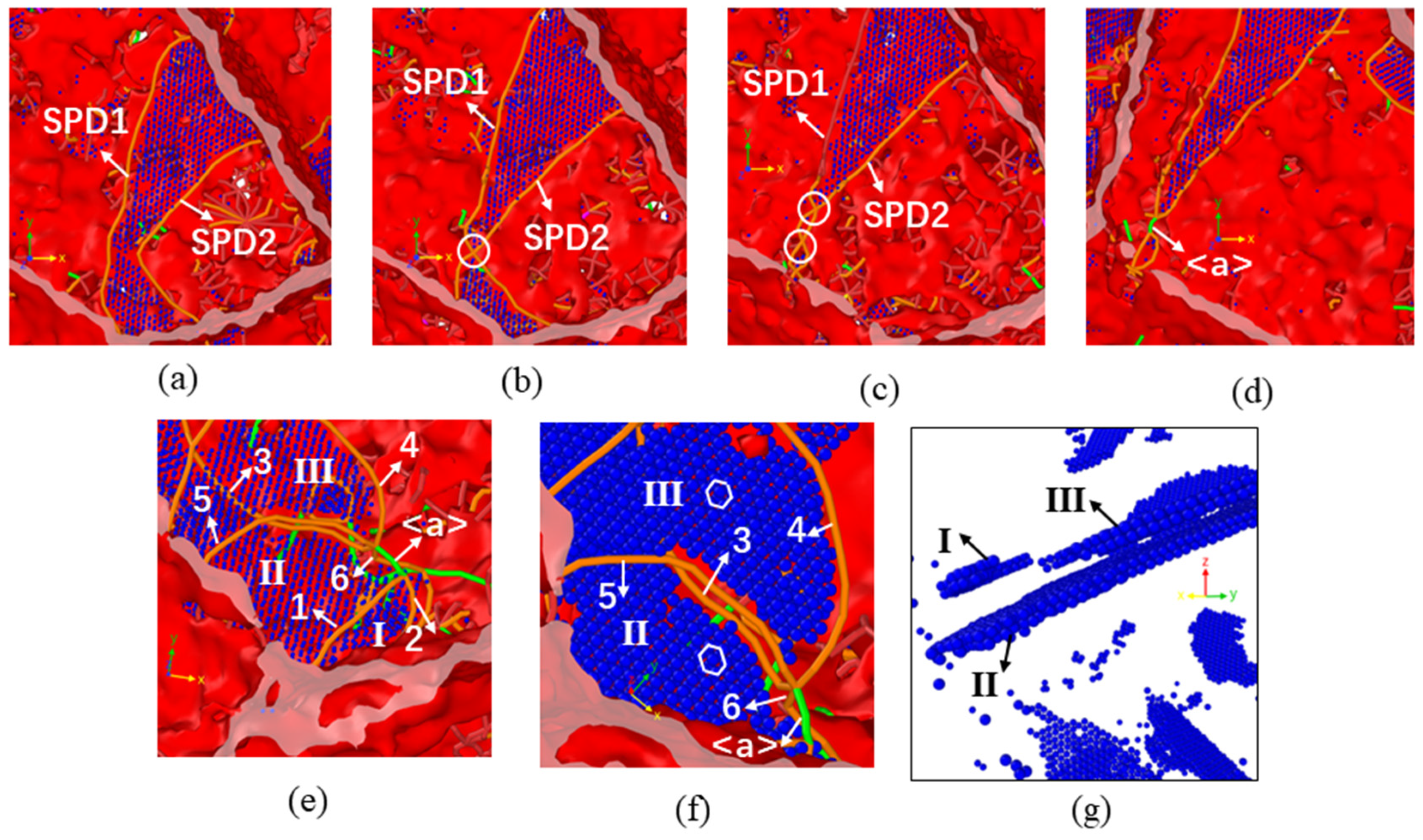
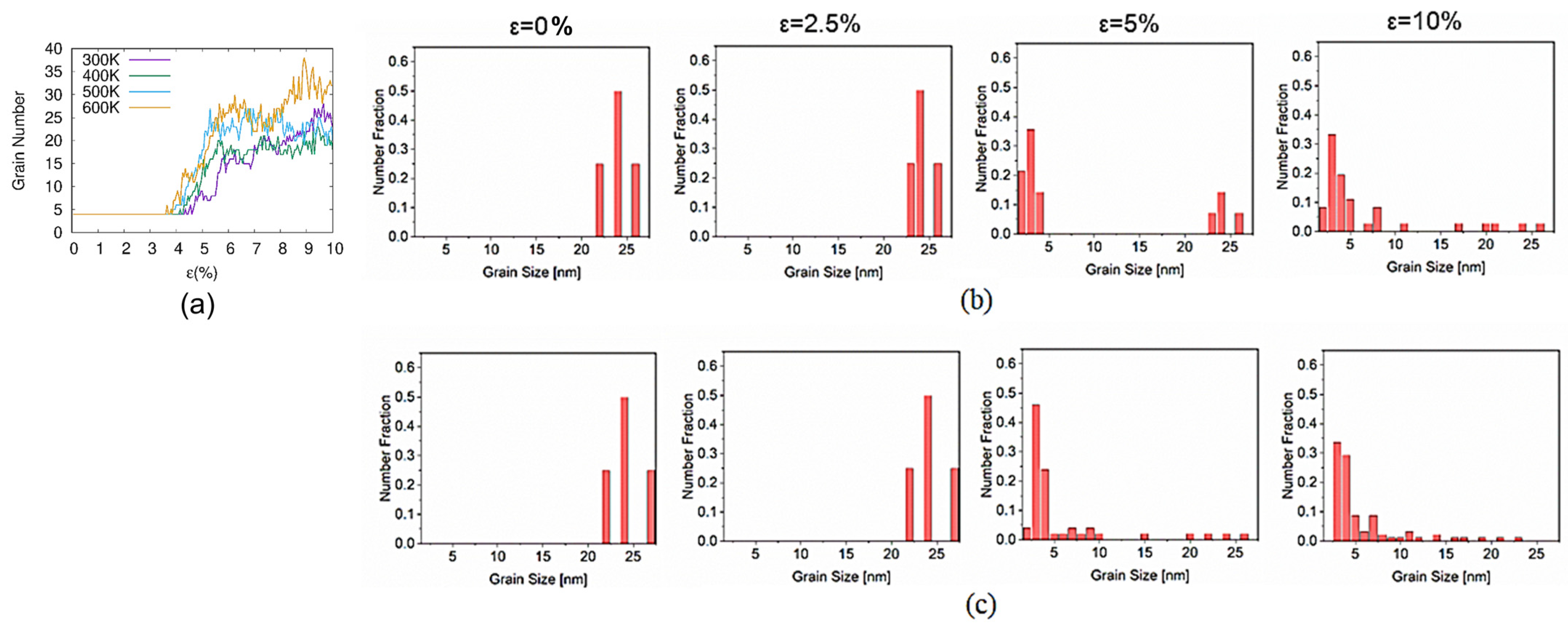
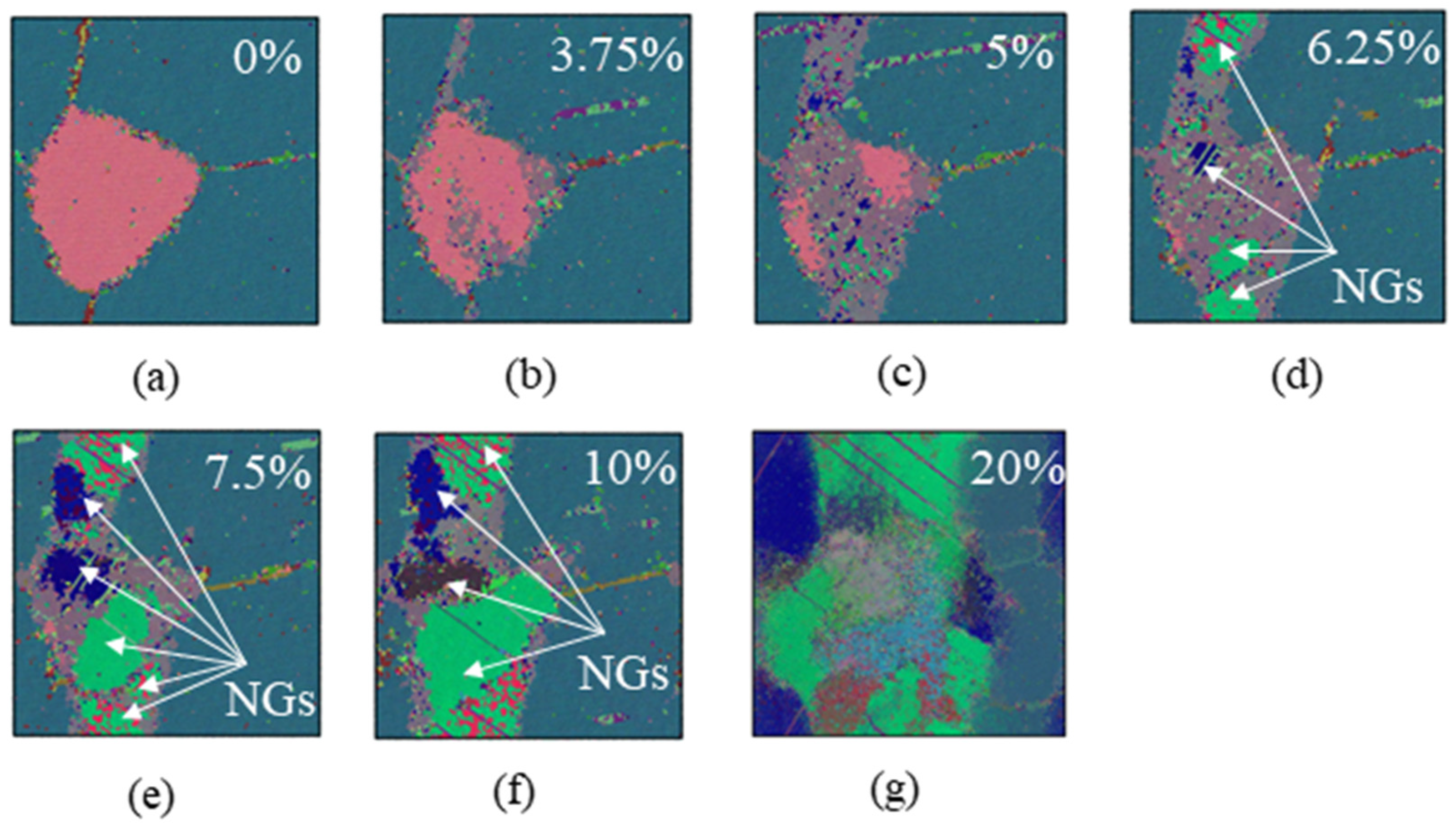
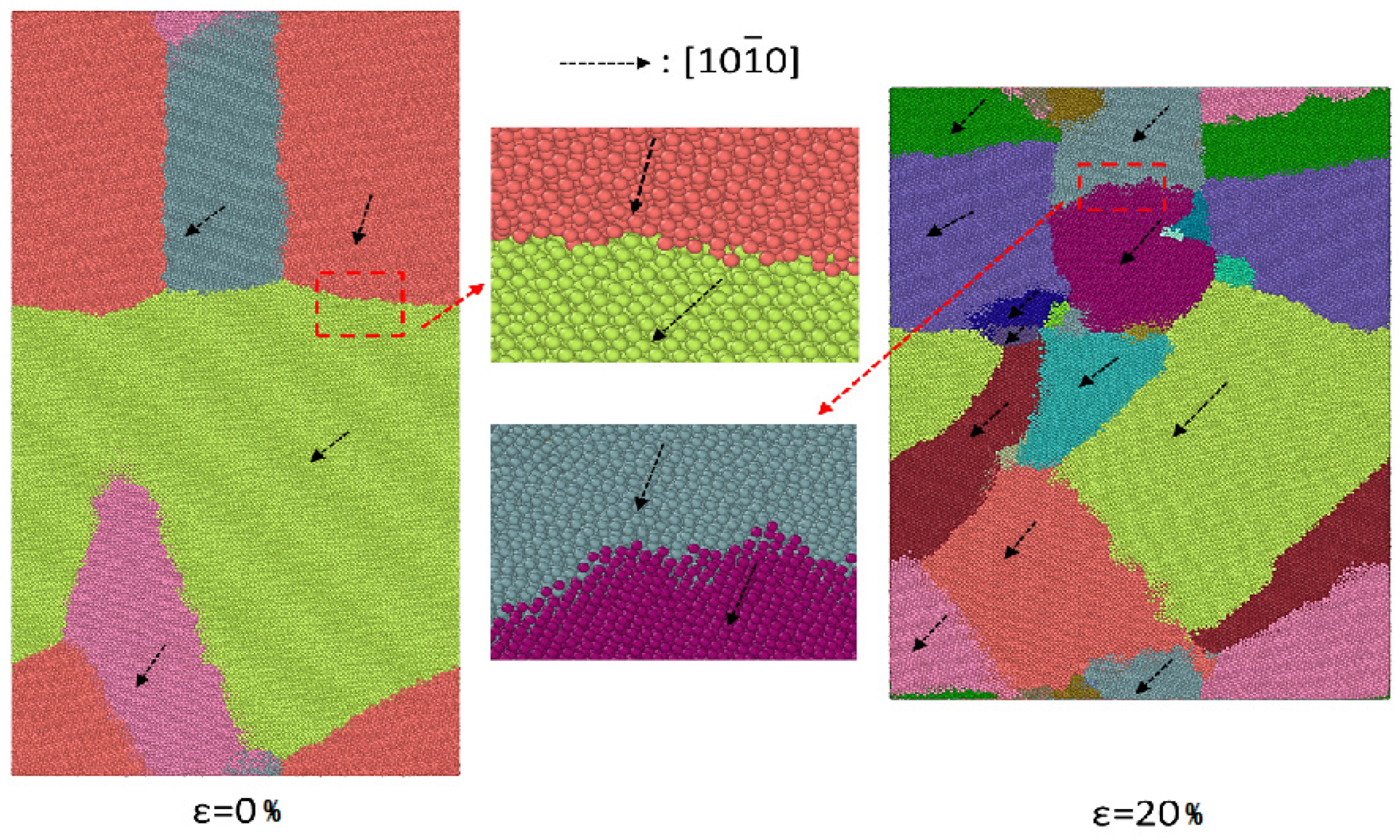
3.3. Grain Boundary Behavior
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Matsunaka, D.; Ohnishi, Y.; Shibutani, Y. Effects of Stacking Fault Energy on Fundamental Deformation Modes in Single Crystalline Magnesium by Molecular Dynamics Simulations. Mater. Trans. 2013, 54, 2093–2097. [Google Scholar] [CrossRef]
- Fan, H.; Tang, J.; Tian, X.; Wang, Q.; Tian, X.; El-Awady, J.A. Core Structures and Mobility of ⟨c⟩ Dislocations in Magnesium. Scr. Mater. 2017, 135, 37–40. [Google Scholar] [CrossRef]
- Tang, X.Z.; Guo, Y.F.; Xu, S.; Wang, Y.S. Atomistic Study of Pyramidal Slips in Pure Magnesium Single Crystal under Nano-Compression. Philos. Mag. 2015, 95, 2013–2025. [Google Scholar] [CrossRef]
- Byer, C.M.; Ramesh, K.T. Effects of the Initial Dislocation Density on Size Effects in Single-crystal Magnesium. Acta Mater. 2013, 61, 3808–3818. [Google Scholar] [CrossRef]
- Fan, H.; Wang, Q.; Tian, X.; El-Awady, J.A. Temperature Effects on the Mobility of Pyramidal <c+a> Dislocations in Magnesium. Scr. Mater. 2017, 127, 68–71. [Google Scholar]
- Aghababaei, R.; Joshi, S.P. Micromechanics of Tensile Twinning in Magnesium Gleaned from Molecular Dynamics Simulations. Acta Mater. 2014, 69, 326–342. [Google Scholar] [CrossRef]
- Shin, J.H.; Kim, S.H.; Ha, T.K.; Oh, K.H.; Choi, I.S.; Han, H.N. Nanoindentation Study for Deformation Twinning of Magnesium Single Crystal. Scr. Mater. 2013, 68, 483–486. [Google Scholar] [CrossRef]
- Yoo, M.H.; Lee, J.K. Deformation Twinning in hcp Metals and Alloys. Philos. Mag. A 1991, 63, 987–1000. [Google Scholar] [CrossRef]
- Kim, G.S.; Yi, S.; Huang, Y.; Lilleodden, E. Twining and Slip Activity in Magnesium Single Crystal. MRS Online Proc. Libr. 2009, 1224, 1224-FF05-03. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Capolungo, L.; Marshall, P.E.; McCabe, R.J.; Tomé, C.N. Statistical Analyses of Deformation Twinning in Magnesium. Philos. Mag. 2010, 90, 2161–2190. [Google Scholar] [CrossRef]
- Yu, Q.; Qi, L.; Chen, K.; Mishra, R.K.; Li, J.; Minor, A.M. The Nanostructured Origin of Deformation Twinning. Nano Lett. 2012, 12, 887–892. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Martín, R.; Pérez-Prado, M.T.; Segurado, J.; Bohlen, J.; Gutiérrez Urrutia, I.; Llorca, J.; Molina Aldareguia, J.M. Measuring the Critical Resolved Shear Stresses in Mg Alloys by Instrumented Nanoindentation. Acta Mater. 2014, 71, 283–292. [Google Scholar] [CrossRef]
- Sánchez-Martín, R.; Pérez-Prado, M.; Segurado, J.; Molina Aldareguia, J. Effect of Indentation Size on the Nucleation and Propagation of Tensile Twinning in Pure Magnesium. Acta Mater. 2015, 93, 114–128. [Google Scholar] [CrossRef]
- Lavrentev, F.F.; Pokhil, Y.u.A.; Zolotukhina, I.N. Analysis of Pairwise Dislocation Interaction and Its Contribution to Flow Stress during Magnesium Crystal Basal Slip. Mater. Sci. Eng. 1978, 32, 113–119. [Google Scholar] [CrossRef]
- Fan, H.; Aubry, S.; Arsenlis, A.; El-Awady, J.A. Discrete Dislocation Dynamics Simulations of Twin Size-Effects in Magnesium. MRS Online Proc. Libr. 2015, 1741, 27–32. [Google Scholar] [CrossRef]
- Ocegueda, E.; Bhattacharya, K. Interaction between Deformation Twinning and Dislocation Slip in Polycrystalline Solids. arXiv 2022, arXiv:2202.02908. [Google Scholar] [CrossRef]
- Gong, M.; Xu, S.; Jiang, Y.; Liu, Y.; Wang, J. Structural Characteristics of {012} Non-Cozone Twin-Twin Interactions in Magnesium. Acta Mater. 2018, 159, 65–76. [Google Scholar] [CrossRef]
- Yu, Q.; Jiang, Y.; Wang, J. Cyclic Deformation and Fatigue Damage in Single-Crystal Magnesium under Fully Reversed Strain-Controlled Tension–Compression in the [100] Direction. Scr. Mater. 2015, 96, 41–44. [Google Scholar] [CrossRef]
- Mordike, B.L.; Ebert, T. Magnesium: Properties-Applications-Potential. Mater. Sci. Eng. A 2001, 302, 37–45. [Google Scholar] [CrossRef]
- Horstemeyer, M.F.; Wang, P. Cradle-to-Grave Simulation-Based Design Incorporating Multiscale Microstructure-Property Modeling: Reinvigorating Design with Science. J. Comput.-Aided Mater. Des. 2003, 10, 13–34. [Google Scholar] [CrossRef]
- Aghion, E.; Bronfin, B.; Eliezer, D. The Role of the Magnesium Industry in Protecting the Environment. J. Mater. Process. Technol. 2001, 117, 381–385. [Google Scholar] [CrossRef]
- Groh, S.; Marin, E.B.; Horstemeyer, M.F.; Bammann, D.J. Dislocation Motion in Magnesium: A Study by Molecular Statics and Molecular Dynamics. Modell. Simul. Mater. Sci. Eng. 2009, 17, 075009. [Google Scholar] [CrossRef]
- Zhu, S.Q.; Yan, H.G.; Chen, J.H.; Wu, Y.Z.; Du, Y.G.; Liao, X.Z. Fabrication of Mg-Al-Zn-Mn Alloy Sheets with Homogeneous Fine-Grained Structures Using High Strain-Rate Rolling in a Wide Temperature Range. Mater. Sci. Eng. A 2013, 559, 765–772. [Google Scholar] [CrossRef]
- Wu, Y.Z.; Yan, H.G.; Chen, J.H.; Zhu, S.Q.; Su, B.; Zeng, P.L. Hot Deformation Behavior and Microstructure Evolution of ZK21 Magnesium Alloy. Mater. Sci. Eng. A 2010, 527, 3670–3675. [Google Scholar] [CrossRef]
- Zhu, S.Q.; Yan, H.G.; Chen, J.H.; Wu, Y.Z.; Su, B.; Du, Y.G.; Liao, X.Z. Feasibility of High Strain-Rate Rolling of a Magnesium Alloy across a Wide Temperature Range. Scr. Mater. 2012, 67, 404–407. [Google Scholar] [CrossRef]
- Cepeda-Jiménez, C.M.; Molina-Aldareguia, J.M.; Pérez-Prado, M.T. Effect of Grain Size on Slip Activity in Pure Magnesium Polycrystals. Acta Mater. 2015, 84, 443–456. [Google Scholar] [CrossRef]
- del Valle, J.A.; Carreño, F.; Ruano, O.A. Influence of Texture and Grain Size on Work Hardening and Ductility in Magnesium-Based Alloys Processed by ECAP and Rolling. Acta Mater. 2006, 54, 4247–4259. [Google Scholar] [CrossRef]
- Shimizu, I. Temperature Dependent Plastic Deformation Behavior of AZ31 Magnesium Alloy in Uniaxial and Biaxial Compressions. Key Eng. Mater. 2016, 725, 421–426. [Google Scholar] [CrossRef]
- Chapuis, A.; Liu, Q. Investigating the Temperature Dependency of Plastic Deformation in a Mg-3Al-1Zn Alloy. Mater. Sci. Eng. A. 2018, 725, 108–118. [Google Scholar] [CrossRef]
- Mohapatra, S.; Prasad, R.; Jain, J. Temperature Dependence of Abnormal Grain Growth in Pure Magnesium. Mater. Lett. 2021, 283, 128851. [Google Scholar] [CrossRef]
- Zhang, H. Atomistic Simulation of Sliding of [100] Tilt Grain Boundaries in Mg. J. Mater. Res. 2009, 24, 3446–3453. [Google Scholar] [CrossRef]
- Song, H.Y.; Li, Y.L. Atomic Simulations of Effect of Grain Size on Deformation Behavior of Nano-Polycrystal Magnesium. J. Appl. Phys. 2012, 111, 044322. [Google Scholar] [CrossRef]
- Moitra, A. Grain Size Effect on Microstructural Properties of 3D Nanocrystalline Magnesium under Tensile Deformation. Comput. Mater. Sci. 2013, 79, 247–251. [Google Scholar] [CrossRef]
- Hasan, M.S.; Lee, R.; Xu, W. Deformation Nanomechanics and Dislocation Quantification at the Atomic Scale in Nanocrystalline Magnesium. J. Magnes. Alloys 2020, 8, 1296–1303. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A Tool for Manipulating and Converting Atomic Data Files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Liu, X.Y.; James, B.A.; Furio, E.; John, A.M. EAM Potential for Magnesium from Quantum Mechanical Forces. Modell. Simul. Mater. Sci. Eng. 1996, 4, 293–303. [Google Scholar] [CrossRef]
- Tang, Y.; El-Awady, J.A. Formation and Slip of Pyramidal Dislocations in Hexagonal Close-Packed Magnesium Single Crystals. Acta Mater. 2014, 71, 319–332. [Google Scholar] [CrossRef]
- Somekawa, H.; Singh, A.; Inoue, T.; Mukai, T. Enhancing Fracture Toughness of Magnesium Alloy by Formation of Low Angle Grain Boundary Structure. Adv. Eng. Mater. 2010, 12, 837–842. [Google Scholar] [CrossRef]
- Panicker, R.; Chokshi, A.H.; Mishra, R.K.; Verma, R.; Krajewski, P.E. Microstructural Evolution and Grain Boundary Sliding in a Superplastic Magnesium AZ31 Alloy. Acta Mater. 2009, 57, 3683–3693. [Google Scholar] [CrossRef]
- Yamakov, V.; Wolf, D.; Phillpot, S.R.; Mukherjee, A.; Gleiter, H. Dislocation–Dislocation and Dislocation–Twin Reactions in Nanocrystalline Al by Molecular Dynamics Simulation. Acta Mater. 2003, 51, 4135–4147. [Google Scholar] [CrossRef]
- Sinmonnin, P.; Schrieber, D.K.; Uberuaga, B.P.; Rosso, K.M. Atomic Diffusion, Segregation, and Grain Boundary Migration in Nickel-based Alloys from Molecular Dynamicks Simulations. Mater. Today Commu. 2023, 35, 105768. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated Identification and Indexing of Dislocations in Crystal Interfaces. Modelling Simul. Mater. Sci. Eng. 2012, 20, 085007. [Google Scholar]
- Rogers, J.P.; Wynblatt, P.; Foiles, S.M.; Baskes, M.I. Monte Carlo Simulation of the Cu Ag (001) Semicoherent Interphase Boundary. Acta Metall. Mater. 1990, 38, 177–184. [Google Scholar] [CrossRef]
- Available online: https://www.lammps.org (accessed on 1 May 2023).
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO–the Open Visualization Tool. Modell. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Stukowski, A. Structure Identification Methods for Atomistic Simulations of Crystalline Materials. Modell. Simul. Mater. Sci. Eng. 2012, 20, 045021. [Google Scholar] [CrossRef]
- Larsen, P.M.; Schmidt, S.; Schiøtz, J. Robust structural identification via polyhedral template matching. Modell. Simul. Mater. Sci. Eng. 2016, 24, 055007. [Google Scholar] [CrossRef]
- Qi, H.; Guo, Y.F.; Tang, X.Z.; Xu, S. Atomistic Simulation of the Structural Evolution in Magnesium Single Crystal under c-axis Tension. Acta Metall. Sin. 2011, 24, 487–494. [Google Scholar]
- Liu, J.; Cui, Z.; Li, C. Modelling of Flow Stress Characterizing Dynamic Recrystallization for Magnesium Alloy AZ31B. Comput. Mater. Sci. 2008, 41, 375–382. [Google Scholar] [CrossRef]
- Wilson, S.R.; Mendelev, M.I. A Unified Relation for the Solid-Liquid Interface Free Energy of Pure FCC, BCC, and HCP Metals. J. Chem. Phys. 2016, 144, 144704. [Google Scholar] [CrossRef]
- Li, W.J.; Zhao, G.Q.; Ma, X.W.; Gao, J. Flow Stress Characteristics of AZ31B Magnesium Alloy Sheet at Elevated Temperatures. Int. J. Appl. Phys. Math. 2012, 2, 83–88. [Google Scholar] [CrossRef]
- Feng, X.; Sun, Y.; Lu, Y.; He, J.; Liu, X.; Wan, S. Effect of the Strain Rate on the Damping and Mechanical Properties of a ZK60 Magnesium Alloy. Materials 2020, 13, 2969. [Google Scholar] [CrossRef] [PubMed]
- Rida, A.; Micoulaut, M.; Rouhaud, E.; Makke, A. Understanding the Strain Rate Sensitivity of Nanocrystalline Copper Using Molecular Dynamics Simulations. Comput. Mater. Sci. 2020, 172, 109294. [Google Scholar] [CrossRef]
- Fukuda, K.; Koyanagi, Y.; Tsushida, M.; Kitahara, H.; Mayama, T.; Ando, S. Activation Stress for Slip Systems of Pure Magnesium Single Crystals in Pure Shear Test. Mater. Trans. 2017, 58, 587–591. [Google Scholar] [CrossRef]
- Karewar, S.; Sietsma, J.; Santofimia, M.J. Effect of Pre-Existing Defects in the Parent Fcc Phase on Atomistic Mechanisms during the Martensitic Transformation in Pure Fe: A Molecular Dynamics Study. Acta Mater. 2017, 142, 71–81. [Google Scholar] [CrossRef]
- Kim, D.H.; Ebrahimi, F.; Manuel, M.V.; Tulenko, J.S.; Phillpot, S.R. Grain-boundary activated pyramidal dislocations in nano-textured Mg by molecular dynamics simulation. Mater. Sci. Eng. A 2011, 528, 5411–5420. [Google Scholar] [CrossRef]
- Liu, J.; Fan, X.; Zheng, W.; Singh, D.J.; Shi, Y. Nanocrystalline Gold with Small Size: Inverse Hall–Petch between Mixed Regime and Super-Soft Regime. Philos. Mag. 2020, 100, 2335–2351. [Google Scholar] [CrossRef]
- Joni, B.; Al-Samman, T.; Chowdhury, S.G.; Csiszar, G.; Ungar, T. Dislocation densities and prevailing slip-system types determined by X-ray line profile analysis in a textured AZ31 magnesium alloy deformed at different temperatures. J. Appl. Crystallogr. 2013, 46, 55–62. [Google Scholar] [CrossRef]
- Wu, Z.; Curtin, W.A. The Origins of High Hardening and Low Ductility in Magnesium. Nature 2015, 526, 62–67. [Google Scholar] [CrossRef]
- He, C.; Zhang, Y.; Liu, C.Q.; Yue, Y.; Chen, H.W.; Nie, J.F. Unexpected partial dislocations within stacking faults in a cold deformed MgBi alloy. Acta Mater. 2020, 188, 328–343. [Google Scholar] [CrossRef]
- Jiang, S.; Liu, T.; Chen, C.; Jiang, X. Law of Atomic Motion during {101} Twinning in Magnesium Alloys. Mater. Trans. 2011, 52, 1585–1588. [Google Scholar] [CrossRef]
- Jiang, L.; Jonas, J.J.; Mishra, R.K.; Luo, A.A.; Sachdev, A.K.; Godet, S. Twinning and Texture Development in Two Mg Alloys Subjected to Loading along Three Different Strain Paths. Acta Mater. 2007, 55, 3899–3910. [Google Scholar] [CrossRef]
- Yoshinaga, H.; Horiuchi, R. Deformation Mechanisms in Magnesium Single Crystals Compressed in the Direction Parallel to Hexagonal Axis. Trans. Jpn. Inst. Met. 1963, 4, 1–8. [Google Scholar] [CrossRef]
- Pueschl, W. Models for Dislocation Cross-Slip in Close-Packed Crystal Structures: A Critical Review. Prog. Mater. Sci. 2002, 47, 415–461. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Chen, Z.; Llorca, J.; Zeng, X. Deformation mechanisms of Mg-Ca-Zn alloys studied by means of micropillar compression tests. Acta Mater. 2021, 217, 117151. [Google Scholar] [CrossRef]
- Yasi, J.A.; Hector, L.G.; Trinkle, D.R. Prediction of thermal cross-slip stress in magnesium alloys from direct first-principles data. Acta Mater. 2011, 59, 5652–5660. [Google Scholar] [CrossRef]
- Máthis, K.; Nyilas, K.; Axt, A.; Dragomir Cernatescu, I.; Ungár, T.; Lukáč, P. The Evolution of Non-Basal Dislocations as a Function of Deformation Temperature in Pure Magnesium Determined by X-Ray Diffraction. Acta Mater. 2004, 52, 2889–2894. [Google Scholar] [CrossRef]
- Kaibyshev, R.; Sitdikov, O. Dynamic Recrystallization of Magnesium at Ambient Temperature. Int. J. Mater. Res. 1994, 85, 738–743. [Google Scholar] [CrossRef]
- Kaibyshev, R.; Sitdikov, O. On the Role of Twinning in Dynamic Recrystallization. Int. J. Mater. Res. 2000, 89, 384–390. [Google Scholar]
- Galiyev, A.; Kaibyshev, R.; Gottstein, G. Correlation of Plastic Deformation and Dynamic Recrystallization in Magnesium alloy ZK60. Acta Mater. 2001, 49, 1199–1207. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, M.P.; Zhu, S.; Jiang, N. Preferential dynamic recrystallization at original grain boundaries in the hot-rolling process of AZ31 alloy. J. Alloys Compd. 2012, 544, 159–165. [Google Scholar] [CrossRef]
- Dai, Y.; Chen, X.H.; Yan, T.; Tang, A.T.; Zhao, D.; Luo, Z.; Liu, C.Q.; Cheng, R.J.; Pan, F.S. Improved Corrosion Resistance in AZ61 Magnesium Alloys Induced by Impurity Reduction. Acta Metall. Sin. 2020, 33, 225–232. [Google Scholar] [CrossRef]
- Barezban, M.H.; Roumina, R.; Mirzadeh, H.; Mahmudi, R. Effect of Gd on Dynamic Recrystallization Behavior of Magnesium During Hot Compression. Met. Mater. Int. 2021, 27, 843–850. [Google Scholar] [CrossRef]
- Mishra, R.K.; Gupta, A.K.; Rao, P.R.; Sachdev, A.K.; Kumar, A.M.; Luo, A.A. Influence of cerium on the texture and ductility of magnesium extrusions. Scr. Mater. 2008, 60, 562–565. [Google Scholar] [CrossRef]
- Liu, P.; Jiang, H.; Cai, Z.; Kang, Q.; Zhang, Y. The effect of Y, Ce and Gd on texture, recrystallization and mechanical property of Mg–Zn alloys. J. Magnes. Alloys 2016, 4, 188–196. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Xu, C.; Li, Y.; Wang, B.; Guo, Y. Temperature Effect on the Deformation Behavior in Nanocrystalline Magnesium under Compression: An Atomistic Study. Crystals 2023, 13, 1479. https://doi.org/10.3390/cryst13101479
Zhang C, Xu C, Li Y, Wang B, Guo Y. Temperature Effect on the Deformation Behavior in Nanocrystalline Magnesium under Compression: An Atomistic Study. Crystals. 2023; 13(10):1479. https://doi.org/10.3390/cryst13101479
Chicago/Turabian StyleZhang, Cheng, Chun Xu, Yu Li, Binjun Wang, and Yanhui Guo. 2023. "Temperature Effect on the Deformation Behavior in Nanocrystalline Magnesium under Compression: An Atomistic Study" Crystals 13, no. 10: 1479. https://doi.org/10.3390/cryst13101479



