Next Article in Journal
Nanocrystalline Iron Oxides with Various Average Crystallite Size Investigated Using Magnetic Resonance Method
Previous Article in Journal
Analysing the Photo-Physical Properties of Liquid Crystals
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 14
Issue 4
10.3390/cryst14040359
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Novel Tetragonal Boron Pnictides BX (X = N, P, As, Sb, Bi) with Square B2X2 Motifs from Crystal Chemistry and First Principles

by
Samir F. Matar
1 and
Vladimir L. Solozhenko
2,*
1
Lebanese German University (LGU), Jounieh P.O. Box 206, Lebanon
2
LSPM–CNRS, Université Sorbonne Paris Nord, 93430 Villetaneuse, France
*
Author to whom correspondence should be addressed.
Crystals 2024, 14(4), 359; https://doi.org/10.3390/cryst14040359
Submission received: 28 March 2024 / Revised: 5 April 2024 / Accepted: 9 April 2024 / Published: 11 April 2024
(This article belongs to the Section Inorganic Crystalline Materials)
Browse Figures
Versions Notes

Abstract

:
Novel tetragonal (P42/mnm) boron pnictides BX (X = N, P, As, Sb, Bi) with chromium boride (crb) topology exhibiting a square B2X2 motif with resulting edge- and corner-sharing tetrahedra were predicted from crystal chemistry and extensively characterized by density functional theory (DFT) calculations. All new BX phases were found to be cohesive with decreasing cohesive energy along the series. Mechanically stable with positive sets of elastic constants, all crb phases exhibit slightly lower hardness than other BX polymorphs due to increased openness of the crystal structures. All-positive phonon frequencies characterize the crb BX family except for X = Bi, which shows a slight acoustic instability; also, the shape of the phonon spectra changes from band-like for X = N, P, As to flat bands for the heavier elements. The electronic band structures reveal insulating to semiconducting properties for crb BX, depending on the pnictogen nature along the series.

1. Introduction

The prediction of novel phases with advanced properties (chemical, thermal, mechanical, electronic, etc.) is a crucial research topic, for which theoretical approaches have recently been developed including computational materials discovery using evolutionary crystal structure prediction [1] and deep machine learning [2]. Despite the availability of structure discovery tools such as Universal Structure Predictor: Evolutionary Xtallography (USPEX) [3] and machine learning programs such as Graph Networks for Materials Exploration (GNoME) [2], the rationalizing role of the scientist (crystallographers, physicists, and chemists) remains unavoidable to establish the relationship between structure, crystal chemistry, and properties to find the optimal way to synthesize new materials. Validation of new structures and stoichiometries requires the support of first principles quantum mechanics calculations within the framework of density functional theory (DFT) [4,5]. A protocol for these calculations is described in the following section. In terms of symmetry, new predicted phases can be analyzed for topology using the online program TopCryst [6].
In 2013, Prasad et al. [7] reported a new hypothetical carbon allotrope called “squaroglitter” with C8 stoichiometry. The designation as “-glitter” is due to the presence of sp2 carbon (in addition to the tetrahedral sp3 carbon) in the structure, which shows similarity to the previously announced C6 “glitter” [8]. Both carbon allotropes are electrically conductive due to the presence of sp2 carbon. C8 “squaroglitter” belongs to the chromium boride (crb) topology, which is a large family of carbon allotropes presented in the SACADA database [9]. The crb topology archetype is identified as SACADA ID 60; the structure is shown in Figure 1a. The polyhedral representation on the right shows a characteristic central square of sp3 carbons bonded to form 2 × 2 edge-sharing tetrahedra that are corner-sharing along the c-axis. The crystal structure belongs to space group I4/mmm (No. 139) (Table 1), with all eight carbon atoms occupying a single Wyckoff position, namely (8h).
In this context of special tetrahedral structural features, we were interested in proposing binary systems with edge- and corner-sharing tetrahedra. For this purpose, the crystal symmetry was redefined in a primitive space group P42/mnm (No. 136) with two four-fold Wyckoff positions, which is also identified with the crb topology. Figure 1b displays the two alternating carbon sites, represented by brown and white spheres, with the structural parameters provided in Table 2, which shows the same interatomic distances and cell volume (cf. Table 1) during the transformation from C8 to (C1)4(C2)4.
Very recently, we have ab initio predicted superdense hexagonal boron pnictides BX (X = N, P, As, Sb, Bi) with quartz (qtz) topology [10,11,12]. In the present work, we used the (C1)4(C2)4 template structure to predict and investigate within DFT a new family of tetragonal equiatomic boron pnictides BX with crb topology that exhibit only B–X bonds, avoiding energetically unfavorable B–B or X–X bonds. Figure 1d displays the square B2X2 motif that characterizes these structures, along with the resulting edge- and corner-sharing BX4 tetrahedra.
Note that all hypothetical tetragonal BX phases are isoelectronic with crb C8, i.e., with a valence electron number of 32 (8 × 4), and are therefore expected to exhibit insulating to semiconducting electronic band structures as shown in the present paper.
The present study examines a family of isostructural and isoelectronic boron pnictides to identify trends in the underlying physics. These investigations report on the crb BX ground state energies (cohesive) as well as the energy derived properties, namely, the mechanical and dynamic stabilities and electronic band structures. This assessment aims to understand the ‘structure–crystal chemistry–physical properties’ relationship throughout the series.

2. Computational Framework

The quantitative search for the ground state energies, the ground state structures, and the related mechanical and dynamical properties required accurate calculations, which were performed within VASP (Vienna Ab initio Simulation Package (VASP) based on the DFT [13,14]. The atomic potentials with all valence states (especially with respect to such light elements as boron and carbon) were considered using the projector augmented wave (PAW) method [14,15]. DFT exchange–correlation effects were considered within a generalized gradient functional (GGA) according to Perdew, Burke, and Ernzerhof [16]. The relaxation of the atoms to the ground state structures was performed with the conjugate gradient algorithm according to Press et al. [17]. The Blöchl tetrahedron method [18] with corrections according to the Methfessel and Paxton scheme [19] was used for geometry optimization and energy calculations, respectively. Brillouin-zone (BZ) integrals were approximated using a special k-point sampling according to Monkhorst and Pack [20]. The structural parameters were optimized until the forces on the atoms were below 0.02 eV/Å, and all stress components were below 0.003 eV/Å3. The calculations were converged at an energy cut-off of 400 eV for the plane-wave basis set regarding the k-point integration in the reciprocal space from kx(6) × ky(6) × kz(6) up to kx(12) × ky(12) × kz(12) for the final convergence and relaxation to zero strains. In the post-treatment process of the ground state electronic structures, the charge density projections were operated onto the carbon atomic sites. The elastic constants Cij and the phonon band structures were calculated to evaluate the mechanical and dynamic stabilities. The electronic band structures were obtained using the all-electrons DFT-based ASW method [21] and the exchange correlation GGA functional [16].

3. Crystal Chemistry

3.1. Developing Binary Equiatomic Compounds

As mentioned above, the archetypical crb C8 carbon allotrope belongs to body-centered tetragonal (“I” centering: from German Innenzentriert) space group I4/mmm (No. 139) with a unique carbon eight-fold Wyckoff position (Table 1). This configuration does not permit the occupation of two chemically distinct elements to form a binary compound. From crystal chemistry engineering, crb C8 was redefined in a lower symmetry primitive “P” space group, specifically, P42/mnm (No. 136), with two distinct four-fold carbon positions. These positions are described in Table 1 and shown in two different colors (brown and white) in Figure 1b. In both configurations, the C–C distances are 1.519 Å and 1.574 Å (square). These values are on either side of the sum of the atomic radii of two carbon atoms with r(C) = 0.77 Å, which is 1.54 Å, i.e., the C-C distance in diamond, the perfectly covalent crystal structure. The cell volume of 47.75 Å3 is the same in both “I” C8 and “P” (C1)4(C2)4, resulting in a density ρ = 3.34 g/cm3 lower than that of diamond: ρ = 3.50 g/cm3 suggesting a slightly lower hardness of both crb allotropes. The peculiarity of the structures with crb topology is the presence of a C4 square with a perfect angle of 90° and another angle of ∠C-C-C1 = 113.62°. The building block tetrahedra are distorted, thus showing a clear difference with respect to diamond, where a unique ideal tetrahedral angle of 109.47° is identified.
Using the (C1)4(C2)4 template (Table 1), the crb binary compounds BX were designed and structurally optimized to the ground state energy following successive calculations with increasing precision of the k-space mesh. The results presented in Table 2 show trends of increasing volume with X, which can be explained by the increase in the atomic radius along the 5A column: r(N) = 0.75 Å, r(P) = 1.10 Å, r(As) = 1.20 Å, r(Sb) = 1.40 Å, and r(Bi) = 1.50 Å. Note that r(B) = 0.83 Å. The angles differ from those observed for C8, especially for the 90° perfect square angle found below this value in the B2X2 square.
The other relevant result is in the values of the cohesive energies (Ecoh) obtained per formula unit (FU) along the series by subtracting the atomic energies (see footnote, Table 2) from the total energy. The most cohesive structure is crb C8 with Ecoh = −2.29 eV/atom compared to Ecoh = −2.47 eV/atom for diamond.
In the BX family, the last row of Table 2 shows the trend of a strong decrease in the cohesive energy counted per FU with a very low magnitude for X = Bi. Note that for BBi, the electronegativity trend is reversed compared to other boron pnictides, χ(Bi) < χ(B), so that it can rather be called a “boride”, i.e., with negatively charged boron (see next section for an illustration). At the same time, the cohesive energy of the ambient pressure zinc-blende BX series was added to establish trends. Again, the decrease in cohesive energy along the BX family is confirmed, but to a systematically greater extent than for crb BX.

3.2. Projection of the Charge Density

Considering the tetragonal crb structures of boron pnictides, it is important to establish the relationship between crystal chemistry and crystal structure due to the expected change in ionocovalent character from template (C1)4(C2)4 to the BX family, which is caused by the difference in Pauling electronegativities χ of pnictogen versus boron. Specifically, χ(C) = 2.55, while for the BX family χ(B) = 2.04, and for pnictogens χ(N) = 3.04, χ(P) = 2.19, χ(As) = 2.18, χ(Sb) = 2.05, and χ(Bi) = 2.02, i.e., there is a noticeable decrease in Pauling electronegativity values along the series. The most appropriate qualitative assessment is provided by the description of the charge density projections onto the different crb BX phases, which are represented by yellow volumes around the atoms shown in Figure 2.
The crb C8 (Figure 2a), made of a single chemical element, shows a purely covalent character with a tetrahedral charge density around the atoms. This is very similar to diamond, with the difference that, unlike crb C8, the environment is perfectly tetrahedral, i.e., not distorted. In crb BN (Figure 2b) with electronegativity difference of the constituents ∆χ(B-N) = −1, a concentration of charge density around N (grey spheres) is observed, so it can be considered as “boron nitride”. For crb BX (X = P, As), (Figure 2c,d) with a small electronegativity difference ∆χ(B-X) ≈ −0.15, the situation changes with respect to the nitride, and the charge density is almost halfway between B and X. Finally, in BX (X = Sb, Bi) (Figure 2e,f), the boron electronegativity is close to that of Sb and higher than that of Bi. Both compounds are rather borides, i.e., with negatively charged boron, as can be observed with the yellow volumes around boron (green spheres).
While the chemical situation of the purely covalent template crb (C1)4(C2)4 is clear, the BX family exhibits different types of chemical bonding, changing from nitride to an ionocovalent behavior for P and As, and finally to borides in the case of Sb and Bi. It is also important to note that the steric factor plays an important role in these changes, as there is a regular increase in the atomic radius of pnictogen along the series.
After analyzing the crystal chemistry, further investigation is required to fully understand the physical properties, as discussed below.

4. Results and Discussion

4.1. Mechanical Properties from Elastic Constants

The mechanical properties of the novel boron pnictides were studied by calculating the elastic tensors through finite distortions of the lattice. The resulting elastic constants Cij (where i and j correspond to the lattice directions) are presented in Table 3. All Cij values of all crb BX are positive, indicating mechanically stable phases. Along the series, there is a clear tendency for the Cij values to decrease due to the increase in atomic radii. As expected, the template (C1)4(C2)4 has the highest Cij values, followed by crb BN. For heavier pnictogens, a significant decrease in the elastic constants is observed, and for Sb and Bi this decrease is particularly pronounced.
The analysis of the elastic tensors was performed using the ELATE software (https://progs.coudert.name/elate) [22], which provides the bulk (B), shear (G) and Young’s (E) moduli Poisson’s ratio (ν) along different averaging methods; in the present work, the Voigt approach [23] was chosen. Table 4 shows the calculated elastic moduli, with values that follow the trends observed for Cij.
Vickers hardness (HV) from elastic properties was evaluated using the empirical Mazhnik–Oganov [24] and Chen–Niu [25] models. Hardness was also estimated in the framework of the thermodynamic model [26,27], which is based on thermodynamic properties and crystal structure, and using the Lyakhov–Oganov approach [28], which takes into account the topology of the crystal structure, the strength of covalent bonds, the degree of ionicity, and directionality. Fracture toughness (KIc) was evaluated using the Mazhnik–Oganov model [24]. Table 4 summarizes the Vickers hardness values for all considered crb boron pnictides calculated using four models. A tendency of a significant decrease in hardness with increasing atomic number of the pnictogen is observed for all four models. Since it has been shown earlier that the thermodynamic model is the most reliable in the case of boron compounds [12,29,30] and shows perfect agreement with the available experimental data for boron pnictides [31,32,33], it is obvious that the hardness values calculated within the empirical models are strongly underestimated. The Oganov–Lyakhov model gives slightly underestimated values for compounds of light pnictogens and does not work in the case of BSb and BBi. It should be noted that all crb phases exhibit 4–7% less hardness than other BX polymorphs due to the increased openness of the crystal structures. However, all crb boron pnictides are hard phases with Vickers hardness exceeding that of cemented tungsten carbide, the conventional hard material.
The fracture toughness of the new boron pnictides decreases from 6.0 MPa·m½ for crb BN, which is twice that of cubic BN (KIc = 2.8 MPa·m½ [34]), down to 0.5 MPa·m½ for crb BBi.

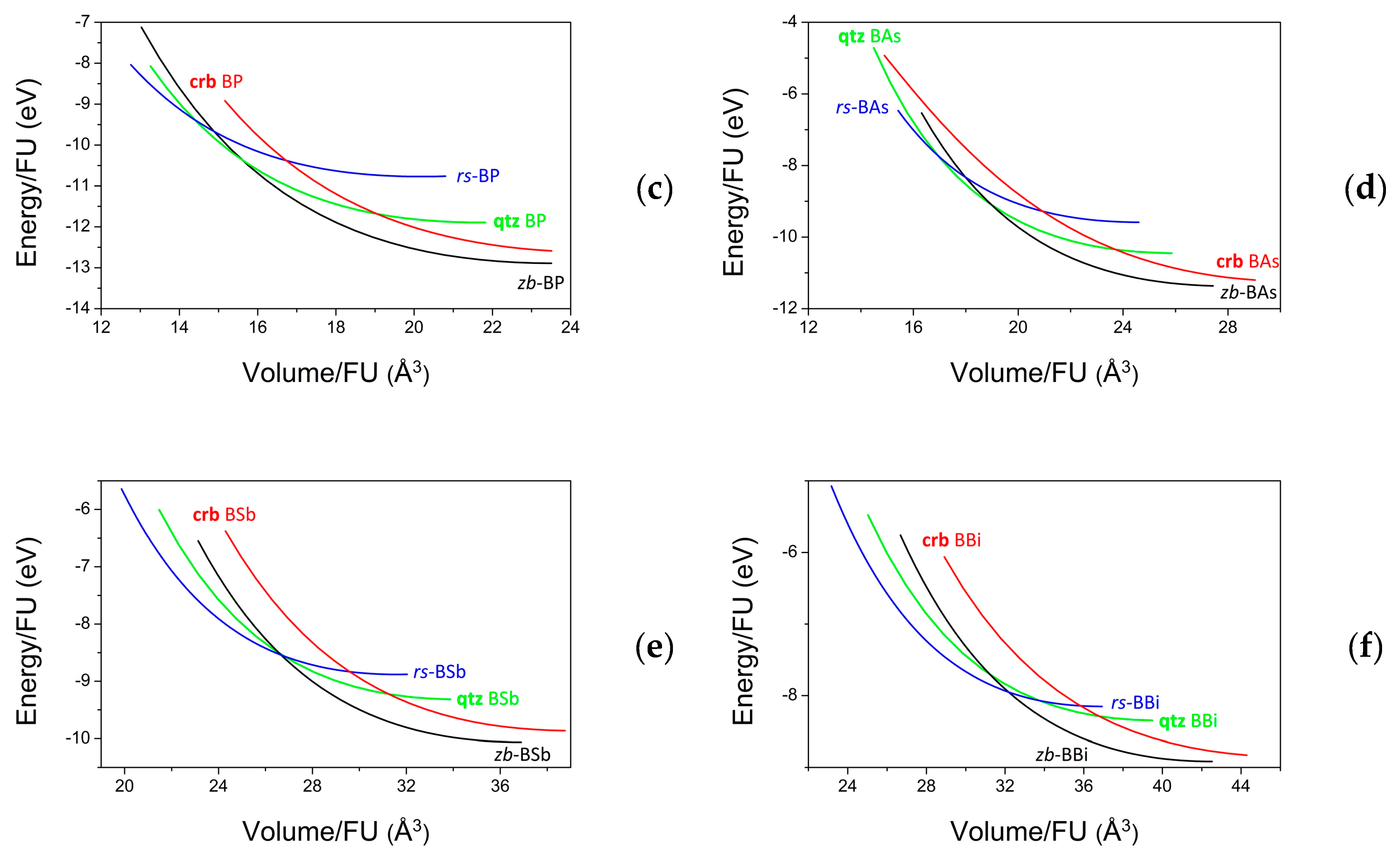
4.2. Equations of State

The comparative energy trends of different crystalline forms for each boron pnictide can be determined from their equations of state. This was achieved based on a series of calculations of total energy as a function of volume for the zinc-blende (zb), rocksalt (rs), qtz, and crb BX polymorphs. The resulting E(V) curves, shown in Figure 3, were fitted to the third-order Birch equations of state [35]:
E(V) = E0(V0) + (9/8)∙V0B0[([(V0)/V])⅔ − 1]2 + (9/16)∙B0(B0′ − 4)V0[([(V0)/V])⅔ − 1]3,
where E0, V0, B0 and B0′ are the equilibrium energy, volume, bulk modulus, and its first pressure derivative, respectively. As can be seen from Figure 3, for all boron pnictides, the polymorphs with crb topology are metastable over the whole range of experimentally accessible pressures. However, the closeness of the cohesive energies of zinc-blende and crb polymorphs (see Table 2) allows for the possibility of the formation of crb BX at high pressures and high temperatures as a result of alternative metastable behavior, most likely in chemical reactions of the elements.

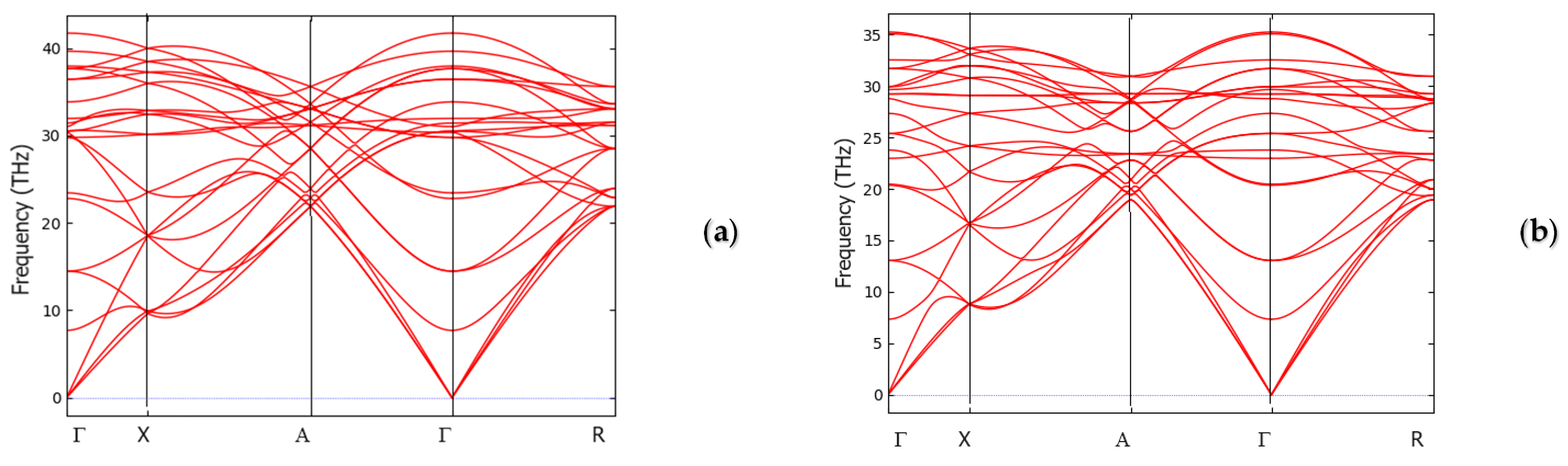
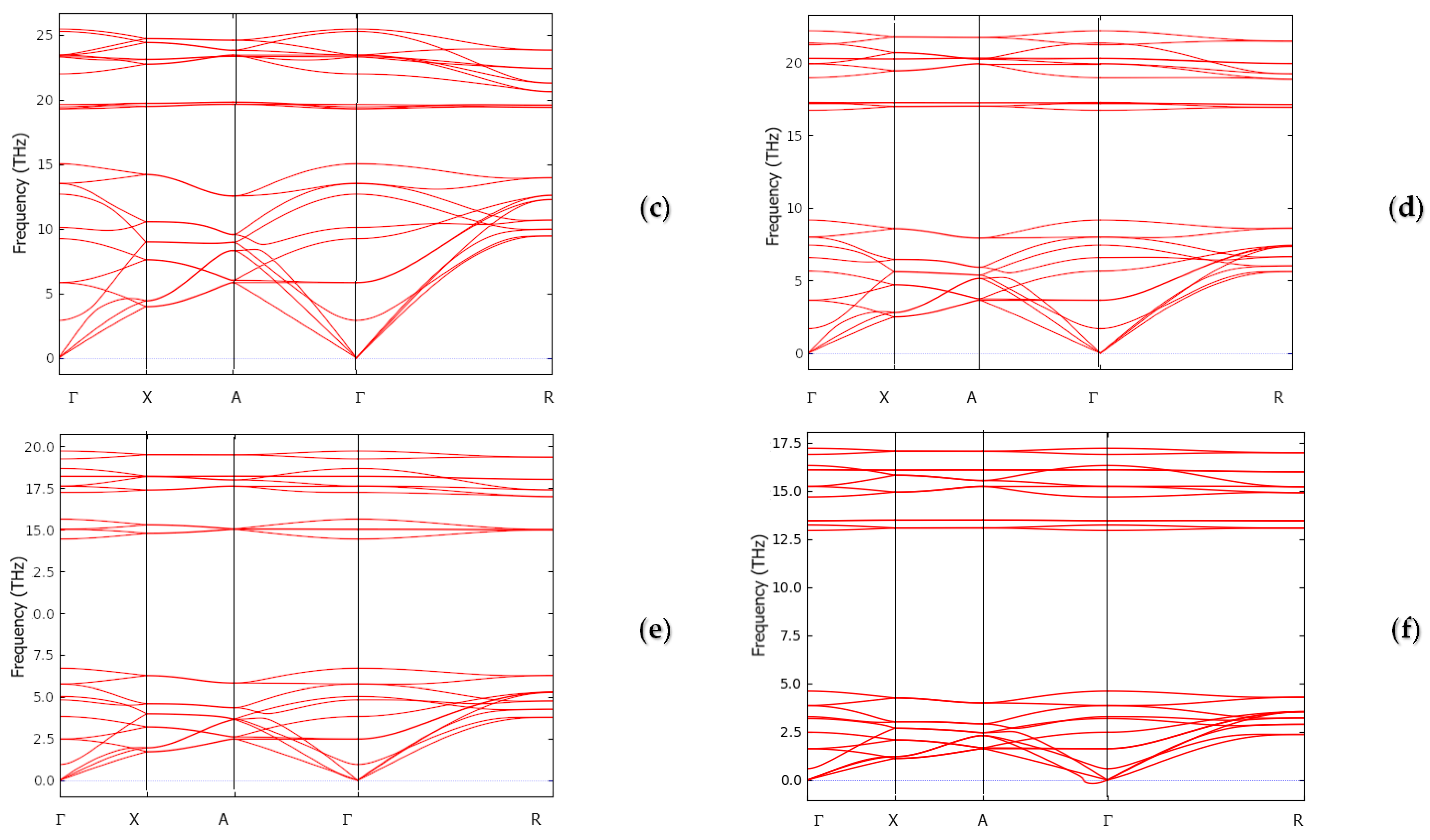
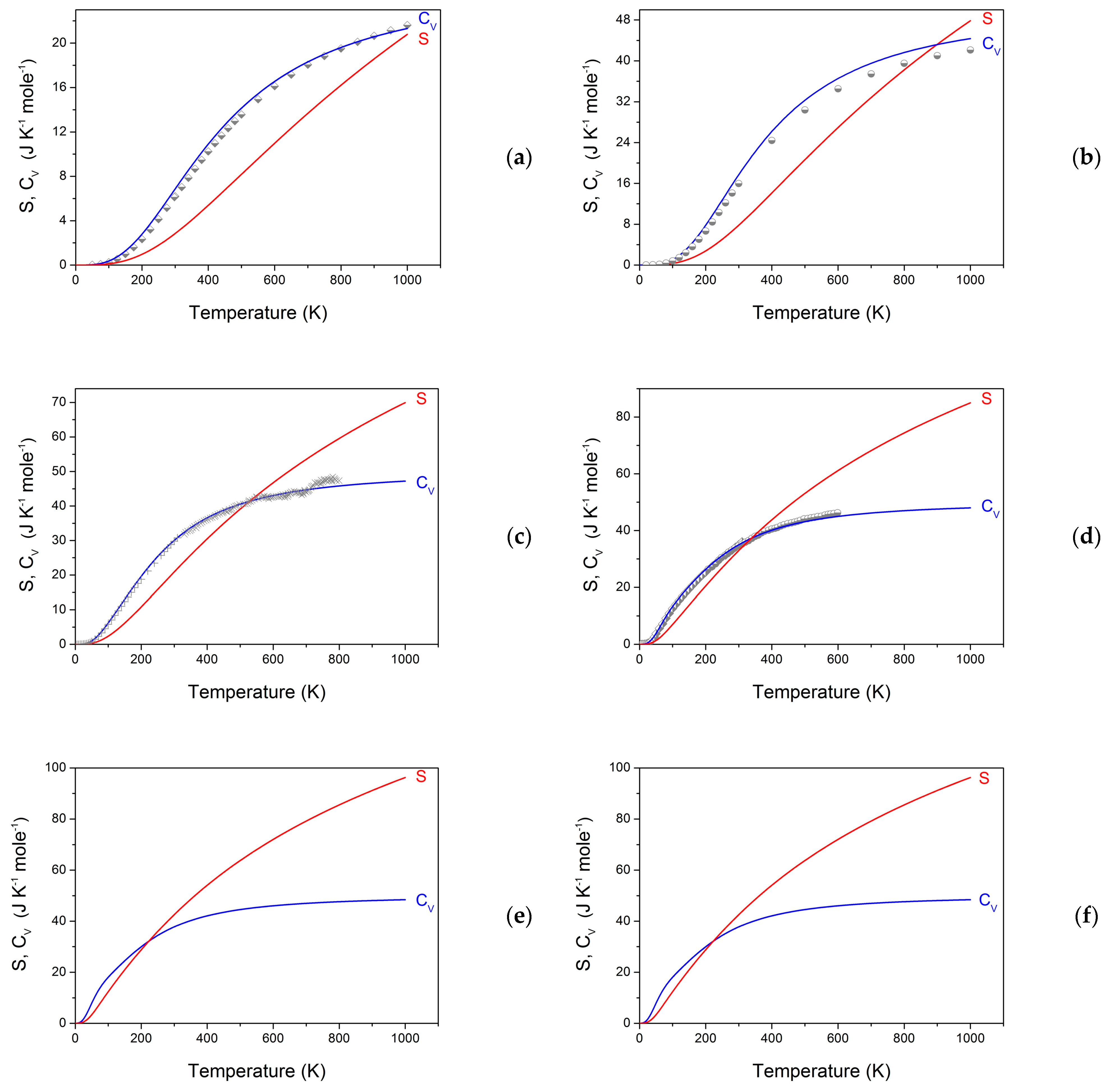
4.3. Dynamic and Thermodynamic Properties from the Phonons

To verify the dynamic stability of the novel boron pnictides, their phonon properties were studied. The phonon band structures (red lines) obtained from a high resolution of the tetragonal Brillouin zone according to Togo et al. [36] are shown in Figure 4. The horizontal direction corresponds to the main directions of the tetragonal Brillouin zone, while the vertical direction shows the frequencies ω, given in terahertz (THz).
The band structures include 3N bands, three acoustic modes starting from zero energy (ω = 0) at the Γ point, the center of the Brillouin zone, up to a few terahertz, and 3N-3 optical modes at higher energies. The acoustic modes correspond to the lattice rigid translation modes of the crystal (two transverse and one longitudinal). All six panels in Figure 4 show positive phonon frequencies, indicating the dynamic stability of all investigated phases. This observation is significant because the crb BX phases become less cohesive along the series (Table 2).
The highest frequencies are observed for crb C8 with bands around 40 THz, the signature of the tetrahedral carbon as in diamond [37]. For BX phases, the lower frequencies are observed due to the trend of increasing d(B–X) along the series (cf. Table 2). This is consistent with the trend of strong decrease in compactness with a change from broadband behavior for BN (Figure 4b) to progressively flattened bands in BP (Figure 4c), BAs (Figure 4d), BSb (Figure 4d), and finally BBi (Figure 4f), which exhibits a dynamic instability characterized by the negative phonons at the Γ point. These trends are consistent with the decreasing cohesive energy along the series.
The thermodynamic properties of the novel boron pnictides were calculated from the phonon frequencies using the statistical thermodynamic approach [38] on a high-precision sampling mesh in the Brillouin zone. The temperature dependencies of heat capacity at constant volume (Cv) and entropy (S) of crb C8 and BX are shown in Figure 5 in comparison with available experimental Cp data for diamond [39,40] and zinc-blende BN [41], BP [42,43], and BAs [44,45]. The observed excellent agreement between the calculated and experimental data for zb-BX indicates the validity of the method used to estimate the thermodynamic properties in the case of boron pnictides. For all three boron pnictides, the heat capacity and entropy of crb phases are slightly higher than those of zb-BX, which is expected for more open crb structures compared to the ideal zinc-blende structure.

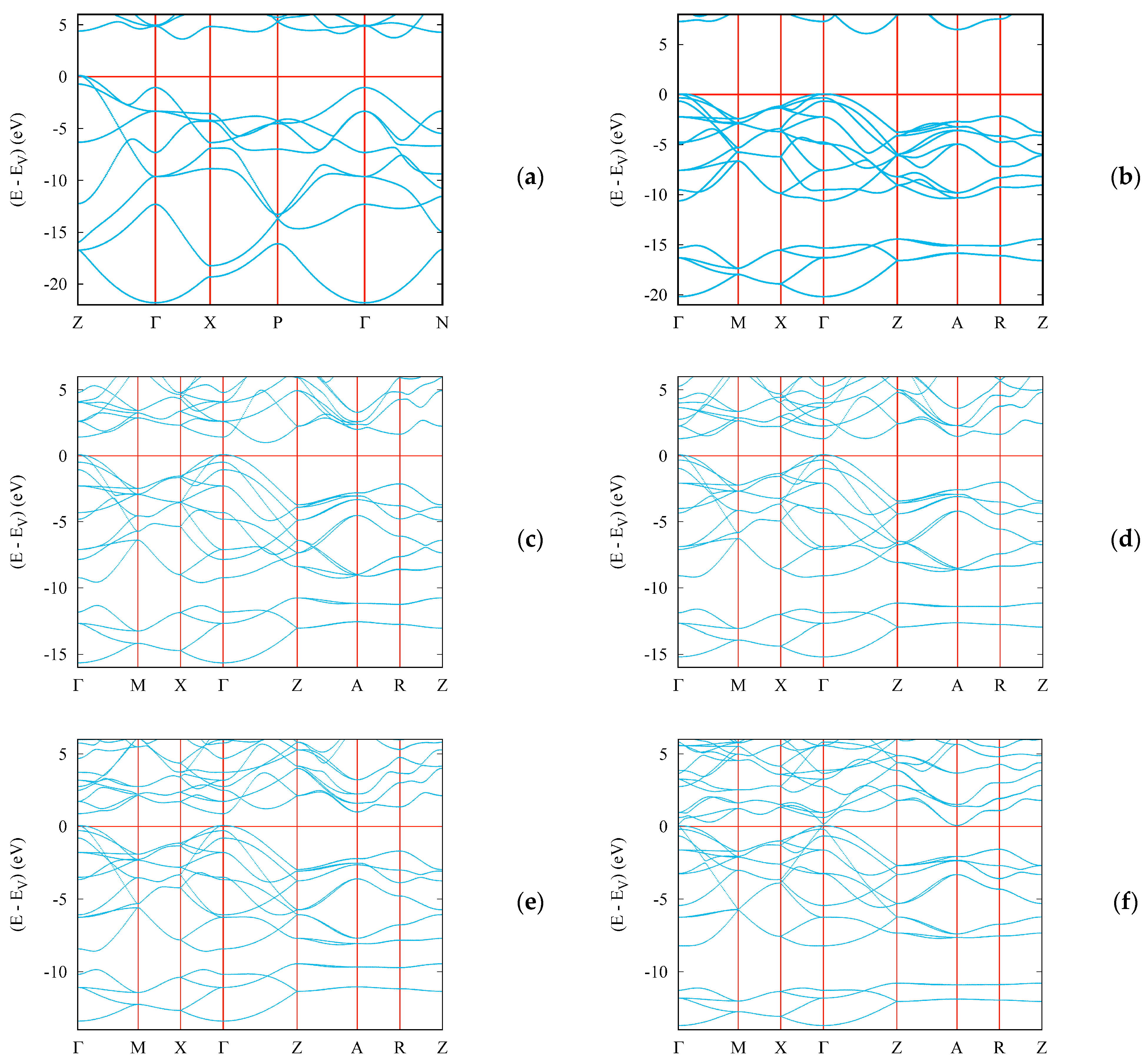
4.4. Electronic Band Structures

The electronic band structures of crb C8 and BX were calculated using the all-electrons DFT-based augmented spherical method (ASW) [21]. The results are shown in Figure 6. The bands (blue lines) develop along the main directions of the tetragonal Brillouin zone. The zero energy along the vertical axis is considered with respect to EV, the top of the filled valence band VB. All six phases have band gaps ranging from widely insulating in C8 and BN (the latter presenting the largest band gap > 5 eV), to semiconducting for the other boron pnictides, with the almost closing gap in BBi. This behavior is related to the continuous change in chemical properties described above.

5. Conclusions

Based on crystal chemistry and density functional theory calculations, a novel family of tetragonal (P42/mnm) boron pnictides BX with crb topology with X element belonging to group 5A (X = N, P, As, Sb, Bi) was predicted. From a crystallographic point of view, these phases exhibit a square B2X2 motif at z = 0, forming edge-sharing BX4 tetrahedra along the square diagonal, connected via corners along the vertical z direction. All new crb BX phases were found to be cohesive, and mechanically stable from elastic constants. As can be seen from the charge density projections, the BX family exhibits different types of chemical bonding, changing from nitride BN to ionocovalent behavior for P and As, and finally to borides in the case of Sb and Bi. A tendency for a significant decrease in hardness with increasing atomic number of the pnictogen was observed (from ~50 GPa for BN to ~13 GPa for BBi); however, all crb boron pnictides are hard phases with Vickers hardness exceeding (or equal to) that of cemented tungsten carbide, the conventional hard material. Dynamically, the new boron pnictides were found to be stable with positive phonon frequencies, except for X = Bi, which exhibits slightly negative acoustic phonons in the center of the Brillouin zone. The heat capacities of the crb BX calculated from the phonon frequencies were found to be slightly higher than those of the corresponding zinc-blende polymorphs, as expected for phases with increased openness of the crystal structures. From the analysis of the electronic band structures, it was found that the properties of the crb boron pnictides change from insulating to semiconducting along the series.

Author Contributions

Conceptualization, S.F.M.; methodology, S.F.M. and V.L.S.; investigation, S.F.M. and V.L.S.; formal analysis, S.F.M. and V.L.S.; data curation, S.F.M. and V.L.S.; visualization, S.F.M. and V.L.S.; validation, S.F.M. and V.L.S.; resources, S.F.M.; writing—original draft preparation, S.F.M.; writing—review and editing, V.L.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Oganov, A.R.; Glass, C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef]
  2. Merchant, A.; Batzner, S.; Schoenholz, S.S.; Aykol, M.; Cheon, G.; Cubuk, E.D. Scaling deep learning for materials discovery. Nature 2023, 624, 80–85. [Google Scholar] [CrossRef]
  3. Glass, C.W.; Oganov, A.R.; Hansen, N. USPEX—Evolutionary crystal structure prediction. Comput. Phys. Comm. 2006, 175, 713–720. [Google Scholar] [CrossRef]
  4. Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, 864–871. [Google Scholar] [CrossRef]
  5. Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
  6. Shevchenko, A.P.; Shabalin, A.A.; Karpukhin, I.Y.; Blatov, V.A. Topological representations of crystal structures: Generation, analysis and implementation in the TopCryst system. Sci. Technol. Adv. Mat. 2022, 2, 250–265. [Google Scholar] [CrossRef]
  7. Prasad, D.L.V.K.; Gerovac, N.M.; Bucknum, M.J.; Hoffmann, R. Squaroglitter: A 3,4-connected carbon net. J. Chem. Theory Comput. 2013, 9, 3855–3859. [Google Scholar] [CrossRef]
  8. Bucknum, M.J.; Hoffmann, R. A hypothetical dense 3,4-connected carbon net and related B2C and CN2 nets built from 1,4-cyclohexadienoid units. J. Am. Chem. Soc. 1994, 116, 11456–11464. [Google Scholar] [CrossRef]
  9. Hoffmann, R.; Kabanov, A.A.; Golov, A.A.; Proserpio, D.M. Homo Citans and carbon allotropes: For an ethics of citation. Angew. Chem. Int. Ed. 2016, 55, 10962–10976. [Google Scholar] [CrossRef] [PubMed]
  10. Matar, S.F.; Solozhenko, V.L. Ultrahigh-density superhard hexagonal BN and SiC with quartz topology from crystal chemistry and first principles. Crystals 2023, 13, 1498. [Google Scholar] [CrossRef]
  11. Solozhenko, V.L.; Matar, S.F. Superdense hexagonal BP and AlP with quartz topology: Crystal chemistry and DFT study. Crystals 2023, 13, 1622. [Google Scholar] [CrossRef]
  12. Solozhenko, V.L.; Matar, S.F. High-pressure phases of boron pnictides BX (X = As, Sb, Bi) with quartz topology from first principles. Crystals 2024, 14, 221. [Google Scholar] [CrossRef]
  13. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
  14. Kresse, G.; Joubert, J. From ultrasoft pseudopotentials to the projector augmented wave. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  15. Blöchl, P.E. Projector augmented wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  16. Perdew, J.; Burke, K.; Ernzerhof, M. The Generalized Gradient Approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  17. Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes, 2nd ed.; Cambridge University Press: New York, NY, USA, 1986. [Google Scholar]
  18. Blöchl, P.; Jepsen, O.; Anderson, O. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef]
  19. Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
  20. Monkhorst, H.J.; Pack, J.D. Special k-points for Brillouin Zone integration. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  21. Eyert, V. Basic notions and applications of the augmented spherical wave method. Int. J. Quantum Chem. 2000, 77, 1007–1031. [Google Scholar] [CrossRef]
  22. Gaillac, R.; Pullumbi, P.; Coudert, F.X. ELATE: An open-source online application for analysis and visualization of elastic tensors. J. Phys. Condens. Matter 2016, 28, 275201. [Google Scholar] [CrossRef] [PubMed]
  23. Voigt, W. Über die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Annal. Phys. 1889, 274, 573–587. [Google Scholar] [CrossRef]
  24. Mazhnik, E.; Oganov, A.R. A model of hardness and fracture toughness of solids. J. Appl. Phys. 2019, 126, 125109. [Google Scholar] [CrossRef]
  25. Chen, X.Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
  26. Mukhanov, V.A.; Kurakevych, O.O.; Solozhenko, V.L. The interrelation between hardness and compressibility of substances and their structure and thermodynamic properties. J. Superhard Mater. 2008, 30, 368–378. [Google Scholar] [CrossRef]
  27. Mukhanov, V.A.; Kurakevych, O.O.; Solozhenko, V.L. Hardness of materials at high temperature and high pressure. Phil. Mag. 2009, 89, 2117–2127. [Google Scholar] [CrossRef]
  28. Lyakhov, A.O.; Oganov, A.R. Evolutionary search for superhard materials: Methodology and applications to forms of carbon and TiO2. Phys. Rev. B 2011, 84, 092103. [Google Scholar] [CrossRef]
  29. Mukhanov, V.A.; Kurakevych, O.O.; Solozhenko, V.L. Thermodynamic model of hardness: Particular case of boron-rich solids. J. Superhard Mater. 2010, 32, 167–176. [Google Scholar] [CrossRef]
  30. Solozhenko, V.L.; Matar, S.F. Prediction of novel ultrahard phases in the B–C–N system from first principles: Progress and problems. Materials 2023, 16, 886. [Google Scholar] [CrossRef]
  31. Solozhenko, V.L.; Bushlya, V. Mechanical properties of boron phosphides. J. Superhard Mater. 2019, 41, 84–89. [Google Scholar] [CrossRef]
  32. Solozhenko, V.L. Hardness of new boron-rich chalcogenides B12S and B12Se. J. Superhard Mater. 2021, 43, 375–377. [Google Scholar] [CrossRef]
  33. Solozhenko, V.L. On hardness of boron subarsenide B12As2. J. Superhard Mater. 2022, 44, 377–378. [Google Scholar] [CrossRef]
  34. Brookes, C.A. The mechanical properties of cubic boron nitride. In Science of Hard Materials. Proceedings of the International Conference; Adam Hilger Ltd.: Accord, MA, USA, 1986; pp. 207–220. [Google Scholar]
  35. Birch, F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300 K. J. Geophys. Res. 1978, 83, 1257–1268. [Google Scholar] [CrossRef]
  36. Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
  37. Krishnan, R.S. Raman spectrum of diamond. Nature 1945, 155, 171. [Google Scholar] [CrossRef]
  38. Dove, M.T. Introduction to Lattice Dynamics; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
  39. DeSorbo, W. Specific heat of diamond at low temperatures. J. Chem. Phys. 1953, 21, 876–880. [Google Scholar] [CrossRef]
  40. Victor, A.C. Heat capacity of diamond at high temperatures. J. Chem. Phys. 1962, 36, 1903–1911. [Google Scholar] [CrossRef]
  41. Solozhenko, V.L.; Gavrichev, K.S. Thermodynamic properties of boron nitride. In Wide Band Gap Electronic Materials; Prelas, M.A., Gielisse, P., Popovici, G., Spitsyn, B.V., Stacy, T., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995; pp. 377–392. [Google Scholar]
  42. Ohsawa, J.; Nishinaga, T.; Uchiyama, S. Measurement of specific heat of boron monophosphide by AC calorimetry. Jpn. J. Appl. Phys. 1978, 17, 1059–1065. [Google Scholar] [CrossRef]
  43. Koshchenko, V.I.; Grinberg, Y.K.; Demidenko, A.F. Thermodynamic properties of AlN (5–2700 K), GaP (5–1500 K) and BP (5–800 K). Izv. Akad. Nauk SSSR Neorg. Mater. 1984, 20, 1787–1790. (In Russian) [Google Scholar]
  44. Kang, J.S.; Li, M.; Wu, H.; Nguyen, H.; Hua, Y. Basic physical properties of cubic boron arsenide. Appl. Phys. Lett. 2019, 115, 122103. [Google Scholar] [CrossRef]
  45. Koshchenko, V.I.; Demidenko, A.F.; Grinberg, Y.K.; Yachmenev, V.E. Specific-heats and thermodynamic functions of BP, BAs and B6As at 5–310 K. Izv. Akad. Nauk SSSR Neorg. Mater. 1981, 17, 1965–1968. (In Russian) [Google Scholar]
Crystals 14 00359 g001
Figure 1. Crystal structures (ball-and-stick and tetrahedral representations) of body-centered tetragonal C8 (a); primitive tetragonal (C1)4(C2)4 in which two carbon substructures C1 (4g) (white spheres) and C2 (4g) (brown spheres) allow accommodation of two different types of atomic constituents to form tetrahedral boron pnictides with crb topology (b); novel crb BX (X = N, P, As, Sb, Bi) (green and blue spheres correspond to B and X atoms, respectively) (c); projection of the crb BX structure onto the a–b plane showing distorted B2X2 square and the edge-sharing tetrahedra connected via corners (d).
Figure 1. Crystal structures (ball-and-stick and tetrahedral representations) of body-centered tetragonal C8 (a); primitive tetragonal (C1)4(C2)4 in which two carbon substructures C1 (4g) (white spheres) and C2 (4g) (brown spheres) allow accommodation of two different types of atomic constituents to form tetrahedral boron pnictides with crb topology (b); novel crb BX (X = N, P, As, Sb, Bi) (green and blue spheres correspond to B and X atoms, respectively) (c); projection of the crb BX structure onto the a–b plane showing distorted B2X2 square and the edge-sharing tetrahedra connected via corners (d).
Crystals 14 00359 g001
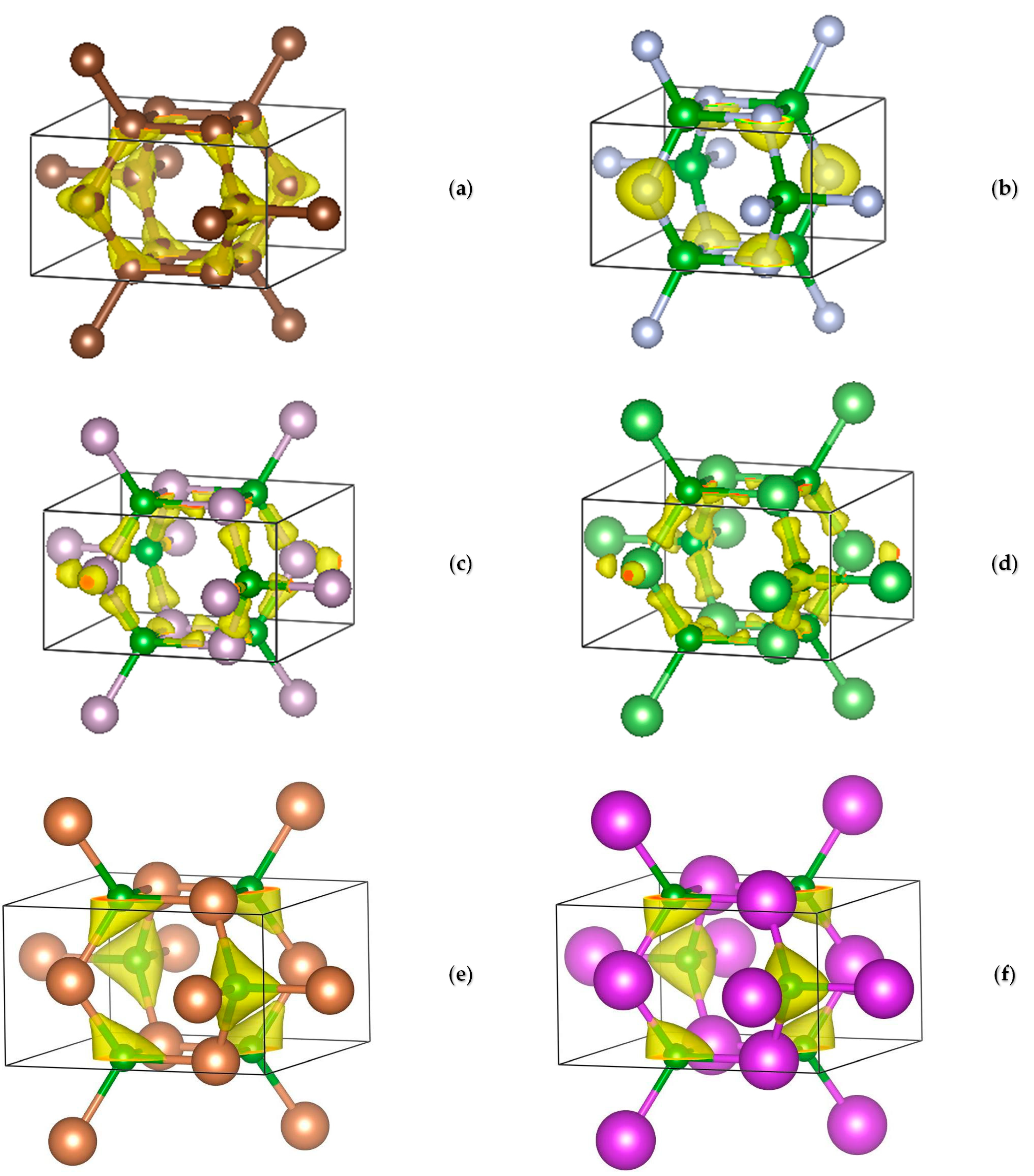
Crystals 14 00359 g002
Figure 2. Charge density projections (yellow volumes) of body centered tetragonal C8 (a) and crb boron pnictides: BN (b), BP (c), BAs (d), BSb (e), and BBi (f). B atoms are represented by green spheres, while the size of the X spheres is proportional to the respective atomic radius of the pnictogen. The c-axis is along the vertical direction.
Figure 2. Charge density projections (yellow volumes) of body centered tetragonal C8 (a) and crb boron pnictides: BN (b), BP (c), BAs (d), BSb (e), and BBi (f). B atoms are represented by green spheres, while the size of the X spheres is proportional to the respective atomic radius of the pnictogen. The c-axis is along the vertical direction.
Crystals 14 00359 g002
Crystals 14 00359 g003aCrystals 14 00359 g003b
Figure 3. Calculated total energy per formula unit as a function of volume for carbon allotropes (a) and boron pnictides polymorphs: BN (b), BP (c), BAs (d), BSb (e), and BBi (f).
Figure 3. Calculated total energy per formula unit as a function of volume for carbon allotropes (a) and boron pnictides polymorphs: BN (b), BP (c), BAs (d), BSb (e), and BBi (f).
Crystals 14 00359 g003aCrystals 14 00359 g003b
Crystals 14 00359 g004aCrystals 14 00359 g004b
Figure 4. Phonon band structures (red lines) of crb phases along the major directions of the simple tetragonal Brillouin zone: C8 (a); BN (b); BP (c); BAs (d); BSb (e); and BBi (f).
Figure 4. Phonon band structures (red lines) of crb phases along the major directions of the simple tetragonal Brillouin zone: C8 (a); BN (b); BP (c); BAs (d); BSb (e); and BBi (f).
Crystals 14 00359 g004aCrystals 14 00359 g004b
Crystals 14 00359 g005
Figure 5. Heat capacity at constant volume (Cv) and entropy (S) of body centered tetragonal C8 (a) and crb boron pnictides as functions of temperature: BN (b), BP (c), BAs (d), BSb (e), and BBi (f). Experimental heat capacity data for diamond and zb-BX (X = N, P, As) are shown as gray symbols.
Figure 5. Heat capacity at constant volume (Cv) and entropy (S) of body centered tetragonal C8 (a) and crb boron pnictides as functions of temperature: BN (b), BP (c), BAs (d), BSb (e), and BBi (f). Experimental heat capacity data for diamond and zb-BX (X = N, P, As) are shown as gray symbols.
Crystals 14 00359 g005
Crystals 14 00359 g006
Figure 6. Electronic band structures (blue lines) of crb phases: C8 (a); BN (b); BP (c); BAs (d); BSb (e); BBi (f).
Figure 6. Electronic band structures (blue lines) of crb phases: C8 (a); BN (b); BP (c); BAs (d); BSb (e); BBi (f).
Crystals 14 00359 g006
Table 1. Calculated crystal structure parameters of tetragonal carbon allotropes with crb topology.
Table 1. Calculated crystal structure parameters of tetragonal carbon allotropes with crb topology.
crb C8
I4/mmm (No. 139)		crb (C1)4(C2)4
P42/mnm (No. 136)
a, Å4.36654.3662
c, Å2.50452.5048
Vcell, Å347.7547.75
Density, g/cm33.343.34
Atomic positionsC (8h) 0.6803, x, 0.0C1 (4g) 0.3197, −x, 0.0
C2 (4f) 0.6803, x, 0.0
Bond lengths, Å1.519 and 1.574 Å1.519 and 1.574 Å
Angles (deg.)∠C-C-C = 90° (within the square)
∠C-C-C = 110.96° (along z direction)		∠C-C-C = 90° (within the square)
∠C-C-C = 110.96° (along z direction)
Etotal, eV−71.33−71.33
Etotal/atom, eV−2.32−2.32
Table 2. Calculated crystal structure parameters of tetragonal boron pnictides with crb topology.
Table 2. Calculated crystal structure parameters of tetragonal boron pnictides with crb topology.
BNBPBAsBSbBBi
P42/mnm (No. 136)
a, Å4.3985.5585.8946.4536.764
c, Å2.5383.1993.3923.7233.900
Vcell, Å349.1198.88117.83155.01178.43
Shortest bond length, Åd(B-N) = 1.53d(B-P) = 1.95d(B-As) = 2.06d(B-Sb) = 2.31d(B-Bi) = 2.38
Angles (deg.)∠BNB = 85.76
∠NBN = 112.44		∠BPB = 90.73
∠PBP = 113.59		∠BAsB = 91. 23
∠AsBAs = 113.50		∠BSbB = 91.36
∠SbBSb = 110.49		∠BBiB = 91. 79
∠BiBBi = 110.28
Atomic positionsB(4g) 0.3258, −x, 0
N(4i) 0.6875, x, 0		B(4g) 0.3217, −x, 0
P(4i) 0.6806, x, 0		B(4g) 0.323, −x, 0
As(4i) 0.681, x, 0		B(4g) 0.3229, −x, 0
Sb(4i) 0.6814, x, 0		B(4g) 0.3238, −x, 0
Bi(4i) 0.6818, x, 0
Etotal, eV−68.86−50.51−45.293−39.45−35.05
Ecoh/FU, eV−5.12−2.13−1.52−0.60−0.053
(zinc-blende)−5.32−2.39−1.57−0.70−0.60
Atomic energies: E(B) = −5.3 eV; E(N) = −6.8 eV; E(P) = −5.2 eV; E(As) = −4.5 eV; E(Sb) = −4.0 eV; E(Bi) = −3.0 eV.
Table 3. Elastic constants (Cij) of tetragonal boron pnictides with crb topology. All values are in GPa.
Table 3. Elastic constants (Cij) of tetragonal boron pnictides with crb topology. All values are in GPa.
C11C12C13C33C44C66
C8949234591202323450
BN757174114988239336
BP2151654840383135
BAs242714031777104
BSb17160382285869
BBi11748311554045
Table 4. Mechanical properties of tetragonal boron pnictides with crb topology: Vickers hardness (HV), bulk modulus (B), shear modulus (G), Young’s modulus (E), Poisson’s ratio (ν), fracture toughness (KIc).
Table 4. Mechanical properties of tetragonal boron pnictides with crb topology: Vickers hardness (HV), bulk modulus (B), shear modulus (G), Young’s modulus (E), Poisson’s ratio (ν), fracture toughness (KIc).
HVBGVEVνKIc *
MO *CN †T ‡LO §B0 ‡BV
GPa MPa·m½
C8676093854234234029160.1397.1
BN434253483633673037130.1776.0
BP10152824173151982420.2321.4
BAs12182220135123952260.1921.3
BSb81217310194661600.2150.8
BBi581328268441080.2350.5
* Mazhnik–Oganov model [24]. † Chen–Niu model [25]. ‡ Thermodynamic model [26,27]. § Lyakhov–Oganov model [28].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Matar, S.F.; Solozhenko, V.L. Novel Tetragonal Boron Pnictides BX (X = N, P, As, Sb, Bi) with Square B2X2 Motifs from Crystal Chemistry and First Principles. Crystals 2024, 14, 359. https://doi.org/10.3390/cryst14040359

AMA Style

Matar SF, Solozhenko VL. Novel Tetragonal Boron Pnictides BX (X = N, P, As, Sb, Bi) with Square B2X2 Motifs from Crystal Chemistry and First Principles. Crystals. 2024; 14(4):359. https://doi.org/10.3390/cryst14040359

Chicago/Turabian Style

Matar, Samir F., and Vladimir L. Solozhenko. 2024. "Novel Tetragonal Boron Pnictides BX (X = N, P, As, Sb, Bi) with Square B2X2 Motifs from Crystal Chemistry and First Principles" Crystals 14, no. 4: 359. https://doi.org/10.3390/cryst14040359

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop