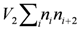Theoretical Studies on Phase Transitions in Quasi-One-Dimensional Molecular Conductors
Abstract
:1. Introduction
 .
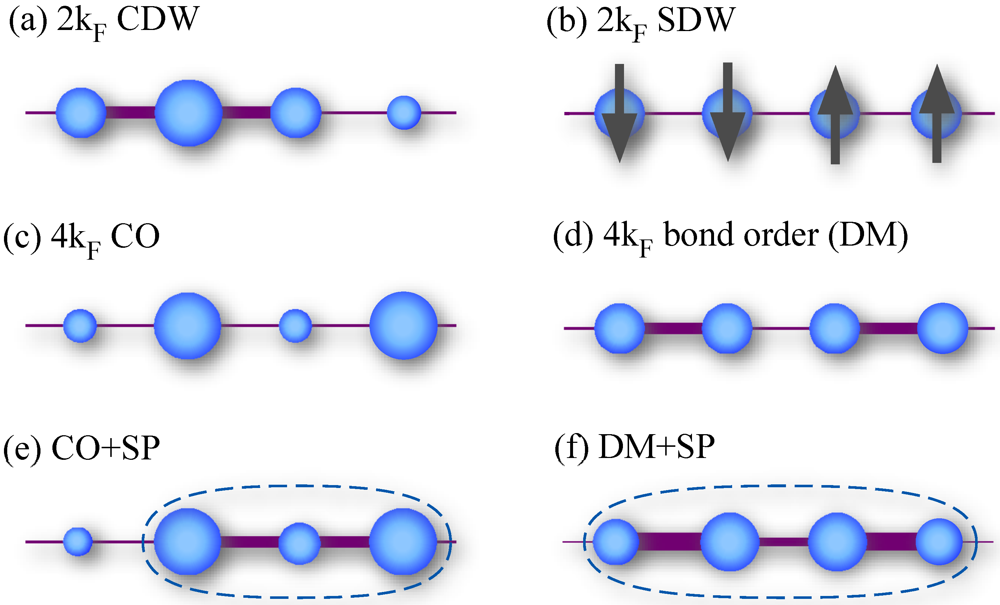
.- 2κF charge density wave (CDW) state: This is a coexistence of modulation of charge density and lattice distortion (bond order) with the period of 4α. The origin is usually the Peierls instability, i.e., the nesting of the Fermi surface, when the electrons are coupled with the lattice degree of freedom (electron-phonon coupling); the modulation opens a gap at the Fermi energy εF in the case of a 1D band. Sometimes the term CDW is used just to represent a charge density modulation, regardless of its physical origin, such as the 4α modulation induced by the spin-Peierls (SP) states mentioned below.
- 2κF spin density wave (SDW) state: This indicates a Peierls instability-induced state as well, mostly, but with magnetic moments which are modulated with the period of 4α, instead of the charge and lattice in the case of CDW. However, for 1D electronic systems, the antiferromagnetic (AF) state in an insulating state due to strong electron correlation, which shows staggered pattern of the localized spin moments, has the same period; therefore they are often mixed up in terminology. These should be distinguished as they have distinct origins.
- 4κF charge order (CO): The intersite Coulomb interaction leads to CO with charge localized on every other site. This is essentially a strongly correlated insulator, where localized spins show up on the “charge rich” sites. We simply call this as the CO state in this review.
- 4κF bond order: 2α modulation of the bonds, namely, dimerization in the transfer integrals makes the system effectively half-filled, then the on-site Coulomb interaction can drive the system to a Mott insulating state. This is called as the dimer-Mott (DM) insulating state. As in the CO state, localized spins appear on the bonding orbitals (anti-bonding orbitals in the case of three quarter-filled band) of the dimerized sites.
- SP state: In the CO and DM insulators, the localized spin degree of freedom is described by the Heisenberg model. 1D Heisenberg chains are susceptible to SP states where spin singlets are aligned periodically. In the quarter-filling case their period is 4α (tetramerization); in other words, 2κF bond order emerges, while 2κF charge modulation is induced as well.
2. Extended Hubbard Model and Ground States
2.1. One-Dimensional Electronic Model

 creates an electron with spin
creates an electron with spin  or
or  at the i-th site along the chain. The density operators are defined as
at the i-th site along the chain. The density operators are defined as 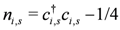 and
and 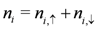 . The interchain coupling is completely neglected in this model. Its ground state consists of two phases for positive U and V: the TLL and the CO insulating states. The latter is stabilized as a long-range order only at T = 0 when both parameters (
. The interchain coupling is completely neglected in this model. Its ground state consists of two phases for positive U and V: the TLL and the CO insulating states. The latter is stabilized as a long-range order only at T = 0 when both parameters (  ,
,  ) are large (see Section 3). In the limit of
) are large (see Section 3). In the limit of  , for example, the TLL (CO insulator) is realized for
, for example, the TLL (CO insulator) is realized for  (
(  ).
).
 is estimated to be around 0.1–0.2, depending on the anion X. Finite dimerization leads to the folding of the Brillouin zone with a gap at the boundary
is estimated to be around 0.1–0.2, depending on the anion X. Finite dimerization leads to the folding of the Brillouin zone with a gap at the boundary  : A half-filled lower band is realized. Then, in the 1D dimerized EHM, the TLL is no longer stable once
: A half-filled lower band is realized. Then, in the 1D dimerized EHM, the TLL is no longer stable once  for positive U and V, and replaced by a Mott insulating state (the DM insulator). The CO region (where intrinsic DM “co-exists” [9]) is shifted toward larger (
for positive U and V, and replaced by a Mott insulating state (the DM insulator). The CO region (where intrinsic DM “co-exists” [9]) is shifted toward larger (  ,
,  ), whose critical line depends on
), whose critical line depends on  . Note that in the CO state with
. Note that in the CO state with  , the system loses the inversion symmetry: Ferrroelectricity arises [10,11,12].
, the system loses the inversion symmetry: Ferrroelectricity arises [10,11,12].2.2. Electron-Lattice Coupling

 increases the lattice energy whose renormalized spring constant is K. The 2κF CDW [Figure 1 (a)] appears in the small Coulomb repulsion region, reflecting its weak-coupling character. In the other diagonal of the phase diagram with large (
increases the lattice energy whose renormalized spring constant is K. The 2κF CDW [Figure 1 (a)] appears in the small Coulomb repulsion region, reflecting its weak-coupling character. In the other diagonal of the phase diagram with large (  ,
,  ), the CO state is realized, as in purely electronic models, while it shows lattice tetramerization due to the SP instability [CO+SP state, Figure 1 (e)]. In between these two, we find the co-existence of dimerization and tetramerization (mixture of bond and charge modulations) [18,19]; This can be interpreted as the spontaneous formation of the DM state, leading to charge localization, then the SP singlet formation [DM+SP state, Figure 1 (f)]. The Holstein coupling added to such a situation enhances the CO+SP region [19].
), the CO state is realized, as in purely electronic models, while it shows lattice tetramerization due to the SP instability [CO+SP state, Figure 1 (e)]. In between these two, we find the co-existence of dimerization and tetramerization (mixture of bond and charge modulations) [18,19]; This can be interpreted as the spontaneous formation of the DM state, leading to charge localization, then the SP singlet formation [DM+SP state, Figure 1 (f)]. The Holstein coupling added to such a situation enhances the CO+SP region [19]. 3. Bosonization and Renormalization Group Study
3.1. One Dimensional Model
 and the spin part
and the spin part  ; this is called charge spin separation. They are written in terms of bosonic phase variables as,
; this is called charge spin separation. They are written in terms of bosonic phase variables as, 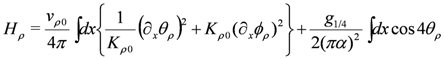
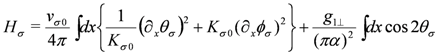
 is a short distance cutoff of the order of the lattice spacing, α. The phase variables satisfy
is a short distance cutoff of the order of the lattice spacing, α. The phase variables satisfy 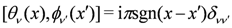 . The quantities,
. The quantities,  ,
,  ,
,  ,
,  ,
,  , and
, and  are bare parameters whose values are non-universal functions of the interaction and the Fermi velocity
are bare parameters whose values are non-universal functions of the interaction and the Fermi velocity  . The non-linear term in the charge sector,
. The non-linear term in the charge sector,  , originates from the 8κF-Umklapp scattering and leads to the insulating ground state with CO. On the other hand, the spin sector is essentially the same as the effective Hamiltonian of a Heisenberg chain. Therefore, the parameters
, originates from the 8κF-Umklapp scattering and leads to the insulating ground state with CO. On the other hand, the spin sector is essentially the same as the effective Hamiltonian of a Heisenberg chain. Therefore, the parameters  and
and  are not independent of each other due to the spin SU(2) symmetry and satisfy the following relation,
are not independent of each other due to the spin SU(2) symmetry and satisfy the following relation, 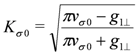
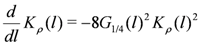
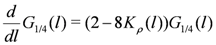

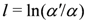 with the new length scale
with the new length scale  . The initial conditions for the above RG equations are given from the bare parameters as
. The initial conditions for the above RG equations are given from the bare parameters as  ,
, 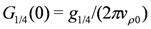 and
and 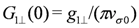 . Note that the relation Equation (6) still holds even under the renormalization procedure; the quantity
. Note that the relation Equation (6) still holds even under the renormalization procedure; the quantity  is written by using the solution of Equation (9) as
is written by using the solution of Equation (9) as 
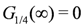 with
with  , whereas the CO insulating state is by
, whereas the CO insulating state is by  . The metal-insulator boundary is characterized by
. The metal-insulator boundary is characterized by 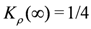 . On the other hand, the spin degree of freedom, as long as we consider repulsive interactions, has gapless excitations with
. On the other hand, the spin degree of freedom, as long as we consider repulsive interactions, has gapless excitations with 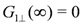 and
and 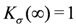 .
. -term in Equation (4). This is because it originates from the interaction processes where four right-going electrons are scattered into four left-going states and vice versa, which include the one-particle states far from Fermi energy as intermediate states. The systematic way to obtain analytical expression for the coupling constant
-term in Equation (4). This is because it originates from the interaction processes where four right-going electrons are scattered into four left-going states and vice versa, which include the one-particle states far from Fermi energy as intermediate states. The systematic way to obtain analytical expression for the coupling constant  is as follows [22,23,24]. The one-particle states are divided into two parts: the states close to
is as follows [22,23,24]. The one-particle states are divided into two parts: the states close to  and those around
and those around  . The effective Hamiltonian for the former states are obtained by integrating out the latter states and treating the interaction processes including both kinds of states in perturbation expansion. The lowest order contribution to the 8κF-Umklapp scattering comes from the third order processes, which are shown in Figure 3. When the bare parameters obtained by the above treatment are used as the initial conditions for the RG equations, one can obtain the ground state phase diagram on the plane of
. The effective Hamiltonian for the former states are obtained by integrating out the latter states and treating the interaction processes including both kinds of states in perturbation expansion. The lowest order contribution to the 8κF-Umklapp scattering comes from the third order processes, which are shown in Figure 3. When the bare parameters obtained by the above treatment are used as the initial conditions for the RG equations, one can obtain the ground state phase diagram on the plane of  and
and  . The CO insulating state is realized for the large
. The CO insulating state is realized for the large  and
and  region, whereas the TLL state with both charge and spin excitation without a gap appears in the other region. The phase diagram is qualitatively the same as that derived from numerical methods [3,8]. We note that, as discussed in the previous section, the alternating transfer integrals change the TLL to the DM insulating state because the
region, whereas the TLL state with both charge and spin excitation without a gap appears in the other region. The phase diagram is qualitatively the same as that derived from numerical methods [3,8]. We note that, as discussed in the previous section, the alternating transfer integrals change the TLL to the DM insulating state because the  -Umklapp scattering is generated by the dimerization gap at
-Umklapp scattering is generated by the dimerization gap at  . In addition, the CO region on the U-V plane is reduced because the CO and the dimerization compete with each other [24]. However, CO is still stabilized even in the presence of the dimerization.
. In addition, the CO region on the U-V plane is reduced because the CO and the dimerization compete with each other [24]. However, CO is still stabilized even in the presence of the dimerization. indicates the right/left going state, and the solid and the dotted lines express the electrons close to
indicates the right/left going state, and the solid and the dotted lines express the electrons close to  and to
and to  , respectively.
, respectively. 
 are taken into account in the analytical bosonization procedure. When the mutual interaction becomes stronger, such a treatment does not endorse quantitatively correct results, because the interaction processes far from the Fermi energy play important roles. One of the most evident example is the 8κF-Umklapp scattering leading to the CO state noted above. However, it is difficult to obtain the accurate values of the initial conditions by such analytical procedures. Instead, the exact diagonalization method for finite size clusters can be used, as demonstrated for the 1D EHM [25]. Here, the size L is related to the variable l, as
are taken into account in the analytical bosonization procedure. When the mutual interaction becomes stronger, such a treatment does not endorse quantitatively correct results, because the interaction processes far from the Fermi energy play important roles. One of the most evident example is the 8κF-Umklapp scattering leading to the CO state noted above. However, it is difficult to obtain the accurate values of the initial conditions by such analytical procedures. Instead, the exact diagonalization method for finite size clusters can be used, as demonstrated for the 1D EHM [25]. Here, the size L is related to the variable l, as  . The initial conditions obtained by such a method lead to the phase diagram which shows good agreement with that by the “purely” numerical methods.
. The initial conditions obtained by such a method lead to the phase diagram which shows good agreement with that by the “purely” numerical methods.3.2. Quasi One Dimension
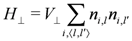
 is the electron number of the i-th site in the l-th chain,
is the electron number of the i-th site in the l-th chain,  denotes a pair of adjacent chains, and the strength of the interchain repulsive interaction is expressed by
denotes a pair of adjacent chains, and the strength of the interchain repulsive interaction is expressed by  . In the following, we apply the mean-field approximation to the interchain interaction (interchain mean-field approximation),
. In the following, we apply the mean-field approximation to the interchain interaction (interchain mean-field approximation), 
 [26,27] as well as the T-dependences of several quantities across
[26,27] as well as the T-dependences of several quantities across  [21] by the bosonization method. Such an interchain mean-field treatment has been applied to different Q1D systems and is known to be accurate as long as we have small interchain couplings [28,29].
[21] by the bosonization method. Such an interchain mean-field treatment has been applied to different Q1D systems and is known to be accurate as long as we have small interchain couplings [28,29].3.2.1. Transition Temperature
 , which is naturally expected to gain the energy for the positive
, which is naturally expected to gain the energy for the positive  . This leads our model to the effective 1D Hamiltonian given by,
. This leads our model to the effective 1D Hamiltonian given by, 
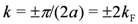 . As a result, the system effectively becomes half-filling, in which the
. As a result, the system effectively becomes half-filling, in which the  -Umklapp scattering appears. In the bosonized form, the Hamiltonian for the charge part (except the quadratic term of n) is written as follows,
-Umklapp scattering appears. In the bosonized form, the Hamiltonian for the charge part (except the quadratic term of n) is written as follows, 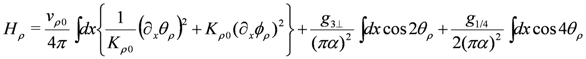
 -Umklapp scattering. Naturally, the bare parameters are functions of the CO order parameter n. Up to the first order of n,
-Umklapp scattering. Naturally, the bare parameters are functions of the CO order parameter n. Up to the first order of n,  is proportional to n, whereas the other parameters are the same as those in the absence of n. Therefore, the transition temperature
is proportional to n, whereas the other parameters are the same as those in the absence of n. Therefore, the transition temperature  is determined by the following equation,
is determined by the following equation, 
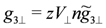 ,
, 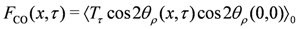 with
with  denoting the thermal average in terms of Equation (4), namely the Hamiltonian of the charge part in the absence of CO. The quantity
denoting the thermal average in terms of Equation (4), namely the Hamiltonian of the charge part in the absence of CO. The quantity  is written by the solution of RG Equation as
is written by the solution of RG Equation as 
 . With regard to the appearance of CO, the
. With regard to the appearance of CO, the  -plane can be separated into the three distinct regions, which is summarized in Figure 4 [26]. In the region (iii) where CO is found even in the absence of
-plane can be separated into the three distinct regions, which is summarized in Figure 4 [26]. In the region (iii) where CO is found even in the absence of  at T = 0, the infinitesimal
at T = 0, the infinitesimal  makes
makes  finite, as is naturally expected. There is another region in which
finite, as is naturally expected. There is another region in which  becomes finite under the infinitesimal
becomes finite under the infinitesimal  ; the region (ii) is specified by
; the region (ii) is specified by  and the metallic TLL state is realized in the strictly 1D case. In contrast, a finite amount of
and the metallic TLL state is realized in the strictly 1D case. In contrast, a finite amount of  is necessary for appearance of CO insulating state at finite T for the region (i) with
is necessary for appearance of CO insulating state at finite T for the region (i) with  . Thus, the parameter region where the finite
. Thus, the parameter region where the finite  appears under the infinitesimal interchain coupling in the Q1D system is different from that where the CO is realized in the 1D system.
appears under the infinitesimal interchain coupling in the Q1D system is different from that where the CO is realized in the 1D system.  in the figure corresponds to the solution
in the figure corresponds to the solution  of the RG equation, Equations (7,8).
of the RG equation, Equations (7,8).
 in the figure corresponds to the solution
in the figure corresponds to the solution  of the RG equation, Equations (7,8).
of the RG equation, Equations (7,8). 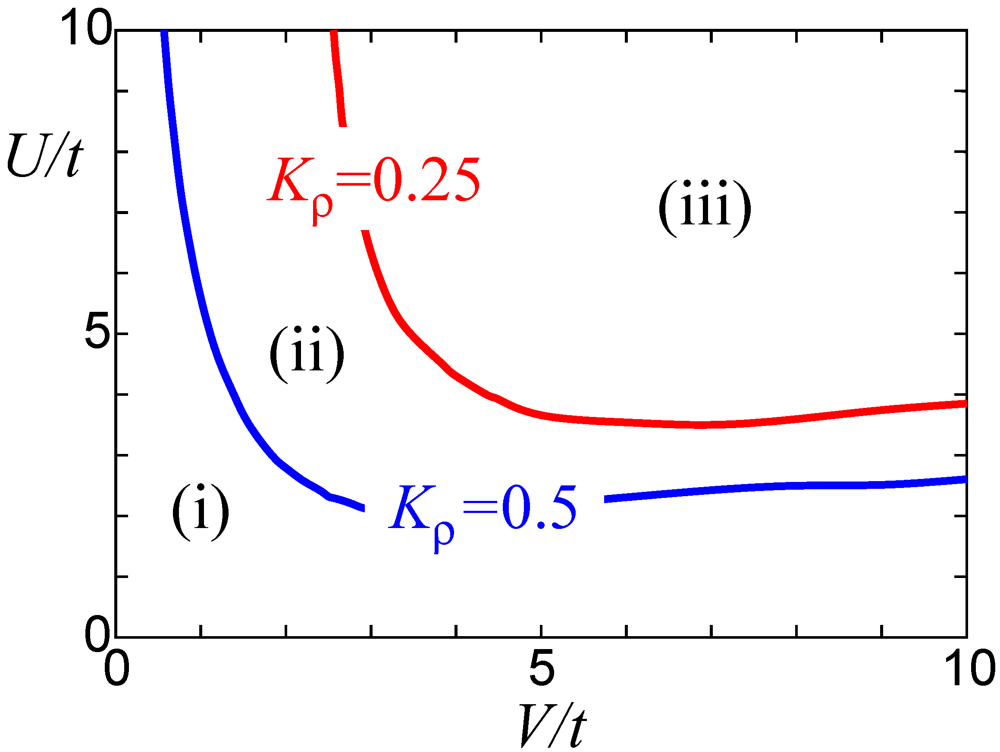
3.2.2. Quantities Across ![Crystals 02 00996 i090]()
 . This is similar to the 1D case as discussed in Section 3.1; we adopt numerical results as “inputs”.
. This is similar to the 1D case as discussed in Section 3.1; we adopt numerical results as “inputs”.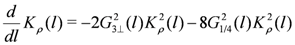


 is given by
is given by  . On the other hand, the spin part of the bosonized Hamiltonian is unchanged (the parameters will be affected). Namely, the Hamiltonian is given by Equation (5) and the RG equation corresponding to it is written by Equation (9) together with the constraint Equation (6) from the SU(2) symmetry.
. On the other hand, the spin part of the bosonized Hamiltonian is unchanged (the parameters will be affected). Namely, the Hamiltonian is given by Equation (5) and the RG equation corresponding to it is written by Equation (9) together with the constraint Equation (6) from the SU(2) symmetry.  and the resistivity
and the resistivity  together with the CO order parameter
together with the CO order parameter  , (a) for the region (ii) in Figure 4[
, (a) for the region (ii) in Figure 4[  ] and (b) for the region (iii) [
] and (b) for the region (iii) [ 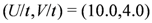 ] [21]. The solid curve shows the data for
] [21]. The solid curve shows the data for  , without charge order at finite T.
, without charge order at finite T. 
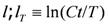 with C being an
with C being an  numerical constant. The initial conditions are obtained by the exact diagonalization method for small size clusters as is introduced above. It should be noted that the T-dependence of the CO order parameter
numerical constant. The initial conditions are obtained by the exact diagonalization method for small size clusters as is introduced above. It should be noted that the T-dependence of the CO order parameter  cannot be obtained within the bosonization and RG procedure because of the ambiguity in the relationship between n and the phase variables. Therefore we determine
cannot be obtained within the bosonization and RG procedure because of the ambiguity in the relationship between n and the phase variables. Therefore we determine  by the quantum Monte Carlo (QMC) method independently. The present procedure is explained in detail in [21]. The spin susceptibility
by the quantum Monte Carlo (QMC) method independently. The present procedure is explained in detail in [21]. The spin susceptibility  [30,31] and the resistivity
[30,31] and the resistivity  [32,33] are respectively written by the T dependent parameters as
[32,33] are respectively written by the T dependent parameters as 
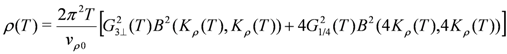
 is the spin susceptibility in the noninteracting case normalized as
is the spin susceptibility in the noninteracting case normalized as  and
and  . It should be noted that
. It should be noted that  is not obtained by the RG scheme; we use usual finite size scaling procedure. The spin susceptibility and the resistivity are shown as a function of T for the region (ii) [
is not obtained by the RG scheme; we use usual finite size scaling procedure. The spin susceptibility and the resistivity are shown as a function of T for the region (ii) [  ] and for the region (iii) [
] and for the region (iii) [ 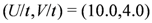 ] in Figure 5. The spin susceptibility is enhanced below
] in Figure 5. The spin susceptibility is enhanced below  without any steep singularity at
without any steep singularity at  . The enhancement originates from the suppression of spin velocity due to the gap formation at
. The enhancement originates from the suppression of spin velocity due to the gap formation at  . On the other hand, the resistivity shows a clear cusp at
. On the other hand, the resistivity shows a clear cusp at  . The abrupt change originates from the emergence of 4κF-Umklapp scattering due to the gap in the energy dispersion at
. The abrupt change originates from the emergence of 4κF-Umklapp scattering due to the gap in the energy dispersion at  . Just below
. Just below  , the resistivity shows a curve which is convex upward in the semi-log plot. The behavior reflects the rapid increase of the CO order parameter n for
, the resistivity shows a curve which is convex upward in the semi-log plot. The behavior reflects the rapid increase of the CO order parameter n for 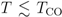 . At lower T, the curve turns convex downward showing an activation type behavior
. At lower T, the curve turns convex downward showing an activation type behavior 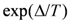 with the weak T-dependence of
with the weak T-dependence of  . We comment that the resistivity is difficult to calculate exactly by solely numerical simulations.
. We comment that the resistivity is difficult to calculate exactly by solely numerical simulations. decreases (increases) as a function of T for
decreases (increases) as a function of T for 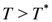 (
( 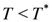 ), where
), where  is of the order of the effective spin-exchange coupling. The present results shown in Figure 5 express the case for
is of the order of the effective spin-exchange coupling. The present results shown in Figure 5 express the case for  . If smaller values of
. If smaller values of  are used, the other case of
are used, the other case of  would be possible. The former case may be observed in DI-DCNQI2Ag [34], whereas
would be possible. The former case may be observed in DI-DCNQI2Ag [34], whereas  of TMTTF2AsF6 seems to be lower than
of TMTTF2AsF6 seems to be lower than  [35].
[35].4. Numerical Study
 . The first term represents the intra-chain part along the stacking direction of molecules,
. The first term represents the intra-chain part along the stacking direction of molecules, 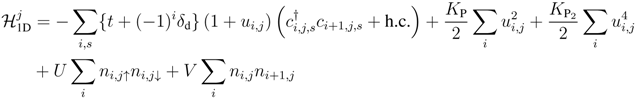
 denotes the intrinsic lattice dimerization (alternation in the transfer integrals),
denotes the intrinsic lattice dimerization (alternation in the transfer integrals),  the renormalized lattice displacement, and,
the renormalized lattice displacement, and,  and
and  the coupling constants of the elastic energy up to the fourth order. The second term in H is the inter-chain Coulomb repulsion,
the coupling constants of the elastic energy up to the fourth order. The second term in H is the inter-chain Coulomb repulsion, 
 , treated as classical variables, are taken into account by the adiabatic approximations, being optimized so as to minimize the free energy. The mean-field approximation is imposed to the inter-chain part,
, treated as classical variables, are taken into account by the adiabatic approximations, being optimized so as to minimize the free energy. The mean-field approximation is imposed to the inter-chain part,  as discussed in Section 3.2. We consider periodicities up to four sites, as seen from Figure 1. The model is then reduced to the effective 1D model, which we can treat with full quantum and thermal fluctuations by numerical methods. We have used quantum transfer matrix method to seek for the rather high-T region [36], while the QMC method can be applied to the whole T range even including low-T phases [38]. For the QMC simulation, we employ the stochastic-series-expansion (SSE) method [46,47,48], which is high-precision and less expensive in computational time so that we can use it in iterative calculations of self-consistent loop needed for the adiabatic and mean-field approximations.
as discussed in Section 3.2. We consider periodicities up to four sites, as seen from Figure 1. The model is then reduced to the effective 1D model, which we can treat with full quantum and thermal fluctuations by numerical methods. We have used quantum transfer matrix method to seek for the rather high-T region [36], while the QMC method can be applied to the whole T range even including low-T phases [38]. For the QMC simulation, we employ the stochastic-series-expansion (SSE) method [46,47,48], which is high-precision and less expensive in computational time so that we can use it in iterative calculations of self-consistent loop needed for the adiabatic and mean-field approximations.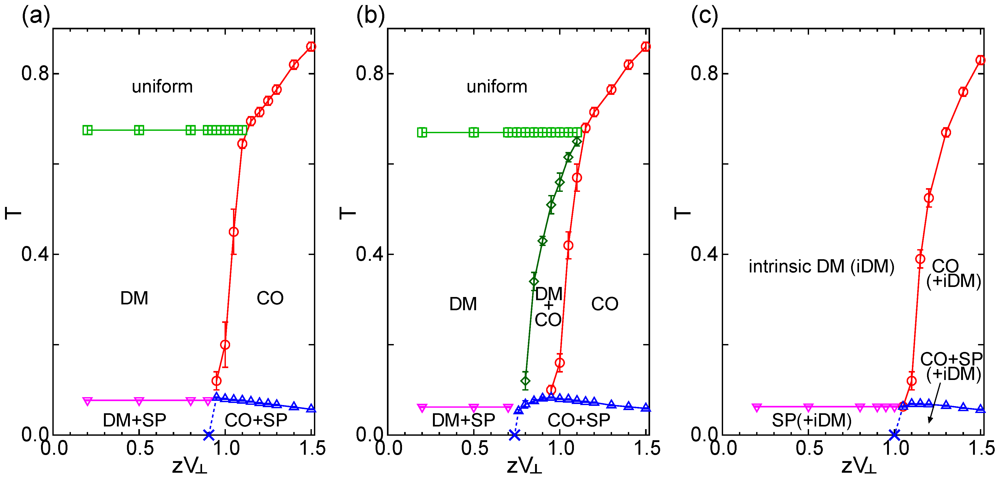
 ,
,  ,
,  ,
,  , and
, and  ; (a)–(c)
; (a)–(c)  ; (d)–(f)
; (d)–(f)  [38]. Open and closed circles represent results for N = 32 and 64, respectively. Statistical errors are smaller than the symbol sizes. Data shown by cross symbols at T=0 are obtained by the exact diagonalization (Lanczos) method for N = 12. The dashed line in (c) (f) shows a Curie–Weiss fit for
[38]. Open and closed circles represent results for N = 32 and 64, respectively. Statistical errors are smaller than the symbol sizes. Data shown by cross symbols at T=0 are obtained by the exact diagonalization (Lanczos) method for N = 12. The dashed line in (c) (f) shows a Curie–Weiss fit for  .
.
 ,
,  ,
,  ,
,  , and
, and  ; (a)–(c)
; (a)–(c)  ; (d)–(f)
; (d)–(f)  [38]. Open and closed circles represent results for N = 32 and 64, respectively. Statistical errors are smaller than the symbol sizes. Data shown by cross symbols at T=0 are obtained by the exact diagonalization (Lanczos) method for N = 12. The dashed line in (c) (f) shows a Curie–Weiss fit for
[38]. Open and closed circles represent results for N = 32 and 64, respectively. Statistical errors are smaller than the symbol sizes. Data shown by cross symbols at T=0 are obtained by the exact diagonalization (Lanczos) method for N = 12. The dashed line in (c) (f) shows a Curie–Weiss fit for  .
. 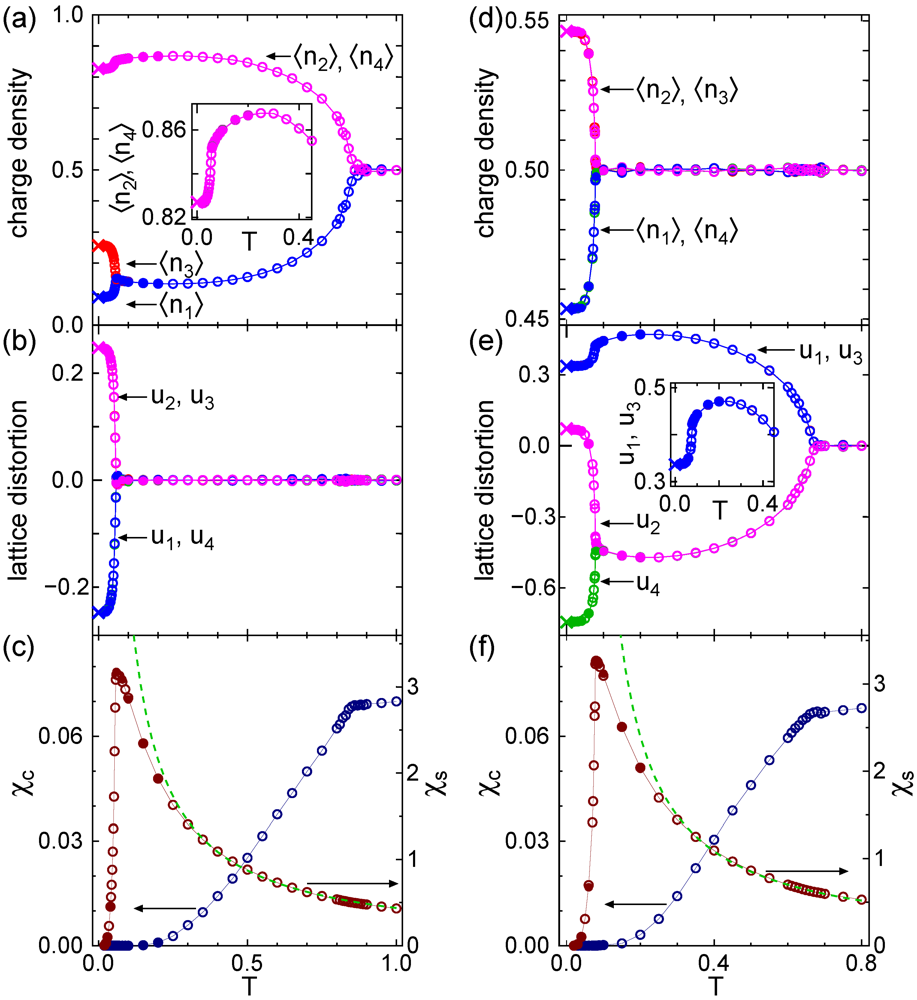
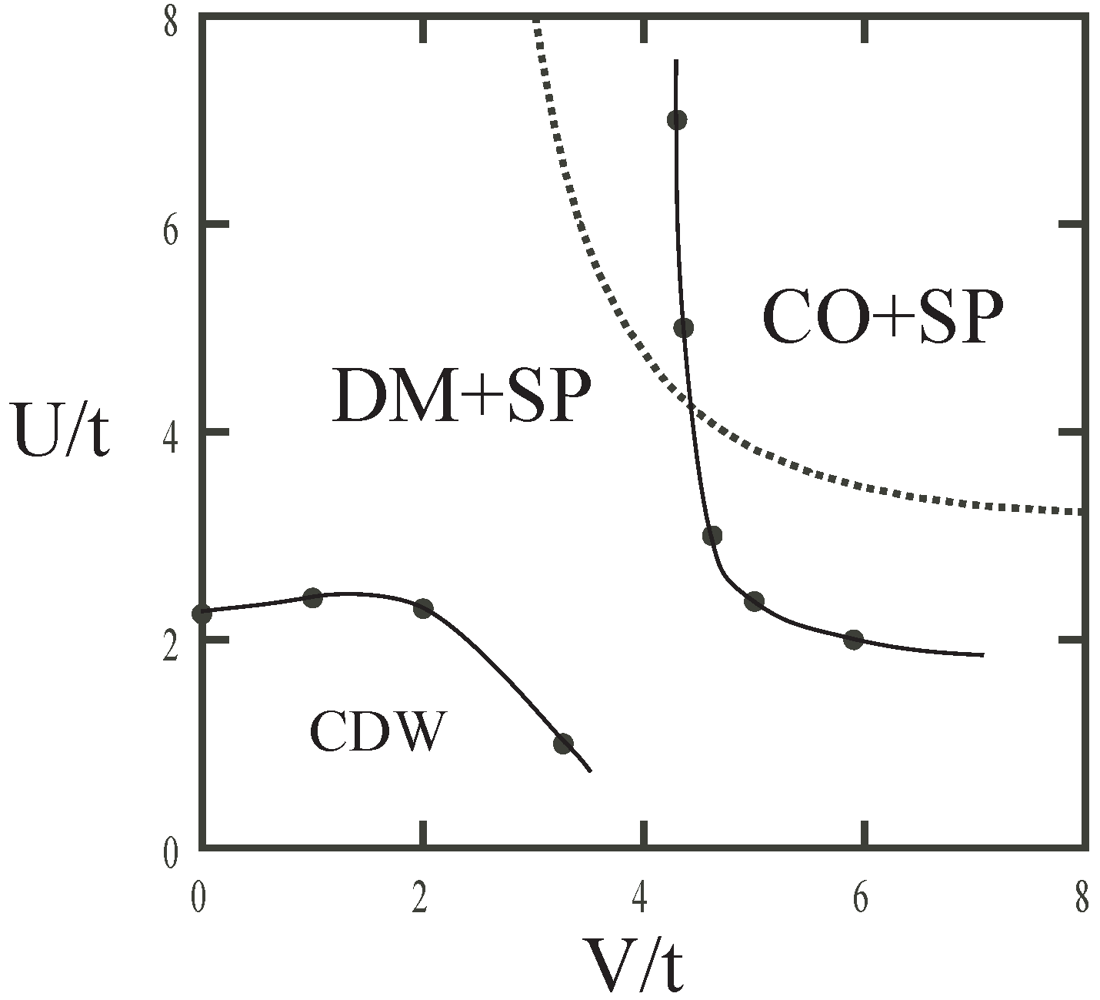
 phase diagrams shown in Figure 6, which are based on direct calculations of T dependences of the order parameters as shown in Figure 7. The global feature is that the uniform, i.e., paramagnetic metallic phase is driven to the insulating state which is DM or CO depending on the strength of
phase diagrams shown in Figure 6, which are based on direct calculations of T dependences of the order parameters as shown in Figure 7. The global feature is that the uniform, i.e., paramagnetic metallic phase is driven to the insulating state which is DM or CO depending on the strength of  when T is lowered. The boundary between DM and CO is very steep and likely of first order for
when T is lowered. The boundary between DM and CO is very steep and likely of first order for  ,
,  [Figure 6(a)]. On the other hand, when the anharmonic term in the elastic energy is finite (
[Figure 6(a)]. On the other hand, when the anharmonic term in the elastic energy is finite (  ), the coexistence phase of DM and CO emerges. This is analogous to the CO phase in the dimerized 1D EHM with electronic ferroelectricity, but different in the sense that the system is uniform at high-T, namely, the ferroelectricity is spontaneously generated [36]. In the case of the intrinsically dimerized lattice (
), the coexistence phase of DM and CO emerges. This is analogous to the CO phase in the dimerized 1D EHM with electronic ferroelectricity, but different in the sense that the system is uniform at high-T, namely, the ferroelectricity is spontaneously generated [36]. In the case of the intrinsically dimerized lattice (  ), the system always has finite dimerization and the transition at intermediate T occurs only to the CO state, which is continuous. Below these insulating phases, with further decreasing T, the system undergoes the SP transition showing tetramerization. The SP phases under DM and CO states are distinguishable [see Figure 1(e,f)] by the eight order parameters, though their T dependences of the charge and spin susceptibilities look alike as shown in Figure 7. We note that the paramagnetic insulating phases at intermediate region can not be obtained by simple one-body approximations such as the Hartree–Fock analysis, which usually needs magnetic ordering to open a charge gap.
), the system always has finite dimerization and the transition at intermediate T occurs only to the CO state, which is continuous. Below these insulating phases, with further decreasing T, the system undergoes the SP transition showing tetramerization. The SP phases under DM and CO states are distinguishable [see Figure 1(e,f)] by the eight order parameters, though their T dependences of the charge and spin susceptibilities look alike as shown in Figure 7. We note that the paramagnetic insulating phases at intermediate region can not be obtained by simple one-body approximations such as the Hartree–Fock analysis, which usually needs magnetic ordering to open a charge gap.5. Discussion
 220 K might be a complex CO, DM mixed state [Kakiuchi ~al.(2007)Kakiuchi, Wakabayashi, Sawa, Itou, and Kanoda, Seo and Motome(2009)].
220 K might be a complex CO, DM mixed state [Kakiuchi ~al.(2007)Kakiuchi, Wakabayashi, Sawa, Itou, and Kanoda, Seo and Motome(2009)]. correspond to the inverse of P; the effect of P acts strongly on transfer integrals, therefore the “effective” Coulomb interaction becomes smaller.
correspond to the inverse of P; the effect of P acts strongly on transfer integrals, therefore the “effective” Coulomb interaction becomes smaller. AsF6 and Br] [56,57]. On the other hand, materials known from early days such as the compounds showing SP transition, MEM-(TCNQ)2 and (BCPTTF)2X (X = PF6, AsF6) [58,59,60], might be interesting to revisit with renewed understandings. In (EDO-TTF)2PF6 [61], a strong first-order phase transition is observed which is not reproduced in theory. More systematic comparisons are required.
AsF6 and Br] [56,57]. On the other hand, materials known from early days such as the compounds showing SP transition, MEM-(TCNQ)2 and (BCPTTF)2X (X = PF6, AsF6) [58,59,60], might be interesting to revisit with renewed understandings. In (EDO-TTF)2PF6 [61], a strong first-order phase transition is observed which is not reproduced in theory. More systematic comparisons are required. lattice distortion), the transition from SP state without CO to that with CO occurs at the ground state with increasing V [62]. For
lattice distortion), the transition from SP state without CO to that with CO occurs at the ground state with increasing V [62]. For  with
with  indicating the phase boundary, the lattice distortion has a maximum value, whereas it is suppressed for
indicating the phase boundary, the lattice distortion has a maximum value, whereas it is suppressed for  . The transition temperature of the SP state shows similar behavior [Sugiura ~al.(2005)Sugiura, Tsuchiizu, and Suzumura], consistent with the QMC results [38]. On the other hand, the alternating lattice modulation leads to the insulating state with spontaneous lattice dimerization, and appears between the metallic state and the CO insulating state [63]. A unified framework including such lattice degree of freedom, on top of the Q1D theory in Section 3, would provide a complementary understanding of the numerical works on the equivalent model in Section 4.
. The transition temperature of the SP state shows similar behavior [Sugiura ~al.(2005)Sugiura, Tsuchiizu, and Suzumura], consistent with the QMC results [38]. On the other hand, the alternating lattice modulation leads to the insulating state with spontaneous lattice dimerization, and appears between the metallic state and the CO insulating state [63]. A unified framework including such lattice degree of freedom, on top of the Q1D theory in Section 3, would provide a complementary understanding of the numerical works on the equivalent model in Section 4.
 denotes the π-d interaction. We also include the AF super-exchange interaction,
denotes the π-d interaction. We also include the AF super-exchange interaction,  , between d spins, whose short-range correlation is experimentally indicated by the analysis of the magnetic susceptibilities [72]. We have elucidated that, at low-T range compared to
, between d spins, whose short-range correlation is experimentally indicated by the analysis of the magnetic susceptibilities [72]. We have elucidated that, at low-T range compared to  , corresponding to a situation where the Ising spins are frozen antiferromagnetically, the π-d coupling,
, corresponding to a situation where the Ising spins are frozen antiferromagnetically, the π-d coupling,  , considerably enhances the correlation of CO [71], consistent with the insulating character seen in the compound. Calculations at finite-T including the magnetic field effect might elucidate the spin-charge coupled behavior in this new type of molecular system [73]. Another interesting example might be (Per)2M(mnt)2 (M = Ni, Pd, Pt, Fe) [74] where localized spins on M(mnt)2 and itinerant carriers on quarter-filled perylene chains interact with each other; in fact, the magnetic response suggests strong coupling of the SP and CDW states [75].
, considerably enhances the correlation of CO [71], consistent with the insulating character seen in the compound. Calculations at finite-T including the magnetic field effect might elucidate the spin-charge coupled behavior in this new type of molecular system [73]. Another interesting example might be (Per)2M(mnt)2 (M = Ni, Pd, Pt, Fe) [74] where localized spins on M(mnt)2 and itinerant carriers on quarter-filled perylene chains interact with each other; in fact, the magnetic response suggests strong coupling of the SP and CDW states [75].6. Summary
 phase diagrams observed experimentally.
phase diagrams observed experimentally.Acknowledgments
References
- Seo, H.; Hotta, C.; Fukuyama, H. Toward systematic understanding of diversity of electronic properties in low-dimensional molecular solids. Chem. Rev. 2004, 104, 5005–5036. [Google Scholar] [CrossRef]
- Lebed, A.G. The Physics of Organic Superconductors and Conductors; Springer-Verlag: Heidelberg, Germany, 2008. [Google Scholar]
- Seo, H.; Merino, J.; Hideo, Y.; Masao, O. Theoretical Aspects of Charge Ordering in Molecular Conductors. J. Phys. Soc. Jpn. 2006, 75, 051009:1–051009:20. [Google Scholar]
- Brown, S.E.; Chaikin, P.M.; Naughton, M.J. La Tour des Sels de Bechgaard. In The Physics of Organic Superconductors and Conductors; Lebed, A.G., Ed.; Springer-Verlag: Berlin, Germany, 2008; pp. 357–512. [Google Scholar]
- Bourbonnais, C.; Jérome, D. Interacting electrons in quasi-one-dimensional organic superconductors. In The Physics of Organic Superconductors and Conductors; Lebed, A.G., Ed.; Springer-Verlag: Berlin, Germany, 2008. [Google Scholar]
- Hünig, S.; Herberth, E. N,N′-dicyanoquinonediimines (DCNQIs): versatile acceptors for organic conductors. Chem. Rev. 2004, 104, 5535–5563. [Google Scholar]
- Mori, T.; Kobayashi, A.; Sasaki, Y.; Kobayashi, H.; Saito, G.; Inokuchi, H. The Intermolecular Interaction of Tetrathiafulvalene and Bis(ethylenedithio)tetrathiafulvalene in Organic Metals. Calculation of Orbital Overlaps and Models of Energy-band Structures. Bull. Chem. Soc. Jpn. 1984, 57, 627–633. [Google Scholar] [CrossRef]
- Mila, F.; Penc, K. Model calculations for 1D correlated systems. J. Electron. Spectrosc. 2001, 117–118, 451–467. [Google Scholar] [CrossRef]
- Seo, H.; Fukuyama, H. Antiferromagnetic Phases of One-Dimensional Quarter-Filled Organic Conductors. J. Phys. Soc. Jpn. 1997, 66, 1249–1252. [Google Scholar] [CrossRef]
- Monceau, P.; Nad, F.; Brazovskii, S. Ferroelectric Mott-Hubbard Phase of Organic (TMTTF)2X Conductors. Phys. Rev. Lett. 2001, 86, 4080–4083. [Google Scholar] [CrossRef]
- Tsuchiizu, M.; Orignac, E. Ising transition in a one-dimensional quarter-filled electron system with dimerization. J. Phys. Chem. Solids. 2002, 63, 1459–1463. [Google Scholar] [CrossRef]
- Ishihara, S. Electronic Ferroelectricity and Frustration. J. Phys. Soc. Jpn. 2010, 79, 011010:1–011010:11. [Google Scholar]
- Emery, V.J.; Noguera, C. Critical properties of a spin-1/2 chain with competing interactions. Phys. Rev. Lett. 1988, 60, 631–634. [Google Scholar] [CrossRef]
- Kobayashi, N.; Ogata, M.; Yonemitsu, K. Coexistence of SDW and Purely-Electronic CDW in Quarter-Filled Organic Conductors. J. Phys. Soc. Jpn. 1998, 67, 1098–1101. [Google Scholar] [CrossRef]
- Kishigi, K.; Hasegawa, Y. Two Kinds of the Coexistent States in One-Dimensional Quarter-Filled Systems under Magnetic Fields and Temperatures. J. Phys. Soc. Jpn. 2000, 69, 3621–3628. [Google Scholar] [CrossRef]
- Tomio, Y.; Suzumura, Y. Quarter-filled spin density wave states with long-range Coulomb interaction. J. Phys. Chem. Solids 2001, 62, 431–434. [Google Scholar] [CrossRef]
- Kuwabara, M.; Seo, H.; Ogata, M. Coexistence of Charge Order and Spin-Peierls Lattice Distortion in One-Dimensional Organic Conductors. J. Phys. Soc. Jpn. 2003, 72, 225–228. [Google Scholar]
- Ung, K.C.; Mazumdar, S.; Toussaint, D. Metal-Insulator and Insulator-Insulator Transitions in the Quarter-Filled Band Organic Conductors. Phys. Rev. Lett. 1994, 73, 2603–2606. [Google Scholar] [CrossRef]
- Clay, R.; Mazumdar, S.; Campbell, D. Pattern of charge ordering in quasi-one-dimensional organic charge-transfer solids. Phys. Rev. B 2003, 67, 115121:1–115121:9. [Google Scholar]
- Fukuyama, H.; Takayama, H. Dynamical Properties of Quasi-One-Dimensional Conductors–Phase Hamiltonian Approach. In Electronic Properties of Inorganic Quasi-One-Dimensional Compounds; Monceau, P., Ed.; Reidel Publishing: Dordrecht, The Nertherlands, 1985; p. 41. [Google Scholar]
- Yoshioka, H.; Tsuchiizu, M.; Otsuka, Y.; Seo, H. Finite-Temperature Properties across the Charge Ordering Transition–Combined Bosonization, Renormalization Group, and Numerical Methods. J. Phys. Soc. Jpn. 2010, 79, 094714:1–094714:9. [Google Scholar]
- Yoshioka, H.; Tsuchiizu, M.; Suzumura, Y. Correlation Effects in a One-Dimensional Quarter-Filled Electron System with Repulsive Interactions. J. Phys. Soc. Jpn. 2000, 69, 651–654. [Google Scholar] [CrossRef]
- Yoshioka, H.; Tsuchiizu, M.; Suzumura, Y. Effects of Next-Nearest-Neighbor Repulsion on One-Dimensional Quarter-Filled Electron Systems. J. Phys. Soc. Jpn. 2001, 70, 762–773. [Google Scholar] [CrossRef]
- Tsuchiizu, M.; Yoshioka, H.; Suzumura, Y. Crossover from Quarter-Filling to Half-Filling in a One-Dimensional Electron System with a Dimerized and Quarter-Filled Band. J. Phys. Soc. Jpn. 2001, 70, 1460–1463. [Google Scholar] [CrossRef]
- Sano, K.; Ōno, Y. Critical behavior near the metal-insulator transition in the one-dimensional extended Hubbard model at quarter filling. Phys. Rev. B 2004, 70, 155102:1–155102:7. [Google Scholar]
- Yoshioka, H.; Tsuchiizu, M.; Seo, H. Finite-Temperature Charge-Ordering Transition and Fluctuation Effects in Quasi One-Dimensional Electron Systems at Quarter Filling. J. Phys. Soc. Jpn. 2006, 75, 063706:1–063706:5. [Google Scholar]
- Yoshioka, H.; Tsuchiizu, M.; Seo, H. Charge-Ordered State versus Dimer-Mott Insulator at Finite Temperatures. J. Phys. Soc. Jpn. 2007, 76, 103701:1–103701:4. [Google Scholar]
- Scalapino, D.; Imry, Y.; Pincus, P. Generalized Ginzburg-Landau theory of pseudo-one-dimensional systems. Phys. Rev. B 1975, 11, 2042–2048. [Google Scholar]
- Schulz, H.J. Dynamics of Coupled Quantum Spin Chains. Phys. Rev. Lett. 1996, 77, 2790–2793. [Google Scholar] [CrossRef]
- Nélisse, H.; Bourbonnais, C.; Touchette, H.; Vilk, Y.; Tremblay, A.M. Spin susceptibility of interacting electrons in one dimension: Luttinger liquid and lattice effects. Eur. Phys. J. B 1999, 12, 351–365. [Google Scholar] [CrossRef]
- Fuseya, Y.; Tsuchiizu, M.; Suzumura, Y.; Bourbonnais, C. Effect of Intersite Repulsions on Magnetic Susceptibility of One-Dimensional Electron Systems at Quarter Filling. J. Phys. Soc. Jpn. 2005, 74, 3159–3162. [Google Scholar] [CrossRef]
- Giamarchi, T. Umklapp process and resistivity in one-dimensional fermion systems. Phys. Rev. B 1991, 44, 2905–2913. [Google Scholar] [CrossRef]
- Giamarchi, T. Resistivity of a one-dimensional interacting quantum fluid. Phys. Rev. B 1992, 46, 342–349. [Google Scholar]
- Hiraki, K.; Kanoda, K. Electronic state of the organic salt (DI-DCNQI)2Ag, where DI-DCNQI is 2,5-diiodo- N,N′-dicyanoquinonediimine. Phys. Rev. B 1996, 54, R17276–R17279. [Google Scholar] [CrossRef]
- Zamborszky, F.; Yu, W.; Raas, W.; Brown, S.; Alavi, B.; Merlic, C.; Baur, A. Competition and coexistence of bond and charge orders in (TMTTF)2AsF6. Phys. Rev. B 2002, 66, 081103:1–081103:4. [Google Scholar]
- Seo, H.; Motome, Y.; Kato, T. Finite-Temperature Phase Transitions in Quasi-One-Dimensional Molecular Conductors. J. Phys. Soc. Jpn. 2007, 76, 013707:1–013707:4. [Google Scholar]
- Clay, R.; Hardikar, R.; Mazumdar, S. Temperature-driven transition from the Wigner crystal to the bond-charge-density wave in the quasi-one-dimensional quarter-filled band. Phys. Rev. B 2007, 76, 205118:1–205118:12. [Google Scholar]
- Otsuka, Y.; Seo, H.; Motome, Y.; Kato, T. Finite-Temperature Phase Diagram of Quasi-One-Dimensional Molecular Conductors: Quantum Monte Carlo Study. J. Phys. Soc. Jpn. 2008, 77, 113705:1–113705:4. [Google Scholar]
- Mila, F.; Zotos, X. Phase Diagram of the One-Dimensional Extended Hubbard Model at Quarter-Filling. Eur. Phys. Lett. 1993, 24, 133–138. [Google Scholar] [CrossRef]
- Penc, K.; Mila, F. Phase diagram of the one-dimensional extended Hubbard model with attractive and/or repulsive interactions at quarter filling. Phys. Rev. B 1994, 49, 9670–9678. [Google Scholar] [CrossRef]
- Hirsch, J.; Scalapino, D. 2pF and 4pF Instabilities in the One-Dimensional Electron Gas. Phys. Rev. Lett. 1983, 50, 1168–1171. [Google Scholar] [CrossRef]
- Hirsch, J.; Scalapino, D. 2pF and 4pF instabilities in a one-quarter-filled-band Hubbard model. Phys. Rev. B 1983, 27, 7169–7185. [Google Scholar] [CrossRef]
- Hirsch, J.; Scalapino, D. 2pF and 4pF instabilities in the one-dimensional Hubbard model. Phys. Rev. B 1984, 29, 5554–5561. [Google Scholar] [CrossRef]
- Hirsch, J. Charge-Density-Wave to Spin-Density-Wave Transition in the Extended Hubbard Model. Phys. Rev. Lett. 1984, 53, 2327–2330. [Google Scholar] [CrossRef]
- Ejima, S.; Gebhard, F.; Nishimoto, S. Tomonaga-Luttinger parameters for doped Mott insulators. Euro. Phys. Lett. 2005, 70, 492–498. [Google Scholar] [CrossRef]
- Sandvik, A.W.; Kurkijärvi, J. Quantum Monte Carlo simulation method for spin systems. Phys. Rev. B 1991, 43, 5950–5961. [Google Scholar]
- Sandvik, A.W. A generalization of Handscomb’s quantum Monte Carlo scheme-application to the 1D Hubbard model. J. Phys. A 1992, 25, 3667–3682. [Google Scholar] [CrossRef]
- Sandvik, A.W. Stochastic series expansion method with operator-loop update. Phys. Rev. B 1999, 59, R14157–R14160. [Google Scholar] [CrossRef]
- Pouget, J.P. Bond and charge ordering in low-dimensional organic conductors. Physica B 2012, 407, 1762–1770. [Google Scholar] [CrossRef]
- Hiraki, K.; Kanoda, K. Wigner Crystal Type of Charge Ordering in an Organic Conductor with a Quarter-Filled Band: (DI-DCNQI)2Ag. Phys. Rev. Lett. 1998, 80, 4737–4740. [Google Scholar] [CrossRef]
- Wigner Crystallization in (DI-DCNQI)2AgDetected by Synchrotron Radiation X-Ray Diffraction. Phys. Rev. Lett. 2007, 98, 066402:1–066402:4.
- Seo, H.; Motome, Y. Spiral Charge Frustration in the Molecular Conductor (DI-DCNQI)2Ag. Phys. Rev. Lett. 2009, 102, 196403:1–196403:4. [Google Scholar]
- Chow, D.; Zamborszky, F.; Alavi, B.; Tantillo, D.; Baur, A.; Merlic, C.; Brown, S. Charge Ordering in the TMTTF Family of Molecular Conductors. Phys. Rev. Lett. 2000, 85, 1698–1701. [Google Scholar] [CrossRef]
- Yu, W.; Zhang, F.; Zamborszky, F.; Alavi, B.; Baur, A.; Merlic, C.; Brown, S. Electron-lattice coupling and broken symmetries of the molecular salt (TMTTF)2SbF6. Phys. Rev. B 2004, 70, 121101:1–121101:4. [Google Scholar]
- Foury-Leylekian, P.; Auban-Senzier, P.; Coulon, C.; Jeannin, O.; Fourmigué, M.; Pasquier, C.; Pouget, J.P. Phase diagram of the correlated quarter-filled-band organic salt series (O-DMTTF)2X (X = Cl, Br, I). Phys. Rev. B 2011, 84, 195134:1–195134:17. [Google Scholar]
- Auban-Senzier, P.; Pasquier, C.; Jérome, D.; Suh, S.; Brown, S.; Mézière, C.; Batail, P. Phase Diagram of Quarter-Filled Band Organic Salts [EDT-TTF-CONMe2]2X, X = AsF2 and Br. Phys. Rev. Lett. 2009, 102, 257001:1–257001:4. [Google Scholar]
- Zorina, L.; Simonov, S.; Mézière, C.; Canadel, E.; Suh, S.; Brown, S.E.; Foury-Leylekian, P.; Fertey, P.; Pouget, J.P.; Batail, P. Charge ordering, symmetry and electronic structure issues and Wigner crystal structure of the quarter-filled band Mott insulators and high pressure metals
-(EDT-TTF-CONMe2)2X, X = Br and AsF6. J. Mater. Chem. 2009, 19, 6980–6994. [Google Scholar]
- Huizinga, S.; Kommandeur, J.; Sawatzky, G.A.; Thole, B.T.; Kopinga, K.; de Jonge, W.J.M.; Roos, J. Spin-Peierls transition in N-methyl-N-ethyl-morpholinium-ditetracyanoquinodimethanide [MEM-(TCNQ)2]. Phys. Rev. B 1979, 19, 4723–4732. [Google Scholar] [CrossRef]
- Liu, Q.; Ravy, S.; Pouget, J.P. Structural fluctuations and spin-peierls transitions revisited. Synth. Met. 1993, 56, 1840–1845. [Google Scholar] [CrossRef]
- Dumoulin, B.; Bourbonnais, C.; Ravy, S.; Pouget, J.P.; Coulon, C. Fluctuation Effects in Low-Dimensional Spin-Peierls Systems: Theory and Experiment. Phys. Rev. Lett. 1996, 76, 1360–1363. [Google Scholar] [CrossRef]
- Ota, A.; Yamochi, H.; Saito, G. A novel metal-insulator phase transition observed in (EDO-TTF)2PF6. J. Mater. Chem. 2002, 12, 2600–2602. [Google Scholar] [CrossRef]
- Sugiura, M.; Suzumura, Y. Competition of Dimerization and Charge Ordering in the Spin-Peierls State of Organic Conductors. J. Phys. Soc. Jpn. 2003, 72, 1458–1468. [Google Scholar] [CrossRef]
- Sugiura, M.; Tsuchiizu, M.; Suzumura, Y. Interplay of Lattice Dimerization and Charge Ordering in One-Dimensional Quarter-Filled Electron Systems. J. Phys. Soc. Jpn. 2004, 73, 2487–2493. [Google Scholar] [CrossRef]
- Sugiura, M.; Tsuchiizu, M.; Suzumura, Y. Spin-Peierls Transition Temperature in Quarter-Filled Organic Conductors. J. Phys. Soc. Jpn. 2005, 74, 983–987. [Google Scholar] [CrossRef]
- Yoshimi, K.; Seo, H.; Ishibashi, S.; Brown, S. Tuning the Magnetic Dimensionality by Charge Ordering in the Molecular TMTTF Salts. Phys. Rev. Lett. 2012, 108, 096402:1–096402:5. [Google Scholar]
- Yoshimi, K.; Seo, H.; Ishibashi, S.; Brown, S.E. Spin frustration, charge ordering, and enhanced antiferromagnetism in TMTTF2SbF6. Physica B 2012, 407, 1783–1786. [Google Scholar]
- Matsuda, M.; Naito, T.; Inabe, T.; Hanasaki, N.; Tajima, H.; Otsuka, T.; Awaga, K.; Narymbetov, B.; Kobayashi, H. A one-dimensional macrocyclic π-ligand conductor carrying a magnetic center.Structure and electrical, optical and magnetic properties of TPP[Fe(Pc)(CN)2]2 {TPP = tetraphenylphosphonium and [Fe(Pc)(CN)2] = dicyano(phthalocyaninato)iron(iii)}. J. Mater. Chem. 2000, 10, 631–636. [Google Scholar] [CrossRef]
- Hanasaki, N.; Matsuda, M.; Tajima, H.; Ohmichi, E.; Osada, T.; Naito, T.; Inabe, T. Giant Negative Magnetoresistance Reflecting Molecular Symmetry in Dicyano(phthalocyaninato)iron Compounds. J. Phys. Soc. Jpn. 2006, 75, 033703:1–033703:4. [Google Scholar]
- Hotta, C.; Ogata, M.; Fukuyama, H. Interaction of the Ground State of Quarter-Filled One-Dimensional Strongly Correlated Electronic System with Localized Spins. Phys. Rev. Lett. 2005, 95, 216402:1–216402:4. [Google Scholar]
- Hotta, C. Interplay of strongly correlated electrons and localized Ising moments in one dimension. Phys. Rev. B 2010, 81, 245104:1–245104:9. [Google Scholar]
- Otsuka, Y.; Seo, H.; Motome, Y. Charge ordering due to π-d coupling in one-dimensional system. Physica B 2010, 405, S317–S320. [Google Scholar]
- Tajima, H.; Yoshida, G.; Matsuda, M.; Hanasaki, N.; Naito, T.; Inabe, T. Magnetic torque and heat capacity measurements on TPP[Fe(Pc)(CN)2]2. Phys. Rev. B 2008, 78, 064424:1–064424:8. [Google Scholar]
- Otsuka, Y.; Seo, H.; Motome, Y. Magnetic field effect on one-dimensional quarter-filled extended Hubbard model. 2012. in preparation. [Google Scholar]
- Gama, V.; Henriques, R.T.; Bonfait, G.; Almeida, M.; Ravy, S.; Pouget, J.P.; Alcácer, L. The Interplay Between Conduction Electrons and Chains of Localised Spins in The Molecular Metals (Per)2M(mnt)2, M = Au, Pt, Pd, Ni, Cu, Co and Fe. Mol. Cryst. Liq. Cryst. 1993, 234, 171–178. [Google Scholar] [CrossRef]
- Green, E.; Brooks, J.; Kuhns, P.; Reyes, A.; Lumata, L.; Almeida, M.; Matos, M.; Henriques, R.; Wright, J.; Brown, S. Interaction of magnetic field-dependent Peierls and spin-Peierls ground states in (Per)2[Pt(mnt)2]. Phys. Rev. B 2011, 84. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yoshioka, H.; Otsuka, Y.; Seo, H. Theoretical Studies on Phase Transitions in Quasi-One-Dimensional Molecular Conductors. Crystals 2012, 2, 996-1016. https://doi.org/10.3390/cryst2030996
Yoshioka H, Otsuka Y, Seo H. Theoretical Studies on Phase Transitions in Quasi-One-Dimensional Molecular Conductors. Crystals. 2012; 2(3):996-1016. https://doi.org/10.3390/cryst2030996
Chicago/Turabian StyleYoshioka, Hideo, Yuichi Otsuka, and Hitoshi Seo. 2012. "Theoretical Studies on Phase Transitions in Quasi-One-Dimensional Molecular Conductors" Crystals 2, no. 3: 996-1016. https://doi.org/10.3390/cryst2030996