Effect of Intra- and Intermolecular Interactions on the Properties of para-Substituted Nitrobenzene Derivatives

Abstract

To study the influence of intra- and intermolecular interactions on properties of the nitro group in para-substituted nitrobenzene derivatives, two sources of data were used: (i) Cambridge Structural Database and (ii) quantum chemistry modeling. In the latter case, “pure” intramolecular interactions were simulated by gradual rotation of the nitro group in para-nitroaniline, whereas H-bond formation at the amino group allowed the intermolecular interactions to be accounted for. BLYP functional with dispersion correction and TZ2P basis set (ADF program) were used to perform all calculations. It was found that properties of the nitro group dramatically depend on both its orientation with respect to the benzene ring as well as on the substituent in the para-position. The nitro group lies in the plane of the benzene ring for only a small number of molecules, whereas the mean value of the twist angle is 7.3 deg, mostly due to intermolecular interactions in the crystals. This distortion from planarity and the nature of para-substituent influence the aromaticity of the ring (described by HOMA index) and properties of the nitro group due to electronic effects. The results obtained by QM calculations fully coincide with observations found for the data set of crystal structures.

1. Introduction

The nitro group is one of the most frequently encountered substituents in organic chemistry [1]. In the Cambridge Structural Database (CSD) [2], 38406 crystal structures of chemical compounds containing the NO₂ group are reported, whereas considering more precise measurements—the numbers are 36030 and 20662 with R-factor equal to or less than 0.10 and 0.05, respectively. This particular interest in nitro-compounds is due to their very important properties. The nitro group is one of the most typical electron-accepting substituents with the substituent constant σ_p = 0.78 [3]. Recently, we analyzed the effect of the nitro group with Kohn-Sham molecular orbital theory to separate inductive and resonance effects [4]. Its electron-accepting power (EAP) originates via two mechanisms. There is a strong inductive activity due to a combined effect of three electronegative atoms (the group electronegativity ${\chi }_{N{O}_2}$ is equal to 4.00 for coplanar and 4.19 for perpendicular orientation with respect to the benzene ring [5]). Furthermore, the two electronegative oxygen atoms cause an electron deficiency on the nitrogen atom and hence the nitro group may also act as a strong π-electron acceptor; the resonance power of the nitro group becomes significant when the electron-donating substituent is present in the para-position, as documented by the σ_p⁻ constants being equal to 1.27 [3,6]. It is important to note that rotation of this group around the C-N bond with respect to the benzene ring decreases the efficiency of the through-resonance interactions and the substituent constant σ_p⁻ reduces by almost a half, from 1.27 for planar conformation to 0.72 for the perpendicular one [7].

Understanding of structural aspects of this group is very important because nitro-compounds belong to very important chemicals applied in medicinal and pharmaceutical chemistry [8], used as explosives [9,10] and fertilizers [11] as well as in other fields of chemistry [1].

Deformations in geometric and electronic structure of the nitro group as well as the deviation from coplanarity with the aromatic moiety are of great importance, since these effects may change significantly both the nature of the group as well as the effect on the substituted system. To study these effects we have chosen para-substituted nitrobenzene derivatives, since one can expect in these systems a substantial variability of aforementioned properties [12]. To this end, we have undertaken detailed studies on: (i) deformations of para-substituted nitrobenzene derivatives found in the solid state; (ii) controlled deformations carried out by rotation of the nitro group in para-nitroaniline (PNA), Scheme 1; (iii) the influence of intermolecular hydrogen (H-) bonding of the amino group on properties of the nitro group in PNA.

2. Experimental and Computational Section

Geometries of the studied derivatives were retrieved from CSD [2] with the following restrictions:

(1)

The search was performed for organic compounds containing para-substituted nitrobenzene fragment(s).

(2)

The search was restricted to structure measurements with the reported mean estimated standard deviation (esd) for the CC bond ≤ 0.005 Å, with 3D coordinates determined, not disordered, without errors, polymeric, ions and powder structures, and with R ≤ 0.05. Sometimes solvent molecules were also present in the crystal latice.

For the analysis of the retrieved data Vista v2.1 [13] was used.

All quantum chemical calculations were carried out using the Amsterdam Density Functional (ADF) program [14,15]. Geometries and energies were calculated using the generalized gradient approximation (GGA) with BLYP functional [16,17] and DFT-D3 correction [18] as the best correction for non-covalent interactions [19]. The MOs were expanded in uncontracted sets of Slater type orbitals (STOs) containing diffuse functions with two sets of polarization functions [20] (TZ2P).

To investigate the effect of the intermolecular H-bond on the NO₂ group properties, two types of H-bonded complexes were studied: (i) with neutral and (ii) charge-assisted hydrogen bonds (Scheme 2). In the first case, N···HF and H···FH interactions were considered. In the second one, N⁻···HF and NH···F⁻ interactions were taken into account.

The total energy of the H-bond consists of two major components: the deformation (ΔE_def) and interaction (ΔE_int) energies.

ΔE_tot = ΔE_def + ΔE_int

(1)

The first term represents the amount of energy required to deform the equilibrium geometries (E′) of two fragments into their geometries in the complex (E).

ΔE_def = (E_A − E_A′) + (E_B − E_B′)

(2)

The second term of Equation (1) corresponds to the actual energy change when the two distorted fragments are combined in the final structure. According to Ziegler-Rauk method [21,22,23], ΔE_int can be decomposed into a number of chemically meaningful components representing different steps toward the formation of a complex from two selected fragments:

ΔE_int = ΔV_elstat + ΔE_Pauli + ΔE_oi + ΔE_disp

(3)

The term ΔV_elstat corresponds to the classical electrostatic interaction between the unperturbed charge distributions of the distorted fragments and is usually attractive. The Pauli repulsion energy, ΔE_Pauli, comprises the destabilizing interactions between occupied orbitals and is responsible for the steric repulsion. The orbital interaction energy, ΔE_oi, represents the donor–acceptor interactions between the occupied molecular orbitals on one fragment with the unoccupied molecular orbitals of the other fragment, as well as the mixing of occupied and virtual orbitals within the same fragment (intrafragment polarization). The term ΔE_disp accounts for the dispersion corrections as introduced by Grimme and co-workers [18,24,25].

The changes in the H-bond strength were achieved by elongation of the distance between N and F atoms from equilibrium to 4.0 Å with step of 0.3 Å. In all H-bonded complexes a linearity of N···H···F atoms was imposed (to maintain the same settings during the modeling of the H-bonded complexes). It is well known that this angle is usually close to 180 deg for strong hydrogen bonds [26,27]. The calculated differences in interaction energies for linear and bent bonding in equilibrium complexes are less than 0.1 kcal/mol. To estimate the effect of para-substitution on the benzene ring the same types of H-bonded complexes for aniline and p-nitroaniline were studied.

The electron-accepting properties of the nitro group were modified with the rotation of this group from coplanar to perpendicular orientation with respect to the benzene ring. This angle φ (0 ≤ φ ≤ 90) was changed with step of 10 and 30 degrees for intra- and intermolecular interactions, respectively (the NH₂ group remains fixed).

The electron density distribution was analyzed using the Voronoi deformation density (VDD) method [28,29], which is an independent basis set and yields chemically meaningful atomic charges.

The charge of the substituent active region, cSAR, [30,31,32] was used to characterize the substituent. It is defined as the sum of atomic charges of the substituent X and the ipso carbon atom:

cSAR(X) = q(X) + q(C_ipso)

(4)

π-Electron delocalization [33] of the phenyl ring was estimated applying the aromaticity index HOMA (Harmonic Oscillator Model of Aromaticity) [34,35] which reads:

$$\text{HOMA}=1-\frac{1}{n}{\displaystyle \sum _{i=1}^n\alpha (R_{opt}-{R_i)}^2}$$

(5)

where n is the number of CC bonds taken into account when carrying out the summation, α is a normalization constant (α_CC = 257.7) fixed to give HOMA = 0 for a model nonaromatic system and HOMA = 1 for the system with all bonds equal to the optimal value R_opt,CC = 1.388 Å, and R_i denotes the computed bond lengths.

3. Results and Discussion

Three sources of molecular geometry deformations in para-substituted nitrobenzene derivatives are discussed: (i) substituents; (ii) intermolecular interactions when the molecule is subjected to chemical reactions, e.g., by protonation process; and (iii) interactions in crystals. The first two cases are relatively simple. The reason for the perturbation is known and its magnitude may be qualitatively estimated by applying the standard rules used for evaluation of substituent effects or by estimation of the rate/equilibrium constants or H-bond energy. In the third case, deformation of every symmetrically independent molecule in the elementary crystal cell may be different even for the same crystal. Consequently, for a data set taken for various para-substituted nitrobenzene derivatives in the crystalline state, the source of the structural deformation is the so-called crystal packing forces and hence presents a collection of chaotically acting reasons.

On these grounds our discussion is carried out in two parts. The first one deals with deformations observed for various para-substituted nitrobenzene derivatives in the crystalline state taken from CSD as a source of information. Then the application of the quantum chemical modeling (QM) enables us to enlighten the experimental data with some controlled quantitative descriptions.

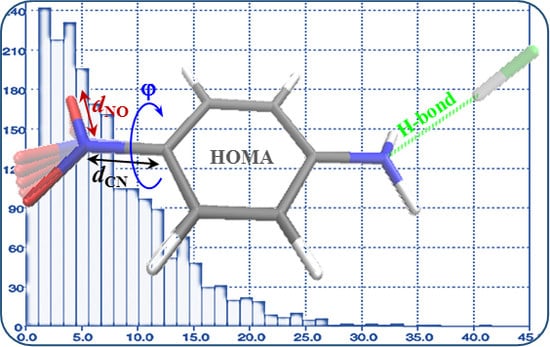
3.1. Analyses of Molecular Geometry Deformations Based on the Cambridge Structural Database

Two kinds of deformations are considered: (i) changes in geometry of the nitro groups, as ONO angle and NO bond lengths; and (ii) changes in the adjacent parts, as the linking the CN bond length as well as the dihedral angle between the C-NO₂ and phenyl ring planes. Figure 1, Figure 2, Figure 3 and Figure 4 represent the above-mentioned characteristics obtained from CSD (1750 hits with 2071 structural studied fragments) for para-substituted nitrobenzene derivatives; phenyl ring aromaticity is shown in Figure 5. All these histograms were prepared using Vista v2.1 [13].

When the ONO angle is considered (Figure 1), the distribution is very symmetrical with a mean value of 123.446 deg. The value of the angle greater than 120 deg, as expected for sp² hybridization, may result from repulsion forces due to the interactions between two N(+)O(–) bond dipoles. Low temperature (104K) X-ray determination found this ONO angle equal to 123.2(1) deg [36], whereas 125.3(2) deg from gas phase electron diffraction determination [37] and 124.35(1) deg from microwave determination [37] were determined. It seems probable that the greater angles estimated for free molecules are due to there being more space around the nitro group than in the crystal state.

A similar analysis was carried out for the NO bond lengths; the difference between them, d(N1O2)-d(N1O3) (labeling of atoms in Scheme 1), is presented by histogram (Figure 2). The maximum value of these differences amounts to 0.134 Å, whereas the range in their variability is equal to 0.193 Å for the retrieved data set. The observed changes seem to be mostly associated with intermolecular interactions between the neighboring molecules, the lengths of both NO bonds can be unequal depending on the surroundings (Figure 3).

The distribution of the dihedral angle between the NO₂ group and phenyl ring planes is illustrated in the histogram in Figure 4. The maximum twist (observed for one structure, MAGTIZ) is 41.06 deg and, surprisingly, the smallest twist of the range 0–1 deg was found for ~120 hits. That is only for ~6% of all cases! This means that coplanarity of the nitro group with the aromatic ring can be very easily broken. This is understandable if one takes into account that even in so weakly interacting molecules as those in crystals of nitrobenzene a very weak O···H-C bond with a neighboring nitrobenzene molecule causes a dihedral angle of 1.7 deg [36]. Additionally, for both oxygen atoms of the nitro group participating in a similar number of intermolecular interactions, the dihedral angle is close to the one found for the mean value; in the case of para-dinitrobenzene it amounts to ca. 10 deg [38,39]. However, if due to intermolecular interactions, the two oxygen atoms significantly differ from each other, then the nitro group becomes much more twisted. Good illustrations are 1,3-thiazolium-5-thiolate derivatives: 4-(4-methoxyphenyl)-3-methyl-2-(4-nitrophenyl)-1,3-thiazolium-5-thiolate (MAGTIZ) and 2-(4-methoxyphenyl)-3-methyl-4-(4-nitrophenyl)-1,3-thiazolium-5-thiolate (MAGTEV) [40], see Figure 3. In the first case the maximum twist angle is observed, whereas for MAGTEV the angle amounts to 6.22 deg.

Changes in CN bond lengths are worthy of deeper analysis because of the large range in their variations, between 1.410 and 1.535 Å. It is well known that the lengths of the exocyclic CN or CC bonds in para-substituted benzene derivatives are good estimators of the aromatic character of the ring described by the HOMA index [41]. Shortening of this bond indicates a large contribution of the quinoid structure of the ring and hence a decrease in its aromatic character. Distribution of the CN bond lengths, shown in Figure 5, suggests a significant variability in aromaticity of para-substituted nitrobenzene derivatives. The length of the CN bond in nitrobenzene is 1.467 Å [36], which is very close to the mean value (1.469 Å). Thus, one can assume that the great range of CN bond lengths results from the intramolecular interactions (electronic effects) between the electron-accepting NO₂ group and counter-substituents located in the para-position. Moreover, it illustrates indirectly the changes in aromaticity due to these influences.

The obtained results for the retrieved data set (Figure 6) confirm this suggestion, showing the range of HOMA values from 0.826 and in a more regular way between 0.88 and 1.00. A relatively small decrease in the aromatic character of the phenyl ring as an effect of the substituent is in line with more detailed studies based on QM modeling of this problem [42,43].

It is important to note that histograms of the data sets for para-substituted nitrobenzene derivatives and measurements with R ≤ 0.075 or 0.1 are characterized by similar shapes and statistical parameters as shown above; only a slightly greater range of variability of the studied parameters and their esds were observed.

Therefore, the aromatic character of the ring in para-substituted nitrobenzene derivatives depends on at least two factors: (i) the twist around the CN bond and (ii) the above-mentioned substituent effect. Figure 7 illustrates a direct dependence of the HOMA index on the angle between planes for NO₂ and carbon atoms of the benzene ring. Taking into account that in the HOMA formula (Equation (5)), differences between the d_opt and the measured bond lengths are considered, with relatively low accuracy of estimation of the latter, then the obtained HOMA values are biased with a large error. Despite this disadvantage, Figure 7 shows some regularity. The lowest values of the HOMA increase with an increase in the dihedral angle. This means that in this direction the possible contribution of the quinoid form decreases and hence the aromatic character increases.

3.2. Quantum Chemistry Modeling

For clarity, this section is divided into two parts. The first one deals with consequences of “pure” intramolecular interactions where changes are modeled by gradual rotation of the nitro group in p-nitroaniline. The second part presents effects of intermolecular interactions that are realized by involving the amino group in H-bond formation. The main object of the study, p-nitroaniline (PNA), is presented in Scheme 1 (including numbering of atoms).

3.2.1. Consequences of the Nitro Group Rotation in p-Nitroaniline

PNA can be considered as a derivative of aniline, nitrobenzene, and benzene. To visualize how the substitution of the benzene ring affects the distribution of charges, we computed the VDD charges of the atoms in benzene (see Figure 8) for the nitro and amino derivatives, and finally in PNA with the planar and perpendicular conformation (PNA90) of the nitro group. To compare the substituent effects, C_s symmetry for all systems has been imposed (energy differences between planar and non-planar conformations of the amino group in aniline and PNA are equal to 0.75 and 0.14 kcal/mol, respectively).

For nitrobenzene derivatives presented in Figure 8, the charge at the nitrogen atom of the nitro group changes less (0.010 e) than at the oxygen atoms (0.028 e). Similar modifications are observed for the amino group of aniline derivatives, where the change in the nitrogen atom charge is smaller (0.017 e) than in hydrogen atoms (0.020 e). In the perpendicular PNA conformation, the acidity of hydrogens in the amino group is clearly less than in a coplanar one (with charges of 0.139 e and 0.149 e, respectively), but in the unsubstituted aniline the H atoms are still less acidic (0.129 e). Conversely, the basicity of the nitrogen atom in the amino group is the largest in aniline (q(N) = −0.185 e), and the smallest one in the coplanar conformation of PNA (q(N) = −0.168 e).

The use of the idea of cSAR(X) enables a deeper look at the substituent effects [44,45]. The application of this concept makes the comparison of group characteristics available and easier to understand.

Table 1. cSAR(X) values (in electrons) for substituents in ortho-, meta- and para- positions of benzene and its nitro and amino derivatives ¹.

Molecule	cSAR(H) (ortho-, meta- and para-Positions)	cSAR(NO2)	cSAR(NH2)
benzene	0.0	-	-
nitrobenzene	0.033, 0.022, 0.036	−0.146	-
aniline	−0.044, −0.001, −0.039	-	0.129
p-nitroaniline 0	−0.017, 0.032, -	−0.219	0.198
p-nitroaniline 90	−0.019, 0.029, -	−0.170	0.156
p-nitroanilide anion	−0.063/−0.085, 2 −0.026, -	−0.509	-
p-nitroanilide anion 90	−0.080/−0.104, 2 −0.045, -	−0.348	-

Notes: ¹ The cSAR(NO₂) and cSAR(NH₂) values taken from [44]; ² Two numbers correspond to different ortho- positions in anions; second number characterizes the position closer to H from NH⁻.

presents the cSAR(X) data for all groups (nitro, amino and CH fragments) in the studied nitro and amino benzene derivatives.

The changes in cSAR(X) values as a result of NO₂ rotation in PNA are almost equivalent for the NO₂ and NH₂ groups. The nitro group loses 0.049 e whereas the amino group only 0.042 e. When absolute cSAR(X) values of these groups in coplanar PNA are compared with the data for nitrobenzene and aniline, then there results a difference of 0.082 e for the NO₂ group, whereas for the amino group this is 0.069 e. Thus, both groups have comparable flexibility in their accepting/donating properties upon activity of another group located in the para position in benzene.

The dependence of cSAR(X) values on the Hammett sigma constants for different p-nitrobenzene-X derivatives has a negative slope with correlation coefficient cc = −0.985 [44] indicating that the more negative cSAR(X), the higher the electron-accepting power of X. It should be stressed that cSAR(X) describes the electronic state of the C-X fragment representing the state after the substituent effect has acted. As can be seen from Table 1, the nitro group has more electron-attracting power in coplanar PNA, then in its perpendicular conformation and finally in nitrobenzene, with cSAR(NO₂) equal to −0.219, −0.170 and −0.146, respectively.

As stated above, rotation of the NO₂ group around the C-N bond in PNA modifies the accepting/donating character of both substituents. Figure 9 shows how the rotation of the nitro group increases the relative energy, E_rel, of the system. Interestingly, in the range 30 < φ < 70 degrees the changes in energy are larger than for small and large values of the rotation angle.

The characteristics of both substituents obtained for the fully applied range of the rotation angle φ are collected in Table S1, whereas the relationships between cSAR(NO₂), cSAR(NH₂) and φ are shown in Figure 10. Rotation of the NO₂ group in PNA leads to a decrease in both the electron-accepting and electron-donating power of the nitro and amino groups, respectively (see also [44]).

Modification of the nitro substituent properties, due to its rotation, causes appropriate changes in cSAR(X) values of both substituents in the para position (Figure 10). Changes in cSAR(NO₂) and cSAR(NH₂) correlate well with cc = −0.985, see Figure S1. This means that the increase in the electron-accepting ability of the NO₂ group is directly associated with an increase in electron-donating ability of NH₂ group. Therefore, an augmentation of the aromaticity of the ring with an increase of φ may be expected. In this direction, the contribution of the quinoid form of PNA decreases, and hence an increase of the HOMA index is observed (Figure 11), in line with the results obtained for the data retrieved from CSD for para-substituted nitrobenzene derivatives.

3.2.2. Consequences of the H-Bond Formation at the Amino Group in p-Nitroaniline

Four types of intermolecular interactions of the amino group with F⁻ and HF were taken into account, see Scheme 2. However, for the studied complexes, only three of them (a, b and d) exist in equilibrium systems since in the fourth one (c) the proton transfer reaction (HNH···F⁻ → HN⁻···HF) occurs and another kind of equilibrium system appears. Therefore, in the case of interaction c (Scheme 2) complexes can only be modeled by gradually varying the distance between the heavy atoms of H-bond from 2.65 Å up to 4.0 Å (in this way, the strength of H-bonding is gradually changed). Data for the strongest studied complexes of aniline and PNA are collected in

Table 2. Energy decomposition analysis (ΔE in kcal/mol) for H-bonded complexes of aniline and p-nitroaniline (X = F for N···H interactions, X = N for H···F ones). For HNH···F⁻ interactions d_N···F = 2.65 Å (no proton transfer).

Complex	Angle φ/deg	dX-H/Å	ΔEdef	ΔEint	ΔEPauli	ΔVelstat	ΔEdisp	ΔEoi	ΔEoiσ	ΔEoiπ	ΔEHB
H2N···HF
aniline		0.971	1.37	−12.72	21.14	−17.91	−1.55	−14.40			−11.35
PNA	0	0.967	1.42	−9.67	17.49	−13.42	−1.58	−12.16			−8.25
	30	0.967	1.41	−9.87	17.78	−13.76	−1.58	−12.31			−8.46
	60	0.968	1.36	−10.43	18.53	−14.66	−1.58	−12.71			−9.07
PNA90	90	0.970	1.29	−10.97	19.20	−15.52	−1.58	−13.06			−9.68
HN−···HF
aniline		1.069	8.70	−40.69	31.63	−41.29	−1.48	−29.54	−27.48	−2.07	−31.99
PNA	0	1.065	8.43	−35.61	50.65	−45.59	−1.54	−39.12	−36.02	−3.10	−27.18
	30	1.067	8.50	−36.07	51.26	−46.05	−1.54	−39.74			−27.57
	60	1.075	9.42	−37.65	53.46	−47.61	−1.53	−41.98			−28.23
PNA90	90	1.175	22.26 1	−53.60	78.08	−61.37	−1.47	−68.86	−63.72	−5.14	−31.34
HNH···F−
aniline		1.174	12.24	−54.36	64.88	−58.37	−0.97	−59.90	−51.22	−8.67	−42.12
PNA	0	1.180	12.82	−67.83	34.89	−54.94	−0.98	−46.80	−37.55	−9.25	−55.01
	30	1.174	12.32	−66.68	34.36	−54.08	−0.98	−45.97			−54.36
	60	1.161	11.30	−63.51	33.19	−51.71	−0.98	−44.01			−52.21
PNA90	90	1.133	8.08	−56.37	30.90	−46.72	−0.99	−39.56	−32.61	−6.95	−48.29
HNH···FH
aniline		1.007	0.01	−1.94	1.78	−2.22	−0.64	−0.86	−0.79	−0.07	−1.93
PNA	0	1.009	0.01	−2.91	2.11	−3.20	−0.69	−1.12	−1.02	−0.10	−2.90
	30	1.012	0.00	−2.78	2.09	−3.09	−0.71	−1.08			−2.78
	60	1.013	0.00	−2.63	2.07	−2.96	−0.71	−1.04			−2.63
PNA90	90	1.008	0.01	−2.54	1.95	−2.82	−0.67	−1.01	−0.92	−0.09	−2.53

Note: ¹ Proton transfer takes place: HN⁻···HF → HNH···F⁻.

, whereas dependences of H-bond energy on elongation of H-bond length are presented in Figure S2.

An interesting effect is observed for dependence of E_HB on the rotation angle φ. For the HNH···F⁻ interactions, the H-bond becomes weaker with an increase of φ, since weakening of the electron-attracting power of the NO₂ group due to its rotation causes a decrease in N-H acidity (see Figure 12). Conversely, for HN⁻···HF and H₂N···HF interactions, an increase of φ is associated with an increase of the H-bonding strength. A similar situation is observed for the dependence of E_HB on σ_p⁻ constants of the NO₂ group estimated for various twist angles of the group [7].

Figure S2 presents typical, close to the linear, dependences of H-bond strength on its distance for the complexes of PNA, its derivative PNA90 and aniline. The effect of the substituent on the strength of intermolecular interactions is consistent with the above-described substituent influence on acidity and basicity of the amino group. For complexes with N···HF interactions, both neutral and charge-assisted, the strongest H-bonds are observed for aniline and the weakest one for PNA. The opposite changes are found in the case of NH···F H-bonds.

The presence of electron-accepting substituents in the para-position to the amino group leads to a decrease in the strength of the N···HF hydrogen bond in comparison with aniline by 3.1 and 4.8 kcal/mol for the equilibrium structure of neutral and charged complexes, respectively (a, d in Scheme 2, Table 2). At the same time, if the amino group acts as a proton donor (b, c in Scheme 2), then NH···F bond becomes stronger by 1.0 and 13.0 kcal/mol for HNH···FH and HNH···F⁻ interactions, respectively. These differences decrease (almost half) when the NO₂ group is turned 90 degrees out of the ring plane because π-electron delocalization is partly switched off as we computed previously [4]. Since the rotation decreases the resonance effect between NO₂ and NH₂ groups, HN⁻···HF interaction will become stronger, whereas HNH···F⁻ one will weaken. This is illustrated by Figure 12, σ_p⁻ taken from ref. [7]. Interestingly, the slopes of the regressions in Figure 12 are the steepest for stronger interactions and much less steep for the weaker ones.

To investigate the nature of the hydrogen bonds in the studied complexes the decomposition of the interaction energy into different components is very helpful. We performed the EDA of the interaction energy to determine information about the importance of specific energy terms (electrostatic, Pauli repulsion, orbital interaction, and dispersion). The results for H-bonded complexes of aniline and PNA are presented in Table 2. It is obvious that for all complexes the most important stabilizing term is the electrostatic one, showing more than 50% of total attractive interactions (i.e., ΔE_oi + ΔV_elstat + ΔE_disp), followed by the orbital interaction and dispersion. For all complexes of PNA, the contribution of the orbital interaction term, ΔE_oi, is also very important (more than 40%), except for the weakest H-bonding, HNH···FH, where the percentage of ΔE_oi is only 22% and is comparable to the magnitude of the dispersion term (15%). For the planar complexes, further decomposition of ΔE_oi into σ and π components shows that ΔE_oi^σ provides the main contribution, thereby indicating a partially covalent character of the corresponding H-bonds.

Variation of VDD charges at nitrogen and hydrogen atoms participating in H-bonding on rotation angle φ is presented in Figure S3. For comparison, appropriate values for “free” PNA and HF are added. It was shown that the rotation of the NO₂ group increases the negative charge at the nitrogen atom in the amino group. This effect depends on the strength of H-bonding: H₂N···HF vs. HN⁻···HF (10 kcal/mol vs. 30 kcal/mol). In a stronger H-bonded system, the VDD(N) charge becomes more negative. A similar picture (decrease of the positive charge as the angle φ increases) is observed for VDD charges at the hydrogen atom of amino group involved in the interaction. Moreover, participation of this atom in intermolecular interaction increases its positive charge in comparison with free PNA and this effect depends also on the H-bond strength. The same is observed for the HF molecule participating in H-bonding and the free HF.

Due to the rotation of the NO₂ group, the atoms of the amino group involved in H-bonding become more negative (N) or less positive (H) (Figure S3). In the case of the N···H hydrogen bond, the increase of negative charge at the N atom causes a slight strengthening of the H-bond improving the electrostatic attraction between the PNA fragment and HF (ΔQ(N) = 0.010 for neutral complexes and 0.057 for charged ones). However, for the H···F hydrogen bond, a reverse situation is observed. The H-bond weakens because of the positive charge at H atom of the PNA fragment and the electrostatic contribution is reduced (ΔQ(H) ≈ −0.01 for both systems).

The electron-accepting ability of the substituent and the strength of H-bonding have both a significant impact on π-electron delocalization and hence on the aromaticity of the phenyl ring (as it is the transmitting moiety), expressed by the HOMA index (Figure 13 and Figure S4, respectively). The changes in the aromaticity are due to changes of the quinoid-like structure contribution and depend on the charge transfer from the electron-donating amino group involved in intermolecular interactions (H-bonding) and on the electron-attracting power of NO₂ which is governed by the rotation angle φ.

For equilibrium complexes, the HOMA values increase with the rotation of the NO₂ group for all types of H-bonded complexes of p-nitroaniline (Figure 13). For all PNA complexes with the NO₂ group in the plane of the ring, the values of the HOMA index are lower than those for aniline complexes (ΔHOMA ~ 0.02 for neutral system and 0.10 for charged ones). When this resonance effect is broken by rotation of the NO₂ group, an increase of aromaticity is observed. HOMA values for systems with a perpendicular NO₂ group are higher or similar to those for aniline complexes. Furthermore, it should also be noted that, as illustrated in Figure 13, the changes in aromaticity are consistent with those obtained for experimental data retrieved from CSD (Figure 7).

When considering the effect of H-bonding on π-electron delocalization of the ring, it can be seen that the aromaticity behaves in two different ways: (i) the formation of H-bond promotes the increase of aromaticity only for complexes with H₂N···HF and HN⁻···HF interactions whereas (ii) for HNH···F⁻ charged complexes the HOMA values are much lower. Finally, the very weak HNH···FH bonds almost do not affect the aromaticity (Figure S4).

Furthermore, in cases of PNA and anilines involved in H-bonding, one may expect changes in pyramidality of the NH₂ group and also changes in the C7-N14 bond length due to resonance effect, similarly as in the case of para-substituted aniline derivatives [46]. Indeed, Figure S5 shows the dependence of pyramidality of the NH₂ group on the C7-N14 bond length, which follows a linear relation with the correlation coefficient cc = 0.998 for H-bonded complexes of aniline and p-nitroaniline. Moreover, the pyramidality of the NH₂ group depends also on the rotation angle of the nitro group in PNA complexes, as presented in Figure S6. As a result of the H₂N···HF bond formation, the deformation (pyramidalization) of the NH₂ group becomes larger from 10.2 to 23.9 degrees when the NO₂ group is coplanar and from 16.3 to 26.4 degrees when the NO₂ group is perpendicular to the plane of the phenyl ring.

4. Conclusions

The nitro group is one of the most common substituents. Results of the analyses of geometrical and electronic parameters of the group extracted from CSD for para-substituted nitrobenzene derivatives as well as results obtained quantum chemically reveal a sensitivity of the properties of this group to intra- and intermolecular interactions. It has been shown that:

(1)

Considering CSD data, deformations of the ONO angle are small, with the mean value (123.4 deg) close to the value for nitrobenzene in the crystal (123.2(1) deg) with a small value of esd (ca. 0.7). This indicates a rather small effect of the chaotic action of the neighboring molecules in the crystal lattice on this angle of the NO₂ group. Similar results are found for the NO bond lengths.

(2)

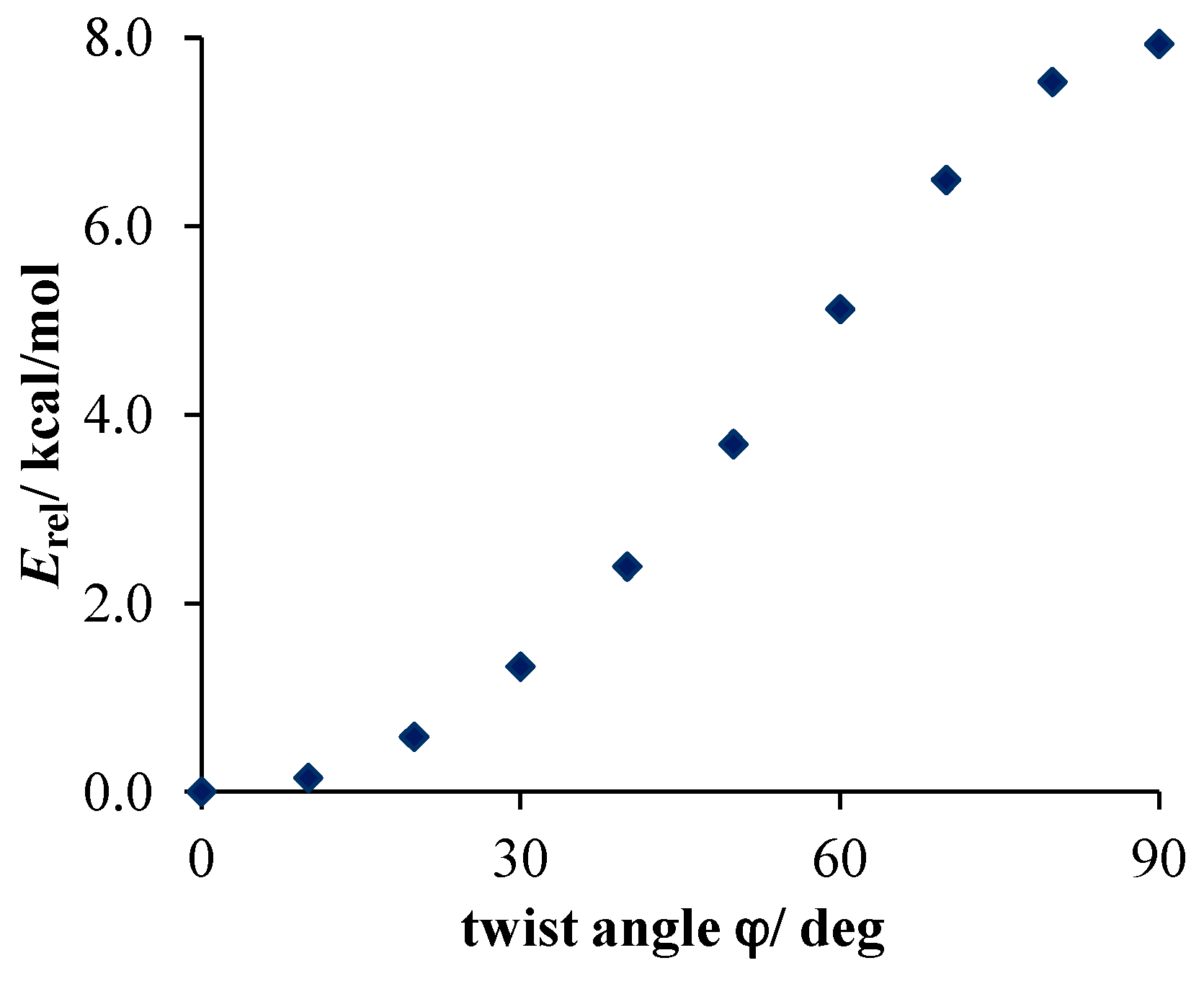
Much stronger deformations are observed for the twist angle, with a maximum value of ~40 deg, but a mean value of 7.3 deg with a rather large esd (5.6 deg). This is in line with QM results for PNA showing that rotation of the NO₂ group with respect to the benzene ring up to 30 degrees is associated with very small changes in energy of the system, namely less than 2.0 kcal/mol, whereas to achieve a perpendicular orientation ca. 8.0 kcal/mol is required.

(3)

Substantial range of the CN bond length is observed in the crystals of nitrobenzene derivatives (from 1.410 to 1.535 Å). Shortening of the CN bond length indicates an increased contribution of the quinoid structure and as a consequence a lower aromaticity of the ring. Such changes can be caused either by distortion from coplanar orientation between the NO₂ group and the phenyl ring or by the effect of a substituent located in the para-position, as was confirmed by QM results for PNA and its H-bonded complexes.

(4)

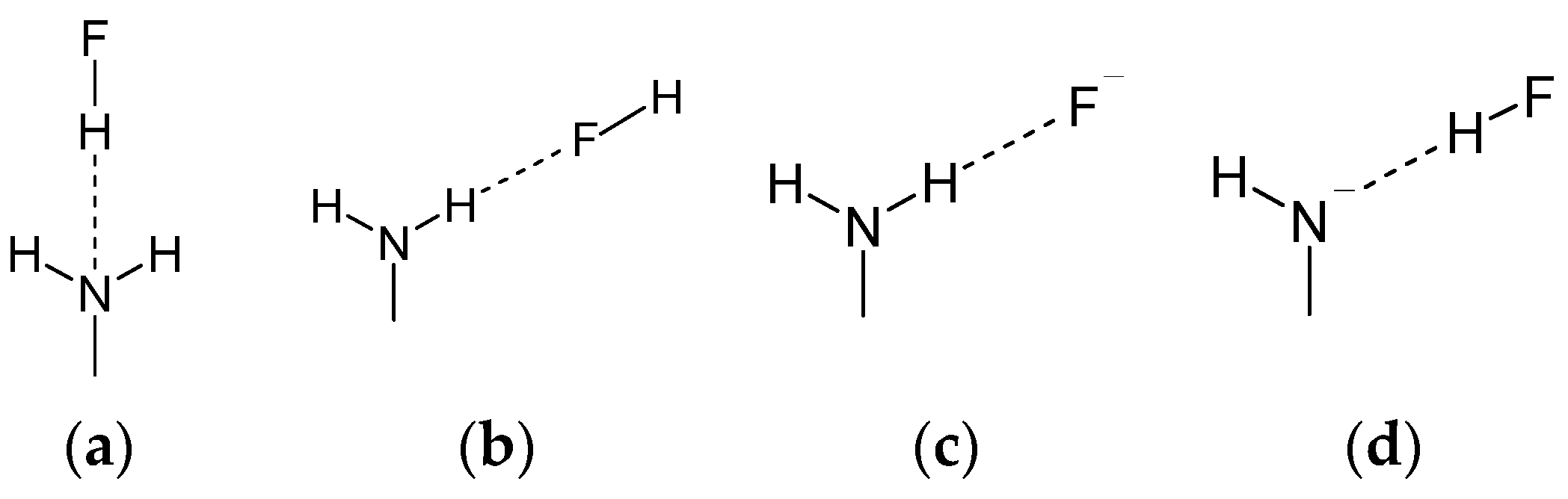
Energy decomposition analysis of the H-bonds in the modeled complexes of aniline and PNA revealed that the amino group can form hydrogen bonds in a wide range of strengths (from −2.0 to −55.0 kcal/mol). The results support the view that these interactions are mostly provided by electrostatic attraction, however a significant covalent contribution has to be considered.

(5)

Application of the VDD atomic charges and the cSAR concept allows an estimation of the magnitude of the intramolecular charge transfer. For all of the studied systems, a mutually dependent change in characteristics of both groups (NO₂ and NH₂) was observed. It was shown that the electron-attracting ability of the nitro group dramatically depends on the moiety to which it is attached (see Table 1) as well as on intermolecular interactions occurring even at distant parts of the studied systems.