1. Introduction
In recent years, it was demonstrated that topology and curvature could be exploited to nucleate diverse complex patterns in nature [
1,
2,
3]. Of particular interest are topological defects (TDs), which, in isolation, are topologically protected and consequently they cannot be destroyed [
4]. They might represent “fundamental particles” of the Standard model (which are from this perspective emergent) if relevant fields represent fundamental entities of nature [
5] as first suggested by Skyrme already in 1962 [
6]. Note that the first theory on coarsening dynamics of TDs was developed in cosmology in order to explain TDs in the Higgs field of the early universe [
7]. Furthermore, recent relativistic simulations imply [
8] that negative curvature of the “empty” part of the universe might explain the origin of the so-called “dark energy”. Since these phenomena show remarkable universalities, it is of interest to find appropriate systems where their fundamental behavior can be relatively easily assessed and probed [
9,
10].
Why are TDs so ubiquitous in nature? The reason behind this is that any continuous symmetry breaking phase transition can be represented by an order parameter field [
11] consisting of two qualitatively different components:
amplitude field and
gauge (also called
symmetry breaking or
non-hydrodynamic) field. For example, the classical para-ferromagnetic transition is described by the vector order parameter field
,
, where
plays the role of
amplitude (
gauge) field. The
amplitude measures the degree of ordering in the symmetry broken phase. For given conditions, it possesses a single equilibrium value. On the other hand, the
gauge component determines a highly degenerated symmetry breaking choice. Due to the latter fact, TDs can be formed.
The key property of TDs is their discrete topological charge [
4,
10]
, which is a conserved property. Its quantum character arises due to degeneracy of equilibrium values of a relevant
gauge field. In three spatial dimensions,
q reveals how many times all possible “orientations” of the
gauge field are realized while crossing a closed surface enclosing the defect [
10]. In two-dimensions (2D), to which we are restricted in this paper,
is equivalent [
10] to the winding number
.
Of particular recent interest is to understand the impact of curvature and topology on the number and position of TDs. A convenient system for such studies, both from experimental and theoretical perspectives, are numerous effectively two-dimensional soft material [
10,
11] films, exhibiting some sort of in-plane ordering [
11,
12,
13,
14,
15]. Typical representative systems are colloidal liquid crystalline (LC) shells [
15] and various biological membranes [
13,
14] composed of anisotropic constituents, or isotropic membranes with adsorbed anisotropic nano-sized complexes (e.g., proteins). We henceforth refer to these orientationally anisotropic effectively 2D (i) open or (ii) closed soft films as (i)
ordered films and (ii)
ordered shells, respectively
. In the case of non-toroidal geometries,
ordered shells unavoidable contain TDs due to the Gauss-Bonnet and Poincare-Hopf theorems [
16]. According to these theorems, the integrated Gaussian curvature
over a closed surface exhibiting orientational ordering determines the total topological charge (i.e., the winding number)
of the system [
16]:
Recently, it has been shown [
12] that one can assign the
effective topological charge to a surface patch
of an
ordered film characterized by its spatially averaged Gaussian curvature
. In the absence of “impurities” it can be expressed as
[
12]. Here,
stands for the total charge of “real” TDs within
and the hypothetical
smeared Gaussian curvature charge [
12,
17] is defined as
In cases where
represents a closed surface, it holds true that
, owing to Equations (1) and (2). In this sense, one could say that any closed system is strictly
neutral. The
neutralization tendency
[
4,
17] is presented also in each finite (unclosed) patch of a surface exhibiting spatial non-homogeneities in
, which is referred to as the
effective topological charge cancellation (ETCC) mechanism [
12]. However, if a
neutralization within a patch cannot be achieved via redistribution of existing TDs, it is necessary that a large enough local curvature exists that has the potential to trigger formation of pairs {
defect,
antidefect} of TDs. Here,
defect (
antidefect) refers to a topological defect bearing
.
Note that
ordered shells could be exploited to nucleate formation of different new materials and even metamaterials. For example, Nelson [
15] proposed that colloidal
nematic shells (i.e., colloids covered with a thin nematic LC film) immersed in isotropic matrix containing appropriate nano-binders could be organized in periodic configurations (i.e., scaled crystals) analogous to “real” crystals (consisting of atoms). In this analogy, the
ordered shells play the role of atoms and TDs determine their valence [
15]. Namely, the nano-binders tend to be attached to the cores of TDs due to the
defect core replacement (DCR) [
18] mechanism. The DCR mechanism is based on the reduction of the defect core penalty by partially replacing an energetically expensive condensation penalty volume with the nano-binder’s volume. In such a way, the nano-binders bind nearby
shells together [
15], nucleating colloidal crystal growth.
By varying the number and position of TDs within an ordered shell, one could control the symmetry of resulting crystals and consequently the key physical characteristics of crystals. For this purpose, it is of strong interest to find ways to form and control different shapes of ordered shells and consequently tame their valence. Note that, in general, much larger diversity of shell geometries, and consequently symmetries, could be realized in comparison to those existing in atoms. Therefore, scaled crystals formed by ordered shells, exhibiting complex geometries, could in general exhibit qualitatively new symmetries (and consequently new physical properties) not encountered in “real” atom-based crystals.
In this paper, we theoretically analyze the impact of different geometries of ordered films and ordered shells on the number and position of TDs. We first illustrate the efficiency of the ETCC mechanism in predicting the presence of TDs. Next, we demonstrate a relatively simple path to switch among different configurations of TDs in ordered shells by varying a single control parameter.
2. Results
In this section, we demonstrate numerically, using mesoscopic description, how one could relatively easily manipulate shapes of effectively two-dimensional soft system exhibiting in-plane ordering and, consequently, control the predetermined number and position of TDs.
To determine shapes of
shells and in-plane orderi ng within these films, we use a mesoscopic modelling, where the system’s properties are described using the curvature tensor
and the tensor nematic order parameter
. The Weingarten curvature tensor
[
19] determines the local curvature of a surface
, which is embedded in 3D Cartesian system:
The unit vectors
point along the surface principal directions exhibiting principal curvatures
. The invariants of
are trace and determinant, yielding the mean local curvature (
) and the Gaussian curvature (
), respectively:
We set that molecules exhibiting nematic orientational ordering are bound to lie in the local tangent plane of the surface and are otherwise unconstrained. The molecules are assumed to be rod-like, exhibiting the so-called head-to-tail invariance. The corresponding local orientational order is described in terms of the 2D tensor order parameter
. In the diagonal form, it can be expressed as [
20]
Here, the orthogonal unit vectors and are the eigenvectors of the tensor , while and are the corresponding eigenvalues. The lower bound corresponds to isotropic local ordering, while the upper bound corresponds to rigidly aligned molecules in a small area along the direction , commonly referred to as the nematic director field.
For numerical convenience, we restrict to axially symmetric surfaces of revolution
with rotational symmetry about the
-axis. We parametrize the position vector
of a generic point lying on
as
where
,
, and the unit vectors {
} determine the Cartesian coordinate system. On the surface of revolution, parallels and meridians are lines of principal curvature. We set that the principal directions (see Equation (3)) {
,
} point along meridians (
) and parallels (
), respectively.
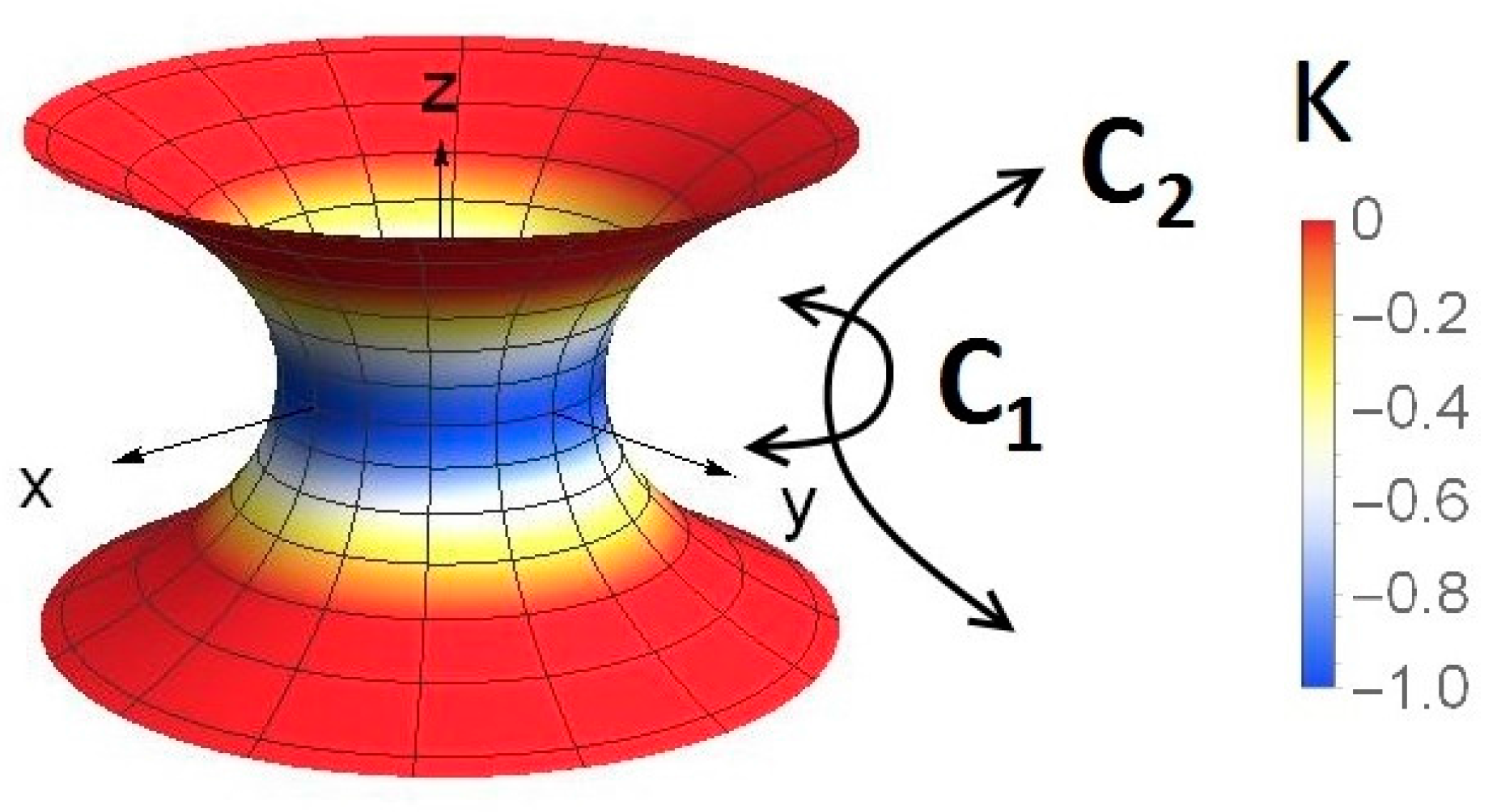
We consider two qualitatively different geometries. First, we study possible defect structures on a catenoid’s [
21] surface (see
Figure 1) defined by
where the length
characterizes a catenoid.
This geometry is interesting for several reasons. Firstly, its mean curvature equals zero everywhere on the surface. In general, surface curvature is energetically expensive. Therefore, such minimal surfaces, characterized by , often represent natural ”structural attractors” (at least locally). Secondly, the integral of the Gaussian curvature over the catenoid’s surface is a constant, i.e., . Therefore, the catenoid’s surface enforces the smeared Gaussian curvature charge , so TDs bearing the total charge should be introduced in order to make the nematic patch neutral (). Note that the film shape in catenoids is prescribed and the variational parameter is solely the nematic tensor order parameter.
Next, we consider also cases of ordered shells exhibiting spherical topology, where the shapes of shells are calculated by minimizing the bending elastic energy for a given relative volume . Here stands for the volume of a film of total surface area , and is the volume of the sphere having the same surface area, where .
2.1. Ordered Films
To demonstrate the adequacy of the
effective charge cancellation mechanism, we first consider open
ordered films. As a testing ground, we chose a catenoid. We show that by squeezing the catenoid’s neck, four TDs bearing
are formed in order to compensate the
smeared Gaussian curvature charge localized at the neck. Numerically calculated order parameter textures are shown in
Figure 2. In column (
a), we depict the catenoid’s shape. Its neck is gradually squeezed on passing downwards. In the case shown in the first row, the curvature and the related nematic elastic distortions are relatively weak. Consequently, it holds
where
denotes the catenoid’s surface. The nematic order parameter exhibits relatively weak spatial variations, see
Figure 2b. The corresponding nematic director profile
is homogeneous in the
plane as shown in
Figure 2c. Therefore,
is aligned along parallels of the catenoid. In the Cartesian coordinates, this corresponds to concentric circles centered at the origin of the
-axis.
In the case shown in the 2nd row of
Figure 2, elastic distortions at the neck are relatively strong and nematic ordering is almost melted at the neck area (
Figure 2b, 2nd row) , where the distortions are the largest. However, the local curvature is still not strong enough to trigger the formation of TDs and the nematic director field is still aligned along the parallels.
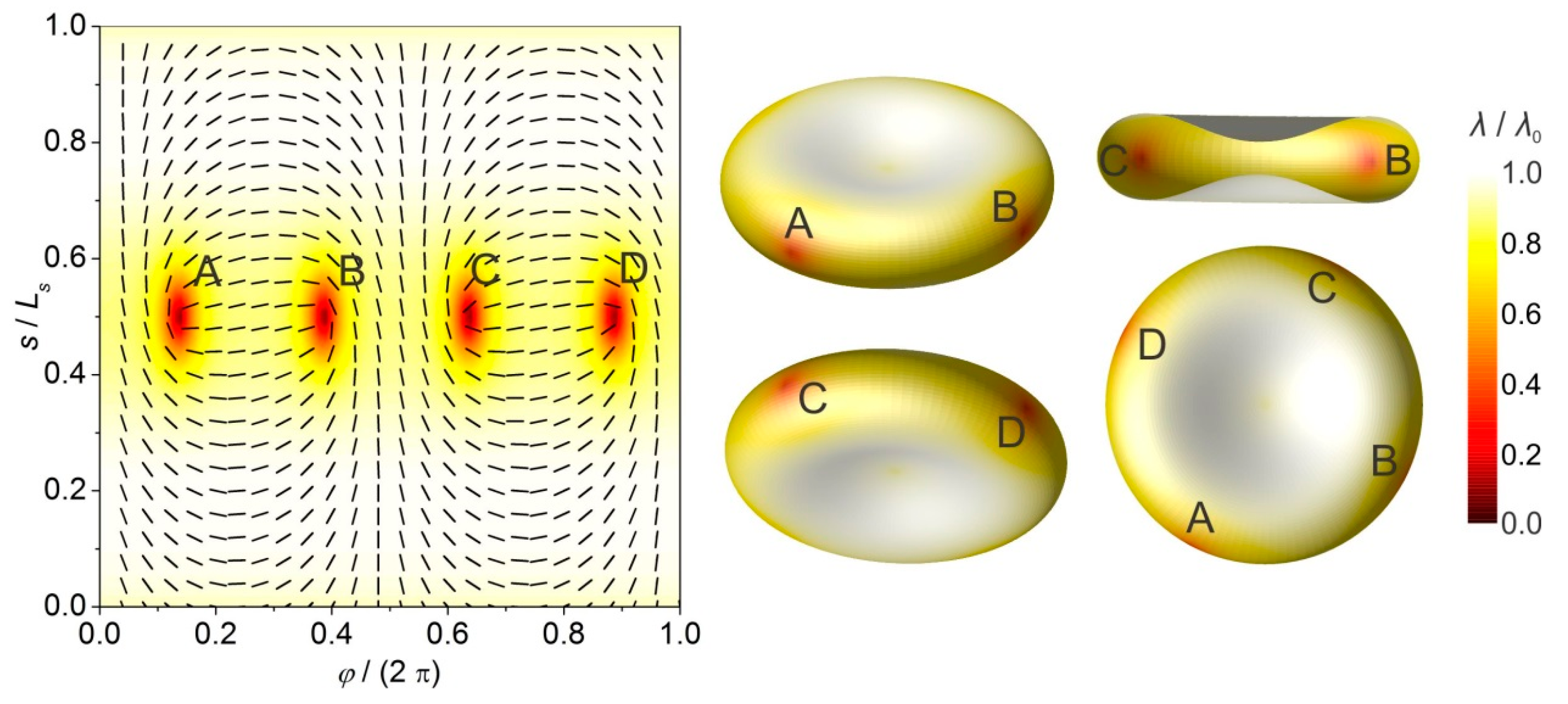
When the critical condition is met, four
defects are created at the neck in order to compensate the
smeared Gaussian curvature charge. The resulting structure exhibits zero effective topological charge and is in this sense
neutral. Representative configurations are depicted in the 3rd row of
Figure 2. At the center of the cores of TDs, the nematic order parameter is melted (
Figure 2b, 3rd row). The characteristic nematic director profile of defects is well visible in the 3rd row of
Figure 2c. In the Cartesian coordinates, this profile corresponds to parallel alignment of
in the regions relatively far from the neck.
2.2. Ordered Shells
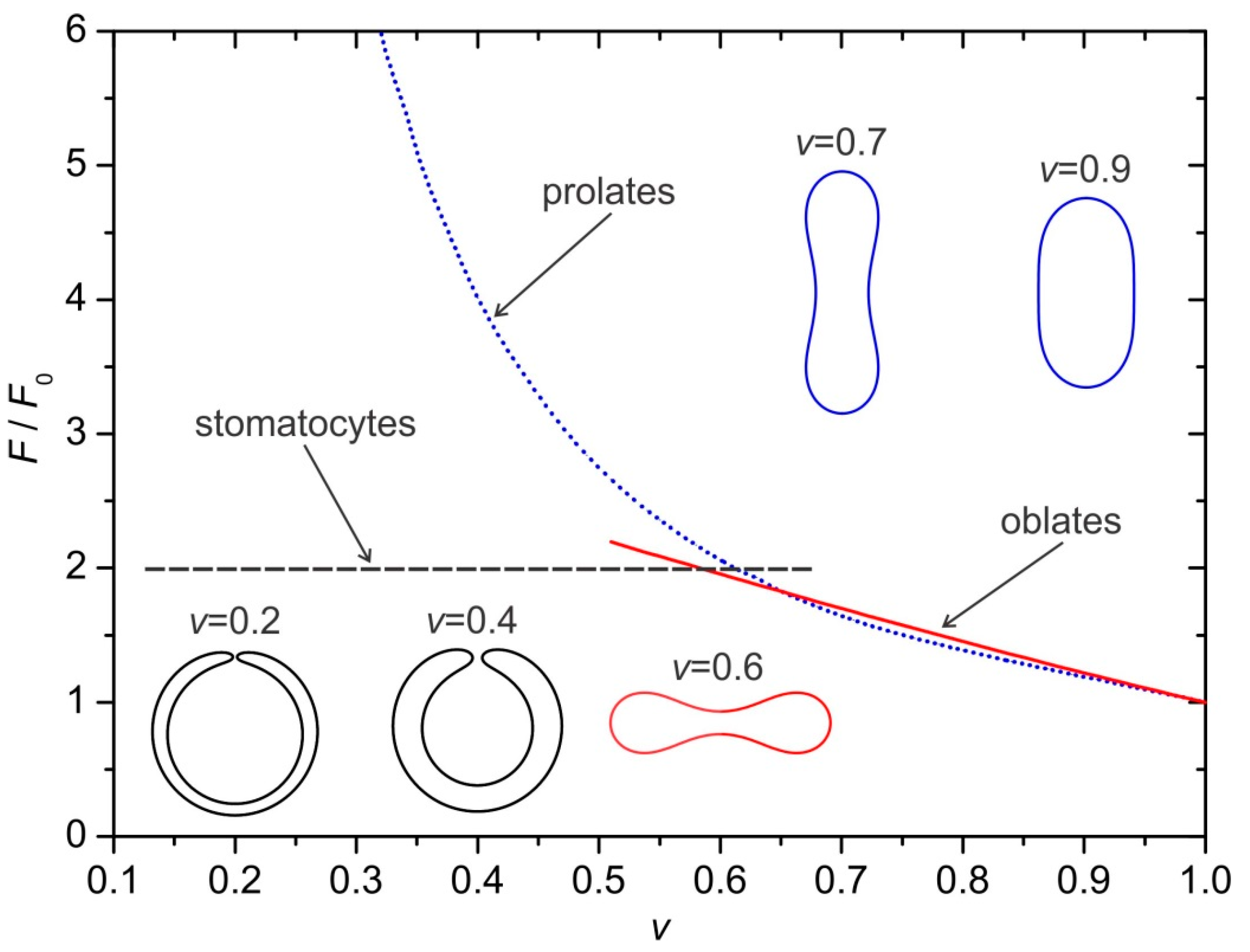
Next, we consider ordered shells where both surface geometry and degree of nematic ordering are varied. We demonstrate that one can efficiently switch between qualitatively different configurations simply by varying the relative volume of a shell.
Using our simple modelling, one can obtain three qualitatively different geometries of
shells by varying
, which is presented in
Figure 3. These structures are commonly referred to as stomatocytes, oblates and prolates [
22,
23,
24]. In
Figure 3, they are depicted with black, red and blue color, respectively. Each class of shapes is stable at a certain range of the reduced volume values. Stomatocytes are globally stable for
, prolates for
, and oblates exist in the interval
.
Note that all the structures in
Figure 3 exhibit the spherical topology. According to the Gauss-Bonnet and Poincare-Hopf theorems, such structures bear the total topological charge
in order to
neutralize the whole
shell. For
,
shells are spherical and the Gaussian curvature is spatially independent (
, where
is the radius of the sphere). Consequently, a sphere typically hosts four
TDs residing at the vertices of a hypothetical tetrahedron inscribed within the sphere in order to maximize the mutual separation among TDs [
19,
20,
25].
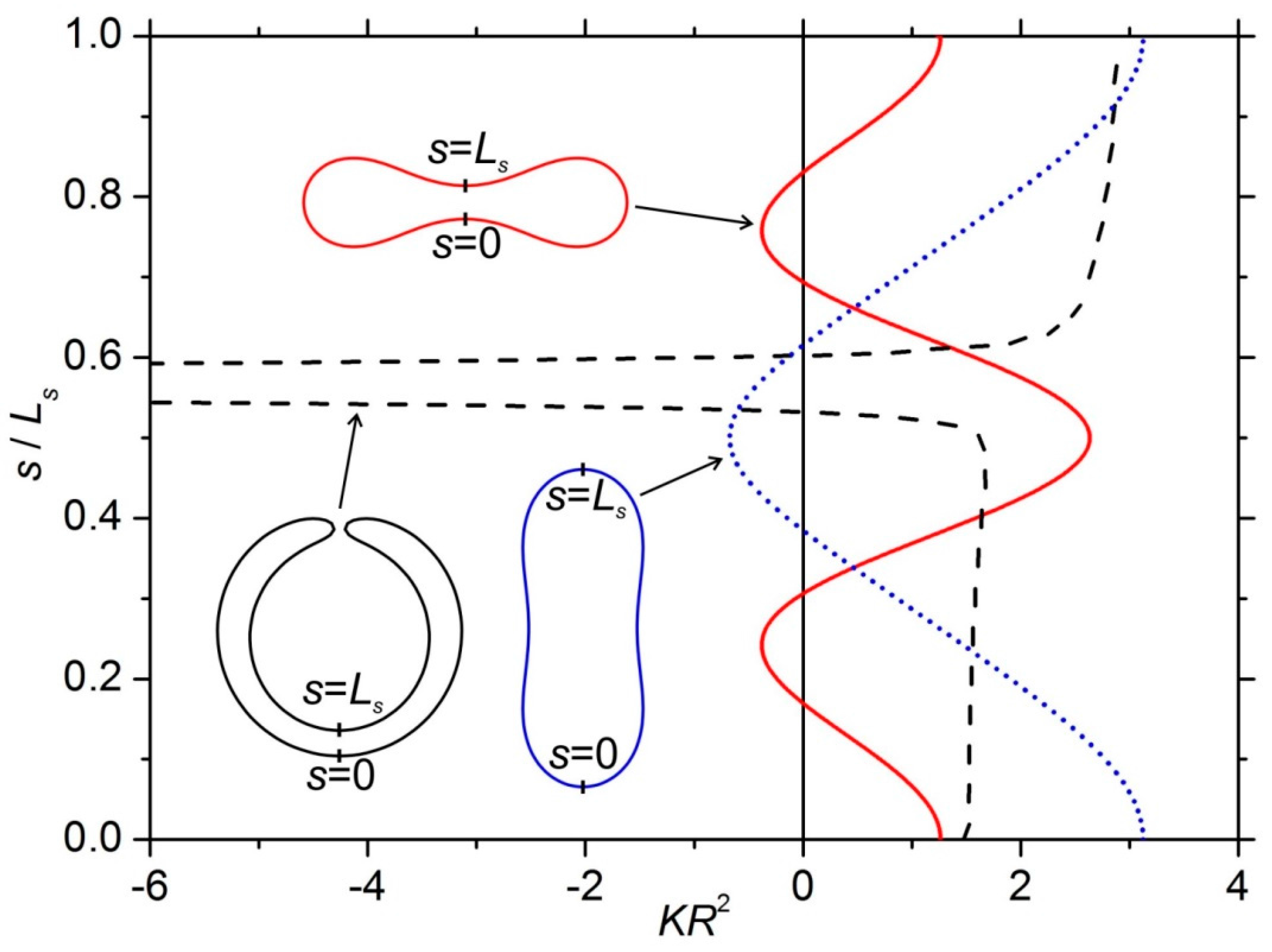
On decreasing
, different patches, characterized by different spatially averaged Gaussian curvature
, become apparent. Consequently, the positions and even the number of TDs are changing. Established configurations of TDs tend to
neutralize each patch according to the ETCC mechanism. Typical spatial variations of
in stomatocytes, oblates and prolates are shown in
Figure 4.
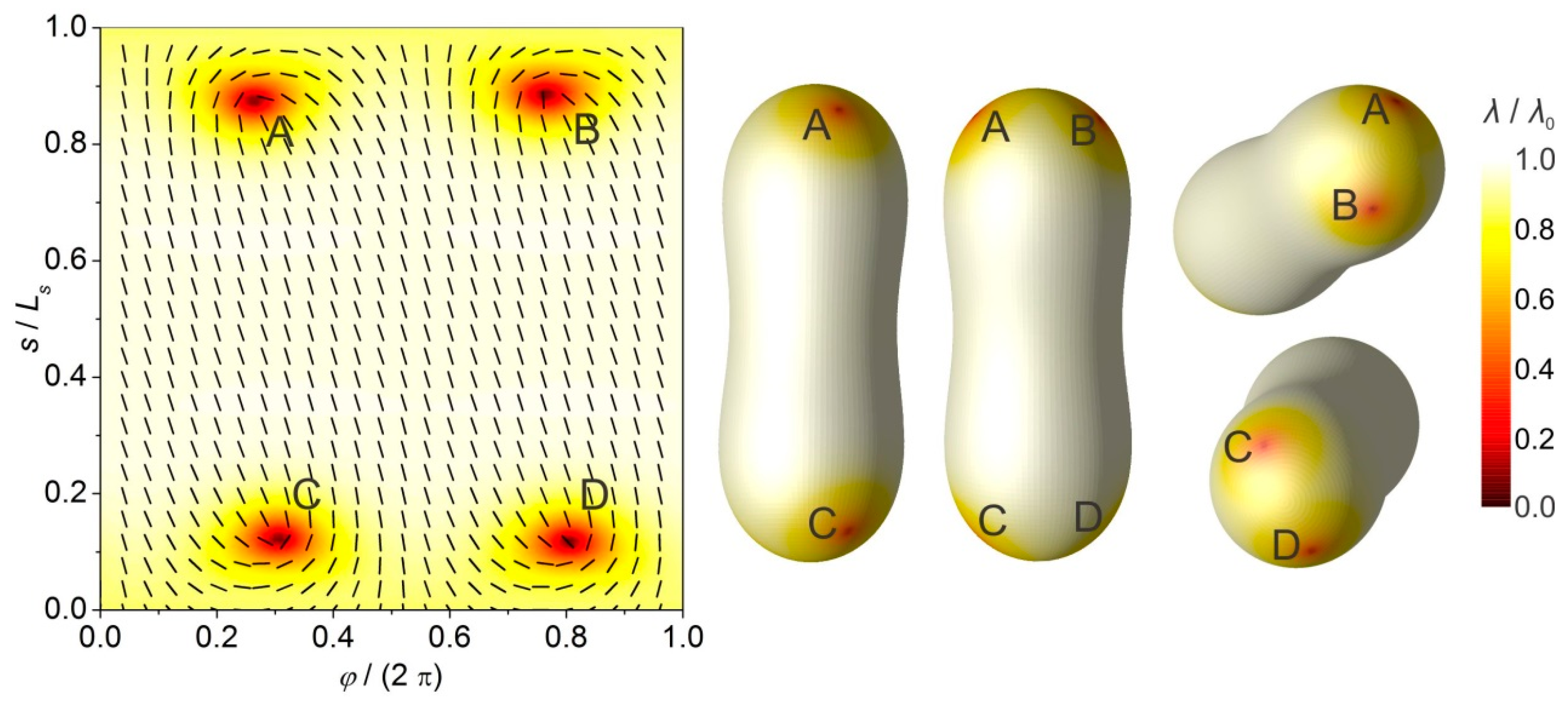
In the first regime (
), the
shells adopt prolate-type shapes where bumps exhibiting progressively bigger positive Gaussian curvatures form at the poles (see
Figure 4). Therefore, in each pole region it roughly holds
, while the equatorial regime is characterized by
. Consequently, to
neutralize each patch, four
TDs are attracted to the poles as illustrated in
Figure 5.
Within the parameter window
, oblate structures are formed (see
Figure 6). For these structures, positive Gaussian curvature exhibits a pronounced maximum at the equatorial ring (
Figure 4). This maximum acts as a strong attractor for TDs. Consequently, four
TDs assemble in the equatorial region.
For
, stomatocyte shapes are formed (
Figure 7). These structures possess the neck, where
(see
Figure 4). The local elastic distortion is strong enough to enable the formation of two additional pairs {
defect,
antidefect}, bearing topological charges
. Consequently, stomatocytes typically host eight TDs, where the total topological charge remains
, i.e., the structure is
neutral. The two
TDs are localized at the neck in order to partially screen
. On the other hand, the six TDs bearing
are distributed in the regime where
.
3. Discussion
Of our interest was to identify a relatively simple and “natural” way to vary shapes of
ordered shells and to predict the number and position of TDs within the resulting configurations. A possible future application based on such systems might be scaled crystals [
15,
25,
26,
27,
28]. Namely, different configurations of TDs on
ordered shells, immersed in an isotropic host, are expected to nucleate self-assembling into periodic structures exhibiting different symmetries and, consequently, quantitatively or even qualitatively different physical properties [
15].
Firstly, we demonstrated that, for a given geometry, one could relatively reliably predict the number and position of TDs. For this purpose, the
effective topological charge cancellation [
12] mechanism can be used. Its predicting power works well in the cases where the so-called intrinsic geometry contributions [
1,
2,
3,
29] are dominant in the free energy terms coupling geometry and orientational ordering. The ETCC mechanism is useful for the geometries that possess surface patches exhibiting significantly different characteristic Gaussian curvatures. We illustrated its efficiency on an open catenoid [
21] geometry, where topology does not require the presence of TDs. Our simulations reveal that if a catenoid’s neck is squeezed enough, so that the local curvature is strong enough to nucleate the formation of pairs {
defect,
antidefect}, four
TDs appear at the neck in order to compensate the local negative Gaussian curvature. Note that the accompanying four
TDs are not visible in equilibrium structures (see
Figure 2, 3rd row) because the catenoid’s surface is “open”.
Afterwards, we considered
ordered shells of spherical topology. We were changing the geometry of
shells by varying the relative volume
. Namely, decreasing
enables switching among three qualitatively different shapes, referred to as oblates, prolates and stomatocytes [
22]. Such structures are among others observed in biological membranes [
14,
22,
23,
24], where
could be relatively easily varied by changing the osmotic pressure of a system. Furthermore, in biological membranes there are several different origins of in-plane ordering [
12]. In our simulations, stability ranges of different structures are as follows: oblates are stable within the window
, prolates for
, and stomatocytes for
. For parameters used in our study, prolate and oblate structures possess four TDs, each bearing
, tending to be assembled in the regions exhibiting relatively high positive Gaussian curvature. Consequently, in prolates, TDs are assembled near the poles and in oblates at the equatorial region. On the other hand, in stomatocytes, a relatively narrow neck exhibiting negative Gaussian curvature is formed. The curvature there is strong enough to nucleate two pairs of {
defect,
antidefect} = {
}. Therefore, the resulting structure has eight TDs carrying the total topological charge equal to two. The two
antidefects are localized within the neck in order to compensate for relatively strong local negative Gaussian curvature. The remaining six TDs, bearing
, are distributed in the remaining part of the structure which exhibits
. Relative position of TDs in these regions is dominated by mutual repulsion among TDs because
exhibits relatively weak spatial variations.
Our work is illustrative and demonstrates a possible way of varying shapes and, consequently, configurations of TDs. Note that, in real configurations, elastic anisotropies [
26,
27,
28] of relevant elastic constants and extrinsic [
2,
3,
29,
30,
31] geometric terms might play an important role in the positioning of TDs. In our modelling, we considered only the so-called intrinsic free energy curvature terms. However, as illustrated in [
3,
21,
29], in general, extrinsic curvature terms are also present. The intrinsic terms penalize in-plane distortions of ordering which are independent of embedding of a 2D manifold in 3D. On the other hand, the extrinsic terms penalize out-of-plane distortions which are sensitive to 3D embedding. Despite the fact that both contributions have common origin (i.e., curvature) their effect on TDs is, in general, contradicting. Namely, the intrinsic terms favor assembling of TDs in regions exhibiting strong curvature. On the other hand, the extrinsic terms act as a local ordering field tending to align an orientational ordering either (depending on values of extrinsic elastic constants) along the maximal or minimal principal curvature direction. The relative role of extrinsic terms increases with the difference
. Therefore, they are absent for cases
. For example, this is realized in a sphere. In the case of catenoids, it holds
. In our simulations, we considered only intrinsic terms. Consequently, in catenoids TDs are created at the catenoid’s neck for strong enough curvature. However, if extrinsic terms are present, their field-like alignment tendency is most effective exactly at the neck. Consequently, on increasing the extrinsic term strength TDs would be expelled from the neck region. This was demonstrated in [
21] where a simple nematic director field description was employed. The competition of these contradicting ordering mechanisms is the focus of our future paper.
4. Methods
We express the total free energy functional of the ordered soft film surface
as
. The free energy density
consists of surface bending
, order condensation
, and intrinsic elastic
term. Here, we took into account only the most essential terms needed to describe the phenomena of our interest. Note that, in general, the so-called extrinsic elastic contribution also exists, but is discarded in this study. We express the densities as [
12,
20]:
Here , , and are material parameters. The bending () and intrinsic () elastic constants are positive, and the orientational ordering exists for positive values of and .
In the eigenframe of
, tensor
can be parametrized as [
20]
where
and
are scalar order parameters and
, see Equation (5).
For simulation purposes, we introduce scaled and dimensionless quantities. We introduce material-dependent order parameter correlation length
and geometrically imposed length
. The former estimates the distance on which a local perturbation in order parameter relaxes on a flat surface. The quantity
describes some characteristic geometrically imposed length in the system, i.e., it equals to the radius of the sphere with the same surface area as the surface of the investigated
shell. Furthermore, we introduce the parameter
that determines the bulk equilibrium value of order parameter in flat geometries. With this in mind, we introduce the scaled order parameter (
), the scaled curvature tensor (
), and we measure all length in units of
. The resulting dimensionless free energy density (
) reads
In case of catenoids, the geometry of ordered films was prescribed. In case of ordered shells, we first minimized the Helfrich curvature contribution (the first term in Equation (12)) for a prescribed value of v. For a given geometry, we then calculated the nematic ordering by minimizing the free energy potential with respect to .