The Continuum Approach to the Description of Semi-Crystalline Polymers Deformation Regimes: The Role of Dynamic and Translational Defects
Abstract
:1. Introduction
2. Materials and Methods
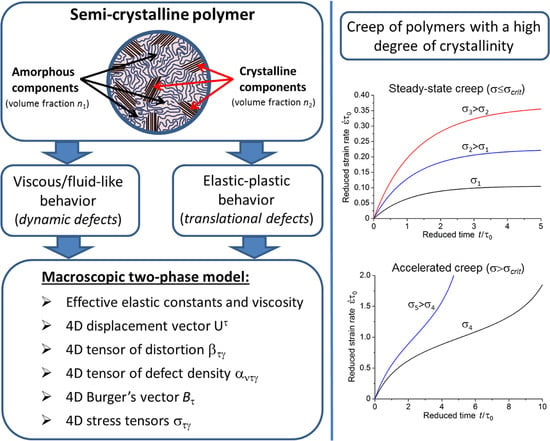
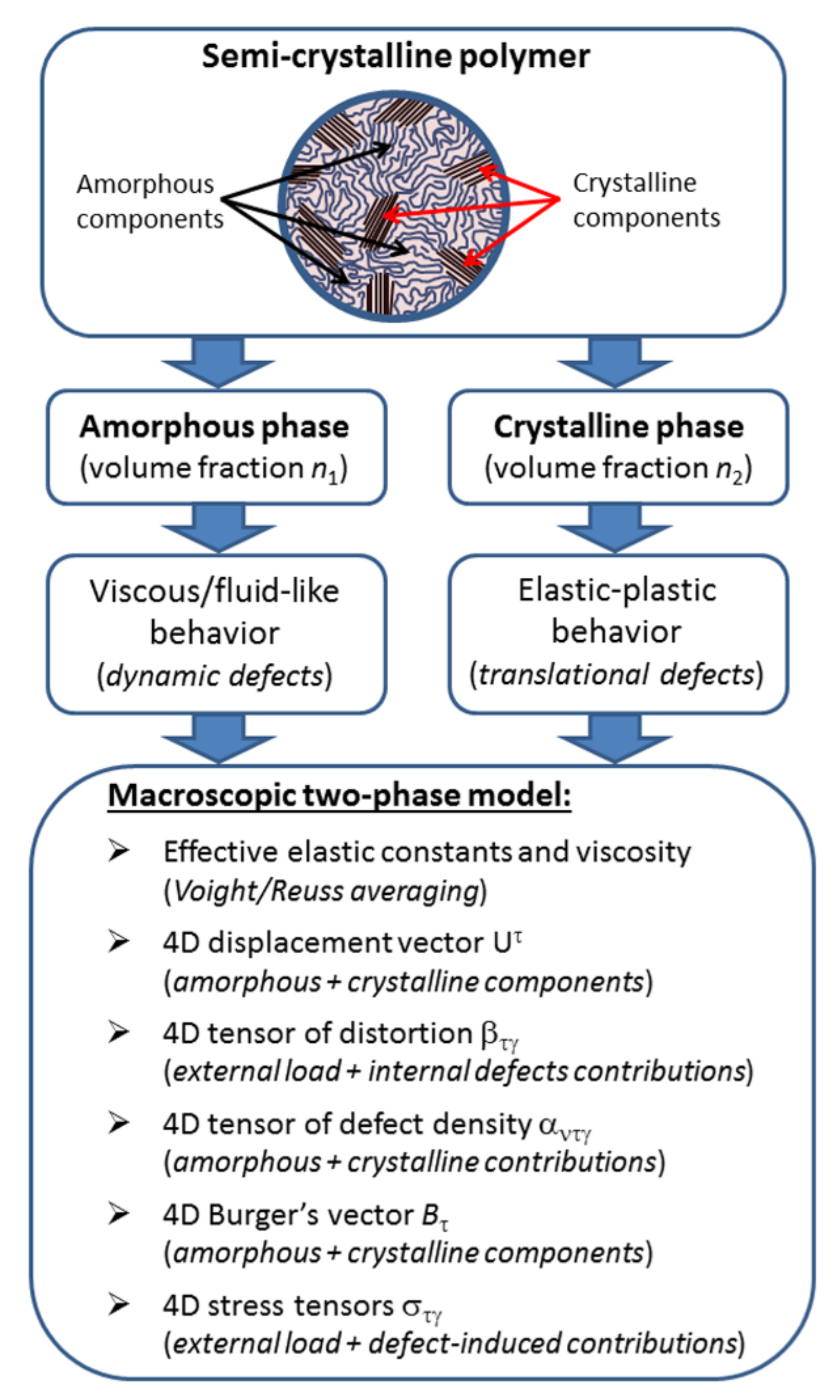
2.1. Definition of a Semi-Crystalline Polymer as a Two-Phase Material
2.2. Macroscopic Definition of Defects in the Classical 3D Continuum Theory of Crystalline Solids
2.3. Definition of Defects in the Developed 4D Continuum Model of Semi-Crystalline Polymers
3. Results and Discussion
3.1. Definition of Defects in a Semi-Crystalline Polymer as an Effective Medium
3.2. Geometric and Dynamic Equations of the Defect Fields
3.3. Interaction between the Defect Fields and the 4D Stress Tensor
3.3.1. Interaction Force between the Field of “Accelerations–Vorticities” and the 4-Stress Tensor
3.3.2. Interaction Force between the Translational Defect Fields and the 4-Stress Tensor
3.4. The System of Dynamic Equations for Defect Fields in Semi-Crystalline Polymers
- Equation (93a) implies that there are no sources and sinks of vorticity in the material (the vortex lines are closed or come to the surface);
- Equation (93b) defines the relationship between accelerations and vorticities in the amorphous phase of the polymer;
- Equation (93c) shows that vorticity is generated by a change in the acceleration of the amorphous phase, a material impulse, and field impulses of defects in amorphous and crystalline phases. This relationship describes the interaction between defects of various types, in particular, it shows that the fluxes of translational defects in the crystalline phase of the polymer can “generate” dynamic defects in the amorphous phase;
- Equation (93d) shows that the sources of accelerations in the amorphous phase are the material density and the densities of the defect fields in both phases. This equation also demonstrates the effect of the fields of translational defects and their fluxes in the crystalline phase on the nucleation of dynamic defects in the amorphous phase;
- Equation (93e) implies that translational defects in the crystalline phase are closed or exit to the surface;
- Equation (93f) defines the relationship between the translational defect flux and the density of translational defects;
- Equation (93g) shows that material impulses and field impulses of defects in the amorphous and crystalline phases cause the fluxes of translational defects. The relationship between defect fluxes in the crystalline and amorphous phases can be illustrated by combining the Equation (93c,g): . The meaning of the relationship is that dynamic defects in the amorphous phase (change in acceleration and/or curl of vorticity) can “generate” the motion (flux) of translational defects in the crystalline phase;
- Equation (93h) shows that defects of the translational type appear in (or disappear from) the crystalline component of some volume of the semi-crystalline polymer as a result of external stresses, and field stresses caused by defects in the amorphous and crystalline phases, as well as changes in the rate of flow of translational defects through the surface of this volume.
- Stresses σ and elastic displacements caused by external loading (Hooke’s law);
- Elastic displacements (or displacement rates) with the characteristics of defect fields in the crystalline phase.
3.5. Discussion
3.6. Some Analytical Solutions for Amorphous and Crystalline Polymer Phases
3.6.1. Analysis of the Natural Vibrations of the Defect Field in the Amorphous Phase of the Polymer
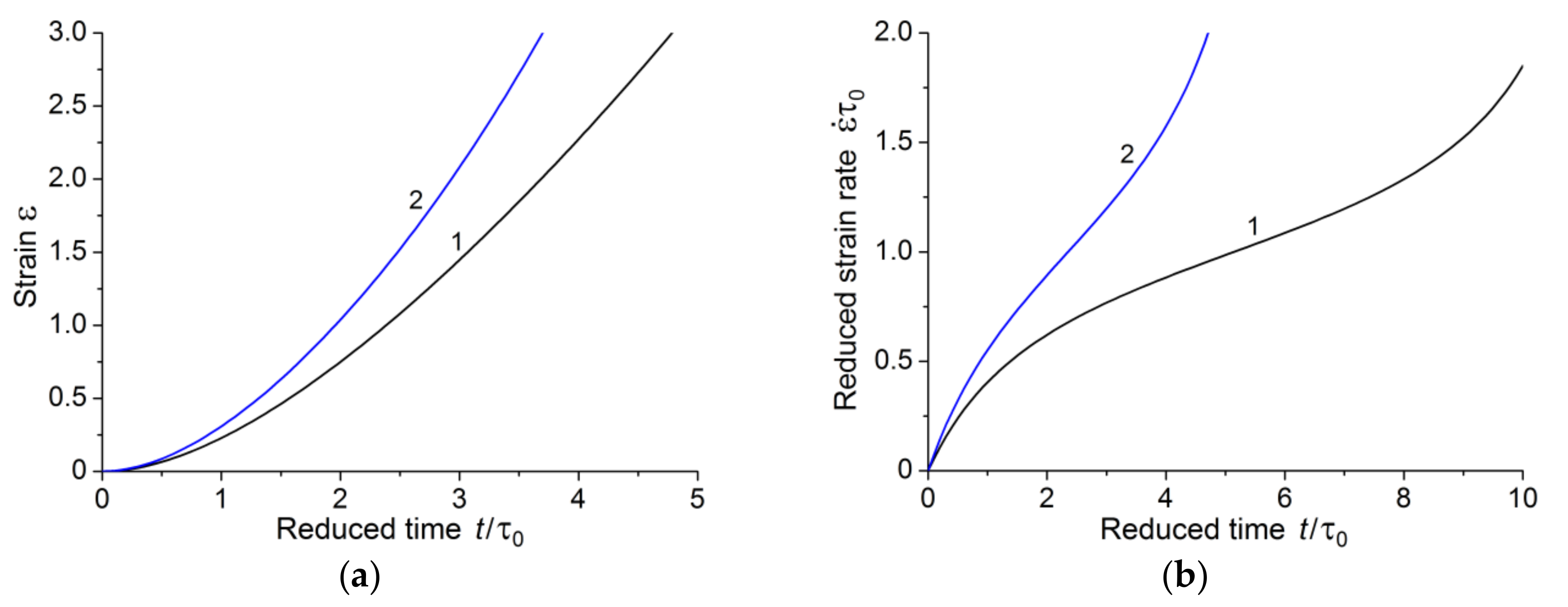
3.6.2. Analysis of General Patterns of Creep of Polymers with a High Degree of Crystallinity under Uniaxial Loading
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Chen, D.T.N.; Wen, Q.; Janmey, P.A.; Crocker, J.C.; Yodh, A.G. Rheology of soft materials. Annu. Rev. Condens. Matter Phys. 2010, 1, 301–322. [Google Scholar] [CrossRef]
- Kleman, M.; Lavretovich, O.D. Soft Matter Physics: An Introduction; Springer: New York, NY, USA, 2003; ISBN 978-0-387-95267-3. [Google Scholar]
- Kolesnikov, V.I.; Bardushkin, V.V.; Sorokin, A.I.; Sychev, A.P.; Yakovlev, V.B. Effect of thermoelastic characteristics of components, shape of non-isometric inclusions, and their orientation on average stresses in matrix structures. Phys. Mesomech. 2018, 21, 258–262. [Google Scholar] [CrossRef]
- Hu, W. The physics of polymer chain-folding. Phys. Rep. 2018, 747, 1–50. [Google Scholar] [CrossRef]
- Wunderlich, B. Macromolecular Physics. Volume 1: Crystal Structure, Morphology, Defects; Academic Press: New York, NY, USA, 1973; ISBN 978-0-12-765601-4. [Google Scholar]
- Khoury, F.; Passaglia, E. The Morphology of Crystalline Synthetic Polymers. In Treatise on Solid State Chemistry; Hannay, N.B., Ed.; Plenum Press: New York, NY, USA, 1976; pp. 336–496. ISBN 978-1-4684-2666-3. [Google Scholar]
- Bartczak, Z. Deformation of semi-crystalline polymers—The contribution of crystalline and amorphous phases. Polimery 2017, 62, 787–799. [Google Scholar] [CrossRef]
- Rozanski, A.; Galeski, A. Plastic yielding of semicrystalline polymers affected by amorphous phase. Int. J. Plast. 2013, 41, 14–29. [Google Scholar] [CrossRef]
- Cangemi, L.; Meimon, Y. A two-phase model for the mechanical behaviour of semicrystalline polymers. Oil Gas Sci. Technol. 2001, 56, 555–580. [Google Scholar] [CrossRef]
- Brusselle-Dupend, N.; Cangemi, L. A two-phase model for the mechanical behaviour of semicrystalline polymers. Part I: Large strains multiaxial validation on HDPE. Mech. Mater. 2008, 40, 743–760. [Google Scholar] [CrossRef]
- Brusselle-Dupend, N.; Cangemi, L. A two-phase model for the mechanical behaviour of semicrystalline polymers. Part II—Modelling of the time-dependent mechanical behaviour of an isotropic and a highly oriented HDPE grade. Mech. Mater. 2008, 40, 761–770. [Google Scholar] [CrossRef]
- Gueguen, O.; Richeton, J.; Ahzi, S.; Makradi, A. Micromechanically based formulation of the cooperative model for the yield behavior of semi-crystalline polymers. Acta Mater. 2008, 56, 1650–1655. [Google Scholar] [CrossRef]
- Regrain, C.; Laiarinandrasana, L.; Toillon, S.; Sai, K. Multi-mechanism models for semi-crystalline polymer: Constitutive relations and finite element implementation. Int. J. Plast. 2009, 25, 1253–1279. [Google Scholar] [CrossRef]
- Abdul-Hameed, H.; Messager, T.; Zairi, F.; Nait-Abdelaziz, M. Large-strain viscoelastic–viscoplastic constitutive modeling of semi-crystalline polymers and model identification by deterministic/evolutionary approach. Comput. Mater. Sci. 2014, 90, 241–252. [Google Scholar] [CrossRef]
- Abdul-Hameed, H.; Messager, T.; Ayoub, G.; Zairi, F.; Nait-Abdelaziz, M.; Qu, Z.; Zairi, F. A two-phase hyperelastic-viscoplastic constitutive model for semi-crystalline polymers: Application to polyethylene materials with a variable range of crystal fractions. J. Mech. Behav. Biomed. Mater. 2014, 37, 323–332. [Google Scholar] [CrossRef] [PubMed]
- Oleinik, E.F.; Rudnev, S.N.; Salomatina, O.B. Evolution in Concepts Concerning the Mechanism of Plasticity in Solid Polymers after the 1950s. Polym. Sci. Ser. A 2007, 49, 1302–1327. [Google Scholar] [CrossRef]
- Bartczak, Z.; Galeski, A. Plasticity of semicrystalline polymers. Macromol. Symp. 2010, 294, 67–90. [Google Scholar] [CrossRef]
- Argon, A.S. The Physics of Deformation and Fracture of Polymers; Cambridge University Press: Cambridge, UK, 2013; ISBN 9781139033046. [Google Scholar]
- Seguela, R. Plasticity of semi-crystalline polymers: Crystal slip versus melting—Recrystallization. e-Polymers 2007, 7, 032–1. [Google Scholar] [CrossRef]
- Young, R.J. A dislocation model for yield in polyethylene. Philos. Mag. 1974, 30, 85–94. [Google Scholar] [CrossRef]
- Seguela, R. Dislocation approach to the plastic deformation of semi-crystalline polymers: Kinetic aspects for polyethylene and polypropylene. J. Polym. Sci. B Polym. Phys. 2002, 40, 593–601. [Google Scholar] [CrossRef]
- Petermann, J.; Gleiter, H. Direct observation of dislocations in polyethylene crystals. Philos. Mag. 1972, 25, 813–816. [Google Scholar] [CrossRef]
- Savin, A.V.; Khalack, J.M.; Christiansen, P.L.; Zolotaryuk, A. Twisted topological solitons and dislocations in a polymer crystal. Phys. Rev. B 2002, 65, 054106. [Google Scholar] [CrossRef] [Green Version]
- Spieckermann, F.; Wilhelm, H.; Polt, G.; Ahzi, S.; Zehetbauer, M. Rate mechanism and dislocation generation in high density polyethylene and other semicrystalline polymers. Polymer 2014, 55, 1217–1222. [Google Scholar] [CrossRef]
- Zabashta, Y.F. On the dislocation mechanism of polymer deformation: Defects of spiral molecules. Polym. Mech. 1974, 10, 493–496. [Google Scholar] [CrossRef]
- Keith, H.D.; Passaglia, E. Dislocations in Polymer Crystals. J. Res. Nat. Stand. Sec. A 1964, 68A, 513–518. [Google Scholar] [CrossRef]
- Jabbari-Farouji, S.; Rottler, J.; Lame, O.; Makke, A.; Perez, M.; Barrat, J.-L. Plastic deformation mechanisms of semicrystalline and amorphous polymers. ACS Macro Lett. 2015, 4, 147–150. [Google Scholar] [CrossRef]
- Ahzi, S.; Makradi, A.; Gregory, R.V.; Edie, D.D. Modeling of deformation behavior and strain-induced crystallization in poly(ethylene terephthalate) above the glass transition temperature. Mech. Mater. 2003, 35, 1139–1148. [Google Scholar] [CrossRef]
- Pouriayevali, H.; Arabnejad, S.; Guo, Y.B.; Shim, V.P.W. A constitutive description of the rate-sensitive response of semi-crystalline polymers. Int. J. Impact Eng. 2013, 62, 35–47. [Google Scholar] [CrossRef]
- Krairi, A.; Doghri, I. A thermodynamically-based constitutive model for thermoplastic polymers coupling viscoelasticity, viscoplasticity and ductile damage. Int. J. Plast. 2014, 60, 163–181. [Google Scholar] [CrossRef]
- Horstemeyer, M.F.; Bammann, D.J. Historical review of internal state variable theory for inelasticity. Int. J. Plast. 2010, 26, 1310–1334. [Google Scholar] [CrossRef]
- Meng, F.; Terentjev, E.M. Transient network at large deformations: Elastic–plastic transition and necking instability. Polymers 2016, 8, 108. [Google Scholar] [CrossRef]
- Fielding, S. Complex dynamics of shear banded flows. Soft Matter 2007, 3, 1262–1279. [Google Scholar] [CrossRef]
- Drummy, L.F.; Voigt-Martin, I.; Martin, D.C. Analysis of displacement fields near dislocation cores in ordered polymers. Macromolecules 2001, 34, 7416–7426. [Google Scholar] [CrossRef]
- Grinyaev, Y.V.; Chertova, N.V. Field theory of defects. Part II. Phys. Mesomech. 2006, 9, 30–36. [Google Scholar]
- Sweeney, J.; Bonner, M.; Ward, I.M. Modelling of loading, stress relaxation and stress recovery in a shape memory polymer. J. Mech. Behav. Biomed. Mater. 2014, 37, 12–23. [Google Scholar] [CrossRef] [PubMed]
- Sweeney, J.; Spencer, P.E. The use of a new viscous process in constitutive models of polymers. Key Eng. Mater. 2015, 651–653, 812–817. [Google Scholar] [CrossRef]
- deWit, R. Theory of disclinations: III. Contiuous and discrete disclinations in isotropic elasticity. J. Res. Nat. Stand. Sec. A 1973, 77A, 359–368. [Google Scholar] [CrossRef]
- Eshelby, J.D. The continuum theory of lattice defects. In Progress in Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: New York, NY, USA, 1956; Volume 3, pp. 79–303. ISBN 9780080864679. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields, 4th ed.; Butterworth-Heinemann: Oxford, UK, 1987; ISBN 9780750627689. [Google Scholar]
- Davydov, A.S. Quantum Mechanics, 2nd ed.; Pergamon Press: Oxford, UK, 1976; ISBN 0080204376. [Google Scholar]
- Takahashi, T.; Konda, A.; Shimizu, Y. Creep characteristics of polypropylene/polyamide 6 blend fiber. FIBER 1994, 50, 241–247. [Google Scholar] [CrossRef]
- Drozdov, A.D. Creep rupture and viscoelasticity of polypropylene. Eng. Fract. Mech. 2010, 77, 2277–2293. [Google Scholar] [CrossRef]
- Drozdov, A.D.; Klitkou, R.; Potarniche, C.G. Viscoelasticity and viscoplasticity of polypropylene/polyethylene blends. Int. J. Solids Struct. 2010, 47, 2498–2507. [Google Scholar] [CrossRef]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grinyaev, Y.V.; Chertova, N.V.; Shilko, E.V.; Psakhie, S.G. The Continuum Approach to the Description of Semi-Crystalline Polymers Deformation Regimes: The Role of Dynamic and Translational Defects. Polymers 2018, 10, 1155. https://doi.org/10.3390/polym10101155
Grinyaev YV, Chertova NV, Shilko EV, Psakhie SG. The Continuum Approach to the Description of Semi-Crystalline Polymers Deformation Regimes: The Role of Dynamic and Translational Defects. Polymers. 2018; 10(10):1155. https://doi.org/10.3390/polym10101155
Chicago/Turabian StyleGrinyaev, Yurii V., Nadezhda V. Chertova, Evgeny V. Shilko, and Sergey G. Psakhie. 2018. "The Continuum Approach to the Description of Semi-Crystalline Polymers Deformation Regimes: The Role of Dynamic and Translational Defects" Polymers 10, no. 10: 1155. https://doi.org/10.3390/polym10101155