Anti-Resonant Hollow Core Fibers with Modified Shape of the Core for the Better Optical Performance in the Visible Spectral Region—A Numerical Study
Abstract
:1. Introduction
2. Modified Kagomé Hollow Core Fiber—Modeling and Optical Properties
2.1. Modeling of the Structure
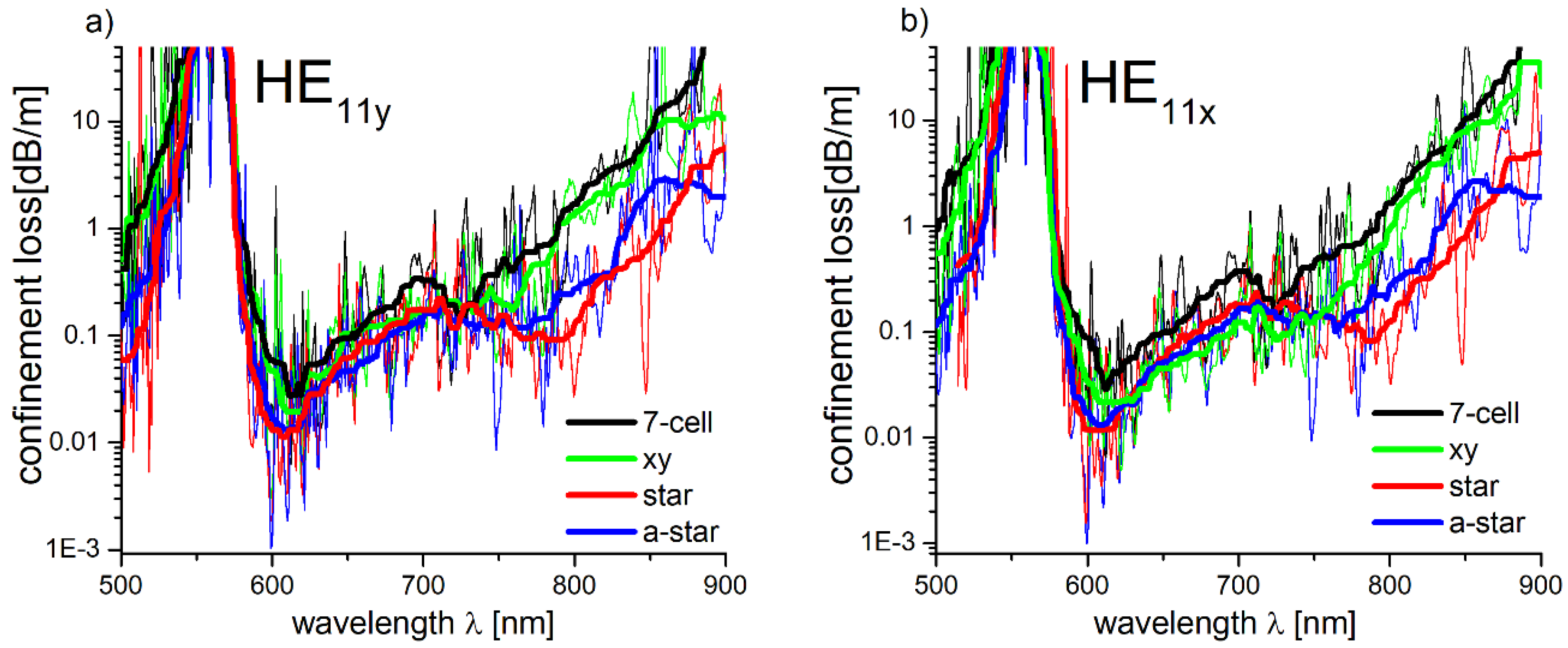
2.2. Fundamental Mode Losses
2.3. Dispersion Properties and Effective Mode Area Calculations
3. The Effect of Struts Dimensions
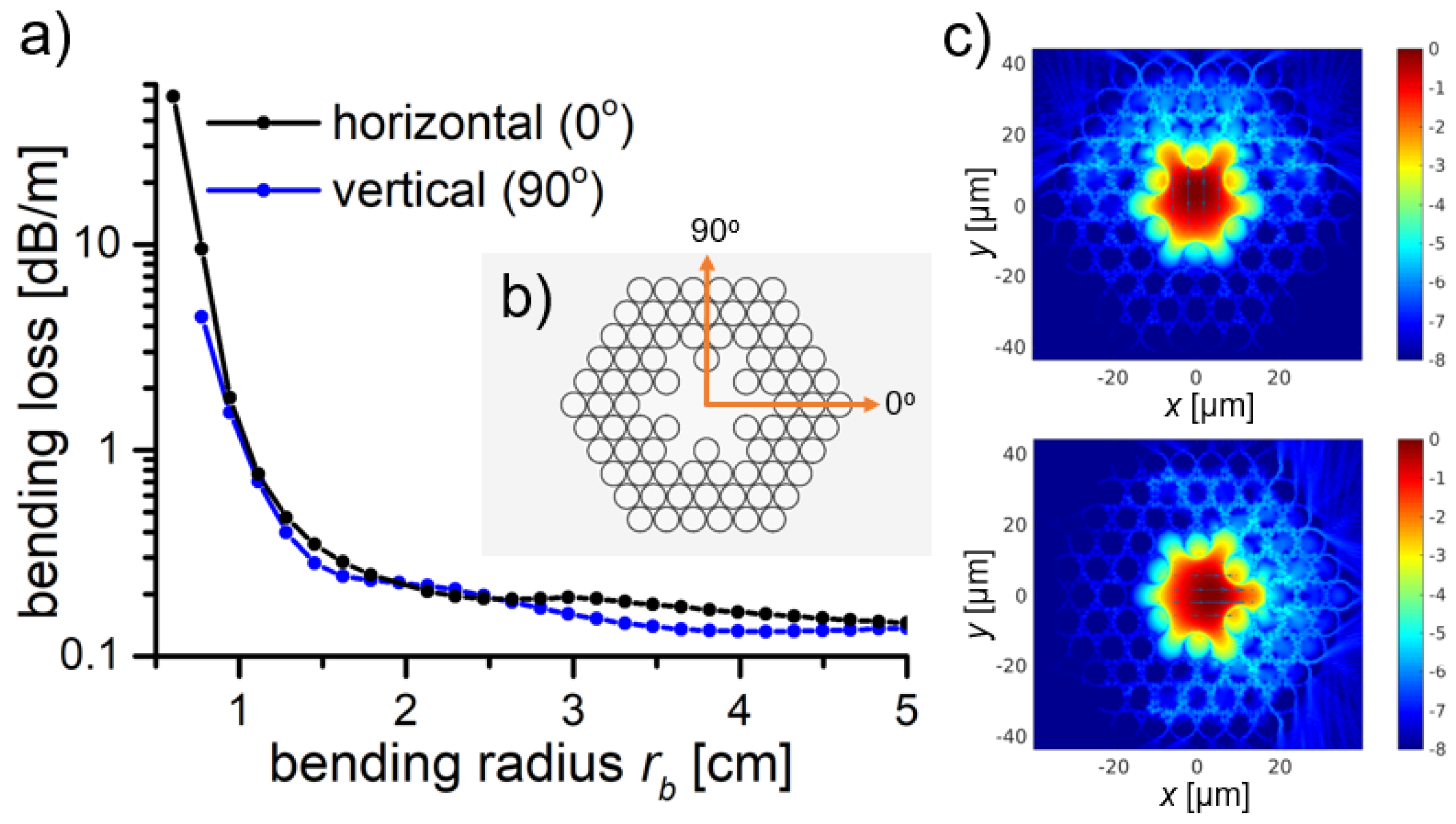
4. Bending Losses
5. Anti-Resonant Hollow Core Fibers—PMMA Simulations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cregan, R.F.; Mangan, B.J.; Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Roberts, P.J.; Allan, D.C. Single-mode photonic band gap guidance of light in air. Science 1999, 285, 1537–1539. [Google Scholar] [CrossRef] [PubMed]
- Roberts, P.J.; Couny, F.; Sabert, H.; Mangan, B.J.; Williams, D.P.; Farr, L.; Mason, M.W.; Tomlinson, A.; Birks, T.A.; Knight, J.C.; et al. Ultimate low loss of hollow-core photonic crystal fibres. Opt. Express 2005, 13, 236–244. [Google Scholar] [CrossRef] [PubMed]
- Roberts, P.J.; Williams, D.P.; Sabert, H.; Mangan, B.J.; Bird, D.M.; Birks, T.A.; Knight, J.C.; Russell, P.S.J. Design of low-loss and highly birefringent hollow-core photonic crystal fiber. Opt. Express 2006, 14, 7329–7341. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amezcua-Correa, R.; Broderick, N.G.R.; Petrovich, M.N.; Poletti, F.; Richardson, D.J. Design of 7 and 19 cells core air-guiding photonic crystal fibers for low-loss, wide bandwidth and dispersion controlled operation. Opt. Express 2007, 15, 17577–17586. [Google Scholar] [CrossRef] [PubMed]
- Jung, Y.; Sleiffer, V.A.J.M.; Baddela, N.; Petrovich, M.N.; Hayes, J.R.; Wheeler, N.V.; Gray, D.R.; Fokoua, E.N.; Wooler, J.P.; Wong, N.H.L.; et al. First demonstration of a broadband 37-cell hollow core photonic bandgap fiber and its application to high capacity mode division multiplexing. In Proceedings of the 2013 Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference (OFC/NFOEC), March Anaheim, CA, USA, 17–21 March 2013; pp. 1–3. [Google Scholar]
- Poletti, F.; Petrovich, M.N.; Richardson, D.J. Hollow-core photonic bandgap fibers: Technology and applications. Nanophotonics 2013, 2, 315–340. [Google Scholar] [CrossRef]
- Benabid, F.; Knight, J.C.; Antonopoulos, G.; Russell, P.S.J. Stimulated Raman scattering in hydrogen-filled hollow-core photonic crystal fiber. Science 2002, 298, 399–402. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Knight, J.C. Negative curvature hollow-core optical fiber. IEEE J. Sel. Top. Quant. Electron. 2016, 22, 146–155. [Google Scholar] [CrossRef]
- Markos, C.; Travers, J.C.; Abdolvand, A.; Eggleton, B.J.; Bang, O. Hybrid photonic-crystal fiber. Rev. Mod. Phys. 2017, 89, 045003. [Google Scholar] [CrossRef]
- Bufetov, I.; Kosolapov, A.; Pryamikov, A.; Gladyshev, A.; Kolyadin, A.; Krylov, A.; Yatsenko, Y.; Biriukov, A. Revolver hollow core optical fibers. Fibers 2018, 6, 39. [Google Scholar] [CrossRef]
- Belardi, W. Design and properties of hollow antiresonant fibers for the visible and near infrared spectral range. J. Lightw. Technol. 2015, 33, 4497–4503. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Wheeler, N.V.; Couny, F.; Roberts, P.J.; Benabid, F. Low loss broadband transmission in hypocycloid-core kagome hollow-core photonic crystal fiber. Opt. Lett. 2011, 36, 669–671. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Couny, F.; Roberts, P.J.; Benabid, F. Low loss broadband transmission in optimized core-shape kagome hollow-core PCF. In Proceedings of the Conference on Lasers and Electro-Optics 2010, San Jose, CA, USA, 16–21 May 2010; p. CPDB4. [Google Scholar]
- Pryamikov, A.D.; Biriukov, A.S.; Kosolapov, A.F.; Plotnichenko, V.G.; Semjonov, S.L.; Dianov, E.M. Demonstration of a waveguide regime for a silica hollow-core microstructured optical fiber with a negative curvature of the core boundary in the spectral region > 3.5 μm. Opt. Express 2011, 19, 1441–1448. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.-F.; Wang, Y.-Y.; Liu, X.-L.; Ding, W.; Wang, P. Bending loss characterization in nodeless hollow-core anti-resonant fiber. Opt. Express 2016, 24, 14801–14811. [Google Scholar] [CrossRef] [PubMed]
- Poletti, F. Nested antiresonant nodeless hollow core fiber. Opt. Express 2014, 22, 23807–23828. [Google Scholar] [CrossRef] [PubMed]
- Habib, M.S.; Bang, O.; Bache, M. Low-loss hollow-core silica fibers with adjacent nested anti-resonant tubes. Opt. Express 2015, 23, 17394–17406. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Fan, Z.; Shi, Z.; Ma, Y.; Yu, J.; Zhang, J. Dual-core antiresonant hollow core fibers. Opt. Express 2016, 24, 17453–17458. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Qi, W.; Ho, D.; Yong, K.-T.; Luan, F.; Yoo, S. Hollow core anti-resonant fiber with split cladding. Opt. Express 2016, 24, 7670–7678. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.-F.; Wang, Y.-Y.; Ding, W.; Jiang, D.-L.; Gu, S.; Zhang, X.; Wang, P. Hollow-core conjoined-tube negative-curvature fibre with ultralow loss. Nat. Commun. 2018, 9, 2828. [Google Scholar] [CrossRef] [PubMed]
- Michieletto, M.; Lyngsø, J.K.; Jakobsen, C.; Lægsgaard, J.; Bang, O.; Alkeskjold, T.T. Hollow-core fibers for high power pulse delivery. Opt. Express 2016, 24, 7103–7119. [Google Scholar] [CrossRef] [PubMed]
- Kolyadin, A.N.; Alagashev, G.K.; Pryamikov, A.D.; Mouradian, L.; Zeytunyan, A.; Toneyan, H.; Kosolapov, A.F.; Bufetov, I.A. Negative curvature hollow-core fibers: Dispersion properties and femtosecond pulse delivery. Phys. Procedia 2015, 73, 59–66. [Google Scholar] [CrossRef]
- Gao, S.-F.; Wang, Y.-Y.; Ding, W.; Wang, P. Hollow-core negative-curvature fiber for uv guidance. Opt. Lett. 2018, 43, 1347–1350. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Cann, M.; Brunton, A.; Wadsworth, W.; Knight, J. Single-mode solarization-free hollow-core fiber for ultraviolet pulse delivery. Opt. Express 2018, 26, 10879–10887. [Google Scholar] [CrossRef] [PubMed]
- Kolyadin, A.N.; Kosolapov, A.F.; Pryamikov, A.D.; Biriukov, A.S.; Plotnichenko, V.G.; Dianov, E.M. Light transmission in negative curvature hollow core fiber in extremely high material loss region. Opt. Express 2013, 21, 9514–9519. [Google Scholar] [CrossRef] [PubMed]
- Debord, B.; Amsanpally, A.; Chafer, M.; Baz, A.; Maurel, M.; Blondy, J.M.; Hugonnot, E.; Scol, F.; Vincetti, L.; Gérôme, F.; et al. Ultralow transmission loss in inhibited-coupling guiding hollow fibers. Optica 2017, 4, 209–217. [Google Scholar] [CrossRef]
- Belli, F.; Abdolvand, A.; Chang, W.; Travers, J.C.; Russell, P.S.J. Vacuum-ultraviolet to infrared supercontinuum in hydrogen-filled photonic crystal fiber. Optica 2015, 2, 292–300. [Google Scholar] [CrossRef]
- Wang, Z.; Belardi, W.; Yu, F.; Wadsworth, W.J.; Knight, J.C. Efficient diode-pumped mid-infrared emission from acetylene-filled hollow-core fiber. Opt. Express 2014, 22, 21872–21878. [Google Scholar] [CrossRef] [PubMed]
- Sherlock, B.; Fei, Y.; Jim, S.; Sean, W.; Carl, P.; Mark, A.A.N.; Paul, M.W.F.; Jonathan, K.; Chris, D. Tunable fibre-coupled multiphoton microscopy with a negative curvature fibre. J. Biophotonics 2016, 9, 715–720. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Popenda, M.A.; Stawska, H.I.; Mazur, L.M.; Jakubowski, K.; Kosolapov, A.; Kolyadin, A.; Bereś-Pawlik, E. Application of negative curvature hollow-core fiber in an optical fiber sensor setup for multiphoton spectroscopy. Sensors 2017, 17, 2278. [Google Scholar] [CrossRef] [PubMed]
- Giovanardi, F.; Cucinotta, A.; Vincetti, L. Inhibited coupling guiding hollow fibers for label-free DNA detection. Opt. Express 2017, 25, 26215–26220. [Google Scholar] [CrossRef] [PubMed]
- Argyros, A.; Pla, J. Hollow-core polymer fibres with a kagome lattice: Potential for transmission in the infrared. Opt. Express 2007, 15, 7713–7719. [Google Scholar] [CrossRef] [PubMed]
- Large, M.C.J.; Poladian, L.; Barton, G.W.; van Eijkelenborg, M.A. Hollow-core microstructured polymer optical fibres. In Microstructured Polymer Optical Fibres; Large, M.C.J., Poladian, L., Barton, G.W., van Eijkelenborg, M.A., Eds.; Springer: Boston, MA, USA, 2008; pp. 165–179. [Google Scholar]
- Anthony, J.; Leonhardt, R.; Leon-Saval, S.G.; Argyros, A. Thz propagation in kagome hollow-core microstructured fibers. Opt. Express 2011, 19, 18470–18478. [Google Scholar] [CrossRef] [PubMed]
- Van Putten, L.D.; Gorecki, J.; Numkam Fokoua, E.; Apostolopoulos, V.; Poletti, F. 3D-printed polymer antiresonant waveguides for short-reach terahertz applications. Appl. Opt. 2018, 57, 3953–3958. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhao, J.; Gong, C.; Tian, H.; Sun, L.; Chen, P.; Lin, L.; Liu, W. 3D printed low-loss THz waveguide based on kagome photonic crystal structure. Opt. Express 2016, 24, 22454–22460. [Google Scholar] [CrossRef] [PubMed]
- Cruz, A.; Cordeiro, C.; Franco, M. 3D printed hollow-core terahertz fibers. Fibers 2018, 6, 43. [Google Scholar] [CrossRef]
- Argyros, A. Microstructured polymer optical fibers. J. Lightw. Technol. 2009, 27, 1571–1579. [Google Scholar] [CrossRef]
- Marques, C.A.F.; Webb, D.J.; Andre, P. Polymer optical fiber sensors in human life safety. Opt. Fiber Technol. 2017, 36, 144–154. [Google Scholar] [CrossRef] [Green Version]
- Bilro, L.; Alberto, N.; Pinto, J.L.; Nogueira, R. Optical sensors based on plastic fibers. Sensors 2012, 12, 12184–12207. [Google Scholar] [CrossRef] [PubMed]
- Stawska, H.; Bereś-Pawlik, E. Enhancement of two photon fluorescence collection by using effectively single mode double clad hollow core fiber with low dispersion at 800 nm. Opt. Quan. Electron. 2015, 47, 67–76. [Google Scholar] [CrossRef]
- Lumerical Mode Solutions. Available online: https://www.lumerical.com/tcad-products/mode/ (accessed on 27 June 2018).
- Zhu, Z.; Brown, T.G. Full-vectorial finite-difference analysis of microstructured optical fibers. Opt. Express 2002, 10, 853–864. [Google Scholar] [CrossRef] [PubMed]
- Lumerical Mode Solutions, Finite Difference Eigenmode. Available online: https://kb.lumerical.com/en/solvers_finite_difference_eigenmode.html (accessed on 26 July 2018).
- Szczurkowski, M. Private Communications. Available online: https://refractiveindex.info/?shelf=organic&book=poly%28methyl_methacrylate%29&page=Szczurowski (accessed on 25 June 2018).
- Malitson, I.H. Interspecimen comparison of the refractive index of fused silica. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Agrawal, G. Chapter 2-Pulse Propagation in Fibers. In Nonlinear Fiber Optics, 5th ed.; Agrawal, G., Ed.; Academic Press: Boston, MA, USA, 2013; pp. 27–56. [Google Scholar]
- Hasan, M.I.; Akhmediev, N.; Chang, W. Empirical formulae for dispersion and effective mode area in hollow-core antiresonant fibers. J. Lightw. Technol. 2018, 1. [Google Scholar] [CrossRef]
- Petermann, K. Constraints for fundamental-mode spot size for broadband dispersion-compensated single-mode fibres. Electron. Lett. 1983, 19, 712–714. [Google Scholar] [CrossRef]
- Moenster, M.; Steinmeyer, G.; Iliew, R.; Lederer, F.; Petermann, K. Analytical relation between effective mode field area and waveguide dispersion in microstructure fibers. Opt. Lett. 2006, 31, 3249–3251. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G. Chapter 3-Group-Velocity Dispersion. In Nonlinear Fiber Optics, 5th ed.; Agrawal, G., Ed.; Academic Press: Boston, MA, USA, 2013; pp. 57–85. [Google Scholar]
- Belardi, W.; Knight, J.C. Effect of core boundary curvature on the confinement losses of hollow antiresonant fibers. Opt. Express 2013, 21, 21912–21917. [Google Scholar] [CrossRef] [PubMed]
- Hayes, J.R.; Poletti, F.; Abokhamis, M.S.; Wheeler, N.V.; Baddela, N.K.; Richardson, D.J. Anti-resonant hexagram hollow core fibers. Opt. Express 2015, 23, 1289–1299. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Ding, W. Confinement loss in hollow-core negative curvature fiber: A multi-layered model. Opt. Express 2017, 25, 33122–33133. [Google Scholar] [CrossRef] [Green Version]
- Lumerical Mode Solutions, (n,k) Material Model. Available online: https://kb.lumerical.com/en/materials_nk_material_model.html (accessed on 27 July 2018).
- Abdullah, O.G.; Aziz, S.B.; Rasheed, M.A. Effect of silicon powder on the optical characterization of poly(methyl methacrylate) polymer composites. J. Mater. Sci. Mater. Electron. 2017, 28, 4513–4520. [Google Scholar] [CrossRef]
- Khashan, M.A.; Nassif, A.Y. Dispersion of the optical constants of quartz and polymethyl methacrylate glasses in a wide spectral range: 0.2–3 μm. Opt. Commu. 2001, 188, 129–139. [Google Scholar] [CrossRef]
- ESKA™ (Mitsubishi Rayon Co., Ltd., Tokyo, Japan) Plastic Fiber Optic & Cable General Technical Information. Available online: http://www.princetel.com/datasheets/ESKA_GK-40.pdf (accessed on 27 July 2018).
- Ayesta, I.; Zubia, J.; Arrue, J.; Illarramendi, A.M.; Azkune, M. Characterization of chromatic dispersion and refractive index of polymer optical fibers. Polymers 2017, 9, 730. [Google Scholar] [CrossRef]











| Rout [µm] | Strut Dimensions [µm] | Resonant Wavelengths λm of mth Order [µm] | ||||
|---|---|---|---|---|---|---|
| m = 1 | m = 2 | m = 3 | m = 4 | m = 5 | ||
| 3.85 | a = 0.98 | 2.07 | 1.034 | 0.68 | 0.51 | 0.41 |
| b = 1.24 | 2.60 | 1.31 | 0.87 | 0.65 | 0.52 | |
| 3.83 | a = 1.02 | 2.15 | 1.07 | 0.71 | 0.54 | 0.43 |
| b = 0.96 | 2.02 | 1.01 | 0.67 | 0.50 | 0.4 | |
| 3.81 | a = 1.06 | 2.24 | 1.11 | 0.745 | 0.56 | 0.44 |
| b = 0.55 | 1.16 | 0.58 | 0.38 | 0.29 | 0.23 | |
| - | d0 = 0.54 | 1.14 | 0.57 | 0.38 | 0.28 | 0.23 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stawska, H.I.; Popenda, M.A.; Bereś-Pawlik, E. Anti-Resonant Hollow Core Fibers with Modified Shape of the Core for the Better Optical Performance in the Visible Spectral Region—A Numerical Study. Polymers 2018, 10, 899. https://doi.org/10.3390/polym10080899
Stawska HI, Popenda MA, Bereś-Pawlik E. Anti-Resonant Hollow Core Fibers with Modified Shape of the Core for the Better Optical Performance in the Visible Spectral Region—A Numerical Study. Polymers. 2018; 10(8):899. https://doi.org/10.3390/polym10080899
Chicago/Turabian StyleStawska, Hanna Izabela, Maciej Andrzej Popenda, and Elżbieta Bereś-Pawlik. 2018. "Anti-Resonant Hollow Core Fibers with Modified Shape of the Core for the Better Optical Performance in the Visible Spectral Region—A Numerical Study" Polymers 10, no. 8: 899. https://doi.org/10.3390/polym10080899
APA StyleStawska, H. I., Popenda, M. A., & Bereś-Pawlik, E. (2018). Anti-Resonant Hollow Core Fibers with Modified Shape of the Core for the Better Optical Performance in the Visible Spectral Region—A Numerical Study. Polymers, 10(8), 899. https://doi.org/10.3390/polym10080899






