Nanoscale Mechanical Properties and Indentation Recovery of PI@GO Composites Measured Using AFM
Abstract
:1. Introduction
2. Materials and Methods
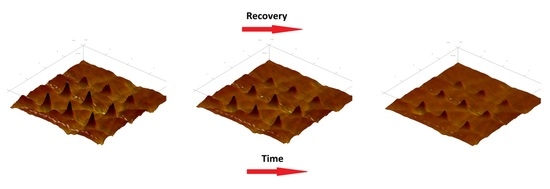
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qu, C.; Hu, J.; Liu, X.; Li, Z.; Ding, Y. Morphology and mechanical properties of polyimide films: The effects of UV irradiation on microscale surface. Materials 2017, 10, 1329. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Cheng, Y.; Wang, Z.; Wang, K.; Feng, A. In situ polymerization of modified graphene/polyimide composite with improved mechanical and thermal properties. J. Mater. Sci. 2017, 28, 576–581. [Google Scholar] [CrossRef]
- Nayak, L.; Rahaman, M.; Aldalbahi, A.; Kumar Chaki, T.; Khastgir, D. Polyimide-carbon nanotubes nanocomposites: Electrical conduction behavior under cryogenic condition. Polym. Eng. Sci. 2017, 57, 291–298. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Ding, Q.; Tan, J.; Chen, Z.; Chen, J.; Zuo, X.; Tang, A.; Zeng, K. Polyimide/Graphene nanocomposites with improved gas barrier and thermal properties due to a “dual-plane” structure effect. Macromol. Mater. Eng. 2018, 303, 1800053. [Google Scholar] [CrossRef]
- Lu, Y.; Hao, J.; Xiao, G.; Zhao, H.; Hu, Z.; Wang, T. In situ polymerization and performance of alicyclic polyimide/graphene oxide nanocomposites derived from 6FAPB and CBDA. Appl. Surf. Sci. 2017, 394, 78–86. [Google Scholar] [CrossRef]
- Chen, M.; Qi, M.; Yao, L.; Su, B.; Yin, J. Effect of surface charged SiO2 nanoparticles on the microstructure and properties of polyimide/SiO2 nanocomposite films. Surf. Coat. Technol. 2017, 320, 59–64. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, T.; Xu, L.; Huang, P. Synthesis and characterization of aramid fiber-reinforced polyimide/carbon black composites and their use in a supercapacitor. Chin. J. Chem. 2017, 35, 1586–1594. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Wang, T.; Wang, Q. In situ synthesis and thermal, tribological properties of thermosetting polyimide/graphene oxide nanocomposites. J. Mater. Sci. 2012, 47, 1867–1874. [Google Scholar] [CrossRef]
- Kong, J.-Y.; Choi, M.-C.; Kim, G.Y.; Park, J.J.; Selvaraj, M.; Han, M.; Ha, C.-S. Preparation and properties of polyimide/graphene oxide nanocomposite films with Mg ion crosslinker. Eur. Polym. J. 2012, 48, 1394–1405. [Google Scholar] [CrossRef]
- Ramakrishnan, S.; Dhakshnamoorthy, M.; Jelmy, E.J.; Vasanthakumari, R.; Kothurkar, N.K. Synthesis and characterization of graphene oxide–polyimide nanofiber composites. RSC Adv. 2014, 4, 9743–9749. [Google Scholar] [CrossRef]
- Díez-Pascual, A.M.; Gómez-Fatou, M.A.; Ania, F.; Flores, A. Nanoindentation in polymer nanocomposites. Prog. Mater. Sci. 2015, 67, 1–94. [Google Scholar] [CrossRef] [Green Version]
- Yongqiang, L.; Chunzheng, P. Improved interfacial properties of PI composites through graphene oxide and carbon nanotubes on carbon fiber surface. Surf. Interface Anal. 2018, 50, 634–639. [Google Scholar] [CrossRef]
- Li, L.; Encarnacao, L.M.; Brown, K.A. Polymer nanomechanics: Separating the size effect from the substrate effect in nanoindentation. Appl. Phys. Lett. 2017, 110, 043105. [Google Scholar] [CrossRef]
- Qu, Z.; Bu, J.; Pan, X.; Hu, X. Probing the nanomechanical properties of PLA/PC blends compatibilized with compatibilizer and nucleation agent by AFM. J. Polym. Res. 2018, 25, 138. [Google Scholar] [CrossRef]
- Zheng, L.; Jiang, X.; Deng, X.H.; Yin, J.R.; Jiang, Y.; Zhang, P.; Ding, Y.H. Mechanical characterization of PMMA by AFM nanoindentation and finite element simulation. Mater. Res. Express 2016, 3, 115302. [Google Scholar] [CrossRef]
- Moeller, G. AFM nanoindentation of viscoelastic materials with large end-radius probes. J. Polym. Sci. Part B 2009, 47, 1573–1587. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Nili, H.; Walia, S.; Bhaskaran, M.; Sriram, S. Nanoscale electro-mechanical dynamics of nano-crystalline platinum thin films: An in situ electrical nanoindentation study. J. Appl. Phys. 2014, 116, 163504. [Google Scholar] [CrossRef]
- Savvides, N.; Bell, T. Microhardness and Young’s modulus of diamond and diamondlike carbon films. J. Appl. Phys. 1992, 72, 2791–2796. [Google Scholar] [CrossRef]
- Doerner, M.F.; Nix, W.D. A method for interpreting the data from depth-sensing indentation instruments. J. Mater. Res. 2011, 1, 601–609. [Google Scholar] [CrossRef]
- Clifford, C.A.; Seah, M.P. Quantification issues in the identification of nanoscale regions of homopolymers using modulus measurement via AFM nanoindentation. Appl. Surf. Sci. 2005, 252, 1915–1933. [Google Scholar] [CrossRef]
- Suk, J.W.; Piner, R.D.; An, J.; Ruoff, R.S. Mechanical properties of monolayer graphene oxide. ACS Nano 2010, 4, 6557–6564. [Google Scholar] [CrossRef] [PubMed]
- Tweedie, C.A.; Van Vliet, K.J. On the indentation recovery and fleeting hardness of polymers. J. Mater. Res. 2011, 21, 3029–3036. [Google Scholar] [CrossRef]
- Ding, Y.H.; Deng, X.H.; Jiang, X.; Zhang, P.; Yin, J.R.; Jiang, Y. Nanoscale mechanical characterization of PMMA by AFM nanoindentation: A theoretical study on the time-dependent viscoelastic recovery. J. Mater. Sci. 2013, 48, 3479–3485. [Google Scholar] [CrossRef]
- Ghosh, P.; Rameshbabu, A.P.; Dhara, S. Citrate cross-linked gels with strain reversibility and viscoelastic behavior accelerate healing of osteochondral defects in a rabbit model. Langmuir 2014, 30, 8442–8451. [Google Scholar] [CrossRef] [PubMed]





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Cai, Q.; Xu, F. Nanoscale Mechanical Properties and Indentation Recovery of PI@GO Composites Measured Using AFM. Polymers 2018, 10, 1020. https://doi.org/10.3390/polym10091020
Zhou J, Cai Q, Xu F. Nanoscale Mechanical Properties and Indentation Recovery of PI@GO Composites Measured Using AFM. Polymers. 2018; 10(9):1020. https://doi.org/10.3390/polym10091020
Chicago/Turabian StyleZhou, Ji, Qiang Cai, and Fu Xu. 2018. "Nanoscale Mechanical Properties and Indentation Recovery of PI@GO Composites Measured Using AFM" Polymers 10, no. 9: 1020. https://doi.org/10.3390/polym10091020
APA StyleZhou, J., Cai, Q., & Xu, F. (2018). Nanoscale Mechanical Properties and Indentation Recovery of PI@GO Composites Measured Using AFM. Polymers, 10(9), 1020. https://doi.org/10.3390/polym10091020